Analisis Transformasi Box Cox Untuk Mengatasi Heteroskedastisitas Dalam Model Regresi Linier Sederhana.

(1)

ANALISIS TRANSFORMASI BOX COX UNTUK MENGATASI

HETEROSKEDASTISITAS DALAM MODEL

REGRESI LINIER SEDERHANA

SKRIPSI

DESRI KRISTINA S

070803055

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

(2)

ANALISIS TRANSFORMASI BOX COX UNTUK MENGATASI

HETEROSKEDASTISITAS DALAM MODEL REGRESI LINIER SEDERHANA

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

DESRI KRISTINA S 070803055

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : ANALISIS TRANSFORMASI BOX COX UNTUK MENGATASI HETEROSKEDASTISITAS DALAM MODEL REGRESI LINIER SEDERHANA

Kategori : SKRIPSI

Nama : DESRI KRISTINA S

Nomor Induk Mahasiswa : 070803055

Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Juni 2011

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Rachmad Sitepu, M.Si Drs. Open Darnius, M.Sc NIP. 19530418 198703 1 001 NIP.19641014 199103 1 004

Diketahui/ Disetujui oleh:

Departemen Matematika FMIPA USU Ketua,

Prof. Dr. Tulus, M.Si.

(4)

PERNYATAAN

ANALISIS TRANSFORMASI BOX COX UNTUK MENGATASI

HETEROSKEDASTISITAS DALAM MODEL REGRESI LINIER SEDERHANA

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juni 2011

DESRI KRISTINA S

(5)

PENGHARGAAN

Segala hormat dan pujian syukur hanya kepada Tuhan Yang Maha Kuasa karena kasihNya yang sungguh besar yang senantiasa memberi pertolongan dan kekuatan, tuntunan bagi penulis untuk mengerjakan skripsi ini sampai waktu yang telah ditetapkan.

Dalam kesempatan ini penulis mengucapkan terimakasih kepada Drs. Open Darnius, M.Sc dan Drs. Rachmad Sitepu, M.Si sebagai dosen pembimbing yang telah memberikan hati dan waktunya untuk mengarahkan dan memberikan masukan kepada penulis dalam menyelesaikan skripsi ini. Penulis juga mengucapkan terima kasih kepada Drs. Pangarapen Bangun, M.Si dan Drs. Ujian Sinulingga, M.Si selaku Dosen penguji yang juga membantu penulis selama pengerjaan skripsi ini. Ucapan terimakasih juga penulis tujukan kepada Dr. Sutarman, M.Sc selaku Dekan FMIPA USU, Ketua dan Sekretaris Departemen Matematika FMIPA USU yaitu Prof. Dr. Tulus, M.Si dan Dra. Mardiningsih, M.Si dan kepada Bapak Ibu dosen beserta semua Staf Administrasi di FMIPA USU.

Penulis juga mengucapkan terima kasih kepada kedua orang tua tercinta Bapak M.Silalahi dan Ibu L.br.Situmorang atas semua dukungan dalam doa, motivasi, kasih sayang, serta semua dukungan materil dan moril yang membantu penulis dalam menyelesaikan skripsi ini. Juga kepada adik-adik yang saya kasihi Marno, Luri, Wenny dan Mario. Penulis juga mengucapkan terima kasih kepada sahabat – sahabat yang telah mendukung saya, terkhusus buat KTB Florence (K’Tiur, Dewi, Anita, Riris dan Rolina) dan adik – adik tercinta KK Evangelium. Terima kasih atas semua doa dan dukungannya. Tak lupa juga penulis mengucapkan terima kasih kepada semuanya teman-teman di Math’07 (tidak muat jika disebutkan namanya satu per satu) atas kebersamaan kita selama ini, atas doa dan saling mendukung diantara kita. Semangat dan doa dari teman-teman juga sangat membantu penulis dalam menyelesaikan skripsi ini. Terimakasih juga buat teman-teman kost 24, juga teman-teman penulis di Sibolga serta keluarga tulang di Helvetia, keluarga Namboru di Sidikalang atas kebaikan, doa dan kasihnya.

(6)

ABSTRAK

(7)

ANALYSIS OF BOX COX TRANSFORMATION TO OVERCOME HETEROSCEDASTICITY IN SIMPLE LINEAR REGRESSION MODEL

ABSTRACT

(8)

DAFTAR ISI

2.1 Regresi Linier Sederhana 7

2.2 Estimasi Parameter 9

2.2.1 Pengertian Estimasi Parameter dan Estimator 9

2.2.2 Sifat – Sifat Estimator 9

2.2.3 Jenis – Jenis Pendugaan 11

2.3 Metode Kemungkinan Maksimum 11

2.3.1 Maksimum Likelihood dalam Regresi Linier Sederhana 12

2.4 Heteroskedastisitas 15

2.4.1 Pengertian Heteroskedastisitas 15 2.4.2 Konsekuensi atau Akibat Adanya Heteroskedastisitas 17 2.4.3 Pengujian Heteroskedastisitas 21

2.5 Transformasi Box Cox 23

2.5.1 Pendugaan Parameter Transformasi Box Cox 24 2.5.2 Selang Kepercayaan Parameter Pada Transformasi Box Cox 26

2.6 Pengujian Model Regresi 27

Bab 3 Pembahasan 29

Bab 4 Kesimpulan Dan Saran 35

4.1 Kesimpulan 35

(9)

Halaman

Daftar Pustaka 36

(10)

DAFTAR TABEL

Halaman

Tabel 2.1 Nilai dan Model Transformasinya 25 Tabel 3.1 Hasil pengujian Heteroskedastisitas dan Analisis Transformasi

Box Cox Pada Model Regresi Linier Sederhana 32 Tabel 3.2 Hasil Analisis Dalam Model Penentuan Regresi Linier Sederhana

Setelah Variabel Respon Ditransformasikan Sesuai dengan Model

(11)

DAFTAR GAMBAR

Halaman

Gambar 2.1 Asumsi Homoskedastisitas 16

(12)

ABSTRAK

(13)

ANALYSIS OF BOX COX TRANSFORMATION TO OVERCOME HETEROSCEDASTICITY IN SIMPLE LINEAR REGRESSION MODEL

ABSTRACT

(14)

BAB 1

PENDAHULUAN

1.1 Latar Belakang

Analisis Regresi adalah analisis statistik yang mempelajari bagaimana memodelkan

sebuah model fungsional dari data untuk dapat menjelaskan ataupun meramalkan

suatu fenomena alami atas dasar fenomena lain. Analisis regresi juga merupakan salah

satu teknik statistika yang digunakan secara luas dalam ilmu pengetahuan terapan

dalam bidang sosial maupun eksakta.

Gujarati (2006) mendefenisikan analisis regresi sebagai kajian terhadap

hubungan satu variabel yang disebut sebagai variabel yang diterangkan (variabel tidak

bebas) dengan satu atau lebih variabel yang menerangkan (variabel bebas). Melalui

analisis regresi ini, model hubungan antar variabel dapat diketahui. Selain itu, analisis

regresi juga dapat dipergunakan sebagai peramalan. Model regresi linear sederhana

dapat dinyatakan sebagai berikut:

(1)

dengan:

Y adalah variabel tidak bebas;

adalah variabel bebas, dengan i = 1, 2, 3, ... , n;

(15)

Model regresi linear sederhana tersebut dapat ditulis dengan menggunakan

persamaan matriks yaitu:

,

, , dan

dengan:

Y adalah vektor kolom berukuran (n baris dan 1 kolom) X adalah matriks berukuran (n baris 2 kolom)

adalah vektor kolom berukuran (2 baris dan 1 kolom) adalah vektor kolom berukuran

dan adalah parameter yang akan diduga dalam model regresi linier

sederhana. Pendugaan parameter tersebut baik dengan menggunakan Metode Kuadrat

Terkecil (Ordinary Least Square) maupun dengan Metode Kemungkinan Maksimum

(Maximum Likelihood Methods) harus memenuhi asumsi – asumsi model ideal tertentu terhadap error . Salah satu asumsi yang penting dan harus dipenuhi adalah

asumsi homoskedastisitas atau disebut juga asumsi kehomogenan varian. Apabila

asumsi homoskedastisitas tidak dipenuhi, berarti varian dari setiap kesalahan

pengganggu untuk variabel bebas yang diketahui tidak sama, sehingga keadaan ini

disebut heteroskedastisitas (keheterogenan ragam).

Dalam model regresi linier terdapat beberapa cara dalam mengatasi masalah

heteroskedastisitas. Menurut Greene (2004) untuk mengatasi heteroskedastisitas dapat

dilakukan dengan Metode Kuadrat Terkecil Tertimbang (Weighted Least Square),

penaksirannya melalui pembobotan yang juga dapat dikatakan kuadrat terkecil yang

diberlakukan secara umum atau disebut Kuadrat Terkecil Umum (General Least

Square). Selain itu, heteroskedastisitas juga dapat diatasi dengan mentransformasikan

variabel - variabelnya, baik variabel bebas, variabel tidak bebas maupun keduanya.

(16)

masalah heteroskedastisitas karena mengingat salah satu tujuan dari transformasi Box

Cox adalah menghomogenkan varian.

1.2 Identifikasi Masalah

Heteroskedastisitas merupakan salah satu faktor yang menyebabkan model regresi

linier sederhana tidak efisien dan akurat, juga mengakibatkan penggunaan metode

kemungkinan maksimum dalam mengestimasi parameter (koefisien) regresi akan

terganggu. Masalah heteroskedastisitas harus diatasi, salah satunya dengan

Transformasi Box Cox yaitu transformasi pangkat berparameter tunggal terhadap

variabel tidak bebas Y yang kisarannya pada interval (-2,2). Sehingga, dalam

penelitian ini akan menunjukkan secara simulasi bahwa parameter pada

Transformasi Box Cox berada di kisaran (-2,2).

1.3 Batasan Masalah

Agar penyelesaian masalah tidak menyimpang dari pembahasan, maka dibuat

pembatasan masalah yaitu dengan menganggap bahwa model analisis regresinya tetap

memenuhi asumsi – asumsi klasik lainnya kecuali asumsi homoskedastisitas tidak terpenuhi.

1.4 Tinjauan Pustaka

Kutner, M.H, Wassamen.W dan Neter J (1990) mengatakan bahwa bentuk fungsi

dari peluang distribusi dengan adanya istilah kesalahan pengganggu (error) yang

ditetapkan serta estimator dari parameter – parameter dan yang dinotasikan dengan dan dapat diperoleh dengan menggunakan Metode Kemungkinan Maksimum (Maximum Likelihood Methods). Metode ini menggunakan distribusi

gabungan dari sampel pengamatannya. Ketika gabungan distribusi ditunjukkan

(17)

inilah yang disebut sebagai fungsi kemungkinannya. Dengan memaksimumkan fungsi

kemungkinannya maka akan diperoleh estimator dari parameter – parameternya.

Supranto J (2004) mengatakan bahwa heteroskesdastisitas merupakan salah satu

pelanggaran terhadap salah satu asumsi model ideal tertentu terhadap galat yang

diberlakukan dalam analisis regresi yaitu asumsi homoskedastisitas yang menyatakan

bahwa varian kesalahan pengganggu pada setiap variabel bebas adalah sama

(konstan). Heteroskedastisitas adalah keadaan bahwa varian kesalahan pengganggu

tidak bersifat konstan atau disimbolkan dengan ar .

Gasperz, Vincent (1991) mengatakan bahwa heteroskedastisitas dapat mengakibatkan pendugaan parameternya tidak efisien sehingga tidak mempunyai

ragam minimum. Karena pendugaan parameter dianggap efisien karena memiliki

ragam yang minimum, sehingga ragam galat bersifat konstan atau disebut juga

bahwa asumsi homoskedastisitas terpenuhi. Salah satu usaha untuk mengatasi

heteroskedastisitas ini dapat dilakukan dengan mentransformasikan variabel – variabelnya, baik variabel bebas, variabel tidak bebas maupun keduanya agar asumsi

homoskedastisitas terpenuhi.

Box, G. E. P. Dan D. R. Cox (1964) mengatakan bahwa Transformasi Box Cox

adalah transformasi yang mempertimbangkan kelas transformasi berparameter tunggal

yaitu yang dipangkatkan pada variabel respon (variabel tidak bebas) Y yang

bertanda positif , sehingga transformasinya menjadi . Dalam analisis regresi apabila kenormalan data, kehomogenen ragam dan linieritas tak dipenuhi,

maka dapat dilakukan transformasi terhadap variabel responnya sesuai dengan

prosedur Transformasi Box Cox. Salah satu cara untuk mengatasi ketidakhomogenan

ragam yaitu dengan Transformasi Box Cox.

Drapper, N dan Smith, H (1992) mengatakan bahwa Transformasi Box Cox

diberlakukan kepada variabel respon, Y, yang harus bertanda positif, dinyatakan

(18)

jika 0 ln jika 0

Famili transformasi kontinu ini bergantung pada satu parameter yang akan diduga.

Salah satu metode pendugaan (penaksiran) yang dapat digunakan ialah dengan

menggunakan Metode Kemungkinan Maksimum. Cara penaksiran agak berbeda

dengan cara penaksiran yang biasa dilakukan, yaitu dengan menentukan nilai pada

kisaran tertentu

1.5 Tujuan Penelitian

Tujuan dari penelitian ini adalah menggunakan prosedur Transformasi Box Cox

untuk mengatasi masalah heteroskedastisitas antara variabel – variabel bebas, sehingga diperoleh persamaan regresi linier sederhana yang lebih baik.

1.6 Manfaat Penelitian

Regresi adalah salah satu metode yang digunakan untuk menaksir suatu peubah tak

bebas dengan memperhatikan faktor – faktor penyebabnya. Dari penulisan ini, penulis berharap dapat memberikan suatu solusi alternatif bagi pengguna analisis regresi linier

sederhana dalam masalah heteroskedastisitas yang terdapat pada data, sehingga model

regresi tersebut dapat diatasi dan menjadi model regresi yang benar.

(19)

1.7 Metode Penelitian

Data yang digunakan untuk analisis ini adalah data simulasi. Data simulasi terdiri dari

dua variabel yaitu variabel bebas (X) dan variabel tak bebas (Y). Data simulasi yang

akan dianalisis merupakan data random yang dibangkitkan berdasarkan distribusi

yang telah ditentukan yaitu berdistribusi normal dengan menggunakan program

Minitab 16. Langkah – langkah yang digunakan untuk menganalisis data tersebut adalah:

1. Mengitung estimator dan dan membentuk model analisis regresi sederhana

dari data tersebut.

2. Mendeteksi keberadaan heteroskedastisitas berdasarkan prosedur pada Uji

Korelasi Rank dari Spearmen yang digunakan.

3. Menduga parameter pada Transformasi Box Cox dengan menggunakan Metode

Kemungkinan Maksimum. Dalam tulisan ini digunakan Program Minitab 16

dengan menjalankan perintah atau rangkaian perintah (command) yang

membentuk suatu fungsi tertentu dalam Minitab yang disebut dengan Macro

Minitab. Dengan menjalankan command tersebut akan diperoleh penduga dan

selang kepercayaan .

4. Menentukan model transformasinya sesuai dengan pendugaan parameter yang

telah didapat.

5. Mentransformasikan data menurut model transformasinya dan membentuk model

analisis regresi.

6. Menguji signifikansi dari model regresi tersebut dan juga dilakukan pengujian

(20)

BAB 2

LANDASAN TEORI

2.1 Regresi Linier Sederhana

Dalam beberapa masalah terdapat dua atau lebih variabel yang hubungannya tidak

dapat dipisahkan karena perubahan nilai suatu variabel tidak selalu terjadi dengan

sendirinya, namun perubahan nilai variabel itu dapat pula disebabkan oleh berubahnya

variabel lain yang berhubungan dengan variabel tersebut. Hal tersebut biasanya

diselidiki sifat hubungannya yaitu dengan mengetahui pola nilai suatu variabel yang

disebabkan oleh variabel lain diperlukan alat analisis yang dapat membuat perkiraan

nilai variabel tersebut pada nilai tertentu variabel yang mempengaruhinya.

Teknik yang umum digunakan untuk menganalisis hubungan antara dua atau

lebih variabel dalam ilmu statistik adalah dengan analisis regresi. Analisis regresi

adalah teknik statistik yang berguna untuk memeriksa dan memodelkan hubungan

diantara variabel-variabel. Analisis regresi berguna untuk menelaah pola dan

mengukur hubungan statistika antara dua atau lebih variabel yang modelnya belum

diketahui dengan sempurna.

Persamaan matematik yang digunakan untuk melakukan peramalan mengenai

(21)

(1822 – 1911) yang berasal dari hasil pengamatan yang dilakukan terhadap manusia yaitu membandingkan tinggi badan anak laki – laki dengan tinggi badan ayahnya.

Galton menyatakan bahwa tinggi badan anak laki – laki dari badan yang tinggi pada beberapa generasi kemudian cenderung “mundur” (regressed) mendekati rata – rata populasi. Dengan kata lain, anak laki – laki dari ayahnya yang mempunyai badannya sangat tinggi cenderung lebih pendek dari ayahnya. Sedangkan anak laki – laki dari ayah yang mempunyai badan sangat pendek cenderung lebih tinggi dari

ayahnya. Dari hasil penelitian ini istilah regresi pada mulanya bertujuan untuk

membuat perkiraan nilai suatu variabel (tinggi badan anak) terhadap suatu variabel

lain (tinggi badan ayah).

Pada perkembangan selanjutnya analisis regresi dapat digunakan sebagai alat

untuk membuat perkiraan ataupun peramalan nilai suatu variabel dengan

menggunakan variabel lain yang berhubungan dengan variabel tersebut. Dalam

analisis regresi, dikenal dua jenis variabel yaitu :

1. Variabel Respon disebut juga variabel dependent yaitu variabel yang tidak bebas

yaitu keberadaannya dipengaruhi oleh variabel lainnya dan dinotasikan dengan Y.

2. Variabel Prediktor disebut juga variabel independent yaitu variabel yang bebas

(tidak dipengaruhi oleh variabel lainnya) dan dinotasikan dengan X.

Analisis regresi yang melibatkan hubungan antara satu variabel respon (tidak

bebas) dengan satu variabel prediktor (bebas) diistilahkan dengan regresi linier

sederhana, dengan model persamaan:

(2.1)

Dimana intercept dan slope merupakan parameter yang tidak diketahui nilainya,

sedangkan adalah error random dengan rata – rata nol dan varians .

Misalkan ada n pasangan observasi, katakan dengan y merupakan variabel tidak bebasnya atau variabel respon yang berhubungan

dengan n variabel bebas diukur dengan errornya dapat diabaikan sehingga nilai

(22)

(2.2)

Tujuan utama dari analisis regresi adalah mendapatkan dugaan (estimation)

dari suatu variabel dengan menggunakan variabel lain yang diketahui.

2.2 Estimasi Parameter

2.2.1 Pengertian Estimasi Parameter dan Estimator

Estimasi (pendugaan) merupakan proses yang menggunakan sampel statistik untuk

menduga atau menaksir hubungan parameter populasi yang tidak diketahui.

Pendugaan merupakan suatu pernyataan mengenai parameter populasi yang diketahui

berdasarkan informasi dari sampel, dalam hal ini sampel random, yang diambil dari

populasi yang bersangkutan. Jadi dengan pendugaan ini, keadaan parameter populasi

dapat diketahui (Hasan 2002).

Menurut Hasan (2002), estimator adalah suatu statistik (harga sampel) yang

digunakan untuk menduga suatu parameter. Dengan penduga, dapat diketahui

seberapa jauh suatu parameter populasi yang tidak diketahui berada di sekitar sampel

(statistik sampel). Besaran sebagai hasil penerapan penduga terhadap data dari sesuatu

contoh disebut nilai duga (estimate). Secara umum, parameter diberi lambang dan

penduganya diberi lambang .

2.2.2 Sifat – Sifat Estimator

(23)

1. Estimator yang tidak bias

Estimator yang tidak bias apabila dapat menghasilkan estimasi yang mengandung nilai

parameter yang diestimasikan. Misalkan, estimator dikatakan estimator yang tidak bias jika rata – rata semua harga yang mungkin akan sama dengan , atau dapat dituliskan .

2. Estimator yang efisien

Estimator dikatakan efisien bagi parameternya apabila estimator tersebut memiliki

varians minimum. Apabila terdapat lebih dari satu penduga, penduga yang efisien

adalah penduga yang memiliki varians terkecil. Dua buah penduga dapat

dibandingkan dengan efisiensi relatif. Misalkan dan adalah sebagai dua estimator untuk , dimana varians penduga lebih kecil dibandingkan varians , maka relatif lebih efisien dibandingkan dengan .

3. Estimator yang konsisten

Estimator dikatakan konsisten apabila nilai penduga cenderung mendekati nilai parameter untuk n (jumlah sampel) yang semakin besar mendekati tak hingga. Jadi,

ukuran sampel yang besar cenderung memberikan penduga titik yang lebih baik

dibandingkan ukuran sampel kecil.

Dalam analisis regresi, diperlukan suatu model yang digunakan untuk

mengetahui hubungan antara variabel tidak bebas (respon) dengan satu atau lebih

variabel bebas (prediktor) dan untuk melakukan peramalan terhadap variabel respon.

Model regresi dapat diperoleh dengan melakukan pendugaan terhadap parameter -

parameternya dengan menggunakan metode tertentu. Metode yang dapat digunakan

mengestimasi parameter model regresi, khususnya parameter model regresi linier

yaitu dengan Metode Kuadrat Terkecil (Ordinary Least Square) dan Metode

(24)

2.3 Metode Kemungkinan Maksimum

Salah satu cara untuk mendapatkan estimator yang baik adalah dengan menggunakan

Metode Kemungkinan Maksimum (Maximum Likelihood Methods) yang

diperkenalkan oleh R. A. Fisher (1890 – 1962). Maksimum likelihood ini adalah metode yang digunakan untuk menduga parameter – parameter dengan memaksimumkan fungsi kemungkinannya yang dibentuk dari gabungan distribusi

pengamatan.

Misalkan X adalah variabel random berukuran n pengamatan dengan

maka fungsi kemungkinannya adalah:

(2.3)

Penduga kemungkinan dengan Metode Kemungkinan Maksimum dari

parameter tunggal adalah sebuah nilai yang memaksimumkan fungsi

kemungkinan . Apabila variabel random dari populasi yang berdistribusi , maka fungsi kemungkinannya didefinisikan sebagai berikut:

( )

Jika fungsi kemungkinannya diturunkan terhadap , maka akan diperoleh

penyelesaian atau estimasi parameter – parameter dengan memaksimumkan persamaan (2.4) dan menyamakan dengan nol, diperoleh:

(25)

Untuk lebih jelasnya, misalkan peubah acak X tersebut tersebar normal dengan

nilai tengah dan varians , dimana dan tidak diketahui sehingga fungsi

kemungkinannya adalah:

( )

Tujuan utama dari analisis regresi adalah mendapatkan dugaan (estimation)

dari suatu variabel dengan menggunakan variabel lain yang diketahui.

2.3.1 Maksimum Likelihood dalam Regresi Linier Sederhana

Maksimum Likelihood adalah metode yang dapat digunakan untuk mengestimasi

suatu parameter dalam regresi.

Dalam model regresi linear sederhana, berdasarkan data diasumsikan bahwa galat dalam model regresi berdistribusi dengan pengamatan – pengamatan dalam percobaan berdistribusi normal dan independen, dengan mean dan variansnya . Maka fungsi kemungkinan nilai pertama Y adalah:

(2.7)

Kemudian kemungkinan nilai kedua Y sama dengan persamaan (2.7), kecuali angka

satu diganti dengan dua dan seterusnya untuk semua nilai Y amatan lainnya.

Untuk nilai Y bebas dengan mengalikan semua kemungkinan bersama, maka

fungsi probabilitas bersamanya adalah:

( ) Dengan menyatakan

(26)

penggunaannya dikenal untuk eksponensial, sehingga persamaan (2.8) dapat

diperlihatkan dengan penjumlahan eksponensial yaitu:

( )

Mengingat yang diberikan dipertimbangkan untuk berbagai nilai dan ,

sehingga fungsi likelihoodnya yaitu:

( 0)

Estimator fungsi kemungkinan maksimum untuk parameter – parameter dan dinotasikan dengan dan diperoleh dengan memaksimumkan L, sehingga:

( )

ln maksimum bila

minimum, ini merupakan jumlah kuadrat error

Dengan mendifferensialkan fungsi kemungkinannya terhadap setiap parameter

dan estimator harus memenuhi:

Penyelesaian dari persamaan tersebut adalah:

(2.12)

(27)

dan adalah estimator untuk intercept (titik potong) dan slope (kemiringan).

Sehingga diperoleh estimator model regresi linier sederhananya adalah:

(2.14)

Selain estimator dan , menurut Kutner, M.H (1990) estimasi juga dibutuhkan dalam uji hipotesis dan pembentukan estimasi yang berhubungan dengan

model regresi. Dengan mendifferensialkan fungsi kemungkinannya terhadap

parameter dan estimator juga harus memenuhi:

Maka, penyelesaian dari persamaan tersebut adalah:

( )

Dengan adalah standard error regresi atau dapat juga dituliskan:

( )

SSE (Sum Square of Error) adalah jumlah kuadrat residual dan penduga ini bias .

Jumlah kuadrat residual mempunyai derajat kebebasan , karena dua derajat kebebasan adalah gabungan dari estimasi dan yang terlibat dalam pembentukan Sehingga estimator tak bias dari adalah :

( 7

Pendugaan (estimasi) yang dilakukan dengan Metode Kemungkinan

Maksimum untuk memperoleh estimatornya, tentu saja tidak lepas dari kesalahan

(error) baik itu sedikit maupun banyak. Namun dengan metode kemungkinan

maksimum, kesalahan penduga dijamin yang terkecil karena estimasi dengan metode

ini akan meminimumkan jumlah kudrat errornya dengan ketentuan memenuhi beberapa

(28)

Dengan demikian dalam melakukan analisis regresi diberlakukan asumsi – asumsi model ideal tertentu terhadap galat , yaitu:

1. Nilai rata – rata kesalahan pengganggu nol, yaitu: , untuk .

2. adalah konstan untuk semua kesalahan pengganggu (asumsi homoskedastisitas).

3. Tidak ada korelasi serial (autocorrelation) antara pengganggu ,

berartikovarian .

4. Peubah bebas konstan dalam sampling yang terulang dan bebas terhadap kesalahan pengganggu .

5. Tidak ada multikolinearitas antar variabel bebas X.

2.4 Heteroskedastisitas

2.4.1 Pengertian Heteroskedastisitas

Salah satu asumsi penting dari model regresi linear klasik adalah varian error pada

setiap nilai – nilai variabel bebas adalah sama (konstan), asumsi ini disebut juga sebagai asumsi homoskedastisitas atau homogenitas varian yang disimbolkan dengan:

, ,

Apabila asumsi ini tidak dipenuhi dalam analisis regresi linier, maka didapatkan

keadaan bahwa varian tidak bersifat konstan. Keadaan ini disebut mengalami

heteroskedastisitas atau disimbolkan dengan:

, , ,

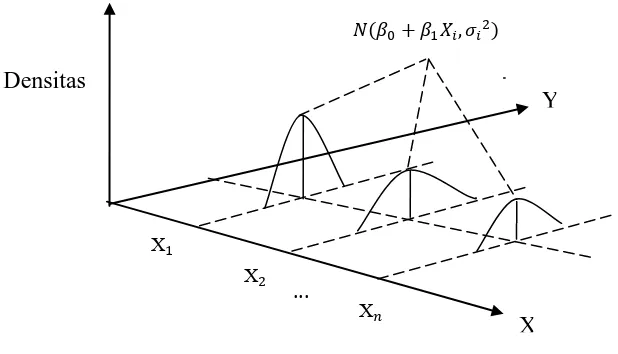
Secara diagram dalam regresi dua variabel, homoskedastisitas dapat

ditunjukkan pada Gambar (2.1) yang menunjukkan bahwa varian setiap rerata nolnya

(29)

setiap titik atau untuk seluruh nilai X (variabel bebas) yang kecil maupun besar, maka

pola tertentu akan terbentuk bila sebaran Y diplot dengan sebaran X. Bila

digambarkan dalam tiga dimensi, polanya akan mendekati pola pada Gambar (2.1).

Gambar 2.1. Asumsi Homoskedastisitas

Sebaliknya, Gambar (2.2) menunjukkan varian kondisional dari yaitu naik

dengan naiknya X atau dikatakan bahwa varian dari pada setiap variabel bebas X

tidak sama (tidak konstan).

Gambar 2.2. Asumsi Heteroskedastisitas

X Y Densitas

...

X Y Densitas

...

(30)

2.4.2 Konsekuensi Atau Akibat Adanya Heteroskedastisitas

Dalam kenyataannya, asumsi homoskedastisitas dari kesalahan pengganggu

mungkin tidak bisa dipenuhi, dengan kata lain varian dari kesalahan pengganggu

bersifat heteroskedastisitas, yaitu . Hal ini dapat dipahami jika diperhitungkan faktor – faktor yang menjadi penyebab adanya kesalahan pengganggu dalam model regresi. Faktor kesalahan pengganggu dimasukkan ke dalam model

untuk dapat memperhitungkan kesalahan – kesalahan yang mungkin terjadi dalam pengukuran dan kesalahan karena mengabaikan variabel – variabel tertentu. Dengan memperhatikan kedua perhitungan itu, maka terdapat alasan untuk memperkirakan

bahwa varian bervariasi secara sistematis dengan variabel bebas X.

Konsekuensi dari pelanggaran asumsi homoskedastisitas adalah sebagai

berikut:

1. Penduga (estimator) yang diperoleh tetap memenuhi persyaratan tidak bias.

(31)

Dengan demikian:

Demikian juga untuk estimator parameter yaitu

Diberikan estimator

( )

Dengan mensubsitusikan ke dalam persamaan (2.19), maka:

Dapat disimpulkan bahwa sifat ketidakbiasan tidak tergantung pada varian galat.

Jika dalam model regresi ada heteroskedastisitas, maka kita tetap memperoleh

nilai parameter yang tidak bias karena sebagai penduga tidak bias tidak

memerlukan asumsi bahwa varian galat harus konstan.

2. Varian penduga yang diperoleh akan menjadi tidak efisien, artinya penduga

(32)

Dengan asumsi adanya homoskedastisitas, maka:

ar

i j

Karena , dan

Sehingga diperoleh:

var

( )

Apabila dengan adanya asumsi heteroskedastisitas maka:

var

( )

Walaupun dikatakan adalah unbiased, tetapi tidak efisien karena varian – variannya lebih besar daripada yang diperlukan. Untuk melihat penggunaan persamaan (2.21)

(33)

Misalnya, dinyatakan bahwa varian dengan asumsi heteroskedastisitas proporsional

terhadap dan maka faktor proporsionalitasnya dinyatakan dengan persamaan:

Dengan mensubstitusikan nilai ke dalam persamaan (2.22), diperoleh:

var

persamaan (2.23) lebih besar daripada satu atau dapat dituliskan:

Maka ar dengan asumsi heteroskedastisitas akan lebih besar daripada ar dengan asumsi homoskedastisitas. Sebagai akibatnya, standar error dari terlalu

rendah (underestimated). Sebagaimana diketahui bahwa standart error ini memiliki peran

dalam pembentukan nilai t hitung yang berkaitan akan menjadi terlalu tinggi

(overestimated) yang mungkin selanjutnya menghasilkan kesimpulan bahwa dalam

(34)

signifikan. Oleh karena itu jika asumsi homoskedastisitas tidak dipenuhi maka hasil uji t

tidak menentu.

Selain uji signifikan tidak dapat diterapkan, batas – batas kepercayaan juga tidak dapat diterapkan. Artinya jika varian penaksir model tidak memenuhi asumsi

homoskedastisitas, maka inferensi dan prediksi mengenai koefisien – koefisien populasinya akan keliru.

Dalam analisis model regresi linear apabila semua asumsi model regresi linear

klasik terpenuhi kecuali asumsi homoskedastisitas yang berarti adanya

heteroskedastisitas, maka estimator dari paramater yang diperoleh masih tetap tak bias

dan konsisten tetapi estimatornya tidak efisien, baik untuk sampel kecil maupun

sampel besar.

2.4.3 Pengujian Heteroskedastisitas

Masalah heteroskedastisitas pada umumnya terjadi di dalam analisis data cross –

sectional. Data cross – sectional yaitu data yang diambil pada satu waktu saja, tetapi

dengan responden yang besar, misalnya jika melakukan survai. Data survai yang

didapatkan dari penelitian tersebut pada intinya adalah membandingkan kondisi satu

dan lain orang pada waktu yang sama. Gejala heteroskedastisitas terjadi akibat

ketidaksamaan data atau bervarisinya data yang diteliti.

Untuk mendeteksi masalah heteroskedastisitas dapat dilakukan dengan

metode formal dan informal. Metode formal dapat dilakukan dengan uji statistik

diantaranya Uji Park, Uji Glejser, Uji Korelasi Rank dari Spearmen dan Uji Goldfeld – Quant. Sedangkan metode informal biasanya dilakukan dengan uji metode grafik dengan memetakan terhadap dan melihat pola penyebaran yang terbentuk

sistematis atau acak. Dalam tulisan ini akan digunakan Uji Korelasi Rank dari

(35)

Pengujian Korelasi Rank dari Spearmen

Sesuai dengan namanya, metode ini pertama kali diperkenalkan oleh Spearmen dan

menggunakan korelasi peringkat X dan . Koefisien Korelasi Rank dari Spearmen dirumuskan:

( )

di mana merupakan selisih rank yang ditempatkan untuk dua karakteristik yang

berbeda dari individu ke-i atau fenomena ke-i dan n adalah banyaknya individu atau

fenomena yang diberi rank.

Langkah – langkah pengujian heteroskedastisitas dengan menggunakan uji

Korelasi Rank dari Spearmen adalah sebagai berikut:

1. Menentukan model regresi dengan meregresikan X dan Y dan didapatkan nilai

galat .

2. Tanpa memperhatikan tanda dari , yaitu ambil nilai mutlaknya yaitu , kemudian merangking kedua variabel dan sesuai dengan urutan yang menaik ataupun menurun selanjutnya menghitung selisih rank keduanya.

3. Menghitung koefisien berdasarkan persamaan (2.24).

4. Tingkat signifikansi koefisien korelasi yang didapatkan dengan persamaan

(2.24) diuji dengan statistik uji t sebagai berikut:

( )

dengan derajat bebas .

5. Pengujian hipotesis:

: tidak ada heteroskedastisitas

: ada heteroskedastisitas

Dengan demikian, kaidah pengambilan keputusan untuk hipotesis di atas adalah

sebagai berikut:

Tolak jika

(36)

Apabila dalam model regresi mencakup lebih dari dua variabel bebas, dapat

dihitung antara dengan setiap variabel bebas X secara terpisah dan juga dapat diuji

untuk mengetahui signifikan tidaknya dengan uji t.

2.5 Transformasi Box Cox

Box dan Cox (1964) telah mengembangkan suatu prosedur dalam pemilihan suatu

transformasi dari suatu transformasi kuasa (power transformation) yang dikenal

dengan Transformasi Box Cox dengan memperhatikan secara sistematis transformasi

variabelnya. Prosedur Transformasi Box Cox bertujuan untuk memeriksa

kecondongan dari distribusi bentuk galatnya atau dengan kata lain untuk menormalkan

data. Selain itu prosedur transformasi ini dapat juga digunakan untuk

menghomogenkan varian dan melinierkan model regresinya.

Transformasi Box Cox merupakan transformasi pangkat pada variabel respon

dan mempertimbangkan kelas transformasi berparameter tunggal, yaitu yang

dipangkatkan pada variabel respon Y. Dengan demikian, model transformasinya

menjadi dan adalah parameter yang perlu diduga.

Menurut Drapper S dan Harry S (1992) Transformasi Box Cox diberlakukan

pada variabel respon Y yang harus bertanda positif , dinyatakan dalam transformasi kuasa dengan persamaan berikut:

jika

jika ( )

Setelah Y ditransformasikan menjadi W, maka model regresi liniernya dalam

persamaan matriks menjadi:

(2.27)

dengan . Dengan demikian, prosedur utama Box Cox adalah menduga parameter transformasi dan dalam model regresi liniernya parameter juga perlu

(37)

2.5.1 Pendugaan Parameter Transformasi Box Cox

Salah satu metode yang dapat digunakan dalam pendugaan parameter pada

Transformasi Box Cox adalah dengan Metode Kemungkinan Maksimum. Cara

penaksiran ini sedikit berbeda dengan penaksiran yang biasa dilakukan yaitu

menentukan nilai pada kisaran nilai tertentu.

Dari model regresi linier diperoleh fungsi kemungkinannya, yaitu:

( ) Dengan mengalikan transformasi Jacobian dari variabel – variabel sampai dengan terhadap fungsi kemungkinannya maka diperoleh:

( )

dengan:

( 0)

Sehingga, fungsi kemungkinannya menjadi:

( )

Penduga parameter pada Transformasi Box Cox diperoleh dengan

memaksimumkan persamaan fungi kemungkinannya. Sehingga diperoleh:

( )

Sehingga untuk nilai yang telah ditetapkan, maka fungsi maksimum likelihoodnya

adalah:

(38)

Dengan adalah

K ( umlah Kuadrat isa) setelah menduga model

regresi dengan yang ditentukan.

Penaksiran parameter yang biasa dilakukan yaitu menentukan nilai pada

kisaran nilai tertentu. Biasanya yang dipakai yaitu dari kisaran 2,2) atau bahkan (-1,1). Sehingga untuk setiap tingkatan nilai yang telah ditetapkan akan diperoleh nilai – nilai maksimum likelihoodnya yaitu nilai . Penduga parameter dikatakan sebagai penduga apabila memiliki nilai maksimum log – likelihoodnya adalah maksimum terhadap yang telah ditetapkan dari antara nilai - nilai

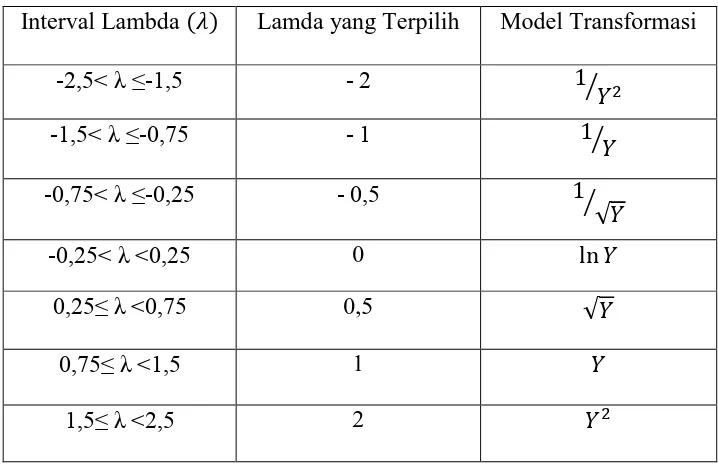
yang diperoleh dari yang lainnya. Pada tabel 2.1 di bawah ini diberikan beberapa nilai dan model transformasinya.

Tabel 2.1 Nilai dan Model Transformasinya

Interval Lambda Lamda yang Terpilih Model Transformasi

, , , 0,7

0,7 0, 0,

0, 0, 0

0, 0,7 0,5

0,7 , 1

(39)

2.5.2 Selang Kepercayaan Parameter Pada Transformasi Box Cox

Pendugaan parameter sering dinyatakan dalam pembentukan selang kepercayaan,

karena hampir tidak pernah ditemukan nilai statistik yang tepat sama dengan nilai

parameternya. Menurut Hasan (2002), pendugaannya sering dinyatakan dalam suatu

daerah atau interval yang dibatasi oleh dua nilai dan digunakan tingkat kepecayaan

(confidence) terhadap daerah nilai sebenarnya atau parameternya berada, sehingga

disebut interval kepercayaan atau selang kepercayaan.

Demikian halnya dalam pendugaan parameter pada Transformasi Box Cox

dinyatakan juga dalam selang kepercayaan terhadap , atas nilai – nilai yang memenuhi pertidaksamaan berikut:

(2.34)

Dengan adalah titik persentase sebaran khi-kuadrat dengan satu derajat bebas yang luas wilayah di sebelah kanannya sebesar . Sebagian nilai – nilai itu adalah:

0,10 0,05 0,025 0,01 0,005

_2,71 _3,841 _5,024 _6,635 _7,879

Untuk menggambarkan persaman (2.34) yaitu dengan menarik garis mendatar

setinggi, pada tebaran dengan pada setiap

perhitungan yang telah diperoleh. Sehingga garis yang terbentuk akan memotong

(40)

2.6 Pengujian Hipotesis dalam Model Regresi Linier Sederhana

Model regresi yang baik diperoleh akan diperiksa setelah variabel respon Y

ditransformasikan sesuai dengan model transformasi. Pemeriksaan ini ditempuh

melalui pengujian hipotesis.

Jika pada percobaan akan dilakukan pengujian terhadap yang sama dengan

sebuah konstanta misalkan , maka pada umumnya hipotesis tersebut dirumuskan

sebagai berikut:

Dan akan diduga alternatifnya dua arah, maka satistik uji yang digunakan pada

pengujian hipotesis ini adalah:

( )

Kaidah pengambilan keputusan untuk pengujian hipotesis ini adalah sebagai berikut:

ditolak jika . Dalam hal lain terima .

Dengan cara yang sama dapat juga digunakan untuk menguji intercept , dan

hipotesisnya adalah sebagai berikut:

Statistik ujinya adalah:

( )

Kaidah pengambilan keputusan untuk pengujian hipotesis ini adalah sebagai berikut:

ditolak jika . Dalam hal lain terima .

Nilai dapat diperoleh dari tabel t dengan menggunakan dengan derajat

(41)

Dalam persamaan (2.35) dan (2.36) di atas dapat dinyatakan dengan persamaan berikut:

( 7

Dengan adalah koreksi atau perbaikan jumlah kuadrat X.

Pengujian hipotesis dalam model regresi tersebut dilakukan secara parsial yang

bertujuan untuk menguji signifikansi pengaruh variabel bebas terhadap variabel

respon. Sehingga, masalah khusus dari pengujian hipotesis dalam model regresi linier

sederhana adalah:

Apabila hipotesis ditolak, maka variabel bebas X berpengaruh terhadap variabel

respon Y. Dengan demikian, model analisis regresi signifikan dan layak digunakan

(42)

BAB 3

PEMBAHASAN

3.1 Transformasi Box Cox Untuk Mengatasi Heteroskedastisitas

Apabila asumsi homoskedastisitas tidak terpenuhi atau terdapat heteroskedastisitas

maka tidak akan mempengaruhi ketakbiasan dan konsistensi dari penduga parameter,

tetapi penduga tersebut menjadi tidak efisien karena tidak memiliki varian yang

minimum, dengan demikian tidak lagi merupakan penduga tak bias linier terbaik atau

disebut juga Best Linear Unbiased Estimator (BLUE). Akibat tidak memiliki varian

yang minimum, maka akan mempengaruhi pengujian hipotesis terhadap parameter

baik menggunakan pendekatan uji signifikan maupun pendekatan selang kepercayaan.

Oleh karena itu tindakan perbaikan perlu dilakukan yaitu dengan mengatasi masalah

heteroskedastisitas. Salah satunya yaitu dengan Transformasi Box Cox yang

mentransformasikan variabel responnya dengan mempertimbangkan kelas

transformasi berparameter tunggal, yaitu yang dipangkatkan pada variabel respon

Y. Dengan demikian, model transformasinya menjadi .

Dengan mentransformasikan variabel responnya sesuai dengan model

transformasinya, maka akan diperoleh model regresi yang baik dengan memenuhi

asumsi homoskedastisitas yaitu masalah heteroskedastisitas akan teratasi. Model

transformasi akan terbentuk, apabila penduga parameter diperoleh dengan

(43)

( )

Persamaan (3.1) dapat juga dituliskan menjadi:

( )

Jika persamaan (3.1) direduksi terhadap konstanta, maka:

( )

Sehingga memaksimalkan nilai yang ditetapkan sama dengan meminimalkan , yaitu meminimalkan Jumlah Kuadrat Sesatan yang diperoleh dari pengepasan model

regresinya.

Misalnya apabila diperoleh penduga parameter pada Transformasi Box Cox

mendekati 0 (nol) atau berada pada interval -0, 0, , maka model transformasinya adalah . Dengan mentranformasikan variabel responnya sesuai model transformasi yang telah diperoleh maka akan memperkecil skala pengukuran

variabel – variabel yang asli. Oleh karena itu mampu mengurangi perbedaan di antara nilai – nilai. Contohnya, apabila terdapat nilai asli 10 dan 100; dimana diketahui bahwa 100 adalah sepuluh kali dari nilai 10 tetapi melalui transformasi logaritma

natural akan menjadi: ln 00 , 0 hanya sekitar dua kali dari ln 0 , 0 .

Untuk memperjelas prosedur Transformasi Box Cox dalam mengatasi masalah

heteroskedastisitas pada variabel – variabel bebas, maka dalam penelitian ini digunakan data simulasi dengan membangkitkan bilangan acak dengan menggunakan

program Minitab 16. Dan data yang dibangkitkan berdasarkan distribusi yang telah

(44)

Data simulasi ini terdiri dari dua variabel yaitu variabel bebas X dan variabel

respon (Y). Dan dengan menggunakan program Minitab 16 akan dibahas setiap data

simulasi berdasarkan distribusi normal dengan parameter rata – rata dan standard deviasi yang telah ditentukan. Kemudian dilakukan analisis regresi untuk

mendapatkan estimator dari model regresi dan dilakukan pengujian adanya

heteroskedastisitas. Dengan adanya masalah heteroskedastisitas dalam model regresi

maka akan diatasi dengan menggunakan Transformasi Box Cox yang dapat dianalisis

(45)

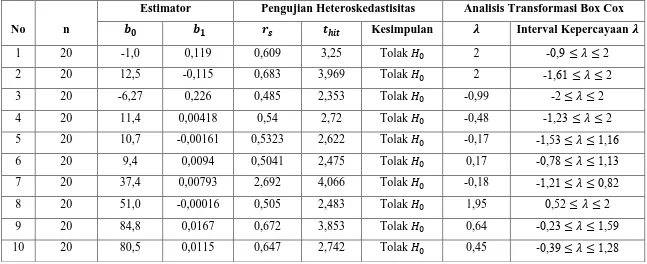
Tabel 3.1 Hasil Pengujian Heteroskedastisitas dan Analisis Transformasi Box Cox Pada Model Regresi Linier Sederhana

No n

Estimator Pengujian Heteroskedastisitas Analisis Transformasi Box Cox

Kesimpulan Interval Kepercayaan

1 20 -1,0 0,119 0,609 3,25 Tolak 2 0,

2 20 12,5 -0,115 0,683 3,969 Tolak 2 ,

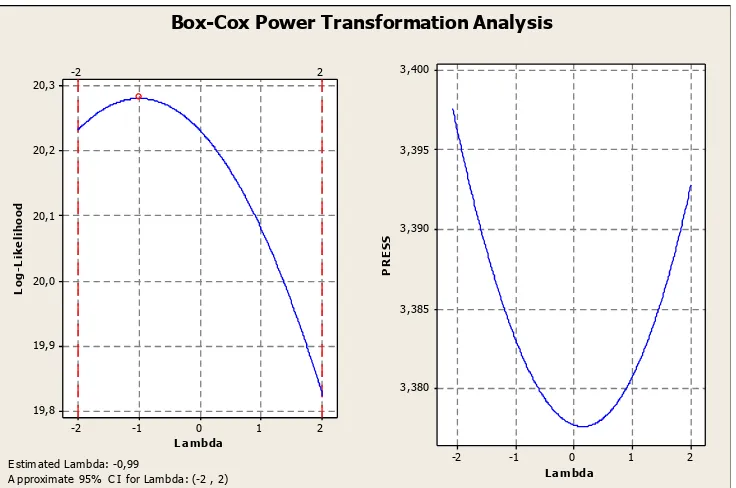
3 20 -6,27 0,226 0,485 2,353 Tolak -0,99

4 20 11,4 0,00418 0,54 2,72 Tolak -0,48 ,

5 20 10,7 -0,00161 0,5323 2,622 Tolak -0,17 , ,

6 20 9,4 0,0094 0,5041 2,475 Tolak 0,17 0,7 ,

7 20 37,4 0,00793 2,692 4,066 Tolak -0,18 , 0,

8 20 51,0 -0,00016 0,505 2,483 Tolak 1,95 0,

9 20 84,8 0,0167 0,672 3,853 Tolak 0,64 0, ,

(46)

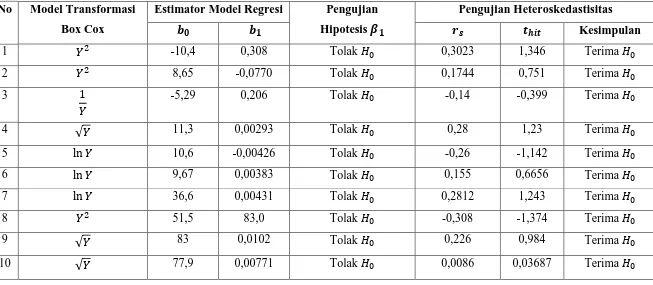
Tabel 3.2 Hasil Analisis Dalam Model Penentuan Regresi Linier Sederhana Setelah Variabel Respon Ditransformasikan Sesuai dengan Model Transformasi Box Cox

No Model Transformasi Box Cox

Estimator Model Regresi Pengujian Hipotesis

Pengujian Heteroskedastisitas

Kesimpulan

1 -10,4 0,308 Tolak 0,3023 1,346 Terima

2 8,65 -0,0770 Tolak 0,1744 0,751 Terima

3 -5,29 0,206 Tolak -0,14 -0,399 Terima

4 11,3 0,00293 Tolak 0,28 1,23 Terima

5 10,6 -0,00426 Tolak -0,26 -1,142 Terima

6 9,67 0,00383 Tolak 0,155 0,6656 Terima

7 36,6 0,00431 Tolak 0,2812 1,243 Terima

8 51,5 83,0 Tolak -0,308 -1,374 Terima

9 83 0,0102 Tolak 0,226 0,984 Terima

(47)

Hasil analisis Transformasi Box Cox untuk data yang berdistribusi normal

yang juga mengandung masalah heteroskedastisitas yaitu diperolehnya penduga

yang didapat pada setiap contoh data simulasinya. Penduga yang diproleh dapat juga

dituliskan dalam selang kepercayaan. Dengan diperolehnya penduga ini maka akan

terbentuk model transformasi Box Cox sesuai dengan nilai penduga seperti yang

ditunjukkan dalam tabel 3.2. Sehingga dengan mentransformasikan variabel

responnya sesuai dengan model transformasi maka akan diperoleh model regresi baru.

Dan apabila model regresi tersebut dilakukan uji signifikansi terhadap model regresi

maka diperoleh kesimpulan bahwa variabel bebas berpengaruh secara signifikan

terhadap variabel respon. Dengan demikian model regresi tersebut signifikan.

Kemudian apabila dilakukan pengujian heteroskedastisitas dengan uji Korelasi

Rank Spearmen maka hipotesis adanya heteroskedastisitas ditolak atau asumsi

homoskedastisitas terpenuhi dalam model regresi yang telah didapat.

(48)

BAB 4

KESIMPULAN DAN SARAN

4.1Kesimpulan

1. Dari hasil analisis untuk semua data simulasi yang dibangkitkan dengan

mengikuti distribusi normal maka dapat disimpulkan bahwa Transformasi Box

Cox dapat mengatasi heteroskedastisitas dalam model regresi, sehingga asumsi

homoskedastisitas akan terpenuhi.

2. Pendugaan parameter dapat juga dituliskan dalam selang kepercayaan. Dan

dari hasil analisis data simulasi, penduga parameter yang diperoleh berada

dikisaran (-2,2).

4.2Saran

Heteroskedastisitas merupakan salah satu pelanggaran asumsi model ideal dalam

analisis regresi. Sehingga dengan adanya masalah heteroskedastisitas dapat

menyebabkan model yang diperoleh kurang baik karena penduga parameternya tidak

efisien. Dengan demikian disarankan untuk terlebih dahulu menghilangkan masalah

heteroskedastisitas tersebut. Salah satu caranya yaitu dengan Transformasi Box Cox.

Dan apabila kenormalan data dan linieritas tidak dipenuhi dalam analisis regresi dapat

(49)

DAFTAR PUSTAKA

Box, G. E. P. Dan D. R. Cox. 1964. An Analysis of Transformations. Journal of the

Royal Statistical Society. 26(2): hal.211-243

Daniel, W.W. 1989. Statistika Nonparametrik Terapan. Jakarta: Gramedia

Drapper, N dan Smith, H. 1992. Analisis Regresi Terapan. Jakarta: Gramedia

Gaspersz, Vincent. 1991. Ekonometrika Terapan 2. Bandung: Tarsito.

Gaudry, Marcel G. 1979. Heteroscedasticity and The Use of Box – Cox

Transformation. 2(3): hal. 225-229.

Greene H William. 2000. Econometric Analysis Fourth Edition. New York: Prentice

Hall International. Inc.

Gujarati, Damodar 1988. Basic Econometrics. United State of America : McGraw – Hill, Inc.

Hasan, Iqbal. 2001. Pokok – Pokok Materi Statistik 2 (Statistik Inferensi). Jakarta: PT

Bumi Aksara.

Ispriyanti, Dwi. 2004. Pemodelan Statistika Dengan Transformasi Box Cox. 7(3):hal.

8-17.

Kutner, M.H, Wassamen.W dan Neter J. 1990. Applied Linear Statistical Models.

(50)

Montgomery DC dan Elizabeth A.P. 1982. Introduction to Linear Regression Analysis

Second Edition. New York: John Wiley & Son.

Sembiring, R.K. 1995. Analisis Regresi. Bandung: ITB.

Sumodinigrat, Gunawan. 1994. Ekonometrika Pengantar. Yogyakarta: BPFE -

Yogyakarta.

Supranto, J. 2004. Ekonometrika. Jakarta: Ghalia Indonesia.

Weisberg, S. 1985. Applied Linier Regression Second Edition. New York: John Wiley

& Son.

Wonnacott, Thomas H dan Wonnacott, Ronald J. 1935. Regression: A Second Course

(51)

(52)

Penyelesaian Model Regresi Linier Sederhana dan Analisis Transformasi Box Cox Pada Data Berdistribusi Normal Yang Mengandung Heteroskedastisitas

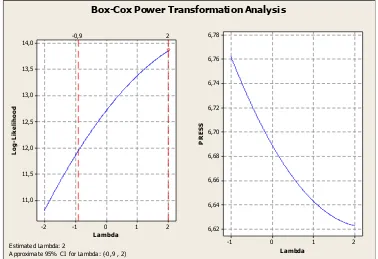
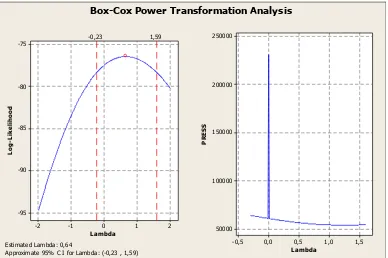
Data Simulasi 1

Welcome to Minitab, press F1 for help.

MTB > Random 20 X;

Regression Analysis: Y versus X

The regression equation is

Macro is running ... please wait

Approximate 95% CI for Lambda: (-0,9 , 2)

(53)

Data Simulasi 2

MTB > Random 20 X;

R denotes an observation with a large standardized residual.

MTB > %bctrans C2 C1.

Executing from file: C:\Program Files\Minitab\Minitab 16\English\Macros\bctrans.MAC

Approximate 95% CI for Lambda: (-1,61 , 2)

(54)

Data Simulasi 3

Welcome to Minitab, press F1 for help. MTB > Random 20 X;

(55)

Data Simulasi 4

MTB > Random 20 X;

(56)

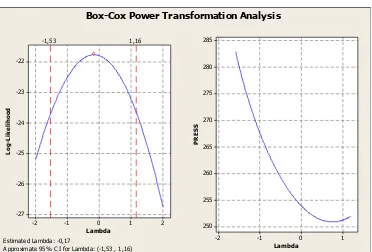
Data Simulasi 5

MTB > Random 20 X;

Approximate 95% CI for Lambda: (-1,53 , 1,16)

(57)

Data Simulasi 6

MTB > Random 20 X;

(58)

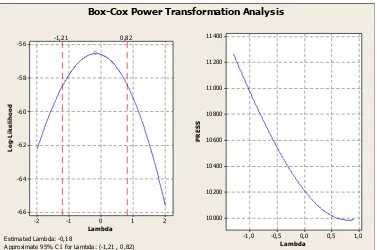
Data Simulasi 7

MTB > Random 20 X;

(59)

Data Simulasi 8

MTB > Random 20 X;

The regression equation is Y = 51,0 - 0,00016 X

20 cases used, 381 cases contain missing values

Predictor Coef SE Coef T P

(60)

Data Simulasi 9

MTB > Random 20 X;

(61)

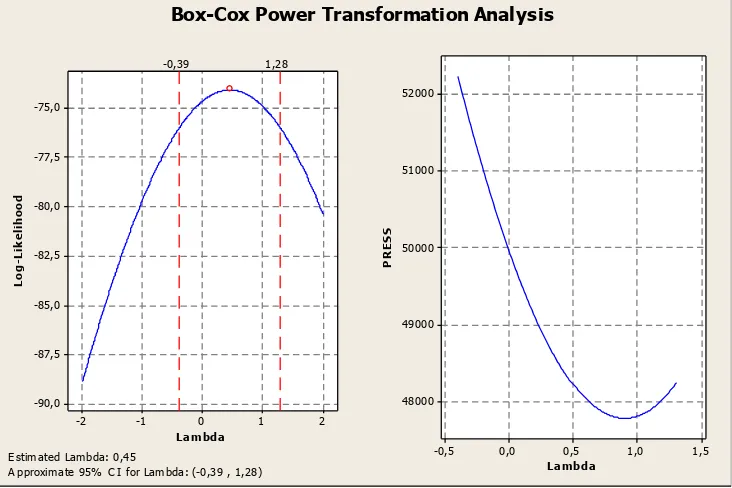
Data Simulasi 10

MTB > Random 20 X;

(62)

Gambar Analisis Transformasi Box Cox Pada Data Berdistribusi Normal Untuk Mengatasi Heteroskedastisitas Pada Model Regresi

(63)

(64)

(65)

(66)

(67)

(68)

Macro Minitab Analisis Transformasi Box Cox

Mcolumns Y X.1-X.n Y1 Lambda Res Trans LL Temp1 Temp2 Junk Mcolumns Conf Col Col1 Col2 Col3 Col4 Col5 Final Case Mesh Mcolumns St1 St2 St3 St4 St5 St6 Oper YY XX.1-XX.n Lev Press Mcolumns HH.1-HH.100 II.1 Bug JJ.1 T1 T2

Mconstants a c e f g h i j k l m t u lo hi lam err one two

note Macro is running ... please wait

mtitle "Box-Cox Power Transformation Analysis"

Note **Error** Response values must be positive. Note

exit ENDIF

IF infstore and not influence brief 2

(69)

Note **Note** Rows with missing values have been deleted from the

# Session window information

kkname ss Y

# Find optimal lambda based on log-likelihood

(70)

ENDIF

code (f:e)1 (-9999:f) '*' Temp1 Conf let Conf = Conf*Temp2

# Compute PRESS for refined lambda range

(71)

Penyelesaian Analisis Model Regresi Setelah Variabel Respon

Ditransformasikan Sesuai Dengan Model Transformasi Box Cox Pada Data Berdistribusi Normal

Data Simulasi 1

Welcome to Minitab, press F1 for help. MTB > Regress 'Y' 1 'X';

SUBC> Constant; SUBC> Brief 2.

The regression equation is Residual Error 18 0,000002 0,000000

Total 19 0,061159

Data Simulasi 2

(72)

Data Simulasi 3

Total 19 0,33524

Data Simulasi 4

(73)

Data Simulasi 5

(74)

Data Simulasi 7

(75)

Data Simulasi 9

(76)

Tabel Distribusi t (df = 1-40)

df 0.25 0.10 0.05 0.025 0.01 0.005 0.001

1 1.00000 3.07768 6.31375 12.70620 31.82052 63.65674 318.30884

(77)

Tabel Nilai Kritis Distribusi F dengan df untuk

penyebut (N2)

df untuk pembilang (N1)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

1 161 199 216 225 230 234 237 239 241 242 243 244 245 245 246 2 18.51 19.00 19.16 19.25 19.30 19.33 19.35 19.37 19.38 19.40 19.40 19.41 19.42 19.42 19.43 3 10.13 9.55 9.28 9.12 9.01 8.94 8.89 8.85 8.81 8.79 8.76 8.74 8.73 8.71 8.70 4 7.71 6.94 6.59 6.39 6.26 6.16 6.09 6.04 6.00 5.96 5.94 5.91 5.89 5.87 5.86 5 6.61 5.79 5.41 5.19 5.05 4.95 4.88 4.82 4.77 4.74 4.70 4.68 4.66 4.64 4.62 6 5.99 5.14 4.76 4.53 4.39 4.28 4.21 4.15 4.10 4.06 4.03 4.00 3.98 3.96 3.94 7 5.59 4.74 4.35 4.12 3.97 3.87 3.79 3.73 3.68 3.64 3.60 3.57 3.55 3.53 3.51 8 5.32 4.46 4.07 3.84 3.69 3.58 3.50 3.44 3.39 3.35 3.31 3.28 3.26 3.24 3.22 9 5.12 4.26 3.86 3.63 3.48 3.37 3.29 3.23 3.18 3.14 3.10 3.07 3.05 3.03 3.01 10 4.96 4.10 3.71 3.48 3.33 3.22 3.14 3.07 3.02 2.98 2.94 2.91 2.89 2.86 2.85 11 4.84 3.98 3.59 3.36 3.20 3.09 3.01 2.95 2.90 2.85 2.82 2.79 2.76 2.74 2.72 12 4.75 3.89 3.49 3.26 3.11 3.00 2.91 2.85 2.80 2.75 2.72 2.69 2.66 2.64 2.62 13 4.67 3.81 3.41 3.18 3.03 2.92 2.83 2.77 2.71 2.67 2.63 2.60 2.58 2.55 2.53 14 4.60 3.74 3.34 3.11 2.96 2.85 2.76 2.70 2.65 2.60 2.57 2.53 2.51 2.48 2.46 15 4.54 3.68 3.29 3.06 2.90 2.79 2.71 2.64 2.59 2.54 2.51 2.48 2.45 2.42 2.40 16 4.49 3.63 3.24 3.01 2.85 2.74 2.66 2.59 2.54 2.49 2.46 2.42 2.40 2.37 2.35 17 4.45 3.59 3.20 2.96 2.81 2.70 2.61 2.55 2.49 2.45 2.41 2.38 2.35 2.33 2.31 18 4.41 3.55 3.16 2.93 2.77 2.66 2.58 2.51 2.46 2.41 2.37 2.34 2.31 2.29 2.27 19 4.38 3.52 3.13 2.90 2.74 2.63 2.54 2.48 2.42 2.38 2.34 2.31 2.28 2.26 2.23 20 4.35 3.49 3.10 2.87 2.71 2.60 2.51 2.45 2.39 2.35 2.31 2.28 2.25 2.22 2.20