MULTIKOLINIERITAS DALAM REGRESI LINIER
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Pendidikan
Program Studi Pendidikan Matematika
Oleh:
Maria Ursula
NIM: 091414084
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ABSTRAK
Maria Ursula, 2013. Multikolinieritas dalam Regresi Linier. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Multikolinieritas merupakan salah satu pelanggaran asumsi di mana
vektor-vektor kolom dari matriks yaitu saling tak bebas linier. Multikolinieritas
itu sendiri terbagi dua, yaitu multikolinieritas sempurna dan multikolinieritas tidak
sempurna. Multikolinieritas sempurna adalah suatu kondisi di mana variabel-variabel
bebas berkorelasi secara sempurna, dengan kondisi sebagai berikut:
Sedangkan multikolinieritas tidak sempurna adalah suatu kondisi di mana
variabel-variabel bebas berkorelasi tetapi tidak secara sempurna, dengan kondisi sebagai berikut:
Di mana merupakan variabel gangguan.
Terjadinya multikolinieritas dalam regresi menyebabkan beberapa hal yaitu, jika
terjadi multikolinieritas sempurna penaksir parameter-parameter regresi tidak dapat
ditentukan, jika multikolinieritas tidak sempurna, penaksir parameter-parameter regresi
masih bisa ditentukan namun dengan tingkat keakuratan yang rendah.
Multikolinieritas dapat dideteksi dengan cara menguji nilai t dan F, serta memeriksa nilai VIF. Masalah multikolinieritas ini dapat diperbaiki dengan cara
menggunakan informasi apriori, menggabungkan data cross section dan data time series, menghilangkan variabel yang berkolinier, dan transformasi variabel.
ABSTRACT
Maria Ursula, 2013. Multicollinearity in Linear Regression. Thesis. Mathematics Education, Department of Mathematics and Natural Sciences, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.
Multicollinearity is a one of infringement of assumption where the column
vectors from matrix namely not mutually linearly independent.
Multicollinearity itself is divided into two, namely perfect multicollinearity and not
perfect multicollinearity. Perfect multicollinearity is a condition, in which the
independent variables are completely correlated, with the following conditions:
Whereas not perfect multicollinearity is a condition in which the independent
variables are correlated yet incompletely, with the following conditions:
In which is a variable interference.
The occurrence of multicollinearity in regression causes some cases, if happen
then perfect multicollinearity estimating regression parameters can not be determined.
While the not perfect one, the regression parameters estimator can still be determined, but
with a low level of accuracy.
Multicollinearity can be detected by testing the value of t and F, as well as
examining the value of VIF. Multicollinearity problem can be corrected by using apriori
information, combining cross section and time series data, eliminating collinear variable, and variable transformation.
Keywords : Multicollinearity, Regression, Linear Regression, infringement of
i
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Pendidikan
Program Studi Pendidikan Matematika
Oleh:
Maria Ursula
NIM: 091414084
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA YOGYAKARTA
iv
Tulisan ini dipersembahkan untuk mereka yang ku cintai
Teruntuk:
TUHAN YESUS KRISTUS yang selalu ada saat penulis
membutuhkan pertolongan-Nya
Bapak , Mamak, dan adik tercinta yang selalu dan tak pernah lelah
memberi dorongan dan motivasi selama penulisan skripsi ini
Teman-teman yang tak pernah lelah memberi semangat dan motivasi
serta kesabaran dalam mendengar keluh kesah penulis selama
penulisan skripsi ini
Almamater Universitas Sanata Dharma Yogyakarta
MOTTO HIDUP
"Kegagalan adalah sesuatu yang bisa kita hindari dengan; tidak
mengatakan apa-apa, tidak melakukan apa-apa dan tidak menjadi
apa-apa."
-Denis Waitley
“Saya telah menemukan paradoks, yaitu bahwa jika kamu mengasihi
sampai kamu tersakiti, maka tidak akan ada lagi sakit hati, hanya ada lebih banyak kasih.”
vi
ABSTRAK
Maria Ursula, 2013. Multikolinieritas dalam Regresi Linier. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Multikolinieritas merupakan salah satu pelanggaran asumsi di mana
vektor-vektor kolom dari matriks � yaitu �1,�2,…,�� saling tak bebas linier.
Multikolinieritas itu sendiri terbagi dua, yaitu multikolinieritas sempurna dan
multikolinieritas tidak sempurna. Multikolinieritas sempurna adalah suatu kondisi
di mana variabel-variabel bebas berkorelasi secara sempurna, dengan kondisi
sebagai berikut:
�1�1+�2�2+�3�3+⋯+���� = 0
Sedangkan multikolinieritas tidak sempurna adalah suatu kondisi di mana
variabel-variabel bebas berkorelasi tetapi tidak secara sempurna, dengan kondisi
sebagai berikut:
�1�1+�2�2+⋯+�� +�� = 0
Di mana � merupakan variabel gangguan.
Terjadinya multikolinieritas dalam regresi menyebabkan beberapa hal
yaitu, jika terjadi multikolinieritas sempurna penaksir parameter-parameter regresi
tidak dapat ditentukan, jika multikolinieritas tidak sempurna, penaksir
parameter-parameter regresi masih bisa ditentukan namun dengan tingkat keakuratan yang
rendah.
Multikolinieritas dapat dideteksi dengan cara menguji nilai t dan F, serta memeriksa nilai VIF. Masalah multikolinieritas ini dapat diperbaiki dengan cara
menggunakan informasi apriori, menggabungkan data cross section dan data time series, menghilangkan variabel yang berkolinier, dan transformasi variabel.
vii
ABSTRACT
Maria Ursula, 2013. Multicollinearity in Linear Regression. Thesis. Mathematics Education, Department of Mathematics and Natural Sciences, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.
Multicollinearity is a one of infringement of assumption where the column
vectors from matrix � namely �1,�2,…,�� not mutually linearly independent.
Multicollinearity itself is divided into two, namely perfect multicollinearity and
not perfect multicollinearity. Perfect multicollinearity is a condition, in which the
independent variables are completely correlated, with the following conditions:
�1�1 +�2�2+�3�3+⋯+���� = 0
Whereas not perfect multicollinearity is a condition in which the
independent variables are correlated yet incompletely, with the following
conditions:
�1�1+�2�2+⋯+���� +�� = 0
In which � is a variable interference.
The occurrence of multicollinearity in regression causes some cases, if
happenthen perfect multicollinearity estimating regression parameters can not be
determined. While the not perfect one, the regression parameters estimator can
still be determined, but with a low level of accuracy.
Multicollinearity can be detected by testing the value of t and F, as well as examining the value of VIF. Multicollinearity problem can be corrected by using
apriori information, combining cross section and time series data, eliminating collinear variable, and variable transformation.
Keywords : Multicollinearity, Regression, Linear Regression, infringement of
viii
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa atas
berkat, rahmat dan penyertaan-Nya sehingga penulis dapat menyelesaikan skripsi
yang berjudul “Multikolinieritas dalam Regresi Linier” sebagai salah satu
syarat untuk memperoleh gelar Sarjana Pendidikan (S.Pd) pada Fakultas
Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma Yogyakarta.
Penulis menyadari bahwa sejak awal masa perkuliahan hingga masa
penyusunan skripsi ini, penulis telah mendapatkan bimbingan, bantuan dan
pengarahan dari berbagai pihak. Penulis mengucapkan terima kasih kepada:
1. Ibu Ch. Enny Murwaningtyas, M.Si sebagai dosen pembimbing skripsi atas
kesediaan memberikan pengajaran, bimbingan, masukkan, kritik dan saran
selama penyusunan skripsi.
2. Bapak Rohandi, Ph.D., selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan
Universitas Sanata Dharma.
3. Bapak Dr. Marcellinus Andi Rudhito, S.Pd , selaku Ketua Program Studi
Pendidikan Matematika, Universitas Sanata Dharma.
4. Bapak Dominikus Arif Budi Prasetyo, M.Si selaku Dosen Pembimbing
Akademik.
5. Bapak Hongki Julie, S.Pd., M.Si., yang telah banyak membantu penulis dalam
penulisan skripsi ini.
6. Bapak Drs. Sukardjono, M.Pd., dan Bapak D. Arif Budi Prasetyo, S.Si., M.Si.,
yang telah menjadi dosen penguji skripsi, terimakasih atas saran dan
bimbinganna selama ini.
7. Segenap dosen Pendidikan Matematika Sanata Dharma atas segala pengajaran
dan bimbingannya selama perkuliahan.
8. Bu Henny, Pak Sugeng, dan Mas Arif yang telah memberikan pelayanan
administrasi selama penulis kuliah.
9. Perpustakaan Universitas Sanata Dharma yang memberikan fasilitas dan
ix
10.Bapak Petrus Rimau, mamak Yusta Fatmawati., adikku tersayang (Leonardus
Perta Morizia) yang selalu memberikan doa, semangat, dukungan dan
perhatian selama proses penyusunan skripsi.
11.Yeremia Wedaring Asmoro sebagai sahabat dan rekan kerja selama
penyusunan skripsi atas dukungan, kerjasama, semangat dan doanya.
12.Chintya, Hellen, sebagai sahabat-sahabat terbaik yang selalu memberi
dukungan dan semangat selama penyusunan skripsi.
13.Semua teman-teman PMAT USD atas kebersamaannya selama kuliah S1 di
prodi pendidikan matematika Universitas Sanata Dharma.
14.Teman-teman Kos Odilia (Kak Lina, Menik, Siska, Ecik, Nover, Stefani, Desi,
Gesti, Maya, Vita, Mita, Neno dan Mega) atas dukungan, bantuan dan
kebersamaannya selama tinggal di Yogyakarta.
15.Semua pihak yang penulis tidak dapat sebutkan satu persatu yang turut
membantu selama penyusunan skripsi ini.
Penulis menyadari bahwa skripsi ini masih kurang kesempurnaan, oleh sebab itu
penulis mengharapkan kesediaan pembaca untuk memberikan kritik dan saran
yang membangun. Akhir kata, semoga segala informasi yang ada dalam skripsi ini
dapat bermanfaat bagi pembaca.
xi
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
LEMBAR PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
ABSTRAK ... vi
ABSTRACT ... vii
KATA PENGANTAR ... viii
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... x
DAFTAR ISI ... xi
DAFTAR TABEL ... xiii
BAB I. PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Rumusan Masalah ... 3
C. Batasan Masalah... 4
D. Tujuan Penulisan ... 4
E. Metode Penulisan ... 4
F. Sistematika Penulisan ... 5
BAB II. LANDASAN TEORI ... 6
A. KONSEP – KONSEP STATISTIK... 6
B. PROBABILITAS ... 10
xii
BAB III. REGRESI LINIER ... 33
A. ANALISIS REGRESI LINIER SEDERHANA ... 34
B. ANALISIS REGRESI LINIER BERGANDA ... 60
C. PENGUJIAN HIPOTESIS ... 90
BAB IV. MULTIKOLINIERITAS... 95
A. KONSEKUENSI MULTIKOLINIERITAS ... 98
B. PENDETEKSIAN MULTIKOLINIERITAS ... 103
C. LANGKAH – LANGKAH PERBAIKAN ... 107
BAB V. KESIMPULAN ... 125
DAFTAR PUSTAKA ... 128
xiii
DAFTAR TABEL
Tabel 2.1 Tabel Percobaan Pelemparan Dua Buah Mata Uang Logam ... 11
Tabel 2.2 Tabel Distribusi Peluang Percobaan Pelemparan Sepasang Dadu ... 13
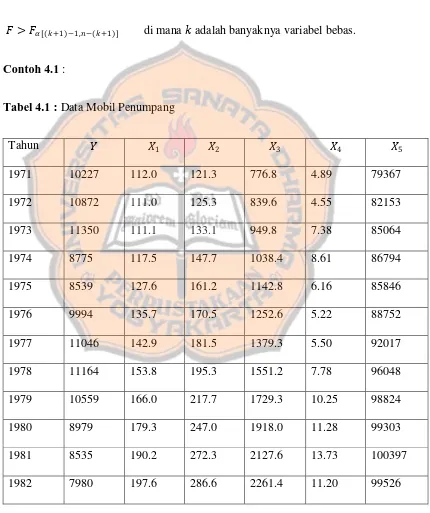
Tabel 4.1 Data Mobil Penumpang ... 103
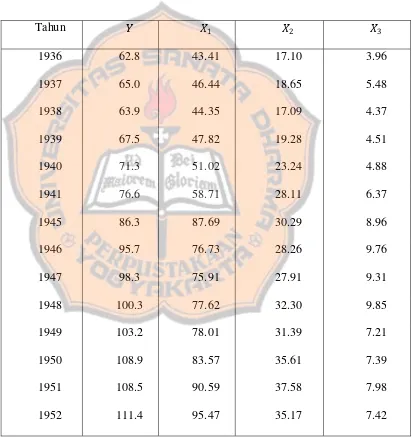
Tabel 4.2 Data tahun 1936 - 1952 ... 108
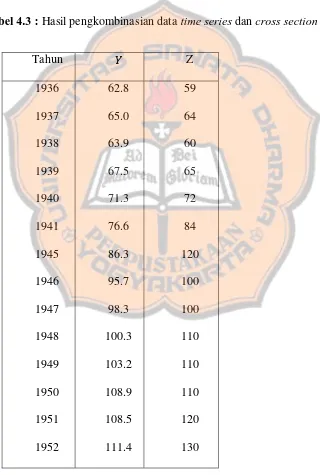
Tabel 4.3 Hasil pengkombinasian data time series dan cross section ... 110
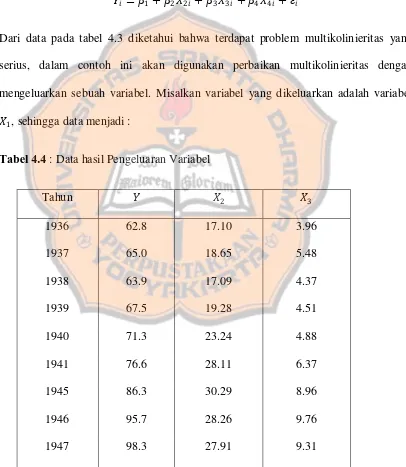
Tabel 4.4 Data hasil Pengeluaran Variabel ... 113
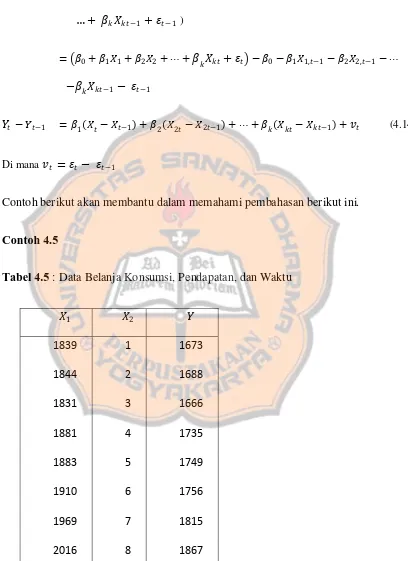
Tabel 4.5 Data Belanja Konsumsi, Pendapatan, dan Waktu ... 116
Tabel 4.6 Data Hasil Transformasi Diferensial Pertama Sebagai ... 118
1
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Istilah regresi pertama kali diperkenalkan oleh Sir Francis Galton (1822-1911)
yang membandingkan tinggi badan anak laki-laki dengan tinggi badan ayahnya. Dia
mengamati setelah beberapa generasi, anak laki-laki dengan ayah yang postur
tubuhnya sangat tinggi cenderung lebih pendek dari ayahnya, sampai mendekati
suatu besaran tinggi badan tertentu, yang tidak lain adalah tinggi rata-rata seluruh
populasi tinggi anak laki-laki, atau tinggi anak laki-laki pada umumnya. Demikian
pula anak laki-laki dengan ayah yang postur tubuhnya sangat pendek, setelah
beberapa generasi cenderung lebih tinggi dari ayahnya, hingga mendekati rata-rata
seluruh populasi.
Dalam kehidupan sehari-hari sering juga dijumpai hubungan antara suatu
variabel dengan satu atau lebih variabel lain. Variabel yang dipengaruhi disebut
variabel terikat yang dilambangkan dengan Y, sedangkan variabel yang
mempengaruhi disebut variabel bebas yang dilambangkan dengan X. Contohnya
dalam bidang ekonomi, ingin diketahui hubungan antara pengeluaran bulanan dalam
satu keluarga dengan banyaknya pendapatan keluarga tersebut dalam satu bulan.
hasil panen, juga dalam bidang pendidikan, hubungan antara hasil tes inteligensi
dengan prestasi belajar siswa. Hubungan-hubungan seperti ini dikenal dengan nama
regresi. Hubungan antara variabel bebas dan variabel terikat ini bentuknya bisa linier
ataupun polynomial. Dalam penulisan ini hanya akan dibahas regresi linier.
Analisis regresi yang linier terbagi menjadi dua, yaitu analisis regresi
sederhana dan analisis regresi berganda. Analisis regresi sederhana dimodelkan
dengan bentuk sebagai berikut:
� =�0+�1 �+��
Sedangkan analisis regresi berganda dimodelkan dalam bentuk matriks sebagai
berikut:
= vektor variabel tak bebas berordo �× 1
= matriks variabel bebas berordo �× (�+ 1)
Dari model tersebut ingin dicari parameter-parameter regresinya. Karena tidak
mungkin untuk memperoleh data populasi maka yang dicari adalah penaksir
parameternya saja. Dalam mencari penaksir parameter-parameter tersebut diperlukan
beberapa asumsi yang mendasari.
Ada beberapa asumsi yang mendasari penaksiran parameter-parameter
regresi, salah satunya adalah tidak adanya multikolinieritas. Pelanggaran asumsi tidak
adanya multikolinieritas ini akan menyebabkan beberapa hal dalam regresi, salah
satunya yaitu penaksir parameter regresi tidak dapat dicari. Jika
parameter-parameter regresi tidak dapat ditentukan, akibatnya model juga tidak dapat
ditentukan. Oleh karena beberapa hal tersebut, multikolinieritas harus diatasi.
Berdasarkan latar belakang di atas penulis memilih judul “Multikolinieritas
dalam Regresi Linier”.
B. Rumusan Masalah
Pokok permasalahan yang akan dibahas dalam tulisan ini adalah sebagai berikut:
1. Apa yang dimaksud dengan multikolinieritas dan apa konsekuensi dari
multikolinieritas?
2. Bagaimana mendeteksi multikolinieritas?
C. Batasan Masalah
Dalam penulisan ini, penulis hanya akan membahas model regresi yang linier, dengan
variabel terikat Y dengan variabel bebas X. Dalam penulisan ini, dalam mendeteksi
multikolinieritas hanya menggunakan uji t , uji F, dan memeriksa nilai VIF. Untuk
langkah-langkah perbaikan penulis hanya akan membahas langkah-langkah perbaikan
dengan informasi apriori, menggabungkan data cross section dan data time series,
mengeluarkan sebuah variabel, transformasi variabel, dan penambahan data baru.
D. Tujuan Penulisan
Tujuan yang akan dicapai dalam penulisan ini adalah:
1. Memahami pengertian dari multikolinieritas dan memahami konsekuensi dari
multikolinieritas.
2. Memahami cara-cara mendeteksi multikolinieritas.
3. Memahami langkah-langkah perbaikan model regresi yang mengalami masalah
multikolinieritas.
E. Metode Penulisan
Metode penulisan makalah ini menggunakan metode studi pustaka, yaitu
dengan menggunakan buku-buku pendukung yang berkaitan dengan regresi linier dan
F. Sistematika Penulisan
Bab I menjelaskan tentang latar belakang masalah, rumusan masalah,
batasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan, dan
sistematika penulisan.
Bab II menjelaskan tentang landasan teori yang menjadi dasar dari
penulisan skripsi ini.
Bab III menjelaskan tentang regresi linier sederhana, regresi linier
berganda, asumsi-asumsi yang mendasari penaksiran parameter regresi linier
sederhana, asumsi – asumsi yang mendasari penaksiran parameter-parameter regresi
linier berganda, dan pengujian hipotesis.
Bab IV menjelaskan tentang pengertian multikolinieritas, konsekuensi
adanya multikolinieritas, bagaimana mendeteksi multikolinieritas, dan
langkah-langkah perbaikan model regresi yang terkena multikolinieritas.
6
BAB II
LANDASAN TEORI
A. KONSEP-KONSEP STATISTIK
Dalam pembahasan mengenai regresi linier yang akan dibahas lebih dalam
pada bab III akan sering menggunakan konsep-konsep statistik. Oleh karena itu dalam
subbab ini akan dibahas terlebih dahulu mengenai konsep-konsep statistik di
antaranya adalah populasi dan sampel, variabel dan konstanta, distribusi, dan
distribusi sampel.
Dalam mempelajari statistika tidak lepas dari istilah data, karena statistika
itu sendiri adalah ilmu mengenai pengolahan data. Regresi sebagai bagian dari
statistika, dan multikolinieritas yang merupakan bagian dari regresi juga tidak lepas
dari pengolahan data. Data didalam statistika dapat dibedakan menjadi dua secara
umum, yaitu data populasi dan data sampel. Oleh karena itu penting untuk diketahui
istilah yang berkaitan dengan data, yakni istilah populasi dan sampel.
Definisi 2.1
Populasi adalah keseluruhan pengamatan atau obyek yang menjadi perhatian(Ronald
Suatu populasi dikatakan terbatas bila banyaknya objek yang bisa diamati
terbatas. Suatu populasi dikatakan tidak terbatas bila banyaknya objek yang bisa
diamati tidak terbatas. Sifat-sifat populasi disebut parameter.
Definisi 2.2
Sampel adalah himpunan objek pengamatan yang dipilih dari populasi(Gunawan
Sumodiningrat,2012).
Banyaknya objek pengamatan dalam sampel disebut ukuran sampel.
Sifat-sifat sampel disebut statistik. Statistik adalah nilai yang diperoleh dari sampel dan
digunakan untuk menaksir nilai parameter.
Dalam model regresi dikenal adanya variabel bebas dan variabel terikat.
Selain itu akan sering dijumpai istilah variabel random dalam pembahasan mengenai
regresi linier. Untuk itu di dalam subbab ini, sebelum membahas mengenai pengertian
dari variabel bebas dan variabel terikat, terlebih dahulu dibahas mengenai pengertian
dari variabel itu sendiri. Tidak kalah pentingnya ketika mempelajari variabel, perlu
juga dipelajari mengenai istilah konstanta, karena umumnya persamaan matematik
juga melibatkan istilah konstanta tersebut.
Definisi 2.3
Variabel adalah suatu kuantitas homogen yang nilainya dapat berubah pada setiap
Variabel terbagi dua berdasarkan bisa atau tidaknya variasi dari variabel itu
dikendalikan, yaitu variabel random dan variabel nir-random. Variabel yang
variasinya tidak dapat dikendalikan disebut variabel random, sedangkan variabel yang
variasinya dapat dikendalikan disebut variabel nir-random.
Definisi 2.4
Variabel random ialah suatu fungsi yang mengaitkan suatu bilangan real pada setiap
unsur dalam ruang sampel(Ronald E Walpole dan Raymond H Mayers,1989).
Variabel random dinyatakan dengan huruf besar, misalnya X, sedangkan
nilainya dinyatakan dengan huruf kecil, x. Pembahasan ini penting dalam
menjelaskan sifat variabel terikat Y di dalam analisis regresi linier, baik sederhana
maupun berganda. Variabel random terbagi lagi menjadi dua yaitu variabel diskrit
dan variabel kontinu.
Definisi 2.5
Konstanta adalah suatu besaran yang tidak berubah pada setiap waktu(Gunawan
Sumodiningrat,2012).
Distribusi adalah konsep yang berkaitan dengan tata aturan data. Di dalam
mempelajari asumsi-asumsi dalam regresi akan dibicarakan mengenai bagaimana
tersebut lebih dalam, maka dibahas terlebih dahulu mengenai hal-hal yang berkaitan
dengan distribusi. Distribusi terbagi dua yaitu distribusi frekuensi dan distribusi
probabilitas.
Definisi 2.6
Distribusi frekuensi adalah suatu bentuk penyajian nilai-nilai pengamatan dari suatu
variabel yang berasal dari sampel menurut tata aturan tertentu(Gunawan
Sumodiningrat,2012).
Distribusi frekuensi dipelajari dengan cara menghitung rerata dan variannya.
Istilah rerata dan varian akan banyak digunakan di bab-bab selanjutnya.
Definisi 2.7
Distribusi probabilitas adalah suatu bentuk penyajian nilai-nilai pengamatan dari
suatu variabel yang berasal dari populasi menurut aturan tertentu(Gunawan
Sumodiningrat,2012).
Variabel-variabel di dalam populasi memiliki distribusi tertentu, oleh sebab
itu setiap nilai dari suatu variabel memiliki probabilitas kejadian tertentu. Setiap nilai
dari suatu variabel ini memiliki sifat random. Seperti halnya distribusi frekuensi
dipelajari dengan mencari rerata dan variannya maka distribusi probabilitas dipelajari
B. PROBABILITAS
Seperti yang telah dipaparkan sebelumnya, bahwa di dalam penaksiran
parameter-parameter regresi di dasari beberapa asumsi, salah satunya adalah variabel
gangguan berdistribusi normal. Pada bagian ini akan dibahas mengenai pengertian
dari distribusi normal. Namun sebelum membahas mengenai distribusi normal, akan
dibahas terlebih dahulu mengenai fungsi probabilitas, distribusi probabilitas, baru
setelah itu dibahas mengenai distribusi normal.
Fungsi probabilitas yang akan dipelajari pada subbab ini juga terbagi dua,
yaitu fungsi probabilitas variabel random diskrit dan fungsi probabilitas variabel
random kontinu.
Jika X adalah variabel random diskrit dengan nilai-nilai : 1, 2, 3,…,
yang sesuai dengan probabilitas : 1 , ( 2), ( 3),…, ( ) maka himpunan
pasangan:
1 ... 1
2 ... ( 2)
3 ... ( 3)
... ( )
disebut fungsi probabilitas diskrit X.
Misalkan dalam pelemparan dua buah mata uang logam sebanyak dua kali.
dianggap sebagai variabel random X. Kemungkinan hasil pelemparan dua buah mata
uang tersebut dinyatakan dalam tabel berikut:
Tabel 2.1: Tabel Percobaan Pelemparan Dua Buah Mata Uang Logam
Hasil Lemparan Banyaknya Gambar Probabilitas dari (X) : f(x)
Angka, Angka 0 ¼
Gambar, Gambar 2 ¼
Angka, Gambar 1 ¼
Gambar, Angka 1 ¼
Fungsi probabilitas merupakan grafik yang menggambarkan hubungan
antara X dan f(x), untuk X suatu variabel diskrit.
Jika sebuah variabel random adalah variabel kontinu dalam intervalnya
terdapat sejumlah nilai-nilai yang banyak sekali (tidak terbatas). Distribusi
probabilitas untuk variabel kontinu berupa sebuah fungsi kontinu dari variabel
random, dan disebut fungsi probabilitas density.
Selanjutnya, jika X adalah sebuah variabel random kontinu, maka
probabilitas nilai X dalam interval dari a sampai b adalah:
Di mana f(x) adalah fungsi probabilitas density. Integral dari 1 ke dalam kasus
variabel kontinu analog dengan penjumlahan probabilitas dalam kasus variabel
diskrit. Oleh karena probabilitas X akan memiliki semua nilai sama dengan 1 maka:
� −∞< <∞ = ( ) ∞
−∞
= 1
Kemudian probabilitas X mempunyai nilai kurang dari atau sama dengan 0 tertentu
adalah:
� −∞< < 0 = 0 = ( )
0
−∞
Di mana F mencerminkan probabilitas kumulatif dari X.
Seperti halnya fungsi probabilitas yang terbagi menjadi fungsi probabilitas
diskrit dan fungsi probabilitas kontinu, distribusi probabilitas yang akan dipelajari
pada subbab ini terbagi dua yaitu, distribusi peluang diskrit dan distribusi peluang
kontinu.
Definisi 2.8
Distribusi peluang diskrit adalah sebuah tabel atau rumus yang mencantumkan semua
kemungkinan nilai suatu peubah acak diskrit berikut peluangnya(Gunawan
Sumodiningrat,2012).
Contoh 2.1
Penyelesaian:
Misalkan X adalah peubah acak yang menyatakan jumlah bilangan dari kedua dadu
tersebut. Maka X dapat mengambil sembarang nilai bulat dari 2 sampai 12. Dua dadu
dapat mendarat dalam 36 cara, masing-masing dengan peluang 1
36. � = 3 =
2 36,
karena jumlah 3 hanya dapat terjadi dalam 2 cara. Dengan memperhatikan
kemungkinan nilai-nilai lainnya. Distribusi peluang yang diperoleh adalah sebagai
berikut:
Tabel 2.2: Tabel Distribusi Peluang Percobaan Pelemparan Sepasang Dadu
x 2 3 4 5 6 7 8 9 10 11 12
Pada distribusi peluang kontinu, tidak mungkin menyajikan semua
kemungkinan data dengan menggunakan tabel. Misalnya ingin diketahui peluang
mengambil secara acak orang yang tingginya tepat 164 cm, di antara orang yang
berusia di atas 21 tahun. Peluang mengambil secara acak orang yang tingginya tepat
164 cm bernilai nol. Hal ini dikarenakan ambilah contoh di antara angka 163.5 dan
164.5 terdapat tak hingga banyaknya ukuran tinggi, dan hanya satu yang tepat 164
cm. Sehingga peluang mengambil secara acak orang yang tingginya 164 cm di antara
tak hingga ukuran tinggi dinilai nol.
Distribusi probabilitas memiliki beberapa sifat yang penting diantaranya
Dalam pembahasan mengenai regresi linier akan dicari nilai harapan dari variabel Y
berdasarkan nilai dari variabel X tertentu, untuk itu terlebih dahulu dipelajari
mengenai nilai harapan itu sendiri.
Definisi 2.10
misalkan bahwa suatu variabel random X mempunyai distribusi diskrit dengan fungsi
peluang (f.p) dari x adalah f. Nilai harapan dari X, ditulis dengan lambang E(X),
adalah suatu jumlah yang didefinisikan sebagai berikut:
E(X) = ( ) (2.10.1)
( ) <∞ (2.10.2)
(Abdus Salam, 1989)
Definisi 2.11
jika sebuah Variabel Random X mempunyai suatu distribusi kontinu dengan
fungsi kepadatan peluang (f.d.p) dari X adalah f maka ekspektasi E(X) didefinisikan
sebagai berikut :
E(X) = −∞∞ (2.3)
Teorema 2.1
Jika Y = aX + b , yang mana aX + b adalah konstanta maka E(Y) = aE(X) + b(Abdus
Salam, 1989).
Bukti :
E(Y) = E (aX + b)
= −∞∞ +
= −∞∞ + −∞∞
E(Y) = +
Definisi 2.12
Misalkan bahwa X adalah sebuah variabel random dengan mean = ( ). Varians
dari X, ditulis dengan lambang Var(X), didefinisikan sebagai berikut:
Var(X) = [( − )]2
(Abdus Salam,1989)
Sifat-sifat varians:
1. ( − )2 = 2 − 2
Pembuktiannya adalah sebagai berikut:
Diketahui = ( )
= 2 −2 + 2
= 2 −2 + 2
= 2 −2 2 + 2
= 2 + 2
2. Jika 1 dan 2 adalah variabel random bebas, maka
� 1+ 2 =� 1 +� ( 2)
Bukti :
1 = 1 dan 2 = 2 maka
1+ 2 = 1+ 2 , sehingga
� 1+ 2 = [( 1+ 2 − 1− 2)]2
= [(( 1− 1 ) + ( 2− 2))2]
= [( 1− 1 )2+ ( 2− 2)2+ 2( 1− 1 )( 2− 2)
= Var( 1) +� 2 + 2 ( 1− 1 )( 2− 2)
Karena 1 dan 2 bebas,
E[( 1− 2 ) ( 2− 2)] = E( 1− 1 )E( 2− 2)
= ( 1− 1)( 2− 2)
= 0
Maka : � 1+ 2 = Var( 1) +� 2
Kovarian antara dua peubah acak adalah suatu bentuk hubungan antara dua
peubah itu, misalkan apabila nilai X yang besar maka nilai Y juga besar, atau X kecil
maka nilai Y juga kecil. Hubungan yang semacam ini disebut hubungan yang positif.
Sebaliknya nilai X yang besar dengan Y yang kecil, atau X yang kecil maka Y
nilainya besar, maka hubungan demikian disebut hubungan yang negatif. Tanda
kovariansi (+ atau -) menunjukan seperti apa hubungan kedua peubah acak itu,
apakah positif ataukah negatif.
Definisi 2.13
Kovarians didefinisikan sebagai berikut:
� = −�=1 ( ) − ( ) �( , ) di mana
= nilai variabel acak X ke-i
= nilai variabel acak Y ke-i
� , = probabilitas terjadinya dan
= 1,2,…,�
Selanjutnya akan dibahas mengenai distibusi normal. Distribusi normal
adalah distribusi yang terpenting dalam seluruh bidang statistika. Grafiknya
cukup baik oleh kurva normal ini. Pengukuran fisik di bidang seperti percobaan
meteorologi, penelitian curah hujan, dan pengukuran suku cadang yang diproduksi
sering dengan baik dapat diterangkan menggunakan distribusi normal. Di samping itu
variabel gangguan dalam pengukuran ilmiah dapat dihampiri dengan baik oleh
distribusi normal. Semakin sangat banyak titik sampel dalam penelitian kita, maka
semakin data itu menghampiri normal.
Distribusi normal sering disebut distribusi Gauss untuk menghormati Karl
Friedrish Gauss (1777-1855), yang juga menemukan persamaannya waktu meneliti
variabel gangguan dalam pengukuran yang berulang-ulang mengenai bahan yang
sama. Peubah acak kontinu yang kurvanya berbentuk lonceng disebut peubah acak
normal.
Definisi 2.9
Distribusi normal adalah fungsi padat peubah acak normal X, dengan rataan dan
variansi �2, ialah ; ,� = 1 2��
− 12 ( −� )2
, − ∞< < ∞ dengan �=
3,14159…dan = 2,71828… (Ronald E Walpole dan Raymond H Mayers, 1995).
Bentuk kurva normal ditentukan oleh dan �. Titik tertinggi kurva normal
berada pada rata-ratanya. Semakin tinggi kurva normal tersebut, semakin ramping
dan runcing bentuk kurvanya, yang menandakan bahwa titik-titik pengamatannya
oleh simpangan baku �. Bentuk ( −
� )2 menandakan kurva normal adalah kurva yang
simetris.
Dengan memperhatikan gambar berikut serta memeriksa turunan pertama
dan kedua dari ; ,� dapat diperoleh lima sifat kurva normal berikut:
Gambar 2.1 Kurva Normal dengan Simpangan baku 0.5
1. Modus, titik pada sumbu datar yang memberikan maksimum kurva, terdapat pada
= ;
2. Kurva setangkup terhadap sumbu tegak yang melalui rataan ;
3. Kurva mempunyai titik belok pada = ±�, cekung dari bawah bila − �<
< +�, dan cekung dari atas untuk nilai x lainnya;
4. Kedua ujung kurva normal mendekati asimptot sumbu datar bila nilai x bergerak
menjauhi baik ke kiri maupun ke kanan;
5. Seluruh luas di bawah kurva dan di atas sumbu datar sama dengan 1.
Setiap hasil pengamatan yang berasal dari sembarang variabel acak normal x
ditransformasikan menjadi variabel acak normal z dengan = 0 dan � = 1, untuk
merupakan bentuk baku dari setiap variaabel acak normal x sehingga penyelesaian
setiap persoalan dengan dan � yang berbeda dapat diselesaikan dengan satu tabel
standar.
Untuk mengubah distribusi normal menjadi distribusi normal baku adalah
dengan cara mengurangi nilai-nilai variabel X dengan rata-rata dan membaginya
dengan standar deviasi � sehingga diperoleh variabel baru Z, yaitu:
= −�
= −
� =
1
� − = −
� = 0
� = [ − ]2 = ( )2 = ( −� )2 =��22 = 1
Sehingga variabel normal baku Z mempunyai rata-rata = 0 dan standar
deviasi �= 1.
C. MATRIKS
Pembahasan tentang matriks berguna dalam mempelajari analisis regresi
berganda yang akan dibahas pada bab III. Dalam subbab ini akan dipelajari mengenai
tipe-tipe matriks, operasi matriks, transpose dan submatriks, determinan, invers
matriks persegi, tetapi sebelumnya akan dibahas terlebih dahulu mengenai matriks itu
Definisi 2.14
Matriks adalah suatu susunan bilangan-bilangan berbentuk segiempat.
Bilangan-bilangan dalam susunan itu disebut elemen dari matriks tersebut(Howard
Anton,2000).
Ukuran matriks atau ordo matriks diberikan oleh jumlah baris (garis
horisontal) dan kolom (vertical) yang menyusunnya. Matriks ditulis dengan huruf
yang dicetak tebal. Jika ada sebuah matriks A yang terdiri baris dan kolom, maka ordo matriks A adalah × . Dalam pembahasan tentang matriks juga dikenal istilah skalar, yaitu angka tunggal atau bilangan real. Sebuah besaran skalar adalah matiks
1 × 1. Sebuah matriks dengan hanya satu kolom disebut vektor kolom, dan sebuah
matriks dengan hanya satu baris adalah vektor baris.
Contoh 2.2
Matriks dalam contoh di atas memiliki 4 baris dan 2 kolom, maka ukuran
atau ordo dari matriks A adalah 3 × 2. Matriks hanya terdiri dari satu baris, maka matriks merupakan vektor baris. Matriks terdiri hanya dari satu kolom, maka
matriks merupakan vektor kolom.
Dalam mempelajari matriks dikenal beberapa tipe-tipe matriks. Tipe-tipe
1. Matriks Persegi
Sebuah matriks dengan setidaknya satu elemen tidak bernilai nol pada diagonal
utama (terletak pada sudut kiri atas hingga sudut kanan bawah) dan bernilai nol
pada elemen lainnya disebut sebagai matriks diagonal.
Contoh 2.7
Sebuah matriks diagonal dengan semua elemen diagonal bernilai 1 disebut
matriks identitas. Matriks identitas dilambangkan dengan I .
4. Matriks Simetris
Matriks simetris adalah sebuah matriks persegi dengan elemen yang berada di
atas diagonal utama merupakan cerminan di bawah elemen dari diagonal utama.
Dalam sebuah matriks simetris, matriks = �.
5. Matriks nol
sebuah matriks dengan semua elemennya bernilai nol disebut matriks nol,
dilambangkan dengan 0 .
6. Vektor nol
Sebuah vektor baris atau vektor kolom yang semua elemennya bernilai nol
disebut sebagai vektor nol, dan juga dilambangkan dengan 0 .
7. Matriks yang Sama
Dua matriks didefinisikan sama jika keduanya mempunyai ukuran yang sama dan
Pada regresi berganda, dalam mencari rumus penaksir � dengan matriks,
melibatkan beberapa operasi matriks. Tidak hanya itu, dalam membuktikan sifat-sifat
dari penaksir, juga menggunakan beberapa operasi matriks. Pada bab IV untuk
membuktikan konsekuensi dari multikolinieritas juga menggunakan beberapa operasi
matriks. Untuk itu penting memahami beberapa operasi matriks, yang akan dibahas
dalam bagian ini. Berikut ini adalah beberapa operasi matriks.
1. Penjumlahan Matriks
Anggap A = dan B = . jika A dan B adalah matriks yang mempunyai order yang sama, penjumlahan matriks didefinisikan sebagai
+ =
Di mana C adalah matriks yang mempunyai order yang sama dengan A dan B,
serta diketahui juga bahwa = + untuk semua I dan j, yaitu C didapatkan dengan menjumlahkan elemen A dan B .
Contoh 2.11
= 2 3 4 5
6 7 8 9 =
1 0 −1 3
−2 0 1 5
+ =
= 2 3 4 5
6 7 8 9 +
1 0 −1 3
= 2 + 1 3 + 0 4−1 5 + 3 6−2 7 + 0 8 + 1 9 + 5
= 3 3 3 8
4 7 9 14
2. Pengurangan Matriks
Pengurangan matriks memiliki prinsip yang sama dengan penjumlahan matriks,
kecuali bahwa − = , yaitu jika elemen dari B dikurangi dari elemen yang berhubungan dengan A untuk mendapatkan C , memberikan order yang sama bagi
A dan B.
3. Perkalian Skalar
Mengalikan sebuah matriks A dengan sebuah skalar (sebuah angka riil), maka setiap elemen dari matriks akan dikalikan dengan ∶
=
4. Perkalian Matriks
Anggap A adalah matriks berorde × dan B adalah matriks yang berorde ×� , maka AB didefinisikan sebagai matriks yang baru C dengan orde ×�, seperti:
= =1 = 1,2,…, = 1,2,…,�
Contoh 2.12
= 2 1
6 3 =
2 3 4
× = 2 1
6 3 ×
2 3 4
6 7 8
= 2 × 2 + (1 × 6) 2 × 3 + (1 × 7) 2 × 4 + (1 × 8) 6 × 2 + (3 × 6) 6 × 3 + (3 × 7) 6 × 4 + (3 × 8)
= 10 13 16 30 39 48
Sifat-sifat perkalian matriks:
a. Perkalian matriks tidak bersifat komutatif, yaitu AB ≠ BA .
b. Walaupun AB dan BA ada, hasil matriks tidak berada dalam orde yang sama, jadi jika A adalah matriks × dan B adalah × , AB adalah × , sementara BA adalah × , dengan demikian AB dan BA berbeda orde. c. Sebuah vektor baris yang telah dikalikan dengan sebuah vektor kolom adalah
sebuah skalar.
d. Sebuah vektor kolom yang telah dikalikan dengan vektor baris adalah sebuah
matriks.
Di dalam regresi berganda untuk mencari penaksir parameter-parameter
regresi menggunakan bentuk matriks. Di dalam rumusan tersebut memuat suatu
transpose matriks. Untuk memahami perhitungan-perhitungan dalam bab III maupun
di dalam bab IV yang melibatkan transpose matrik, dalam subbab ini dibahas terlebih
Definisi 2.15
Jika A adalah sebarang matriks × , maka transpose A, dinyatakan dengan , didefinisikan sebagai matriks × yang didapatkan dengan mempertukarkan baris
dan kolom dari A, yaitu kolom pertama dari adalah baris pertama dari A, kolom kedua dari adalah baris kedua dari A, dan sterusnya.
Contoh 2.3
=
4 5
3 5
1 0
= 4 3 5
5 1 0
Pengubahan susunan sebuah vektor baris merupakan sebuah vektor kolom
dan sebaliknya, pengubahan susunan sebuah vektor kolom merupakan sebuah vektor
baris.
Contoh 2.4
� = 4 5 6
� = 4 5 6
Dengan matriks A berordo × , jika semua kecuali baris dan kolom matriks A
dihapus, matriks yang dihasilkan dari ordo × yang disebut submatriks A.
=
3 5 7
8 3
2 2
1 1
Dan baris ketiga dan kolom ketiga matriks A, didapat:
= 3 5
8 2
Matriks adalah sebuah submatriks dengan ordo 2 × 2.
Berikut ini adalah sifat-sifat dari transpose matriks:
a. Pengubahan susunan dari sebuah matriks yang telah mengalami pengubahan
adalah matriks asli itu sendiri. Jadi ( ) =
b. C = A + B dan = ( + ) = +
c. ( ) =
( ) =
d. � =� , � adalah matriks identitas
e. = , adalah sebuah skalar (sebuah angka riil) f. ( ) = = =
g. Apabila A adalah matriks persegi dengan = , maka adalah sebuah matriks simetris.
Determinan dari matriks A dinyatakan dengan det atau dengan simbol , di mana berarti “determinan dari”. Proses menemukan nilai sebuah determinan
Untuk mencari determinan A berorde 2 × 2 dilakukan perkalian silang secara berlawanan elemen diagonal utama dan mengurangi produk perkalian silang dengan
elemen diagonal lainnya dari matriks A. Ekspansi dari determinan untuk matriks
Sedangkan ekspansi dari determinan berorde 3 × 3 adalah sebagai berikut:
Jika =
1. Sebuah matriks dengan nilai determinan nol disebut sebagai matriks singular,
sedangkan sebuah matriks dengan nilai determinan tidak nol disebut sebagai
matriks nonsingular, di mana matriks singular tidak mempunyai invers.
3. = �
4. Dengan menukar dua baris atau dua kolom manapun dari matriks A akan mengubah tanda dari .
5. Jika setiap elemen dari sebuah baris atau sebuah kolom dari matriks A dikalikan dengan sebuah skalar , maka dikalikan dengan .
6. Jika dua baris atau dua kolom sebuah matriks identik, determinannya adalah nol.
7. Jika satu baris atau satu kolom dari sebuah matriks merupakan perkalian baris
atau kolom lainnya, determinannya adalah nol. Jika baris atau kolom manapun
sebuah matriks merupakan kombinasi linear dari baris (kolom) lainnya,
determinannya adalah nol.
8. = , artinya bahwa determinan dari produk dua matriks adalah produk
dari determinannya masing-masing.
Teorema 2.4
Anggap adalah suatu matriks ×
Jika B adalah matriks yang dihasilkan jika suatu penggandaan suatu baris A
ditambahkan pada baris lainnya atau jika suatu penggandaan suatu kolom
ditambahkan pada kolom lainnya, maka det = det( ) .
Bukti:
=
11 + 12 12 13
21 + 22 22 23
31 + 32 32 33
=
11 12 13
21 22 23
= 11+ 12 22 33+ 12 23 31 + 32 + 13( 21 + 22) 32 −
12 21+ 22 33+ 11+ 12 23 32+ 13 22( 31+ 32)
= ( 11 22 33) + ( 12 22 33) + ( 12 23 31) + ( 12 23 32) + ( 13 21 32) +
( 13 22 32) − ( 12 21 33) + ( 12 22 33) + ( 11 23 32) + ( 12 23 32) +
( 13 22 31) + ( 13 22 32)
= {( 11 22 33) + ( 12 23 31) + ( 13 21 32)−[ ( 12 21 33) + ( 11 23 32) +
( 13 22 31)]} + { ( 12 22 33) + ( 12 23 32) + ( 13 22 32)−
[ ( 12 22 33) + ( 12 23 32) + ( 13 22 32)]}
= + 0
=
Jika baris ke-i dan kolom ke-j dari matriks A dihapus, determinan dari submatriks disebut minor dari elemen dan dilambangkan dengan �
Kofaktor elemen dari sebuah matriks A berorde �� dilambangkan dengan dinyatakan sebagai
= (−1)+ �
Matriks kofaktor adalah sebuah matriks yang diperoleh dengan menggantikan elemen
dari sebuah matriks A dengan kofaktornya, dilambangkan dengan (cof A). Sedangkan matrika adjoin adalah pengubahan susunan dari matriks kofaktor, yaitu
Sebuah invers dari matriks persegi A , dilambangkan dengan −1jika ada merupakan sebuah matriks persegi yang unik, dan memenuhi :
−1 = −1 =�
Di mana �adalah matriks identitas. Sifat-sifat invers matriks :
a. ( )−1 = −1 −1
b. ( −1) = ( )−1
Jika matriks A adalah matriks persegi dan non singular, di mana ≠ 0 , invers −1 dapat ditemukan sebagai:
−1 = 1
( )
Berikut ini adalah langkah-langkah dalam mencari invers matriks:
1. Mencari nilai determinan, jika nilainya tidak nol maka lanjut ke langkah nomor
dua.
2. Mengganti setiap elemen matriks A dengan kofaktornya untuk mendapatkan matriks kofaktor.
3. Mengubah susunan dari matriks kofaktor untuk mendapatkan matriks adjoin.
33
BAB III
ANALISIS REGRESI
Dalam kehidupan sehari – hari sering ditemui adanya hubungan antar
variabel. Contohnya di dalam bidang ekonomi, adanya hubungan antara pengeluaran
suatu keluarga selama satu bulan dengan pendapatan keluarga tersebut selama satu
bulan. Di dalam bidang pendidikan, adanya hubungan antara hasil tes inteligensi
siswa dengan nilai ulangan kimia siswa, ataupun hubungan antara hasil panen dengan
jenis pupuk dan kadar air di dalam bidang pertanian. Hubungan yang semacam itu di
dalam statistika di namakan regresi.
Definisi 3.1
Analisis regresi berkaitan dengan studi mengenai ketergantungan satu variabel, yaitu
variabel terikat, terhadap satu atau lebih variabel lainnya, yaitu variabel bebas,
dengan tujuan untuk mengestimasi dan/atau memperkirakan nilai rata-rata (populasi)
variabel terikat dari nilai yang diketahui atau nilai tetap dari variabel bebas(Damodar
N. Gujarati,2012).
Variabel yang mempengaruhi variabel lain disebut variabel bebas,
sedangkan variabel yang nilainya dipengaruhi atau tergantung dengan nilai variabel
variabel terikat dilambangkan dengan Y. Bentuk hubungan variabel bebas dan terikat
ini bisa linier, kuadratik, logaritma, eksponensial, atau hiperbola. Dalam penulisan ini
hanya akan dibahas hubungan yang linier.
Pembahasan mengenai analisis regresi ini terdiri dari analisis regresi
sederhana dan analisis regresi berganda. Tetapi sebelumnya terlebih dahulu akan
dibahas mengenai sifat variabel bebas dan variabel terikat.
Variabel bebas diasumsikan bersifat tetap karena memiliki nilai yang sama
dalam berbagai sampel. Nilai dari variabel bebas sudah ditentukan sebelumnya oleh
peneliti. Satu variabel bebas dapat menentukan lebih dari satu variabel terikat.
Variabel terikat bersifat random, karena nilainya ditentukan oleh suatu eksperimen
acak.
A. ANALISIS REGRESI LINIER SEDERHANA
Analisis regresi linier sederhana adalah analisis regresi linier di mana nilai
variabel terikat Y hanya dipengaruhi oleh satu variabel penjelas X. Contoh,
pengeluaran keluarga mingguan dipengaruhi oleh pendapatan mingguan keluarga.
Dengan pengetahuan sebelumnya bahwa hubungan X dan Y yang linier
maka dapat dinyatakan dengan persamaan matematik berikut:
0 merupakan intercept atau jarak dari titik O(0,0) dengan titik potong terhadap
sumbu ordinat (sumbu y), 1 adalah slope atau gradient atau kemiringan garis,
merupakan galat atau error. 0 dan 1 merupakan koefisien-koefisien regresi.
Asumsi-asumsi di dalam regresi linier yang harus dipenuhi, yaitu:
1. = 0
Dengan kata-kata bahwa nilai harapan bersyarat terhadap X tertentu
adalah 0. Nilai-nilai Y untuk X tertentu dapat berada di atas maupun di bawah garis
regresi, jarak antara Y dengan nilai harapannya adalah .
2. , = − [ − ]
= ( ) karena asusmsi 1
= 0 ≠
, = 0 berarti pula bahwa dan tidak saling mempengaruhi,
atau tidak berhubungan, atau tidak berkorelasi satu sama lain. Apabila terjadi korelasi
antara yang satu dengan yang lainnya maka akan timbul masalah autokorelasi atau
korelasi berurutan, dan yang dikehendaki oleh asumsi 2 adalah tidak ada masalah
autokorelasi, atau , = 0.
3. = [ − ]2
= [ ]2 karena asumsi 1
Varians bersyarat untuk X tertentu adalah suatu angka konstan positif
yang sama dengan �2. Apa yang diinginkan oleh asumsi ini adalah varians untuk X
tertentu adalah sama. Apabila terjadi pelanggaran terhadap asumsi ini maka akan
muncul masalah heteroskedastisitas, yaitu bilamana varians untuk X tertentu tidak
sama.
4. berdistribusi normal dengan rata-rata 0 dan varians �2, ditulis ~�(0,�2).
Asumsi kenormalan ini penting dalam pengujian hipotesis, pada pengambilan
kesimpulan. Jika berdistribusi normal, maka tidak dapat dilakukan uji F dan uji
t.
Nilai harapan dari terhadap X tertentu adalah :
= ( 0+ 1 + )
= ( 0) + 1 ( ) + ( )
Karena 0 , 1 , bersifat konstan sehingga 0 = 0dan = dan akibat
dari asumsi 1 di mana ( ) = 0 maka:
= 0+ 1 (3.2)
Varians dari adalah :
Var ( ) = [ − ( )]2
= [ 0+ 1 + − 0− 1 )]2
= [ )]2
Akibat dari asumsi 3 di mana [ )]2 =�2 maka;
Var ( ) =�2 (3.3)
Dari (3.2) dan (3.3) dapat dikatakan bahwa regresi linier sederhana dapat dinyatakan
dengan persamaan = 0+ 1 + dengan nilai harapan = 0+ 1
dan varians �2.
Besarnya nilai koefisien-koefisien regresi tidak dapat ditentukan secara
tepat, melainkan merupakan suatu taksiran. Hal ini disebabkan karena tidak mungkin
untuk memperoleh data populasi, namun koefisien-koefisien regresi ini dapat diduga
berdasarkan koefisien-koefisien regresi sampel. Persamaan regresi sampel dinyatakan
sebagai berikut,
= 0+ 1 + (3.4)
Dengan Ý = 0 + 1 (3.5)
Ý= estimator E Y Xi , 0= estimator β0; 1= estimator β1. di sini menunjukan nilai
galat. dinyatakan analog dengan , sehingga dikatakan sebagai estimator .
Garis regresi sampel dapat dihasilkan sebanyak n buah. Dari garis-garis
namun mungkin saja salah satu garis tersebut merupakan garis regresi terbaik yang
mewakili garis regresi yang sesungguhnya.
Untuk mengetahui garis mana yang terbaik yang sesuai dengan garis regresi
yang sesungguhnya, dapat digunakan sebuah metode. Metode ini adalah Metode
Kuadrat Terkecil Biasa atau Ordinary Least Square (OLS) Methode. Metode ini
digunakan untuk menaksir regresi populasi atas dasar regresi sampel seakurat
mungkin, dengan cara mengestimasi β0 dan β1 setepat mungkin.
Metode Kuadrat Terkecil (Ordinary Least Square Methode)
Jika ketiga asumsi di atas dipenuhi maka penaksir OLS memenuhi beberapa
sifat statistik yang diinginkan, yaitu linier, tidak bias dan varians yang minimum.
Penaksir koefisien regresi tetap dapat ditentukan jika ketiga asumsi tidak dipenuhi,
namun penaksir yang diperoleh tidak memiliki sifat statistik yang diinginkan tersebut.
Metode kuadrat terkecil merupakan salah satu metode yang digunakan untuk
mengestimasi β0 dan β1. Dari persamaan = 0+ 1 + , diperoleh;
= Ý + (3.6)
= −Ý
Prinsip dari metode OLS adalah memilih fungsi regresi sampel sedemikian
rupa sehingga jumlah residual (sisa) 2 = ( −Ý )2 sekecil mungkin.
= ( − 0− 1 )2
terhadap 1, dan menyamakan hasilnya dengan nol seperti berikut ini,
� 2 =1 � 1 =
� =1 − 0− 1 2
Dari persamaan (3.7) di mana 0 = =1 − 1 =1 dan disubstitusikan ke persamaan
1 = =1 =1 − =1
Dengan menyelesaikan bagian pembilang persamaan (3.9), didapat:
= 2
Maka dari persamaan (3.10) dan (3.11) diperoleh,
0 = − 1 (3.13)
Menurut Teori Gauss-Markov yaitu estimator OLS merupakan estimator
terbaik jika memiliki sifat linier, tidak bias, dan memiliki varians yang minimum
(best linear unbiased estimator disingkat BLUE). Sifat-sifat tersebut dibuktikan
dengan langkah-langkah berikut:
1. Penaksir-penaksir kuadrat terkecil merupakan fungsi linier dari Y
Terlebih dahulu akan dibuktikan = 0
Dari definisi , di mana = – maka;
= ( – )
= ( – )
= 1+ 2+ + −
= −
= −
= 0 (3.14)
Selanjutnya akan dibuktikan 1 adalah penaksir linier dari Y
Dari persamaan (3.12) di mana 1 = =1
Dari definisi di mana = – , maka
1 = =1 2 =1
= ( 2– )
= ( 2)− 2)
Akibat dari persamaan (3.14) di mana = 0 maka;
= ( 2)− ) 2
= (2) (3.15)
1 = (3.16)
di mana didefinisikan 2 , Jadi terbukti bahwa 1 merupakan fungsi linier dari Y
Akan dibuktikan 0 merupakan fungsi linier dari Y
dari persamaan (3.13) di mana 0 = − 1 , maka;
0 = − 1
= − 1
= − 1
= −
0 = (1− ) (3.17)
Jadi terbukti bahwa 0 merupakan fungsi linier dari Y.
2. Penaksir-penaksir tersebut tidak bias
Sebelumnya akan dibuktikan = 0, = 1, 2 = 12
= 0
Definisi di mana = 2 , maka;
= ( 2)
= 2
Karena dari persamaan (3.14) di mana = 0 , maka;
= 0 (3.18)
= ( + )
= +
Karena dari persamaan (3.18) di mana = 0, maka;
=
Definisi di mana = 2 , maka;
= 22
= 1 (3.19)
Karena = 2 , maka;
2 = (
2)2
= 2 ( 2)
= 22 ( 12)
= 22 ( 12)
2 = 1
2 (3.20)
Bentuk lain dari 0 yaitu;
Dari persamaan (3.17) di mana 0 = (1− ) , maka
0 = (1− )
substitusi persamaan (3.1) di mana = 0+ 1 +
0 = 1− ( 0+ 1 + )
= 1 0+ 1 + − ( 0+ 1 + )
= 0+ 1 + − 0 − 1 −
Dari persamaan (3.18) di mana = 0 dan persamaan (3.19) di mana = 1 ,
maka;
0= 0+ − (3.21)
Selanjutnya akan dibuktikan 0 = 0
substitusi persamaan (3.21) di mana 0= 0+ − ,
0 = 0 + −
= 0 +1 ( )− ( )
Karena asumsi 1 di mana = 0, maka;
= 0 +1 ( )− ( )
0 = 0 (3.22)
Jadi terbukti bahwa 0 = 0
Bentuk lain dari 1 adalah;
Dari persamaan (3.16), di mana 1 = , maka;
1 =
Substitusi dengan persamaan (3.1) di mana = 0+ 1 +
1 = ( 0+ 1 + )
= 0 + 1 +
Karena persamaan (3.18) di mana = 0 dan persamaan (3.19) di mana =
1, maka;
1 = 1+ (3.23)
Akan dibuktikan 1 = 1
Substitusi persamaan (3.23) di mana 1 = 1 +
= 1 + ( )
Karena asumsi 1 di mana ( ) = 0, maka;
1 = 1 (3.24)
3. Penaksir-penaksir tersebut memiliki varian yang minimum
Sebelumnya akan ditentukan terlebih dahulu varians 1 dan varians 0 . Dari
persamaan (3.24) di mana 1 = 1 , maka;
Var 1 = ( 1− ( 1))2
= ( 1− 1)2
Substitusi persamaan (3.23) di mana 1 = 1 +
= ( 1 − 1)2
= ( 1 + − 1)2
= ( )2
= ( 12 12 + 22 22+ + 2 1 2 1 2 + + 2 −1 −1 )
= ( 2 2+ 2 )
= 2 2 + 2 ( )
dari asumsi 3 di mana 2 = �2 dan asumsi 2 di mana = 0
= 2�2
Dari persamaan (3.20) di mana 2 = 12 , maka;
Var 1 =�2 12 (3.25)
Dari persamaan (3.22) di mana 0 = 0 , maka;
= �2(
2−2( )2 +2( )2
2 )
Var ( 0) =�2(
2
2) (3.26)
Untuk menentukan varians 0 dan 1 minimum perlu dibandingkan dengan
varians dari beberapa penaksir * yang tidak bias. Dimisalkan 1* = di mana
≠ tetapi = + , sehingga
1* = ( 0+ 1 + )
= ( 0+ 1 + )
= 0 + 1 +
( 1*) = 0 + 1 + ( )
Karena asumsi 1 di mana ( ) = 0 , maka;
( 1*) = 0 + 1 + ( )
= 0 + 1 (3.27)
Karena * penaksir yang tidak bias, maka pada persamaan (3.18) = 0
dan = 1, dan diketahui = + , maka,
= +
= +
Karena pada persamaan (3.18) = 0, maka haruslah = 0
= ( + )
= +
Karena pada persamaan (3,19) = 1 ,maka haruslah
Selanjutnya akan dibuktikan 1 memiliki varians yang minimum.
Bukti :
Var ( 1*)= [ 1∗− 1 2]
= [( )2]
= �2 2
= �2 ( + )2
= �2( 2 + 2 + 2 )
= �2( 2 + 2 + 2 2)
karena = = 0
Var ( 1∗) =�2( 2+ 2)
Var ( 1*) =�2 2 +�2 2
Dari persamaan (3.25) di mana Var 1 =�2 12
Var ( 1*)=�2 2 +�2 2
= var ( 1)+ �2 2 (3.28)
Oleh karena 2 selalu positif, maka Var ( 1*) > var ( 1), hanya apabila 2 = 0
maka Var ( 1*) = var ( 1). Hal ini menunjukan bahwa 1 memiliki varians yang
minimum.
Selanjutnya Akan dibuktikan bahwa 0 memiliki varians yang minimum, namun
sebelumnya akan dilakakan langkah-langkah berikut ini,
Dimisalkan 0∗ = (1− )
0∗ = (1− ) 0+ 1 +
0∗ = 0(1− ) + 1( − ) + (
1
− )
( 0∗) = 0(1− ) + 1( − ) + ( − )
( 0∗) = 0(1− ) + 1 ( − ) + ( )−
Karena asumsi 1 di mana = 0 , maka;
( 0∗) = 0(1− ) + 1 ( − ) + ( )−
( 0∗) = 0(1− ) + 1 ( − )−
Agar ( 0∗) = 0 maka = 0, = 1, dan = 0, diketahui = +
sehingga = 0 dan = 0.
Akan dibuktikan 0 memiliki varians yang minimum
Var ( 0∗) = [ 0∗− ( 0∗ ]2
Dari persamaan (3.21) di mana 0 = 0, maka;
Var ( 0∗) = [ 0∗− 0 ]2
= ( [(1− ) ]2
= �2 (1− )2
= �2 ( 1
2+ 2 2−2 1
)
= �2 (1+ 2 2 −2 )
karena definisi = + dan = 0, maka ;
= �2 (1+ 2 ( + )2)
= �2 (1+ 2 2+ 2 2)
= �2 (1+ 2 2+ 2 2)
= �2 (1+ 2 2) +�2 2 2
= �2 1+ 2 1
2 +�2 2 2
Dari proses persamaan (3.26) di mana Var ( 0) =�2 1+ 2 12 , maka;
= var ( 0) +�2 2 2 (3.29)
Oleh karena 2 selalu positif, maka Var ( 0*) > var ( 0), hanya apabila 2 = 0
maka Var ( 0*) = var ( 0). Hal ini menunjukan bahwa 0 memiliki varians yang
minimum.
Data yang ada di dalam statistika cenderung berubah-ubah dari satu sampel
ke sampel lainnya, maka estimasi akan berubah dengan sendirinya (ipso facto),
karena hal tersebut diperlukan sebuah keakuratan dari sebuah estimator. Keakuratan
sebuah estimator tersebut diukur berdasarkan standar error-nya. Standar error adalah
sebuah alat ukur keakuratan estimator. Standar error dapat dicari dengan cara sebagai
berikut;
0 = � ( 0) (3.30)
Di mana Var ( 0) = �2(
2
2) (dari persamaan (3.26)), sehingga persamaan (3.30)
0 = �2( 2
2)
0 = � ( 2
2) (3.31)
1 = � ( 1) (3.32)
Di mana Var 1 = �2 12 ( dari persamaan (3.25)), sehingga persamaan (3.32)
menjadi,
1 = �2 1
2
1 =� 12 (3.33)
Di mana adalah standar error dan � adalah varians. Standar error tidak lain
adalah standar deviasi sebuah distribusi sampling dari sebuah estimator.
Kebaikan suatu garis regresi diukur dengan koefisien determinasi. Koefisien
determinasi adalah ukuran ikhtisar yang mengatakan seberapa baik garis regresi
sampel mencocokan data. Koefisien determinasi untuk kasus dua variabel
dilambangkan dengan 2 sedangkan untuk regresi berganda dilambangkan dengan
2.
Sebelum membahas lebih jauh mengenai koefisien determinasi, terlebih
merupakan bentuk alternatif di mana baik X maupun Y dinyatakan sebagai
simpangan dari nilai rata-ratanya.
= 0+ 1 + (3.4)
Kedua ruas dijumlahkan
= 0 + 1 +
karena = 0, maka
= 0 + 1 +
= 0+ 1
kedua ruas dibagi dengan n
= 0+ 1
= 0+ 1 (3.34)
Dengan mengurangkan (3.34) dengan (3.4), diperoleh,
− = ( 0+ 1 + )− 0+ 1
− = 1 − +
dari definisi dan di mana = − dan = − , sehingga;
− = 1 − +
= 1 + (3.35)
Sehingga
= − 1 (3.36)
Persamaan (3.34) ini merupakan persamaan dalam bentuk simpangan.
Ý = 0+ 1 (3.5)
Ý = 0+ 1
Kedua ruas dibagi dengan n
Ý
= 0+ 1
Ý= 0+ 1 (3.37)
Dengan mengurangkan (3.37) dengan (3.5) diperoleh;
Ý−Ý= ( 0+ 1 )− 0+ 1
Ý−Ý= 1 − (3.38)
didefinisikan Ý−Ý, dan dari definisi di mana = − ,sehingga persamaan
(3.37) menjadi:
= 1 (3.39)
akan dibuktikan = 0
= 1 (3.40)
kedua ruas dikalikan dengan
= 1
= 1
kedua ruas dijumlahkan
= 1
Substitusi persamaan (3.36) di mana = − 1
= 1
= 1 ( − 1 )
= 1
Untuk menghitung 2 dilakukan langkah-langkah berikut ini:
Di mana 2 = ( − )2 adalah variasi total dari nilai Y nyata untuk
rerata sampelnya yang dapat juga dinamakan total jumlah kuadrat( total sum of
squares-TSS). 2 = (Ý−Ý)2= (Ý− )2 = 12 2 adalah penjelasan atas
jumlah kuadrat (explained sum of squares-ESS). 2 adalah residual atau variasi
nilai Y yang tidak terjelaskan di sekitar garis regresi, lebih dikenal RSS, sehingga
persamaan (3.42) dapat ditulis:
TSS = ESS + RSS (3.43)
2 didefinisikan sebagai berikut:
2 =
= 12 2
2 (3.44)
Dari persamaan (3.42) di mana 2= 12 2+ 2 maka, 12 2 = 2−
2
Sehingga,
= 12 2 2
= 2− 2 2
= 22− 2
2
2 = 1− 2
2 (3.45)
atau dalam bentuk lain sebagai berikut;
Dari persamaan (3.45), jika taksiran memiliki ketepatan sempurna, maka:
Nilai 2 = 1 menunjukan ketepatan terbaik ( best fit). Jika garis regresi sampel adalah
garis horizontal ( 1 = 0) maka;
2 =
12 2 + 2 (3.49)
= 0 + 2
2 = 2 (3.50)
Akibat dari persamaan (3.50) adalah