KARAKTERISTIK HAZARD RATE PADA DISTRIBUSI GOMPERTZ

ABSTRAK

KARAKTERISTIK HAZARD RATE PADA DISTRIBUSI GOMPERTZ

Oleh

Andri Antoro

Waktu kelangsungan hidup adalah data yang mengukur waktu untuk kejadian tertentu seperti kematian, kegagalan, sembuhnya dari suatu penyakit tertentu dan sebagainya. Distribusi dari waktu kelangsungan hidup digolongkan oleh tiga fungsi yakni Fungsi Kelangsungan Hidup, Fungsi Kepekatan Peluang (fkp), dan Fungsi Kegagalan (Hazard). Dari ketiganya dapat dikaji bentuk Hazard Rate distribusi Gompertz. Distribusi Gompertz hanya mempunyai 1 bentuk hazard rate yakni meningkat (increasing).

KARAKTERISTIK HAZARD RATE PADA DISTRIBUSI GOMPERTZ

Skripsi

Sebagai Salah Satu Syarat Untuk Mencapai Gelar SARJANA SAINS

Pada

Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

BANDAR LAMPUNG 2015

RIWAYAT HIDUP

Penulis dilahirkan pada 3 Oktober 1990 di Bandar Lampung dan adalah anak

kedua dari tiga bersaudara, dari pasangan Bapak Mamik dan Ibu Saodah.

Penulis memulai pendidikan dari TK Handayani Tanjung Karang Barat pada

tahun 1995. Kemudian pendidikan sekolah dasar diselesaikan di SD Negeri 2

Gedong Air Bandar Lampung pada tahun 2002, sekolah lanjutan tingkat

menengah di SLTP Negeri 7 Bandar Lampung pada tahun 2005, dan sekolah

lanjutan tingkat atas di SMA Negeri 7 Bandar Lampung pada tahun 2008.

Tahun 2008 penulis terdaftar sebagai mahasiswa Jurusan Matematika Fakultas

MIPA Universitas Lampung melalui jalur PKAB. Selama menjadi mahasiswa

penulis pernah menjadi anggota Bidang Keilmuan di HIMATIKA selama dua

periode yaitu periode 2009-2010 dan 2010-2011. Sebagai bentuk aplikasi bidang

ilmu kepada masyarakat, penulis telah menyelesaikan mata kuliah wajib Kuliah

Kerja Nyata yang dilaksanakan pada 01 Juli 2011 – 10 Agustus 2011 di Desa Liman Benawi, Lampung Tengah serta Kerja Praktik di Dinas Pendidikan Kota

Bandar Lampung selama 13 - 27 Juni 2011 dan mendapatkan kesempatan

bergabung dalam organisasi pemuda internasional AIESEC sebagai anggota

“Be the change that you wish to see in the world” (Mahatma Gandhi)

“If you believe you can achieve”

“Don’t cry because it’s over, smile because it happened” (Dr. Seuss)

“Bila anda berani mimpi tentang sukses berarti anda sudah memegang kunci kesuksesan hanya tinggal berusaha mencari lubang kuncinya untuk membuka

gerbang kesuksesan” (John Savique Capone)

PERSEMBAHAN

Aku persembahkan karya sederhana ini untuk kedua orang tua ku serta semua

orang yang telah mendukung dan dengan tulus mendoakan kelancaran terciptanya

karya sederhana ini, terima kasih atas segala bentuk cinta dan kasih sayang kalian.

Ayah, Mama serta kakak dan adik perempuan saya Iin dan Iis. Terima kasih atas cinta yang melimpah, do’a yang tulus, nasehat, semangat serta kesabaran yang

kalian berikan dalam mengiringiku meraih kesuksesan.

Keluarga, sahabat, dan teman-teman yang senantiasa memberikan semangat dan

dukungan dalam menyelesaian skripsi ini. Semoga memberi manfaat yang tidak

SANWACANA

Alhamdulillahi robbil ‘alamin, puji dan syukur penulis kepada Allah SWT atas

izin ridho-Nya dalam menyelesaikan skripsi ini. Shalawat juga salam atas Nabi

Muhammad SAW, tuntunan dan tauladan utama.

Pada proses penyusunan skripsi ini, penulis memperoleh banyak dukungan, kritik,

dan saran yang membangun sehingga skripsi ini mampu penulis selesaikan. Untuk

itu penulis ingin mengucapkan terima kasih kepada :

1. Bapak Warsono, Ph.D., selaku dosen pembimbing utama yang telah

meluangkan waktu dari padatnya kesibukan beliau untuk membimbing dan

mengoreksi, hingga skripsi ini selesai.

2. Bapak Drs. Rudi Ruswandi, M.Si., selaku dosen pembimbing pembantu yang

telah banyak membantu dan selalu sabar memberikan pengarahan dalam

proses penyusunan skripsi ini.

3. Ibu Dian Kurniasari, S.Si., M.Sc., selaku dosen penguji bukan pembimbing

yang memberi penulis masukan dan saran.

4. Bapak Drs. Mustofa Usman, M.A.,Ph.D., selaku pembimbing akademik.

5. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D., selaku Ketua Jurusan Matematika

FMIPA Universitas Lampung.

x 7. Dosen, staf dan karyawan Jurusan Matematika FMIPA UNILA yang telah

memberikan ilmu pengetahuan dan bantuan kepada penulis.

8. Ayah, Mama, Mba Iin, Dek Iis dan Kak Hadi yang telah memberikan

dukungan secara finansial dan moril, mengirimkan doa, nasihat dan semangat

yang sangat membantu selama penyusunan skripsi.

9. Teman-teman seperjuangan Matematika ‘08 Wiwid, Achi, Noven, Edo,

Yayat, Ida, Selvi, Mia, Wiwik, Rendy, Recan serta teman – teman Exotic

lainnya, terimakasih atas saran, dukungan dan semangat kebersamaannya.

10. My best mate Alec Storey, thanks for your support bud!

11. Angga, Ben, Feriza, Winnie dan teman-teman Toshihiro Brothers, terima

kasih buat dukungan dan semangatnya kepada penulis.

12. Adik-adik tingkat Matematika Angkatan 2009, terima kasih untuk masukan

dan bantuannya kepada penulis.

13. Semua pihak yang telah membantu selama ini, yang tidak dapat disebutkan

satu persatu.

Bandar Lampung, Agustus 2015 Penulis

xi

2.4 Fungsi Distribusi Waktu Kegagalan ... 7

2.5 Fungsi Kelangsungan Hidup (Fungsi Survival)... 8

2.6 Fungsi Hazard ... 8

2.7 Aturan Glaser ... 11

2.8 Distribusi Gompertz ... 12

III. METODOLOGI PENELITIAN 3.1 Langkah-langkah Penelitian ... 16

3.1.1 Algoritma (Diagram Alir) Penelitian ... 17

3.1.2 Turunan Pertama dari Fungsi Kepekatan Gompertz ... 18

3.1.3 Nilai � � dan Turunan Pertamanya (�′ � ) ... 19

3.1.3.1Nilai � � ... 19

3.1.3.2Turunan Pertama Nilai (� � ) ... 20

3.1.4 Fungsi Kelangsungan Hidup Distribusi Gompertz ... 20

3.1.5 Karakteristik Fungsi Hazard Distribusi Gompertz ... 22

IV. HASIL DAN PEMBAHASAN 4.1 Analisis Bentuk Hazard Distribusi Gompertz ... 24

xii

V. KESIMPULAN

DAFTAR PUSTAKA

I. PENDAHULUAN

1.1 Latar Belakang

Analisis kelangsungan hidup adalah analisis mengenai data yang diperoleh dari

catatan waktu yang dicapai suatu objek sampai terjadinya peristiwa gagal (failure

event) dengan tujuan utamanya adalah menganalisis peluang waktu hidup. Dalam

menentukan waktu kelangsungan hidup, terdapat tiga hal yang harus diperhatikan

yaitu waktu awal (time origin), definisi failure time yang harus jelas, dan skala

waktu sebagai satuan pengukuran

Misalkan T adalah peubah acak waktu kelangsungan hidup yang mempunyai

fungsi kepekatan peluang f(t) dan fungsi distribusi kumulatif F(t). Dengan

� � = �( <�) yang merupakan peluang terjadinya kegagalan (kematian) atau

peluang hidup sampai dengan t. Jika T adalah peubah acak yang menunjukkan

waktu untuk mati atau gagal (waktu kegagalan), maka fungsi kelangsungan hidup

(survival) pada saat t adalah � =�( >�) yang merupakan peluang hidup

melebihi waktu t dengan � ∈[0,∞) dan jangkauan peluang � ∈[0,1].

Distribusi kumulatif untuk fungsi kegagalan F(t) adalah komplemen S(t) sehingga

� +� � = 1. Diasumsikan bahwa � 0 = 0 sehingga 0 = 1 yang berarti

2

Hal terpenting yang berkaitan dengan analisis data kelangsungan hidup adalah

tingkat kematian (kegagalan) pada suatu sistem atau individu, yang dinyatakan

sebagai fungsi hazard yaitu peluang bahwa suatu sistem atau individu akan gagal

atau mati pada saat �+∆�. Bersyarat bahwa sistem atau objek yang diamati masih

hidup pada saat t. Fungsi hazard ini menyatakan peluang mati sesaat (laju

kegagalan sesaat) suatu individu atau sistem yang masih hidup pada waktu t.

Pada saat sebuah model distribusi peluang untuk masa hidup telah ditentukan

dalam bentuk fungsi kepekatan peluang, fungsi kelangsungan hidup dan fungsi

hazard yang sesuai dapat dihasilkan dari hubungan � = 1− � � = 1−

Dalam menganalisis data kelangsungan hidup suatu individu atau sistem langkah

penting yang harus diperhatikan adalah menentukan model peluang, hal ini

dilakukan untuk melihat apakah model sesuai dengan keadaan data. Dan

kelengkapan lain yang juga harus diperhatikan yaitu laju kegagalan (hazard rate).

Laju kegagalan (hazard rate) adalah peluang suatu sistem pada umur t akan gagal

dalam interval (t, t+Δt). Atau dalam istilah lain, laju kegagalan (hazard rate)

adalah perbandingan dari fungsi kepekatan peluang (fkp) terhadap fungsi

3

(I)) dimana kurva yang terbentuk akan meningkat secara monoton, menurun

(decreasing (D)) dengan bentuk kurva menurun secara monoton, bathtub ( ),

upside-down bathtub ( ), dan konstan.

Tidak semua model peluang memiliki bentuk-bentuk hazard rate seperti yang

dijelaskan di atas. Demikian pula dengan distribusi Gompertz, itulah sebabnya

sangat menarik untuk meneliti karakteristik bentuk fungsi hazard rate dengan

distribusi Gompertz.

Mengingat pentingnya hazard rate dalam pengepasan model peluang dan

keistimewaan distribusi Gompertz, maka dalam penelitian ini akan dikaji

mengenai karakteristik hazard rate dari distribusi Gompertz dengan parameter �,

dan parameter bentuk �.

1.3 Tujuan Penelitian

Tujuan penelitian ini adalah sebagai berikut :

a. Mendapatkan fungsi kelangsungan hidup distribusi Gompertz dan fungsi

hazard distribusi Gompertz.

b. Mengkaji karakteristik hazard rate dalam bentuk increasing, decreasing,

bathtub, upside-down bathtub atau konstan yang akan terjadi pada distribusi

Gompertz.

II. LANDASAN TEORI

2.1Peubah Acak

Suatu percobaan yang dapat diulang pada kondisi yang sama dan hasil dari

percobaan tersebut tidak diketahui secara pasti sebelum percobaan itu dilakukan

disebut sebagai Percobaan Acak. Dalam percobaan acak akan menghasilkan suatu

peubah acak yang dapat disajikan dalam ruang sampel. Ada dua macam peubah,

yaitu kuantitatif dan kualitatif. Pengamatan yang berasal dari peubah kuantitatif

dapat diklasifikasikan atas kontinu dan diskrit.

Definisi 2.1 Peubah Acak dan Ruang Sampel

Peubah acak adalah suatu fungsi yang nilainya berupa bilangan nyata yang

ditentukan oleh setiap unsur dalam ruang sampel yang memetakkan setiap elemen

∈ � dengan satu dan hanya satu bilangan real � = � (Hogg & Craigg,

1986).

Ruang sampel didefinisikan sebagai himpunan dari semua gugusyang

unsur-unsurnya terdiri atas semua kemungkinan hasil percobaan, dan dilambangkan

dengan huruf C (Walpole, 1995).

Definisi 2.2 Peubah Kuantitatif dan Peubah Kualitatif

Peubah kuantitatif adalah peubah yang pengamatannya dapat diukur, sebab

5

yang tidak memungkinkan dilakukannya pengukuran numerik. Pada peubah

kualitatif pengamatannya berupa memasukkan suatu individu ke dalam satu dari

beberapa kategori yang saling terpisah. Pengamatan-pengamatan tersebut tidak

dapat diurutkan secara berarti ataupun diukur, hanya diklasifikasikan dan

kemudian dicacah (Steel & Torrie, 1995).

Definisi 2.3 Ruang Sampel Diskrit dan Peubah Acak Diskrit

Bila suatu ruang sampel mengandung jumlah titik sampel yang terhingga atau

suatu barisan unsur yang tidak pernah berakhir tetapi yang sama banyaknya

dengan bilangan cacah, maka disebut Ruang Sampel Diskrit (Walpole, 1995).

Pandang peubah acak X, dengan ruang sampel berdimensi satu C, C merupakan

himpunan titik-titik, sehingga setiap selang hingga mengandung berhingga

banyaknya titik C.

Misalkan ada fungsi (�) yang memenuhi :

1. � 0,∀� ∈ �

2. � = 1

3. Untuk � ⊂ �, berlaku � � = Pr ��� = (�)

maka X disebut Peubah Acak diskrit dan (�) disebut fungsi peluang dari X

(Hoog & Craigg, 1986).

Definisi 2.3 Ruang Sampel Kontinu dan Peubah Acak Kontinu

Bila suatu ruang sampel mengandung tak hingga banyaknya titik sampel yang

6

Sampel Kontinu (Walpole, 1995). Pandang peubah acak X, dengan sampel

berdimensi satu C yang kontinu, misalkan ada fungsi (�) yang memenuhi :

1. � 0,∀� ∈ �

2. � = 1

3. Untuk � ⊂ �, berlaku � � = Pr ��� = (�)

maka X disebut Peubah Acak Kontinu dan (�) disebut fungsi peluang dari X

(Hoog & Craigg, 1986).

2.2Analisis Survival

Analisis survival adalah analisis mengenai data yang diperoleh dari catatan waktu

yang dicapai suatu objek sampai terjadinya peristiwa gagal (failure event). Dalam

menentukan waktu survival, T, terdapat tiga elemen yang harus diperhatikan yaitu

waktu awal (time origin), definisi failure time yang harus jelas, dan skala waktu

sebagai satuan pengukuran.

2.3Fungsi Kepekatan Peluang

Menurut Elisa T Lee (1920), seperti beberapa peubah acak kontinu lainnya, waktu

kelangsungan hidup T mempunyai fungsi kepekatan peluang (f.k.p) didefinisikan

sebagai limit dari peluang suatu individu yang gagal dalam interval pendek t ke

+∆ per satuan lebar ∆ , atau peluang kegagalan dalam interval kecil per

satuan waktu. Itu dapat dijelaskan sebagai:

= lim_∆t→0�( < < +∆)

∆ (2.1)

adalah fungsi non negatif , yaitu

7

= 0 untuk < 0

2.4Fungsi Distribusi Waktu Kegagalan

Misalkan T adalah peubah acak kontinu yang menyatakan waktu kegagalan

dimana T diasumsikan saling bebas yang didefinisikan pada interval waktu (0,∞)

Fungsi distribusi waktu kegagalan didefinisikan sebagai :

� = Pr = � �₀ (2.2)

Fungsi distribusi kumulatif ini menyatakan peluang suatu sistem yang mengalami

kegagalan hingga batas waktu t. Sifat-sifat dari fungsi distribusi :

a) 0 � ( ) 1 karena 0 Pr⁡{ } 1

Bukti : Misalkan ∈ Σ dengan Σ adalah ruang kejadian (event space) dari

himpunan semua kejadian (outcomes) yang mungkin terjadi (�), maka:

→ ∅ Ω, dengan Ω adalah ruang sampel dari �

→0 Pr⁡( ) 1∎

b) � ( ) fungsi tidak turun (non decreasing)

Bukti : Misalkan F adalah suatu fungsi yang bernilai real pada interval

[0,∞). Fungsi F disebut fungsi non decreasing pada interval [0,∞), jika

untuk sebarang titik ₁ dan ₂ pada interval [0,∞), dimana ₁ < ₂ maka

� ( 1) � ( 2)∎

c) � ∞ = lim_{∆ →}0� = 1 dan � −∞ = lim∆ →0� = 0

Bukti : � ∞ = 1 dan � −∞ = 0 karena { ∶ ∞} adalah seluruh

8

2.5Fungsi Kelangsungan Hidup (Fungsi Survival)

Menurut Elisa T. Lee (1920), fungsi kelangsungan hidup (fungsi survival)

dinotasikan dengan � didefinisikan sebagai peluang suatu individu yang

bertahan lebih dari t:

� = � (suatu individu bertahan lebih dari t)

=� > = ∞ � � (2.3)

Dari definisi fungsi distribusi kumulatif � , maka

� = 1− � ( > )

= 1− �( ) (2.4)

Dengan � adalah fungsi tidak naik (non increasing) yaitu suatu fungsi yang

bernilai real, jika untuk sebarang titik ₁ dan ₂ pada interval [0,∞) dengan

1 2 maka �( 1) �( 2). Jadi dapat disimpulkan bahwa

� 0 = 0 dan � ∞ = 1

Akan ekuivalen terhadap

� ∞ = 0dan � 0 = 1

2.6Fungsi Hazard

Menurut Elisa T Lee (1920), fungsi hazard ℎ dari waktu kelangsungan hidup T

tergantung pada failure rate. Ini didefinisikan sebagai peluang gagal selama

interval waktu yang sangat kecil, diasumsikan bahwa individu memiliki hidup

yang lebih lama untuk awal dari interval, atau sebagai limit dari peluang individu

9

fungsi hazard kumulatif didefinisikan sebagai :

� = ℎ � �₀ (2.6)

Dari persamaan (2.4) dan (2.5), maka diperoleh

ℎ = ( )

�( ) (2.7)

adalah turunan dari fungsi kumulatif distribusi, maka:

= � = 1− � =− �( ) (2.8)

Maka dari persamaan (2.8) dapat diperoleh :

10

Dan diperoleh persamaan untuk fungsi kelangsungan hidup, yaitu:

� = �� −�( ) = �� − ℎ � �₀ (2.11)

dari persamaan (2.6) dan persamaan (2.10) maka diperoleh :

= ℎ �� − ℎ � �₀ ; 0 (2.12)

(Elisa T. Lee, 1992).

Dari persamaan (2.5) telah kita ketahui bahwa ℎ =_�( )

( ), kemudian untuk

mengetahui karakteristik fungsi hazardnya h(t) diturunkan terhadap t sehingga:

ℎ( )

turun atau konstan maka langkah selanjutnya adalah membuat ℎ( )= 0

11

Dari persamaan di atas sekarang dapat diketahui bahwa sebuah distribusi akan

1. Memiliki laju hazard naik (increasing) jika 2

Syarat cukup sebuah fungsi kepekatan bukan merupakan suatu kondisi yang

diperlukan untuk menentukan karakteristik laju hazardnya.

2.7 Aturan Glaser

Untuk melihat bagaimana laju hazard yang dipengaruhi oleh kombinasi dari

nilai-nilai parameter maka Glaser (1980) membuat metode untuk menentukan bentuk

laju hazard dengan satu turning point (titik belok). Dalam metodenya, Glaser

menggunakan fungsi kepekatan peluang. Titik belok (turning point) dari suatu

fungsi adalah suatu titik maksimum atau minimum dalam suatu fungsi atau kurva

dan didefinisikan sebagai berikut :

�

=

−

′ �

� (2.13)

Fungsi eta ini memiliki peranan penting dalam mengkaji fungsi dan bentuk laju

hazard. Aturan Glaser (1980) sendiri adalah sebagai berikut :

1. Jika ′ � > 0 untuk semua �> 0 maka Increasing (I)

2. Jika ′ � < 0 untuk semua �> 0 maka Decreasing (D)

3. Misalkan terdapat �0 > 0 sehingga ′(�0) < 0 untuk semua � ∈ 0,�0 ,

12

a. Jika lim_�→0 � = 0, maka Increasing (I)

b. Jika lim_�→0 � →∞, maka Bathtub ( )

4. Misalkan terdapat �0 > 0 sehingga ′ �0 > 0 untuk semua � ∈ 0,�0 ,

′ _{�0 = 0 ,} ′_{(�0) < 0 untuk semua �> �0 dan}

a. Jika lim_�→0 � = 0, maka Upside-down Bathtub ( )

b. Jika lim_�→0 � →∞, maka Decreasing (D)

2.8 Distribusi Gompertz

Distribusi Gompertz secara luas dipakai untuk menggambarkan suatu pola

kematian pada manusia. Distribusi Gompertz memiliki fungsi kepekatan peluang

dengan parameter lokasi dan parameter bentuk �,

� = �� −� ��−1 ; ,� > 0 ,� 0 (2.14)

13

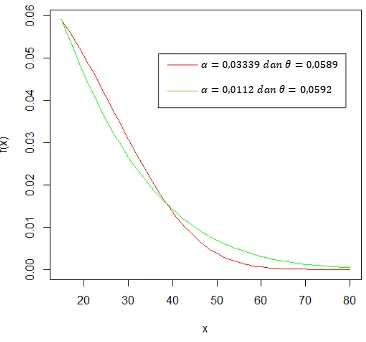
Berikut merupakan grafik fungsi kepekatan peluang distribusi Gompertz

Gambar 2.1 Grafik Fungsi Kepekatan Peluang Distribusi Gompertz

Fungsi distributif kumulatif Gompertz didapatkan dari pengintegralan fungsi

kepekatan peluang Gompertz, maka fungsi distributif kumulatif Gompertz adalah

sebagai berikut

� � = 1− −�( ��−1) (2.15)

�= 0,03339 �� = 0,0589

14

Dan berikut grafik fungsi distributif kumulatif Gompertz

Gambar 2. Grafik Fungsi Distribusi Kumulatif Gompertz

Dari fungsi distribusi kumulatif di atas maka didapatkan bentuk fungsi survival

sebagai berikut

� � = 1− � �

= 1−(1− −� ��−1 )

= −� ��−1 (2.16)

�= 0,03339 �� = 0,0589

15

Setelah fungsi kelangsungan hidup distribusi Gompertz didapatkan, maka

selanjutnya mencari fungsi hazard dari distribusi Gompertz.

ℎ �

=

(�)

�(�)

=

�� −� �� −

1

−� �� −1

=

�� −�

�� −1

−� �� −1

=

III. METODOLOGI PENELITIAN

3.1 Langkah-langkah Penelitian

Untuk melihat karakteristik laju hazard distribusi Gompertz dalam penelitian ini

peneliti menggunkan aturan Glaser (1980). Adapun lagkah-langkah yang

dilakukan dalam menyelidiki laju hazard distribusi Gompertz ini adalah sebagai

berikut :

1. Menentukan turunan pertama dari fungsi kepekatan distribusi Gompertz.

2. Menentukan nilai

�

=

−

′_(�)

(�) dan turunan pertamanya.

3. Menentukan fungsi kelangsungan hidup dari distribusi Gompertz.

4. Menentukani fungsi hazard dari distribusi Gompertz.

5. Melakukan analisis fungsi hazard dengan menggunakan aturan Glaser.

6. Membuat grafik fungsi hazard dari distribusi Gompertz dengan

17

3.1.1 Algoritma (Diagram Alir) Penelitian

Berikut ini merupakan langkah-langkah yang dilakukan dalam menyelidiki laju

hazard distribusi Gompertz yang digambarkan dalam diagram alir.

Gambar 3.1 Diagram Alir Penelitian

Mencari nilai � dan ′ �

Mencari nilai �(�)

Mencari nilai ℎ(�)

Analisis fungsi ℎ(�) dengan aturan Glaser

Membuat grafik fungsi hazard ℎ(�) Mencari nilai ′(�)

Mulai

18

3.1.2 Turunan Pertama Dari Fungsi Kepekatan Gompertz

Sebelum melakukan analisis laju hazard langkah awal yang harus dilakukan

adalah mencari turunan pertama dari fungsi kepekatan peluang distribusi

Gompertz. Turunan pertama dari fungsi kepekatan peluang distribusi Gompertz

adalah sebagai berikut:

� = �� −� ��−1

� = �� −� ��

+_�

� � ∶ =�� −

� �� −�

� = � − ��

′ _{� =}

�( )

′ _{� =} �� −_� ��+� _{� − ��}

′ _{� = � −} �� �� −_� ��+�

′ _{� = � −} 2 �� �� −_� ��+�

19

3.1.3 Nilai �(�) dan Turunan Pertamanya (�′(�))

Untuk melihat bagaimana laju hazard yang dipengaruhi oleh kombinasi dari

nilai-nilai parameter maka Glaser (1980) membuat metode untuk menentukan bentuk

laju hazard dengan satu turning point (titik belok). Dalam metodenya, Glaser

menggunakan fungsi kepekatan peluang. Titik belok (turning point) dari suatu

fungsi adalah suatu titik maksimum atau minimum dalam suatu fungsi atau kurva

dan dilambangkan dengan � .

hazardnya harus sama dengan nol. Ini berarti persamaan (3.2) dibuat sama dengan

nol sehingga diperoleh

20

kemiringan positif ini bukan berarti fkp tersebut memenuhi kondisi laju hazard

meningkat. Oleh karena itu langkah selanjutnya adalah mencari nilai dari � .

� = −

selanjutnya adalah mencari turunan pertama dari � .

3.1.3.2 Turunan Pertama Nilai �(�)

Turunan pertaman dari � pada distribusi Gompertz adalah:

′ _{� =}

� (�)

=

� �� − �

= � �� (3.4)

3.1.4 Fungsi Kelangsungan Hidup Distribusi Gompertz

Sebelum mencari fungsi kelangsungan hidup, langkah pertama yang harus

dilakukan adalah mencari fungsi distribusi kumulatif. Fungsi distribusi kumulatif

distribusi Gompertz adalah sebagai berikut:

22

Setelah mendapatkan fungsi distribusi kumulatif distribusi Gompertz, maka

langkah selanjutnya adalah mencari fungsi kelangungan hidup dari distribusi

Gompertz, yang dituliskan sebagai berikut:

� � = 1− � �

= 1−(1− −� ��−1 )

= −� ��−1 (3.6)

Setelah fungsi kelangsungan hidup distribusi Gompertz didapatkan, maka

selanjutnya mencari fungsi hazard dari distribusi Gompertz.

ℎ � =_�(�)

(�)

= �� −� ��₋₁

−� ��₋₁

= �� −� ��₋₁

−� ��₋₁

= �� (3.7)

3.1.5 Karakteristik fungsi hazard distribusi Gompertz

Menurut McDonald dan Richard (1987) bahwa pola dari laju hazard dapat diduga

oleh ′ � = 0 dan tanda dari koefisien-koefisiennya. Dari persamaan (3.4) yaitu:

23

Kemudian untuk melihat karakteristik laju hazard-nya digunakan ′ � = 0, hal

ini dikarenakan dengan menurunkan suatu fungsi dan membuatnya sama dengan

nol maka akan diketahui titik-titik kritis fungsi tersebut. Sehingga dapat dilihat

bentuk naik (Increasing) dan turunnya (Decreasing) fungsi hazard dan bentuk

kecekungan laju hazard-nya yang dalam hal ini bila cekung ke atas dikatakan

bathtub dan bila cekung ke bawah dikatakan upside-down bathtub.

′ _{� = �} �� _{= 0}

Dari persamaan di atas didapatkan koefisien konstanta sebagai berikut :

V. KESIMPULAN

Berdasarkan hasil dari penelitian yang telah dilakukan, maka dapat ditarik

kesimpulan sebagai berikut :

1. Karakteristik hazard rate dari distribusi Gompertz yang telah dianalisis

berdasarkan aturan Glaser berbentuk increasing.

2. Hazard rate dari distribusi Gompertz dengan �, � > 0 akan meningkat

(increasing) secara eksponensial.

3. Secara grafis, karakteristik hazard rate distribusi Gompertz juga

DAFTAR PUSTAKA

Dobson, A. J. 2001. An Introduction to Generalized Linear Model. Chapman

Hall/CRC Texts in Statistical Science Series.

Glaser, R. E. 1980. Bathtub and Related Failur Rate Characterizations. J. American

Statistical Association, 75, pp 667-672.

Hogg, R.V. and Craigg, A. T.. 1986. Introduction to Mathematical Statistics. Fifth

Edition. Prentice-hall Inc., New Jersey.

Klein, J. P. and Moescberger, M. L. 1997. Survival Analysis: Techniques for

Censored and Truncated Data. Springer-Verlag Inc., New York.

Lenart, Adam. 2011. The Gompertz Distribution and Maximum Likelihood

Estimation of Its Parameters. 1: 2-3.

Lee, E. T. 1992. Statistical Methods for Survival Data Analysis. Second Edition. John

Wiley & Sons Inc., Canada.

McDonald, J. B. and Ricards, D. O. 1987. Hazard Rates and Generalized Beta

Distributions. Transactions On Reliability, R-36, 463-466.

Walpole, E. R. 1995. Pengantar Statistika. Edisi Ketiga. Gramedia Pustaka Utama,

Jakarta.