PENENTUAN NILAI UMUM ASURANSI MENGGUNAKAN
TEORI KONTROL OPTIMUM
RAFIDHA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRACT
RAFIDHA. Pricing of General Insurance with Optimal Control Theory. Supervised by I GUSTI PUTU PURNABA and SISWANDI.
Generally, premium calculations are essential in the discussion of insurance products, such as expected value principles, higher order moments, and utility theory. However, all of these principles fail to account for the competitive nature of insurance pricing. Furthermore, Taylor (1986) formulates this problem as a model based on a demand law and distribution of claims. He uses a simple discrete time deterministic model, which is analyzed using pontryagin’s maximum principle to maximize the final wealth of an insurer. This leads to a bang-bang optimal premium strategy, which cannot be optimal for the insurer in realistic applications. The model is then modified by introducing a new premium rate representing the accumulated premium rates received from the existing and new customers. This model has two demand functions, i.e. power law and linear demand functions. For these demand functions, it is known that withdrawal from the market, setting a premium above the break even point, or loss leading can be optimal. Furthermore, the optimal premium strategy is sensitive to the form of the demand function.
ABSTRAK
RAFIDHA. Penentuan Nilai Umum Asuransi Menggunakan Teori Kontrol Optimum. Dibimbing oleh I GUSTI PUTU PURNABA dan SISWANDI.
Secara umum, penghitungan premi dari suatu produk asuransi antara lain prinsip nilai harapan, momen orde tertinggi, dan teori utilitas. Namun, ternyata semua prinsip ini gagal untuk menghitung sifat kompetitif alami dari penentuan harga asuransi. Oleh karena itu Taylor (1986) membawa permasalahan ini ke suatu model formulasi berdasarkan permintaan dan sebaran klaim. Ia menggunakan model deterministik diskret, di mana analisisnya menggunakan teori kontrol optimum sehingga memaksimumkan kekayaan akhir asuransi. Hal ini membawa ke suatu strategi premi bang-bang optimum, dimana pada aplikasinya di asuransi tidak bisa optimum. Model kemudian dimodifikasi dengan memperkenalkan tingkat premi yang diperoleh yang merepresentasikan tingkat akumulasi premi yang diterima dari nasabah baru dan lama. Model ini mempunyai dua fungsi permintaan yaitu fungsi permintaan hukum pangkat dan fungsi permintaan linear. Untuk dua fungsi permintaan diketahui bahwa keputusan untuk keluar dari pasar, menetapkan premi di atas break even point atau loss leading bisa optimum. Oleh karena itu strategi premi optimum peka terhadap bentuk fungsi permintaan.
PENENTUAN NILAI UMUM ASURANSI MENGGUNAKAN
TEORI KONTROL OPTIMUM
RAFIDHA
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul : Penentuan Nilai Umum Asuransi Menggunakan Teori Kontrol Optimum
Nama : Rafidha
NIM : G54054308
Menyetujui,
Pembimbing I
Dr. Ir. I Gusti Putu Purnaba, DEA.
NIP. 19651218 199002 1 001
Pembimbing II
Drs. Siswandi, M.Si.
NIP. 19640629 199103 1 001
Mengetahui,
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Dr. drh. Hasim, DEA.
NIP. 19610328 198601 1 002
KATA PENGANTAR
Alhamdulillah, puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Serta shalawat dan salam selalu tercurahkan untuk Nabi Muhammad SAW, sahabat, dan keluarganya. Penyusunan karya ilmiah ini juga tidak terlepas dari dukungan dan bantuan berbagai pihak. Penulis mengucapkan terimakasih yang sebesar-besarnya kepada:
1. Keluarga tercinta atas semua semangat dan dukungannya. Ayah dan Mama yang telah memberikan kasih sayang, doa, didikan, serta dukungan baik secara moril dan materi, nasihat, dan motivasi yang sangat berharga bagi penulis. Semangat dan kesabaranmu adalah motivasi bagiku. Untuk Bang Ari, Kak Dhia, Ina, dan Dhila terimakasih atas doa dan dukungannya; 2. Keluarga besar yang selalu memberikan doa, semangat dan dukungannya.
3. Bapak I Gusti Putu Purnaba selaku dosen pembimbing I serta Bapak Siswandi selaku pembimbing II. Terimakasih atas waktu, ilmu yang diberikan dan kesabarannya dalam membimbing penulis. Semua ilmu yang Pak Pur dan Pak Siswandi berikan sangat bermanfaat bagi penulis. TERIMA KASIH;
4. Bapak Toni Bakhtiar selaku dosen penguji. Terimakasih atas waktu dan ilmu yang telah diberikan bagi penulis;
5. Semua dosen Departemen Matematika, terimakasih atas ilmu yang sanagt bermanfaat dan nasihatnya selama ini;
6. Ibu Susi, Ibu Ade, Bapak Yono, Mas Bono, Mas Heri, Mas Deni dan seluruh staf pegawai Departemen Matematika, terimakasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis di departemen Matematika;
7. Danish: Icha, Nesh, Hida, Tante, Mba Ind, Rizki atas persahabatan, doa, semangat dan nasihatnya selama ini;
8. Erlin, Eyyi. Jane, Niken , dan Obi terimakasih atas persahabatan, doa, dukungan semangat, dan bantuannya yang sangat berharga bagi penulis;
9. Sahabat-sahabat idha: Fara, Mija, Dwi, Hilda, Ophie, Mayang, Qkee, Gita, dan Ella terimakasih atas persahabatan, doa, semangat dan dukungannya selama ini.
10.Teman-teman satu bimbingan: Nyoman dan Mega, terima kasih atas doa, bantuan, dukungan semangat, dan nasehatnya.
11.Eyyi, Ocoy, dan Luri, terimakasih atas bantuannya telah pembahas serta saran dan kritiknya. 12.Teman-teman Math’42: Erlin, Eyyi, Jane, Niken, Obi, Achy, Hap-hap, Die-die, Vino, Lisda,
Vita, Hikmah, Ryu, Luri, Okta, Gita, Vera , Rita, Mega, Ricken, Agnes, Ayu, Ocoy, Nyomie, Hesti, Nola, Titi, Mira, Rima, Sima, Tia, Lina, Zil, Dewi, Lela, Pipit, Nofita, Ety, Yuni, Wiwi, Fachri , Ilyas, Iputh, Yusep, Warno , Sapto, Djawa, Bima, Awi, Ayeep, Danu, Dandy, Yudi, , Eko, Mocco, Qnun, Rendi, Acuy, Ridwan, Herry, Boy, Septian, Mas Mukhtar, terima kasih atas doa, dukungan semangatnya, terimakasih atas kebersamaannya selama 3 tahun di Math’42;
13.Adik-adik 43: Apri, Chopy, Nia, Buncit, Cupid, Tami, Arum, dan lainnya yang tidak dapat dituliskan satu per satu, terima kasih atas doa dan dukungan semangatnya;
14.Teman-teman TPB: Wildan, Nopeq, Lukman, Mutia ,dan Ragil terima kasih atas doa, dukungan semangatnya, dan semoga persahabatan ini akan terus terjalin;
15.Teman-teman SD: Ai, Ky, Mbe, Dinul, Eno, Eko, Chica, Cina, Nitya, Oetie, Rifki, Gita, Ukhen, dan Vemmy terima kasih atas pertemanan, doa, semangat dan dukungannya;
16.Semua civitas Matematika angkatan 40, 41, 43, dan 44, terimakasih untuk semuanya;
Penulis menyadari tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca.
Semoga karya ilmiah ini bermanfaat bagi dunia ilmu pengetahuan khususnya Matematika.
Bogor, November 2009
RIWAYAT HIDUP
Penulis dilahirkan di Pontianak pada tanggal 13 Juli 1987 sebagai anak ketiga dari lima bersaudara, anak dari pasangan Amri H. Machjus dan Aisyah.
Pendidikan formal yang ditempuh penulis yaitu di SD Muhammadiyah 2 Pontianak pada tahun 1999, SLTP Negeri 3 Pontianak pada tahun 2002, SMU Negeri 1 Pontianak pada tahun2005, dan pada tahun yang sama penulis diterima di Institut Pertanian Bogor melalui jalur SPMB (Seleksi Penerimaan Mahasiswa Baru). Pada tahun 2006, penulis diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
DAFTAR ISI
Halaman
DAFTAR ISI ... vii
DAFTAR TABEL ... viii
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... viii
I PENDAHULUAN ... 1
1.1. Latar Belakang ... 1
1.2. Tujuan ... 1
II LANDASAN TEORI ... 1
2.1 Asuransi dan Polis Asuransi ... 1
2.2 Barisan dan Deret ... 2
2.3 Persamaan Diferensial Orde Satu ... 2
2.4 Proses Stokastik ... 2
2.5 Proses Markov ... 2
2.6 Persamaan Bernoulli ... 2
2.7 Persamaan Riccati ... 2
2.8 Masalah Kontrol Optimum ... 3
2.9 State Sistem Dinamik dan Peubah Kontrol ... 3
2.10 Reachability, Controllability, dan Observability... 3
2.11 Fungsional Objektif ... 3
2.12 Formulasi Masalah Kontrol Optimum ... 4
2.13 Prinsip Maksimum Pontryagin ... 4
2.14 Kontrol Optimum Linear ... 5
III HASIL dan PEMBAHASAN ... 5
3.1 Formulasi Model ... 5
3.2 Strategi Premi ... 6
3.3 Prinsip Maksimum Pontryagin dan Hamiltonian ... 7
3.4 Akumulasi Pendapatan Premi ... 8
3.4.1 Fungsi Permintaan Hukum Pangkat ... 10
3.4.2 Fungsi Permintaan Linear ... 12
IV SIMPULAN ... 16
DAFTAR PUSTAKA ... 17
DAFTAR TABEL
Halaman
1. Nilai Parameter Fungsi Permintaan Hukum Pangkat ... 11
2. Nilai Parameter Fungsi Permintaan Linear ... 14
DAFTAR GAMBAR
Halaman 1. Pengaruh polis pada pendapatan premi perusahaan asuransi ... 62. Perubahan akumulasi pendapatan premi ... 8
3. Profil harga premi pada waktu t ... 9
4. Strategi optimum untuk fungsi permintaan hukum pangkat G dengan parameter pada Tabel 1 ... 11
5. Sensitifitas strategi optimum terhadap model parameter untuk fungsi permintaan hukum pangkat G ... 11
6. Strategi optimum untuk fungsi permintaan linear G dengan parameter pada Tabel 2 ... 14
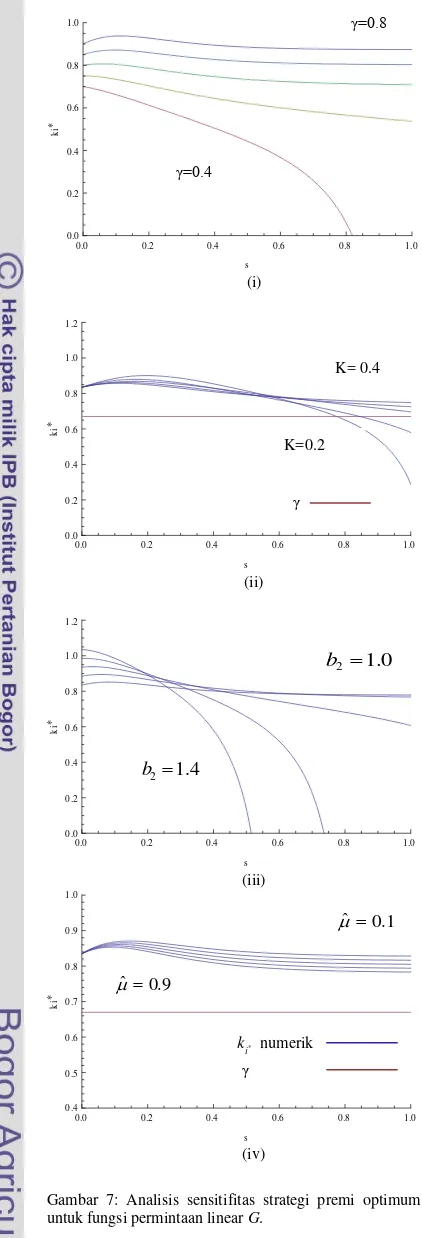
7. Analisis sensitifitas strategi premi optimum untuk fungsi permintaan linear ... 14
DAFTAR LAMPIRAN
Halaman 1. Persamaan permintaan ... 192. Nilai harapan persamaan kekayaan ... 20
3. Persamaan nilai harapan akumulasi pendapatan premi ... 21
4. Persamaan nilai harapan akumulasi pendapatan premi dengan nilai awal ... 21
5. Nilai harapan persamaan kekayaan ... 21
6. Solusi nilai awal persamaan adjoin ... 22
7. Pengali Lagrange ... 23
8. Persamaan adjoin nondimensional ... 24
9. Nilai omega ... 25
10. Batas perilaku untuk lambda ... 26
11. Persamaan adjoin ... 26
12. Persamaan Riccati nondimensional ... 27
13. Batas perilaku untuk lambda dan kontrol optimum ... 28
14. Nilai lambda pada persamaan Riccati ... 29
15. Nilai awal untuk persamaan adjoint ... 30
16. Grafik lambda fungsi permintaan hukum pangkat ... 30
17. Grafik strategi premi ... 30
18. Grafik strategi premi dengan bervariasi ... 31
19. Grafik strategi premi dengan K bervariasi ... 31
20. Grafik strategi premi dengan a1 bervariasi... 32
21. Grafik lambda fungsi permintaan linear ... 32
22. Grafik strategi premi ... 33
23. Grafik strategi premi dengan bervariasi ... 33
24. Grafik strategi premi dengan K bervariasi ... 33
25. Grafik strategi premi dengan b1bervariasi ... 34
I.
PENDAHULUAN
1.1 Latar Belakang
Secara umum produk asuransi
memerlukan penghitungan premi. Prinsip
penghitungan premi saat ini semakin
berkembang dengan berbagai pendekatan. Pendekatan paling sederhana adalah prinsip nilai harapan yaitu premi bersih sama dengan nilai harapan klaim dikalikan konstanta tertentu. Dalam menentukan harga premi asuransi disarankan menggunakan momen orde tertinggi dari sebaran klaim atau menggunakan teori utilitas. Kenyataannya, semua prinsip ini gagal untuk menghitung sifat kompetitif alami dari penentuan harga asuransi (Emms & Haberman 2005).
Penjelasan mengenai permodelan premi asuransi yang harus ditentukan di pasar yang kompetitif dan reaksi mereka terhadap perubahan premi yang ditawarkan perusahaan kompetitor sangat sedikit dibahas dalam literatur asuransi. Walaupun faktanya bahwa siklus pertanggungan pada non-life insurance yang dikenal sekarang dan analisis objektif diperlukan untuk merumuskan strategi pertanggungan dengan baik dibandingkan dengan mengikuti trend (Emms & Haberman 2005).
Kebijakan perusahaan asuransi
dipengaruhi oleh harga yang ditawarkan oleh
perusahaan lain. Selama siklus
pertanggungan, masing-masing perusahaan asuransi mengikuti pasar. Ketika premi pasar menurun maka premi perusahaan asuransi juga menurun. Sebaliknya ketika premi pasar
mengalami peningkatan maka premi
perusahaan asuransi juga meningkat (Emms & Haberman 2005).
Harga premi relatif yang lebih rendah menghasilkan resiko di dalam pasar asuransi pada keuntungan yang lebih rendah untuk perusahaan asuransi. Premi adalah sebuah bentuk yang ditetapkan dalam upaya mengoptimumkan kekayaan dengan cara menjual asuransi sesuai permintaan. Secara implisit, strategi masing-masing perusahaan asuransi tidak mempengaruhi pasar. Hal ini masuk akal sepanjang perusahaan asuransi relatif kecil dibanding dengan ukuran pasar (Emms & Haberman 2005).
Taylor (1986) mengasumsikan bahwa kompetisi dapat memberikan pengaruh pada strategi premi perusahaan asuransi. Taylor meneliti perubahan drastis tingkat premi yang ditawarkan oleh perusahaan asuransi di pasar asuransi Australia. Harga asuransi setelah kejadian bencana besar, misalnya bencana alam, sering diikuti oleh periode tingkat premi yang lebih tinggi dan memperhitungkan
keuntungan. Masing-masing perusahaan
asuransi cenderung mengikuti pasar daripada harga asuransi berdasarkan prediksi sebaran klaim. Permasalahan ini membawa ke suatu model formulasi yang berdasarkan permintaan dan sebaran klaim. Taylor menggunakan model deterministik diskret. Sebelumnya telah
dibuat secara umum pendekatannya
menggunakan model stokastik kontinu, dengan analisisnya menggunakan teori kontrol optimum (Emms & Haberman 2005).
1.2 Tujuan
Adapun tujuan dari karya tulis ini adalah menemukan strategi premi asuransi optimal
yang memaksimumkan kekayaan akhir
perusahaan asuransi dengan strategi
deterministik.
II LANDASAN TEORI
Untuk memahami penentuan nilai umum asuransi menggunakan teori kontrol optimum, berikut ini diberikan beberapa definisi dan teorema-teorema yang berkaitan di antaranya
2.1Asuransi dan Polis Asuransi Definisi 2.1.1 (Asuransi)
Asuransi adalah suatu kontrak antara dua pihak dengan satu pihak menyetujui untuk
mengganti kerugian dari pihak lain. Pihak yang menyetujui mengganti kerugian disebut penanggung dan pihak yang mengalami
kerugian disebut tertanggung. Pihak
tertanggung membayar klaim pembayaran yang disebut premi kepada pihak penanggung.
Definisi 2.1.2 (Polis Asuransi)
Polis asuransi adalah kontrak asuransi
antara pihak penanggung dan pihak
tertanggung.
(Dorfman 2004)
2.2 Barisan dan Deret
Definisi 2.2.1 (Barisan Takhingga)
Barisan takhingga adalah suatu susunan bilangan yang dituliskan dalam suatu urutan tertentu a a a1, 2, 3,...,an. Barisan
a a a1, 2, 3,...
dapat dinyatakan dengan
a
n n 1 .
(Stewart 1999)
Definisi 2.2.1 (Deret Takhingga)
Deret takhingga adalah penjumlahan suku-suku dari suatu barisan takhingga
an n1 yaitu a1a2a3 ... an... dan dinotasikan dengan
1 n n
a
.( Stewart 1999)
Definisi 2.2.1 (Deret Taylor)
Fungsi f sebarang di a (atau di sekitar a atau yang berpusat di a) disebut deret Taylor jika memenuhi persamaan
( )
0
(1) (2)
1 2
( )
( ) ( )
!
( ) ( )
( ) ( ) ( ) ...
1! 2!
n
n n
f a
f x x a
n
f a f a
f a x a x a
Bukti:lihat Stewart 1999, hal 188.
(Stewart 1999)
2.3 Persamaan Diferensial Orde Satu Definisi 2.3.1 (Persamaan Linear Orde Satu)
Persamaan linear orde satu dapat ditulis sebagai berikut
0( ) 1( ) ( ), dy
a x a x y F x dx
dengan a x a x0( ) , 1( ) ,dan F x( )adalah fungsi tertentu yang didefinisikan pada interval tertentu I. Diasumsikan bahwa a x0( )0 untuk semua xI , kemudian masing-masing ruas dibagi oleh a x0( )dan menulis ulang persamaan menjadi
( ) ( )
y p x y f x
denganp x( )a x a x0( ) 1( )dan f x( )F x a x( ) 0( ).
Diasumsikan bahwa p(x) dan f(x) adalah kontinu untuk x pada interval I.
Persamaan ini mempunyai solusi umum yaitu
( ) ax ( ) ax ax
y x e
f x e xceBukti:lihat Farlow 1994, hal 30-31.
(Farlow 1994)
2.4 Proses Stokastik
Definisi 2.4.1 (Proses Stokastik)
Proses stokastik X { ( ),X t tT}adalah suatu himpunan dari peubah acak yang
memetakan suatu ruang contoh Ω ke suatu
ruang state S.
(Ross 2007)
2.5 Proses Markov
Definisi 2.5.1 (Proses Markov)
Proses Markov adalah suatu proses acak yang peluang nilai yang akan datang ditentukan oleh nilai saat ini. Suatu proses stokastik x(t) disebut Markov jika untuk setiap n dan t1<t2…<tn maka
1 1 1
( ( )n n| (n ),..., ( )) ( ( )n n| (n ))
P x t x x t x t P x t x x t
Karena t1<t2…<tn maka persamaan ini
ekivalen terhadap
1 1
( ( )n n| ( ), n ) ( ( )n n| (n )) P x t x x t t t P x t x x t
(Papoulis 1984)
2.6 Persamaan Bernoulli
Definisi 2.6.1 (Persamaan Bernoulli)
Persamaan diferensial biasa berbentuk
' ( ) ( ) n
yP x yQ x y disebut persamaan Bernoulli saat n1, 0.Persamaan Bernoulli
khusus karena merupakan persamaan
diferensial tak linear dengan diketahui solusi eksaknya.
(Farlow 1994)
2.7 Persamaan Riccati
Definisi 2.7.1 (Persamaan Riccati)
Persamaan umum Riccati diberikan oleh 2
( )
( ) ( ) ( ) ( ) ( )
d y x
a x y x b x y x c x
d x
mempunyai solusi dalam bentuk prosedur infinit
2 2
1 1
( ) ( 4 ( ( ( 4 ( (...))))))
2 2
d d
y x b b a c b b a c
a d x a d x
Prosedur yang dijelaskan di atas dapat diekspresikan dalam bentuk iterasi
2 0
1
( ) [ ( ) ( ) 4 ( ) ( )]
2 ( )
y x b x b x a x c x
a x
dan
2 1
1
( ) [ ( ) ( ) 4 ( ) ( ( ) ], 0. 2 ( )
n n
d y
y x b x b x a x c x n
a x d x
(Agnew R.P. 1960)
Berikut diberikan beberapa definisi mengenai dasar dari kontrol optimum.
2.8 Masalah Kontrol Optimum
Definisi 2.8.1 (Masalah Kontrol Optimum)
Masalah kontrol optimum adalah memilih peubah kontrol u(t) di antara semua peubah kontrol yang admissible, yaitu kontrol yang membawa sistem dari state awal x t( )0 pada waktu t0kepada state akhir x T( ) pada waktu
akhir T, sedemikian sehingga memberikan nilai maksimum atau nilai minimum untuk fungsional objektif. Fungsional objektif adalah fungsi dari beberapa fungsi lainnya untuk memaksimumkan atau meminimumkan suatu permasalahan.
(Tu 1983)
2.9 State Sistem Dinamik dan Peubah Kontrol
Definisi 2.9.1 (State Sistem Dinamik dan Peubah Kontrol)
State atau keadaan sistem dinamik adalah koleksi dari x t( )( ( ),x t x t1 2( ),...,x tn( )) yang apabila diberikan suatu nilai pada waktu
0
tt , maka nilainya akan dapat ditentukan pada tt0 melalui pilihan vektor peubah kontrol u t( )( ( ),u t u t1 2( ),...,u tn( )).
Vektor x t( ) disebut vektor peubah state sedangkan x ti( ) disebut peubah state untuk
0
(1 i n t, t T). Ruang state adalah ruang dimensi n yang memuat koordinat x ti( )
di mana 1 i n .
State suatu sistem kontinu pada waktu t dinyatakan dalam bentuk sistem persamaan diferensial yaitu x t( ) f x t u t t[ ( ), ( ), ]
sedangkan state suatu sitem diskret
dinyatakan dalam sistem persamaan beda yaitu x k( 1) f x k u k k[ ( ), ( ), ]. Sistem ini juga dapat berbentuk deterministik dan stokastik.
Peubah kontrol adalah peubah yang memengaruhi suatu sistem dilambangkan dengan u ti( ) dengan (1 i n t, 0 t T). Secara umum, kendala peubah kontrol dinyatakan dengan persyaratan bahwa peubah kontrol harus dipilih dari kumpulan kontrol-kontrol yang admissible, yang dilambangkan
( ( ))u t
, artinya kontrol u ti( )( ( ))u t .
Apabila kontrol u t( )hanya fungsi dari t, maka disebut kontrol open-loop dan apabila kontrol u t( )juga merupakan fungsi dari peubah state x t( ) yaitu u t( )u x t t[ ( ), ], maka disebut kontrol closed-loop .
(Tu 1983)
2.10 Reachability, Controllability, dan Observability
Definisi 2.10.1 (Reachability, Controllability,
dan Observability)
Suatu keadaan 1
x dikatakan dapat dicapai (reachable) dari sebarang keadaan x0 pada waktu t0 jika kontrol u T1( )( ( ))u T dapat
ditemukan sedemikian sehingga
0 1 1
1
( , , )
x u x t x untuk waktu t1t0 . Koleksi dari semua x1 tersebut disebut reachable state pada waktu t.
Istilah controllability merujuk pada kenyataan bahwa beberapa state terminal 1
x
dapat dicapai dari state awal x0 dengan
pilihan kontrol u t( ) yang tepat,
1( ) ( ( ))
u T u T . Jadi, controllability
merupakan syarat perlu untuk adanya suatu solusi.
Observability adalah kemampuan untuk menentukan state awal x0 dari observasi data dan output. Output menyatakan hubungan antara peubah state dengan peubah kontrol, misalnya y t( )g x t u t t[ ( ), ( ), ].
(Tu 1983)
2.11Fungsional Objektif
Definisi 2.11.1 (Fungsional Objektif)
Peubah kontrol u t( ) harus dipilih dalam
rangka memaksimumkan atau
meminimumkan fungsional objektif J u t[ ( )], yaitu
0 0
[ ( )] ( ( ), ( ), ) ,
T t
J u t
f x t u t t dtSecara umum, terdapat tiga alternatif untuk menyajikan formulasi fungsional objektif, yaitu:
1. Formulasi Bolza
Formulasi fungsional objektif bentuk Bolza merupakan formulasi yang lebih umum.
0
[ ( )] [ ( ), ] ( ( ), ( ), ) ,
T t
J u t S x T T
f x t u t t dtdengan f0 dan S adalah fungsi kontinu yang dapat diturunkan. Fungsi S x T T[ ( ), ] dikenal
dengan fungsi ‘scrap value’ pada waktu
terminal T .
2. Formulasi Lagrange
Formulasi Lagrange adalah bentuk khusus dari formulasi Bolza dengan S x T T[ ( ), ]0, yaitu
0
[ ( )] ( ( ), ( ), ) .
T t
J u t
f x t u t t dt3. Formulasi Mayer
Formulasi Mayer juga merupakan bentuk
khusus dari formulasi Bolza, dengan
0
( ( ), ( ), ) 0
T t
f x t u t t dt
, yaitu[ ( )] [ ( ), ].
J u t S x T T
Dengan mendefinisikan kembali
peubah-peubahnya, maka ketiga Bolza dapat
dikonversikan menjadi formulasi Mayer dengan mendefinisikan peubah tambahan
1( ) n
x t sebagai
0
1( ) 0( , , ) t
n t
x t
f x u dt, xn1( )t0 0 akan menghasilkan Jxn1( )t S x T T[ ( ), ].(Tu 1983)
2.12 Formulasi Masalah Kontrol Optimum Definisi 2.12.1 (Formulasi Masalah Kontrol Optimum)
Misalkan U menyatakan himpunan dari semua fungsi yang kontinu sesepenggal (piecewise). Masalah kontrol optimum adalah masalah menentukan fungsi kontrol u*(t) di antara fungsi admissible u(t) yang membawa sistem dari state awal x0 kepada state akhir /
terminal xT yang memenuhi kondisi akhir /
terminal, melalui
( ) ( ( ), ( ), )
x t f x t u t t
sehingga fungsional J mencapai nilai
maksimum. Dengan perkataan lain, masalah kontrol optimum adalah memaksimumkan fungsional objektif
0 0 ( )
max [ ( )] ( ), ( ( ), ( ), )
T u t U
t
J u t S x T T f x t u t t
terhadap kendala
0 0
( ) ( ( ), ( ), ); ( ) , ( ) n.
x t f x t u t t x t x x t R
(Tu 1983)
Berikut adalah syarat perlu kontrol optimum
2.13 Prinsip Maksimum Pontryagin
Teorema 2.13.1 (Prinsip Maksimum Pontryagin)
Misalkan u*(t) sebagai kontrol admissible yang membawa state awal
0 0
( ( ), )x t t kepada target state terminal
( ( ), )x T T , dengan x T( )dan T secara umum tidak ditentukan. Misalkan *
( )
x t merupakan
trajektori atau lintasan dari sistem yang berkaitan dengan u*(t). Supaya kontrol u*(t) merupakan kontrol optimum adalah perlu terdapat fungsi vektor p t*( )0
, sedemikian sehingga
1. p t*( )
dan x t*( )
merupakan solusi dari sistem kanonik
* * * *
( ) H( ( ), ( ), ( ), )
x t x t u t p t t
p
*( ) H( *( ), *( ), *( ), ) p t x t u t p t t
x
dengan fungsi Hamiltonian H diberikan oleh
0
( , , , ) ( ( ), ( ), ) ( ( ), ( ), )
H x u p t f x t u t t p f x t u t t
2. * * *
( ( ), ( ), ( ), ) ( ( ), ( ), ( ), )
H x t u t p t t H x t u t p t t . 3. Semua syarat batas terpenuhi.
* * *
( ( ), ( ), ( ), ) ( ( ), ( ), ( ), ) H x t u t p t t H x t u t p t t
disebut Prinsip Maksimum Pontryagin.
Kondisi ini dipenuhi oleh Hu 0 dan 0
uu
H . Jika uU dan U himpunan
tertutup, maka Hu 0 tidak memiliki arti,
kecuali maksimum dari H diberikan oleh bagian dalam himpunan U.
Jika H fungsi monoton naik dalam peubah u, dan U tertutup, maka kontrol optimum adalah
u
maxuntuk masalah memaksimumkan danu
minuntuk masalah meminimumkan. Hal ini juga berlaku apabila H adalah fungsi linear dalam u. Sehingga peubah kontrol optimumverteks ke verteks yang lainnya. Ini adalah
kasus khusus dari kontrol ‘bang-bang’.
Syarat cukup mencakup
* * *
( ( ), ( ), ( ), ) ( ( ), ( ), ( ), ) H x t u t p t t H x t u t p t t .
Vektor p disebut juga vektor adjoin yang memiliki peranan sebagai pengali Lagrange. Dalam masalah optimisasi dinamis, peubah atau vektor adjoin merupakan ‘shadow price’ dari vektor atau peubah x, menunjukkan jumlah kenaikan/penurunan untuk setiap kenaikan/penurunan dalam nilai x pada
waktu t yang berkontribusi terhadap
fungsional objektif optimum J. Sedangkan p
sebagai tingkat kenaikan (apresiasi untuk
0
p ), atau penurunan (depresiasi untuk
0
p ) dalam nilai dari tiap unit modal. Nilai dari suatu dH H
dt t
. Syarat perlu
untuk masalah kontrol optimum adalah x
p H ,Hu0 , xHp. Syarat batas diberikan oleh persamaa
n
0 0
(Sx p)xt tt T [ ( )H t St]tt Tt t 0
Apabila scrap S=0, maka persamaan menjadi
0 0
( ) ( )t Tt t ( ) t Tt t 0
p t x t H t t
Khususnya jika waktu awal t0danx t( )0 telah ditentukan, sedangkan T dan x T( )belum ditentukan, maka syarat batas menjadi
( ) ( ) ( ) 0
p T x T H T T
.
Bukti: lihat Tu 1983, hal 114-118.
(Tu 1983)
2.14 Kontrol Optimum Linear
Definisi 2.14.1 (Kontrol Optimum Linear)
Masalah kontrol optimum linear adalah masalah kontrol optimum dengan fungsi Hamiltonian merupakan fungsi linear dari peubah kontrol. Sifat linear tersebut dapat muncul pada Hamiltonian karena fungsi objektif dan atau fungsi kendala merupakan fungsi linear dari peubah kontrol.
Secara umum, fungsi Hamiltonian dalam bentuk linear dapat dituliskan dalam bentuk berikut :
( , , ) ( , , ) ( )
H x p t x p t u t
dengan ( , , )x p t menyatakan kumpulan koefisien dari u t( )yang disebut sebagai switching function dan ( , , )x p t merupakan kumpulan koefisien yang tidak memuat u t( ). Secara umum, untuk kontrol yang tidak bounded, kontrol ekstremum tidak ada. Jika kontrol terbatas maka kontrol ekstremum tersebut akan terdapat pada batas-batasnya.
Misalkan u berbatas, untuk semua i,
i i i
m u M
,
dengan midan Miberturut-turut merupakan nilai minimum dan
maksimum yang dapat dicapai oleh ui. Apabila mi dan Mi merupakan konstanta maka dapat ditulis sebagai 1 ui 1.
Dengan menerapkan prinsip maksimum
Pontryagin pada masalah tersebut diperoleh kontrol optimum *
i
u berikut
* 1 jika 0
1 jika 0
i i
i
u
Jadi, jika u t( ) muncul linear dalam fungsi Hamiltonian dan tiap komponen uiterbatas, maka kontrol optimum *
( ) i
u t tak kontinu : loncat dari nilai minimum ke nilai maksimum atau sebaliknya sebagai respons terhadap perubahan tanda dari i. Dengan kata lain,
( , , )x p t
disebut sebagai switching function dan kontrol *
i
u disebut sebagai kontrol ‘ bang-bang’.
(Tu 1983)
III HASIL DAN PEMBAHASAN
3.1 Formulasi ModelExposure adalah kemungkinan kerugian-kerugian yang bisa terjadi atas suatu risiko disebabkan oleh keadaan lingkungan sekitar. Misalnya pada asuransi kendaraan, exposure adalah tahun kendaraan, tariff premi adalah rupiah per tahun kendaraan. Pada waktu t, q
(1986), proses berikut adalah deskripsi dari sebuah pasar asuransi
( )
dqq g p p dt
(1)
( )
dw w dtq p dt (2) (Penurunan rumus lihat Lampiran 1)
dengan fungsi permintaan adalah
( , ) exp ( )
f p p g , g adalah parameter fungsi
permintaan dan α adalah excess return yaitu biaya yang dikeluarkan perusahaan asuransi kepada pemegang saham. Premi rata-rata pasar diasumsikan sebagai proses acak positif dengan rata-rata terbatas pada waktu t dan sebaran tidak ditentukan.
Diketahui bahwa tarif premi ditentukan pada waktu t sehingga semua premi memiliki satuan per unit waktu per unit exposure. Dengan formulasi ini, wadalah refleksi yang akurat untuk kekayaan perusahaan pada waktu t karena setiap pemegang polis membayar premi p per unit exposure untuk setiap t.
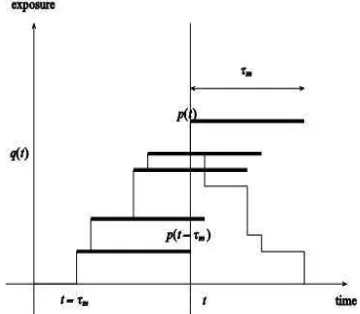
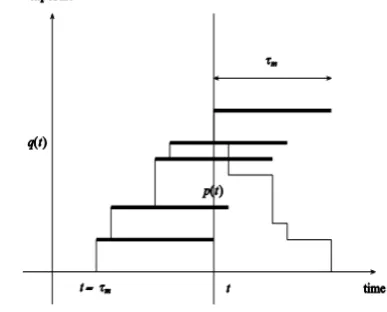
Prinsip pada asumsi model ini adalah semua pemegang polis baik yang baru maupun yang lama diharuskan membayar tarif premi p yang berlaku. Gambar 1 menunjukkan bagaimana polis mempengaruhi pendapatan premi perusahaan asuransi pada kondisi diskret.
Gambar 1 Pengaruh polis pada pendapatan premi perusahaan asuransi
Pada Gambar 1 exposure sebagai fungsi dari waktu dengan pemegang polis membayar premi p(t) yang saat ini berlaku untuk jangka waktu rata-rata polis yang dinotasikan dengan
τm. Garis tebal menyatakan jangka waktu polis
dengan tanggal mulai yang sama. Tarif pendapatan premi yang diakui pada waktu t dari semua polis yang berlaku adalah p(t) q(t).
Perubahan kekayaan pada waktu t
disebabkan oleh pendapatan premi yang dinotasikan oleh pq dt pada persamaan (2). Asumsi ini menarik karena artinya semua
proses acak adalah Markov. Hal ini masuk akal sepanjang tingkat premi tidak berubah secara drastis selama jangka waktu polis.
3.1.1 Parameter
Fungsi permintaan memerlukan parameter sebagai variabel bantu untuk menyelesaikan suatu permasalahan. Taylor (1986) mengambil dua bentuk parameter g p p( / ) untuk fungsi permintaan yaitu
1. Parameter untuk fungsi permintaan eksponensial berbentuk
( ) (1 ) .
g p p a p p (3)
Bentuk tersebut diperoleh dari
( )
( 1)
( ) (1 )
( , )
( ) (1 )
a p p p a p p g p p a p p
f p p e
e
e e
g p p a p p
2. Parameter untuk fungsi permintaan elastisitas harga konstan berbentuk
( ) log( ) .
g p p a p p (4) Bentuk tersebut diperoleh dari
( )
( )
( , ) ( )
( )
log log( )
( ) log( )
a a g p p
a g p p
f p p p p
e p p
e p p
g p p a p p
dengan a konstan yang menjelaskan berapa banyak exposure yang ditingkatkan oleh perubahan premi relatif. Bentuk persamaan (3) telah dijelaskan oleh Taylor (1986) sedangkan bentuk persamaan (4) mengacu pada Lilien & Koetler 1983.
3.2 Strategi Premi
Terdapat dua strategi premi, yaitu fungsi linear premi rata-rata pasar serta fungsi linear premi rata-rata pasar dan premi break-even (Emms, Haberman & Savoulli 2004). Pada karya tulis ini hanya dijelaskan mengenai strategi pertama yaitu fungsi linear terhadap premi rata-rata pasar.
Untuk memaksimumkan nilai harapan dari total kekayaan pada akhir waktu T jika diketahui state S pada saat t=0 maka dibentuk fungsi objektif
max{ [ ( ) | (0)]}
p
V E w T S
Strategi premi yang digunakan adalah
( )
Fungsi deterministik k(t) digunakan untuk analisis model seperti pada persamaan (1)-(2). Untuk premi tidak negatif makak0.
Fungsi permintaan dan bentuk strategi
menghasilkan exposure q(t) yang
deterministik. Hal ini menjadikan model lebih sederhana dan alasan mengapa strategi yang
ada pada persamaan (5) digunakan.
Berdasarkan terminologi dari teori kontrol optimum maka peubah kontrol adalah k dan peubah state adalah q dengan
( ) .
dqq g k dt
Untuk fungsi permintaan elastisitas harga konstan dan fungsi permintaan eksponensial, parameter g adalah fungsi menurun terhadap k.
Dari persamaan (2) diperoleh nilai harapan persamaan kekayaan sebagai berikut
0
[ ( )] T[ (0) T ],
E w T e w
F dt (Bukti lihat Lampiran 2)dengan
( , , ) ( )
( )
t t
F F q k t e q p
e q k p
( , , ) t ( )
p
FF q k t e q k m m (6)
dan
( ; ) [ ( ) | (0) ],
X X
m m t s E X t S s (7)
dengan S adalah state dari sistemdan X adalah peubah yang ingin kita cari.
Akibatnya masalah strategi premi ditulis sebagai suatu bentuk baku untuk teori kontrol (Sethi & Thompson 2000).
Kemudian menentukan fungsi nilai
0 0
max{ T ( , , ) },
k
V J F q k t dt
(8)dengan kontrol optimum k*. Nilai dari fungsi
objektif ini menentukan nilai maksimum dari harapan akhir kekayaan.
3.3 Prinsip Maksimum Pontryagin dan Hamiltonian
Kondisi yang dibutuhkan untuk kontrol optimum ditentukan oleh Prinsip Maksimum Pontryagin yang dapat dinyatakan dalam bentuk Hamiltonian
( , , , ) ( , , ) ( , )
( , , ) ( , )
H x u p t F x u t p f x u
F q k t
f q k
( , , , ) ( , , ) ( ),
H q k t F q k t q g k
(9)
dengan adalah pengali Lagrange (Tu 1983). Prinsip Maksimum dinyatakan dalam
* * *
( , , , ) ( , , , ),
H x u p t H x u p t
* * *
( , , , ) ( , , , ),
H q k t H q k t
untuk semua k0.
Untuk fungsi permintaan eksponensial
(1 )
ga k , Hamiltonian merupakan fungsi linear dari peubah kontrol. Kontrol
optimumnya adalah bang-bang: untuk
*
0 ,k
dan 0,k*0 atau
tergantung dari parameter model. Jika *
0 dan k 0
maka hal ini adalah loss
leader: perusahaan asuransi melepas asuransi untuk mendapatkan pasar dan menagih nasabah premi tanpa batas pada saat t=T supaya meningkatkan kekayaan tanpa batas. Jika k* untuk t[0, ]T yang artinya optimum untuk tidak menjual asuransi.
Untuk fungsi permintaan elastisitas harga konstan g a logk , Hamiltoniannya adalah
( , , , ) ( , , ) ( )
H q k t f q k t q g k
( , , , ) t ( ) log
p
H q k t e q k m m q a k (10)
Jika maksimum dari H melalui
(0, )
k diberikan oleh Hk=0 yaitu turunan
Hamiltonian terhadap k kemudian
menggunakan persamaan (10) maka
0
0 k
t p H
qa e q m
k
e mt p a 0. k
(11)
Karena k harus positif maka juga positif. Persamaan ini ketika dipasangkan dengan persamaan adjoint menentukan suatu kontrol optimum. (Gelfand & Fomin 2000). Persamaan adjointnya adalah
t( ) log
q p
H e k m m a k
(12) Untuk maksimum, turunan kedua dari H adalah Hkk 0saat kk*. Dari persamaan (10) diperoleh
2 0
kk a q H
k
untuk k0, titiknya minimum.
Dari bentuk Hamiltonian pada fungsi permintaan eksponensial diketahui kontrol optimumnya menurun dan tidak unik : jika
0
maka k* sementara jika
0
maka k* 0atau .
sebuah perusahaan asuransi memerlukan semua pelanggan yang ada untuk membayar tarif premi yang saat ini berlaku. Terdapat batasan pada seberapa besar peningkatan pemegang polis yang diperlukan untuk membayar premi asuransi sebelum jangka waktu polis habis. Strategi yang optimum akan bergantung pada peningkatan nilai ini. Solusi untuk masalah ini adalah dengan menempatkan kendala pada strategi premi sehingga harga premi asuransi tidak dapat mengubah polis asuransi secara drastis (Emms, Haberman & Savoulli 2004). Pendekatan alternatifnya adalah dengan mengubah asumsi dari model ini.
3.4 Akumulasi Pendapatan Premi
Diberikan model kontinu yang sederhana oleh Gerrad & Glass (2004). Penyebab perubahan exposure adalah kerugian akibat penghentian polis serta adanya new business atau polis yang dilanjutkan. Oleh karena itu diperlukan parameter untuk tarif new business. New business adalah produk dan polis baru yang belum pernah dipasarkan oleh perusahaan asuransi. Persamaan exposure dipecah menjadi new busines dan penghentian polis selama parameter new business memiliki bentuk yang mirip dengan fungsi
permintaan pada persamaan (3) dan
persamaan (4). Berdasarkan fungsi permintaan pada persamaan (3) dan persamaan (4), diperoleh persamaan new business sebagai berikut
nq G p p( ), (13) dengan G adalah fungsi permintaan tak negatif. Parameter ini mencerminkan gagasan bahwa reputasi sebuah perusahaan adalah sebanding dengan exposure di pasar dan hal ini merupakan bagian dari reputasi sebuah perusahaan asuransi yang dapat meningkatkan kemungkinan untuk menghasilkan peluang new business (Emms & Haberman 2005). New business ini juga ditentukan oleh premi asuransi yang ditetapkan relatif pada pasar yang diwakili oleh fungsi permintaan G.
Jangka waktu rata-rata sebuah polis asuransi termasuk polis yang dilanjutkan dilambangkan dengan τm. Perubahan exposure
pada saat t bergantung pada new business dari t-τm hingga t (lihat Gambar 2). Oleh karena itu
proses q non-Markov, yang sangat sulit dimodelkan. Untuk tetap membuat model tersebut Markov dan menggunakan teori
kontrol konvensional maka digunakan
parameter kehilangan exposure akibat
penghentian polis yaitu q dengan 1 m
.
Nasabah yang ada tidak diwajibkan membayar premi saat ini sebagai gantinya nasabah membayar premi pada awal waktu polis. Artinya bahwa pada saat t ada kisaran harga premi yang dibayarkan kepada asuransi
sehingga terdapat tingkat akumulasi
pendapatan premi Q sehingga Q juga non-Markov. Untuk model Markov dimisalkan bahwa penurunan akumulasi pendapatan premi akibat penghentian polis sebanding dengan akumulasi pendapatan premi saat ini
Q.
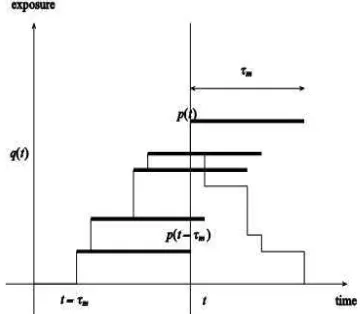
Berikut ini diberikan gambar perubahan akumulasi pendapatan tergantung pada new business dan tarif premi antara t-τm dan t.
Gambar 2 Perubahan akumulasi pendapatan premi
Pada Gambar 2, exposure asuransi sebagai fungsi dari waktu dengan premi dimulai dari awal polis dan konstan selama jangka waktu
polis. Pendapatan premi adalah
( ) ( )
m
t t
Q p s n s ds
.Dimisalkan bahwa π konstan dan
pmenyebar lognormal, yaitu sebaran
kemungkinan dari p yang logaritmanya menyebar normal. Hal ini tidak realistis karena diasumsikan bahwa π dan p bebas karena π dan p tidak saling mempengaruhi. Jika pasar menggunakan prinsip nilai harapan maka p sebanding dengan π . Oleh karena itu
,
p
Dengan asumsi ini didapat model
( )
dq nq dt (15)
( )
dQ pnQ dt (16)
( ) .
dw w Q p q dt
(17) Berdasarkan strategi (5) maka exposure q dan new business n adalah deterministik. Diasumsikan bahwa terdapat
m
p bebas terhadap peubah state lainnya sehingga terdapat dua peubah state baru yaitu q dan mQ.Misalnya jika p menyebar log-normal
dengan perubahan μ maka mp p(0)et
, menggunakan notasi pada persamaan (7). Dari persamaan (16) diperoleh
( ) .
Q
p Q
dm
q k G k m m
dt
Dengan mengintegralkan persamaan ini
didapat
( ) 0
( ) ( ( ) ) 0
( ) (0) ( ) ( )
(0) ( ( )) (18)
t s t
Q Q p
B t b s t
Q p
m t m e m s n s ds
m e m b s db
(Bukti lihat Lampiran 3)
dengan
0
( ) ( )
t
B t
n s dsadalah total bisnisyang dihasilkan sepanjang waktu t.
Dimisalkan bahwa B adalah fungsi monoton naik terhadap t sehingga invers dari tt B( )
terdefinisi.
Gambar 3 Profil harga premi pada waktu t
Gambar 3 menunjukkan profil harga premi yang diperoleh model ini pada waktu t. Profil premi yang benar tergantung pada sejarah harga premi antara t-τm dan t. Dengan
membuat model tersebut Markov, persamaan
(18) menyatakan bahwa profil ini adalah fungsi terboboti dari seluruh premi pada [0, t], walaupun demikian hanya nilai premi dalam rentang [t-τm , t] yang penting. Namun, perlu
diketahui bahwa hal ini memaksakan sebuah struktur premi tiruan yang berbeda dari yang sebenarnya diterima, kecuali dalam kasus tarif premi konstan. Jika mp konstan dengan
menggunakan persamaan (15) dan (16) dan integral dihasilkan mQ q mp menggunakan
(0) (0)
Q p
m q m yang artinya pendapatan
akumulasi premi perusahaan asuransi didapat dari exposure q (Bukti lihat Lampiran 4).
Pada Gambar 3, rataan tarif profil premi diterima pada saat t dengan tarif premi dimulai pada awal polis dan konstan selama jangka waktu. Polis individu dijelaskan oleh garis tebal. Jika tingkat premi konstan kemudian premi yang terjadi Q(t) diberikan oleh wilayah yang berbayang. Pendapatan premi yang sebenarnya di model kontinu adalah yang ditutupi oleh garis titik-titik.
Dengan nilai harapan dari persamaan (17) dan integral didapat
0
( ) [ (0) ( ( ) ( )) ]
t
t s
w w Q p
m t e m
e m s qm s ds(Bukti lihat Lampiran 5).
Fungsi kekayaan dijelaskan dalam bentuk Lagrange sebagai
0
max{ T }
k
V J
F dtdengan
( , ) t( Q p)
F x t e m qm (19) dengan mQ pada persamaan (18) dan vektor
statenya adalah ( , )T
Q
x q m .
Persamaan statenya adalah
( ( ) )
( , , )
( ) p Q
q G k
x f x k t
q k G k m m
(20) Hamiltonian diberikan oleh
1 2
( , , , )
( ) ( ( ) ) ( ( ) ),
t
Q p p Q
H x k t F f
e m qm q G k q k G k m m
dengan vektor pengali Lagrange adalah 1 2
( , )
Dimisalkan kontrol optimum k* diberikan
oleh turunan pertama untuk memaksimumkan H. Persamaan state dan persamaan adjoin yang merupakan syarat perlu suatu kontrol optimum adalah
0 k
H
(21) x H (22)
x
H
Untuk turunan kedua Hkk 0 saat kk*. Syarat batasnya adalah
(0) ( (0), Q(0)) , ( )T 0.
x q m
T Untuk menentukan kontrol optimum k* ,
hanya perlu memecahkan masalah nilai awal yang terdiri dari persamaan adjoin (23) dan syarat batas.
Persamaan adjoin yang kedua bebas terhadap pilihan fungsi permintaan G. Dari persamaan (19) dan (20) didapat
2 2 ,
t Q
Hm e
(24) dengan syarat batas2( )T 0. Persamaan ini kemudian diintegralkan sehingga diperoleh
( ) ( )
2 (1 ),
t t T e e
(25) (Bukti lihat Lampiran 6)
Akibatnya untuk 0 t Tmaka 2 0. 3.4.1 Fungsi Permintaan Hukum Pangkat
Fungsi permintaan G merupakan fungsi tak naik tak negatif dari harga relatif premi. Oleh karena itu terdapat parameter yang sesuai yang didefinisikan untuk semua premi positif dengan bentuk
1
1 ,
a
Gb k (26) dengan a b1, 10: a1 konstan dan satuan
1
b adalah per unit waktu. Walaupun G didefinisikan untuk semuak0, persamaan (26) akan menjadi parameter yang tidak realistik karena k menjadi besar. Jika strategi optimum tergantung pada generasi new bussiness untuk tarif premi relatif besar maka hal ini bukan model yang baik untuk fungsi permintaan (Emss & Haberman 2005).
Hamiltonian untuk fungsi permintaan ini adalah
1 1
1 1
1 1 2 1
1
1 1 2 1
( ) ( ) ( )
( ) ( ) ( ).
a a
t
Q p p Q
a a
t
Q p p Q
H F f
e m qm q b k qkb k m m
e m qm q b k qb k m m
Dengan melakukan turunan pertama dan kedua fungsi H diperoleh
1 1 1 1 1 1 1 1 1
1 1 1 1 1 2
1
1 1 2 1 1
2 1
1 1 1 1 1 1 1 2
2 1
1 1 1 1 1 1 1 2
2
1 1 1 1 1 2
(1 )
((1 ) )
( 1) (1 )
(1 ) (1 )
( (1 ) (1 ) ).
a a k p a p a a kk p a a p a p
H a q b k a q b k m
q b k a k m a
H a a q b k a a q b k m
a a q b k a a q b k m
a q b k a a k m
Misalkan ekstremum dari H pada titik interior *
i
k , dengan * (0, )
i
k . Oleh karena itu
strategi optimum diberikan oleh Hk 0:
1
* 1
1 1 2 1 1
1 2 1 1
1 1
1 2
((1 ) ) 0
(1 ) (27) (1 ) a p p i p
qb k a km a
a k m a
a k a m
yang memberikan hasil maksimum
jikaHkk 0
1 * 1 * 1 * 1 * 2
1 1 1 1 1 2
2 1 1
1 1 1 1 1 2
1 2
2
1 1 1 1 1 1
2 1 1
( (1 ) (1 ) )
( (1 ) (1 ) )
(1 )
( (1 ) )
0
a
kk i p
a p i p a i a i
H a qb k a a km
a
a qb k a a m
a m
a qb k a a
a qb k
Akibatnya terdapat maksimum interior dari H jika 1 0dan ki* 0. Selanjutnya dari (25) dan (27) makaa11.
Pengali Lagrange ditentukan oleh
1
1 2
1 1 1 1
1 1 1
(1 ) 1 ( ) ( ) 1 p a t p a m
m e b
a a (28) (Bukti lihat Lampiran 7)
menggunakan persamaan (25) dengan syarat batas1( )T 0. Hal ini mirip dengan persamaan Bernoulli tetapi tak homogen sehingga secara umum tidak mempunyai solusi analitik.
Kemudian dilakukan penondimensionalan
pada premi rata-rata pasar untuk
penyederhanaan persamaan sehingga
diperoleh solusi numerik dengan
menggunakan nilai awal. Skala yang
digunakan adalah
1 2 1 1
1
1 1
ˆ
(0) (1 )
( ) p (0) ( )
b b p t T s T
K b b T m p M s
Substitusikan skala tersebut ke dalam persamaan (28) sehingga diperoleh persamaan adjoint nondimensional yaitu
1
ˆ(1 ) 1
1 1
(1 ) ( ) 1
[ ( ) ( )( ) ].
1
a
s a M s
d
M s e K
ds a a
(29) (Bukti lihat Lampiran 8).
Dari persamaan (25) diperoleh
ˆ(1 ) (ˆ )
(1 ) ˆ ( ) K s s e e K
(Bukti lihat Lampiran 9). dan strategi optimum
* 1 1 1 2 1 1 1 (0)
1 (0) ( )
i p a k a m a p
a p M s
* 1
1
(30)
1 ( )
i
a k
a M s
Saat s0, 0 sehingga ki* tidak terdefinisi. Dalam hal ini hanya bisa ditemukan sifat batas secara numerik dengan mensubstitusikan ekspansi deret Taylor untuk
dan ω saat s0sehingga persamaan
aljabarnya ˆ '(0) M(0)e.
(Bukti lihat Lampiran 10).
Diberikan akar numerik dari persamaan ini, kemudian dapat diintegralkan persamaan (29)
secara numerik dengan nilai awal
( s) '(0) s.
Jika dimisalkan 1 maka orde utama ˆ(1 s)
e K
dan persamaan aljabar untuk :
1
ˆ(1 )
ˆ(1 ) 1
1 1
( 1) ( ) 1
( ) ( ) ( ) ( ) 0.
1 ( )
s a
s a M s e
M s e K
a a K
(31) Secara umum, solusi persamaan ini hanya bisa ditentukan secara numerik.
Untuk lebih sederhana, dimisalkan p
adalah konstan sehingga M 1. Untuk menetapkan bentuk parameter, dimisalkan bahwa asuransi menetapkan preminya 80% terhadap premi pasar sehingga exposure asuransi akan meningkat sebesar 40% setelah satu tahun. Jadi, dipilih a12 dan diperoleh
1 0.256
b dari persamaan (26). Lama rata-rata polis ditetapkan selama satu tahun dan perencanaan horizon selama 10 tahun. Excess return diambil sebesar 6% dan rasio premi sebesar 0.67.
Tabel 1 Nilai Parameter Fungsi Permintaan Hukum Pangkat
Waktu Horizon T 10 tahun
Pertumbuhan permintaan a1
2
Parameter Permintaan b1 0.256 per tahun
Penurunan Kekayaan α 0.06 per tahun
Rasio break-even terhadap premi rata-rata γ
0.67
Lama rata-rata polis
τ = -1
1 per tahun
Berikut diberikan hasil simulasi untuk fungsi permintaan hukum pangkat dengan menggunakan parameter pada Tabel 1.
0.2 0.4 0.6 0.8 1.0
1.0 0.8 0.6 0.4 0.2 0.0
s (i)
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
s (ii)
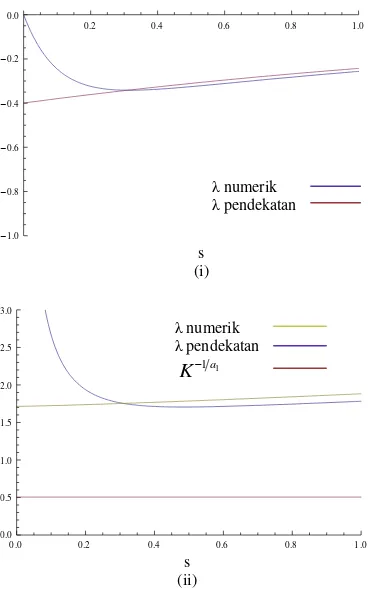
Gambar 4 Strategi optimum untuk fungsi permintaan hukum pangkat G dengan parameter pada Tabel 1
Gambar 4 menunjukkan solusi numerik dari persamaan (29) dan (31) untuk perbandingan dengan data pada Tabel 1. Strategi dimulai dari s1 bersesuaian dengan
0
t sampai s0 bersesuaian dengan
tT. Dari persamaan (15), persamaan state untuk exposure adalah
1
1
1 1
1
( )
( ( ) )
( )
( ) . (32)
a a
dq n q dt
q G k q dt
q b k K b q dt
dq q b k K dt
Hal ini bisa dilihat Gambar 4 (ii) bahwa strategi optimum ki* selalu di atas 1
1a K
sehingga exposure menurun secara
eksponensial dengan waktu t meningkat. Jadi parameter ini menetapkan strategi optimum yang menjelaskan strategi keluar dari pasar.
numerik pendekatan
numerik pendekatan
0.0 0.2 0.4 0.6 0.8 1.0 0.0
0.5 1.0 1.5 2.0 2.5 3.0
s
ki
(i)
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
s
ki
(ii)
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
s
ki
(iii)
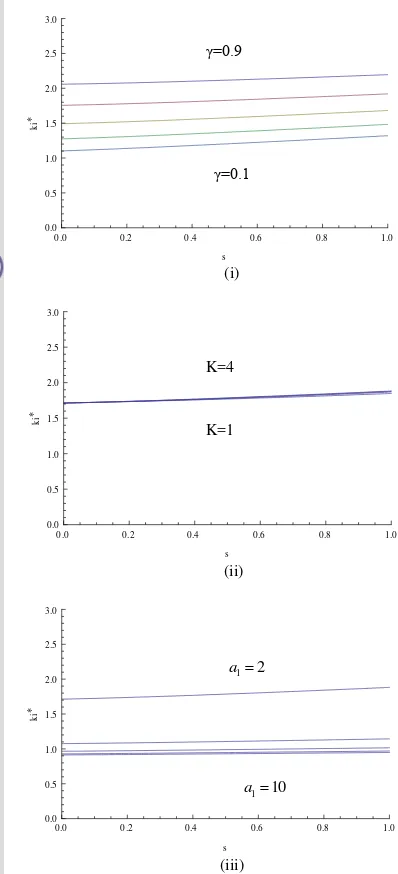
Gambar 5 Sensitifitas strategi optimum terhadap model parameter untuk fungsi permintaan hukum pangkat G
Kontrol optimum adalah fungsi dari parameter γ, K, a1, ε, dan ˆ. Gambar 5
menunjukkan kontrol optimum yang berbeda jika salah satu parameter bervariasi sedangkan sisanya diambil dari Tabel 1. Kontrol optimum menunjukkan untuk γ = 0.1 sampai dengan 0.9 dengan langkah 0.2 pada Gambar 5 (i), K = 1 sampai dengan 4 dengan langkah 1 pada Gambar 5 (ii), dan a1 = 2 sampai
dengan 10 dengan langkah 2 pada Gambar 5 (iii).
Dengan meningkatkan γ, premi relatif optimum meningkat dan perusahaan asuransi melakukan repricing. Untuk K, strategi optimum tidak terpengaruh oleh K. Jika K cukup kecil (sesuai dengan lama polis) maka persamaan (32) menunjukkan bahwa exposure
bisa tumbuh secara eksponensial tetapi premi relatif optimum masih besar dibandingkan premi rata-rata pasar. Pada saat lama rata-rata waktu polis lebih panjang dari perencanaan horizon T maka sangat sedikit pemegang polis
meninggalkan asuransi dengan premi
berapapun yang ditetapkan: nasabah terus membayar tingkat premi yang ditetapkan saat awal polis. Keterbatasan model ini adalah lama rata-rata waktu polis bebas terhadap tingkat premi.
Dari Gambar 5 (iii) bisa dilihat bahwa parameter pertumbuhan permintaan a1
meningkat, premi optimum menurun di bawah premi rata-rata pasar. Untuk kisaran parameter dikaji pada premi relatif optimum di atas
1 1
0.5
a
K sehingga strategi premi menuju ke penarikan dari pasar. Hal ini jelas bahwa strategi premi sangat bergantung pada parameter permintaan. Diketahui bahwa untuk parameter yang dipilih menetapkan premi relatif optimum ki*
, yang berarti bahwapsehingga tidak ada strategi yang loss-leading.
3.4.2 Fungsi Permintaan Linear
Parameter produk dan polis baru
disederhanakan dengan
2 2 2
2
( ) jika
0 jika
a b k k b
G
k b
dengan a2 0memiliki satuan per unit waktu dan b2 konstan. Diketahui bahwa G adalah parameter yang berbeda dengan g di (3) karena G adalah fungsi tak negatif yang menjelaskan karakteristik permintaan pada new business dibanding perubahan di bagian tertentu pada eksposure.
Hamiltonian pada kasus ini adalah
1 2 2 2 2 2
( ) ( ( ) ) ( ( ) ) t
Q p p Q
H F f
e m q m q a b k q k a b k m m
dengan turunan pertama dan kedua
2 1 2 2 2 2 2
2 1 2 2 2
2 2
2
( 2 )
2
k p p
p kk
H a q q a b m q a k m
a q q a m b k
H q a k
jika kb2. Oleh karena itu maksimum H pada saat
1 2
a
K=4
K=1
γ=0.λ
γ=0.1
1 10
2 1 2 2 2 2 1 2 2 2 1 2 2 0
( 2 ) 0
2 2 k p p p H
a q q a m b k
a q
b k
q a m
b k m * 1 2 2 1 ( ) 2 i p k b m
(34)
yang memberikan strategi interior optimum dengan 0ki* b2dan 2 0.
Persamaan adjoin menentukan kontrol interior optimum:
* * *
1
1 2 2 2 2 2
1 2 2 2 2 2
( ( ( ) ) ( ) ) ( ( ) ) ( ) q t p p t
p i i i p
H
m e a b k a k b k m
m e a b k a k b k m
(35) dengan syarat batas1( )T 0. Pengali Lagrange kedua hanya merupakan fungsi dari t sehingga persamaan (34) dapat disubstitusi ke (35) sehingga diperoleh:
2 2
2 2 2
2 2 2 1
1 1
2
( )
2 4 4
p t
p
p
a b m
a b a
m e m (36) (Bukti lihat Lampiran 11)
yang merupakan persamaan Riccati.
Kemudian dilakukan skala ulang
menggunakan peubah:
2 2 2 1 (0) (1 ) p (0) ( )
a a p tT s m p M s
(37) dan parameter penondimensionalan:
1
2 ( 2 ) ˆ .
K a a T T
Diketahui bahwa definisi dari K dan ε telah berubah dari bagian sebelumnya karena perubahan fungsi permintaan. Dari persamaan (15) eksposure dibentuk oleh:
2 2 2
2 2
( ) ;
(38) ;
q a b k K k b
dq
q a K k b
Jika kb2maka polis berakhir pada tarif yang lebih tinggi daripada tarif dimana new business yang dihasilkan terlepas dari tarif premi relatif. Hal ini tidak realistik sehinggakb2.
Persamaan Riccati dengan skala ulang adalah
2 2
ˆ(1 )
2 ( ) 2
( ) ( ) ,
4 2 4 ( )
s
b M s b
d
K M s e
ds M s
(39) (Bukti lihat Lampiran 12)
dengan
ˆ(1 ) ˆ
( ) (1 ) ˆ ( ) K s s e e K
(40)
dan syarat batas adalah (0)0. Dalam hal ini peubah baru strategi interior optimum adalah * 1 2 2 2 1 ( ) 2 (0) 1 ( )
2 (0) ( )
i p k b m p b
p M s
* 2 1 ( )
2 ( )
i
k b
M s
(41)
asalkan
M
. Karena 0 saat 0s maka *
i
k tidak terdefinisi pada akhir
waktu horizon. Jika dimisalkan cukup dekat
dengan s0 maka ekspansi deret Taylor
disubstitusikan pada persamaan (39) sehingga diperoleh
* 2
1
( ) ; 0 .
2
i
k b s (42) (Bukti lihat Lampiran 13)
Ekspresi ini memberikan tarif premi relatif optimum akhir.
Dimisalkan 1 maka untuk orde utama ˆ(1 s)
e K
dan
2 1/ 2
2 2
ˆ( 1)
2 2 ( ) )
( )
s
K b K b K K
M
K e
(43) (Bukti lihat Lampiran 14)
dengan
2 .
c b K
(44)
Dimisalkan bahwa jika perusahaan
asuransi menetapkan premi 80% terhadap
premi pasar maka akan mendapatkan
ekspo