Penentuan Premi Sistem Bonus Malus dengan Menggunakan Fungsi Utilitas Eksponensial

(1)

ABSTRAK

MEGAWATI. Penentuan Premi Sistem Bonus Malus dengan Menggunakan Fungsi Utilitas Eksponensial. Dibimbing oleh I GUSTI PUTU PURNABA dan RETNO BUDIARTI.

Sistem Bonus Malus merupakan salah satu sistem yang digunakan dalam asuransi mobil. Sistem ini memperkenalkan pembagian kelas premi yang dipengaruhi oleh banyaknya klaim yang diajukan oleh pemegang polis tiap tahunnya.

Dalam karya ilmiah ini, dibahas mengenai penghitungan premi pada sistem Bonus Malus untuk pertanggung-jawaban pihak ketiga pada asuransi mobil dengan menggunakan dua cara yang berbeda, namun keduanya tetap menggunakan fungsi utilitas eksponensial. Cara yang pertama yaitu dengan menerapkan prinsip utilitas nol (zero utility) menggunakan fungsi utilitas eksponensial. Cara yang kedua adalah memperoleh kesimetrisan antara biaya yang lebih (overcharges) dan biaya yang kurang (undercharges) dengan memberikan bobot pada keduanya melalui pendekatan fungsi utilitas, dengan tujuan memberikan pinalti pada kelebihan biaya (penalization of overcharges) tersebut.

Untuk membandingkan sistem perhitungan pada kedua pendekatan tersebut, sebelumnya diberikan prinsip nilai harapan. Banyaknya klaim masing-masing polis diasumsikan menyebar Poisson dengan fungsi sebaran parameternya adalah sebaran gamma; dan menghasilkan sebaran tak bersyaratnya yaitu sebaran binomial negatif. Dicari sebaran posterior dari parameter frekuensi klaim, kemudian parameter tersebut diduga menggunakan teknik pendugaan Bayes.

(2)

ABSTRACT

MEGAWATI. Determination of Bonus Malus System’s Premium Using Utility Exponential Function. Under supervision of I GUSTI PUTU PURNABA and RETNO BUDIARTI.

A Bonus Malus system is one of systems used in the automobile insurance. This system introduces the clasification of premium level, which is influenced by the number of claims from the policyholder every year.

This paper discusses premium calculation on Bonus Malus system for automobile third party liability insurance with two different methods, which both are based on exponential utility functions. The first method is carried out by applying the principle of zero utility using the exponential utlilty function. The second method is formulated by breaking the symmetry between overcharges and undercharges by weighting them differently in the utility function in order to penalize the overcharges.

In order to compare the calculation methods of both approaches, the expected value principle should be given in advance. Number of claims from each policyholder is assumed to follow Poisson distribution, while the parameters follow the gamma distribution. This leads to an unconditional negative binomial distribution. The posterior distribution of frequency claim parameter is to be determined in order to estimate the parameters using Bayes estimation technique.

The premium calculation on Bonus Malus system using expected value and zero utility principle implies very high cost for high risk. In the Bonus Malus premium using the penalization of overcharges approach, the ratio between extreme premiums is reduced to produce a smaller Malus. Therefore, the most appropriate premium for policyholder in every class is the premium which applies penalization of overcharges.

(3)

I PENDAHULUAN

Latar Belakang

Asuransi merupakan transaksi pertanggungan yang melibatkan dua pihak yaitu tertanggung dan penanggung. Pihak penanggung menjamin pihak tertanggung yang akan mendapatkan penggantian terhadap suatu kerugian yang mungkin akan dideritanya sebagai akibat dari suatu peristiwa yang semula belum tentu akan terjadi atau belum dapat ditentukan saat atau kapan terjadinya. Di lain pihak si tertanggung diwajibkan membayar sejumlah uang kepada si penanggung yang besarnya sekian persen dari nilai pertanggungan, yang biasa disebut premi. Setiap perusahaan asuransi menerapkan sistem penetapan premi yang berbeda-beda. Salah satu sistem yang ditawarkan oleh perusahaan asuransi adalah sistem Bonus Malus.

Sistem Bonus Malus merupakan salah satu sistem yang digunakan dalam asuransi mobil. Sistem ini memperkenalkan pembagian kelas premi yang dipengaruhi oleh banyaknya klaim yang diajukan oleh pemegang polis tiap tahunnya. Pada sistem ini, pemegang polis yang tidak mengajukan klaim akan diberikan penurunan premi yang disebut sebagai ’Bonus’ sedangkan bagi pemegang polis yang telah mengajukan satu atau lebih klaim akan dikenakan kenaikan premi yang disebut sebagai ’Malus’.

Pada karya ilmiah ini dibahas mengenai penghitungan premi pada sistem Bonus Malus untuk pertanggung-jawaban pihak ketiga pada asuransi mobil dengan menggunakan dua cara berbeda, namun keduanya tetap menggunakan fungsi utilitas eksponensial. Cara pertama yaitu dengan menerapkan prinsip utilitas nol (zero utility) menggunakan fungsi utilitas eksponensial dan cara kedua yaitu memperoleh kesimetrisan antara biaya yang lebih (overcharges) dan biaya yang kurang (undercharges) dengan memberikan bobot pada kedua-duanya melalui pendekatan fungsi utilitas, dengan tujuan memberikan pinalti terhadap overcharges tersebut.

Tujuan

Tujuan penulisan karya ilmiah ini adalah:

1. Mempelajari penghitungan premi pada sistem Bonus Malus untuk pertanggung-jawaban pihak ketiga pada asuransi mobil.

2. Mempelajari perbandingan penghitungan premi pada sistem Bonus Malus dengan dua pendekatan yang berbeda yaitu utilitas nol (zero utility) dan pinalti pada

kelebihan biaya (penalization of

overcharges).

II LANDASAN TEORI

Ruang Contoh, Kejadian dan Peluang

Definisi 1 (Percobaan Acak)

Dalam suatu percobaan seringkali dilakukan pengulangan yang dilakukan dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul adalah diketahui, tetapi hasil pada percobaan berikutnya tidak dapat diduga dengan tepat. Percobaan semacam ini disebut percobaan acak.

(Hogg & Craig 1995)

Definisi 2 (Ruang Contoh dan Kejadian)

Himpunan dari semua kemungkinan hasil dari suatu percobaan acak disebut ruang

contoh, dinotasikan dengan Ω. Suatu

kejadian A adalah himpunan bagian dari Ω. (Grimmett & Stirzaker 1992)

Definisi 3 (Medan-σ)

Medan-σ adalah suatu himpunan F

yang anggotanya terdiri atas himpunan bagian dari ruang contoh Ω, yang memenuhi kondisi berikut:

1. ∅ ∈F _,

2. Jika A A1, 2,...∈ F maka 1

i i

A

∞ =

∈

U

F _,

3. Jika A∈F _maka c

A ∈F _.

(Grimmett & Stirzaker 1992)

Definisi 4 (Ukuran Peluang)

Misalkan F _{adalah medan-}σ _{dari ruang}

contoh Ω. Ukuran peluang adalah suatu fungsi P:F → ⎡ ⎤_{⎣ ⎦}0,1 pada (Ω,F < yang memenuhi:

(4)

I PENDAHULUAN

Latar Belakang

Tujuan

overcharges).

II LANDASAN TEORI

Ruang Contoh, Kejadian dan Peluang

(Hogg & Craig 1995)

Definisi 3 (Medan-σ)

1. ∅ ∈F _,

2. Jika A A1, 2,...∈ F maka 1

i i

A

∞ =

∈

U

F _,

A ∈F _.

(5)

2. Jika A A1, 2,...∈F adalah himpunan yang

saling lepas yaitu A1∩A2= ∅ untuk

setiap pasangan i≠j, maka

( )

1 1

i i

P A P A

∞ ∞

= =

⎛ ⎞

=

⎜ ⎟

⎝

U

⎠

∑

.

Peubah Acak dan Fungsi Sebaran

Definisi 5 (Peubah Acak)

Misalkan F _{adalah medan-}σ_{dari ruang}

contoh Ω. Suatu peubah acak Xadalah suatu fungsi X:Ω→ℜ dengan sifat

( )

{

ω∈Ω:X ω ≤x

}

∈F _{untuk setiap}x∈ℜ. (Grimmett & Stirzaker 1992)

Definisi 6 (Peubah Acak Diskret)

Peubah acak Xdikatakan diskret jika nilainya hanya pada himpunan bagian yang terhitung dari ℜ.

Catatan:

Suatu himpunan bilangan C disebut terhitung jika C terdiri atas bilangan terhingga atau anggota C dapat dikorespondensikan 1-1 dengan bilangan bulat positif.

Definisi 7 (Fungsi Sebaran)

MisalkanX adalah suatu peubah acak dengan ruang contoh Ω. Misalkan kejadian

(

, ,

A= −∞x⎤⎦⊂ Ω maka peluang dari kejadianA

adalah

( )

(

)

( )

X X

P A =P X≤x =F x .

Fungsi FX disebut fungsi sebaran dari peubah

acak X.

(Hogg & Craig 1995)

Definisi 8 (Peubah Acak Kontinu)

Peubah acak X dikatakan kontinu jika ada fungsi fX(x) sehingga fungsi sebaran

∫

∞ −

= x

X X x f u du

F ( ) ( ) ,

x∈ℜ, dengan f:ℜ →⎡⎣0,∞

)

adalah fungsi yang terintegralkan. Fungsi fXdisebut fungsi

kepekatan peluang dari X.

Definisi 9 (Fungsi Massa Peluang Untuk Peubah Acak Diskret)

Fungsi massa peluang dari peubah acak diskret X adalah fungsi p:ℜ→

[ ]

0,1 yang diberikan oleh

) ( )

(x P X x

p_X = = .

Definisi 10 (Sebaran Poisson)

Suatu peubah acak X dikatakan

menyebar Poisson dengan parameter ,λ jika memiliki fungsi massa peluang

! ) ; (

x e x p

x X

λ

λ = −λ ,x=0,1,2,...dengan λ>0.

(Hogg & Craig 1995)

Definisi 11 (Sebaran Binomial Negatif)

Suatu peubah acak N dikatakan menyebar binomial negatif dengan parameter r dan p, dinotasikan BN(r,p) jika memiliki fungsi massa peluang:

;

1

( ) [ ] r n 0,1, 2,...,

N

r n

p n N n p q n

n

+ −

= Ρ = =

⎛

⎜

⎞

⎟

=

⎝

⎠

denganr>0,0< <p 1, dan q= −1 p. (Hogg & Craig 1995)

Definisi 12 (Sebaran Gamma)

menyebar gamma dengan parameter α dan β, dinotasikan gamma

(

α β,

)

, jika memiliki fungsi kepekatan peluang

∈ Γ

= − −

x e x x

f x;

) ( )

( α 1 β

α

α β

ℜ+_,

dengan α>0, β>0, dan Γ(α)>0, dimana

∫

∞ − −

= Γ

0

1 _.

)

(α yα e ydy

(Hogg & Craig 1995)

Definisi 13 (Fungsi Sebaran Bersama Dua Peubah Acak)

Fungsi sebaran bersama dua peubah acak

X dan Y merupakan suatu fungsi

2

: [0,1]

F ℜ → yang didefinisikan sebagai

( )

,

(

,

)

XY

F x y =P X≤x Y≤y .

Definisi 14 (Fungsi Kepekatan Peluang Bersama dan Marjinal)

Misalkan X dan Y peubah acak kontinu, maka fungsi kepekatan peluang bersama dari

(6)

( )

2

( )

,

, XY

XY

F x y

f x y

x y

∂ =

∂ ∂ ,

dan fungsi kepekatan peluang marjinal dari peubah acak Y adalah

( )

,

Y XY

f y f x y dx

∞

−∞

=

∫

.

Definisi 15 (Fungsi Kepekatan Peluang Bersyarat)

Misalkan X dan Y adalah peubah acak kontinu dengan fungsi kepekatan peluang marjinal dari Y adalah fY

( )

y > 0. Maka fungsi kepekatan peluang bersyarat dari X dengan syarat Y=y adalah

(

)

( )

|

,

| XY

X Y

Y

f x y

f y

= .

Definisi 16 (Sebaran Khi-kuadrat)

menyebar khi-kuadrat dengan parameterr, jika memiliki fungsi kepekatan peluang

( )

21 2

2

; , 0 2 2

r x

X r

x e

f x r x

r

− ₋

= < < ∞

⎛ ⎞ Γ⎜ ⎟ ⎝ ⎠

,

dengan r>0

.

(Hogg & Craig 1995)

Definisi 17 (Sebaran Prior)

Suatu peubah acak X dengan parameter

θ memiliki fungsi kepekatan peluang

bersyarat yang dinotasikan dengan

(

1,..., n|

)

f x x θ dan u

( )

θ adalah fungsi

kepekatan marjinal dari θ, dinamakan

sebaran prior.

(Arnold 1990)

Definisi 18 (Sebaran Posterior)

Suatu peubah acak X merupakan

sebaran prior dengan fungsi kepekatan peluang bersyarat f x

(

1,...,xnθ

)

dan θ

memiliki fungsi kepekatan peluang u

( )

θ , maka fungsi kepekatan peluang bersama dari

( )

x,θ dinotasikan dengan U

(

θ x x1, 2,...,xn

)

,

dinamakan sebaran posterior, dinyatakan dengan

(

)

(

1 2

) ( )

2 1

1 2

, ,..., | , ,...,

, ,..., |

n n

n

f x x x u U x x x

f x x x u d

θ θ

θ

θ θ θ

=

∫

.

(Arnold 1990)

Nilai Harapan, Ragam dan Momen

Definisi 19 (Nilai Harapan)

1. Jika X adalah peubah acak diskret

dengan fungsi massa peluang pX

( )

x ,

maka nilai harapan dari X, dinotasikan dengan E X

( )

, adalah

( )

X

( )

x

E X =

∑

x p x ,

asalkan jumlah di atas konvergen mutlak. 2. Jika X adalah peubah acak kontinu

dengan fungsi kepekatan peluang fX

( )

x ,

maka nilai harapan dari Xadalah

E X

( )

x fX

( )

x dx

∞ −∞

=

∫

,

asalkan integral di atas konvergen mutlak. (Hogg & Craig 1995)

Definisi 20 (Nilai Harapan Bersyarat)

Misalkan X dan Y adalah peubah acak kontinu dan fX Y|

(

x y|

)

adalah fungsi

kepekatan peluang bersyarat dari X dengan syarat Y=y, maka nilai harapan dari X dengan syarat Y=y adalah

[

|

]

X Y|

(

|

)

E X Y y x f x y dx

∞

−∞

= =

∫

.

(Hogg & Craig 1995)

Definisi 21 (Ragam)

Ragam dari peubah acak X adalah nilai harapan kuadrat selisih antara X dengan nilai harapannya. Secara matematis dapat dituliskan sebagai

( )

(

)

(

)

2

2 2

. Var X E X E X

E X E X

⎡ ⎤

= _⎢ − ⎡ ⎤_{⎣ ⎦} _⎥

⎣ ⎦

⎡ ⎤

= _⎣ _⎦− ⎡ ⎤_{⎣ ⎦}

(Hogg & Craig 1995)

Definisi 22 (Momen)

1. Jika X adalah peubah acak diskret

dengan fungsi massa peluang p_X(x), maka momen ke-k dari X, didefinisikan sebagai

( ) ( )

1

i X i

k i k

x p x X

E

∑

∞

=

= ,

jika jumlah di atas konvergen. Jika jumlah di atas divergen, maka momen ke-k dari peubah acake-k X adalah tidake-k ada. 2. Jika X adalah peubah acak kontinu

dengan fungsi kepekatan peluang fX

( )

x ,

(7)

∫

∞

∞ −

= x f x dx X

E( k) k _X( ) ,

jika integral di atas konvergen. Jika integral di atas divergen, maka momen ke-k dari peubah acak X adalah tidak ada.

Definisi 23 (Fungsi Pembangkit Momen)

Fungsi pembangkit momen dari suatu peubah acak X didefinisikan sebagai

) ( )

( tX

X t Ee

M = .

untuk t∈ℜ sehingga nilai harapan di atas ada.

Fungsi Kemungkinan (Likelihood)

Definisi 24 (Fungsi Kemungkinan)

Misalkan X1,...,Xn adalah contoh acak

dari suatu sebaran dengan fungsi kepekatan peluang f x

( )

;θ , maka fungsi kepekatan peluang bersama dari X1,...,Xn yang

merupakan fungsi kemungkinannya adalah

( )

(

1;

) (

2;

) (

... n;

)

L θ = f x θ f x θ f x θ

(Hogg & Craig 1995)

Definisi 25 (Penduga Kemungkinan Maksimum )

Misalkan X1, X2,..., Xn adalah contoh acak

berukuran n dari suatu sebaran dengan fungsi kepekatan peluang f(x;θ). Penduga kemungkinan maksimum bagi θ dinotasikan

dengan θˆ , adalah nilai θ yang

memaksimumkan fungsi kemungkinan )

; ,..., (X1 Xn θ

L .

(Hogg & Craig 1995)

Statistik dan Penduga

Definisi 26 (Statistik)

Statistik adalah suatu fungsi dari satu atau lebih peubah acak yang tidak bergantung pada satu atau beberapa parameter yang nilainya tidak diketahui.

(Hogg & Craig 1995)

Definisi 27 (Penduga)

Misalkan X1,...,Xn adalah contoh acak.

Suatu statistik U X

(

1,...,Xn

)

yang digunakan

untuk menduga fungsi parameter g

( )

θ ,

dikatakan sebagai penduga (estimator) bagi

( )

g θ , dilambangkan oleh gˆ

( )

θ .

Jika nilai X1=x X1, 2 =x2,...,Xn=xn, maka

nilai U(x1,...,xn) disebut sebagai dugaan (estimate) bagi g

( )

θ .

(Hogg & Craig 1995)

Definisi 28 (Penduga Takbias)

(i) Suatu penduga yang nilai harapannya sama dengan parameter g

( )

θ yaitu

(

1,..., n

)

( )

E U X⎡_⎣ X ⎤_⎦=g θ disebut

penduga takbias bagi parameter g

( )

θ . Jika sebaliknya, penduga tersebut disebut berbias.

(ii) Jika lim_n_→∞E U X⎣⎡

(

1,...,Xn

)

⎤⎦=g

( )

θ untuk

n→ ∞, maka U X

(

1,...,Xn

)

disebut

penduga takbias asimtotik.

(Hogg & Craig 1995)

Definisi 29 (Uji Kebaikan-Suai)

Uji Kebaikan-Suai antara frekuensi yang teramati dengan frekuensi harapan didasarkan pada besaran

(

)

∑

=

− = k

i i i i

e e o

1

2

2 _,

χ

sedangkan χ2 merupakan statistika yang menyebar khi-kuadrat. Lambang oi dan ei

menyatakan frekuensi teramati dan frekuensi harapan bagi sel ke-i.

(Walpole 1995)

Definisi 30 (Hipotesis Uji Kebaikan-Suai)

Uji hipotesis adalah salah satu uji statistika yang dilakukan untuk pengujian kesesuaian parametrik β_i yang dibuat. Dengan hipotesis sebagai berikut:

H0: β_i=0

H1: βi ≠0

Maka dengan menggunakan nilai dari khi-kuadrat hitung dan khi-khi-kuadrat tabel akan berlaku pengambilan kaidah keputusan sebagai berikut. Jika χ_hit2 >χ_tabel2 maka hipotesis nol di atas ditolak dan jika

2 2

tabel hit χ

χ < maka hipotesis nol diterima.

Dalam penentuan khi-kuadrat tabel diperlukan besaran nilai p-value tertentu berdasarkan penyesuaiannya.

(8)

III PEMBAHASAN

Setiap perusahaan asuransi menerapkan sistem penetapan premi yang berbeda-beda. Salah satu sistem yang ditawarkan adalah sistem Bonus Malus.

Penghitungan premi pada sistem Bonus Malus pada karya ilmiah ini menggunakan dua pendekatan yang berbeda, namun pendekatan tersebut tetap menggunakan fungsi utilitas eksponensial.

Sebelumnya diberikan prinsip nilai harapan untuk membandingkan sistem penghitungan premi pada kedua pendekatan tersebut.

Prinsip Nilai Harapan

Dalam penentuan tarif untuk pertanggung-jawaban pihak ketiga pada asuransi mobil, para pemegang polis biasanya dibedakan oleh dua macam variabel pembeda yaitu himpunan dari faktor-faktor prior (misalnya jenis dan penggunaan mobil, umur dan jenis kelamin dari pengemudi, lokasi) dan skema klasifikasi posterior (berdasarkan banyaknya kecelakaan yang dialami oleh pemegang polis).

Terlebih dahulu diberikan kelas-kelas dari resiko yang ada, dengan faktor-faktor prior yang sudah ditetapkan dan diasumsikan variabel-variabel lainnya tidak berpengaruh terhadap kehomogenan kelas-kelas resiko tersebut. Masalah yang dihadapi adalah mencari besarnya premi yang optimal pada sistem Bonus Malus dengan tujuan untuk membiayai masing-masing polis sebesar nilai yang proporsional terhadap banyaknya klaim diharapkan yaitu

]. [S E

P= Pernyataan di atas merupakan

prinsip nilai harapan.

Dari contoh-contoh numerik, dapat diasumsikan bahwa banyak dari klaim untuk masing-masing polis adalah menyebar Poisson. ), 0 ( ! ) |

( = = >

− λ λ λ λ k e k K P k

K (1)

dengan λmerupakan nilai dari suatu peubah

acak Λ yang menyebar gamma dengan

fungsi sebaran U(λ), sehingga dU(λ) dapat dituliskan:

( , 0).

) ( ) ( 1 > Γ =τ − λ − λ τ

λ τ d a

a e dU a a a (2)

Sebaran Λ memiliki rata-rata

τ

a

m= ,

ragam 2 ₂

τ

σ = a dan fungsi pembangkit

momen () 1 ( τ)

τ⎟⎠ < ⎞ ⎜ ⎝ ⎛ − = − t t t M a .

Bukti disajikan pada Lampiran 1.

Sebaran tak bersyarat dari peubah acak K merupakan sebaran binomial negatif dengan fungsi massa peluangnya adalah

( )

∫

∞ − − − ∞ Γ = = = 0 1 0 ! ) ( ) ( ) ( λ λ τ λ λ λ τλ λ d a e k e dU k K P k P a a k K

( )

λ λ

τ _e λ τ _d

a k a k a

∫

∞ − + + − Γ = 0 1 ) 1 ( !

( )

( ) 1 1 ! 1 1 ! ₀ 1 a k a k du u e a k a k a a k u a k a + Γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + Γ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + Γ = + ∞ − + − +

∫

τ τ τ τ

( )

a k a k a k _⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + Γ + Γ = τ τ τ 1 1 1 ! ) ( a k a k a k ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − − + = τ τ τ 1 1 1 )! 1 ( ! )! 1 ( . 1 1 1

1 k a

k a k ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + − = τ τ

τ (3)

Dari hasil yang diperoleh di atas, kemungkinan banyaknya klaim dalam portofolio pada suatu periode tertentu memiliki sebaran binomial negatif dengan parameter

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ +τ τ 1 ,

a . Penguraian sebaran binomial negatif

tersebut disajikan pada Lampiran 2.

(9)

Tabel l Data banyaknya kecelakaan kendaraan bermotor

Banyak klaim Frekuensi

Teramati Dugaan (Poisson) Dugaan (binomial negatif)

0 96978 96689.5 96985.6

1 9240 9773.5 9222.3

2 704 494 711.7

3 43 16.6 50.7

4 9 0.4 3.5

Lebih dari 4 0 0 0.2

Total 106974 106974 106974

.

Misalkan kelas-kelas resiko telah diperoleh dari hasil amatan selama t tahun, dan didefinisikan kl(l=1,....,t) sebagai banyaknya klaim yang muncul selama tahun

l. k_l tersebut merupakan nilai dari peubah

acak Kl, yang diasumsikan bebas

(independent) dan memiliki sebaran yang sama (equidistributed). Untuk setiap himpunan dari amatan (k₁,...,k_t), harus dikaitkan pada suatu premi

) ,...., ( 1 1

1 t t

t P k k

P+ = + .

Jika P(k₁,....,ktλ) dinotasikan sebagai kemungkinan bahwa pemegang polis dengan

parameter λ akan mengajukan klaim

dengan urutan (k₁,...,k_t), maka sebaran posterior dari λ yaitu

) (

) ( ) ,..., (

) ( ) ,..., ( ) ,..., (

1 ) ( 1 0

1 1 1

1 1

a k

t e

dU k k P

dU k k P k k dU

t

l l

a k t

a k

t t t

t

l l t

l l

+ Γ

+ =

=

∑

∫

=

+ +

− − + ∞

∑ ∑

=

= τ

λ

λ λ

λ λ λ

τ λ

. ) ' (

' '

' 1 '

λ τ

λ λτ

d a

e a

a Γ

= − −

(4) Sebaran posterior tersebut memiliki parameter a'=a+k dan τ'=t+τ dengan

∑

=

= t l

l

k k

1

adalah total dari banyaknya

klaim. Uraian sebaran posterior tersebut disajikan pada Lampiran 3.

Dari hasil yang diperoleh ternyata sebaran posterior terhadap frekuensi klaim

λ juga merupakan sebaran gamma dengan parameter 'a dan 'τ .

Prinsip nilai harapan merupakan definisi dari premi Pt+1(k1,....,kt) dengan

∫

∞

+ = +

0

1

1 (1 ) ( ,..., t)

t K dU k k

P α λ λ

, ' ' ) 1 (

τ α a

K +

= (5)

K merupakan nilai konstan dan αadalah biaya tambahan keselamatan (safety loading). Penguraian prinsip nilai harapan tersebut disajikan pada Lampiran 4

Safety loading biasa disebut sebagai premi kotor atau beban pada premi bersih. Misalnya biaya tambahan yang harus disediakan untuk administrasi, pajak, keuntungan perusahaan dan untuk beberapa jaminan kerugian yang menyimpang dari kejadian yang biasa terjadi.

Jadi rumus relativitas sistem Bonus Malus pada kasus ini yaitu:

∫

∞ ∞

0 0

1

) (

) ,..., ( . 100

λ λ

dU k k

dU t

τ τ

a a ' ' . 100

⇔

100 ⎟.

⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

+ + ⇔

a t

k

a τ

τ (6)

Dengan kata lain rumus tersebut merupakan premi yang harus dibayarkan oleh pemegang polis jika premi awal (t=0)sebesar 100.

(10)

Pertama-tama akan diperiksa apakah data tersebut berasal dari populasi yang

menyebar Poisson (λ). Untuk itu

digunakan uji kebaikan-suai untuk sebaran Poisson dari data tersebut dengan hipotesis:

H0: Contoh berasal dari populasi yang

menyebar Poisson.

H1: Contoh bukan berasal dari populasi yang

menyebar Poisson.

Kemudian hipotesis tersebut di uji dengan menggunakan statistik uji berikut.

Statistik uji χ2:

(

) (

)

3127 . 191

0588 . 72 2713 . 89 1218 . 29 8608 . 0

17 17 52 494

494 704 5

. 9773

5 . 9773 9240 5

. 96689

) 5 . 96689 96978 ( )

( 2 2 2 2

4 1

2 2

=

+ +

+ =

− + − + −

+ −

= − =

∑

=

i i i i

e e o

χ

Dengan

♦ oi merupakan frekuensi teramati di

kelas i, i = 1,...,6 , dan

♦ e_i merupakan frekuensi harapan dari data teramati di kelas i saat H0

benar.

Karena nilai χ2 =191.3127 > 815

. 7

2 ₌

tabel

χ maka tolak H0. Jadi dapat

disimpulkan bahwa belum cukup bukti untuk mengatakan bahwa contoh berasal dari populasi yang menyebar Poisson (0.101081). (lihat Lampiran 5)

Selanjutnya dilakukan uji kebaikan-suai untuk menguji apakah data tersebut berasal

dari populasi yang menyebar binomial negatif

⎟ ⎠ ⎞ ⎜ ⎝ ⎛

+τ τ

1 ,

a dengan hipotesis:

H0: Contoh berasal dari sebaran binomial

negatif dengan parameter ⎟

⎠ ⎞ ⎜ ⎝ ⎛

+τ τ

1 ,

a .

H1: Contoh bukan berasal dari sebaran binomial

negatif dengan parameter ⎟

⎠ ⎞ ⎜ ⎝ ⎛

+τ τ

1 ,

a .

Kemudian hipotesis tersebut di uji dengan menggunakan statistik uji berikut.

Statistik uji χ2:

(

) (

)

87001 . 8

59189 . 7 1607 . 1 0828794 . 0 0339431 . 0 10 0218 . 6

7 . 3

7 . 3 9 7 . 50

7 . 50 43 711.7

711.7 704 9222.3

9222.3 9240 96985.6

) 96985.6 96978

( ) (

4

2 2

2 5

1 2 2

=

+ + +

+ × =

− + − + −

+ −

= − =

− =

∑

i i

e e o

χ

dengan

♦ o_i merupakan frekuensi teramati di kelas i, i = 1,...,6 dan

♦ ei merupakan frekuensi harapan

dari data teramati dikelas i saat H0

benar.

Karena nilai χ2 =8.87001 <

488 . 9

2 ₌

tabel

χ maka tidak ada alasan untuk

menolak H0.

Jadi dapat disimpulkan bahwa contoh berasal dari populasi yang menyebar

binomial negatif (1.6049,0.9408). (lihat Lampiran 6)

Karena contoh data yang telah diketahui memenuhi asumsi bahwa banyaknya klaim menyebar binomial negatif maka tabel premi dapat dihitung dengan rumus

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

+ +

a t

k

a τ

τ

100 dan dengan menggunakan

(11)

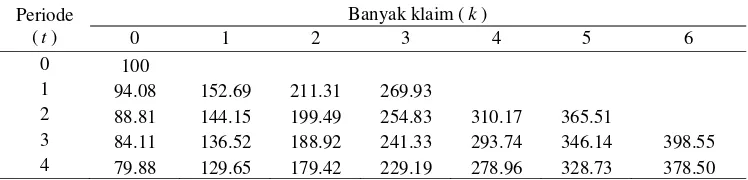
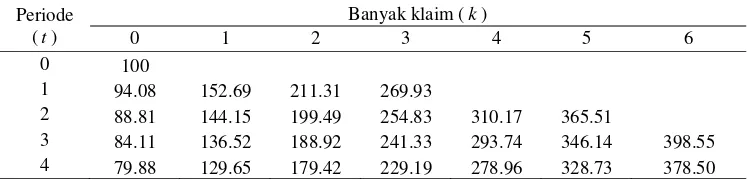
Tabel 2 Premi sistem Bonus Malus berdasarkan prinsip nilai harapan

Periode (t)

Banyak klaim (k)

0 1 2 3 4 5 6

0 100

1 94.08 152.69 211.31 269.93

2 88.81 144.15 199.49 254.83 310.17 365.51

3 84.11 136.52 188.92 241.33 293.74 346.14 398.55

4 79.88 129.65 179.42 229.19 278.96 328.73 378.50

Dari Tabel 2 di atas dapat diketahui bahwa:

♦ Pada awal mengikuti asuransi,

pemegang polis membayar premi sebesar 100 kepada perusahaan asuransi;

♦ Jika pemegang polis tidak

mengalami kecelakaan pada periode satu, maka pada periode berikutnya pemegang polis akan mendapatkan bonus sebesar 5,92% dari premi awal atau dia hanya membayar premi sebesar 94.08;

♦ Apabila pada periode berikutnya atau periode dua, pemegang polis mengalami kecelakaan maka dia dikenakan malus sebesar 50,07% dari premi periode satu atau sebesar 144.15 sehingga dia pindah kelas ke grup 1.

Pada bagian berikutnya, dapat digunakan dua pendekatan yang berbeda untuk menentukan premi sistem Bonus Malus yaitu prinsip utilitas nol (zero utility) dan pinalti pada kelebihan biaya (penalization of overcharges). Kedua pendekatan tersebut memiliki kesamaan yaitu menggunakan fungsi utilitas eksponensial. Fungsi utilitas eksponensial memiliki bentuk formula

) 1 ( 1 )

( e cx

c x

u = − − , ckonstanta positif.

(Gerber 1974a, 1974b)

(7) Fungsi utilitas u(x) merupakan fungsi kekayaan dari penanggung dan diasumsikan merupakan fungsi naik dan cekung ke bawah. Bentuk khusus ini akan digunakan kemudian.

Prinsip Utilitas Nol

Pada penerapan formula (19) pada Gerber (1974a) untuk degenerate distribution (penghitungan premi pada sistem Bonus Malus yang hanya berdasarkan pada banyaknya klaim dan tidak berdasarkan besarnya klaim secara nominal), diperoleh persamaan:

)]. 1 ( [ ; 1 1

1 ⎟⎟ < +

⎠ ⎞ ⎜

⎜ ⎝ ⎛

+ − − +

=

+ _τ c Logτ

t e Log c

k a K P

c t

(8) (Gerber 1974b)

Kredibilitas premi di atas merupakan fungsi kontinu yang tidak menurun terhadap c. Pilihan suatu c=0.4 menghasilkan suatu premi awal yang pantas (masuk akal) yaitu P1=0.1262. Saat premi murni (pure premi/premi tanpa tambahan loading) adalah sebesar 0.1011, maka akan mengakibatkan terjadinya keterkaitan terhadap biaya tambahan keselamatan (safety loading) sekitar 25%.

Pada prinsip ini jika pada awal mengikuti asuransi pemegang polis dikenakan premi sebesar 100 maka rumus sistem Bonus Malus adalah sebagai berikut:

, 1 1

1 1 100

⎟ ⎟ ⎠ ⎞ ⎜

⎜ ⎝

⎛ ₋ −

⎟ ⎟ ⎠ ⎞ ⎜

⎜ ⎝ ⎛

+ − − +

τ τ c

c

e Log c a K

t e Log c

k a K

dengan syarat

. 2273 . 1 )] 1 (

[c<Logτ+ ⇔c<

(12)

Tabel 3 Premi sistem Bonus Malus dengan pendekatan prinsip utilitas nol untuk nilai c=0.4

Periode (t)

Banyak klaim (k)

0 1 2 3 4 5 6

0 100

1 93.987 152.549 211.111 269.673

2 88.655 143.896 199.136 254.377 309.617 364.857

3 83.987 136.172 188.447 240.722 292.997 345.273 397.548

4 79.623 129.235 178.847 228.459 278.071 327.683 377.296

Perbedaan-perbedaan yang muncul sangat kecil sekali, bahkan untuk nilai c yang tidak masuk akal. Misalnya digunakan

nilai c=1.65 yaitu nilai yang

mengakibatkan terjadinya keterkaitan

terhadap biaya tambahan keselamatan (safety loading) sebesar 200%. Program untuk memperoleh nilai premi pada Tabel 4 berikut juga disajikan pada Lampiran 7.

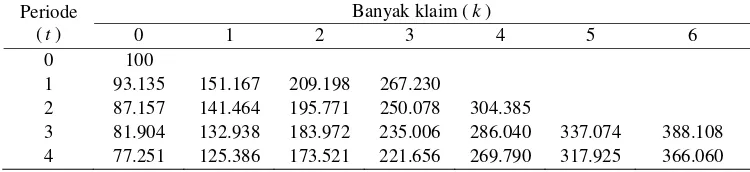
Tabel 4 Premi sistem Bonus Malus dengan pendekatan prinsip utilitas nol untuk nilai c=1.65

Periode (t)

Banyak klaim (k)

0 1 2 3 4 5 6

0 100

1 93.135 151.167 209.198 267.230

2 87.157 141.464 195.771 250.078 304.385

3 81.904 132.938 183.972 235.006 286.040 337.074 388.108

4 77.251 125.386 173.521 221.656 269.790 317.925 366.060

Nilai c tersebut menghasilkan suatu premi yang besarnya tiga kali lipat dari premi awal.

Satu hal yang perlu dicatat bahwa pada kedua kasus di atas memiliki nilai premi yang lebih rendah dibandingkan dengan Tabel 2. Hal ini secara alami akan berimplikasi terhadap nilai premi awal yang lebih tinggi.

Pinalti pada Kelebihan Biaya

Pada sebaran posterior untuk frekuensi klaim seperti yang terdapat pada prinsip utilitas nol (lihat Gambar 1), akan ditelusuri bahwa sebaran-sebaran tersebut secara substansial berpotongan. Perolehan Gambar 1 disajikan pada Lampiran 8. Semua pemegang polis dari grup 2 harus membayar premi yang lebih besar 2.24 kali

(13)

Gambar 1 Grafik perpotongan pada sebaran posterior untuk frekuensi klaim antara grup awal )

0

(k= saat t = 3 dan grup 2 (k=2) saat t = 3 Tarif yang diperoleh melalui prinsip

nilai harapan memiliki sifat yang khas yaitu dengan cara meminimumkan jumlah dari kuadrat galat yang muncul untuk overcharges dan undercharges keseluruhan polis pada grup yang ada serta menjamin stabilitas keuangan yang berkaitan terhadap premi-premi yang akan berpengaruh dan berkompensasi terhadap harapan kerugian yang muncul pada waktu t. Bagaimanapun juga hal ini terlihat tidak wajar (tidak adil) dalam sudut pandang pemegang polis,

dimana overcharges dan undercharges

dirumuskan secara simetris sehingga pemegang polis yang membayar premi terlampau mahal atau terlampau murah diperlakukan dan dinilai sama. Satu sisi akan berpendapat bahwa galat yang terjadi akan lebih parah dibandingkan yang lainnya. Oleh

karena itu perlu adanya perlakuan adil untuk membedakannya yaitu dengan cara memboboti tingkat galat pada keduanya menggunakan pinalti pada kelebihan biaya (penalizing of overcharges).

Saat semua peserta pada grup 2 harus membayar pada jumlah yang sama, maka premi juga harus diperkecil. Konsekuensinya premi pada grup awal harus ditingkatkan dengan tujuan untuk menutupi keseimbangan keuangan. Bagaimanapun juga, sebagai kelas resiko yang lebih tinggi biasanya selalu merupakan populasi terkecil sehingga peningkatan terhadap premi pada grup awal akan sedikit sekali.

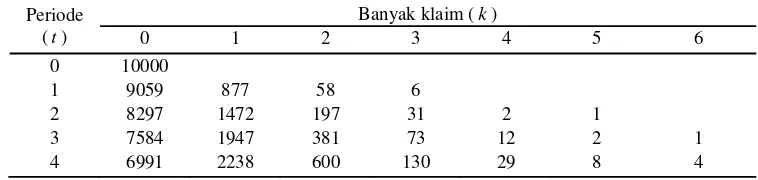
Pada kenyataannya, populasi pada subgrup akan menurun seiring terjadinya penambahan pada nilai k. Di bawah ini merupakan ilustrasi dari populasi yang dimaksud.

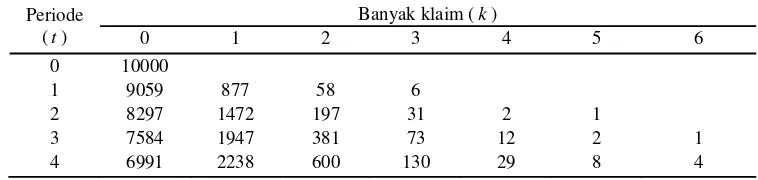
Tabel 5 Banyaknya populasi tiap subgrup pada kelas-kelas resiko

Periode (t)

Banyak klaim (k)

0 1 2 3 4 5 6

0 10000

1 9059 877 58 6

2 8297 1472 197 31 2 1

3 7584 1947 381 73 12 2 1

4 6991 2238 600 130 29 8 4

Konsekuensinya adalah hanya diperlukan peningkatan premi pada grup awal sebesar 1 satuan untuk kontribusi terhadap grup 2 sebesar 20 satuan. (Lemaire 1979).

Satu cara untuk menyelesaikan masalah ketidaksimetrisan yaitu dengan mengindeks

(14)

Kemudian dicari rumus untuk penentuan premi sistem Bonus Malus dengan menggunakan pendekatan pinalti pada kelebihan biaya.

Untuk memberikan nilai t, terlebih dahulu perlu dinotasikan:

♦ m+1 merupakan jumlah dari grup (m adalah nilai maksimum dari k),

♦ N_k merupakan ukuran populasi grup ke-k, ♦

∑

= = m k k N N 0 ,

♦ pk =Pt+1(k1,...,kt),

♦ dU(λk)=dU(λk₁,...,k_t), dan

♦ ( ). 0

∫

∞ = λ λ λ dU

Dengan menggunakan fungsi utilitas eksponensial dan menggunakan argumen yang sama dengan perbedaan antara premi

k

P dan nilai nyata λ, akan

memaksimumkan:

[

1

]

( ),

1 1 0 0 ) (

∑ ∫

= ∞ − − − = m k p c

k e dU k

c N N

Z λ k λ

(9)

dengan kendala

∑

= = m k k kp N N ₀ 1 _λ

.

Atau dengan meminimumkan fungsi Lagrange . 1 ) ( 1 1 0 0 ) (

0

∫

∑

∞ = − − = ⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ − − = m k k k p c m k

k N p

N k dU e N N c

k λ α λ

ψ λ

(10) Hal ini diperoleh dengan menurunkan ψ terhadap αdan ψterhadap pk

∑

= = → = ∂ ∂ m k k kp N N ₀ 1 0 λ α ψ (11)

∫

∞ − ₌ → = ∂ ∂ 0 ) ( 1

0 _k cp c _k

k N N k dU e e N N p

k λ α

ψ λ

,

k=0,....,m

.

(12) Jika a x k x k dU e x M − ∞ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = =

∫

τ λ

λ ₍ ₎ ₁

) (

0

dinotasikan sebagai fungsi pembangkit momen dari sebaran posterior λ, persamaan (12) akan disederhanakan menjadi: m k c M e k cpk ,..., 0 ) (− =α = (13) atau m k c M Log c Log c

pk k( ) 0,...,

1

1 ₋ ₋ ₌

= α

(14)

dan β Logα

c 1

= .

β dapat diperoleh dengan mengalikan

persamaan (14) dengan N_k

,

menjumlahkan semua nilai k dan membagi dengan N sehingga diperoleh: . 1 1 1 1

0 0 0

) (

∑

= = = − − = m k m k m k c k k k k

k N LogM

c N N N p N N β

Dan disubtitusi dengan persamaan (11), didapat:

∑

= − + = m k k kLogM c

N

Nc ₀ ( )

1

λ β

Sehingga akan diperoleh:

. ) ( ) ( 1 1 ) ,..., ( 0 1 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − + = =

∑

= + m i k i i t t

k NLogM c LogM c

N c k k P p λ

Penguraian rumus tersebut disajikan pada Lampiran 9.

Nilai c dapat dipilih dengan tujuan untuk merefleksikan satu preferensi ketidaksimetrisan pada galat. Jika dipilih nilai c=11.5 berarti perlu untuk menurunkan biaya dua polis sebesar 0.03, masing-masing untuk mengkompensasi terhadap overcharges sebesar 0.04. dan jika dipilih c=17.5 berarti diperlukan dua undercharges sebesar 0.04 untuk menyeimbangkan satu overcharges sebesar 0.04.

Dengan menggunakan fungsi struktur Λ dan populasi pada Tabel 5 diperoleh rumus penentuan premi untuk pembayaran premi awal sebesar 100 sebagai berikut:

( ) ( ) ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + +

∑

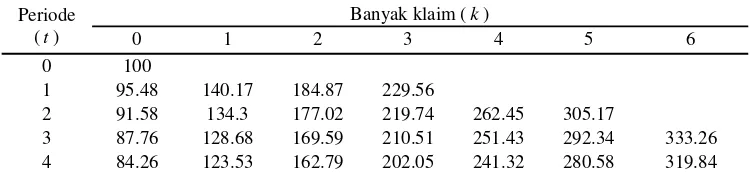
= − − = + − + − m i a a i m i k a k a i c Log c N N c t c Log t c N N c 0 0 1 1 1 1 1 1 1 1 100 τ τ λ τ τ λ

(15)

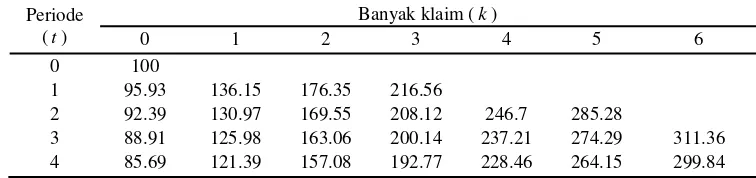
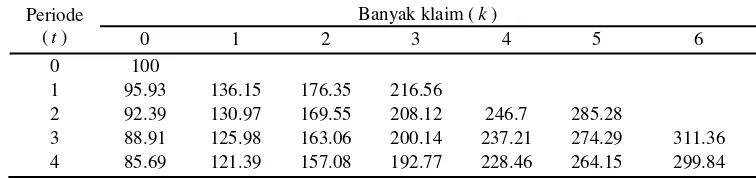
Tabel 6 Premi sistem Bonus Malus dengan pendekatan pinalti pada kelebihan biaya untuk nilai c=11.5

Periode (t)

Banyak klaim (k)

0 1 2 3 4 5 6

0 100

1 95.48 140.17 184.87 229.56

2 91.58 134.3 177.02 219.74 262.45 305.17

3 87.76 128.68 169.59 210.51 251.43 292.34 333.26

4 84.26 123.53 162.79 202.05 241.32 280.58 319.84

Berikut tabel nilai premi untuk c=17.5

Tabel 7 Premi sistem Bonus Malus dengan pendekatan pinalti pada kelebihan biaya untuk nilai 5

. 17

=

c

Periode (t)

Banyak klaim (k)

0 1 2 3 4 5 6

0 100

1 95.93 136.15 176.35 216.56

2 92.39 130.97 169.55 208.12 246.7 285.28

3 88.91 125.98 163.06 200.14 237.21 274.29 311.36

4 85.69 121.39 157.08 192.77 228.46 264.15 299.84

Pada kedua tabel di atas dapat dilihat bahwa terjadi penurunan premi pada

1

≥

k dan kenaikan sedikit premi pada grup

awal yang bertujuan untuk menutupi keseimbangan keuangan.

.

V SIMPULAN

Karya ilmiah ini membandingkan penghitungan premi pada sistem Bonus Malus dengan dua pendekatan yang berbeda yaitu utilitas nol (zero utility) dan pinalti pada kelebihan biaya (penalization of overcharges).

Dapat dilihat dari aplikasinya, premi sistem Bonus Malus yang diperoleh dengan menggunakan prinsip nilai harapan dan pendekatan prinsip utilitas nol membutuhkan biaya yang sangat tinggi untuk resiko yang besar meskipun terjustifikasi sempurna, hal ini terlihat sangat sulit untuk menggunakan tabel tersebut pada prakteknya terutama untuk

alasan yang bersifat komersial (kepentingan bisnis).

(16)

Tabel 6 Premi sistem Bonus Malus dengan pendekatan pinalti pada kelebihan biaya untuk nilai c=11.5

Periode (t)

Banyak klaim (k)

0 1 2 3 4 5 6

0 100

1 95.48 140.17 184.87 229.56

2 91.58 134.3 177.02 219.74 262.45 305.17

3 87.76 128.68 169.59 210.51 251.43 292.34 333.26

4 84.26 123.53 162.79 202.05 241.32 280.58 319.84

Berikut tabel nilai premi untuk c=17.5

Tabel 7 Premi sistem Bonus Malus dengan pendekatan pinalti pada kelebihan biaya untuk nilai 5

. 17

=

c

Periode (t)

Banyak klaim (k)

0 1 2 3 4 5 6

0 100

1 95.93 136.15 176.35 216.56

2 92.39 130.97 169.55 208.12 246.7 285.28

3 88.91 125.98 163.06 200.14 237.21 274.29 311.36

4 85.69 121.39 157.08 192.77 228.46 264.15 299.84

Pada kedua tabel di atas dapat dilihat bahwa terjadi penurunan premi pada

1

≥

k dan kenaikan sedikit premi pada grup

awal yang bertujuan untuk menutupi keseimbangan keuangan.

.

V SIMPULAN

Karya ilmiah ini membandingkan penghitungan premi pada sistem Bonus Malus dengan dua pendekatan yang berbeda yaitu utilitas nol (zero utility) dan pinalti pada kelebihan biaya (penalization of overcharges).

Dapat dilihat dari aplikasinya, premi sistem Bonus Malus yang diperoleh dengan menggunakan prinsip nilai harapan dan pendekatan prinsip utilitas nol membutuhkan biaya yang sangat tinggi untuk resiko yang besar meskipun terjustifikasi sempurna, hal ini terlihat sangat sulit untuk menggunakan tabel tersebut pada prakteknya terutama untuk

alasan yang bersifat komersial (kepentingan bisnis).

(17)

MEGAWATI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(18)

DAFTAR PUSTAKA

Arnold SF. 1990. Mathematical Statistics. New Jersey: Prentice Hall, Inc.

Ayuningtyas V. 2007. Penentuan Premi pada Sistem Bonus Malus yang Optimal. Skripsi Sarjana Departemen Matematika FMIPA Universitas Indonesia, Depok. Indonesia.

Corlier F, Lemaire J dan Muhokolo D. 1979. Simulation of an automobile portofolio. The Geneva papers on risk and insurance. 12: 40-46.

Gerber H. 1974a. On Additive Premium Calculation Principles. ASTIN Bulletin. 7: 215-222.

Gerber H. 1974b. On Iterative Premium Calculation Principles. ASTIN Bulletin. 74. 163-172.

Grimmet GR, Stirzaker DR. 1992. Probability and Random Processes.

Edisi ke-2. New York: Clarendon Press Oxford.

Hogg RV, Craig AT. 1995. Introduction to Mathematical Statistics. Edisi ke-5. New Jersey: Prentice Hall, Inc.

Hosmer DW Jr, Lemeshow S. 1989. Applied

Logistic Regression. New York: John Wiley and Sons.

Lemaire J. 1977. Selection Procedures of Regression Analysis Applied to Automobile Insurance. ASTIN Bulletin. 77: 65-72.

Lemaire J. 1979. How to Define a Bonus Malus System with an exponential Utility Function. ASTIN Bulletin. 10: 274-282.

(19)

MEGAWATI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(20)

ABSTRAK

MEGAWATI. Penentuan Premi Sistem Bonus Malus dengan Menggunakan Fungsi Utilitas Eksponensial. Dibimbing oleh I GUSTI PUTU PURNABA dan RETNO BUDIARTI.

Sistem Bonus Malus merupakan salah satu sistem yang digunakan dalam asuransi mobil. Sistem ini memperkenalkan pembagian kelas premi yang dipengaruhi oleh banyaknya klaim yang diajukan oleh pemegang polis tiap tahunnya.

Dalam karya ilmiah ini, dibahas mengenai penghitungan premi pada sistem Bonus Malus untuk pertanggung-jawaban pihak ketiga pada asuransi mobil dengan menggunakan dua cara yang berbeda, namun keduanya tetap menggunakan fungsi utilitas eksponensial. Cara yang pertama yaitu dengan menerapkan prinsip utilitas nol (zero utility) menggunakan fungsi utilitas eksponensial. Cara yang kedua adalah memperoleh kesimetrisan antara biaya yang lebih (overcharges) dan biaya yang kurang (undercharges) dengan memberikan bobot pada keduanya melalui pendekatan fungsi utilitas, dengan tujuan memberikan pinalti pada kelebihan biaya (penalization of overcharges) tersebut.

Untuk membandingkan sistem perhitungan pada kedua pendekatan tersebut, sebelumnya diberikan prinsip nilai harapan. Banyaknya klaim masing-masing polis diasumsikan menyebar Poisson dengan fungsi sebaran parameternya adalah sebaran gamma; dan menghasilkan sebaran tak bersyaratnya yaitu sebaran binomial negatif. Dicari sebaran posterior dari parameter frekuensi klaim, kemudian parameter tersebut diduga menggunakan teknik pendugaan Bayes.

(21)

ABSTRACT

MEGAWATI. Determination of Bonus Malus System’s Premium Using Utility Exponential Function. Under supervision of I GUSTI PUTU PURNABA and RETNO BUDIARTI.

A Bonus Malus system is one of systems used in the automobile insurance. This system introduces the clasification of premium level, which is influenced by the number of claims from the policyholder every year.

This paper discusses premium calculation on Bonus Malus system for automobile third party liability insurance with two different methods, which both are based on exponential utility functions. The first method is carried out by applying the principle of zero utility using the exponential utlilty function. The second method is formulated by breaking the symmetry between overcharges and undercharges by weighting them differently in the utility function in order to penalize the overcharges.

In order to compare the calculation methods of both approaches, the expected value principle should be given in advance. Number of claims from each policyholder is assumed to follow Poisson distribution, while the parameters follow the gamma distribution. This leads to an unconditional negative binomial distribution. The posterior distribution of frequency claim parameter is to be determined in order to estimate the parameters using Bayes estimation technique.

The premium calculation on Bonus Malus system using expected value and zero utility principle implies very high cost for high risk. In the Bonus Malus premium using the penalization of overcharges approach, the ratio between extreme premiums is reduced to produce a smaller Malus. Therefore, the most appropriate premium for policyholder in every class is the premium which applies penalization of overcharges.

(22)

PENENTUAN PREMI SISTEM BONUS MALUS DENGAN

MENGGUNAKAN FUNGSI UTILITAS EKSPONENSIAL

Skripsi

sebagai salah satu syarat untuk memperoleh Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh:

MEGAWATI

G54050912

DEPARTEMEN MATEMATIKA

FAKULTAS METEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(23)

Judul

: Penentuan Premi Sistem Bonus Malus dengan Menggunakan

Fungsi Utilitas Eksponensial

Nama :

Megawati

NRP :

G54050912

Menyetujui:

Pembimbing I,

Pembimbing II,

(Dr. Ir. I. G. Putu Purnaba, DEA.)

NIP: 19651218 199002 1 001

(Ir. Retno Budiarti, Ms.)

NIP: 19610729 198903 2 001

Mengetahui:

Ketua Departemen,

(Dr. Berlian Setiawaty, MS.)

NIP: 19650505 198903 2 004

(24)

KATA PENGANTAR

Puji dan syukur penulis panjatkan kehadirat Allah SWT atas rahmat, berkah serta nikmat sehat sehingga penulis mampu menyelesaikan tugas akhir ini yang berjudul Penentuan Premi Sistem Bonus Malus dengan Menggunakan Fungsi Utilitas Eksponensial. Shalawat serta salam tercurah kepada junjungan kita nabi besar Muhammad SAW yang telah memberikan suri tauladan tak henti-hentinya kepada umatnya hingga akhir jaman.

Tugas akhir ini penulis persembahkan untuk kedua orang tua dan seluruh keluarga yang selalu mendukung, menasehati dan mendoakan penulis dengan dukungan yang luar biasa. Tak lupa penulis mengucapkan terimakasih kepada pihak-pihak yang telah memberikan dorongan terhadap penulisan dalam menyelesaikan tugas akhir ini, yaitu:

1. Bapak Dr. Ir. I G. Putu Purnaba, DEA selaku dosen pembimbing I dan ibu Ir. Retno Budiarti, Ms selaku dosen pembimbing II yang telah meluangkan waktu, tenaga dan pikiran untuk memberikan bimbingan, saran, koreksi dan pengarahan dalam penyusunan tugas akhir ini serta bapak Dr. Ir. I Wayan Mangku, M.Sc atas kesediaannya menjadi dosen penguji penulis saat sidang.

2. Seluruh dosen matematika IPB atas segala ilmu yang telah diberikan selama 4 tahun menuntut ilmu di Departemen Matematika IPB dan TU matematika IPB, bu Susi, bu Ade, pak Yono, mas Deni, mas Bono, mas Hery dan lain-lain, atas bantuan yang telah diberikan kepada penulis.

3. Untuk papa, mama, kak Lenny dan bang chokey, bang Benny, bang Andy dan kak Nur, bang Dian, bang Hendy, serta keluarga besar papa dan mama yang telah memberikan kasih sayang, nasehat, dukungan, serta doanya.

4. Puthut dan keluarga yang juga selalu mendukung dan mendoakan penulis dalam situasi apapun dalam menyelesaikan karya ilmiah ini (makasih printernya ndut).

5. Teman-teman kristal, Ami, mba Vin, mba Ik, mbo Rie, Vence, Bundo, Die2 dan Nidha, atas doa dan kebersamaannya.

6. Sahabat-sahabatku, Sisca yang telah memberikan pinjaman untuk keperluan seminar dan Nunk yang selalu memberikan dorongan semangat penulis. Tak lupa untuk harry makasih banyak bantuannya.

7. Teman-teman matematika angkatan 42, Eyyi, Yuni dan Sapto yang sudah bersedia menjadi pembahas penulis saat seminar, Nyoman dan Idha yang selalu memberikan dorongan semangat dan bantuannya selama ini, Ocoy, Yusep, Warno, Pepe, Ilie, Agnez, Die2, Vino, Riyu, Nola, Hesti, Titi, Djawa, Vitha, Hikmah, Octa, Githa, Siti, Titi, Acy, Boy, Danu, Dendy, Dewi, Hap2, Iput, Jane, Lina, Lisda, Ayeep, Mira, Moko, Oby, Rendy, Ricken, Ridwan, Septian, Acuy, Wie2, mas Mukthar, Tia, Zil, Acuy, Yudy, Ardy, Facjri, Bayu, Erlyn, Ayu, Bima, Niken, Hery, Awi, Rima, Siti, Ety, Acy, Nofita, Eko, Luri. Kalian adalah teman-teman terbaikku di Departemen Matematika, teman-teman seperjuangan untuk menuntut ilmu di Departemen Matematika IPB.

8. Kakak-kakak kelasku dan adik-adik kelasku, kak Tities dan kak Ani terimakasih atas tugas akhirnya yang sedikit banyak membantu penulis dalam hal bahasan ataupun materinya, kak Rofah, kak Rijal dan Apri terimakasih atas segala bantuannya dalam menyelesaikan tugas akhir ini. Dan semua kakak dan adik kelas matematika yang lainnya.

9. Dan semua pihak yang tidak bisa disebutkan satu persatu yang telah banyak membantu selesainya tugas akhir ini, terimakasih banyak untuk semuanya.

Penulis banyak menyadari bahwa banyak kekurangan dalam penulisan tugas akhir ini, oleh sebab itu kritik dan saran dari pembaca sangat diharapkan. Semoga tugas akhir ini bermanfaat bagi pembaca.

Bogor, November 2009

(25)

RIWAYAT HIDUP

Penulis lahir di Jakarta pada tanggal 1 Januari 1987 sebagai anak keenam dari enam bersaudara dari pasangan Asrial dan Mawarni.

(26)

DAFTAR ISI

Halaman

DAFTAR TABEL ...

DAFTAR GAMBAR ...

DAFTAR LAMPIRAN ...

I PENDAHULUAN ... Latar Belakang ... Tujuan ...

II LANDASAN TEORI... Ruang Contoh, Kejadian dan peluang ... Peubah Acak dan Fungsi Sebaran... Nilai Harapan, Ragam dan Momen ... Fungsi kemungkinan (likelihood) ... Statistik dan Penduga ...

III PEMBAHASAN... Prinsip Nilai Harapan... Prinsip Utilitas Nol... Pinalti pada Kelebihan Biaya ...

IV SIMPULAN………...

DAFTAR PUSTAKA………...

viii

1 1 1

1 1 2 3 4 4

5 5 8 9

12

(27)

DAFTAR TABEL

Halaman

1 Data banyaknya kecelakaan kendaraan bermotor... 2 Premi sistem Bonus Malus berdasarkan prinsip nilai harapan... 3 Premi sistem Bonus Malus dengan pendekatan utilitas nol untuk nilai c=0.4... 4 Premi sistem Bonus Malus dengan pendekatan utilitas nol untuk nilai c=1.65... 5 Banyaknya populasi tiap subgrup pada kelas-kelas resiko... 6 Premi sistem Bonus Malus dengan pendekatan pinalti pada kelebihan biaya untuk nilai

5 . 11

=

c ... 7 Premi sistem Bonus Malus dengan pendekatan pinalti pada kelebihan biaya untuk nilai

5 . 17

=

c ... 6 8 9 9 10

12

DAFTAR GAMBAR

Halaman

Grafik perpotongan pada sebaran posterior untuk frekuensi klaim antara grup awal (k=0)

saat t=3dan grup 2 (k=2) saat t=3………

' 10

DAFTAR LAMPIRAN

Halaman

1 Bukti rata-rata, ragam dan fungsi pembangkit momen untuk sebaran Λ ………. 2 Fungsi massa peluang dari sebaran binomial negatif ……….. 3 Sebaran posterior dari λuntuk banyaknya data klaim dengan menggunakan teorema

Bayes ... 4 Prinsip nilai harapan untuk menghitung premi sistem Bonus Malus ……… 5 Uji kebaikan-suai untuk sebaran Poisson ………... 6 Uji kebaikan-suai untuk sebaran binomial negatif………... 7 Program-program untuk menghitung nilai pada Tabel 3, Tabel 4, Tabel 6 dan Tabel 7... 8 Program untuk memperoleh grafik pada Gambar 1... 9 Bukti rumus untuk menghitung premi Bonus Malus dengan pendekatan pinalti pada

kelebihan biaya ………...

15 18

19 21 22 25 32 38

39

(28)

I PENDAHULUAN

Latar Belakang

Tujuan

overcharges).

II LANDASAN TEORI

Ruang Contoh, Kejadian dan Peluang

(Hogg & Craig 1995)

Definisi 3 (Medan-σ)

1. ∅ ∈F _,

2. Jika A A1, 2,...∈ F maka 1

i i

A

∞ =

∈

U

F _,

A ∈F _.

(29)

2. Jika A A1, 2,...∈F adalah himpunan yang

saling lepas yaitu A1∩A2= ∅ untuk

setiap pasangan i≠j, maka

( )

1 1

i i

P A P A

∞ ∞

= =

⎛ ⎞

=

⎜ ⎟

⎝

U

⎠

∑

.

Peubah Acak dan Fungsi Sebaran

Definisi 5 (Peubah Acak)

Misalkan F _{adalah medan-}σ_{dari ruang}

contoh Ω. Suatu peubah acak Xadalah suatu fungsi X:Ω→ℜ dengan sifat

( )

{

ω∈Ω:X ω ≤x

}

∈F _{untuk setiap}x∈ℜ. (Grimmett & Stirzaker 1992)

Definisi 6 (Peubah Acak Diskret)

Peubah acak Xdikatakan diskret jika nilainya hanya pada himpunan bagian yang terhitung dari ℜ.

Catatan:

Suatu himpunan bilangan C disebut terhitung jika C terdiri atas bilangan terhingga atau anggota C dapat dikorespondensikan 1-1 dengan bilangan bulat positif.

Definisi 7 (Fungsi Sebaran)

MisalkanX adalah suatu peubah acak dengan ruang contoh Ω. Misalkan kejadian

(

, ,

A= −∞x⎤⎦⊂ Ω maka peluang dari kejadianA

adalah

( )

(

)

( )

X X

P A =P X≤x =F x .

Fungsi FX disebut fungsi sebaran dari peubah

acak X.

(Hogg & Craig 1995)

Definisi 8 (Peubah Acak Kontinu)

Peubah acak X dikatakan kontinu jika ada fungsi fX(x) sehingga fungsi sebaran

∫

∞ −

= x

X X x f u du

F ( ) ( ) ,

x∈ℜ, dengan f:ℜ →⎡⎣0,∞

)

adalah fungsi yang terintegralkan. Fungsi fXdisebut fungsi

kepekatan peluang dari X.

Definisi 9 (Fungsi Massa Peluang Untuk Peubah Acak Diskret)

Fungsi massa peluang dari peubah acak diskret X adalah fungsi p:ℜ→

[ ]

0,1 yang diberikan oleh

) ( )

(x P X x

p_X = = .

Definisi 10 (Sebaran Poisson)

menyebar Poisson dengan parameter ,λ jika memiliki fungsi massa peluang

! ) ; (

x e x p

x X

λ

λ = −λ ,x=0,1,2,...dengan λ>0.

(Hogg & Craig 1995)

Definisi 11 (Sebaran Binomial Negatif)

Suatu peubah acak N dikatakan menyebar binomial negatif dengan parameter r dan p, dinotasikan BN(r,p) jika memiliki fungsi massa peluang:

;

1

( ) [ ] r n 0,1, 2,...,

N

r n

p n N n p q n

n

+ −

= Ρ = =

⎛

⎜

⎞

⎟

=

⎝

⎠

denganr>0,0< <p 1, dan q= −1 p. (Hogg & Craig 1995)

Definisi 12 (Sebaran Gamma)

menyebar gamma dengan parameter α dan β, dinotasikan gamma

(

α β,

)

, jika memiliki fungsi kepekatan peluang

∈ Γ

= − −

x e x x

f x;

) ( )

( α 1 β

α

α β

ℜ+_,

dengan α>0, β>0, dan Γ(α)>0, dimana

∫

∞ − −

= Γ

0

1 _.

)

(α yα e ydy

(Hogg & Craig 1995)

Definisi 13 (Fungsi Sebaran Bersama Dua Peubah Acak)

Fungsi sebaran bersama dua peubah acak

X dan Y merupakan suatu fungsi

2

: [0,1]

F ℜ → yang didefinisikan sebagai

( )

,

(

,

)

XY

F x y =P X≤x Y≤y .

Definisi 14 (Fungsi Kepekatan Peluang Bersama dan Marjinal)

Misalkan X dan Y peubah acak kontinu, maka fungsi kepekatan peluang bersama dari

(30)

( )

2

( )

,

, XY

XY

F x y

f x y

x y

∂ =

∂ ∂ ,

dan fungsi kepekatan peluang marjinal dari peubah acak Y adalah

( )

,

Y XY

f y f x y dx

∞

−∞

=

∫

.

Definisi 15 (Fungsi Kepekatan Peluang Bersyarat)

Misalkan X dan Y adalah peubah acak kontinu dengan fungsi kepekatan peluang marjinal dari Y adalah fY

( )

y > 0. Maka fungsi kepekatan peluang bersyarat dari X dengan syarat Y=y adalah

(

)

( )

|

,

| XY

X Y

Y

f x y

f y

= .

Definisi 16 (Sebaran Khi-kuadrat)

menyebar khi-kuadrat dengan parameterr, jika memiliki fungsi kepekatan peluang

( )

21 2

2

; , 0 2 2

r x

X r

x e

f