Sistem Bonus-Malus dengan Banyak Klaim Berdistribusi Geometrik dan Besar Kerugian Berdistribusi Weibull Terpotong

SISTEM

BONUS-MALUS

DENGAN BANYAK KLAIM

BERDISTRIBUSI GEOMETRIK DAN BESAR KERUGIAN

BERDISTRIBUSI WEIBULL TERPOTONG

DIAN NURITA SANTI

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa tesis berjudul “Sistem Bonus-Malus dengan Banyak Klaim Berdistribusi Geometrik dan Besar Kerugian Berdistribusi Weibull Terpotong”  adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Agustus 2015

RINGKASAN

DIAN NURITA SANTI. Sistem Bonus-Malus dengan Banyak Klaim Berdistribusi Geometrik dan Besar Kerugian Berdistribusi Weibull Terpotong. Dibimbing oleh I GUSTI PUTU PURNABA dan I WAYAN MANGKU.

Asuransi merupakan salah satu cara untuk mengurangi kerugian finansial dengan menyalurkan risiko kerugian dari seseorang ke badan lainnya, contohnya asuransi kendaraan bermotor. Penentuan harga premi risiko asuransi kendaraan bermotor berdasarkan data yang diketahui asuransi di masa lalu (experience rating). Sistem experience rating seperti ini dikenal sebagai sistem Bonus-Malus. Berdasarkan sistem Bonus-Malus, pemegang polis yang telah mengajukan satu atau lebih klaim akan dikenakan kenaikan premi risiko (malus), sedangkan bagi pemegang polis yang tidak mengajukan klaim akan diberikan penghargaan berupa penurunan premi risiko (bonus) di periode pembayaran premi risiko berikutnya. Sistem Bonus-Malus dikatakan optimal jika seimbang secara finansial bagi perusahaan asuransi dan adil bagi para pemegang polis. Sehingga pada penentuan premi risiko tidak hanya berdasarkan banyak klaim tetapi juga berdasarkan besar kerugian yang ditimbulkan.

Penelitian ini menggabungkan sistem Bonus-Malus yang telah dibahas oleh Mert dan Saykan (2005) dan Ni et al. (2014). Namun, penentuan premi risiko pada sistem Bonus-Malus tersebut diterapkan untuk besar kerugian pemegang polis yang ditanggung seluruhnya oleh perusahaan asuransi. Pada kenyataannya tidak semua besar kerugian yang diajukan pemegang polis dapat ditanggung oleh perusahaan asuransi. Ketika perusahaan asuransi menetapkan batas maksimum besar kerugian yang ditanggung, maka perlu memodifikasi model distribusi besar kerugian menjadi distribusi besar kerugian terpotong. Distribusi banyak klaim yang digunakan adalah geometrik yang merupakan gabungan dari distribusi Poisson dan eksponensial. Sedangkan distribusi besar kerugian yang digunakan oleh Ni et al. (2014) dimodifikasi menjadi distribusi besar kerugian terpotong yaitu Weibull terpotong. Distribusi Weibull terpotong merupakan gabungan distribusi eksponensial terpotong dan Levy. Penelitian ini juga membandingkan premi risiko antara besar kerugian yang ditanggung penuh dan besar kerugian yang ditanggung dengan batas maksimum santunan.

Berdasarkan hasil pembahasan, diperoleh simpulan bahwa persamaan premi risiko dengan batas kerugian maksimum adalah





















3

2 t 1

1

2

2 1

Premi K

K

B c N u K n

N u K n

K

t c _{B c N u K n}



 



 _{ } 

 

   

  

  

 

 _{    }

 

 

,

dengan adalah total banyak klaim, adalah batas maksimum yang mampu ditanggung perusahaan asuransi, adalah total besar kerugian di bawah batas , adalah banyak klaim di bawah batas , �_{�− /} adalah fungsi Bessel dengan indeks

distribusi Weibull sama besarnya dengan premi risiko berdasarkan distribusi Weibull terpotong ketika besar kerugian lebih kecil dari batas maksimum kerugian. Sedangkan, premi risiko berdasarkan distribusi Weibull menjadi lebih mahal dari premi risiko berdasarkan distribusi Weibull terpotong ketika besar kerugian lebih besar dari batas maksimum kerugian. Semakin kecil kerugian menyebabkan semakin sedikit premi risiko yang dibayarkan dan semakin besar kerugian berakibat semakin besar premi risiko yang dibayarkan.

SUMMARY

DIAN NURITA SANTI. Bonus-Malus System with the Claim Frequency Distribution is Geometric and the Severity Distribution is Truncated Weibull. Supervised by I GUSTI PUTU PURNABA and I WAYAN MANGKU.

Insurance is one way to denigrate financial loss by channeling the risk of loss of the person to another entity, for example automobile insurance. The risk premium of the automobile insurance is determined by insurance that is known data in the past (experience rating). System experience rating could call as Bonus-Malus system. In the Bonus-Malus system, policyholders who has submitted one or more claims will be subjected to a risk premium increase (malus), whereas for policyholders who did not file a claim would be rewarded with a decrease in risk premium (bonus) in the next premium payment period.Bonus-Malus system is said to be optimal if it is financially balanced for insurance companies and fair for policyholders. That is, the determination of the risk premium is not only based on the claims frequency but also based on the severity.

In this study, we used the Bonus-Malus system by Mert and Saykan (2005) and Ni et al. (2014). But, previous research concern with the determination of the risk premium Bonus-Malus system which is applied to all of the severity that guaranteed by the insurance company. In fact, all of the severity proposed by policyholder could not be covered by insurance company. When an insurance company sets a maximum bound of the severity incurred, it is necessary to modify the model of the severity distribution into the truncated severity distribution. The claim frequency is geometric distribution as a combination of Poisson and exponential distribution. While, the severity distribution by Ni et al. (2014) modified to be the severity distribution with maximum bound is truncated Weibull distribution. Truncated Weibull distribution is a combination of truncated exponential and Levy distribution. In this study, we also compared the risk premium between the full severity and the severity with the maximum bound.

The result shows that the risk premium equation with maximum bound is





















3

2 t 1

1

2

2 1

Premium K

K

B c N u K n

N u K n

K

t c _{B c N u K n}



 



 _{ } 

 

   

  

 _{ } 

 _{    }

 

 

,

the severity, the less of the risk premium to be paid and the greater of the severity, the greater of the risk premium must be paid.

© Hak Cipta Milik IPB, Tahun 2015

Hak Cipta Dilindungi Undang-Undang

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

SISTEM

BONUS-MALUS

DENGAN BANYAK KLAIM

BERDISTRIBUSI GEOMETRIK DAN BESAR KERUGIAN

BERDISTRIBUSI WEIBULL TERPOTONG

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2015

PRAKATA

Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa, yang telah melimpahkan rahmat dan karunia-Nya, sehingga karya ilmiah yang berjudul

“Sistem Bonus-Malus dengan Banyak Klaim Berdistribusi Geometrik dan Besar Kerugian Berdistribusi Weibull Terpotong” ini dapat terselesaikan.

Terima kasih penulis ucapkan kepada Bapak Dr Ir I Gusti Putu Purnaba, DEA dan Bapak Prof Dr Ir I Wayan Mangku, MSc selaku pembimbing, atas kesediaan dan kesabaran untuk membimbing dan membagi ilmunya kepada penulis dalam penyusunan karya ilmiah ini. Ucapan terima kasih juga penulis sampaikan sebesar-besarnya kepada seluruh Dosen Departemen Matematika IPB yang telah mengasuh dan mendidik penulis selama di bangku kuliah hingga berhasil menyelesaikan studi, serta seluruh staf Departemen Matematika IPB atas bantuan, pelayanan, dan kerjasamanya selama ini.

Ucapan terima kasih yang tulus dan penghargaan yang tak terhingga juga penulis ucapkan kepada Ayahanda dan Ibunda tercinta Widjiatmoko dan Tanem yang telah membesarkan dan mendidik penulis dengan penuh kasih sayang demi keberhasilan penulis selama menjalani proses pendidikan, juga kakak tersayang Aloysius Beni Ditya Havian serta keluarga besarku atas doa dan semangatnya.

Terakhir tak lupa penulis juga menyampaikan terima kasih kepada seluruh mahasiswa Pascasarjana Departemen Matematika Terapan atas segala bantuan dan kebersamaannya selama menghadapi masa-masa terindah maupun tersulit dalam menuntut ilmu, serta semua pihak yang telah banyak membantu dan tak sempat penulis sebutkan satu per satu.

Semoga karya ilmiah ini dapat bermanfaat bagi semua pihak yang membutuhkan.

Bogor, Agustus 2015

DAFTAR ISI

DAFTAR TABEL vi

DAFTAR LAMPIRAN vi

PENDAHULUAN

Latar Belakang 1

Perumusan Masalah 2

Tujuan Penelitian 2

TINJAUAN PUSTAKA

Pengertian Asuransi 2

Sistem Bonus-Malus dengan Banyak Klaim 3

Sistem Bonus-Malus Optimal 4

METODE PENELITIAN 6

HASIL DAN PEMBAHASAN

Modifikasi Distribusi Besar Kerugian 7

Simulasi Numerik Sistem Bonus-Malus 14

SIMPULAN 18

DAFTAR PUSTAKA 18

LAMPIRAN 20

DAFTAR TABEL

1 Banyak klaim 15

2 Besar kerugian dan banyak klaim data sebenarnya 15 3 Besar kerugian dan banyak klaim dengan u = 2300 15 4 Hasil perhitungan harga premi risiko dengan total besar kerugian 8000 16 5 Hasil perhitungan harga premi risiko dengan total besar kerugian 10000 16 6 Hasil perhitungan harga premi risiko dengan u = 2300 17

DAFTAR LAMPIRAN

1 Beberapa Definisi dan Teorema 20

2 Bukti Beberapa Persamaan 28

PENDAHULUAN

Latar Belakang

Berbagai persoalan hidup sering kali dialami dalam kehidupan sehari-hari, salah satunya kemungkinan sering tertimpa kerugian dalam menjalani aktifitas keseharian. Banyaknya risiko yang terjadi karena faktor bencana maupun faktor manusia membuat manusia mulai memikirkan harta dan jiwa mereka. Untuk mengurangi beban tersebut, maka seseorang membuat perjanjian yang memberikan kerugian-kerugian dimaksud kepada badan atau pihak lainnya yang juga terbuka dengan kerugian-kerugian tersebut. Perjanjian ini dikenal sebagai kontrak asuransi atau polis. Asuransi adalah sebuah sistem untuk mengurangi kerugian finansial dengan menyalurkan risiko kerugian dari seseorang ke badan atau pihak lainnya. Tujuan pembelian dari suatu produk asuransi adalah untuk menutup kerugian finansial karena bahaya yang mungkin merugikan seseorang.

Secara garis besar, bidang asuransi terdiri dari dua kategori yaitu asuransi jiwa dan asuransi non jiwa. Asuransi jiwa adalah asuransi yang memberikan santunan dalam jumlah tertentu yang berhubungan dengan hidup matinya seseorang. Sedangkan asuransi non jiwa adalah asuransi yang memberikan ganti rugi kepada tertanggung yang menderita kerugian barang atau benda miliknya, contohnya asuransi kendaraan bermotor. Salah satu sistem dalam penentuan premi risiko asuransi kendaraan bermotor adalah sistem Bonus-Malus.

Sistem Bonus-Malus adalah suatu sistem dimana pemegang polis yang telah mengajukan satu atau lebih klaim akan dikenakan kenaikan premi risiko (malus), sedangkan bagi pemegang polis yang tidak mengajukan klaim akan diberikan penghargaan berupa penurunan premi risiko (bonus) di periode pembayaran premi risiko berikutnya (Denuit et al. 2007). Sistem Bonus-Malus dikatakan optimal jika seimbang secara finansial bagi perusahaan asuransi, yaitu total bonus sama dengan total malus dan adil bagi para pemegang polis yaitu setiap pemegang polis membayar premi risiko yang proporsional dengan risiko yang terjadi.

2

Perumusan Masalah

Penelitian ini menggabungkan sistem Bonus-Malus yang telah dibahas oleh Mert dan Saykan (2005) dan Ni et al. (2014). Namun, sistem Bonus-Malus penelitian tersebut diterapkan untuk besar kerugian pemegang polis yang ditanggung seluruhnya oleh perusahaan asuransi. Pada kenyataannya tidak semua besar kerugian yang diajukan pemegang polis dapat ditanggung oleh perusahaan asuransi. Ketika perusahaan asuransi menetapkan batas maksimum besar kerugian yang ditanggung, maka perlu memodifikasi model distribusi besar kerugian yang telah diteliti oleh Ni et al. (2014) menjadi distribusi besar kerugian terpotong. Berdasarkan uraian tersebut, dapat dirumuskan beberapa masalah sebagai berikut: 1. Bagaimana menentukan premi risiko pada sistem Bonus-Malus dengan banyak

klaim berdistribusi geometrik dan besar kerugian berdistribusi Weibull terpotong.

2. Bagaimana perbandingan premi risiko antara besar kerugian yang ditanggung penuh dan besar kerugian yang ditanggung dengan batas maksimum santunan.

Tujuan Penelitian

Berdasarkan uraian perumusan masalah, tujuan yang akan dicapai pada penelitian ini adalah sebagai berikut:

1. Menentukan persamaan premi risiko sistem Bonus-Malus dengan banyak klaim berdistribusi geometrik dan besar kerugian berdistribusi Weibull.

2. Membandingkan premi risiko antara besar kerugian yang ditanggung penuh dan besar kerugian yang ditanggung dengan batas maksimum santunan.

TINJAUAN PUSTAKA

Pengertian Asuransi

Pengertian asuransi secara umum adalah menyerahkan pertanggungan risiko kepada penanggung yaitu perusahaan asuransi untuk jangka waktu dan perjanjian-perjanjian yang telah disepakati. Definisi asuransi menurut Kitab Undang-Undang

Hukum  Dagang  (KUHD)  Pasal  246  disebutkan  bahwa  “Asuransi atau

3 Sistem Bonus-Malus dengan Banyak Klaim

Sistem Bonus-Malus dengan banyak klaim merupakan sistem penentuan premi risiko yang hanya berdasarkan banyaknya klaim. Banyaknya klaim yang diajukan oleh setiap pemegang polis berbeda (heterogen), karena setiap pemegang polis memiliki risiko yang tidak sama untuk kejadian yang dialami. Klugman et al. (2012) menyebutkan bahwa distribusi campuran cocok untuk memodelkan data yang heterogen pada asuransi kendaraan bermotor. Dionne dan Vanasse (1989), Tremblay (1992) menggunakan distribusi campuran Poisson sebagai distribusi dari banyak klaim yang diajukan oleh setiap pemegang polis.

Fungsi distribusi banyak klaim dari setiap pemegang polis diasumsikan berdistribusi Poisson yang dituliskan sebagai berikut:



|



, 0,1, 2,...; 0 !

k

e

P k k

k

_

      , (2.1) dengan menyatakan rata-rata banyak klaim yang diajukan dari setiap pemegang polis dan k adalah banyaknya klaim yang diajukan.

Dionne dan Vanasse (1989) mengasumsikan parameter persamaan (2.1) berdistribusi gamma dengan parameter dan . Fungsi kepekatan peluang parameter adalah

 

1

 

1 /

, 0, 0, dan 0

f  _  e     

 

 

   

 . (2.2)

Berdasarkan persamaan (2.1) dan (2.2) diperoleh fungsi massa peluang banyak klaim sebagai berikut:

 

1 1

.

1 1

k k

P k

k



 

 

 

    

   _   _ 

   

  (2.3)

Persamaan (2.3) menunjukkan bahwa fungsi kepekatan peluang berdistribusi binomial negatif dengan parameter dan . Adapun premi risiko periode selanjutnya diperoleh dari persamaan sebagai berikut:

 

1 1

1

1

1

, e

ˆ ˆ

xp ,

,

,

t t i

i i

i

t j

i i i

t j i i

j t

j i i

j

a Y

P M

a x u

Y Y





 

 

 







  

  



 

  





(2.4)

4

Tremblay (1992) mengasumsikan parameter persamaan (2.1) berdistribusi generalised inverse Gaussian dengan parameter dan . Fungsi kepekatan peluang parameter adalah

 

 2

2

3 , 0, 0, dan 0.

2

f e

  



   



 _ 

 

_{ }

 

    (2.5)

Berdasarkan persamaan (2.1) dan (2.5) dihasilkan fungsi kepekatan peluang banyak klaim sebagai berikut:

 



1 1 2 1 



.

k

P k e

 _

   

 (2.6)

Persamaan (2.6) menunjukkan bahwa fungsi kepekatan peluang berdistribusi Poisson inverse Gaussian dengan parameter dan . Adapun persamaan premi risiko periode selanjutnya dituliskan sebagai berikut:





1









1 1 2

'

'

' '/ '

, , , ,

'/ ' 1

, 1

2 1

, 1 2

v

t t

v

K

P k k k

K

t

t

  

  

  





  

  



(2.7)

dengan _�+ adalah fungsi Bessel berindeks + . Persamaan (2.7) menunjukkan bahwa premi risiko periode selanjutnya berdasarkan banyak klaim yang diajukan selama periode waktu t.

Sistem Bonus-Malus Optimal

Sistem Bonus-Malus optimal adalah sistem penentuan premi risiko tidak hanya berdasarkan banyak klaim tetapi juga besar kerugian dari setiap klaim. Frangos dan Vrontos (2001), Mert dan Saykan (2005), Mahmoudvand dan Hassani (2009), Ni et al. (2014) mengasumsikan besar kerugian berdistribusi campuran eksponensial dengan fungsi kepekatan peluang sebagai berikut.



|



x, 0,

f X x  e x (2.8)

dengan x merupakan besar kerugian dan � adalah parameter distribusi besar kerugian.

Frangos dan Vrontos (2001), Mert dan Saykan (2005), serta Mahmoudvand dan Hassani (2009) mengasumsikan parameter � persamaan (2.8) berdistribusi inverse gamma dengan parameter dan . Fungsi kepekatan peluang parameter � adalah

 

 

/ 1

1

, 0, 0, dan 0.

Γ

m

s e m

f s m

s m



 

  

   

     

5 Berdasarkan persamaan (2.8) dan (2.9) diperoleh fungsi kepekatan peluang besar kerugian sebagai berikut:

 





 1

, 0.

s s

f x s m x m   x (2.10) Persamaan (2.10) menunjukkan bahwa fungsi kepekatan peluang besar kerugian berdistribusi pareto dengan parameter dan .

Frangos dan Vrontos (2001) membuat sistem Bonus-Malus optimal berdasarkan distribusi binomial negatif untuk banyak klaim dan distribusi pareto untuk besar kerugian. Pada penelitian tersebut digunakan tiga persamaan untuk menghitung premi risiko periode selanjutnya, yaitu

1 ,

t

K P

t

  

 

 (2.11)

1

1 ,

1

K k k t

m x

K P

t s K



 



 _ 

  



 _   _



_(2.12)





 





₁





₁ ,

1 1

1

1

1 exp

1

exp ,

1 exp

t _{j j} K

t _j

t _{i j} i _k i k

j j j

t i _j

j _i

s d X

K

t

P c

t t c s K

 



 

 

 



 _   

 



    

 









(2.13)

dengan dan � adalah parameter distribusi banyak klaim, m dan s adalah parameter distribusi besar kerugian, adalah total banyak klaim, t adalah periode waktu, adalah besar kerugian ke-k, dan adalah vector karakteristik individu ke-i periode ke-j, dan adalah vektor koefisien periode ke- j.

Sistem Bonus-Malus persamaan (2.11) digunakan untuk menghitung premi risiko hanya berdasarkan banyak klaim yang berdistribusi binomial negatif. Penentuan premi risiko persamaan (2.11) telah dijelaskan pada penelitian Dionne dan Vanasse (1989). Sedangkan, sistem Bonus-Malus berdasarkan banyak klaim dan besar kerugian menggunakan persamaan (2.12) dan (2.13). Persamaan (2.13) merupakan perhitungan premi risiko yang menggabungan secara simultan karakteristik individu, jumlah kecelakaan, dan besar kerugian dari setiap kecelakaan.

Mert dan Saykan (2005) menggunakan sistem Bonus-Malus dengan banyak klaim berdistribusi geometrik dan besar kerugian berdistribusi pareto. Banyak klaim pada penelitian ini mengasumsikan parameter persamaan (2.1) berdistribusi eksponensial seperti persamaan (2.8). Berdasarkan persamaan (2.1) dan (2.8) dihasilkan fungsi kepekatan peluang banyak klaim berdistribusi geometrik sebagai berikut:

 

1

, 0 1.

1 1 1

k

P k  

  

 

 _{ }  

     (2.14)

Fungsi kepekatan peluang besar kerugian yang digunakan pada penelitian ini sama seperti persamaan (2.10). Adapun model premi risiko yang digunakan adalah

1 1

1

. 1

K k k t

m x

K P

t  s K

 

  

  



6

Persamaan (2.15) menunjukkan bahwa premi risiko yang dibayarkan bergantung pada parameter distribusi geometrik � , parameter distribusi pareto ( dan ), periode waktu , total banyak klaim (K), dan total besar kerugian (

1

K k k

x 



).

Ni et al. (2014) menganalisis besar kerugian berdasarkan distribusi eksponensial dengan parameter �. Parameter � diasumsikan berdistribusi Levy dengan dengan parameter . Fungsi kepekatan peluang parameter � adalah

 

₃ exp 2 , 0 dan 0.

4 2

c c

f   c

  

 

 _ _  

  (2.16)

Berdasarkan persamaan (2.8) dan (2.16) diperoleh fungsi kepekatan peluang besar kerugian sebagai berikut:

 

, 0.

2

c x c x e

f x x

x



  (2.17)

Persamaan (2.17) menunjukkan bahwa fungsi kepekatan peluang berdistribusi Weibull dengan parameter − , .

Penentuan premi risiko sistem Bonus-Malus oleh Ni et al. (2014) dengan distribusi binomial negatif pada banyak klaim dan distribusi Weibull pada besar kerugian adalah









3

2 1

1

2 2

,

K t

K

B c M

K M

P

t c _{B c M}

 

 



 

 



 _{ }

  

 

(2.18)

1 | 0 2

2 ,

t M P

t c

      

   (2.19)

dengan M adalah total besar kerugian, �_{� − /} adalah fungsi Bessel dengan indeks

− / , dan adalah parameter distribusi Weibull. Premi risiko persamaan (2.19) digunakan ketika tidak ada klaim yang diajukan, sedangkan persamaan (2.18) digunakan untuk menghitung premi risiko jika ada klaim yang diajukan.

METODE PENELITIAN

Pada penelitian ini, difokuskan penyelesaian premi risiko yang melibatkan banyak klaim dan besar kerugian terpotong dari setiap pemegang polis. Diasumsikan bahwa banyak klaim dari setiap pemegang polis saling bebas dengan besar kerugian dari setiap klaim. Berikut langkah-langkah umum yang dilakukan. 1. Memodifikasi distribusi besar kerugian yang sudah ada menjadi distribusi

terpotong.

7

HASIL DAN PEMBAHASAN

Modifikasi Distribusi Besar Kerugian

Perhitungan premi risiko sistem Bonus-Malus optimal yang wajib dibayarkan oleh setiap pemegang polis asuransi didasarkan pada komponen banyak klaim dan besar kerugian yang ditimbulkan akibat kecelakaan. Model komponen banyak klaim yang digunakan seperti pada penelitian Mert dan Saykan (2005) yaitu menggunakan distribusi geometrik yang merupakan gabungan dari distribusi Poisson dan eksponensial. Estimasi rata-rata banyak klaim periode selanjutnya adalah









1 1 2

0

1

| | , ,

ˆ _{, ,}

t t

K

E K u k k k d

t

    

 





   





(4.1)

dengan

1

t i i

K k







menyatakan total banyak klaim selama periode dan

� menyatakan banyak klaim dari setiap pemegang polis periode waktu ke-�,

� = , , … , . Persamaan (4.1) menunjukkan bahwa premi risiko yang harus dibayarkan pada periode + dengan banyak klaim � , � , … , �_�, hanya bergantung pada total banyak klaim (K) yang diajukan setiap pemegang polis dan periode waktu (t). Bukti persamaan (4.1) tersaji dalam lampiran.

Model besar kerugian berdasarkan Ni et al. (2014) menggunakan distribusi Weibull. Estimasi rata-rata besar kerugian periode selanjutnya dengan besar kerugian , , … , _� dan total besar kerugian selama periode waktu t menggunakan bagian dari persamaan (2.18) yaitu









3

2 1

1

2

2

ˆ K _.

t

K

B c M

M

c _{B c M}

_ 



 

 _ _

  (4.2)

Persamaan (4.2) menunjukkan bahwa estimasi rata-rata besar kerugian periode selanjutnya bergantung pada total besar kerugian (M) dan banyak klaim (K) selama t periode.

Sistem Bonus-Malus besar kerugian pada penelitian Ni et al. (2014) tidak mempertimbangkan besar kerugian maksimum yang mampu ditanggung perusahaan asuransi, sehingga model tersebut perlu dimodifikasi dengan besar kerugian yang terpotong. Ketika perusahaan asuransi hanya mampu menanggung besar kerugian dari setiap pemegang polis sebesar , maka besar kerugian yang ditanggung perusahaan asuransi di atas nilai adalah sebesar . Besar kerugian diasumsikan berdistribusi campuran eksponensial terpotong dengan Levy. Misalkan besar kerugian dari setiap pemegang polis adalah x dan berdistribusi eksponensial terpotong, maka fungsi kepekatan peluangnya adalah





, 0

,

| ,

x u e

f X x u

x u x

e





   _

  

 





8





, 0

, 1 1 | . x x F X u e x u x          _{ } 

Parameter � diasumsikan berdistribusi dengan parameter c yang memiliki fungsi kepekatan peluang:





42

3

Θ  ,   0.

2 c c e         

Fungsi distribusi kumulatif besar kerugian untuk 0 x u adalah

 



 







 

2 2 2 0 4 3 0 4 4 3 3 0 0 | Θ 1 2

2 2

c x

c c

x

F x F X x d

c

e e d

c c

e d e e d

 _                _   _  _        









2 2 4 4 3 3 0 0 .

2 2

c

c _x

c c

e d e d

   _{ }      _  _  _  









(4.3)

Misalkan 2 4 3 0 1, 2 c c

e d



 _





2 2

2 3 ,

4 2 c c d d         

ketika    0  dan      0,maka persamaan (4.3) dapat dituliskan menjadi

 

2 2 2 0 2 4 3 3 2 2 1 . 2 2 4 c x c c

F x e d

c   _          _ _ _{ }          _ _        



(4.4)

Keterangan:

 

 

 

 

0

lim lim lim .

a b b

b b b

b a a

f x dx f x dx f x dx f x dx

  



    









Persamaan (4.4) menjadi

2 2 2 2 2 2 2 4 3 3 2 0 2 3 4 3 0 3

( ) 1

2 2

4 1

2 2

2

c x

c x

c c

F x e d

9 2 2 2 2 4 0 2

1 , 0

4

c x

c x

e d a

  _     _{  }      



  2 2 0 2 1 . a e d   _     _  _  

 



(4.5)

Selanjutnya, untuk menyelesaikan persamaan (4.5) digunakan persamaan berikut

2 2 2 2 2 2 2 0 0 2 0 0 2 0 0 a a a a a a

I e d

a

e d

a

e d e d

a

e d e d

                        _  _       _ _        _{  }  _{  }              _  _  _  _         _  _       _ _       _ _  













2 2 0 1 . a a e d   _      _ _      _  _  



(4.6)

Misalkan



,



, a g        2 1 0. dg a

d   

Penyelesaian persamaan (4.6) adalah

2 2 2 2 1 1 1 . g g a

I e dg

a e dg             _  _{ }   _{  }    





Langkah berikutnya diperlukan penyelesaikan bentuk lain dari persamaan (4.6) sedemikian sehingga didapat penyelesaian dari persamaan

2 0 . a e d   _     _ _  



Misalkan 2 , a d d a       

10 2 2 2 2 2 2 2 0 0 0 2 2 0 2 2 0 0 0 a a a a a a a

I e d e d

a

e d e d

a a

e d e d

a e                             _{  }  _{  }               _ _ _  _           _{  }  _{  }              _{ }        _{ } _          _ _     















2 2 2 2 2 0 0 0 0 2 . a a a a a

d e d

e d e d

e d                  _   _  _  _ _          _{  }  _{  }             _ _      









Karena 2 0 2 a

I e d



 _

    _ _  





dan I  , maka diperoleh penyelesaian persamaan (4.6) sebagai berikut:

2 2 2 2 2 0 0 0 0 2 1 2 . 2 a a a a a

I e d e d

e d e d                     _{  }  _{  }             _ _       _ _       _  _    









Persamaan (4.5) dijabarkan kembali sebagai berikut:

 

2 2

2 2 0 2 0 2 0 2 2 2 1 . 2 1 2 1 2 1 2 1 a a a a a a a

F x e d

e d

e e d

11 2 2 4 1 1 . c x c x e e      

Fungsi distribusi kumulatif besar kerugian terpotong adalah

 



 



0

| Θ

F x F X x   d

 



  2 2 0 2 1 exp 1 , 0 , 1 , 0 1 , c x x u x u a d x u e x u        _ _ _          _        _      



1 2 2 , 0

, 1 1 x c e x x u u     _ _      _    (4.7) Fungsi distribusi kumulatif persamaan (4.7) merupakan fungsi distribusi Weibull terpotong dengan parameter − , .

Besar kerugian { , , … , _�} dari setiap pemegang polis sebanyak klaim, besar kerugian untuk 0 x_i u adalah klaim, maka banyaknya kerugian untuk

i

x u adalah Kn klaim. Misalkan merupakan total besar kerugian untuk 0 x_i u maka

1 . n i i N x 





dan total besar kerugian dari klaim adalah









1 1 . K n i i i i

x x u K n N u K n

 

     





Fungsi kepekatan peluang bersama

untuk besar kerugian sebanyak klaim adalah





 

1

1 1 1

| i

n i i

K K n

i i n x u i i x

u K n n

f x e e

e e                    







      1 . n i i

x u K n n

N u K n n e e           _   _        

Estimasi parameter besar kerugian dengan pendekatan Bayes, diperoleh fungsi distribusi posterior sebagai berikut:







  



  

1 1 2 1 0 | | , , , | K i i K _K i i f x x x x

f x d

12                 2 2 2 2 3 ₄ 2 3 ₄ 2 0 3 ₄ 2 3 4 2 0 2 2 c

N u K n n

K n K n c

N u K n n

c

N u K n K n n

c

N u K n K n n

c e c e d e e d          _                 _ _            _ _           _ _            _ _  





        2 2 3 ₄ 2 3 ₄ 2 0 . c

N u K n K

c

N u K n K e e d                _ _          _ _ 



(4.8)

Memodifikasi persamaan (4.8) sedemikian sehingga diperoleh









   





    2 2 1 2 3 ₄ 2

1 2 1

2 3 4 2 0 2 | , , , 2 K c

N u K n K

K

K

c

N u K n K

c

e N u K n

x x x

c

e d

N u K n

           _  _{  }   _{    }  _ _   _  _{  }   _{    }   _ _      _{ }           _{ }   







   









      2 1

2 3 4 2 3 2 2 2 2 0 2 2 2 K c

N u K n K

K c N u K n N u K n c c N u K n c

e

N u K n

N u K n N u K n

e d c c          _  _{  }   _{    }  _ _     _     _         _{ }   _      _{ }      _{ }  _{ }      







   





     





2 1

2 3 4 2 3 2 2 2 2 0 2 . 2 2 K c

N u K n K

K c N u K n N u K n c c N u K n c

e

N u K n

N u K n N u K n

e d c c          _  _         _ _     _     _         _{ }   _      _{ }      _{ }   _{ }             



(4.9) Bentuk integral pada bagian penyebut persamaan (4.9) dapat diselesaikan dengan menggunakan fungsi Bessel sebagai berikut:

 

1 2 1 0 1 . 2 x y y v v

B x y e dy

 

 _{   }

  





13









   









2 1 2 _{3 4} 2 1 2 1 2 2 | , , , . 2 K c

N u K n K

K

K

c

e

N u K n

x x x

B c N u K n

       _  _         _ _       _{ }       

Estimasi rata-rata besar kerugian periode selanjutnya _t1 menggunakan fungsi kerugian kuadrat, jika diketahui besar kerugian , , … , _� selama periode waktu t dan K klaim adalah





   













   













2 2 1

2 3 4 2 1 1 2 1 2 _{5 4} 2 1 2 1 2 2 1 2 2 2 2 ˆ K c

N u K n K

t o

K

K _c

N u K n K o K K o c e

N u K n

d

B c N u K n

c

e

N u K n

d

B c N u K n

c

N u K n

            _  _         _ _      _  _{  }   _{    }                 _{ }            _{ }            _{ }    







   

































    2 2 3 1 ₄ 2 1 2 3 2 1 2 3 1 2 3 1 ₄ 2 3 2 2 2 2 2 c

N u K n K K K K K c

N u K n K

o

K

e

d

B c N u K n

B c N u K n

N u K n

c

B c N u K n

c

e

N u K n

B c N u K

               _ _{     }              _  _{  }    _ _{     }               _{   }        _{ }      _{ }    



































   









2 3 2 1 2 1 2 1 1 ₄ 2 3 2 2 2 2 K K K c

N u K n K

o

K

d n

B c N u K n

N u K n

c

B c N u K n

c

e

N u K n

d

B c N u K n

14





















3 2 1 2 2 K K

B c N u K n

N u K n

c

B c N u K n

    _{   }        _{ }





















3 2 1 2 2 . K K

B c N u K n

N u K n

c _{B c N u K n}

     _{ }       _{ }   (4.10)

Persamaan (4.10) menunjukkan bahwa estimasi rata-rata besar kerugian periode selanjutnya bergantung pada total besar kerugian ( + − ) dan banyak klaim ( ) selama t periode. Ketika ≤ + − maka estimasi rata-rata besar kerugian _t1 persamaan (4.2) memberikan hasil yang sama besarnya dengan persamaan (4.10). Sedangkan untuk > + − , maka estimasi _t1 persamaan (4.2) lebih besar dari persamaan (4.10).

Premi risiko periode t +1 berdasarkan banyak klaim � , � , … , �_� dan besar kerugian , , … , _� yang wajib dibayarkan oleh pemegang polis untuk besar kerugian yang tidak terpotong adalah









3 2 t 1 1 2 1 2

Premi K .

K

B c M

K M

t c _{B c M}

            _ _ _        (4.11)

Sedangkan, premi risiko periode t +1 dengan besar kerugian yang terpotong adalah





















3 2 t 1 1 2 2 1

Premi K .

K

B c N u K n

N u K n

K

t c _{B c N u K n}

     _{ }            _ _{ }    _{ }      (4.12)

Persamaan (4.11) dan (4.12) menunjukkan bahwa premi risiko periode selanjutnya bergantung pada banyak klaim, periode waktu, dan besar kerugian. Besar kerugian persamaan (4.11) adalah sebesar . Sedangkan, besar kerugian persamaan (4.12) terbagi menjadi dua bagian yaitu besar kerugian yang berada di bawah batas maksimum kerugian sebesar dan besar kerugian di atas batas maksimum

kerugian sebesar − . Ketika besar kerugian = maupun

+ − = atau pada saat tidak ada klaim yang diajukan = , perhitungan premi risiko persamaan (4.11) dan (4.12) tidak terdefinisi sehingga

perlu dianalisis ulang. Analisis premi risiko untuk besar kerugian

+ − = disajikan dalam lampiran dan hasilnya sebagai berikut:

 

1| 0 2

1 2

Premi_{t N u K n} .

t  c

   

 

 _{ }

   (4.13)

Premi risiko persamaan (4.13) menunjukkan bahwa semakin bertambahnya waktu (t), semakin kecil harga premi risiko ketika tidak ada klaim yang diajukan.

Simulasi Numerik Sistem Bonus-Malus

15

= . . Batas maksimum yang ditanggung perusahaan asuransi adalah

= . Premi risiko yang dihitung untuk bulan = , , … , dan banyak klaim

= , , … , .

Tabel 1 Banyak klaim

Banyak klaim Jumlah kejadian Total klaim

0 48 0

1 29 29

2 12 24

3 11 33

4 9 36

5 6 30

6 3 18

7 1 7

8 1 8

Total 120 185

Tabel 2 Besar kerugian dan banyak klaim data sebenarnya Besar kerugian Banyak klaim

0-50 52

50-100 14

100-200 22

200-400 23

400-800 22

800-1600 23

1600-3200 19

3200-6400 6

6400-12800 1

12800-25600 3

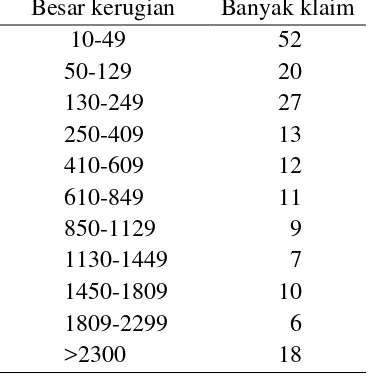
Tabel 3 Besar kerugian dan banyak klaim dengan u = 2300 Besar kerugian Banyak klaim

10-49 52

50-129 20

130-249 27

250-409 13

410-609 12

610-849 11

850-1129 9

1130-1449 7

1450-1809 10

1809-2299 6

16

Tabel 1 menunjukkan data banyak klaim dari 0 hingga 8, serta jumlah kejadian dan total klaim. Tabel 2 menunjukkan banyak klaim dari besar kerugian yang diajukan oleh para pemegang polis. Pada tabel terlihat bahwa banyak klaim terbesar pada rentang 0 hingga 50. Sedangkan, Tabel 3 menunjukkan data besar kerugian dan banyak klaim yang telah terpotong besar kerugiannya. Besar kerugian 10-49 memiliki banyak klaim terbanyak yaitu sebesar 52.

Sistem Bonus-Malus tanpa Distribusi Terpotong

Sistem Bonus-Malus tanpa distribusi terpotong, perhitungan premi risiko yang harus dibayarkan oleh setiap pemegang polis menggunakan persamaan (4.11) jika terdapat klaim yang diajukan, sedangkan apabila tidak ada klaim yang diajukan menggunakan persamaan (4.13). Total besar kerugian yang digunakan adalah 8000 dan 10000.

Tabel 4 Hasil perhitungan harga premi risiko dengan total besar kerugian 8000

Bulan Banyak klaim (K)

(t) 0 1 2 3 4 5

0 493

1 296 2752 3398 3749 3918 3980 2 211 1966 2427 2678 2798 2843 3 164 1529 1888 2083 2176 2211 4 134 1251 1544 1704 1781 1809 5 114 1058 1307 1442 1507 1531 6 99 917 1133 1250 1306 1327 7 87 809 999 1103 1152 1171

Tabel 5 Hasil perhitungan harga premi risiko dengan total besar kerugian 10000

Bulan Banyak klaim (K)

(t) 0 1 2 3 4 5

0 493

1 296 3077 3871 4347 4612 4744 2 211 2198 2765 3105 3294 3389 3 164 1709 2151 2415 2562 2636 4 134 1399 1760 1976 2096 2156 5 114 1183 1489 1672 1774 1825 6 99 1026 1290 1449 1537 1581 7 87 905 1139 1279 1356 1395

17 total besar kerugian menjadi 10000, pemegang polis diwajibkan membayar premi risiko sebesar 3105 yang dapat dilihat pada Tabel 5.

Sistem Bonus-Malus dengan Distribusi Terpotong

Sistem Bonus-Malus dengan distribusi terpotong, perhitungan premi risiko yang harus dibayarkan oleh setiap pemegang polis menggunakan persamaan (4.12) jika terdapat klaim yang diajukan, sedangkan apabila tidak ada klaim yang diajukan menggunakan persamaan (4.13). Besar kerugian diasumsikan sebagai besar kerugian di bawah batas maksimum yaitu .

Tabel 6 Hasil perhitungan harga premi risiko dengan u = 2300 Bulan

(t)

Banyak klaim (K)

0 1 2 3

Banyak klaim kurang dari u (n)

0 1 0 1 2 0 1 2 3

0 493

1 296 1476 973 2439 1986 1443 3393 2940 2441 1879 2 211 1054 695 1742 1419 1031 2424 2100 1744 1342 3 164 820 541 1355 1104 802 1885 1633 1356 1044 4 134 671 442 1109 903 656 1542 1336 1110 854 5 114 568 374 938 764 555 1305 1131 939 723 6 99 492 324 813 662 481 1131 980 814 626 7 87 434 286 717 584 425 998 865 718 553 Tabel 6 Hasil perhitungan harga premi risiko dengan u = 2300 (lanjutan) Bulan

(t)

Banyak klaim (K)

4 5

Banyak klaim kurang dari u (n)

0 1 2 3 4 0 1 2 3 4 5

0

1 4341 3881 3393 2868 2299 5284 4818 4331 3820 3282 2711 2 3101 2772 2423 2049 1642 3774 3441 3093 2729 2344 1936 3 2412 2156 1885 1594 1277 2936 2677 2406 2122 1823 1506 4 1973 1764 1542 1304 1045 2402 2190 1969 1736 1492 1232 5 1670 1493 1305 1103 884 2032 1853 1666 1469 1262 1043 6 1447 1294 1131 956 766 1761 1606 1444 1273 1094 904 7 1277 1142 998 844 676 1554 1417 1274 1124 965 797

Tabel 6 menunjukkan bahwa di awal bulan pemegang polis membayarkan premi risiko awal sebesar 493, apabila pada bulan pertama tidak mengajukan klaim maka pembayaran premi risiko berkurang menjadi 296. Ketika pada bulan pertama pemegang polis mengajukan klaim sebanyak satu kali maka diwajibkan membayar sebesar 1476 jika klaim yang diajukan lebih dari 2300. Sedangkan jika klaim yang diajukan dibawah 2300 maka premi risiko yang wajib dibayarkan sebesar 973.

18

kerugian ≤ + − , maka premi risiko berdasarkan distribusi besar kerugian Weibull akan sama besarnya dengan premi risiko berdasarkan distribusi Weibull terpotong. Sedangkan untuk besar kerugian > + − , premi risiko berdasarkan distribusi besar kerugian Weibull lebih mahal daripada premi risiko berdasarkan distribusi Weibull terpotong.

SIMPULAN

Penelitian ini telah membahas sistem Bonus-Malus optimal dengan besar kerugian yang terpotong, bergantung pada kemampuan perusahaan asuransi dalam memberikan santunan kepada pemegang polis. Berdasarkan hasil pembahasan, diperoleh simpulan bahwa persamaan premi risiko dengan batas kerugian maksimum adalah

Premit+ = _{� +}+

(

( √ + − )�� − √ + −

�_{� −} √ + −

) ,

dengan adalah total banyak klaim, adalah batas maksimum yang mampu ditanggung perusahaan asuransi, adalah total besar kerugian di bawah batas , adalah banyak klaim di bawah batas , �_{�− /} adalah fungsi Bessel dengan indeks

− / , � adalah parameter distribusi banyak klaim, dan adalah parameter distribusi besar kerugian. Persamaan premi risiko periode selanjutnya menunjukkan bahwa premi risiko bergantung pada banyak klaim, waktu, dan total besar kerugian. Premi risiko sistem Bonus-Malus dengan komponen besar kerugian berdasarkan distribusi Weibull sama besarnya dengan premi risiko berdasarkan distribusi Weibull terpotong ketika besar kerugian lebih kecil dari batas maksimum kerugian ( ≤ + − ). Sedangkan, premi risiko berdasarkan distribusi Weibull menjadi lebih mahal dari premi risiko berdasarkan distribusi Weibull terpotong

ketika besar kerugian lebih besar dari batas maksimum kerugian ( > + − ). Semakin besar kerugian yang ditimbulkan maka semakin

besar pula premi risiko yang harus dibayarkan oleh pemegang polis dan sebaliknya untuk kerugian yang semakin kecil.

DAFTAR PUSTAKA

Bowers NL, Gerber HU, Hickman JC, Jones DA, Nesbitt CJ. 1997. Actuarial Mathematics. Schaumburg (US). The Society of Actuaries.

Denuit M, Marechal X, Pitrebois S, Walhin JF. 2007. Actuarial Modelling of Claim Counts. England (GB): John Wiley & Sons.

Dionne G, Vanasse C. 1989. A Generalization of Automobile Insurance Rating Models: The Negative Binomial Distribution with a Regression Component.

ASTIN Bulletin. 19:199-212.

19

Ghahramani S. 2005. Fundamentals of Probability with Stochastic Processes. 3rd ed. United States of America (US): Pearson Prentice Hall.

Hogg RV, McKean J, Craig AT. 2014. Introduction to Mathematical Statistics. United States of America (US): Pearson Education.

Klugman SA, Panjer HH, Willmot GE. 2012. Loss Models. United States of America (US): John Wiley & Sons.

Mahmoudvand R, Hassani H. 2009. Generalized Bonus-Malus Systems with a Frequency and a Severity Component on an Individual Basis in Automobile Insurance. ASTIN Bulletin. 39(1):307-315.

Mert M, Saykan Y. 2005. On a Bonus Malus System where the Claim Frequency Distribution is Geometric and the Claim Severity Distribution is Pareto. Hacettepe Journal of Mathematics and Statistics. 34:75-81.

Ni W, Constantinescu C, Pantelous AA. 2014. Bonus-Malus Systems with Weibull Distributed Claim Severities. Annals of Actuarial Science. 8(2):217-233. Ross SM. 2010. Introduction to Probability Models. 10th ed. United States of

America (US): Elsevier Inc.

Tremblay L. 1992. Using the Poisson Inverse Gaussian in Bonus-Malus Systems.

20

LAMPIRAN

Lampiran 1 Beberapa Definisi dan Teorema

Definisi L.1 (Peubah Acak)

Misalkan kejadian acak dengan suatu ruang sampel C, terdapat fungsi X yang memetakan tepat satu elemen cC dan hanya ada satu nilai X c

 

x x, R

disebut sebagai peubah acak (Hogg et al. 2014).

Definisi L.2 (Fungsi Sebaran)

Fungsi sebaran dari suatu peubah acak adalah fungsi F_X :R[0,1] _yang

diberikan oleh F_X

 

x P X



x



(Ross 2010).

Definisi L.3 (Peubah Acak Diskret)

Peubah acak X adalah suatu peubah acak diskret dengan hasil yang mungkin

, , … , �, …, dan fungsi massa peluangnya merupakan suatu fungsi yang memenuhi kondisi sebagai berikut:

1. p x

 

_i P X



x_i



,

2. p x

 

_i 0, i1, 2, 

3.

 

1

1.

i i

p x

 





Fungsi distribusi kumulatif � dari kondisi � adalah

 

( )

i

i x x

F x p x

 





(Ross

2010).

Definisi L.4 (Peubah Acak Kontinu)

Peubah acak X dikatakan suatu peubah acak kontinu jika fungsi sebarannya dapat dinyatakan sebagai

 

 

x X

F x f u du







untuk suatu fungsi f :R[0,1] _yang

terintegralkan. Fungsi f  f_X merupakan fungsi kepekatan peluang dari . Kondisi yang harus dipenuhi pada peubah acak kontinu:

1. f x

 

0,

2. P X(



,



f x dx

 

1,

 

   





3.





( ) ,

b a

21

4.





( ) 0.

a a

P X a 



f x dx

Selanjutnya, fungsi distribusi kumulatif dari peubah acak kontinu adalah

 





,





( ) .

a

F a P X a f x dx



   



Hubungan fungsi distribusi kumulatif dan fungsi kepekatan peluang ditunjukkan dengan d F a

 

f a

 

da  (Ross 2010).

Definisi L.5 (Peubah Acak dengan Batas)

Misalkan sebuah peubah acak kontinu dengan batas , diberikan oleh

, , ,

X X u

Y

u X u

 

  _



dengan merupakan peubah acak dengan batas tak berhingga (Klugman et al. 2012).

Definisi L.6 (Sebaran Bersama Dua Peubah Acak)

Peubah acak dan disebut dua peubah acak kontinu yang menyebar bersama jika untuk setiap , ∈ fungsi distribusi sebaran bersamanya dapat diekspresikan sebagai

 

 





 

, , , , ,

y x X Y

F x y F x y P X x Y y f u v dudv



    

 

untuk satu fungsi : → [ , ] yang terintegralkan (Ghahramani 2005).

Definisi L.7 (Fungsi Kepekatan Peluang Bersama)

Fungsi f_{X Y,} ( , )x y disebut fungsi kepekatan peluang bersama dari peubah acak kontinu dan jika

 

2 ,

 

,

,

, X Y

X Y

F x y

f x y

x y  

 

(Ghahramani 2005).

Definisi L.8 (Fungsi Kepekatan Peluang Marginal)

22

 

 

 

 

,

,

, ,

,

X X Y

Y X Y

f x F x y dy

f y F x y dx



 



 





(Ghahramani 2005).

Definisi L.9 (Fungsi Kepekatan Peluang Bersyarat)

Misalkan dan peubah acak kontinu dengan fungsi kepekatan peluang marginal f_Y

 

y 0.Fungsi kepekatan peluang bersyarat dari dengan syarat

= adalah

 

 

 

|

,

| X

X Y

Y Y f x y f x y

f y 

(Ross 2010).

Definisi L.10 (Nilai Harapan Peubah Acak Diskret)

Misalkan X peubah acak diskret dengan fungsi massa peluang

 





,

p x P X x maka nilai harapan dari X adalah

 

( )

x E X 



xp x

(Ross 2010).

Definisi L.11 (Nilai Harapan Peubah Acak Kontinu)

Misalkan X peubah acak kontinu, dengan fungsi kepekatan peluang f_X

 

x ,

maka nilai harapan dari X adalah

 

( )

E X xf x dx

 





(Ross 2010).

Definisi L.12 (Ragam Peubah Acak Diskret)

Misalkan X peubah acak diskret, dengan fungsi massa peluang

 





,

p x P X x maka ragam dari X adalah

 

2

 

 

2

x x

Var X  x p x   xp x _

 





23 Definisi L.13 (Ragam Peubah Acak Kontinu)

Misalkan X peubah acak kontinu, dengan fungsi kepekatan peluang f_X

 

x ,

maka ragam dari X adalah

 

2

 

 

2

X

Var X x f x dx xf x dx

 

 

 

 _{  }

 





(Ross 2010).

Definisi L.14 (Fungsi Bessel Termodifikasi)

Misalkan B x_v

 

merupakan fungsi Bessel termodifikasi dengan indeks , maka B x_v

 

direpresentasikan sebagai

 

cosh

 

 

0

cosh , 0, 0,

x t

v v

B x e vt dt B x x v R

 





   

(Ni et al. 2014).

Definisi L.15 (Distribusi Poisson)

Banyaknya hasil X dalam suatu percobaan Poisson disebut suatu peubah acak Poisson dan distribusi peluangnya disebut distribusi Poisson. Distribusi peluang peubah acak Poisson X, yang menyatakan banyaknya sukses yang terjadi dalam suatu selang waktu atau daerah tertentu, diberikan oleh

 

; , 0,1, 2, !

x

e

f x x

x

_

    

dengan menyatakan rata-rata banyaknya sukses yang terjadi dalam selang waktu atau daerah tertentu tersebut dan e = 2,71828. Distribusi Poisson memiliki nilai harapan dan ragam yang sama yaitu

 

 

E X Var X  (Hogg et al. 2014).

Definisi L.16 (Distribus