Representasi Algoritma Kuhn-Munkres Padagraf Bipartit

REPRESENTASI ALGORITMA KUHN-MUNKRES

PADA GRAF BIPARTIT UNTUK MENYELESAIKAN

OPTIMAL ASSIGNMENT PROBLEM

SKRIPSI

DESNI RAHMALINA. P

070823014

PROGRAM STUDI SARJANA MATEMATIKA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

REPRESENTASI ALGORITMA KUHN-MUNKRES

PADA GRAF BIPARTIT UNTUK MENYELESAIKAN

OPTIMAL ASSIGNMENT PROBLEM

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

DESNI RAHMALINA. P

070823014

PROGRAM STUDI SARJANA MATEMATIKA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

JUDUL : REPRESENTASI ALGORITMA KUHN-MUNKRES PADAGRAF BIPARTIT

Kategori : SKRIPSI

Nama : DESNI RAHMALINA PULUNGAN

Nomor Induk Mahasiswa : 070823014

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas :MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Medan, Juni 2010

KOMISI PEMBIMBING:

PEMBIMBING 2, PEMBIMBING 1

Drs. Sawaluddin, M.IT

NIP 195912311998021001 NIP194612251974031001 Drs. Marwan Harahap,M.Eng

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

PERNYATAAN

REPRESENTASI ALGORITMA KUHN-MUNKRES PADA GRAF BIPARTIT

UNTUK MENYELESAIKAN OPTIMAL ASSIGNMENT PROBLEM

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing- masing disebutkan sumbernya.

Medan, Juni 2010

070823014

PENGHARGAAN

Puji dan syukur penulis panjatkan kepada Allah SWT, dengan limpahan dan

karuniaNya skripsi ini berhasil diselesaikan dalam waktu yang telah ditetapkan.

Ucapan terima kasih saya sampaikan kepada Drs. Marwan Harahap, M.Eng

dan Drs. Sawaluddin, M. IT selaku pembimbing pada penyelesaian skripsi ini yang

telah memberikan panduan dan penuh kepercayaan kepada saya untuk

menyempurnakan kajian ini. Panduan ringkas, padat dan professional telah diberikan

kepada saya agar penulis dapat menyelesaikan tugas ini. Ucapan terima kasih juga

ditujukan kepada Ketua dan Sekretaris Departemen Matematika FMIPA USU Dr.

Saib Suwilo, M.Sc dan Drs Henry Rani Sitepu, M.Si, Dekan dan Pembantu Dekan

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara,semua

dosen pada Departemen Matematika FMIPA USU, pegawai di FMIPA USU, dan

rekan-rekan kuliah. Akhirnya, tidak terlupakan kepada orang tua dan semua ahli

keluarga dan rekan terdekat saya yang selama ini memberikan bantuan dan dorongan

ABSTRAK

Semakin meningkatnya kompetisi global menuntut setiap perusahaan untuk

meningkatkan kualitas serta efektifitas kinerja karyawannya yang pada akhirnya

diharapkan dapat mendongkrak profit ( keuntungan). Salah satu cara yang sering

digunakan adalah dengan mengadakan rolling. Sistem ini dapat digunakan untuk

mengetahui penempatan terbaik (optimal) bagi karyawan. Pencarian solusi pada

optimal assignment problem ini dapat diperoleh dengan menerapkan konsep teori

graf. Dalam hal ini permasalahan dinyatakan sebagai graf bipartit khususnya graf

bipartit lengkap berbobot yang menerapkan konsep matching, yaitu pencarian

matching sempurna dengan bobot paling optimal. Pencarian matching sempurna pada

graf bipartit lengkap berbobot mempunyai kemungkinan sebanyak n!. Oleh karena itu

mengefisienkan yaitu algoritma optimal tersebut, maka dapat digunakan sebuah

ABSTRACT

Increasing global competition requires each company to improve the quality and

effectiveness of employee performance which in turn is expected to increase profits.

One frequently used way is by performing rolling. This system is used to determine

the best placement(optimal) for employees. On the optimum placement of some x

employees at y type of job, if the number of employees likened equal to the amount of

job by considering the optimization benefits.finding solution to optimal assignment

problem can be obtained by applying the concept of graphs teory. in this case the

problems are stated as a bipartite graph, especially the complete weighted bipartite

graph that implements the concept of matching, Search is perfectly matched with the

optimal weights. Searching perfectly to the weighted bipertite graph has the

possibility of as many as n!. Therefore, the search is inefficient for a large value of n.

then to further streamline the search for optimal solutions can be used an optimization

DAFTAR ISI

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel ix

Daftar Gambar xii

BAB1. PENDAHULUAN 1

1.1Latar Belakang 1

1.2Perumusan Masalah 2

1.3Batasan Masalah 3

1.4Tujuan Masalah 3

1.5Kontribusi Penelitian 3

1.6Tinjauan Pustaka 3

1.7Metode Penelitian 4

BAB2. LANDASAN TEORI 5

2.1 Himpunan 5

2.1.1 Beda Simetri 6

2.2 Pengertian Graf 7

2.2.1 Istilah-istilah dalam Graf 9

2.2.2 Graf Bipartit 13

2.2.3 Spanning Subgraph 14

2.3 Matching Graf 16

2.3.1 Matching pada Graf Bipartit 23

BAB3. REPRESENTASI ALGORITMA KUHN-MUNKRES 26

3.1.1 Feasible vertex Labeling 28

3.1.2 Equality Subgraph 31

3.2 Algoritma Kuhn- Munkres 33

3.3 Penentuan Bobot Minimum 38

3.4 Implementasi dan Pengujian 51

3.4.1 Tampilan Program dan Hasil Pengujian 52

BAB4. KESIMPULAN DAN SARAN 54

4.1 Kesimpulan 54

4.2 Saran 55

DAFTAR PUSTAKA 56

DAFTAR TABEL

TABEL 3.1 Daftar Nilai Karyawan 26

TABEL 3.2 Daftar Bobot 29

TABEL 3.3 l (y)=0 30

TABEL 3.4 Nilai x Maksimum 30

TABEL 3.5 Feasible vertex labelling dari Graf Bipartit 31

TABEL 3.6 Feasible vertex labelling ke-1 35

TABEL 3.7 Feasible vertex labelling ke-2 37

TABEL 3.8 Daftar kecepatan kinerja tim 39

TABEL 3.9 Bobot W* 40

TABEL 3.10 Feasible vertex labelling ke-1 41

TABEL 3.11 Feasible vertex labelling ke-2 43

TABEL 3.12 l’’ 45

TABEL 3.13 l’’’ 48

DAFTAR GAMBAR .

Gambar 2.1 Graf G 8

Gambar 2.2 Simpul Terisolasi 10

Gambar 2.3 Graf Sederhana dan Graf bukan Sederhana 12

Gambar 2.4 Graf Kosong 12

Gambar 2.5 Graf lengkap dengan 4 simpul 13

Gambar 2.6 Graf berbobot 13

Gambar 2.7 Graf bipartit lengkap 14

Gambar 2.8 Graf H (Spanning subgraph dari Graf G) 15

Gambar 2.9 Contoh matching 16

Gambar 2.10 Contoh Simpul unsaturated M 17

Gambar 2.11 Contoh M-augmenting dan M-alternating 18

Gambar 2.12 Graf dengan matching M dan matching M’ 19

Gambar 2.13 H= G(M∆M’) 19

Gambar 2.14 Graf G dengan matching M dan matching M’ 20

Gambar 2.15 H = G(M∆M’) dari Graf 21

Gambar 3.1 Graf bipartit berbobot 26

Gambar 3.2 Contoh Graf Bipartit berbobot 29

Gambar 3.3 Equality subgraph dari Graf bipartit berbobot 32

Gambar 3.4 Bentuk Flowchart algoritma Kuhn-Munkres 34

Gambar 3.4 Equality subgraph ke-1 36

Gambar 3.5 Sebarang matching M 36

Gambar 3.6 Equality subgraph ke-2 38

Gambar 3.7 Equality subgraph ke-1 41

Gambar3.8 Graf dengan matching M 42

Gambar 3.9 Equality subgraph ke-2 44

Gambar 3.10 Equality subgraph ke-3 46

Gambar 3.11 Matching pada Gl’’ 47

Gambar 3.12 Equality subgraph dan sebarang matching 48

Gambar 3.14 Permasalahan maksimum 52

Gambar 3.15 Hasil Perhitungan maksimum 52

Gambar 3.16 Permasalahan minimum 53

Gambar 3.17 Hasil perhitungan permasalahan 53

ABSTRAK

Semakin meningkatnya kompetisi global menuntut setiap perusahaan untuk

meningkatkan kualitas serta efektifitas kinerja karyawannya yang pada akhirnya

diharapkan dapat mendongkrak profit ( keuntungan). Salah satu cara yang sering

digunakan adalah dengan mengadakan rolling. Sistem ini dapat digunakan untuk

mengetahui penempatan terbaik (optimal) bagi karyawan. Pencarian solusi pada

optimal assignment problem ini dapat diperoleh dengan menerapkan konsep teori

graf. Dalam hal ini permasalahan dinyatakan sebagai graf bipartit khususnya graf

bipartit lengkap berbobot yang menerapkan konsep matching, yaitu pencarian

matching sempurna dengan bobot paling optimal. Pencarian matching sempurna pada

graf bipartit lengkap berbobot mempunyai kemungkinan sebanyak n!. Oleh karena itu

mengefisienkan yaitu algoritma optimal tersebut, maka dapat digunakan sebuah

ABSTRACT

Increasing global competition requires each company to improve the quality and

effectiveness of employee performance which in turn is expected to increase profits.

One frequently used way is by performing rolling. This system is used to determine

the best placement(optimal) for employees. On the optimum placement of some x

employees at y type of job, if the number of employees likened equal to the amount of

job by considering the optimization benefits.finding solution to optimal assignment

problem can be obtained by applying the concept of graphs teory. in this case the

problems are stated as a bipartite graph, especially the complete weighted bipartite

graph that implements the concept of matching, Search is perfectly matched with the

optimal weights. Searching perfectly to the weighted bipertite graph has the

possibility of as many as n!. Therefore, the search is inefficient for a large value of n.

then to further streamline the search for optimal solutions can be used an optimization

BAB I

PENDAHULUAN

1.1 Latar Belakang

Kompetisi Global yang kian hari kian meningkat memaksa perusahaan untuk

menggunakan aset intelektual mereka dengan lebih baik. Berbagai metode digunakan

demi meningkatkan produktivitas perusahaan yang pada akhirnya akan meningkatkan

profit (keuntungan). Salah satu hal yang mempengaruhi perkembangan suatu

perusahaan adalah kualitas kinerja karyawannya. Ketersediaan tenaga ahli (

karyawan) saja tidaklah cukup, namun yang harus lebih diperhatikan adalah

bagaimana mengelola tenaga ahli (karyawan) yang ada agar kinerjanya lebih optimal.

Salah satunya dengan menempatkan karyawan pada pekerjaan dimana penempatan

tersebut merupakan penempatan yang optimal.

Istilah rolling pada perusahaan sudah sering didengar. Sistem ini digunakan

untuk beberapa alasan seperti memaksimalkan kemampuan karyawan, mencegah

terjadinya kekosongan formasi untuk pekerjaan-pekerjaan tertentu dikarenakan tidak

adanya karyawan yang mampu menggantikan karyawan sebelumnya, serta

mengetahui penempatan terbaik (optimal) untuk seseorang karyawan.

Penempatan sejumlah X karyawan pada Y buah pekerjaan, jika banyaknya

karyawan diibaratkan sama dengan banyaknya pekerjaan dengan mempertimbangkan

aspek tertentu seperti pengoptimalkan profit ( keuntungan) yang didapat dari

penempatan X karyawan terhadapY buah pekerjaan dikenal dengan optimal

assignment problem. Penerapan graf pada optimal assignment problem ini dapat

Graf bipartit didefinisikan sebagai suatu graf sederhana G yang himpunan

node V-nya dapat dipartisi menjadi dua himpunan tak kosong V1 dan V2 yang

beririsan sedemikian hingga setiap rusuk dalam graf menghubungkan suatu simpul di

V1 dengan simpul di V2 (sedemikian hingga tak ada rusuk di dalam G

menghubungkan dua simpul di V1 maupu n di V2). Karyawan dianggap sebagai V1 dan

pekerjaan sebagai V2. Karena dalam optimal assignment problem aspek yang

dioptimalkan dianggap sebagai bobot dan peluang penempatan tiap X karyawan pada

Y buah pekerjaan dianggap sama, maka untuk mencari solusinya graf bipartit yang

digunakan adalah graf bipartit lengkap berbobot.(Lovasz, 1986:3)

Untuk mencari solusi dari optimal assignment problem yang dinyatakan

sebagai graf bipartit lengkap berbobot adalah dengan menerapkan konsep matching,

khususnya matching sempurna pada graf bipartit lengkap berbobot. Matching

sempurna dengan bobot paling maksimal adalah solusinya.(Brualdi,2004)

Algoritma Kuhn-Munkres adalah algoritma yang dapat digunakan untuk

menyelesaikan optimal assignment problem. Pada tahun 1955, Harold Kuhn (seorang

matematikawan asal Amerika) mempublikasikan sebuah metode yang diberi nama

Hungarian method( untuk menghormati dua orang matematikawan asal Hungaria,

yaitu D.König dan E.Egervăry), yaitu sebuah algoritma kombinatorik untuk optimasi

yang dapat digunakan untuk menemukan solusi optimal dari assignment problem.

Pada tahun 1957, James Raymond Munkres seorang Professor Emeritus of

mathematics dari MIT merevisi algoritma Kuhn. Oleh karena itu, algoritma ini sering

disebut algoritma Kuhn-Munkres.

Untuk mencari solusi dari optimal assignment problem dengan menggunakan

algoritma Kuhn-Munkres salah satunya dapat dilakukan dengan merepresentasikan

algoritma ini pada graf bipartit. Oleh karena itu, penulis mengangkat judul

“Representasi Algoritma Kuhn-Munkres pada Graf Bipartit untuk menyelesaikan

Optimal Assignment Problem”.

Berdasarkan latar belakang, rumusan masalah yang akan dibahas adalah yang

dimaksud dengan optimal assignment problem dan Bagaimana langkah langkah dan

representasi algoritma Kuhn-Munkres pada graf bipartit dapat menyelesaikan optimal

assignment problem.

1.3 Batasan Masalah

Dalam penulisan tugas akhir ini, penulis membatasi masalah mengenai representasi

algoritma Kuhn-Munkres pada graf bipartit khususnya graf bipartit lengkap dengan

jumlah bipartisi pada masing-masing partisinya sama untuk menyelesaikan contoh

dari optimal assignment problem.

1.4 Tujuan Penelitian

Adapun tujuan dalam penulisan ini adalah:

1. Mendeskripsikan optimal assignment problem.

2. Menjelaskan langkah-langkah dan representasi algoritma Kuhn-Munkres pada

graf bipartit.

3. Menjelaskan langkah dan penerapan algoritma Kuhn-Munkres graf bipartit

untuk menyelesaikan optimal assignment problem untuk permasalahan

maksimum dan minimum.

1.5 Kontribusi Penelitian

Sebagai bahan untuk menambah pemahaman dan pengetahuan mengenai algoritma

Kuhn-Munkres pada graf bipartit untuk menyelesaikan optimal assignment problem

1.6 Tinjauan Pustaka

Assignment problem, seperti juga masalah transportasi merupakan suatu

kasus khusus yang ditemukan dalam pemrograman linear (linear programming).

Dalam assignment problem akan mendelegasikan sejumlah tugas (assignment) kepada

sejumlah penerima tugas (assigne) dalam basis satu-satu. Jadi pada assignment

problem ini diasumsikan bahwa jumlah assignment sama dengan jumlah assigne. Jadi

data pokok pertama yang harus dimiliki dalam menyelesaikan suatu assignment

problem adalah jumlah assigne dan jumlah assignment. Selain data jumlah assigne

dan jumlah assignment yang terlibat, data lain yang biasa diperlukan adalah besar

kerugian yang ditimbulkan atau besar keuntungan yang didapatkan

maksima.(Bazaraa, 1977)

Misalkan G=(V,E) adalah graf sederhana dan bukan graf kosong. Maka,

matching M didefinisikan sebagai himpunan bagian tidak kosong dari rusuk E(G)

sedemikan hingga tidak ada dua rusuk dari M yang saling ajasen di G. Untuk mencari

solusi dari Optimal Assignment problem yang dinyatakan sebagai graf bipartit lengkap

berbobot adalah dengan menerapkan konsep matching, khususnya matching sempurna

pada graf bipartit lengkap berbobot.(Brualdi, 2004)

Pada dasarnya pencarian matching sempurna dengan bobot maksimal dapat

dilakukan dengan mendaftar semua matching sempurna yang berbeda, dan

menghitung jumlah bobot dari tiap matching sempurna yang diperoleh. Banyaknya

matching sempurna yang berbeda pada suatu graf bipartit lengkap dengan n pada

masing-masing partisinya adalah n!. Sangat tidak efisien jika cara ini digunakan,

karena semakin banyak jumlah simpul maka semakin banyak pula matching sempurna

yang berbeda. (Brualdi, 2004)

1.7 Metode Penelitian

Secara umum penelitian yang dilakukan dengan beberapa tahapan, yaitu:

1. Menguraikan mengenai konsep graf, optimal assignment problem, dan

2. Menerapkan algoritma Kuhn-Munkres secara lansung untuk menyelesaikan

contoh dari optimal assignment problem

3. Melakukan pengujian kebenaran solusi yang dihasilkan dengan menggunakan

sebuah program sederhana yang merupakan implementasi dari algoritma

BAB 2

LANDASAN TEORI

Pada bab ini akan dijelaskan himpunan dan beberapa definisi yang berkaitan dengan

himpunan, serta konsep dasar dan teori graf yang akan digunakan pada bab

selanjutnya.

2.1 Himpunan

Sebelum mendefinisikan graf akan dijelaskan terlebih dahulu apa yang disebut dengan

himpunan berdasarkan definisi-definisi yang sudah ada mengenai himpunan, karena

graf merupakan bagian dari himpunan.

Definisi 2.1 Objek dalam suatu himpunan disebut elemen atau anggota dari himpunan. Himpunan dinyatakan sebagai kumpulan dari elemen-elemennya.(Rosen, 1999).

Ada beberapa cara untuk mendeskripsikan suatu himpunan. Salah satu caranya

adalah dengan mendaftar anggota dari himpunan tersebut bila hal itu mungkin

dilakukan.

Contoh 2.1

1. Himpunan bilangan bulat positif yang kurang dari 5 dari dapat ditulis dengan

Z = {1,2,3,4}.

2. Himpunan bilangan bulat positif kurang dari 1000 dapat ditulis dengan Z =

{1,2,3,....,999}.

Suatu himpunan mungkin saja memiliki anggota yang sama banyaknya, bahkan

mungkin memiliki anggota yang sama.

Definisi 2.2 Duah buah himpunan disebut sama jika dan hanya jika memiliki elemen

atau anggota yang sama.

Contoh 2.2

Definisi 2.3 Himpunan A disebut subset dari B jika dan hanya jika setiap elemen di A

juga merupakan elemen di B. Kita gunakan notasi A B untuk menyatakan A subset

dari B (Rosen, 1999:41)

Contoh 2.3:

Misalkan himpunan A= {1,2,3,6} dan {1,2,3,4,5,6,7} maka himpunan A dapat

disebut sebagai subset dari himpunan B ditulis A .

Definisi 2.4 Misalkan S adalah suatu himpunan, jika terdapat tepat n buah elemen

yang berbeda pada S dimana n adalah bilangan bulat tak negatif, dikatakan S adalah

himpunan berhingga dan n adalah banyaknya bilangan (cardinality) dari S. Cardinality

himpunan S dinotasikan dengan |S| .(Rosen, 1999)

2.1.1. Beda Simetri

Misalkan terdapat dua buah himpunan A dan B. Maka beda simetri dari himpunan A

dan B didefinisikan sebagai himpunan yang elemennya terdiri dari gabungan

masing-masing elemen himpunan A dan elemen himpunan B tetapi tidak memuat elemen

yang terdapat pada himpunan A sekaligus terdapat pada himpunan B. Beda simetris

himpunan A dan B dapat dinotasikan dengan A (Rosen, 1999)

Karena beda simetri himpunan A dan B terdiri dari gabungan masing-masing

elemen himpunan A dan elemen himpunan B tetapi tidak memuat elemen yang

terdapat pada himpunan A sekaligus terdapat pada himpunan B, maka beda simetri

dapat dinyatakan dengan (A Pernyataan ini ekivalen dengan

(A\B) ).(Rosen, 1999)

Contoh 2.4:

Misalkan himpunan A = {1,2,3,4,5,6,11,12,13} dan B = {2,6,7,8.9,10} maka

A B = {1,3,4,5,7,8,9,10,11,12,13}.

2.2. Pengertian Graf

Tulisan pertama tentang teori graf adalah karya Leonhard Eulerr pada tahun 1736.

Tulisan ini menyajikan sebuah teori umum yang menyertakan sebuah solusi yang

terdapat dua pulau yang terhampar di sungai Pregel yang terletak di kota K igsberg

( kota tua di Prusia Timur yang sekarang dikenal dengan Kaliningrad) yang saling

terhubung oleh tujuh buah jembatan. Permaasalahan yang muncul yaitu apakah ada

sebuah rute yang memungkinkan agar ketujuh jembatan tersebut dapat dilewati tepat

satu kali. Konfigurasi dari jembatan tersebut dapat dimodelkan dengan sebuah graf,

yang pada akhirnya masalah tersebut terjawab bahwa tidak ada sebuah rute yang

memungkinkan agar ketujuh jembatan tersebut dapat dilewati tepat satu kali.(Rinaldi

Munir, 2007)

Ada beberapa definisi mengenai graf diantaranya:

Graf G didefinisikan sebagai pasangan himpunan (V,E), ditulis dengan notasi G=

(V,E), yang dalam hal ini V adalah himpunan tidak-kosong dari simpul-simpul yang

sering disebut vertices atau node, dan E adalah himpunan rusuk yang sering disebut

edges atau arcs yang menghubungkan sepasang simpul .

Graf dapat digambarkan atau diilustrasikan dengan 3 cara, yaitu dengan

himpunan simpul dan sisi, matriks atau diagram. Jika digambarkan dalam bentuk

diagram, simpul diwakili oleh titik atau noktah ( yang kita gambarkan sebagai

lingkaran kecil) dan rusuk e= {u,v} diwakili oleh segmen garis atau kurva yang

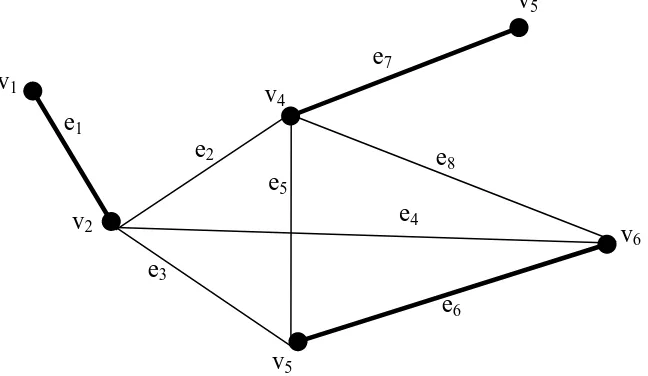
mengaitkan titik u dan titik v. Untuk lebih jelasnya dapat dilihat contoh graf G seperti

gambar 2.1.

e4

v1

e5

v3

e1

e2

e6

v2

e3

v4

e7

e8

v5

Pada Graf G ini, yang merupakan himpunan nodenya

adalahV G( )={ ,v v v v v_{1 2}, ,_{3 4}, }₅ , sedangkan himpunan edgenya

1 2 3 4 5 6 7 8

( ) { , , , , , , , }

E G = e e e e e e e e . Jadi graf G pada Gambar 2.1 terdiri dari 5 node dan

8 edge.

Suatu edge e ditulis e={u,v} dapat juga ditulis dengan uv atau vu disebut

sebagai garis penghubung antara simpul u dan v. Pada Gambar 2.1 e₁ ={ , }v v_{1 2} ,

2 { , }1 2

e = v v ,e₃ ={ , }v v_{2 5} merupakan beberapa contoh edge yang dapat juga disebut

garis penghubung.

Suatu node u dan v disebut sebagai node ujung dari edge e, jika e merupakan

garis penghubung dari node u dan v. Pada gambar 2.1v dan₄ v adalah node yang ₅

merupakan simpul ujung dari edge e . ₇

Pada graf-graf tertentu, terkadang sebuah edge terhubung ke node yang sama,

edge seperti ini dapat disebut sebagai loop. Pada gambar 2.2 graf G mempunyai 1

loop yaitue . ₇

Suatu graf dikatakan mempunyai edge ganda jika pada graf tersebut minimal

dua edge yang menghubungkan dua node yang berlainan. Pada Gambar 2.1, e dan ₁

2

e merupakan edge ganda.

2.2.1 Istilah- istilah dalam graf

Pada suatu graf G node u dan v disebut sebagai node yang saling ajasen jika node u

dan v merupakan node-node ujung atau node u dan v menempel pada edge yang sama.

Pada Gambar 2.1, node v dan ₁ v , ₂ v dan ₁ v , ₃ v dan ₃ v adalah pasangan node yang ₄

saling ajasen.

Edge e dan ₁ e didefinisikan sebagai edge yang saling ajasen jika salah satu ₂

node dari kedua edge tersebut sama. Pada Gambar 2.1 beberapa contoh edge yang

Node u dan edge e, node v dan edge dan rusuk e disebut berisiden, jika u dan v

merupakan node ujung dari edge e. Pada Gambar 2.1, v dan ₃ e , ₈ v dan ₄ e adalah ₈

contoh node dan edge yang berinsiden.

Misalkan terdapat suatu graf G. Maka node pada graf G disebut node terisolasi

jika node tersebut tidak berajasen dengan edge manapun. Perhatikan Gambar 2.2,

dalam hal iniv disebut node terisolasi. ₃

v3

v2

v4

v1

v5

Gambar 2.2 Simpul Terisolasi

Derajat (degree) dari suatu node v yang dinotasikan dengan G(V) adalah

banyaknya edge pada graf G yang berinsiden dengan node v. Khusus pada loop

derajatnya dihitung dua kali. Suatu node v disebut berderajat n jika mempunyai

derajat sebanyak n.

Contoh 2.4:

Perhatikan Gambar 2.1

1. v disebut berderajat 3 karena banyak edge yang berisiden dengan₃ v ada 3, 3

yaitue₅,e₆dan e . ₈

2. v disebut berderajat 4 walaupun banyaknya edge yang berisiden dengan ₅ v ₅

ada 3, yaitue₃, e dan₄ e , tetapi 7 e merupakan loop. Oleh karena itu, banyak 4

Derajat minimum dari graf G dinotasikan dengan δ(G) adalah jika banyaknya

edge yang berisiden dengan node v paling sedikit dari node lain pada graf G.

Sebaliknya, jika node yang berisiden dengan node v tersebut paling banyak, maka

node v dikatakan mempunyai derajat maksimum dan biasa dinotasikan dengan ∆(G).

Misalkan terdapat G, jalan (walk) pada graf G didefinisikan sebagai suatu

barisan yang tak kosong dan berhingga yang suku-sukunya bergantian antara node

dan edge. Jalan boleh saja memuat edge dan node yang sama. Jalan dinyatakan

dengan W. Pada Gambar 2.1,

{v e v e v e v e v_{1 5 3 6 2 6 3 8 4}} merupakan contoh jalan, dan dapat ditulis dengan W

={v e v e v e v e v_{1 5 3 6 2 6 3 8 4}} . Karena jalan pada contoh ini dimulai dari node v dan berakhir ₁

pada node v , maka ₄ v disebut sebagai node awal dan ₁ v disebut sebagai node akhir, ₄

sedangkan node-node selain v dan ₁ v disebut node-node internal dari W. ₄

Selanjutnya, panjang dari suatu jalan dapat didefinisikan sebagai banyaknya edge

yang terdapat didalam suatu jalan.

Jejak (trail) pada suatu graf G didefinisikan sebagai suatu barisan yang tak

kosong dan berhingga yang suku-sukunya bergantian antara node dan edge dan

masing-masing edge tidak boleh termuat lebih dari satu kali. Pada jejak, node boleh

saja termuat lebih dari satu kali. Jejak dinyatakan dengan T. Pada Gambar 2.1

{v e v e v v e v_{2 3 5 4 5 3 7 4}} adalah contoh jejak dan dapat ditulis T={v e v e v v e v_{2 3 5 4 5 3 7 4}}.

Selanjutnya jika pada suatu jejak node awal dan node akhirnya sama maka jejak

tersebut disebut jejak tertutup. Pada Gambar 2.1 T = {v e v e v e v_{1 5 3 6 2 2 1}} adalah contoh

jejak tertutup karena v merupakan node awal sekaligus node akhir. ₁

Jika pada suatu jejak tertutup node awal dan simpul internalnya berbeda, maka

jejak tertutup tersebut dinamakan siklus (cycle). Siklus dinotasikan dengan Cn dengan

n adalah banyaknya node yang termuat dalam suatu siklus. Pada Gambar 2.1

Lintasan (path) dinotasikan dengan P, didefinisikan sebagai suatu barisan yang

tak kosong yang suku-sukunya bergantian antara node dan edge, serta node- nodenya

berlainan

( tidak ada node yang termuat lebih dari satu kali). Pada Gambar 2.1 yang merupakan

contoh lintasan yaitu {v e v e v e v_{1 5 3 8 4 7 5}}, sehingga dapat ditulis P = {v e v e v e v_{1 5 3 8 4 7 5}}.

Suatu graf dikatakan sebagai graf sederhana jika pada graf tersebut tidak

mengandung edge ganda dan loop. Perhatikan Gambar 2.3, graf G bukanlah graf

sederhana, karena mengandung edge ganda e dan ₃ e serta mengandung loop yaitu ₄ e ₈

, sedangkan Graf H merupakan contoh graf sederhana. Graf yang mengandung edge

ganda dan loop biasanya disebut sebagai graf ganda.

e4

v2

v4

v1 e1

e2 e5 e6

e7

v3

v5

e8

e3

v2

v4

v1 e1

e2

v3

v5

e3

e4 e5

e6

Graf 2.3a (Graf G) Graf 2.3b(Graf H)

Gambar 2.3a Graf sederhana dan bukan sederhana Gambar 2.3.b

Suatu graf G dikatakan sebagai graf kosong jika graf tersebut hanya terdiri dari

himpunan simpul. Graf kosong yang terdiri dari n simpul dinotasikan dengan Nn.

N

1

N

2

N

₃

N

₄

Gambar 2.4 Graf Kosong

Suatu graf G dikatakan sebagai graf lengkap jika tiap node pada graf tersebut

berajasen dengan tiap node lainnya. Suatu graf lengkap dengan n yang menyatakan

banyaknya node, dinotasikan dengan Nn. Gambar 2.5 merupakan contoh graf

lengkap dengan 4 simpul.

v

1

e

1

v

3

e

2

v

2

e

4

v

4

e

3

Gambar 2.5 Graf lengkap dengan 4 simpul

Suatu graf G dikatakan sebagai graf berbobot jika setiap edgenya mempunyai

nilai atau bobot tertentu. Bobot pada graf biasanya dinotasikan dengan wij dimana i

dan j sebagai node yang berisiden dengan edge yang memiliki bobot w tersebut. Pada

v

1

4

v

2

v

3

13

9

v

4

Gambar 2.6 Graf Berbobot

2.2.2 Graf Bipartit

Graf Bipartit didefinisikan sebagai graf yang memiliki himpunan node V yang dapat

dipartisi menjadi dua himpunan bagian X dan Y, sehingga masing-masing edgenya

memiliki titik ujung pada X dan titik ujung lainnya pada Y, dengan demikian {X,Y}

dapat disebut sebagai bipartisi pada graf. Jika tiap node pada himpunan X berajasen

dengan semua node pada Y maka graf bipartit tersebut dinamakan graf bipartit

lengkap.

Graf bipartit lengkap dengan banyaknya node pada X atau |X| = m dan

banyaknya node pada Y atau |Y| = n, dinotasikan dengan Km,n.

v

1

v

2

v

3

v

4

v

5

v

6

v

7

Pada Gambar 2.7, dapat dilihat graf tersebut dapat dipartisi menjadi 2

himpunan bagian X dan Y dimana X = { ,v v v v_{1 2}, , }_{3 4} dan Y{ ,v v v . Tiap-tiap node _{5 6}, }₇

pada himpunan X berajasensi dengan semua node pada himpunan Y.

2.2.3 Spanning Subgraph

Subgraph dari G didefinisikan sebagai graf yang merupakan himpunan bagian dari

himpunan node dan edge pada graf G. Sedangkan spanning subgraph dari graf G

adalah subgraph yang memuat semua node dari graf G. Graf H pada Gambar 2.8

merupakan salah satu contoh spanning subgraph dari graf G pada Gambar 2.1.

e5 v1

v3 v4

e8 e6

v2

e3

e7 v5

2.3. Matching graf

Sebelum membahas lebih jauh mengenai optimal assignment problem dan cara

penyelesaiannya, akan dibahas mengenai definisi matching dan matching pada graf

bipartit, karena penyelesaian optimal assignment problem akan menggunakan

penerapan matching pada graf bipartit.

Misalkan G=(V,E) adalah graf sederhana dan bukan graf kosong. Maka,

matching M didefinisikan sebagai himpunan bagian yang tidak kosong dari edge E(G)

sedemikian hingga tidak ada edge dari M yang saling ajasen di G. Selanjutnya

node-node ujung dari matching M disebut matched di bawah M. Untuk lebih jelasnya,

perhatikan Gambar 2.9. M = { ,e e e_{1 6}, }₇ adalah salah satu contoh matching yang dapat

dibuat pada graf G.

v1

e1

v2

e2

e3

v4

e5

v5

e6 e4 e7

e8

[image:30.595.142.466.348.536.2]

v6 v5

Gambar 2.9 Contoh Matching

Jika M adalah suatu Matching, maka suatu node v dikatakan saturated oleh _i

matching M atau matching M saturates terhadap node v jika ada sebuah edge dari _i

matching M menempel pada node v tersebut. Sebaliknya jika tidak ada maka node _i v_i

disebut unsaturated M. Perhatikan Gambar 2.9, v dan ₁ v disebut saturated oleh M, ₂

sebaliknya pada Gambar 2.10. , v disebut unsaturated karena tidak ada matching M ₁

[image:31.595.231.382.83.315.2]

v

1

Gambar 2.10 Contoh simpul unsaturated M

Matching M disebut matching sempurna jika setiap node pada G saturated

oleh matching M. Pada Gambar 2.9 semua node saturated oleh matching M, maka

graf pada Gambar 2.9 merupakan contoh matching sempurna. Sedangkan pada

Gambar 2.10 ada satu node yaitu v yang tidak saturated oleh matching M, maka graf ₁

pada Gambar 2.10 bukan contoh matching sempurna.

Dari sebuah graf G, bisa saja diperoleh lebih dari satu matching M. Suatu

matching M disebut matching maksimum jika untuk setiap matching pada graf G

tidak terdapat matching M dengan |M’|≥|M|. Sehingga setiap matching sempurna

adalah matching maksimum. Namun sebaliknya, jika M adalah matching maksimum

belum tentu M merupakan matching sempurna. Gambar 2.9 merupakan matching

sempurna sekaligus matching maksimum dan Gambar 2.10 merupakan contoh

matching maksimum tetapi bukan matching sempurna.

Misalkan M adalah matching dan P adalah lintasan pada graf G. Lintasan P

disebut M-alternating jika edge-edgenya pada P terbentang dalam M dan berada pada

E(G)\M, dengan kata lain edgenya bergantian antara M dan E(G)\M. Selanjutnya

node akhir dari Lintasan P merupakan M- unsaturated. Untuk lebih jelasnya

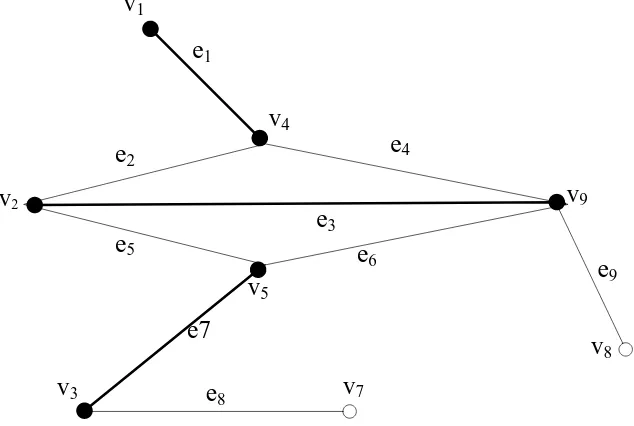
perhatikan Gambar 2.11.

e3 v1

e1

v4 e2

v2

e6 v5

e5

e7

v3 e₈ v7

[image:32.595.143.460.122.335.2]

v8 e9 v9 e4

Gambar 2.11 Contoh M-Augmenting dan M-Alternating

Pada Gambar 2.11, yang merupakan contoh lintasan M-alternating yaitu

4 2 2 3 6 6 5 7 3

{v e v e v e v e v . Sedangkan } {v e v e v e v e v e v_{8 9 6 3 2 5 5 7 3 8 7}} merupakan contoh lintasan

M-augmenting karena node awalnya yaitu v dan node akhirnya yaitu ₈ v merupakan 7

node yang berada pada E(G)\M dan unsaturated M.

Misalkan M adalah matching pada graf G, dan terdapat matching lain, sebut

saja M’ dengan M∆M’ menunjukkan perbedaan simetris M dan M’. Maka dapat

diperoleh suatu graf H=G(M∆M’) yang merupakan graf yang direntang oleh edge

M∆M’ dengan menghapus semua edge M∩M’ dan edge (G\M)∩(G\M’). Untuk lebih

jelasnya perhatikan contoh 2.5.

Contoh 2.5

Diberika graf G yang memuat matching M dan matching M’ seperti pada Gambar

v1

v7

v2 v3 v4 v₅ v₆

v8 v9 v10 v11

Gambar 2.12 Graf G dengan matching M dan matching M’

Edge yang menghubungkan node v5 dan node v8 merupakan anggota-anggota

matching M sekaligus anggota matching M’(M∩M’). Maka, edge tersebut dihapus.

Edge yang menghubungkan node v5 dan node v11 serta edge yang menghubungkan

node v6 dan node v8 bukan anggota matching M sekaligus bukan anggota matching

M’((G\M)∩(G\M’)), oleh karena itu dihapus. Selanjutnya diperoleh H=G(M∆M’),

seperti Gambar 2.13.

v₃

v7 v9

v4

v1 v2 v5 v6

v₈ v10 v11

Gambar 2.13 H =G M M( ∆ ')

Lemma 2.1 Misalkan M dan M’ adalah dua matching yang berbeda pada G, H = G

(M∆M’), dengan M∆M’ menunjukkan beda simetris dari M dan M’. Setiap komponen

dari H pasti berkaitan dengan salah satu dari ketiga bentuk dibawah ini:

2. Siklus (M,M’)-alternating dengan orde genap.

3. Lintasan (M,M’)-alternating.

Bukti:

Misalkan V adalah himpunan node dan E adalah himpunan edge pada graf G

dengan M dan M’ adalah dua matching yang berbeda, maka akan terdapat tiga kasus:

1. Node yang berisiden dengan edge M∩M’ atau edge(G\M)∩(G\M’) tetapi

tidak berinsiden dengan matching M maupun M’, maka pada graf H node

tersebut merupakan node terisolasi.

M’

M

v1 v2 v3 v4 v5 v6

v7 v8 v9 v10 v11

Gambar 3.14 Contoh Graf G dengan matching M dan matching M’

v1 _v

2 v3 v4 v5 v6

v7 _v

8 v9 v10

v11

Gambar 3.15 H =G M M( ∆ ') dari Graf

2. Andaikan P adalah komponen dari H. Dalam hal ini 1 ≤∆P ≤2. Jika semua

dengan satu edge pada M dan satu edge pada M’. Maka dapat disimpulkan

bahwa siklus (M, M’)-alternating dengan orde genap.

3. Ada x V P∈ ( ) sedemikian hingga dengan H(x) = 1. Maka terdapat paling sedikit satu node misalkan saja node y, dengan derajat satu selain node x.

Ketika ∆(P)≤2, P adalah lintasan yang menghubungkan x dan y. Node-node

internalnya (jika ada) merupakan node berderajat dua, maka P adalah lintasan

(M, M’)-alternating.

Contoh 2.6:

1. Perhatikan Gambar 2.14 dan Gambar 2.15. Node { ,v v v_{2 4}, }₇ pada graf G

menjadi node terisolasi pada graf H.

2. Pada Gambar 2.15, {v v v v_{1 7 3 10}} adalah lintasan (M, M’)-alternating.

3. Pada Gambar 2.15, {v v v v v_{5 8 6 1 15}}, adalah siklus (M,M’)-alternating dengan orde genap.

Teorema 2.1(Teorema Berge) Matching M pada graf G adalah matching maksimum

jika dan hanya jika G tidak mengandung lintasan M-augmenting.

Bukti:

1. Akan dibuktikan dengan kontradiksi. Misalkan M adalah matching maksimum

pada graf G dan terdapat lintasan M-augmenting P. Dalam hal ini, P haruslah

memiliki jumlah edge yang ganjil, karena agar suatu lintasan P merupakan

lintasan M-augmenting, setiap satu edge yang merupakan matching M harus

berajasen dengan dua rusuk lainnya yang bukan matching (E(G)\M).

Untuk lebih jelasnya, misalkan lintasan M-augmenting P= { _{0 1 2}

1

... v_k k v v v v

− }.

Perhatikan bahwa k jumlah edge berjumlah ganjil, karena v dan ₀ v unsarated _k

M, artinyav v dan _{0 1} 1vk k

v − harus bukan anggota matching M.

Selanjutnya definisikan himpunan edge M’⊆(G) dengan M’=

1

1 2 3 4 ₂ 0 1 2 3

( { , ... }) { , ... 1 }k v_k

v k k

M v v v v v ₋ v v v v v

−

− ∪ − , maka M’ merupakan

matching pada graf G dengan nilai |M’| = |M|+1. Hal ini kontradiksi dengan M

adalah matching maksimum. Oleh karena itu, jika M adalah matching maksimum

2. Akan dibuktikan dengan kontradiksi. Misalkan M bukan matching maksimum

dan M’ adalah matching maksimum di G. Akibatnya |M’|≥ |M|. Definisikan,

H=G(M∆M’) dengan M∆M’ menunjukkan beda simetri di M dan M’.

Dari pembuktian lemma 2.1, diperoleh setiap node di H berderajat 1 atau 2,

karena setiap node di H berinsiden dengan paling banyak satu edge di M dan satu

edge di M. Dengan demikian, komponen H adalah lintasan yang edgenya

bergantian di M dan M’atau siklus dengan banyak edgenya adalah genap. Karena

M’ dimisalkan sebagai matching maksimum, dari penjelasan sebelumnya

diperoleh |M’|≥|M|. Akibatnya, H mempunyai lebih banyak edge M dibandingkan

edge M. Sehingga lintasan P di H yang edge awal dan edge akhirnya adalah

anggota dari M’. Dengan kata lain node awal serta node akhir dari lintasan P

merupakan M-unsaturated. Maka lintasan P adalah lintasan M-augmenting.

Kita peroleh pernyataan, jika M bukan matching maksimum di G maka

mengandung lintasan M-augmenting. Pernyataan ini ekivalen dengan jika G tidak

mengandung lintasan M-augmenting, maka M adalah matching maksimum di G.

Seperti yang telah dijelaskan sebelumnya, algoritma Kuhn-Munkres dapat

direpresentasikan dengan graf bipartit. Representasi algoritma Kuhn-Munkres

pada graf bipartit melibatkan penerapan matching, maka akan dibahas mengenai

matching pada graf bipartit.

2.3.2 Matching Pada Graf Bipartit

Sebelum membahas lebih jauh mengenai matching pada graf bipartit, akan dijelaskan

dulu mengenai himpunan persekitaran. Misalkan terdapat graf sebarang G=(V,E),

dengan V adalah himpunan node pada G dan S merupakan subset dari V(G), maka

himpunan persekitaran dari S (neighbour set of S) adalah himpunan semua node yang

berajasen dengan node-node di S. Himpunan persekitaran biasanya dinotasikan

dengan NG(S).

Teorema 2.2 (Teorema Hall) Misalkan G adalah graf bipartit dengan bipartisi {X,Y}.

Maka G mengandung sebuah matching yang saturates untuk setiap node di X jika dan

hanya jika |S|≤| NG(S)| untuk setiap S ⊆ X.

1. Misalkan G mengandung matching M yang saturated pada tiap node di X dan

S adalah subset dari X. Karena tiap node pada S matched di bawah M dengan

berbeda di | NG(S|, maka diperoleh |S|≤| NG(S)|.

2. Akan dibuktikan dengan kontradiksi. Misalkan G adalah graf bipartit yang

memenuhi S|≤| NG(S)| untuk setiap S⊆X, tetapi G tidak mempunyai matching

yang saturated pada setiap node dari X. Misalkan M* adalah matching

maksimum pada G, maka akan terdapat node u di X yang merupakan

unsaturated M*.

Selanjutnya definisikan himpunan node di G dengan Z= {v∈V(G): terdapat

lintasan M*alternating dari u ke v}, dengan kata lain Z adalah himpunan

semua node yang terhubung ke u oleh lintasan M*-alternating. Karena M*

adalah matching dan u unsaturated M*, dari teorema 3.1 (teorema Berge)

diperoleh u adalah satu-satunya node yang unsaturated M* pada Z.

Misalkan S= Z∩X dan T = Z∩Y. Maka diperoleh node pada S\{u} matched di

bawah M* dengan node pada T. Sehingga |T| = |S|-1 dari T subset dari NG(S).

Lebih tepat lagi NG(S)=T karena setiap node di NG(S) terhubung ke u oleh

suatu lintasan M*-alternating. Tetapi |T|=|S|-1 dan NG(S) = T, jadi diperoleh |

NG(S)| = (|S|-1<|S| hal ini kontradiksi dengan pernyataan |S|≤| N G(S)|. Maka

haruslah G memiliki matching yang saturates terhadap setiap node di X.

Akibat 1(Teorema Marriage, Forbenius) Graf bipartit G dengan bipartisi

{X,Y}, memiliki matching sempurna jika dan hanya jika |X|=|Y| dan |S|≤| N G(S)|

untuk setiap S⊆X atau Y.

Akibat 2 (König) Jika G adalah graf bipartit k-reguler dengan k>0, maka G

memiliki sebuah matching sempurna.

Bukti:

Misalkan G adalah graf bipartit k- reguler dengan bipartisi {X,Y}. Karena G

adalah k-reguler, maka k|X|=k|Y|. Karena k>0, maka |X| = |Y|.

Misalkan S subset dari X, dengan E1 adalah himpunan edge yang berinsiden

dengan node di S dan E2 adalah himpunan node yang berinsiden dengan node

karena itu diperoleh k| NG(S)|≥|S|, maka berdasarkan Teorema2.2 (Teorema

Hall) diperoleh pernyataan bahwa G memiliki matching M yang saturates

terhadap setiap simpul di X, dan karena |X|= |Y|, maka M adalah matching

Bab 3

REPRESENTASI ALGORITMA KUHN-MUNKRES

3.1 Deskripsi Probem Assignment

Dalam suatu perusahaan sering bermunculan permasalahan yang pada dasarnya dapat

diselesaikan dengan menggunakan konsep graf, salah satunya adalah optimal

assignment problem. Misalkan pada sebuah perusahaan terdapat sebanyak X

karyawan dan Y pekerjaan, dalam hal ini banyak X dan Y diasumsikan sama. Maka

penempatan X karyawan ke Y pekerjaan memperhatikan faktor tertentu seperti profit

(keuntungan) sehingga diperoleh hasil yang optimal biasa dikenal dengan optimal

assignment problem.

Pada penjelasan sebelumnya, banyaknya karyawan dinyatakan dengan X dan

banyaknya pekerjaan dinyatakan dengan Y. Jika banyaknya X karyawan dan Y

karyawan masih dalam ruang lingkup kecil, maka dengan cara perhitungan biasa kita

dapat menemukan solusi optimalnya.

Contoh masalah 3.1

Dalam suatu perusahaan terdapat 3 posisi pekerjaan ( ,y y y yang masih kosong. _{1 2}, ₃)

Perusahaan telah mengadakan penilaian terhadap 3 orang karyawan ( ,x x x . _{1 2}, ₃)

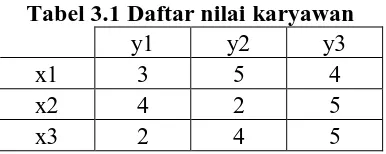
Penilaian setiap karyawan terhadap masing- masing pekerjaan disajikan dalam Tabel

3.1 . Akan ditentukan solusi agar masing- masing karyawan menepati posisi pekerjaan

[image:39.595.202.395.677.754.2]

sehingga menjadi penempatan paling optimal bagi perusahaan.

Tabel 3.1 Daftar nilai karyawan

y1 y2 y3

x1 3 5 4

x2 4 2 5

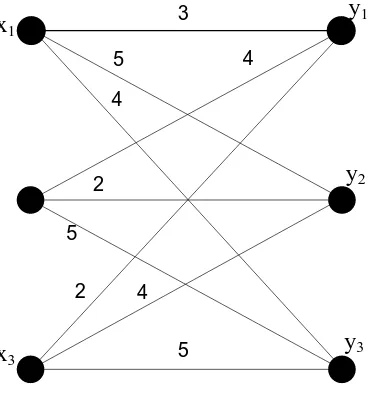
Penyelesaian:

[image:40.595.206.391.119.318.2]

Tabel 3.1 dapat diilustrasikan dengan graf bipartit berbobot seperti gambar berikut: 3 4 5 4 2 5 2 4 5 x1 x3 y1 y2 y3

Gambar 3.1. Graf bipartit berbobot

Untuk mencari solusi optimalnya sama halnya dengan matching sempurna

dengan bobot maksimum pada graf bipartit pada Gambar 3.1. Karena graf G

merupakan graf bipartit yang memiliki partisi {X,Y}dengan|X|=|Y|, berdasarkan

teorema marriage yang telah dijelaskan pada bab sebelumnya, maka pada graf bipartit

ini terdapat matching sempurna. Dalam hal ini karena |X|=|Y|=3 maka dapat

ditentukan kemungkinan matching sempurnanya sebanyak 3!=6 , yaitu:

1. M₁=(x y x y x y_{1 1}, _{2 2}, _{3 3}) dengan

1 1 1 2 2 3 3

M x y x y x y

w =w +w +w

3 2 5

10

= + +

=

2. M₂ =(x y x y x y_{1 1}, _{2 3}, _{3 2}) dengan

2 1 1 2 3 3 2

M x y x y x y

w =w +w +w

3 5 4

12

= + + =

3. M₃ =(x y x y x y_{1 3}, _{2 2}, _{3 1}) dengan

3 1 3 2 2 3 1

M x y x y x y

w =w +w +w

4 2 2

8

= + + =

4. M₄ =(x y x y x y_{1 2}, _{2 1}, _{3 3}) dengan

4 1 2 2 1 3 3

M x y x y x y

w =w +w +w

5 4 5

14

5. M₅ =(x y x y x y_{1 3}, _{2 1}, _{3 2}) dengan

5 1 3 2 1 3 2

M x y x y x y

w =w +w +w

4 4 4

12

= + + =

6. M₆ =(x y x y x y_{1 2}, _{2 3}, _{3 1}) dengan

6 1 2 2 3 3 1

M x y x y x y

w =w +w +w

5 5 2

12

= + + =

Dari keenam kemungkinan diperoleh matching sempurna dengan bobot

maksimum yaitu 14 untuk matching sempurna M₄ =(x y x y x y_{1 2}, _{2 1}, _{3 3}). Maka solusi

optimal dari Contoh 3.1 yaitu:

Karyawan ke-1 ditempatkan pada pekerjaan ke-2

Karyawan ke-2 ditempatkan pada pekerjaan ke-1

Karyawan ke-3 ditempatkan pada pekerjaan ke-3

Contoh masalah 3.1 adalah contoh optimal assignment problem yang

diibaratkan dengan graf bipartit lengkap. Masing-masing simpul pada bipartisi X dan

bipartisi Y sebanyak 3, kemungkinan matching sempurnanya sebanyak n! yaitu 3!=6.

Dalam masalah ini, karena kemungkinan matching sebanyak 6, jadi pencarian

solusi masih bisa dilakukan dengan mendaftar semua matching yang mungkin pada

graf bipartit tersebut dan kemudian menghitung bobot masing-masing. Matching

sempurna dengan bobot paling maksimal adalah solusinya. Namun, lain halnya jika

masing-masing simpul pada bipartisi X dan Y sangat banyak, dengan kata lain nilai n!

sangat besar. Sangat tidak efisien jika dilakukan perhitungan dengan mendaftar semua

kemungkinan matching sempurna seperti Contoh 3.1 . Oleh karena itu, untuk

memudahkan pencarian solusi optimal assignment problem, akan digunakan sebuah

algoritma optimasi yaitu algoritma Kuhn-Munkers. Namun sebelum menguraikan

langkah-langkah dalam algoritma Kuhn-Munkers, akan didefinisikan terlebih dahulu

Feasible vertex labeling dan Equality graph.

Misalkan terdapat suatu graf bipartit lengkap G dengan bobot w yang dinotasikan

dengan (G,w). Feasible vertex labelling pada graf G didefinisikan sebagai fungsi nilai

real l pada X U Y sedemikian sehingga untuk setiap x∈X dany∈Y berlaku: l(x)+ l (y)≥ w(x,y)

Selalu terdapat kemungkinan untuk menemukan feasible vertex labelling.

Salah satu caranya dengan mendefinisikan semua l(y)=0 untuk y Y dan untuk setiap

x X, ambil bobot maksimum pada rusuk yang berajasen dengan x.

( ) max_{y Y} ( , )

l x = _∈ w x y untuk x X

l (y)=0 untuk y Y

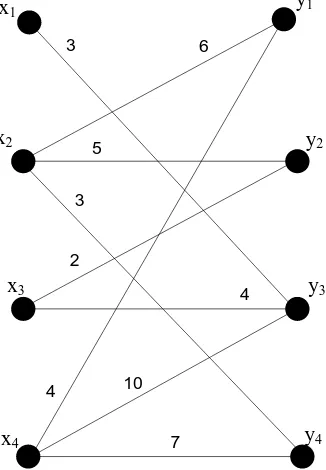
Contoh 3.2:

Akan ditentukan Feasible vertex labelling dari graf bipartit berbobot pada Gambar 3.2

x1

3 6

y1

4 5

x2 y2

x3

3

2

4

10

7

y3

x4 y4

Gambar 3.2 Contoh graf bipartit berbobot

Penyelesaian:

[image:42.595.217.380.357.592.2]

Untuk memudahkan, maka masing-masing bobot kita daftarkan kedalam Tabel 3.2

Tabel 3.2 Daftar bobot

y1 y2 y3 y4

x1 0 0 3 0

x3 0 2 4 0

x4 4 0 10 7

Dari penjelesan sebelumnya, selalu terdapat kemungkinan untuk menemukan

feasible vertex labelling. Salah satu caranya dengan mendefinisikan semua l (y)=0

untuk y Y dan untuk setiap x X, ambil nilai maksimum pada deretan yang sama.

( ) max_{y Y} ( , )

l x = _∈ w x y untuk x X

l (y)=0 untuk y Y

Dari hal ini untuk mendefenisika semua l (y)=0, y Y dapat dilakukan dengan

cara menuliskan 0 di bagian bawah tabel, untuk masing-masing y (perhatikan Tabel

3.3).

Tabel 3.3 l (y)=0

Selanjutnya untuk setiap x X , ambil nilai maksimum pada deretan yang

sama. Hal ini dapat dilakukan dengan cara menentukan nilai x maksimum ditiap

deretan yang sama, kemudian menuliskannya pada kanan tabel(perhatikan Tabel 3.4).

Tabel 3.4 Nilai x maksimum

y1 y2 y3 y4 X max

x1 0 0 3 0 3

x2 6 5 0 3 6

x3 0 2 4 0 4

x4 4 0 10 7 10

Maka diperoleh feasible vertex labelling yang diilustrasikan dengan Tabel 3.5.

y1 y2 y3 y4

x1 0 0 3 0

x2 6 5 0 3

x3 0 2 4 0

x4 4 0 10 7

Tabel 3.5 Feasible vertex labeling dari graf bipartit berbobot

y1 y2 y3 y4

x1 0 0 3 0 3

x2 6 5 0 3 6

x3 0 2 4 0 4

x4 4 0 10 7 10

0 0 0 0

3.1.2 Equality Subgraph

Misalkan terdapat suatu feasible vertex labelling pada graf G. Maka equality

subgraph yang berkorespodensi dengan feasible vertex labelling l didefinisikan

sebagai spanning subgraph dari G dengan himpunan edge El dengan El= {x,y E(G):

l (x)+ l (y)= w(x,y)}, dan dinotasikan dengan Gl.

Contoh 3.3:

Akan ditentukan equality subgraph dari graf bipartit berbobot pada Gambar 3.2.

Penyelesaian:

Langkah pertama yaitu menghimpun edge El. Dari contoh 3.2 telah ditentukan

feasible vertex labelling dari graf bipartit berbobot pada Gambar 3.2. El={x,y E(G):

l (x)+ l (y)=w(x,y)}, maka rusuk El adalah edge-edge yang mempunyai bobot yang

sama dengan bobot feasible vertex labelling yang telah diperoleh, yaitu

1 3 2 1 3 3 4 3

(x y x y x y x y . , , , )

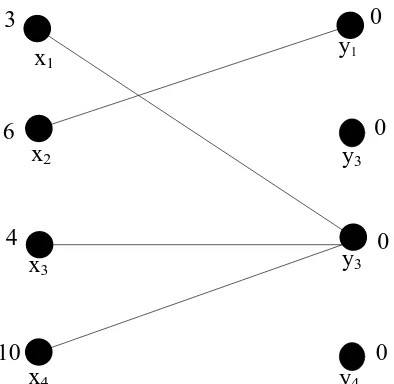
Selanjutnya equality subgraph dapat diilustrasikan dengan Gambar 3.3. Dalam

x1 3

x2 6

4 x3

x4 10

y4 0 y3 0 y1

0

[image:45.595.217.414.78.270.2]

y3 0

Gambar 3.3 Equality subgraph dari graf bipartit berbobot

Teorema 3.1 Misalkan l adalah feasible vertex labelling dari G. Jika equality

subgraph Gl mengandung sebuah matching sempurna M*, maka M* adalah matching

optimal pada G.

Bukti:

Misalkan M* adalah matching sempurna dari suatu equality subgraph Gl,

maka M* juga merupakan matching sempurna dari G karena Gl adalah

spanning subgraph dari G. Masing-masing e M* merupakan anggota dari

Gl dan simpul-simpul akhir dari edge pada M* cover setiap node tepat satu kali

maka diperoleh:

*

( ) ( ) ( )

e M x V

w M w e l x

∈ ∈

=

∑

=

∑

(3...1)

jika M adalah sebarang matching sempurna lain dari G, maka

*

( ) ( ) ( )

e M x V

w M w e l x

∈ ∈

=

∑

≤

∑

(3...2)

dari (1) dan (2) diperoleh w(M*) ≥ w(M). Maka M* adalah matching optimal dari G.

3.2 Algoritma Kuhn-Munkres

Untuk menyelesaikan optimal assignment problem, algoritma Kuhn-Munkres dapat

direpresentasikan dengan graf bipartit. Adapun langkah-langkah dalam Algoritma

Dimulai dengan sebarang feasible vertex labeling l, tentukan Gl, dan pilih

sebarang matching M di Gl.

1. Jika X saturated oleh matching M, maka M adalah matching sempurna

pada G (karena |X| = |Y|). maka M optimal. Stop.

Sebaliknya, jika terdapat beberapa unmatched x X. Definisikan S={X}

dan T = Ø (S⊆X dan T⊆Y, S dan T adalah himpunan simpul yang

unsaturated M pada lintasan M-alternating Gl Lanjutkan ke langkah (2).

2. Jika NGl(S)≠T dengan NGl adalah himpunan persekitaran dari S pada

equality subgraph Gl, maka lanjutkan ke langkah (3). Sebaliknya jika

NGl(S)=T, hitunglah:

,

min { ( ) ( ) ( , )}

c l

x S y T

l x l y w x y

α = _{∈ ∉} + −

dan tentukan feasible vertex labelling l baru dengan:

1 1 ( ) ' ( ) ( ) l v

l l v

l v α α −   =_ +  untuk untuk untuk v S v T v lainnya ∈ ∈

Catatan : α_l> 0 dan NGl (S)≠T. Ganti l dengan l’dan Gl dengan Gl.

3. Pilih node y di NGl (S), yang tidak pada T. Jika y matched di bawah M,

dengan z∈X dan zyadalah matching maka ganti S dengan S ∪ {z} dan

T dengan T ∪ {y}, ulangi ke langkah (2) dalam algoritma Kuhn-Munkres.

Sebaliknya akan terdapat M-augmenting path dari x ke y, dan kita dapat

menggunakannya untuk menemukan matching M’ yang lebih besar pada

Gl. Ganti M dengan M’ dan ulangi langkah(1).

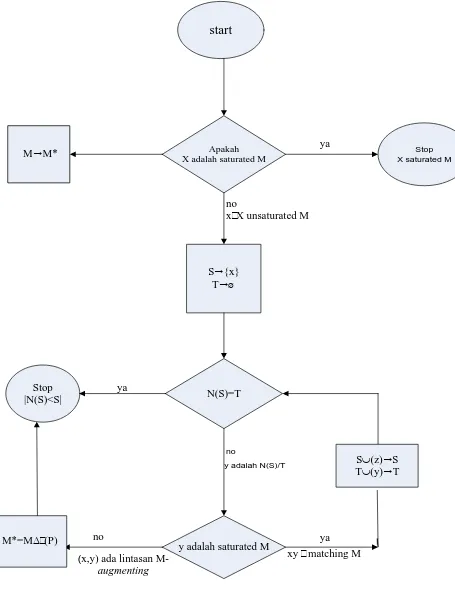
Bentuk flowchart dalam algoritma Kuhn-Munkres dalam menyelesaikan optimal

start

Apakah X adalah saturated M

Stop X saturated M

ya M"M*

S"{x} T"Ø

[image:47.595.105.560.72.664.2]

N(S)=T Stop

|N(S)<S|

S∪(z)"S T∪(y)"T

y adalah saturated M no

x฀X unsaturated M

ya

ya

xy ฀ matching M no

(x,y) ada lintasan

M-augmenting

no

y adalah N(S)/T

M*=MΔ฀(P)

Contoh masalah 3.4:

Akan dicari solusi dari masalah 3.1 dengan menggunakan algoritma

Kuhn-Munkres.

Penyelesaian:

1. Akan ditentukan feasible vertex labeling dan equality subgraph

Seperti yang telah dijelaskan sebelumnya, selalu terdapat kemungkinan untuk

menemukan feasible vertex labeling. Salah satu caranya dengan menghimpun

semua l y( )=0 dan y∈Ydan untuk setiap x∈X , ambil nilai maksimum pada deretan yang sama.

( ) max_{y Y} ( , )

l x = _∈ w x y untuk x∈X

( ) 0

l y = untuk y∈Y

Hal ini dapat diilustrasikan dengan Tabel 3.6, dengan menuliskan bobot

maksimum xyyaitu w xy( )di kiri tabel untuk x∈X dan menuliskan 0 untuk y∈Y pada bagian bawah tabel.

Tabel 3.6 Feasible vertex labeling ke-1

y1 y2 y3

x1 3 5 4 5

x2 4 2 5 5

x3 2 4 5 5

0 0 0

Selanjutnya karena equality subgraph G_l didefinisikan sebagai spanning

subgraph dari G dengan himpunan edge E2 dengan

{ ( ) : ( ) ( ) ( , )}

l

E = xy∈E G l x +l y =w x y , maka equality subgraph dapat

x1 5

y1 0

x2 5

x3 5

y3 0 y2

[image:49.595.222.410.78.224.2]

0

Gambar 3.5 Equality subgraph ke-1

2. Akan dipilih sebarang matching M (ditandai dengan edge yang dicetak

tebal) di Gl , yang diilustrasikan dengan Gambar 3.6.

x1

x2

x3 5

5

5

y1 0

y2 0

y3 0

Gambar 3.6 Sebarang matching M

3. Dari Gambar 3.5 dapat dilihat masih terdapat unmatched x₂∈X ,

sehingga S ={ }x₂ dan T =Ø. Lanjutkan pada langkah(2) dalam algoritma

Kuhn-Munkres.

4. Karena NGl(S)≠T, maka dilanjutkan pada langkah ke-3 dalam algoritma

Kuhn-Munkres. Yaitu, pilih node y di NGl(S), yang bukan pada T. Jika y

matched di bawah M, dengan z∈Xdan zyadalah matching maka ganti S dengan S ∪ {Z} dan T dengan T∪{y}.

5. Dalam hal ini y3 matched di bawah M. Karena x3 X dan

3 3

[image:49.595.220.414.333.477.2]

dengan T∪{ }y₃ atau T ={ }y₃ . Selanjutnya kembali ke langkah (2) dalam

algoritma Kuhn-Munkres.

Karena

l G

N (S)=T maka akan dicari α_l.

,

min { ( ) ( ) ( )}

c l

x S y T

l x l y w xy

α = _{∈ ∈} + −

,

5 0 4,

5 0 2, min

5 0 2,

5 0 4,

c l

x S y T

α _{∈ ∈} + −   + −  = _{ + −}   + −  2 1 2 2 3 1 3 2 ( ) ( ) ( ) ( ) x y x y x y x y =1

Selanjutnya akan dikonstruksi feasible vertex labeling baru dengan:

1 1 ( ) ' ( ) ( ) l v

l l v

l v α α −   =_ +  untuk untuk untuk v S v T v lainnya ∈ ∈

[image:50.595.205.396.561.719.2]

Diperoleh l’ pada Tabel 3.7

Tabel 3.7 Feasible vertex labeling ke-2

y1 y2 y3

x1 3 5 4 5

x2 4 2 5 4

x3 2 4 5 4

0 0 1

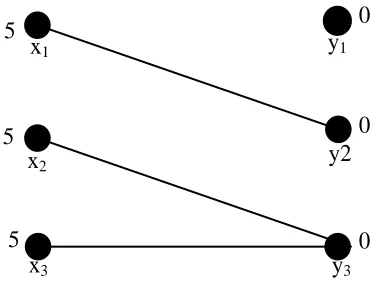
dan diperoleh equality subgraph baru dan sebarang matching M yang ditandai

dengan edge yang dicetak tebal, diilustrasikan dengan Gambar 3.7.

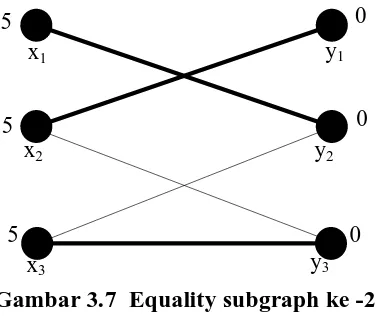
x1 5 x2 5 x3 5 y3 0 y2 0 y1 0

Gambar 3.7 Equality subgraph ke -2

Karena equality subgraph baru Gl telah mengandung matching sempurna

solusi optimal dengan menjumlahkan nilai-nilai feasible vertex labeling baru,

yaitu 5+4+4+0+0+1=14. Perhatikan bahwa nilai ini akan sama dengan total

bobot dari matching sempurnaMyaitu:M = wx1y2+wx2y1+wx3y3=5+5+4=14

3.3 Penentuan Bobot Minimum

Dalam permasalahan tertentu, suatu solusi optimal tercapai jika nilai yang dihasilkan

adalah nilai yang paling minimum. Seperti meminimumkan waktu, kerusakan dan

beberapa kasus lainnya.

Untuk menyelesaikan permasalahan ini, maka dapat dilakukan dengan mencari

jumlah paling minimum dari masing-masing bobot edge yang merupakan matching.

Pencarian jumlah bobot minimum sangat berkaitan erat dengan pencarian bobot

maksimum, dan hubungan antara keduannya dijelaskan oleh Teorema 4.2.

Teorema 3.2 Misalkan (K_{n n, '}, )w dengan adalah graf bipartit lengkap berbobot dengan

bobot matriks W =(w_xy), α adalah entri maksimum di W, Jn adalah matriks kuadrat n

yang semua entrinya satu. Misalkan W* =αJ_n−W adalah matriks berbobot dari

, '

(K_{n n},W*). Maka M adalah matching sempurna dengan bobot minimum dari jika dan

hanya M adalah matching sempurna dengan bobot maksimum dari (Kn n_{, '},W*).

Dengan demikian, w M( )= −na w* (M). Contoh 3.3

Sebuah restoran ternama mengadakan lomba adu kecepatan dalam memasak, lomba

ini diikuti oleh beberapa tim. Tiap tim terdiri 6 koki dan mendapatkan tugas untuk

membuat 6 menu wajib. Tiap koki hanya boleh membuat satu menu. Koki selanjutnya

dapat membuat satu menu berikutnya setelah koki sebelumnya selesai membuat satu

menu sebelumnya. Daftar kecepatan salah satu tim dalam membuat satu menu

sebelumnya. Daftar kecepatan salah satu tim dalam membuat setiap menu disajikan

dalam Tabel 3.8, tentukan urutan koki dan menu yang dibuat, sehingga tim ini dapat

[image:52.595.129.469.93.238.2]

Tabel 3.8 Daftar kecepatan kinerja tim

Koki

Menu

1 2 3 4 5 6

1 20 32 16 30 28 21

2 27 14 20 47 18 15

3 34 23 17 43 21 24

4 21 22 18 26 12 15

5 41 34 15 32 25 17

6 32 20 18 20 17 23

Penyelesaian

Masalah ini dapat diselesaikan dengan mengguanakan algoritma

Kuhn-Munkres. Himpunan koki dianggap sebagai partisi X dan menu sebagai partisi Y.

Dengan teorema 3.2 diperoleh α = 47. Karena *

n

W =αJ −W maka *

47 _n

W = J −W.

1 1 1 1 1 1

20

32 16

30

28

21

1 1 1 1 1 1

27 14

20

47 18

15

1 1 1 1 1 1

34

23 17

43

21 24

*

47

1 1 1 1 1 1

21

22 18

26 12

15

1 1 1 1 1 1

41 34

15

32

25 17

1 1 1 1 1 1

32

20 18

20 17

23

W



 





 





 





 



=− 

 





 





 





 





 



47 47 47 47 47 47 20 32 16 30 28 21

47 47 47 47 47 47 27 14 20 47 18 15

47 47 47 47 47 47 34 23 17 43 21 24

47 47 47 47 47 47 21 22 18 26 12 15

47 47 47 47 47 47 41 34 15 32 25 17

47 47 47 47 47 47 32 20 18 20 17 23

27 15 31 17 19 26

20 33 2

                =−                    =

7 0 29 32

13 24 30 4 26 23

26 25 29 21 35 32

6 13 32 15 22 30

15 27 29 27 30 24

Selanjutnya akan ditentukan nilai W*(M). Hal ini berarti menentukan

matching sempurna M dengan bobot maksimum pada W*. Bobot dari masing-masing

[image:53.595.127.470.154.291.2]

entri pada W* digambarkan pada Tabel 3.9.

Tabel 3.9 Bobot W*

y1 y2 y3 y4 y5 y6

x1 27 15 31 17 19 26

x2 20 33 27 0 29 32

x3 13 24 30 4 26 23

x4 26 25 29 21 35 32

x5 6 13 32 15 22 30

x6 15 27 29 27 30 24

Akan dicari matching sempurna M dengan bobot maksimum pada W* dengan

menggunakan langkah-langkah algoritma Kuhn-Munkres.

1. Menentukan feasible vertex labeling dan equality subgraph. Diperoleh feasible

vertex labeling pada Tabel 3.10, dan equality subgraph pada Gambar3.8.

Tabel 3.10 Feasible vertex labeling ke-1

y1 y2 y3 y4 y5 y6

x1 27 15 31 17 19 26 31

x2 20 33 27 0 29 32 33

x3 13 24 30 4 26 23 30

[image:53.595.103.475.459.560.2]

[image:54.595.199.396.79.320.2]

x1 31 x2 33 x3 30 x4 35 x5 32 x6 30 y1 0 y2 0 y3 y4 0 y5 0 y6 0 0

Gambar 3.8 Equality Subgraph ke-1

2. Menentukan sebarang matching M (ditandai dengan edge yang dicetak tebal)

di Gl yang diilustrasikan dengan Gambar 3.8.

x1 31 x2 33 x3 30 x4 35 x5 32 x6 30 y1 0 y2 0 y3 y4 0 y5 0 y6 0 0

[image:54.595.216.412.422.661.2]

3. Dari Gambar 3.9 matching M belum sempurna, masih terdapat unmatched

6

3, 5,

x x x ∈X, sehingga

6

3, 5

{ , }

S = x x x , ( ) { ,_{3 5}}

l G

N S = y y dan T =φ. Karena

itu dilanjutkan pada langkah(2) dalam algoritma Kuhn-Munkres.

4. Karena ( )

l G

N S ≠T, maka dilanjutkan pada langkah(3) dalam algoritma

Kuhn-Munkres. Yaitu, pilih node y di NGl(S) yang bukan pada T. Jika y matched di

bawah M, dengan z∈X dan zy adalah matching maka ganti S dengan

{ }

S∪ z dan T dengan T∪{ }y . Dalam hal ini y y matched di bawah M. ₃, ₅

Karena x x_{1, 4}∈X

{

x y x y_{1 3}, _{4 5}

}

matching, maka ganti S dengan

{ }

6

3, 5 1, 4

{x x x, }∪ x x atau

{

}

6

1, 3, 4, 5,

S= x x x x x dan ganti T dengan

3 5

{ , }

T∪ y y atau T ={ ,y y_{3 5}}. Selanjutnya kembali ke langkah (2) dalam

algoritma Kuhn-Munkres.

5. Karena ( )

l G

N S =T maka akan dicari αl .

,

min { ( ) ( ) ( )}

c l

x S y T l x l y w xy

,

31 0 27,

31 0 15,

31 0 17,

31 0 26,

30 0 13,

30 0 24,

3 00 4,

30 0 23,

35 0 26,

35 0 25, min

35 0 21,

35 0 32,

32 0 6,

32 0 13,

32 0 15,

32 0 30,

30 0 15,

30 0 27,

30 0 27,

30 0 24,

c l

x S y T

α _{∈ ∈} + −   + −   + −  + −   + −  + −   + −  + −   + −   + − = _{ + −}   + −  + −   + −  + −   + −   + −  + − + − + −    

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

( )

2 1 2 2 2 4 2 6 3 1 3 2 3 4 3 6 4 1 4 2