SOLUSI PERSAMAAN KONVEKSI DIFUSI DENGAN MENGGUNAKAN METODE ANALISIS HOMOTOPI (HAM)
( Skripsi )
Oleh
Eka Zuliana Sari
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
ABSTRAK
SOLUSI PERSAMAAN KONVEKSI DIFUSI DENGAN MENGGUNAKAN METODE ANALISIS HOMOTOPI (HAM)
Oleh Eka Zuliana Sari
Persamaan konveksi difusi adalah salah satu persamaan diferensial parsial taklinear yang sering ditemukan dalam kehidupan sehari-hari. Persamaan ini merupakan jenis persamaan parabolik dengan nilai diskriminan 2− 4 = 0. Berkaitan dengan hal tersebut, maka dikembangkanlah berbagai metode untuk menyelesaikan berbagai masalah dalam bentuk persamaan taklinear. Salah satu metode yang dapat digunakan untuk menyelesaikan persamaan ini adalah metode analisis homotopi (HAM). Metode Analisis Homotopi memiliki beberapa keunggulan dibandingkan dengan metode-metode sebelumnya, diantaranya adalah tidak bergantung pada besar kecilnya parameter dan tetap valid walaupun masalah taklinear tersebut memiliki sembarang parameter.
Pada penelitian ini menunjukkan bahwa solusi dari masalah atau persamaan konveksi difusi yang digunakan dapat diselesaikan dengan menggunakan Metode Analisis Homotopi dengan solusi yang diperoleh sama dengan solusi eksaknya.
RIWAYAT HIDUP
Penulis dilahirkan di Raman Utara pada tanggal 31 Mei 1993, sebagai anak pertama dari dua bersaudara dari pasangan Bapak Jumaadi dan Ibu Sutarmi, serta merupakan kakak dari Ardi Kurniawan.
Penulis menyelesaikan pendidikan Taman Kanak-kanak di TK LKMD Ratna Daya, Raman Utara, Lampung Timur pada tahun 1999. Pendidikan sekolah dasar di SD N 2 Ratna Daya, Raman Utara, Lampung Timur pada tahun 2005. Sekolah menengah pertama di MTs N Raman Utara, Lampung Timur pada tahun 2008. Dan selanjutnya menyelesaikan pendidikan sekolah menengah atas di MAN 1 Metro pada tahun 2011.
penulis diamanahkan sebagai Sekretaris Bidang Keilmuan Himpunan Mahasiswa Matematika (HIMATIKA) FMIPA Universitas Lampung.
MOTO
Man Jadda Wa Jadda
Siapa bersungguh-
su gguh aka aka berhasil
(Pepatah Arab)
Man Shabara Zhafira
Siapa yang bersabar maka akan beruntung
(Pepatah Arab)
“Tidak Ada Kata Terlambat Untuk Memulai
Suatu Hal Yang Baik”
PERSEMBAHAN
Puji dan syukur kehadirat Allah SWT , karena atas segala nikmat, karunia
dan juga ridho-Nya lah skripsi ini dapat terselesaikan, dan dengan setulus hati,
ku persembahkan karya sederhanaku ini teruntuk:
Kedua orangtuaku tersayang Ibunda Sutarmi dan Ayahanda Jumadi
terimakasih untuk s
etiap do’a , dukungan, semangat,
kasih sayang dan juga
perhatian luar biasa yang tiada henti-hentinya. Adikku Ardi Kurniawan yang
selalu memberikan dorongan dan semangat untuk segera menyelesaikan tugas
akhir ini.
Keluarga besar baik dari pihak ayah maupun ibu yang selalu memberikan
semangat, dukungan
serta do’a
yang tiada hentinya pula untuk kesuksesanku.
Sahabat-sahabat terbaik dan luar biasa yang selalu ada untukku saat susah
ataupun senang. Terimakasih banyak atas dukungan, nasihat, semangat dan
SANWACANA
Puji dan syukur penulis panjatkan kehadirat Allah SWT, yang telah memberikan kesehatan serta segala karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini dengan judul “Solusi Persamaan Konveksi Difusi Dengan Menggunakan Metode Analisis Homotopi (HAM)” tepat pada waktunya. Tak lupa shalawat serta salam selalu penulis panjatkan pula kepada Nabi Muhammad SAW yang telah menjadi suri tauladan yang baik bagi kita semua.
Dalam proses menyelesaikan penulisan skripsi ini, tentunya tak lepas dari motivasi, pengarahan serta dukungan dari berbagai pihak. Oleh karena itu, dengan segala kerendahan hati penulis ingin mengucapkan banyak terima kasih kepada :
1. Bapak Prof. Suharso, Ph.D. selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung.
2. Bapak Drs. Tiryono Ruby, M.Sc., Ph.D. selaku Ketua Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung serta selaku Dosen Penguji, terimakasih atas kesediaan dan waktunya untuk menguji, memberikan kritik, saran dan berbagai pengetahuan yang sangat bermanfaat dalam proses penyelesaian skripsi ini.
Lampung dan sekaligus sebagai Dosen Pembimbing Akademik yang telah membimbing dan memberikan arahan selama masa perkuliahan.
4. Bapak Suharsono. S, M.Si., M.Sc., Ph.D. selaku Dosen Pembimbing I, terimakasih atas kesediaan serta kesabaran Bapak dalam membimbing dan memberikan arahan kepada penulis dalam proses menyelesaikan penulisan skripsi ini.
5. Ibu Dra. Dorrah Aziz, M.Si. selaku Dosen Pembimbing II, terimakasih atas waktu dan kesediaan Ibu dalam membimbing, memberikan arahan, semangat serta dukungan sehingga penulisan skripsi ini dapat terselesaikan dengan baik. 6. Seluruh dosen Jurusan Matematika FMIPA Universitas Lampung yang telah memberikan begitu banyak ilmu pengetahuan, serta staff dan juga karyawan di lingkungan FMIPA Universitas Lampung yang telah banyak membantu untuk segala urusan administrasi.
7. Kedua orang tuaku tersayang, adikku Ardi Kurniawan, dan juga seluruh keluarga yang tak henti-hentinya selalu mendo’akan, memberikan dukungan, semangat dan kasih sayang kepada penulis.
8. Sahabat-sahabat yang selalu mendukung, Annastasia Nika S, Andzirnie Bil Haqqi, Rizka Pitri, Faradhika Nitasya, Dian Surida, Nafisah dan Ahmad Antoni terimakasih banyak atas segala nasihat, semangat, bantuan, serta suka dukanya selama ini.
10. Teman-teman Matematika 2011, terimakasih telah menjadi teman terbaik selama masa perkuliahan, semoga tali silaturahmi tak pernah terputus dan sukses untuk kita semua.
11. Keluarga besar HIMATIKA FMIPA Universitas Lampung, khususnya para Pimpinan dan Presidium serta rekan-rekan Bidang Keilmuan periode 2013-2014 atas pembelajaran serta pengalaman yang sangat luar biasa yang penulis dapatkan ketika bersama kalian.
12. Almamaterku tercinta Universitas Lampung dan seluruh pihak yang telah membantu dalam penyususnan skripsi ini yang tidak dapat disebutkan satu persatu.
Bandar Lampung, Februari 2015 Penulis,
DAFTAR ISI 2.1 Persamaan Diferensial Parsial ... 4
2.2 Persamaan Difusi ... 6
2.3 Persamaan Konveksi Difusi ... 8
2.4 Metode Analisis Homotopi (HAM) ... 9
2.5 Parameter Kontrol Kekonvergenan ... 13
2.6 Konsep Deret Taylor dan Deret Maclaurin ... 13
III. METODOLOGI PENELITIAN 3.1 Waktu dan Tempat Penelitian ... 15
3.2 Metodologi Penelitian ... 15
IV. HASIL DAN PEMBAHASAN V. KESIMPULAN DAN SARAN 5.1Kesimpulan ... 21
5.2Saran ... 22
I. PENDAHULUAN
1.1 Latar Belakang dan Masalah
Banyak fenomena yang terjadi di alam dapat dijelaskan dalam suatu model matematika. Model matematika tersebut umumnya dinyatakan dalam bentuk persamaan taklinear. Masalah taklinear ini biasanya sulit diselesaikan baik secara analitik maupun secara numerik jika dihadapkan pada perhitungan komputasi yang rumit. Model matematika sering muncul dalam permasalahan diberbagai cabang ilmu pengetahuan. Misalnya permasalahan dalam bidang biologi, fisika, ekonomi, teknik, dan lainnya. Salah satu contoh dalam bidang fisika adalah masalah konveksi dan difusi.
2
Namun karena metode perturbasi dan non-perturbasi tersebut tidak dapat menentukan cara sederhana untuk mengontrol kekonvergenan dari pendekatan daerah penyelesaiannya. Tahun 1992, Liao menggunakan ide-ide dasar homotopi dari topologi untuk mengusulkan suatu metode untuk menyelesaikan masalah taklinear secara umum yang dinamakan metode homotopi. Terdapat beberapa keunggulan dari metode ini yaitu tetap valid walaupun masalah taklinear tersebut memiliki sembarang parameter.
Dalam penelitian ini akan digunakan metode analisis homotopi (Liao, 2004) yang merupakan suatu metode pendekatan analitik untuk menyelesaikan suatu masalah taklinear. Dalam metode ini, akan didefinisikan suatu operator taklinear yang didasarkan pada bentuk taklinear dari masalah taklinear tersebut.
1.2 Tujuan Penelitian
Adapun tujuan dari dilakukannya penelitian ini adalah :
1. Memahami secara lebih dalam tentang konsep metode analisis homotopi (HAM).
2. Menerapkan metode analisis homotopi untuk memperoleh solusi dari persamaan konveksi difusi.
1.3 Manfaat Penelitian
3
II. TINJAUAN PUSTAKA
2.1 Persamaan Diferensial Parsial
Persamaan yang mengandung satu atau lebih turunan parsial suatu fungsi (yang diketahui) dengan dua atau lebih peubah bebas dinamakan persamaan diferensial parsial.
Persamaan diferensial parsial memegang peranan penting di dalam penggambaran keadaan fisis, di mana besaran-besaran yang terlibat di dalamnya berubah terhadap ruang dan waktu. Di dalam pembahasan tentang persamaan diferensial biasa, variabel bebas yang terlibat dalam masalah hanya satu, sedangkan untuk persamaan diferensial parsial variabel bebas berjumlah lebih dari satu.
5
homogen. Dan bila tidak, maka persamaan itu dikatakan tak homogen.
Bentuk umum dari persamaan diferensial parsial ini adalah:
∑ � �
2�
���2
�= + ∑�= � �����+ + = (2.1)
Orde dari persamaan diferensial parsial ini adalah turunan tertinggi yang muncul pada persamaan diferensial parsial tersebut.
Persamaan diferensial orde 1
��
��
−
��
�
=
(2.2) Persamaan diferensial orde 2
�2 �
��2
+
��
�
=
(2.3) Persamaan diferensial orde 3
�
Selanjutnya, persamaan diferensial parsial juga dibagi menjadi tiga jenis, yaitu persamaan diferensial eliptik, parabolik, dan hiperbolik. Misal, diberikan suatu persamaan diferensial parsial orde dua dalam variable ruang x dan waktu t,
�2
kelas persamaan diferensial parsial tersebut adalah pada nilai diskriminan
6
a. Persamaan diferensial parsial dikatakan persamaan hiperbolik jika nilai
diskriminan − > (2.6)
Salah satu contoh persamaan hiperbolik adalah pada persamaan gelombang
�2
� 2 −
�2
��2 = (2.7)
b. Persamaan diferensial parsial dikatakan persamaan parabolik jika nilai
diskriminan − = (2.8)
Salah satu contoh persamaan parabolik adalah pada persamaan difusi dalam
bentuk �
� − �
�2
��2 = (2.9)
c. Persamaan diferensial parsial dikatakan persamaan eliptik jika nilai
diskriminan − < (2.10)
Salah satu contoh persamaan eliptik adalah pada persamaan Laplace dalam
bentuk �2
7
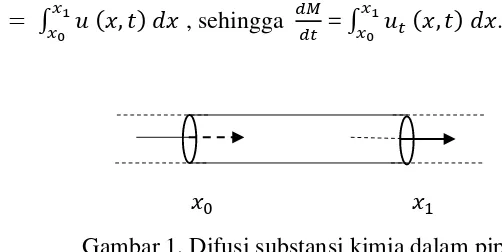
Gambar 1. Difusi substansi kimia dalam pipa
Massa pada bagian ini tidak dapat berubah kecuali oleh adanya perubahan pada aliran masuk (flowing in ) atau aliran keluar ( flowing out). Dengan menggunakan Fick’s Law,
�
� = aliran masuk – aliran keluar = −� � � , − [−� � � , ]. (2.13)
dengan k adalah konstan. Dengan demikian persamaan (2.12) dan persamaan (2.13) sama dengan :
∫�� �, �= � � � , − � � � , . (2.14)
ruas kanan pada persamaan (2.14) sama dengan � ∫�� �� �, � sehingga persamaan (2.14) dapat ditulis menjadi
= � �� (2.15)
8
Konduksi panas diilustrasikan dalam persamaan difusi dengan �, didefinisikan sebagai temperatur pada posisi-x dan waktu-t(Riancelona, 2007).
2.3 Persamaan Konveksi Difusi
Misalkan pada reservoir dengan panjang x dan ketebalan y kemudian dilakukan injeksi uap dengan temperatur tertentu dan kecepatan V. Pada saat injeksi uap dilakukan, terjadi konveksi di dalam reservoir sehingga panas yang dihasilkan oleh uap tersebut akan berpindah ke minyak. Panas tersebut akan mengurangi viskositas dari minyak tersebut agar mudah terangkat. Bersamaan dengan itu, uap tersebut akan kehilangan panas yang disebut dengan konduksi. Dengan demikian, temperatur dari uap yang diinjeksikan tersebut akan semakin menurun hingga pada nantinya akan sama dengan temperatur reservoir.
Pada reservoir ini, konduksi panas yang bisa diilustrasikan dalam persamaan difusi yang dijelaskan sebelumnya sedangkan konveksi yang merupakan perpindahan dari minyak, air dan uap dari reservoir ke arah sumur produksi diilustrasikan dengan persamaan ��
�� sehingga persamaan konveksi dan
konduksi panas yang terjadi saat injeksi uap tersebut dapat diilustrasikan dalam persamaan
dengan �, mendefinisikan temperatur pada posisi-x dan waktu-t.
9
atau transport equation. Persamaan konveksi difusi ini juga merupakan salah satu contoh persamaan difensial parsial yang memiliki banyak aplikasi. Persamaan diferensial parsial adalah suatu bentuk persamaan matematika yang mengandung satu atau lebih operator diferensial parsial pada variable bebas dari suatu fungsi peubah banyak (Riancelona, 2007).
2.4 Metode Analisis Homotopi (HAM)
Metode analisis homotopi (HAM) pertama kali dirancang pada tahun 1992 merupakan teknik semianalitis untuk memecahkan masalah taklinear biasa atau persamaan diferensial parsial.
Metode analisis homotopi (HAM) didasarkan pada konsep topologi dan diferensial geometri untuk menghasilkan kekonvergenan deret dari sistem taklinear. Homotopi menjelaskan semacam variasi deformasi dalam matematika. Sebagai contoh, sebuah lingkaran dapat dideformasikan secara kontinu menjadi elips dan bentuk dari cangkir kopi dapat dideformasikan secara kontinu menjadi bentuk donat. Pada intinya, homotopi didefinisikan sebagai penghubung antara benda yang berbeda dalam matematika yang memiliki karakteristik yang sama di berbagai aspek.
Akan ditunjukkan konsep dasar dari HAM, dengan menggunakan persamaan diferensial :
10
di mana N merupakan operator taklinear, x dan t dinotasikan sebagai variable bebas dan u adalah suatu fungsi yang tidak diketahui.
[ , ] dinotasikan sebagai himpunan fungsi real kontinu dalam interval
� . Secara umum, jika suatu fungsi ∈ [ , ] dapat dideformasikan secara kontinu ke fungsi kontinu ∈ [ , ] lain, maka dapat terbentuk suatu homotopi dari produk ruang X dengan interval [0,1] ke Y sedemikian sehingga jika
� ∈ maka � �; = � � �; = � .
Definisi 2 :
Parameter pelengkap� ∈ [ , ]di dalam suatu fungsi atau persamaan homotopi disebut parameter homotopi.
Definisi 3 :
11
dari � ke solusi yang tidak diketahui u dari � . Jenis dari persamaan homotopi ini disebut persamaan deformasi orde nol.
Definisi 4 :
Diberikan sebuah persamaan taklinear dinotasikan oleh �, yang paling tidak memiliki satu solusi �, , di mana x dan t merupakan variable bebas.
� ∈ [ , ] menunjukkan parameter homotopi dan � � menunjukkan
persamaan deformasi orde nol, yang menghubungkan persamaan asli �, dan persamaan awal � dengan kondisi awal yang diketahui �, .
Asumsikan bahwa persamaan orde nol � � memiliki solusi analitik di q = 1, sehingga diperoleh homotopi deret Maclaurin :
� �, ; � ~ �, + ∑+∞�= � �, �� , � ∈ [ , ] (2.18)
dan deret homotopi
� �, ; ~ �, + ∑+∞�= � �, (2.19)
Persamaan yang berhubungan dengan � �, yang nilainya tidak diketahui disebut persamaan deformasi orde ke-m.
Definisi 5 :
Jika solusi � �, ; � dari persamaan deformasi orde nol � � : � ~ � ada dan analitik di � ∈ [ , ], maka diperoleh solusi deret homotopi dari persamaan asli
� :
�, = �, + ∑+∞�= � �, (2.20)
12
�, ≈ �, + ∑�= � �, (2.21)
(Liao, 2012)
Berdasarkan definisi dari HAM, dapat dibentuk suatu persamaan yang disebut dengan persamaan deformasi orde-nol
� �, = − � �[� �, ; � − �, ] − �ℎ�[� �, ; � ] (2.22)
di mana � ∈ [ , ] merupakan parameter pelengkap, ℎ ≠ merupakan parameter kontrol kekonvergenan, L adalah operator linear pelengkap,
� �, ; � adalah fungsi yang tidak diketahui, �, adalah kondisi awal dari dengan memperhatikan �, maka terdapat
13
kekonvergenan dari deret pada persamaan (2.24) tergantung pada parameter pelengkap ℎ. Jika ini konvergen saat � = , maka terdapat :
�, = �, + ∑∞�= � �, (2.26)
yang mana satu dari solusi-solusinya adalah pada persamaan taklinear awal (Gupta, 2012).
2.5 Parameter Kontrol Kekonvergenan
Karena pada deret Maclaurin tidak ada jaminan bahwa deret konvergen pada
� = melainkan hanya asumsi, sehingga Liao memodifikasi konsep
Homotopi dengan memperkenalkan ℎ sebagai parameter kontrol kekonvergenan.
ℎ membangun persamaan deformasi orde-nol sebagai berikut:
� �, � = − � [� − � ] − �ℎ[� ] ; ℎ ≠ (2.27)
(Liao, 2012)
2.6 Konsep Deret Taylor dan Deret Maclaurin
Deret Taylor adalah bentuk khusus dari suatu fungsi yang dapat digunakan sebagai pendekatan dari integral suatu fungsi yang tidak memiliki anti turunan elementer dan dapat digunakan untuk menyelesaikan persamaan diferensial.
Misalkan f(x) adalah suatu fungsi sebarang yang dapat dinyatakan sebagai suatu deret pangkat sebagai berikut :
14
dengan , = , , , . . . menyatakan koefisien deret pangkat dan a
menyatakan titik pusatnya.
Fungsi f(x) pada persamaan ( 2.28 ) dapat dinyatakan dalam bentuk :
� = ∑ !
∞
=
� −
= +�′ !� � − +�′′!� � − + . . . (2.29)
III. METODOLOGI PENELITIAN
3.1 Waktu dan Tempat Penelitian
Penelitian ini dilaksanakan pada semester ganjil tahun ajaran 2014/2015 bertempat di gedung Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Lampung.
3.2 Metode Penelitian
Adapaun metodologi yang digunakan dalam penelitian ini adalah sebagai berikut :
1. merumuskan masalah dalam bentuk persamaan konveksi difusi.
2. menerapkan metode analisis homotopi (HAM) untuk menentukan solusi dari persamaan konveksi difusi.
Adapun langkah-langkah yang dilakukan untuk menyelesaiakan persamaan konveksi difusi dengan metode analisis homotopi ini adalah sebagai berikut : Diberikan suatu persamaan konveksi difusi :
�
� =
�2
��2− 4 , �, ∈ � atau = ��−4 (3.1)
16
Selanjutnya :
a. Mentransformasi persamaan (3.1) menjadi :
− ��+4 = (3.3)
b. Menganalisis sifat asimtotik. Hal ini dilakukan jika masalah taklinear memiliki batas tak hingga.
c. Menentukan aproksimasi awal dan operator linear L berdasarkan persamaan (3.3).
d. Mengkontruksikan dan memasukkan fungsi ke dalam bentuk persamaan homotopi berikut:
− � �[� �, , � − �, ] − �ℎ�[� �, ; � ] = (3.4)
dengan ℎ ≠ merupakan parameter kontrol kekonvergenan dan dengan
� ∈ [ , ] merupakan parameter benaman.
e. Mengkontruksikan persamaan deformasi orde m, dengan mendiferensialkan persamaan yang diperoleh pada tahap d sebanyak m kali terhadap q, lalu sederhanakan untuk � = sehingga diperoleh
� �, , � = �� �, ,�
��� |
�= , untuk
f. Menentukan solusi persamaan deformasi pada persamaan yang diperoleh dari langkah ke (d) untuk setiap = , , , … dengan � �, =
�!
��� �, ;�
��� |�=
V. KESIMPULAN DAN SARAN
5.1 Kesimpulan
Berdasarkan pada hal-hal yang telah diuraikan pada bab-bab sebelumnya, maka dapat diperoleh kesimpulan sebagai berikut :
1. Metode Analisis Homotopi merupakan salah satu metode analitik yang dapat digunakan untuk menyelesaikan suatu masalah taklinear, yang memiliki beberapa keunggulan yang salah satunya adalah tidak bergantung pada besar kecilnya parameter atau tetap valid walaupun masalah taklinear tersebut memiliki sebarang parameter .
2. Persamaan konveksi difusi yang sering ditemukan dalam kehidupan sehari-hari misalnya dalam proses perpindahan kalor merupakan salah satu masalah taklinear yang dapat diselesaikan dengan menggunakan Metode Analisis Homotopi.
22
5.2 Saran
DAFTAR PUSTAKA
Arti, E.J. 2010. Penggunaan Metode Homotopi untuk Menyelesaikan Model Populasi Volterra. Skripsi. Departemen Matematika FMIPA Institut Pertanian Bogor, Bogor.
Farlow, S.J. 1982. Partial Differential Equations for Scientist and Engineers. Mc Graw-Hill Inc. Canada.
Ghasemi, M. dan Kajani, M.T. 2010. Applications of He's homotopy perturbation method to solve a diffusion convection problem. Mathematical Sciences. 4 (2), 171-186.
Gupta, S. dan Gupta, V. G. 2012. Homotopy Analysis Methode and Diffusion-Convection Equation. International Journal of Mathematical Archive. Vol 3 (2), 767-771.
Kreyzig E. 1998. Advanced Engineering Mathematics 8th Edition.John Wiley. New York
Liao, S. 2012. Homotopy Analysis Method in Nonlinear Differential Equation. Heigher Education Press, Beijing.
Purwanti, T. 2012. Penggunaan Metode Homotopi untuk Menyelesaikan Masalah Getaran Taklinear. Skripsi. Departemen Matematika FMIPA Institut Pertanian Bogor, Bogor.
Riancelona. 2007. Convection Diffusion Equation and Advection Diffusion Equation.