ALGORITMA EKSAK UNTUK MENYELESAIKAN
PERSOALAN BIN COVERING
TESIS
Oleh
ERI SAPUTRA 097021080/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
ALGORITMA EKSAK UNTUK MENYELESAIKAN
PERSOALAN BIN COVERING
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
ERI SAPUTRA
097021080/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
Judul Tesis : ALGORITMA EKSAK UNTUK MENYELESAIKAN PERSOALAN BIN COVERING
Nama Mahasiswa : Eri Saputra Nomor Pokok : 097021080 Program Studi : Matematika
Menyetujui,
Komisi Pembimbing
(Prof. Dr. Opim Salim S, M.Sc) (Prof. Dr. Herman Mawengkang)
Ketua Anggota
Ketua Program Studi Dekan
Telah diuji pada
Tanggal 19 Januari 2012
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Opim Salim S, M.Sc
Anggota : 1. Prof. Dr. Herman Mawengkang 2. Prof. Dr. Tulus, M.Si
ABSTRAK
Tesis ini menjelaskan tentang algoritma eksak untuk menyelesaikan permasalahan bin covering. Penyelesaiannya dengan menggunakan prosedur branch and bound dan teknik generasi kolom. Dalam permasalahan integer programming, generasi kolom digunakan untuk menyelesaikan linear programming relaksasi. Branch and bound dapat digunakan untuk banyak kelas pada masalah skala besar seperti sebuah prosedur yang dapat menjadi penghalang berat dalam hal total waktu komputasi. Setelah diambil pendekatan untuk menguji pengurangan masalah dimana sebagian besar variabel integer tetap konstan dan hanya sebagian kecil diperbolehkan untuk bervariasi dalam langkah-langkah diskrit. Hal ini dapat di implementasikan dalam struktur dari sebuah program dengan memperhatikan se-mua variabel integer pada batas solusi yang selanjutnya sebagai non basic dan penyelesaian masalah berkurang dengan mempertahankan non basic.
ABSTRACT
This tesis present an exact algorithm for solving the problems of bin covering. Us-ing the branch and bound procedures and the technique of column generation. In the problem of integer programming, column generation is used to solve the relax-ation of linear programming. While a straightforward branch and bound approach could be adopted, for many classes of large scale problems such a procedure would be prohibitively expensive in terms of total computing time. After have adopted the approach of examining a reduced problem in which most of the integer variables are held constant and only a small subset allowed to vary in discrete steps. This may be implemented within the structure of a program by examining all integer variables at their bounds at the continuous solution as nonbasic and solving the reduced problem with these maintained nonbasic
KATA PENGANTAR
Syukur Alhamdulillah kehadirat ALLAH SWT, penulis panjatkan atas limpa-han Rahmat dan KaruniaNya yang telah diberikan sehingga penulis dapat menye-lesaikan tesis dengan judul : ”Algoritma Eksak Untuk Menyemenye-lesaikan Permasala-han Bin Covering”. Selawat dan salam kepada junjungan Nabi Muhammad SAW beserta keluarga dan sahabat sekalian.
Tesis ini merupakan salah satu persyaratan penyelesaian studi pada Program Studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
Pada kesempatan ini penulis menyampaikan terima kasih dan penghargaan yang sebesar-besarnya kepada:
Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara
Dr. Sutarman, M.Sc selaku Dekan Fakultas Matematika dan Ilmu Penge-tahuan Alam yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Studi Magister Matematika di FMIPA Universitas Sumatera Utara
Prof. Dr. Herman Mawengkangselaku ketua Program Studi Magister Mate-matika FMIPA Universitas Sumatera Utara dan juga sebagai pembimbing pada penulisan tesis ini yang berkat dorongan dan bantuan beliau sehingga penulisan tesis ini dapat diselesaikan.
Prof. Dr. Opim Salim S, M.Sc juga sebagai pembimbing dalam penulisan tesis ini atas saran dan bantuan sehingga penulisan ini dapat diselesaikan.
Prof. Dr. Tulus, M.Si selaku pembanding atas saran dan bantuannya untuk kesempurnaan penulisan tesis ini serta bimbingan selama perkuliahan berlang-sung.
Seluruh Staf Pengajarpada Program Studi Magister Matematika FMIPA Uni-versitas Sumatera Utara yang telah banyak memberikan ilmu pengetahuan selama masa perkuliahan.
Ibu Misiani, S.Siselaku Staf Administrasi Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.
Seluruh sahabat serta rekan - rekan seperjuangan mahasiswa angkatan 2009 genap atas kebersamaan dan bantuan dalam mengatasi masalah selama perku-liahan berlangsung.
Ucapan terima kasih yang tak terhingga dan penghargaan setinggi tingginya penulis ucapkan kepada ayahanda H. Abubakar Yunus, SP dan Ibunda Hj. Nurmiati, S.Pd yang telah mencurahkan kasih sayang dan dukungan kepada penulis. Terima kasih juga kepada adik - adik penulis (Emira Laura Putri, Evira Agustina Putri, Esar Alkautsar)dan buat seluruh keluarga yang telah membantu, memberikan semangat dan dorongan kepada penulis hingga penulisan tesis ini selesai.
Terima kasih juga kepada sahabat dan rekan - rekan lainnya yang tidak dapat disebutkan satu persatu, yang telah membantu dan memberikan semangat untuk penulis hingga tesis ini selesai.
Akhir kata penulis menyadari bahwa tesis ini masih jauh dari sempurna. Untuk itu penulis mengharapkan kritik dan saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak pihak lainnya yang memerlukannya.
Medan, Januari 2012
Penulis,
RIWAYAT HIDUP
DAFTAR ISI
Halaman
ABSTRAK i
ABSTRACT ii
KATA PENGANTAR iii
RIWAYAT HIDUP v
DAFTAR ISI vi
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 3
1.3 Tujuan Penelitian 3
1.4 Manfaat Penelitian 3
1.5 Metode Penelitian 3
BAB 2 TINJAUAN PUSTAKA 5
BAB 3 LANDASAN TEORI 10
3.1 Program Linear Integer 10
3.2 Algoritma Eksak 11
3.3 Pemodelan Matematika 11
BAB 4 HASIL DAN PEMBAHASAN 16
4.1 Algoritma Branch and Bound 16
4.2 Generasi Kolom 19
4.4 Heuristik Pencarian Sekitar Layak 24
BAB 5 KESIMPULAN 27
ABSTRAK
Tesis ini menjelaskan tentang algoritma eksak untuk menyelesaikan permasalahan bin covering. Penyelesaiannya dengan menggunakan prosedur branch and bound dan teknik generasi kolom. Dalam permasalahan integer programming, generasi kolom digunakan untuk menyelesaikan linear programming relaksasi. Branch and bound dapat digunakan untuk banyak kelas pada masalah skala besar seperti sebuah prosedur yang dapat menjadi penghalang berat dalam hal total waktu komputasi. Setelah diambil pendekatan untuk menguji pengurangan masalah dimana sebagian besar variabel integer tetap konstan dan hanya sebagian kecil diperbolehkan untuk bervariasi dalam langkah-langkah diskrit. Hal ini dapat di implementasikan dalam struktur dari sebuah program dengan memperhatikan se-mua variabel integer pada batas solusi yang selanjutnya sebagai non basic dan penyelesaian masalah berkurang dengan mempertahankan non basic.
ABSTRACT
This tesis present an exact algorithm for solving the problems of bin covering. Us-ing the branch and bound procedures and the technique of column generation. In the problem of integer programming, column generation is used to solve the relax-ation of linear programming. While a straightforward branch and bound approach could be adopted, for many classes of large scale problems such a procedure would be prohibitively expensive in terms of total computing time. After have adopted the approach of examining a reduced problem in which most of the integer variables are held constant and only a small subset allowed to vary in discrete steps. This may be implemented within the structure of a program by examining all integer variables at their bounds at the continuous solution as nonbasic and solving the reduced problem with these maintained nonbasic
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Permasalahan bin covering dinyatakan sebagai berikut : misalkan ada n item (barang) dengan ukuranl1, l2,· · · , lndan tidak terbatas persediaannya pada
bin dengan kapasitas C, untuk ukuran item antara nol dan satu menjadi jumlah maksimum dari unit ukuran bin agar tingkat (ukuran total dari semua item yang didapat) dari setiap bin sama atau melebihi kapasitas. Permasalahan bin cove-ring pertama kali dipelajari oleh Assmann et al. (1984) sebagai permasalahan dari dual bin packing pada persoalan kelas NP-Hard. Dalam prakteknya bin co-vering ditemukan dalam dunia industri, seperti industri transportasi, manajemen operasional perusahaan dan lain sebagainya.
Permasalahan bin covering dapat dimodelkan dengan program integer dan merupakan salah satu dari NP-Hard optimasi kombinatorial yang dapat dipe-cahkan oleh berbagai algoritma eksak seperti branch and bound dan generasi kolom. Jen Clausen (1999) memecahkan masalah NP-Hard untuk optimalitas seiring banyaknya pekerjaan yang membutuhkan algoritma yang sangat efisien, dan paradigma branch and bound merupakan salah satu alat utama yang digu-nakan.Branch and boundmerupakan teknik standar untuk menyelesaikan program integer dengan barisan relaksasi dari problema asli yang diselesaikan untuk mem-peroleh solusi yang optimal. Algoritma branch and bound dapat digunakan pada pencarian lengkap untuk solusi waktu yang terbaik.
permasala-2
han Linear Programming(LP) relaksasi. Relaksasi ini telah terbukti memberikan batas bawah yang sangat baik dalam pelaksanaannya. Dua dekade kemudian, Marcotte (1985) menunjukkan bahwa nilai optimal sangat sering menghasilkan LP relaksasi.
Prosedur gabungan generasi kolom dan branch and bound telah digunakan pada permasalahan lainnya, contohnya permasalahan rute dengan time windows
(Desrosier et al. 1984) dan masalah pewarnaanedge(Nemhauser and Park, 1991). Secara umum, Implementasi prosedur gabungan metode branch and bound dan generasi kolom untuk mengatasi kesulitan pada permasalahan loss (kehilangan) ”struktur” kendala percabangan yang ditambahkan keRestricted Master Problem
(RMP), dan jenis subproblems yang harus diselesaikan pada setiap iterasi dapat berubah.
Setelah penyelesaian akar node pada pohon pencarian yang sesuai untuk penyelesaian linear programming relaksasi akan diperkenalkan kendala percaba-ngan pada RMP. kolom dibangkitkan saat penyelesaian LP relaksasi cukup untuk mendapatkan solusi integer. Namun, di dalam pohon branch and bound, satu set kolom yang tidak di bangkitkan diperlukan untuk mendapatkan solusi opti-mal untuk node, dan jika ada himpunan yang hilang, solusi yang diperoleh tidak optimal.
Generasi kolom pada setiap node dari pohon branch and bound terjadi sete-lah diperkenalkannya kendala percabangan dalam RMP. Dengan demikian sub-problem berubah, dan solusi yang optimal dari subproblem asli yang mungkin kolom seharusnya tidak diperkenalkan di dalam restricted master problem. ke-nyataannya, kolom tertentu yang diset ke nol oleh kendala percabangan berubah menjadi kolom paling menarik yang dihasilkan oleh subproblem.
3
dalam langkah-langkah diskrit. Hal ini dapat di implementasikan dalam struktur dari sebuah program dengan memperhatikan semua variabel integer pada batas solusi yang selanjutnya sebagai non basic dan penyelesaian masalah berkurang dengan mempertahankan non basic.
1.2 Perumusan Masalah
Perumusan masalah dalam penelitian ini adalah bagaimana pelaksanaan prosedur yang menggabungkan branch and bound dan generasi kolom untuk me-ngatasi kesulitan masalah kehilangan ”struktur” pada formulasi skala besar.
1.3 Tujuan Penelitian
Adapun yang menjadi tujuan penelitian ini adalah untuk menyelesaikan per-soalan bin covering dengan algoritma eksak melalui metode heuristik pada pen-carian sekitar layak. Dimana akan dilaksanakan prosedur yang menggabungkan branch and bound dan generasi kolom.
1.4 Manfaat Penelitian
Konstribusi dari penelitian ini adalah ditemukannya suatu metode untuk menyelesaikan permasalahan bin coveringuntuk mendapatkan solusi yang efisien, serta menjadi acuan bagi peneliti lainnya dalam melakukan penelitian yang sama atau lebih kompleks lagi.
1.5 Metode Penelitian
Metode penelitian ini bersifat literatur dan kajian pustaka. Sedangkan prosedur yang dilakukan adalah sebagai berikut :
1. Memperkenalkan perumusan bin covering dan memperkenalkan beberapa kriteria untuk mengurangi variabel bilangan,
4
3. Prosedur column generation diberikan untuk memecahkan subproblem pa-da setiap simpul branch and bound dan algoritma bin covering flow exact
(BCFE),
BAB 2
TINJAUAN PUSTAKA
Masalah Bin Covering dapat dinyatakan sebagai berikut : Misalkan ada n item dengan ukuran l1, l2, . . . , ln dan nilainya tidak terbatas pada bin yang sama
dengan kapasitas C. Kumpulan item pada banyak tempat bin yang mungkin, sehingga total ukuran setiapbin sama atau melebihi kapasitas.
Di asumsikan, bahwa :
l1 ≥l2 ≥. . .≥ln
dan
lj < C, j= 1, . . . , n
Saat beberapa item dengan lj ≥C dapat diberikan sendirian untuk satu bin, dan
n
X
j=1
lj ≥2C (2.1)
Karena sebaliknya solusi nilai 0 atau 1 dapat dengan mudah ditetapkan.
Permasalahan Bin Covering dapat di modelkan sebagai program integer :
6
C = Kapasitas masing-masing bin
7
Proposisi berikut sudah dibuktikan oleh Labbˆe et al. (1995)
Proposisi 1. : U berlaku batas atas pada z∗ dan U ≤2z∗
Andaikan W =C+ maxi{li} −1
Proposisi 2. : Batas bawah pada BC adalah L=
Labbˆe et al, (1995) Menyatakan algoritma yang mampu untuk menyele-saikan secara optimal bin covering adalah algoritma branch and bound. Item dipilih pada ukuran urutan yang tidak meningkat. Setiap node merupakan kepu-tusan sebagai bin untuk menempatkan item kedalamnya. Pada setiap node, batas bawah berdasarkan argumen kombinatorial dihitung, dan subproblem yang ter-sisa dikurangi dengan menggunakan dua kriteria pengurangan. Pada akar node, himpunan heuristik diterapkan pada perintah untuk menghitung solusi awal dan batas bawah.
Kendala (2.3) memastikan bahwa kuota terpenuhi untuk setiap bin yang dipakai, dan kendala (2.4) memastikan item yang ditetapkan paling banyak satu bin. Sebuah batas bawah untuk optimal dari masalah bin covering dapat diperoleh dari LP relaksasi yang optimum, yang hasilnya dari substitisi dua kendala terakhir untuk 0≤yi ≤1 dan 0≤xij ≤1
Sebuah metode klasik program integer (0 - 1) yang banyak digunakan untuk menyelesaikan hard kombinatorial adalah dasar untuk memformulasi permasala-han set-partitioning. Hal ini biasanya di kerjakan untuk permasalahan penjad-walan crew (Hoffman et al, 1993), masalah vehicle routing (Desrochers et al, 1992), masalah bin packing (Villerio de Carvalho, 1999; Chan et al, 1998) dan lain sebagainya.
Untuk masalahbin covering, andaikan F himpunanfeasible columns, yaitu :
8
Andaikan|F|menjadi kardinal F. Untuk lebih sederhana dapat di tunjukkan
F =
ai :i= 1, . . . ,|F|
jika dilihat pada permasalahan bin covering dapat dirumuskan sebagai :
BC
Francois (Vanderbeck et al, 1996) menghasilkan algoritma eksak generasi kolom untuk integer programming dengan sebuah nomor kolom besar. Masalah terdekat yang dapat ditangani meliputi tidak hanya masalah partisi standar seper-ti masalah bin packing dan rute jarak tertentu di mana kolom yang dibangkitkan harus 0 - 1 komponen dan sebelah kanan sisi vektor 1, tetapi juga masalah cutting stock yang mana kolom dan sebelah kanan sisi adalah vektor integer non negatif
Chen dan Yao (2001) mengajukan suatu model baru persoalan bin cove-ring satu-dimensi serta menyelesaikan model ini dengan menggabungkan metode-metode branch and bound dan metode generasi kolom. Namun untuk skala besar metode penelitian ini perlu di modifikasi.
9
BAB 3
LANDASAN TEORI
3.1 Program Linear Integer
Jika variabel tak diketahui diharuskan integer maka problema ini disebut program integer atau program linier integer. Perbedaan dengan program linier adalah dapat diselesaikan lebih efisien pada kasus yang tidak layak ataupun ni-lai optimal tidak tercapai. Program integer 0-1 adalah kasus yang khusus dari program integer dimana variabel diharuskan nol atau satu. Masalah ini juga diklasifikasikan sebagai masalah hard non polynomial.
IP adalah salah satu pemodelan untuk pencarian suatu solusi yang optimal dari suatu permasalahan dan juga merupakan bentuk dari program linier dimana asumsi divisibilitasnya melemah atau hilang sama sekali. Bentuk ini muncul kare-na dalam kenyataannya tidak semua variabel keputusan dapat berubah berupa bilangan pecahan. Asumsi divisibilitas melemah artinya sebagian dari variabel keputusan harus berupa bilangan integer dan sebagian lainnya boleh berupa bi-langan pecahan.
Terdapat tiga tipe dasar model pemrograman integer yaitu:
a. Model integer total(pure), semua variabel keputusan harus bernilai bilangan bulat.
b. Model integer 0-1 (binery), semua variabel keputusan harus bernilai 0 atau 1.
c. Model integer campuran (mixed), dari semua variabel keputusan, hanya beberapa (tidak semua) yang harus bernilai bilangan bulat.
11
3.2 Algoritma Eksak
Umumnya program linear integer diselesaikan dengan menggunakan algorit-ma eksak. Algoritalgorit-ma eksak yang akan digunakan untuk menyelesaikan algorit-masalah
bin covering di bagi menjadi dua bagian yaitu :
1. Metode branch and bound
Metode Branch and bound memakai strategi dimana daerah layak di bagi
menjadi himpunan bagian yang lebih kecil. Setiap himpunan bagian beruru-tan diperiksa sehingga penyelesaian yang layak menghasilkan nilai optimal dari fungsi objektif yang diperoleh.
2. Metode generasi kolom
Generasi kolom telah menjadi teknik yang banyak digunakan untuk menye-lesaikan program linear skala besar. Konsep dasar dari pembangkit kolom adalah menyelesaikan program linier dengan membangkitkan hanya him-punan bagian dari variabel yang dijamin merupakan solusi optimalitas atas keseluruhan variabel.
Hasil dari algoritma eksak ini adalah sebuah solusi optimal. Artinya, bahwa tidak
terdapat penyelesaian lain dengan nilai objektifnya lebih baik.
3.3 Pemodelan Matematika
Karena ada lebih dari satu item dengan ukuran yang sama tanpa kehila-ngan persamaan umumnya, andaikan P adalah himpunan item dengan ukuran yang berbeda di L. Misalkan P ={l1, l2, . . . , lm} dan l1 ≥l2 ≥. . .≥lm. Jumlah
masing-masing ukuran dinotasikan sebagai b1, b2, . . . , bm berturut-turut. Hal ini
juga dapat dimodelkan dengan cara grapsG= (V, A) denganV ={0,1,2, . . . , W}
dan A = (i, j)|0≤i≤j ≤W dan j−i= lk, untuk setiap k ≤m. Untuk nomor
arc adalah 0 (mW).
Selanjutnya dilakukan penambahan arc diantara
12
sesuai dengan fungsi kosong yang keluar dari bin. Pembuktiannya bahwa jika ada
feasible column memungkinkan ada path diantara titik 0 danW. Panjangnya arc merupakan path untuk menentukan ukuran item pada cover.
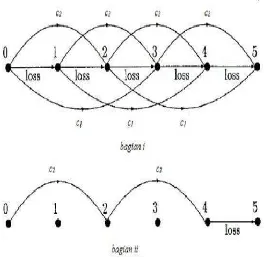
Misalkan pada gambar 1 menunjukkan graph yang terkait dengan sebuah contoh bin dari kapasitas C = 5 dan ukuran item 3 dan 2
Gambar 3.1 Graph and a cutting pattern (Villerio., 1999)
Pada gambar bagian pertama item dengan ukuran 2 dimulai dari bin 1, path antara 0 - 1 adalah loss sedangkan 1 - 5 terpenuhi. Sedangkan item ukuran 3 dimulai dari bin 0, path antara 3 - 5 adalah loss sedangkan 0 - 3 terpenuhi. Untuk item ukuran 3 dimulai dari bin 1, path antara 1 - 4 terpenuhi sedangkan 0 - 1 dan 4 - 5 adalah loss. Pada gambar bagian kedua, yaitu penjelasan dari gambar bagian pertama, path ditampilkan sesuai untuk ukuran item 2 dan 1 unit
loss. Arti dari loss disini adalah bagian yang belum terisi (kosong).
pe-13
Shapiro (1968). Jika solusi covering dari sebuah bin tunggal sesuai dengan flow dari 1 unit antara titik 0 danW, maka sebuah path yang membawa flow yang lebih besar akan sesuai untuk menggunakan solusi cover yang sama pada banyaknya bin.
Dengan flow decomposition properties, setiap flow yang tidak negatif pada grap diatas dapat digambarkan oleh path connecting lebih dari node 0 hingga defisit node W. Permasalahan bin covering dapat dirumuskan sebagai masalah untuk menentukan flow maksimum antara vertex 0 dan vertexW dengan kendala tambahan diketahui bahwa setiap item akan digunakan paling banyak satu kali. Dianggap pengambilan variabel biner xijyang menghubungkan dengan arc yang
diberikan diatas sesuai untuk nilai pada ukuran j − i ditempatkan dalam bin pada jarakiunit dari permulaan bin. Variabelz dapat dinotasikan sebagai x(W0). berikut ini adalah pemodelannya.
BCF
Matriks yang mendefinisikan masalah ini tidak memiliki bentuk umum, se-tiap properti khusus menjamin bahwa solusi basic yang diperoleh adalah integer dan mungkin perlu untuk menggunakan branch and bound setelah menyelesaikan LP relaksasi. Dengan menggunakan variabel yang diberikan sejauh ini, memung-kinkan banyak solusi alternatif dengan item yang persis sama pada masing-masing bin. Dilakukan percobaan untuk mereduksikan kedua kedua simetri pada ruang solusi dan ukuran model dengan mempertimbangkan hanya arc himpunan bagian dari A.
14
Kriteria 1. Sebuah arc dengan ukuranledibuat olehxk,k+le hanya dapat memiliki bagian belakang pada node k itu juga bagian depan arc yang lain dengan ukuran ld, xk−ld,k untuk ld≥le untuk lainnya dari node 0, yaitu batas kiri pada bin.
Contoh (Chen dan Yao., 2001) :
Diberikan sebuah contoh dengan bin kapasitas C = 7 dan P = {6,5,3,2,1} B = (b1, b2,· · · , bm) = (1, 1, 3, 1). Menerapkan kriteria diatas pada A:
˜
A={(0,1), (0,2), (0,3), (0,5), (0,6), (1,2), (2,3), (2,4), (3,4), (3,5), (3,6), (4,5),(4,6), (5,6), (5,7), (5,8), (5,10), (6,7), (6,8), (6,9), (6,11), (6,12), (7,8), (7,9), (8,9), (8,10), (8,11), (9,10), (9,11), (9,12), (10,11), (10,12), (11,12)}
Suatu item tidak diperlukan untuk dimasukkan ke dalam bin yang sudah berisi. Pada flow model, kriterianya dapat diberikan sebagai berikut:
Kriteria 2. Bagian belakang dari arc kurang dari C.
Sesuai dengan kriteria, A dimodifikasi:
˜
A = {(0,1), (0,2), (0,3), (0,5), (0,6), (1,2), (2,3), (2,4), (3,4), (3,5), (3,6), (4,5), (4,6), (5,6), (5,7), (5,8), (5,10), (6,7), (6,8), (6,9), (6,11), (6,12)}
Secara umum, dibatasi oleh sejumlah item yang memiliki ukuran yang sama dalam covering, yakni tidak lebih dari min nbd,
j
w ld
ko
. Meskipun sulit untuk terpenuhi seperti yang diinginkan. Berikut kriteria yang berguna untuk memenuhi permintaan approksimasi.
Kriteria 3. Node k adalah bagian depan arc yang lain dengan ukuran ld(ld > le)
atau k = 0, hanya berlaku arc untuk ukuran le dimulai dari node k+ ile, i =
0,1,· · · , be−1 dank+ile≤W
Oleh kriteria ini, ˜A berubah menjadi
˜
15
Pada kondisi kriteria diatas sebuah arc tidak valid dimana jika ada kekura-ngan arc yang tidak dapat digunakan untuk konstruksi sebuah flow dekekura-ngan busur.
Andaikan
Ti =max
(
0, C −
m
X
j=i+1 bjlj
)
, i= 1, ..., m−1
Kriteria 4. Bagian depan setiap arc dimana jarak li tidak kurang dari Ti.
Sesudah diaplikasikan pada kriteria di atas untuk ˜A. Maka ˜Aadalah sebagai berikut :
˜
A = {(0,2), (0,3), (0,5), (0,6), (2,4), (3,5), (4,6), (5,7), (5,8), (6,7), (6,8), (6,9), (6,11)}
BAB 4
HASIL DAN PEMBAHASAN
4.1 Algoritma Branch and Bound
Algoritmabranch and boundmerupakan pendekatan umum untuk menyele-saikan masalah kombinatorial tujuan tunggal. Metode branch and bound meru-pakan metode pencarian terstruktur dalam ruang solusi yang layak. Ruang solusi di partisi secara berulang-ulang menjadi himpunan bagian yang lebih kecil, dan se-buah batas atas dari fungsi objektif dihiitung dalam setiap subset, subset-subset dengan bound yang diluar solusi terbaik akan di keluarkan dari proses partisi berikutnya.
Dalam permasalahan tujuan ganda, batas haruslah dikembangkan untuk se-tiap percabangan yang bisa diukur hanya bila didominasi oleh penyelesaian yang layak, yaitu bila batas bawah dari semua tujuan sama dengan atau lebih besar dari tujuan penyelesaian yang ada. Aspek penting lainnya dalam keberhasilan implementasi branch and bound adalah rangkaian percabangan. Dalam masa-lah tujuan-tunggal, secara umum lebih menginginkan pengembangan satu penye-lesaian parsial ketimbang yang lainnya berdasarkan pada batas yang dihitung. Karena beberapa batas dihasilkan untuk setiap node dalam masalah multitujuan, kaidah preferensi yang berbeda haruslah diajukan.
Permasalahan optimasi dipecahkan sebagai urutan masalah keputusan di mana akan dicari ada atau tidaknya solusi integer dengan nilai objektif sama dengan lebih kecil dari batas bawah yang di ketahui yang selalu akan menjadi nilai integer, dinotasikan sebagai U.
17
setiap node pencarian depth-first akan di gunakan dengan kendala percabangan, berikut adalah tipenya :
xij ≤ ⌊xij⌋ (4.1)
xij ≥ ⌈xij⌉ (4.2)
dimana, xl
ij variabel pecahan tunggal untuk solusi pada node yang sekarang,
de-ngan demikian penyelesaian programming berikut digolongkan pada kendala kar-dinalitas yang timbul dari percabangan.
18
dimana, Gu dan Hu merupakan index himpunan dari kendala percabangan pada nodeudari tipe (4.1) dan (4.2). RMP yang diformulasikan dalam bentukarc flow. Perhatikan bahwa pada setiap iterasi terdapat satu himpunan arc yang dimiliki RMP, sementara sisanya bisa keluar hasil secara satu persatu.
Remark 1. Pada akar node
Gu =Hu =∅
Setelah kendala percabangan di tambahkan, masalah percabangan di opti-malkan kembali, jika salah satu kasus berikut terjadi:
1. Solusinya adalah integer dengan nilai sama dengan U, yang berarti adalah optimal
2. Solusinya adalah pecahan dengan nilai besar dariU, sehingga perlu diperke-nalkan kendala percabangan yang baru
3. Solusinya memiliki nilai yang kurang dariU, node adalah terukur.
Manfaat pendekatan branch and bound adalah pasti tersedia batas atas maupun batas bawah pada penyelesaian integer terbaik yang mungkin. Asum-sikan fungsi tujuan minimum, batas atas di peroleh dari penyelesaian integer layak terbaik saat ini, dan batas bawah di berikan dari penyelesaian terbaik inte-gral parsial dari subproblem lainnya. Biasanya proses branch and bound berakhir jika beda di antara dua batas ini berada pada toleransi yang ditetapkan.
Remark 2. Pada kenyataannya, jika didapat sebuah solusi layak dan nilai objektif lebih besar atau sama dengan U, dapat dilakukan pencarian depth-first tanpa menemukan solusi optimal dari node saat ini.
19
4.2 Generasi Kolom
Generasi kolom telah menjadi teknik yang banyak digunakan untuk menye-lesaikan program linier skala besar. Konsep dasar dari generasi kolom adalah menyelesaikan program linier dengan membangkitkan hanya himpunan bagian dari variabel yang dijamin merupakan solusi optimalitas atas keseluruhan varia-bel.
Untuk model permasalahan algoritma eksak untuk penyelesaian bin cove-ring akan digunakan generasi kolom untuk menyelesaikan relaksasi program li-nier. Selanjutnya akan digunakan RMP untuk menandakan versi terbatas dari relaksasi program linier yang mengandung hanya himpunan bagian dari variabel. Permasalahan optimisasi akan diselesaikan dengan problema pricing untuk mengi-dentifikasi kolom yang akan ditambahkan dalam RMP. Dari teori program linier, diketahui bahwa biaya reduksi untuk setiap variabel pada solusi optimal adalah tak negatif untuk minimasi.
Generasi kolom menyediakan penguraian dari sebuah permasalahan menjadi master dan sub problem. Penguraian ini memungkinkan adanya penafsiran dalam pengaturan kontektual untuk penambahan beberapa batasan penting, terdapat beberapa kesulitan dalam penggunaan teknikcolumn generation untuk LP dalam solusi IP, yaitu :
1. Integer programming konvensional bercabang pada variabel yang mungkin tidak efektif karena memperbaiki variabel dapat merusak struktur princing problem. Menyelesaikan LP dan subproblem menjadi optimal mungkin men-jadi tidak efisien, dimana beberapa aturan berbeda akan digunakan untuk menangani tree branch and price.
20
Masalah krusial pada pembahasan prosedur branch and bound adalah ba-gaimana menyelesaikan BCFu lebih efektif pada node u pada percabangan tree
(branching tree). Dalam Vanderbeck et al.,(1996) generasi kolom dapat digunakan sebagai pertimbangan rangkaian pemrograman dengan subset variabel untuk me-ningkatkan subset variabel. Dapat dirumuskan sebagai berikut :
SBCFu
Dimana ˜A masih berlaku variabel himpunan yang telah dipertimbangkan. J˜ adalah himpunan kardinat pada vertex yang dianggap bagian subproblem. Se-tiap xij ∈A˜ dapat disamakan untuk kolom Aiji ∈RW dengan A
ij
i =−1 ; A ij i = 1
dan 0 untuk komponen lain.
Setelah menambahkan kendala percabangan dan mengoptimalkan kembali pemrogramanSBCFudiduga solusi optimal sangat kurang dariU. Andaikanπ =
(u, v) menjadi vektor variabel ganda yang berhubungan dengan konservasi flow dan jumlah kendala item dan µ, v vektor dari variabel ganda yang berhubungan dengan kendala percabangan dari tipe (4.1) dan (4.2) berturut turut
Dari teori ganda dapat meningkatkan hasil variabel xij pada node u adalah
˜
de-21
node W, dan P semua himpunan path valid. Kolom Aij merupakan atraktif jika dinaikkan hasil ˜cij lebih besar dari nol. Untuk menentukan path yang paling
at-traktif, subproblem adalah penyelesaian yang sesuai untuk path terpanjang pada
acyclic digraphdengan hasil arc yang tergantung pada nilai variabel ganda. Pem-rograman itu biasanya nilai yang keluar path atraktif, memiliki sifat integralitas dan dapat dilihat seperti berikut ini :
ABCFu
Karena semua arc pada SBCFu ada yang tidak positif hasilnya direduksi,
berikut kondisi yang digunakan.
Proposisi 4.1. Terdapat sebuah path atraktif seandainya sebuah arc dengan hasil positif dinaikkan pada keluaran dari RMP.
Proposisi 4.2. Nilai yang direduksi pada path p adalah sama dengan :
¯
Proof. Nilai yang direduksi dari path p adalah sama dengan jumlah arc
¯
22
Corollary 1. Himpunan arc sesuai untuk path p attraktif jika :
X
Remark 3. Sebagai aturan permasalahan percabangan SBCFu dan subproblem
ABCFu harus kompatibel. Diberikan node u pada branch and bound tree,
terda-pat himpunan kendala percabangan yang diterapkan pada RMP. Untuk memas-tikan kecocokan, variabel di masukkan pada masalah percabanganSBCFu
meng-gunakan generasi kolom tidak harus membuat sebuah point yang layak untuk ru-ang solusi pada master problem ini bertentru-angan dengan kendala percabru-angan yang diterapkan sebelumnya. Oleh karena itu, kolom path dijelaskan pada RMP tidak perlu dimasukkan secara bebas sebagai variabel non negatif.
Kriteria 5. Variabel (arc) yang sudah di set untuk nol pada SBCFu dapat
dire-generasikan oleh sub-problem ABCFu sabagai bagian dari path atraktif. Untuk
menghindari regenerasi, arc dapat dihapus dari subproblemABCFu untuk dapat diterapkan sebagai contoh dengan menerapkan biaya sampai−∞
Kriteria 6. Andaikan Ad = {(i, j)|j−i=ld}, d = 1,2, ..., m, merupakan
him-punan arc yang valid untuk urutanld. Misalkan terdapat himpunan ˆAd⊂Addari
arc sedemikian rupa sehingga jumlah dari batas bawah diterapkan pada jumlah sampai dengan permintaan yang dibutuhkan, yaitu P
l∈Hdu
xij =bddimanaHdu ⊂Hu
adalah himpunan kendala percabangan diterapkan pada arc yang panjang sampai ˆ
Ad. Tidak ada solusi optimal dengan kelebihan produksi. Oleh karena itu, semua
arc yang tersisa (i, j)∈Ad
.
ˆ
Ad dapat di hapus untuk subproblem ABCF u.
Kriteria 6 diatas equivalent dengan observasi 8 dalam Vanderbeck et al. (1996).
23
Itu diketahui dengan adanya kurang optimal point ekstrim yang memiliki basis yang optimal dan basis yang masih memiliki variabel atraktif. Intuitif, jika mengabaikan atraktif arc cadangan dari turunan pivot sebelum menyimpulkan bahwa point extreme adalah optimal.
4.3 Algoritma Bin Covering Flow Exact
Algoritma Bin Covering Flow Exact (BCFE) adalah sebuah algoritma di-mana akan dibahas bagaidi-mana mendapatkan model arc flow yang baru dengan cara menggunakan prosedure algoritmabranch and bounddancolumn generation. Berikut langkah-langkah untuk menyelesaikan algoritma BCFE (Chen dan Yao. 2001) :
Langkah 1. Berdasarkan kriteria 1-4 dapat dibuat himpunan yang valid pada arc ¯A. Seandainya Gu =Hu =∅. u=1, k(u)=0
Langkah 2. Memilih Subset ˜A⊂ A¯
Langkah 3. Menyelesaikan program SBCFu dan di peroleh solusi ˜x dan
nilai objektif ˜zu
Langkah 4. Jika ˜zu ≥U,
Maka jika xu
ij ∈Z1 Untuk setiap Aij ∈A˜.
Maka ˜xu adalah solusi optimal, stop dan keluar solusinya.
Jika ada yang lain ˜xuij merupakan pecahan, andaikan
d= 2k(u)+2(u−1) + 1.
k(d) =k(u) + 1
Gd =Gu∪{x¯u ij}
Hd=Hu
24
Gd =Gu
Hd=Hu∪{x¯uij}
AndaikanGu =Hu =∅ dan pilihan node pterpenuhi olehGp atau Hp 6=∅.
Andaikan u=planjut kelangkah 3. Kalau tidak lanjut ke langkah 5
Langkah 5. ABCFudiselesaikan dan diperoleh solusi ˜xa, yang sesuai untuk
path dari 0 ke vertex W. jika nilai objektif lebih besar dari 0, maka andaikan ˜
Langkah 7. Andaikan U=U-1, kembali ke langkah 1.
Menurut penelitian Kojima et al. (1989),SBCFu dapat diselesaikan dalam
0(
) waktu. Dari kalkulasi yang simpel, dapat dilihat bahwa algoritma
BCFE akan diambil (U −z∗)2|A¯|+1− 2 +A¯
iterasi, dan bahwa setiap iterasi
akan diambil tidak kurang dari 0(A¯
) waktu. Sebenarnya hampir
se-mua waktu komputasi dihabiskan dalam memecahkan mixed integer subproblem
ABCFu. Ternyata algoritma diatas berakhir pada langkah terbatas.
4.4 Heuristik Pencarian Sekitar Layak
Pada kenyataannya pendekatan branch and bound dapat digunakan untuk banyak kelas pada masalah skala besar seperti sebuah prosedur yang dapat men-jadi penghalang berat dalam hal total waktu komputasi. Setelah diambil pen-dekatan untuk menguji pengurangan masalah dimana sebagian besar variabel integer tetap konstan dan hanya sebagian kecil diperbolehkan untuk bervariasi dalam langkah-langkah diskrit.
de-25
sebagai non basic dan penyelesaian masalah berkurang dengan mempertahankan non basic.
Berikut adalah langkah-langkah prosedurnya :
Langkah 1. Penyelesaian masalah mengabaikan syarat integralitas
Langkah 2. Mendapatkan (sub-optimal) integer solusi layak, menggunakan pembulatan heuristic dari solusi berkelanjutan
Langkah 3. Membagi himpunan l pada variabel integer kedalam himpunan l1 pada batas yang non basic pada solusi selanjutnya dan pada himpunan l2. l =l1+l2
Langkah 4. Melakukan pencarian pada fungsi objektif, mempertahankan va-riabel padal1 non basic dan mungkin hanya perubahan diskret pada nilai variabel l2
Langkah 5. Solusi yang didapat pada langkah 4, di uji untuk mengurangi biaya pada variabel l1
Jika salah satu harus dikeluarkan dari aturan, maka tambahkan untuk him-punan l2 dan ulangi dari langkah 4, jikalau tidak berhenti.
Ringkasan diatas memberikan kerangka kerja untuk pengembangan strategi khusus untuk masalah kelas tertentu. Contohnya, pembulatan heuristik pada langkah kedua dapat disesuaikan dengan sifat dasar dari kendala, dan langkah 5 dapat melibatkan dengan hanya menambahkan satu variabel pada suatu waktu kehimpunan l2
26
BAB 5
KESIMPULAN
Dari hasil penelitian dapat disimpulkan :
1. Metode branch and boundmerupakan metode pencarian terstruktur dalam ruang solusi yang layak. Ruang solusi di partisi secara berulang-ulang men-jadi himpunan bagian yang lebih kecil, dan sebuah batas atas dari fungsi objektif dihitung dalam setiap subset. Subset-subset dengan bound yang diluar solusi terbaik akan di keluarkan dari proses partisi berikutnya.
2. Metode generasi kolom digunakan untuk menyelesaikan program linear re-laksasi.
3. Metode heuristik pencarian sekitar layak dapat menyelesaikan permasalahan
bin covering. Metode ini mengambil pendekatan branch and bound untuk banyak kelas pada skala besar seperti sebuah prosedur yang dapat menjadi penghalang berat dalam hal total waktu komputasi.
DAFTAR PUSTAKA
Assmann, S. F. Johnson, D.S. Kleitman, D.J. dkk. (1984). On a dual version of the one-dimensional Bin packing problem. journal Of Algorithms5: 502-525.
Bansal, Nikhil. Caprara, Alberto. Sviridenko, Maxim. (2009). A New Approxima-tion Method for Set Covering Problems, with ApplicaApproxima-tions to Multidimen-sional Bin Packing. SIAM Journal on Computing 39(4) : 1256-1278
Chan, L. Simehi-Levi, D. Bramel, J. (1998). Worst case analyses, linear program-ming and the bin packing problem. Mathematical Programming, 83:213-217
Chen, Feng. and Yao, Enyu. (2001). Exact algorithm for bin covering. Jurnal of Zhejiang University, 3:241-246
Clausen, Jens. (1999). Branch and bound algorithm prinsiples and examples. De-partemen of Computer Sains, University Of Copenhagen
Desrochers, M., Desrosiers, J., Solomon, M., (1992). A new optimization algo-rithm for the vehicle routing problem with time windows.Operation Research, 40:342
Desrosiers, J. F. Soumis, M. Desrochers. (1984). Routing with time windows by-column generation. Networks 14, 545-565.
Fukunaga, Alex S. and Korf, Richard E. (2007). Bin completion algorithms for mul-ticontainer packing, knapsack, and covering problems. Journal of Artificial Intelligence Research28, 393-429
Fukunaga, A. (2005).Bin-Completion Algorithms for One Dimensional, Multicon-tainer Packing Problems. Ph.D. thesis, UCLA.
Gilmore, P.C. dan Gomory, R.E. (1961). A linear programming approach to the cutting stock problem. Operations Research9, 849-859
Gilmore, P.C. dan Gomory, R.E. (1963). A linear programming approach to the cutting stock problem Part II.. Operations Research11, 863-888
Hooffman, K.L. Padberg, M. (1993). Solving airline crew scheduling problems by branch and cut.Management Sciens, 39:657-682
Kojima, M. Mizuno, S. Yoshise, A. (1989). A primal dual interior point method for linear programming, In: N. Meggido (ed.),Progress in Mathematical Pro-gramming. Spinger-Verlag, New York, p. 29 47
Labbˆe, M. Laporte, G. Martello, S. (1995). An exact algorithm for the dual bin packing problem. Operation Research Letter, 17 : 9 -18.
Mawengkang, H. and Murtagh, B.A., (1986) . Solving nonlinear integer program with large-scale optimizations software. Annals of Operations Research 5 : 425 - 437
Ope-29
Shapiro, J.F. (1968). Dynamic programming algorithm for the integer program-ming problem I: The integer programprogram-ming problem viewed as a knapsack type problem, operations research16, 103-121.
Srisuannapa, Chanin. Charnsethikul, Peerayuth. (2007). An exact algorithm for the unbounded knapsack problem with minimizing maximum processing time. Jurnal of Computer Science 3,3:138-143
Taha, A. Hamdy. (2003). Operations Research: An Introduction, Seventh Edition, Prentice Hall, University of Arkansas.
Taylor III, W. Bernard. (1999). Introduction to Management Science, Sixth Edi-tion, Prentice Hall, Virginia Polytechnic Institute and State University.
Vanderbeck, F. Laurence Wolsey, A. (1996). An exact algorithm for IP colomn generation. Operations Research Letters, 19:151-159