PERANAN KESEIMBANGAN NASH DALAM TEORI PERMAINAN
SKRIPSI
BREDTY MAULINA SINAGA 050813011
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERANAN KESEIMBANGAN NASH DALAM TEORI PERMAINAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
BREDTY MAULINA SINAGA
050813011
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : PERANAN KESEIMBANGAN NASH
DALAM TEORI PERMAINAN
Kategori : SKRIPSI
Nama : BREDTY MAULINA SINAGA
Nomor Induk Mahasiswa : 050813011
Program Studi : SARJANA (S-1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU
PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di
Medan, Desember 2007
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dra. Mardiningsih, MSi Drs. Marwan Harahap,M.Eng NIP :131 803 344 NIP : 130 422 443
Diketahui oleh
Departemen Matematika FMIPA USU Ketua
PERNYATAAN
PERANAN KESEIMBANGAN NASH DALAM TEORI PERMAINAN
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri. kecuali beberapa kutipan dari ringkasan yang masing masing disebutkan sumbernya.
Medan, Desember 2007
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Pengasih. dengan limpah karunia-Nya skripsi ini berhasil diselasaikan dalam waktu yang telah ditetapkan.
ABSTRAK
Keseimbangan secara umum adalah nilai yang secara simultan
merupakan nilai minimum dari baris dan maksimum dari kolom dari hasil payoff
tersebut.
Keseimbangan Nash adalah ada serangkaian strategi untuk permainan
dimana tidak ada pemain yang bisa memperoleh keuntungan dengan mengubah
strateginya sementara pemain lain menjaga strategi mereka tetap tidak berubah.
Dalam hal ini keseimbangan Nash ini dapat diselesaikan dengan contoh kasus
yaitu dengan menggunakan strategi dominasi, bila tidak ada strategi mendominasi
akan dilakukan dengan mencari titik pelana dan kedua ini tidak ada dalam suatu
contoh tersebut dapat dilakukan dengan strategi campuran. Disinilah peranan
THE ROLE NASH EQUILIBRIUM IN GAME THEORY
ABSTRACT
The Balance in the general is the value in the simultanly is assessing minimum of line and maximum from column and the result of payoff .
DAFTAR TABEL
Halaman
ABSTRAK
Keseimbangan secara umum adalah nilai yang secara simultan
merupakan nilai minimum dari baris dan maksimum dari kolom dari hasil payoff
tersebut.
Keseimbangan Nash adalah ada serangkaian strategi untuk permainan
dimana tidak ada pemain yang bisa memperoleh keuntungan dengan mengubah
strateginya sementara pemain lain menjaga strategi mereka tetap tidak berubah.
Dalam hal ini keseimbangan Nash ini dapat diselesaikan dengan contoh kasus
yaitu dengan menggunakan strategi dominasi, bila tidak ada strategi mendominasi
akan dilakukan dengan mencari titik pelana dan kedua ini tidak ada dalam suatu
contoh tersebut dapat dilakukan dengan strategi campuran. Disinilah peranan
THE ROLE NASH EQUILIBRIUM IN GAME THEORY
ABSTRACT
The Balance in the general is the value in the simultanly is assessing minimum of line and maximum from column and the result of payoff .
BAB I PENDAHULUAN
1.1 Latar Belakang
Dalam teori permainan dikenal orang kembali setelah munculnya karya
bersama yang gemilang dari John Von Neuman dan V Mergenstern pada tahun
1944 dengan judul Theory of Games and economic behavior. Teori ini bertitik
tolak dari keadaaan dimana seseorang pengambil keputusan harus berhadapan
dengan orang lain dengan kepentingan yang bertentangan. Masa depan yang
dilandasi keputusan yang ia ambil dipengaruhi oleh keputusan yang diambil oleh
orang lain. Itu sebabnya penyelesaian dari pertentangan antara dua pihak yang
bersaingan ini adalah inti dari teori permainan.
Dan setelah ada beberapa terlihat dari hasil karya kedua penemu diatas
yang belum sempurna didalam keseimbangan nash, maka sekarang muncullah
penemu yang ber nama John Nash pada tahun 1950-1953, ia menunjukkan
keseimbangan didalam permainan n-orang, “permainan tak koperatif”, dan dua
orang di dalam permainan koperatif. Nash menguraikan suatu paradigma yang
baru untuk matematik dan pemikir-pemikir ekonomi dengan penggunaan
kepeloporannya dari Teori Keseimbangan ini. Ia telah diterima untuk belajar di
New Jersey dari Barat aslinya Virginia di suatu Scolarship untuk matematika, dan
bekerja dengan singkat dibawah Albert Einstein.
Menurut John Nash, keseimbangan adalah jika ada serangkaian strategi
untuk permainan dimana tidak ada pemain yang bisa memperoleh keuntungan
dengan mengubah strateginya sementara pemain lagi menjaga strategi mereka
tetap tidak berubah, kemudian rangkaian strategi hasil yang bersesuaian
membentuk keseimbangan Nash. Didalam keseimbangan Nash inilah yang
menunjukkan bahwa untuk setiap permainan dengan jumlah pemain dan strategi
yang terbatas terdapat minimal satu solusi yang merupakan himpunan pasangan
berurut strategi yang optimal bagi setiap pemain didalam permainan tersebut. Dari
uraian diatas penulis memilih judul “ Peranan Keseimbangan Nash Dalam
1.2 Identifikasi Masalah
Dalam tulisan ini yang menjadi masalah adalah bagaimana cara
menentukan titik keseimbangan dalam sebuah permainan dimana permainan yang
akan dibahas adalah dalam matrik pembayaran (payoff). Sebagai contoh: si-A dan
si-B mempunyai dua mata uang yang masing-masing kedua sisinya
berbeda.Masing-masing orang menentukan sisi yang akan ditunjukkan kepada
lawannya. Apabila sisi-sisi uang logam yang akan ditunjukkan oleh kedua orang
itu sama, maka si-A menang. Tepati apabila sisi-sisi yang akan ditujukkan oleh
kedua orang itu berbeda, maka si-B menang. Pernyataannya adalah strategi apa
yang harus dijalankan oleh kedua pemain sehingga pemain ini memiliki
equilibrium point?
Permainan ini dapat digambarkan dengan menggunakan matriks yang disebut
payoff-matrik sebagai berikut :
A x y
X 1 -1
Y -1 1
Salah satu strategi yang dapat dilakukan oleh kedua pemain diatas adalah dengan
menggunakan strategi maksimum dan minimum yaitu suatu strategi yang
meminimumkan resiko yang mungkin bagi setiap pemain. Tetapi dati payoff
matriks diatas dapat dilihat bahwa setiap pemain memiliki resiko yang sama untuk
setiap strategi yang dapat digunakan. Bila pemain A menggunakan strategi X atau
Y maka perolehan minimumnya adalah –1. Demikian juga bila pemain B
menggunakan strategi x atau t, maka perolehan minimumnya adalah –1. Hal ini
mengakibatkan permainan diatas menjadi tidak memiliki equlibrium point,yakni
setiap pemain dapat mengambil keuntungan dengan merubah strateginya secara
unilateral. Sebagai contoh, apabila strategi pemain A telah diketahui yakni strategi
X maka pemain B akan menggunakan strategi y untuk memperoleh perolehan
maksimum, selanjutnya apabila pemain A mengetahui pemain B menggunakan
meningkatkan perolehannya juga pada saat yang bersamaan akan mengurangi
perolehan pemain B.
1.3 Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah menganalisa keseimbangan Nash dan menerapkan aplikasi kedalam contoh kasus keputusan dalam sebuah teori permainan.
1.4Metode Penelitian
Penelitian ini bersifat studi literatur yaitu disusun berdasarkan rujukan pustaka
dengan langkah-langkah sebagai berikut :
a. Menerangkan definisi keseimbangan dalam teori permainan
b. Menerangkan definisi teori permainan dalam strategi murni dan
strategi campuran
c. Menyelesaikan permasalahan nilai permainan yang bersifat
seimbang/stabil.
d. Melihat keseimbangan Nash dalam teori permainan.
e. Membuat kedalam contoh kasus.
1.5Tinjauan Pustaka
Menurut John V Neumann teori permainan adalah suatu pendekatan
matematis untuk merumuskan situasi persaingan dan konflik antara
berbagai kepentingan.
Menurut J. Supranto (1998), matriks adalah suatu kumpulan angka-angka
(elemen-elemen) yang disusun berdasarkan baris dan kolom sehingga
berbentuk empat persegi panjang dimana panjangnya dan lebarnya
ditunjukkan oleh banyaknya baris dan kolom.
Menurut John Nash (1953), Nash Equilibrium adalah kondisi dimana
strategi-strategi yang digunakan oleh setiap pemain adalah strategi yang
optimal baginya jika diberikan strategi pemain lainnya dalam permainan
tersebut dimana setiap pemain tidak dapat meningkatkan hasil
Disini agar dapat melakukan penyelesaian dalam teori permainan secara
umum kita perlu menggunakan simbol matematika. Misalnya dalam matriks
pembayaran sebagai berikut :
A =
= Besarnya nilai pembayaran yang diterima oleh A
j = 1,2,3,………,n
Strategi optimal untuk Pemain I :
max{Pi} = max [min. {H(I,j)}] =V
i i
i = 1,2,3,………,m
j = 1,2,3,………,n
Ini disebut kriteria maksimin
Strategi optimal untuk Pemain II :
min{Pi} = min [max. {H(I,j)}] =V
i i
i = 1,2,3,………,m
j = 1,2,3,………,n
1.6 Kontribusi Penelitian
Teori permainan (Game Theory) menerapkan teori permainan yang stabil
dimana apabila keadaan stabil diperoleh dapat digunakan dengan mixed stratery
(strategi campuran). Adapun dibahas disini unsur-unsur dari teori permainan.
Teori permainan ini dapat dilihat dalam bidang ekonmi misalnya: teori permainan
digunakan dalam suatu pasar oligopoli dimana setipa pelaku pasar menggunakan
BAB II
LANDASAN TEORI
2.1 Matriks dan Operasi Matriks 2.1.1 Definisi
Matriks adalah suatu kumpulan angka-angka sering disebut juga
elemen-elemen yang disusun berdasarkan baris dan kolom sehingga berbentuk empat
persegi panjang dimana panjang dan lebarnya ditentukan oleh banyaknya kolom
dan baris yang dibatasi dengan tanda kurung.
A =
Atau disingkat dengan :
( aij
j = 1, 2, ……, n ) , i = 1, 2, ….. , m
Matriks diatas disebut matriks berukuran mxn terdiri dari m baris dan n kolom.
Setiap aij disebut elemen (unsur) dari matriks itu sedangkan indeks i dan j
berturut-turut menyatakan baris dan kolom. Jadi elemen aij terdapat pada baris
ke-i dan kolom ke-j. Matrke-iks bujur sangkar adalah matrke-iks dke-imana banyaknya barke-is
sama dengan banyaknya kolom (m=n).
2.1.2 Teorema Matriks
1. Jika A =
( )
aij dan B =( )
bij keduanya adalah matriks berukuran mxn,maka A+B =
(
aij + bij)
2. Jika A =
( )
aij matriks berukuran mxn dan k adalah skalar, maka k.A =3. Jika A =
( )
aij matriks berukuran mxp dan B =( )
bij matriks berukuranpxn maka perkalian matriks AxB berlaku apabila sejumlah kolom
matriks A sama dengan jumlah matriks B.
AB =
5. Matriks bujur sangkar (square) adalah matriks dimana jumlah banyaknya
baris sama dengan banyaknya kolom (m=n).
A =
6. Matriks Identitas (In) adalah matriks bujur sangkar yang mempunyai
angka satu disepanjang diagonal utama (diagonal dari kiri atas menuju
kanan bawah) elemen yang lainnya adalah nol.
7. Matriks transpos adalah jika baris dan kolom dari suatu matriks mxn
dipertukarkan (baris pertama dengan kolom pertama dan seterusnya),
maka diperoleh suatu matriks nxm yang disebut transpos. Atau disingkat
dengan At atu AI
8. Matriks Kuadrat adalah matriks yang memiliki baris dan kolom yang
sama banyak. Dalam suatu matriks kuadrat, elemen-elemen a11, a22,…..,
ann
disebut elemen diagonal utama. Jumlah elemen-elemen diagonal
utama suatu matriks kuadrat A disebut trace A ditulis tr (A). tr (A) =
Amxn =
4A =
2.2.2 Perkalian Matriks Definisi :
Jika A = [aij] adalah matriks mxp dan B = [bij
C
] adalah matriks pxn maka
hasil kali dari matriks A dan matriks B yang ditulis dengan AB adalah C matriks
mxn. Secara matematik dapat ditulis sebagai berikut :
ij = aijbij + ai2b2j + ……..+ aipbpj
2.2.3 Penjumlahan Matriks Definisi :
Jika A = [aij] adalah matriks mxp dan B = [bij] adalah matriks pxn maka
penjumlahan matriks dari matriks A dan matriks B yang ditulis dengan C = [Cij]
dimana Cij = aij + bij (i = 1,2,……., m ; j = 1,2,…….,n)
2.2.4 Pengurangan Matriks Definisi :
Jika Jika A = [aij] adalah matriks mxp dan B = [bij] adalah matriks pxn
maka pengurangan dari matriks A dan matriks B yang ditulis dengan C = [Cij]
dimana Cij = aij - bij (i = 1,2,……., m ; j = 1,2, ……,n)
2.2.5 Invers Matriks Definisi :
Misalkan A matriks nxn disebut nonsingular jika terdapat matriks B maka
AB = BA = I
Matriks B disebut invers dari A. Jika tidak terdapat matriks B maka matriks A
disebut singular.
Contoh :
2.2.6 Determinan Matriks Definisi :
Misalkan A = [aij
det(A)=[A]
] adalah matriks nxn. Fungsi determinan dari A ditulis
dengan det (A) atau [A]. Secara matematikanya ditulis dengan :
( )
{
}
∑
± aIjIa2j2....anjndengan j1j2....jnmerupakan himpunanS = 1,2,..,n2.2.7 Teorema :
Jika A = [aij
Contoh : A
] adalah matriks nxn yang mengandung sebaris bilangan nol,
maka [A] = 0
2.3 Teori Permainan (Game Theory) 2.3.1 Definisi
Teori permainan adalah pendekatan matematis untuk merumuskan
dikembangkan untuk menganalisa proses pengambilan keputusan dari
situasi-situasi persaingan yang berbeda-beda dan melibatkan dua atau lebih kepentingan.
Kepentingan-kepentingan yang bersaing dalam permainan disebut para pemain
(players). Model-model teori permainan dapat diklasifikasikan dengan sejumlah
cara, seperti jumlah pemain, keuntungan dan kerugian dan jumlah strategi yang
digunakan dalam permainan. Sebagai contoh, bila jumlah pemain adalah dua,
permainan disebut sebagai permainan dua-permain. Begitu juga, bila jumlah
pemain adalah N permainan disebut N-pemain.
Dalam studi formal tentang konflik dan kooperasi konsep teori permainan
dapat diterapkan ketika setiap kegiatan dari objek pelaku adalah saling bergantung
satu dengan yang lainnya. Objek pelaku ini dapat berupa individu, group,
perusahaan, atau kombinasinya. Konsep teori permainan menyediakan sebuah
bahasa untuk memformulasi, menstruktur, menganalisa dan mengerti skenario
strategi.
Ide dasar dari teori permainan adalah tingkah laku strategis dari pemain atau
pengambil keputusan (player or decision maker). Setiap pemain dianggap
mempunyai suatu seri rencana atau model tingkah laku darimana dia bisa
memilih, kalau kita memiliki suatu himpunan strategi. Perlu diperhatikan disini
bahwa teori permainan menekankan tidak hanya menekankan strategi atau
gerakan-gerakan yang diambil bagi pengambil keputusan (pemain) yang tunggal,
akan tetapi tindakan yang dilakukan dalam situasi dimana pemain lainnya sebagai
lawannya juga berbuat sesuatu untuk melakukan gerakan-gerakan sesuai dengan
strategi yang dipilihnya. Lebih lanjut tindakan seorang pemain akan
mempengaruhi gerakan pemain lawannya secara langsung. Dengan perkataan lain,
setiap pemain berada dalam lingkukan yang dinamis bukan statis.
Kegunaan dari teori permainan adalah metodologi yang disediakannya
untuk menstruktur dan menganalisa masalah pemilihan strategi. Untuk
menggunakan teori permainan, maka langkah pertama adalah menentukan secara
eksplisit pemain, strategi yang ada, dan juga menentukan preferensi serta reaksi
Tujuan dari teori permainan adalah menentukan suatu strategi yang
memenuhi kriteria Nash equilibrium sehingga setiap pemaian dalam suatu
permainan tidak dapat mengambil keuntungan dengan cara mengubah strateginya
secara sepihak.
2.4Unsur – unsur Dasar Teori Permainan
Berikut ini akan diuraikan beberapa unsur atau elemen dasar yang penting
dalam penyelesaian dari setiap kasus dengan teori permainan dengan mengambil
permainan dua pemain jumlah nol.
Tabel 2.1 Permainan Dua Pemain Jumlah Nol
Pemain
A
Pemain B
B1 B2 B3
A1 6 9 2
A2 8 5 4
Dari tabel diatas dapat diuraikan unsur-unsur dasar teori permainan :
1. Angka-angka dalam matriks payoff, atau biasa disebut matriks permainan,
menunjukkan hasil-hasil dari strategi-strategi permainan yang berbeda-beda.
Hasil-hasil ini dinyatakan dalam suatu bentuk ukutan efektivitas, seperti uang,
persentase market share. Dalam permainan dua-pemain jumlah nol,
bilangan-bilangan positif menunjukkan keuntungan bagi pemain baris (maximizing
player), dan merupakan kerugian bagi pemain kolom (maximizing player).
Sebagai contoh, bila pemain A mempergunakan strategi A1 dan pemain B
memilih strategi B2
2. Suatu strategi permainan adalah rangkaian kegiatan atau rencana yang
menyeluruh dari seorang pemain, sebagai reaksi atas aksi yang mungkin
dilakukan oleh pemain lain yang menjadi pesaingnya. Dalam hal ini dianggap
bahwa suatu strategi tidak dapat dirusak oleh para pesaing atau faktor lain. , maka hasilnya A memperoleh keuntungan 9 dan B
Dalam tabel 2.1 pemain A mempunyai 2 strategi yaitu A1 dan A2 dan pemain
B mempunyai 3 strategi yaitu (B1, B2, B3
3. Aturan-aturan permainan menggambarkan kerangka dengan mana para
pemain memilih strategi mereka. Sebagi contoh, dipakai anggapan bahwa para
pemain harus memilih strategi-strategi mereka secara simultan dan bahwa
permainan adalah berulang.
).
4. Nilai permainan adalah hasil yang diperkirakan permainan atau payoff
rata-rata dari sepanjang rangkaian permainan, dimana kedua pemain mengikuti
atau mempergunakan strategi mereka yang paling baik atau optimal. Suatu
permainan dikatakan “adil” (fair) apabila nilainya nol, dimana tak ada pemain
yang memperoleh keuntungan atau kemenangan. Permainan dikatakan “tidak
adil” (unfair) apabila nilainya bukan nol.
5. Suatu strategi dikatakan dominan bila setiap payoff dalam strategi adalah
superior terhadap setiap payoff yang berhubungan dalam suatu strategi
alternatif. Sebagai contoh, untuk pemain B, kedua strategi B1 dan B2
didominasi oleh strategi B3. Oleh karena itu untuk maksud pemecahan
permainan ini, kolom-kolom B1 dan B2 dapat dihilangkan dari matrik payoff.
Kemudian permainan dipecahkan dengan pemain B memilih B3 dan pemain A
memilih A2
6. Suatu strategi optimal adalah rangkaian kegiatan, atau rencana yang
menyeluruh, yang menyebabkan seorang pemain dalam posisi yang paling
menguntungkan tanpa memperhatikan kegiatan-kegiatan para pesaingnya.
Pengertian posisi menguntungkan adalah bahwa adanya devisi
(penyimpangan) dari strategi optimal, atau rencana optimal, akan menurunkan
payoff.
. Nilai permainan adalah 4. Aturan dominan ini dapat digunakan
untuk mengurangi ukuran matriks payoff dan upaya perhitungan.
7. Tujuan dari model permainan adalah mengindentifikasikan stratagi atau
rencana optimal untuk setiap pemain. Dari contoh diatas, strategi optimal
untuk A adalah A2, B3 adalah strategi optimal untuk B.
2.4.1 Jenis Situasi Permainan
1) Situasi permainan jumlah dua pemain (two person game)
2) Situasi permainan jumlah lebih dari n- pemain (n-person game)
Klasifikasi pemain dibagi 2 yaitu:
1) Zero sum game (Permainan jumlah nol) adalah
Permainan jumlah nol adalah jika jumlah kerugian dan keuntungan kedua
pemain sama dengan nol. Artinya hasil dari maksimin dan minimaks selalu
sama. Seperti tabel dibawah ini:
Tabel 2.2 Permainan Jumlah Nol
Zero sum game 1 Player II
A B
Player I a 8 4
b 4 2
2) Non- zero sum game (Permainan jumlah tidak nol adalah) :
Disini ditemukan dalam kehidupan riil. Dalam permainan ini hasil dari
keuntungan dan kerugian tidak sama dengan nol. Dan ini sering diselesaikan
dengan metode strategi campuran. Seperti gambar dibawah ini :
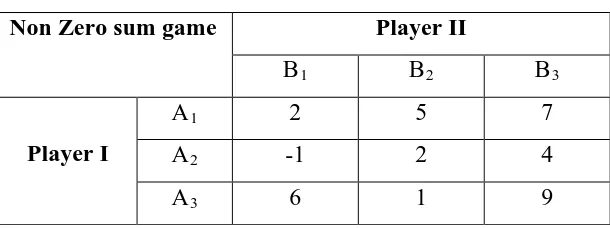
Tabel 2.3 Permainan Jumlah Tidak Nol
Non Zero sum game Player II
B1 B2 B3
Player I
A1 2 5 7
A2 -1 2 4
2.4.2 Strategi
2.4.2.1 Definisi rencana tindakan yang diikuti oleh seorang pemain. Setiap
pemain memiliki dua atau lebih strategi, hanya satu yang dipilih untuk dimainkan.
Ada dua jenis strategi dalam permainan yaitu :
a. Strategi murni (Pure Strategy) adalah disini pemain mempergunakan
strategi tunggal. Dalam permainan strategi murni, pemain baris
mengidentifikasikan strategi optimalnya melalui aplikasi kriteria maksimin
(maximin). Sedangkan pemain kolom (minimizing player) menggunakan
kriteria minimaks (minimax) untuk mengidentifikasikan strategi
optimalnya. Dalam hal ini nilai yang dicapai harus merupakan maksimum
dan minimaks bari dan minimum dari maksimin kolom sekaligus. Pada
kasus tersebut suatu titik keseimbanngan telah dicapai, dan titik ini sering
dikenal sebagai titik pelana (saddle point).
Bila nilai maksimin tidak sama dengan nilai minimaks, titik pelana tidak
dapat dicapai, sehingga permainan tidak dapat dipecahkan dengan
mempergunakan strategi murni. Permainan tanpa titik pelana dapat
dipecahkan dengan menggunakan strategi campuran (mixed strategy).
Contoh :
Kasus teori permainan dalam strategi murni
Misalkan dalam suatu perusahaan A dan B akan melihat seberapa besar
keuntungan yang diperoleh dalam proyek yang akan diteliti oleh kedua
perusahaan tersebut. Maka dapat digambarkan dalam suatu tabel matriks.
Dalam suatu perusahaan ini dianggap A mempunyai 2 strategi dan B
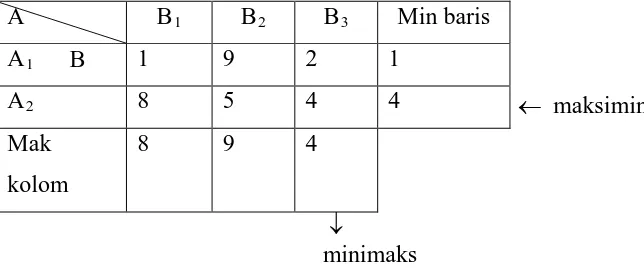
Tabel 2.4 Permainan dengan kriteria maksimin dan minimaks
A B1 B2 B3 Min baris
A1 1 9 2 1
A2 8 5 4 4
Mak
kolom
8 9 4
Dari tabel diatas A mempunyai 2 strategi /pilihan yang tersedia dan B
mempunyai 3 strategi/pilihan yang tersedia. Sekarang A dapat memilih strategi A1
dan A2. Hasilnya dari pemilihan tersebut adalah sebagai berikut :
Strategi Perolehan pilihan
B
Perolehan minimum
tergangtung pilihan B
Pemain A
memilih
A1 (1, 9, 2) Min (1, 9, 2) = 1
A2 (8, 5, 4) Min (8, 5, 4) = 4
Tujuan A : Memaksimumkan perolehan minimum sehingga :
{ } { }
pi = 1,4 i = 1, 2dan : =max.
{ }
i =max.{ }
1,4 =4i p
V
Maka pemain A memilih strategi A2 sebagai strategi optimal dan tidak mau
mundur dari situ. Selanjutnya bagi pemain B terdapat alternatif sebagai berikut:
Strategi Derita tergantung
Pilihan A
Derita max tidak
tergantung pilihan
A
Pemain B
memilih
B1 (1, 8) Max (1,8) = 8
B2 (9, 5) Max (9,5) = 9
B3 (2,4) Max (2,4) = 4
B
← maksimin
↓
Tujuan B : Meminimumkan derita maksimum, sehingga :
{ }
pj ={
8,9,4}
j=1, 2, 3dan : V =
min
.{ }
j =min{
8,9,4}
=4 iP
Disini pemain B memilih strategi B3
4 =
=V
V
sebagai strategi optimal. Dengan demikian
pemain A dan B masing-masing telah memainkan strategi bersih (pure strategi).
Dan didapat titik equilibrium/titik pelana dengan dan harga ini terdapat
pada kotak H (A2, B3) dari tabel diatas. Jadi strategi optimal untuk perusahaan A
adalah A2 dan strategi optimal untuk perusahaan B adalah
b. Mixed strategy (Strategi Campuran) adalah memainkan lebih dari satu
pilihan (alternatif) dan tidak menggunakan urutan tertentu tetapi dalam
bentuk acak. Dalam suatu permainan tidak memiliki strategi deterministik
yang menghasilkan solusi optimal bagi setiap pemain dalam permainan
tersebut. Oleh karenanya, kita membutuhkan suatu teori lain yang dapat
membantu kita mengambil keputusan dalam situasi pemilihan strategi,
apabila strategi deterministik tidak dapat menghasilkan solusi yang
optimal.
Contoh :
Kasus teori permainan dalam strategi campuran
Perusahaan Coloroid Camera (yang akan kita anggap sebagai Perusahaan I) akan
memperkenalkan kamera baru ke dalam ini produknya dan berharap akan
memperoleh peningkatan pangsa pasar sebesar mungkin. Di lain pihak,
perusahaan Comco Camera (yang akan anggap sebagai Perusahaan II) ingin
meminimasi peningkatan pangsa pasar Coloroid. Coloroid dan Camco
menghasilkan penurunan pangsa pasar yang sama untuk Camco. Strategi-strategi
untuk setiap perusahaan didasarkan pada kampanye promosi mereka,
pembungkusan,dan perbedaan aksesori antar produk. Tabel hasil prtukaran, yang
mencakup strategi dan hasil untuk setiap perusahaan (I= Coloroid dan II =
Camco), ditunjukkan dalam Tabel contoh:2. Nilai-nilai dalam Tabel contoh 3.2
adalah persentase peningkatan atau penurunan pangsa pasar untuk Perusahaan I.
Tabel contoh :
Tabel 2.5 Untuk Perusahaan Kamera
Strategi
Perusahaan Kamera I
Strategi Perusahaan Kamera II
A B C
Langkah pertama adalah memeriksa tabel untuk mencari strategi dominan.
Dari melakukan hal tersebut, kita menemukan bahwa strategi 2 mendominasi
strategi 1, dan strategi B mendominasi strategi A. Jadi, strategi 1 dan A dapat
dihilangkan dari tabel hasil pertukaran, seperti ditunjukkan dalam tabel diatas
maka :
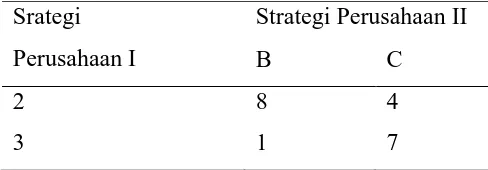
Tabel 2.6 Hasil Pertukaran dengan Menghilangkan Strategi 1 dan A
Srategi
Perusahaan I
Strategi Perusahaan II
B C
Maka perusahaan I menerapkan Kriteria Maksimin seperti ditunjukkan dalam
Tabel 2.7 Tabel Hasil Pertukaran dengan Kriteria Maximin
Srategi
Perusahaan I
Strategi Perusahaan II
B C
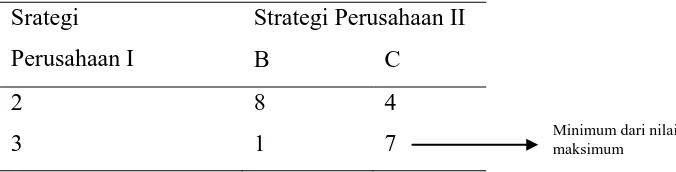
Maka Kriteria minimax diterapkan untuk perusahaan II dalam tabel 3.4 nilai
maksimum untuk strategi B adalah 8%, nilai maksimum untuk strategi C adalah
7%. Dari kedua nilai maksimum ini, 7% merupakan minimum, Jadi strategi
optimal untuk Perusahaan II adalah C.
Tabel 2.8 Hasil Pertukaran dengan Kriteria Minimaks
Srategi
Perusahaan I
Strategi Perusahaan II
B C
Tabel diatas merupakan hasil gabungan dari penerapan kriteria maksimin
dan minimaks dari kedua perusahaan tersebut.
Tabel 2.9 Gabungan Strategi Perusahaan I dan II
Srategi
Perusahaan I
Strategi Perusahaan II
B C
Dari tabel 2.9 dapat kita lihat strategi – strategi yang akan dipilih oleh kedua
perusahaan tidak menghasilkan titik keseimbangan. Oleh karena itu, ini bukanlah
permainan strategi murni. Pada kenyataannya, kondisi keseimbangan ini tidak
akan terjadi pada strategi manapun dari kedua perusahaan ini. Perusahaan I
memaksimumkan persentase peningkatan pangsa pasarnya dengan memilih
Maksimin dari nilai minimum
strategi 2. Perusahaan II memilih strategi C untuk meminimumkan pangsa pasar
perusahaan I. walaupun demikian perusahaan I melihat bahwa perusahaan II
menggunakan strategi C, ia akan berpindah ke strategi 3 untuk meningkatkan
pangsa pasarnay menjadi 7%. Pergerakan ini tidak akan terjadi tanpa terlihat oleh
perusahaan II yang kemudian akan berpindah ke strategi B untuk mengurangi
pangsa pasar perusahaan I menjadi 1 %. Tindakan oleh perusahaan B untuk
mengurangi pangsa pasar perusahaan I segera berpindah ke strategi 2 untuk
memaksimumkan peningkatan pangsa pasarnya menjadi 8%. Berdasarkan
tindakan perusahaan I, perusahaan II akan berpindah ke strategi C untuk
meminimumkan peningkatan pangsa pasar perusahaan I ke 4 %. Sekarang kita
akan melihat bahwa kedua perusahaan kembali ketempat semula. Seperti
dilihatkan pada tabel dibawah ini :
Tabel 2. 10 Hasil dengan Putaran Tertutup
Srategi
Perusahaan I
Strategi Perusahaan II
B C
2
3
8
1
4
7
Permainan strategi campuran bagi kedua perusahaan kamera diatas dapat
dilakukan dengan menggunakan strategi campuran. Salah satu metode lain yang
dapat digunakan yaitu dengan metode ekpektasi keuntungan dan kerugian.
Perusahaan I secara sistematis mengasumsikan bahwa perusahaan II akan memilih
strategi B. Berdasarkan keadaan ini ada probabilitas sebesar p untuk perusahaan I
akan memilih strategi 2 dan probabilitas sebesar (1-p) bahwa perusahaan I akan
memilih strategi 3. jadi, jika perusahaan II memilih B, ekspektasi keuntungan bagi
perusahaan I adalah :
8p + 1(1 –p) = 1 + 7p
Kemudian perusahaan I mengasumsikan bahwa perusahaan II akan memilih
akan memilih strategi 2. Jadi, ekspektasi keuntungan dari perusahaan I
berdasarkan strategi C adalah
4p + 7(1-p) = 7 – 3p
Kita telah tahu sebelumnya bahwa metode ini didasarkan pada ide bahwa
perusahaan I akan mengembangkan rencana yang menghasilkan Perusahaan II.
Jadi jika Perusahaan I merasa apa pun pilihan Perusahaan II, ekspektasi
keuntungan dan setiap strategi tersebut:
1 + 7p = 7 – 3p
10p = 6
p = 6/10 = 0.6
Ingat bahwa p adalah probabilitas memakai strategi 2, atau persentase
waktu penggunaan strategi 2. Jadi, rencana Perusahaan I adalah menggunakan
strategi 2 selama 60% dari seluruh waktu yang ada dan menggunakan strategi 3
selama 40% dari seluruh waktu yang ada. Ekspektasi keuntungan (peningkatan
pangsa pasar untuk Perusahaan I) dapat dihitung menggunakan hasil pertukaran
strategi B atau C, karena keuntungan yang diperoleh sama. Dengan menggunakan
pertukaran strategi B,
E (Perusahaan I) = 0,60(8) + 0,40(1)
= 5,2 % peningkatan pangsa pasar
Untuk memeriksa hasil ini, kita akan menghitung ekspektasi keuntungan
jika strategi C digunakan oleh Perusahaan II
EG (Perusahaan II) = 0,60(4) + 0,40(7)
= 5,2 % peningkatan pangsa pasar
Sekarang kira harus mengulangi proses ini bagi Perusahaan II untuk
mengembangkan strategi campuran yang merupakan ekspektasi keuntungan bagi
Perusahaan I sekarang merupakan ekspektasi kerugian bagi perusahaan II.
Pertama kita asumsikan bahwa Perusahaan I akan memilih strategi 2. Jadi
yang ada dan C selama (1 – p) dan waktu yang ada. Ekspektasi kerugian bagi
Perusahaan II atas strategi 2 adalah :
8p+4(1-p)=4+4p
Kemudian kita hitung ekspektasi kerugian untuk Perusahaan II
berdasarkan anggarai bahwa Perusahaan I memilih strategi 3:
1p + 7(1-p) = 7-6p
Dengan menyamakan kedua ekspektasi kerugian untuk strategi 2 dan 3
akan didapatkan nilai untuk p dan (1-p)
4+ 4p = 7 – 6p
10p = 3
p = 3/10 = 0,30
dan
1p + 7 = 0,70
Karena p adalah probabilitas menggunakan strategi B, perusahaan II akan
menggunakan strategi B selama 30 % dari seluruh waktu yang ada, dan demikian
strategi C akan digunakan selama 70% dari waktu yang ada. Ekspektasi kerugian
aktual berdasrkan strategi 2 dapat dihitung sebagai berikut :
E (Perusahaan II) = 0,30 + 0,70 (4)
= 5,2 % kehilangan pangsa pasar
Strategi campuran utnuk setiap perusahaan didapatkan sebagai berikut
Perusahaan I Perusahaan II
Strategi 2: 60 % waktu yang ada Strategi B: 30 % waktu yang ada
Strategi 3: 40 % waktu yang ada Strategi C: 70 % waktu yang ada
sebesar 5,2 % dan ekspektasi kerugian untuk Perusahaan I juga pangsa pasar
sebesar 5,2 %. Jadi, strategi campuran untuk masing-masing perusahaan
menghasikan titik keseimbangan dimana 5,2 % ekspektasi keuntungan untuk
Perusahaan I pada saat yang sama merupakan 5,2 ekpektasi kerugian untuk
Perusahaan II.
Maka masing-masing perusahaan telah memperbaiki posisinya terhadap hasil
yang dicapai dengan menggunakan strategi maximin dan minimax. Dimana Hasil
pertukaran untuk Perusahaan I hanya berupa peningkatan pasar sebesar 4 %
sementara strategi campuran menghasilkan ekspektasi keuntungan sebesar 5,2 %.
Hasil dari strategi minimax dari perusahaan I adalah kerugian sebesar 7 %,
namun strategi campuran menunjukkan kerugian 5,2 %. Jadi, masing-masing
perusahaan menempatkan dirinya pada situasi yang lebih baik dengan
menggunakan pendekatan strategi campuran.
Pendekatan ini mengasumsikan bahwa permainan bersifat pengulangan dan
akan dimainkan selama periode waktu tertentu sehingga strategi dapat digunakan
selama persentase waktu tertentu dari periode tersebut. Untuk contoh diatas dapat
secara logis diasumsikan bahwa pemasaran kamera baru oleh Perusahaan I akan
membutuhkan waktu yang lama. Jadi setiap perusahaan dapat menggunakan
strategi campuran yang dimiliki.
Secara matematis, defenisi mixed-strategy adalah sebagai berikut:
Suatu mixed-strategy untuk P1 adalah suatu vector X=(x1,x2,……., xn)
dimana entri-entrinya adalah bilangan riil positif sehingga x1+x2+…….+xm = 1,
dengan pengertian bahwa P1akan memainkan strategi si dengan peluang xi , 1 I ≤ ≤ m.
Oleh karena defenisi strategi dalam konsep mixed-strategy telah berubah
menjadi stokastik, maka perolehan dari setiap pemain juga harus diubah.Jika
dalam permainan yang bersifat deterministik perolehan untuk setiap pemain
ditentukan oleh nilai dalam tabel perolehan, maka dalam permainan yang bersifat
stokastik dalam mixed-strategy perolehan untuk setiap pemain adalah berupa nilai
ekspektasi bagi pemain tersebut. Nilai ekspektasi didefenisikan sebagai hasil
yang mungkin terjadi.Sebuah permainan dengan tabel perolehan dalam matriks
A= (aij), jika P1 menggunakan strategi X= (x1,x2,…….,xn) dan P
Menggunakan strategi Y= (y
2
1,y2,…….., yn) maka peluang munculnya aij adalah
xiyj.Oleh karennya untuk permainan ini adalah hasil penjumlahan dari perkalian
xiaijyj
atau dapat dinotasikan sebagai berikut:
j
Atau dengan kata lain diatas adalah identik dengan XAYt dimana ‘X’
adalah strategi yang mungkin bagi pemain-I dan Y adalah stratagi yang mungkin
bagi pemain-II dan A adalah tabel perolehan untuk permainan tersebut.
Pemecahan masalah dalam permainan strategi campuran dapat dilakukan dengan :
(1) metode analitis, (2) metode aljabar matriks.
Metode campuran dapat dilakukan dengan 2 cara yaitu :
1. Metode analitis
Bentuk umum :
p = proporsi waktu pemain A untuk menggunakan strategi 1
1-p = proporsi waktu pemain A untuk menggunakan strategi 2
q = proporsi waktu pemain B untuk menggunakan strategi 1
1-q = proporsi waktu pemain B untuk menggunakan strategi 2
2. Metode Aljabar Matriks
dimana Pij
Strategi optimal perusahaan A =
menunjukkan jumlah payoff dala baris ke i dan kolom ke j. Dan dapat
dicari dengan rumus sebagai berikut :
[ ]
[ ]
2.5 Nash Equilibrium 2.5.1 Definisi :
Keseimbangan adalah Suatu strategi si dikatakan strategi dominan bagi Pi
jika u(si) u(s≥ j), dengan u(si) dan u(sj) adalah perolehan dari strategi si dan sj
≠
dimana i j untuk semua s ∈ S.
Dalam setiap permainan, setiap pemaian akan selalu menggunakan
dominan karena sifat rasional yang diasumsikan pada setiap pemain. Tetapi dalam
beberapa permainan, tidak terdapat strategi dominan sehingga pemain harus
menggunakan mixed-strategy seorang pemain dapat menentukan strategi yang
akan digunakannya dengan cara memilih strategi yang akan digunakannya dengan
suatu distribusi peluang sehingga strategi yang akan digunakan bukan bersifat
deterministik tetapi bersifat stokastik. Dengan menggunakan mixed-strategy
komposisi strategi yang akan digunakan oleh pemain adalah berupa himpunan
pasangan berurut distribusi-distribusi peluang yang akan digunakan oleh setiap
pemain.
Defenisi lain tentang keseimbangan Nash adalah kondisi dimana
strategi-strategi yang digunakan oleh setiap pemain adalah strategi yang
optimal baginya jika diberikan strategi pemain lainnya dalam permainan
tersebut dimana setiap pemain tidak dapat meningkatkan hasil perolehannya
dengan menggantikan strateginya.
Arti keseimbangan Nash menurut John Nash adalah jika ada serangkaian
strategi untuk sebuah permainan dimana tidak ada pemain yang bisa beruntung
dengan mengubah strateginya sedangkan pemain lain mempertahankan
strateginya tidak berubah, maka serangkaian strategi tersebut dan perimbangan
(payoff) yang koresponden membentuk keseimbangan Nash.
2.6 Memilih Strategi
Dalam permainan dua pemain berjumlah nol ini tujuannya adalah
menemukan jawab yang kokoh bagi kedua pemain. Memilih strategi sama artinya
dengan menemukan jawab permainan. Jawab yang dimaksud hanya ada bila tiap
pemain berusaha memperkecil derita atau memperbesar perolehan, dengan kata
lain tiap pemain berusaha meraih strategi optimal bagi dirinya sehingga tidak ada
lagi dari antara pemain yang dapat meningkatkan posisi masing-masing dengan
memilih strategi lain. Hasil yang diharapkan bila kedua pemain telah
menggunakan strategi optimalnya disebut “harga permainan”. Salah satu langkah
dari satu permainan adalah pemilihan satu strategi oleh tiap pemain. Usaha
permainan dan langkah berikutnya tidak boleh lagi dilanjutkan dan permainan
telah selesai.
2.6.1 Kriteria Maksimin dan Minimaks
Tujuan utama menyelesaikan suatu permainan adalah menentukan strategi
optimal. Strategi optimal dapat ditentukan dengan menggunakan teori yang
disebut teori minimaks yang pada prinsipnya mengatakan bahwa tiap pemain
secara sepihak mencari tingkat keamanan yang maksimum bagi diri sendiri.
Dalam memilih strategi optimal, beberapa asumsi ditetapkan terlebih dahulu
yaitu:
1) Bahwa kedua pemain memiliki kepintaran yang sama
2) Tiap pemain sudah mengetahui strategi yang lain
3) Tiap pemain mengetahui jumlah perolehan sendiri dan derita pemain lain
4) Tiap pemain harus menentukan strategi (pilihan).
Berdasarkan asumsi diatas, tiap pemain mengetahui bahwa pemain yang
lain cukup rasional serta mempunyai tujuan yang sama yaitu memaksimumkan
perolehan sendiri. Pemain I memeriksa tiap baris dari matriks perolehan dan
memilih harga maksimum dari harga minimum. Cara menentukan pilihan seperti
ini adalah cara yang konservatif dan biasa disebut sebagai cara memilih yang
terbaik dari antara yang terburuk. Cara ini juga disebut kriteria maksimum dari
minimum disingkat dengan kriteria maksimin.
Sebaliknya, pemain II menyelesaikan permainan untuk menentukan
strategi optimal dengan menggunakan teori yangn dinamakan teori minimaks.
Teori ini menetapkan bahwa pemain secara sepihak mencari tingkat keamanan
yang maksimum bagi dirinya sendiri, yaitu dengan memilih derita terkecil dari
antara sejumlah derita maksimum. Cara ini ialah memilih kriteria minimum dari
2.7 Peranan Dominasi
Pemain B
x y z Keuntungan minimum
8 (4) 7,5
7 3,5 3
Kerugian 8 (4) 7,5
maksimum minimax
Lihat kembali contoh yang diatas, terlihat bahwa strategi 1 menghasilkan
keuntungan maksimum bagi A, tanpa memperhatikan strategi mana yang dipilih
B. Sehingga strategi 1 dikatakan mendominasi strategi 2. untuk kasus dimana
suatu strategi secara sempurna didominasi oleh strategi lain, strategi yang
didominasi dapat dibuang dari matriks pay-off karena pemain tidak pernah
memilihnya.
Untuk pemain B, strategi x didominasi oleh strategi y karena kerugian
strategi x selalu lebih besar daripada kerugian strategi y tanpa memperhatikan
strategi yang dipilih A. strategi x juga didominasi oleh strategi z. Karena itu,
strategi x dapat dibuang.
Pemain A hanya dapat memilih strategi 1, yanng berarti B akan memilih
strategi y untuk meminimumkan kerugian menjadi 4 daripada 7,5. Ingat bahwa
solusinya tetap sama. Jadi, jika setiap pemain memiliki sebuah strategi dominan,
games akan mencapai keseimbangan atau memiliki saddle point. 1
2
(4) maximin
BAB III
PEMBAHASAN
3.1 Pengantar
Keseimbangan Nash adalah jika ada serangkaian strategi untuk permainan
dimana tidak ada pemain yang bisa memperoleh keuntungan dengan mengubah
strateginya sementara pemain lain menjaga strategi mereka tetap tidak berubah,
kemudian rangkaian strategi tersebut dan hasil yang bersesuaian membentuk
keseimbangan Nash.
Setiap permainan berhingga mempunyai setidak-tidaknya satu
keseimbangan Nash dalam strategi murni dan strategi campuran. Pemain disebut
menggunakan strategi campuran jika ia menggunakan strategi acak untuk
memutuskan apa yang harus dilakukan dalam permainan. Idealnya, para pemain
hanya akan menggunakan strategi campuran bila tidak ada perbedaan antara
beberapa strategi murni dan membiarkan lawan tetap menduga strategi yang
diinginkan.
Adapun dua permainan menurut John Nash yaitu
1) Permainan zero sum
Dalam permainan zero sum adalah jumlah hasil para pemain selalu sama
dengan nol tidak soal strategi apa yang digunakan yaitu keuntungan untuk
Pemain I akan berarti kerugian yang sama bagi Pemain II. Dengan
menggunakan strategi dominan.Contoh 1:
Tabel 3.1 Dengan Stategi Dominan Permainan zero sum Pemain 2
a b
Pemain 1 a 1,-1 2,-2
Dalam permainan diatas tampak jelas bahwa kedua Pemain I (b)
mendominasi kuat strategi pertamanya (a). Secara matematik, istilah mendominasi kuat berarti bahwa (1<3) dan (2<4) atau (1,2) << (3,4). Strategi
Pemain I adalah strategi mendominasi kuat. Ini berarti apapun strategi yang
dipilih Pemain II, Pemain I akan memperoleh hasil yang lebih baik bila memilih
strategi b. Karena disimpulkan bahwa jika Pemain I dianggap rasional, ia akan
selalu memilih strategi kedua.
Karena baris I tidak akan digunakan Pemain I, Pemain II dihadapkan dengan
“permainan tereduksi”. Dalam permainan tereduksi ini, strategi (b) Pemain II
mendominasi kuat strategi (a). Solusi permainan ini adalah (b,b) yang member
hasil 3 kepada Pemain I dan -3 kepada Pemain II. Ini disebut keseimbangan Nash.
Akan tetapi, agar ini berlaku kita tidak perlu mengasumsikan bahwa semua
pemain rasional tetapi juga bahwa Pemain II tahu bahwa Pemain I rasional sampai
tingkat dimana ia akan memainkan yang menguasai dengan kuat.
Contoh 2:
Tabel 3.2 Dengan menggunakan titik pelana
Permainan zero sum
Pemain 2
A B C
Pemain 1 A 1,-1 4,-4 0,0
B 2,-2 3,-3 4,-4
C 1,-1 0,0 6,-6
Dalam tabel diatas bahwa tidak ada strategi murni didominasi, tetapi profil
strategi (B,A) yaitu baris B dan kolom A adalah titik pelana matriks. Dalam teori
titik permainan titik pelana berarti bahwa nilai “2” adalah yang terkecil pada baris
dan terbesar pada kolom. Karena itu, strategi B Pemain I adalah reaksi optimal
terhadap pilihan strategi A oleh pemain II, dan secara simultan strategi A
Pemain II adalah reaksi optimal terhadap pilihan strategi B oleh Pemain I. Dari
Contoh 3 :
Bila tidak ada strategi mendominasi dan titik pelana
Tabel 3.3 Dengan strategi campuran
Permainan zero sum
Pemain 2
X Y
Pemain 1 J 1 4
K 3 2
Dalam permainan ini tidak ada titik pelana dan tidak ada strategi
mendominasi. Ini menunjukkan bahwa tidak ada keseimbangan Nash dalam
strategi murni. Akan tetapi keseimbangan Nash ada asalkan strategi campuran
dilakukan. Andaikan bahwa Pemain II memilih strategi campuran (1-q,q). Ini
berarti probabilitas yang akan ia gunakan strategi pertamanya (X) adalah 1-q dan
strategi keduanya (Y) adalah q. Dengan menggunakan informasi ini persamaan
untuk hasil yang diperkirakan bagi Pemain I bisa dibentuk bila ia menggunakan
strategi pertamanya J atau strategi kedua K.
(J) E1
(K) E
= (1-q) + 4q = 1+3q………(1)
2
Jika (1-p,p) adalah reaksi optimal Pemain I terhadap (1-q,q) oleh Pemain II, maka
E
= 3(1-q) + 2q = 3-q …….(2)
1 >E2 (dari persamaan diatas bahwa q> 0,5). Pemain I ingin memilih strategi
pertamanya J sehingga p= 0. Jika E1< E2 ini berarti bahwa q <0,5. Maka reaksi
optimal untuknya adalah memilih strategi keduanya yaitu K, sehingga p=1. Jika
E1 = E2, maka setiap reaksi sama baiknya dank arena dalam kasus ini probalitas
peluang yaitu 0 < p < 1. Begitu juga sebaliknya analisis reasksi optimal dengan
cara yang sama pada Pemain II dalam kasus ini q= 0 bila p < 0,75, q=1 bila p
>0,75 dan bila p = 0,75 maka 0 < q <1. Dari sini didapat reaski optimum di q =0,5
dan p =0,75. Ini mengindikasikan bahwa p= 0,75 adalah reaksi optimum terhadap
q= 0,5 dan sebaliknya. Karena inilah keseimbangan Nash untuk Pemain I adalah
menggunakan strategi keduanya dengan probabilitas 0, 75 dan untuk Pemain II
mengimplikasikan bahwa perkiraan hasil untuk Pemain I adalah 5/2 dan -5/2
untuk Pemain II
2) Permainan non- zero sum
Permainan non- zero sum lebih sering ditemui dalam kehidupan nyata. satu-
satunya perbedaan antara permainan zero sum dan permainan non-zero sum
adalah bahwa keuntungan oleh satu pemain tidak selamanya berarti kerugian
yang sama oleh pemain lain.
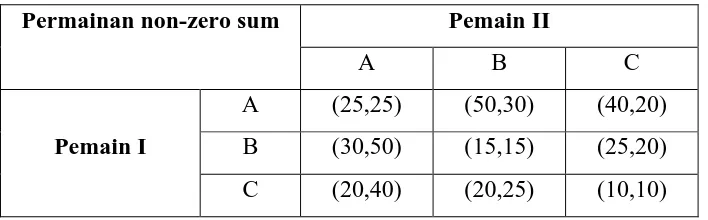
Tabel 3.4 Permainan non-zero sum Permainan non-zero sum Pemain II
A B C
Pemain I
A (25,25) (50,30) (40,20)
B (30,50) (15,15) (25,20)
C (20,40) (20,25) (10,10)
Cara paling mudah untuk menganalisa permaian non zero sum adalah
menganalisanya dengan cara yang sama seperti pada permainan zero- sum. Catat
bahwa pada permainan non- zero sum diperlukan memperlihatkan hasil kedua
pemain karena tidak lagi disimpulkan dari hasil pemain lain, seperti yang bisa
dilakukan dalam permainan zero sum. Menganalisa permainan diatas ada dua titik
keseimbangan Nash pada sel tengah atas (A,B) dan sel tengah kiri (B,A). Untuk
membuktikan perhatikan pilihan (A,B) kemudian Pemain I tidak bisa
meningkatkan hasilnya dengan Pemain 2 memilih B dan demikian sebaliknya.
Karena itu, ini merupakan titik keseimbangan alasanyang sama juga berlaku pada
strategi (B,A).
Kedua kasus akan menghasilkan total hasil 80, yang juga merupakan pilihan
strategi paling efisien karena tidak ada total hasil yang lebih besar dari 80 dalam
permainan ini. Akan tetapi, bila dikaji lebih dalam permainan ini ada bahaya
kedua pemain memilin A, maka total hasil berkurang menjadi 50 dengan hasil 25
kepada masing-masing pemain. Ini jelas tidak diinginkan kedua pemain, bahkan
yang paling buruk diantara kedua pemain bisa mengharapkan pemain lain
kedua pemain memilih B. Dalam kasus ini mereka akan berakhir dengan hasil
BAB IV
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Dari uraian bab-bab sebelumnya, maka dapatlah dibuat beberapa
kesimpulan sebagai berikut :
1. Pada kondisi tertentu, suatu permainan tidak memiliki titik keseimbangan
(equilibrium point). Oleh karenanya dibutuhkan solusi lain yang bersifat
stokastik agar permainan tersebut memiliki equilibrium point. Solusi
optimal dari suatu permainan dapat dipecahkan dengan menggunakan
strategy campuran (mixed strategy)
2. Untuk setiap pemain yang terdiri dari beberapa pemain dan beberapa
strategy bagi setiap pemain, maka ada minimal satu solusi optimal bagi
setiap pemain atau terdapat equilibrium point (titik keseimbangan pada
permainan tersebut.)
3. Dari contoh kasus 1, didapat bahwa nilai maksimin dan minimaks sebesar
4.Dengan menggunakan strategy campuran didapat nilai p = 0,625, q=
0,50 dengan keuntungan yang diharapkan perusahaan A sebesar 3,5 dan
perusahaan B= 3,5.
4. Dari contoh kasus 2 didapat nilai p = 0,60 dan q = 0,70 sehingga
keuntungan untuk perusahaan I mengalami peningkatan sebesar 5,2 % dan
kerugian untuk perusahaan II sebesar 5,2 %dan perusahan tersebut
menghasilkan titik keseimbangan sebesar 5,2 %.
4.2 Saran
Dari uraian bab-bab sebelumnya dapat disimpulkan Game Theory dapat
digunakan oleh pengambil keputusan untuk menentukan strategy yang paling
optimal baginya. Dengan demikian, Game Theory dapat dijadikan sebagai alat
ukur strategy yang ada dalam mencari titik perusahaan tersebut. Oleh karenanya
keputusan hendaklah menggunakan Game Theory untuk menilai strateginya
sehingga strategy yang akan dijalankan menjadi lebih efektif, penulis juga
menyarankan agar penyesuaian Game Theory tidak dilakukan dengan cara manual
DAFTAR PUSTAKA
Hiller, Liebermen,”Introduction To Operation Research”, McGraw Hill, Stanford University, 2001, menjelaskan defenisi game theory.
Squintani, Francesco, “Notes for Non Cooperative Game Theory”, Fall 2001, memberikan teorema Nash yang menyatakan untuk setiap permainan yang terdiri dari n-pemain, maka terdapat minimal satu titik keseimbangan.
P. Siagian, “Strategi dan Teori Permainan”, hal 349.
Supranto, Johannes, 1998. ”Tehnik Pengambilan Keputusan”, Jakarta, Rineka Cipta.
Sri Mulyono, SE, M.Sc.1996. “Teori Pengambilan Keputusan”, Jakarta-Lembaga Penerbit Fakultas Ekonomi Universitas Indonesia.
Kockesen, Levent, “Mixed Strategy Equilibrium” Menjelaskan Kriteria Permainan yang Tidak Memiliki Solusi Titik Equilibrium
Drs. Pangesty Subagyo, M.B.A, Drs. Manuan Asri, M.B.A, Dr. T Hani Handoko, M.B.A.2000 “ Dasar-dasar Operations Research”. Yogyakarta-Lembaga Penerbit Fakultas Ekonomi Universitas Gadjamada 2000
2004.