STUDI PENENTUAN MATRIKS PEMBOBOT SPASIAL
OPTIMUM DALAM PENDUGAAN AREA KECIL
ASFAR
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN SUMBER
INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa tesis berjudul Studi Penentuan Matriks Pembobot Spasial Optimum dalam Pendugaan Area Kecil adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir disertasi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Agustus 2016
Asfar
RINGKASAN
ASFAR. Studi Penentuan Matriks Pembobot Spasial Optimum dalam Pendugaan Area Kecil. Dibimbing oleh ANANG KURNIA dan KUSMAN SADIK.
Statistik area kecil di Indonesia saat ini telah menjadi perhatian oleh para statistisi seiring dengan bergesernya sistem ketatanegaraan dari sistem sentralisasi ke sistem desentralisasi. Pada sistem desentralisasi, pemerintah daerah memiliki kewenangan yang lebih besar untuk mengatur dirinya sendiri, khususnya pada level pemerintah kabupaten/kota. Dengan demikian kebutuhan statistik sampai pada level desa/kelurahan menjadi suatu kebutuhan dasar sebagai landasan bagi pemerintah daerah kabupaten/kota untuk menyusun sistem perencanaan, pemantauan dan penilaian pembangunan daerah atau kebijakan penting lainnya.
Pada umumnya survey yang digunakan hanya dirancang untuk menduga parameter populasi berskala nasional. Sehingga permasalahan akan muncul ketika ingin memperoleh informasi untuk area yang lebih kecil, misalnya pada level propinsi, level kabupaten atau level kecematan. Ukuran contoh pada level area tersebut biasanya sangat kecil sehingga statistik yang diperoleh akan memiliki ragam yang besar. Guna mengatasi hal ini, diperlukan suatu prosedur statistika yang dapat mengkombinasikan data dari contoh kecil dan besar, dengan mengambil keuntungan secara detil dalam survei contoh dan sensus. Metode yang tepat untuk memberi solusi dalam hal ini adalah metode pendugaan area kecil (Small Area Estimation, SAE). Metode ini membantu memperbaiki informasi dan ukuran contoh menjadi lebih efektif. Salah satu metode dalam pendugaan area kecil adalah
Empirical Best Linear Unbiased Prediction (EBLUP).
Fay dan Herriot (1979) merupakan peneliti pertama yang mengembangkan pendugaan area kecil berdasarkan model linier campuran. Model yang kemudian menjadi rujukan dalam pengembangan penelitian pendugaan area kecil lebih lanjut. Model Fay-Herriot yang menjadi dasar dalam pendugaan area kecil mengasumsikan bahwa pengaruh acak galat area saling bebas. Namun dalam beberapa kasus, asumsi ini sering dilanggar. Penyebabnya adalah keragaman suatu area dipengaruhi area sekitarnya, sehingga pengaruh spasial dapat dimasukkan ke dalam pengaruh acak. Efek spasial merupakan hal yang lazim terjadi antara satu area dengan area yang lain, ini berarti bahwa area yang satu mempengaruhi area lainnya. Selain itu, dasar dalam analisis spasial adalah segala sesuatu saling berhubungan satu dengan yang lainnya, tetapi sesuatu yang lebih dekat akan lebih berpengaruh daripada sesuatu yang jauh. Berdasarkan hal tersebut, informasi spasial dapat digunakan dalam model pendugaan area kecil. Dengan memasukkan efek korelasi spasial ke dalam efek acak area, maka akan diperoleh pendugaan area kecil yang mempertimbangkan efek korelasi spasial antar area.
penggunaan informasi tambahan spasial dapat memperkecil ragam dan bias dari penduga EBLUP.
Walaupun para peneliti sebelumnya telah menjelaskan tentang pendekatan spasial dalam pendugaan area kecil, namun terdapat masalah, yaitu masalah dalam penentuan matriks pembobot spasial yang akan akan digunakan dalam pendugaan area kecil. Sebagaimana dijelaskan oleh Getis dan Aldstads (2004) bahwa dalam model spasial, matriks pembobot spasial merupakan komponen penting dalam kebanyakan model ketika representasi struktur spasial dibutuhkan. Oleh karena itu perlu dilakukan pengkajian khusus mengenai pembentukan matriks pembobot yang optimum dalam pendugaan area kecil.
Hasil dari kajian simulasi menunjukkan bahwa banyaknya area kecil mempengaruhi pemilihan metode pembentukan matriks pembobot spasial yang optimum dalam pendugaan area kecil. Penduga SEBLUP dengan rekomendasi matriks pembobot spasial untuk jumlah area yang berbeda memberikan nilai ARRMSE yang lebih kecil dibandingkan dengan nilai ARRMSE pada penduga EBLUP. Hasil simulasi ini sejalan dengan hasil studi kasus rata-rata pengeluaran per rumah tangga per bulan pada level kecamatan di Kota dan Kabupaten Bogor berdasarkan data SUSENAS tahun 2010 dengan menggunakan rekomendasi pembentukan matriks pembobot spasial yang diperoleh pada kajian simulasi. Sehingga dapat disimpulkan bahwa banyaknya area sangat mempengaruhi pemilihan matriks pembobot spasial yang bisa memberikan pendugaan area kecil yang terbaik dengan pendekatan SEBLUP.
SUMMARY
ASFAR. Study of Determining Optimum Spatial Weighting Matrix in Small Area Estimation. Supervised by ANANG KURNIA and KUSMAN SADIK.
Small area statistic in Indonesia has given attention by statisticians in line with the constitutional system shifting from a centralized system to a decentralized system. In the decentralized system, local governments have greater authority to regulate themselves, especially at the level of district/city governments. Thus the need for statistics to the level of villages/wards a basic requirement as a basis for local government district /city to construct a system of planning, monitoring and assessment of regional development or other important policy.
In general surveys are used only designed to estimate population parameters in nationwide scale. So that problems may arise when you want to obtain information for a smaller area, for example at the provincial level, district level or sub district level. The sample size at the level of the area is usually very small so the statistics obtained will have a large variances. To overcome this problems, we need a statistical procedure to combine data from a small sample and large, by taking advantage in detail in the survey sample and census. The proper method to give a solution in this case is a small area estimation methods (SAE). This method helps to improve the information and the sample size to be more effective. One method of estimating a small area is Empirical Best Linear Unbiased Prediction (EBLUP).
Fay and Herriot (1979) was the first researcher to develop a small area estimation based on linear mixed models. The model then becomes a reference in the development of small area estimation further research. Model Fay-Herriot is the basis for small area estimation assumes that the influence of random error-free each area. But in some cases, this assumption is often violated. The reason is the diversity in an area influenced by the surrounding area, so that the spatial effect can be put into a random effect. Spatial effects are normal, occurs between one area to another area, this means that one area affects other areas. In addition, the foundation of spatial analysis are all interconnected with each other, but something closer to be more influential than something much. Based on this, the spatial information can be used in small area estimation models. By entering into the spatial correlation effects random effects area, you will get a small area estimation poise effects of spatial correlation between areas.
EBLUP estimator probe by observing the random influences that correlate spatial area known as the probe Spatial Empirical Best Linear Unbiased Prediction (SEBLUP). Models with random effects of spatial correlation in SAE problem was first introduced by Cressie (Cressie 1991 referred to under Rao 2003b). Researchers had previously mentioned that the EBLUP spatial approach can produce good confidence intervals that depend on the influence of the spatial correlation and the probe of variances. In addition, the use of additional spatial information can reduce both the variance and the bias of the EBLUP estimator.
component in most models when the representation of the spatial structure is needed. Therefore it is necessary to do a special assessment regarding the optimum weighting matrix formation in a small area estimation.
The results of the simulation study shows that a lot of small areas influence the selection method of forming the optimum spatial weighting matrix in the small area estimation. SEBLUP estimator with spatial weighting matrix has recommended for the number of different areas providing value of ARRMSE much smaller than the ARRMSE value of EBLUP estimator. The simulation result is in line with the results of the case study that the average spending per household per month for sub-district in the city and district Bogor uses data of SUSENAS year 2010 by using recommendation weighting matrix formation obtained in the simulation study. It can be concluded that, the number of areas affecting the selection of spatial weighting matrix that can provide the best estimate in small area estimation with SEBLUP approach.
© Hak Cipta Milik IPB, Tahun 2016
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Statistika Terapan
STUDI PENENTUAN MATRIKS PEMBOBOT SPASIAL
OPTIMUM DALAM PENDUGAAN AREA KECIL
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah Subhanahu wa Ta’ala atas segala karunia-Nya sehingga karya ilmiah yang berjudul Studi Penentuan Matriks Pembobot Spasial Optimum dalam Pendugaan Area Kecil berhasil diselesaikan. Keberhasilan penulisan karya ilmiah ini tidak lepas dari bantuan, bimbingan, dan petunjuk dari berbagai pihak.
Dalam penyusunan Tesis ini, penulis telah banyak dibantu oleh berbagai pihak. Oleh karena itu, dalam kesempatan ini penulis ingin menyampaikan ucapan terima kasih kepada:
1. Dr. Anang Kurnia, S. Si, M. Si dan Dr. Ir. Kusman Sadik M. Si selaku dosen pembimbing atas waktu dan bimbingan, arahan serta saran kepada penulis. 2. Dr. Ir. Indahwati, M. Si selaku dosen penguji luar.
3. Seluruh staf Depertemen Statistika atas bantuan dan kerjasamanya.
4. Muhammd Nusrang, S. Si, M.Si atas bimbingan, arahan serta saran kepada penulis.
5. Ibu, Bapak, kakak dan seluruh keluarga atas cinta, kasih sayang, doa dan dukungannya.
6. Teman-tman S2 dan S3 Program studi statistika dan statistika terapan angkatan
2011 dan 2012 atas do’a, kebersamaan dan dukungan yang berlimpah.
7. DIKTI Kementerian Riset, Teknologi dan Pendidikan Tinggi atas beasiswa BPDN-Calon Dosen.
8. Semua pihak yang telah membantu dalam penyelasian tesis. Semoga karya ilmiah ini bermanfaat.
Bogor, Agustus 2016
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
1 PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
2 TINJAUAN PUSTAKA 3 Model Area Kecil 3
Model Level Area 3
Model Level Unit 3
Pendugaan Area Kecil 4
Prediksi Tak Bias Linier Terbaik Empiris (EBLUP) 5
Prediksi Tak Bias Linier Terbaik Empiris Spasial (SEBLUP) 6
Review Matriks Pembobot Spasial 8
Matriks Pembobot Berdasarkan Kedekatan Geografis 8
Matriks Pembobot Berdasarkan Prilaku Data 11
Matriks Pembobot Berdasarkan Pendugaan 12
3 METODE PENELITIAN 14 Data 14
Metode Analisis 14
4 HASIL DAN PEMBAHASAN 18 Kajian Simulasi 18
Matriks Pembobot Spasial 18
Hasil Simulasi Matriks Pembobot Spasial 22
Studi Kasus 26
Pendugaan Pengeluaran Rata-rata Rumah Tangga 27
Pendugaan MSE dan RMSE 28
5 SIMPULAN DAN SARAN 29 Simpulan 29
Saran 29
DAFTAR PUSTAKA 30
LAMPIRAN 32
DAFTAR TABEL
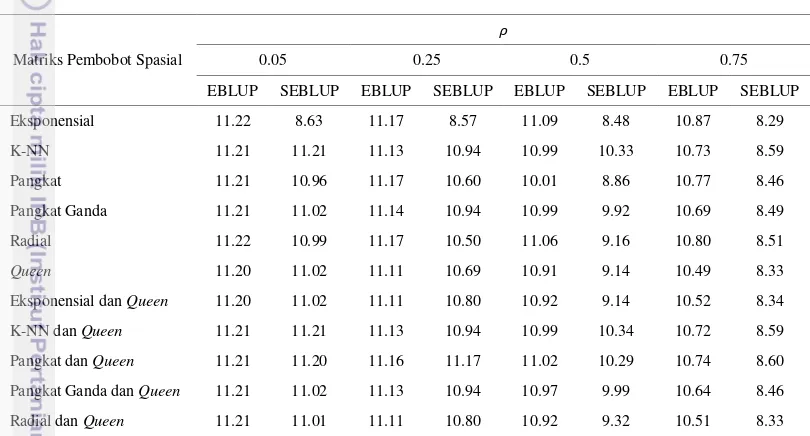
1 Nila ARRMSE untuk m = 16 22
2 Nila ARRMSE untuk m = 64 24
3 Nila ARRMSE untuk m = 144 25
4 Hasil uji autokorelasi spasial dengan Indeks Moran 26
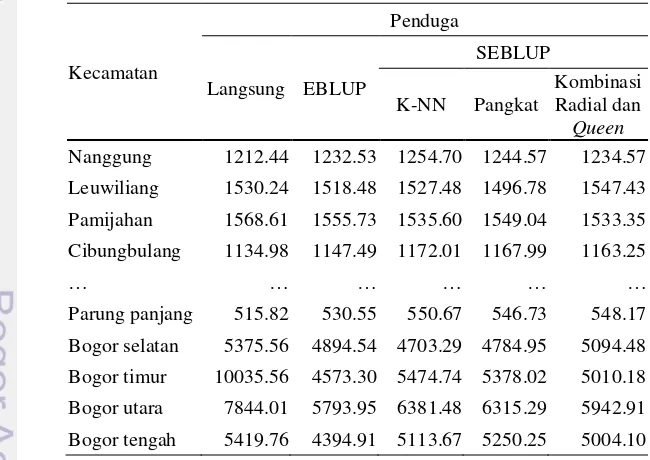
5 Penduga pengeluaran per rumah tangga pada level Kecamatan di Kabupaten dan Kota Bogor berdasarkan data SUSENAS tahun 2010 (Ribu Rupiah) 27
6 Penduga ARMSE (AverageRootMeanSquareError) 28
DAFTAR GAMBAR
1 Ilustrasimatriks kontiguitas tipe rook (b), bishop (c) dan queen (d) dari unit-unit spasial (a) yang bertetangga terhadap F 102 Peta untuk 16 area 18
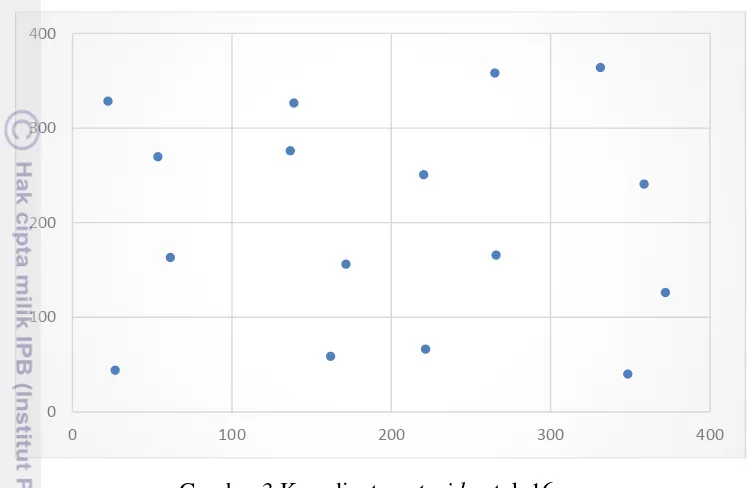
3 Koordinat centroid untuk 16 area 19
4 Peta untuk 64 area 19
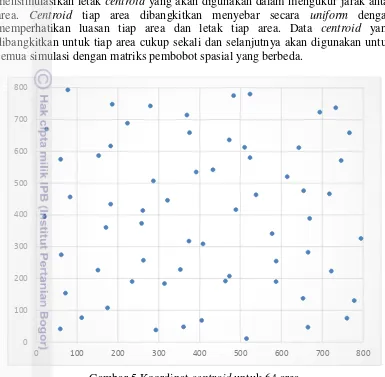
5 Koordinat centroid untuk 64 area 20
6 Peta untuk 144 area 21
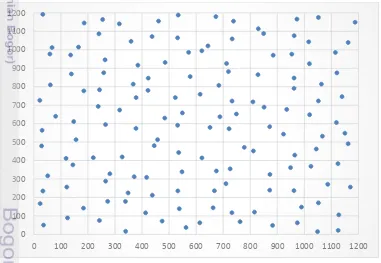
7 Koordinat centroid untuk 144 area 21
DAFTAR LAMPIRAN
1 Keterangan komponen-komponen pada penduga MSE SEBLUP 322 Peubah penyerta dalam pendugaan area kecil pada level kecematan di Kabupaten dan Kota Bogor berdasarkan data PODES tahun 2011 33
3 Peta letak kecamatan di Kabupaten dan Kota Bogor 34
4 Koordinat centroid kecamatan di Kabupaten dan Kota Bogor 35
1
1
PENDAHULUAN
Latar Belakang
Statistik area kecil saat ini telah menjadi perhatian para statistisi dunia secara sangat serius. Telah banyak penelitian yang dikembangkan baik untuk perbaikan teknik dan pengembangan metode maupun aplikasi dalam berbagai kasus dan persoalan nyata yang dihadapi. Terlebih lagi di Indonesia dengan era otonomi daerahnya, dimana sistem ketatanegaraan bergeser dari sistem sentralisasi ke sistem desentralisasi. Pada sistem desentralisasi, pemerintah daerah memiliki kewenangan yang lebih besar untuk mengatur dirinya sendiri, khususnya pada level pemerintah kabupaten/kota. Dengan demikian kebutuhan statistik sampai pada level desa/kelurahan menjadi suatu kebutuhan dasar sebagai landasan bagi pemerintah daerah kabupaten/kota untuk menyusun sistem perencanaan, pemantauan dan penilaian pembangunan daerah atau kebijakan penting lainnya (Kurnia 2009).
Permasalahan muncul ketika akan menduga sampai pada level desa/kelurahan yaitu kondisi ukuran contoh yang kecil karena survey yang menjadi sumber informasi umumnya dirancang untuk menduga parameter populasi berskala nasional. Pendugaan yang umum digunakan didasarkan pada model desain penarikan contoh dalam survey. Sehingga dengan kondisi ukuran contoh yang kecil, metode pendugaan ini idak dapat memberikan hasil dugaan yang akurat dan presisi. Oleh karenanya diperlukan suatu prosedur statistika yang dapat mengkombinasikan data dari contoh kecil dan informasi tambahan. Metode yang tepat untuk memberi solusi dalam hal ini adalah pendugaan area kecil (SmallArea Estimation, SAE) (Elbers et al. 2003, Rao 2003b).
Chand dan Alexander (1995) menyebutkan bahwa prosedur pendugaan area kecil pada dasarnya memanfaatkan kekuatan informasi area sekitarnya dan sumber data dari luar area yang statistiknya ingin diperoleh melalui pembentukan model yang tepat untuk meningkatkan efektifitas ukuran contoh. Secara umum pendugaan area kecil dapat dikatakan sebagai suatu metode untuk menduga parameter pada suatu area yang relatif kecil dalam percontohan survei dengan memanfaatkan informasi dari luar area, dari dalam area itu sendiri dan dari luar survei.
Petrucci dan Salvati (2004b) menyebutkan bahwa model area kecil mengasumsikan bahwa pengaruh acak galat area saling bebas. Namun dalam beberapa kasus, asumsi ini sering dilanggar. Penyebabnya adalah keragaman suatu area dipengaruhi area sekitarnya, sehingga pengaruh spasial dapat dimasukkan ke dalam pengaruh acak. Pengaruh spasial merupakan hal yang lazim terjadi antara satu area dengan area yang lain, ini berarti bahwa area yang satu mempengaruhi area lainnya.
2
Pendekatan spasial EBLUP bisa menghasilkan selang kepercayaan yang baik yang bergantung pada pengaruh korelasi spasial dan nilai dari ragam pendugaannya. Pratesi dan Salvati (2008) menunjukkan bahwa penggunaan informasi tambahan spasial dapat mengurangi bias dan galat penarikan contoh dalam pendugaan area kecil.
Walaupun para peneliti sebelumnya telah menjelaskan tentang pendekatan spasial dalam pendugaan area kecil, namun terdapat masalah, yaitu masalah dalam penentuan matriks pembobot spasial yang akan digunakan dalam pendugaan area kecil. Semua peneliti sebelumnya hanya menggunakan matriks pembobot spasial yang sederhana dan mudah dibentuk, yaitu matriks pembobot yang didasarkan pada ketetanggaan terdekat. Padahal dalam analisis yang menggunakan pengaruh spasial penentuan matriks pembobot merupakan hal penting dan dasar dalam memperoleh pendugaan yang akurat. Sebagaimana dijelaskan oleh Getis dan Aldstads (2004) bahwa dalam model spasial, matriks pembobot spasial merupakan komponen penting dalam kebanyakan model ketika representasi struktur spasial dibutuhkan. Karena hasil analisis sensitif terhadap spesifikasi matriks bobot spasial, matriks bobot spasial yang berbeda mungkin diperlukan untuk berbagai jenis studi.
Oleh karena itu perlu dilakukan pengkajian khusus mengenai pembentukan matriks pembobot yang optimum dalam pendugaan area kecil. Stakhovych dan Bijmolt (2008) menyebutkan bahwa pembentukan matriks pembobot spasial sendiri digolongkan ke dalam tiga kelompok besar, yaitu (1) memperlakukan matriks pembobot sebagai completely exogenous construct, (2) membiarkan data menentukan matriks pembobot sendiri, (3) menduga matriks pembobot.
Metode yang peneliti gunakan dalam menentukan matriks pembobot spasial yang optimum adalah metode kajian kepustakaan dan metode simulasi. Simulasi dilakukan pada beberapa kondisi untuk menentukan matriks pembobot yang optimum. Matriks pembobot optimum yang diperoleh dalam simulasi selanjutnya yang digunakan dalam pendugaan pengeluaran per rumah tangga per bulan pada level kecamatan di Kabupaten dan Kota Bogor pada tahun 2010.
Tujuan Penelitian
Merujuk pada permasalahan di atas, tujuan penelitian ini adalah:
1. Mengkaji kelebihan dan kekurangan masing-masing metode pembentukan matriks pembobot spasial.
3
2
TINJAUAN PUSTAKA
Model Area Kecil
Area kecil menggambarkan suatu subpopulasi kecil untuk demografi maupun kelompok orang yang memiliki sosial ekonomi (ras, jenis kelamin, umur) tertentu yang berada dalam area geografis yang lebih luas. Area kecil sering digunakan sebagai gambaran sebuah area geografis kecil, seperti kabupaten, kecamatan, maupun kelurahan/desa dari suatu negara (Rao 2003b).
Tipe model pendugaan area kecil terbagi menjadi dua, yaitu model level area (basicarea level models) dan model level unit (unit level area models) (Rao 1999, 2003a, 2003b, 2014). Model level area digunakan jika data penyerta yang bersesuaian dengan data peubah yang diamati tidak tersedia hingga level unit contoh, sedangkan model level unit digunakan jika data penyerta yang bersesuaian dengan data peubah yang diamati tersedia hingga level unit contoh.
Model Level Area
Model level area merupakan model yang didasarkan pada ketersediaan data pendukung yang hanya ada untuk level area tertentu, misalkan = ,
, … , � dengan parameter yang akan diduga adalah � yang diasumsikan mempunyai hubungan dengan dengan mengikuti model sebagai berikut:
� = � + , = , … , dengan adalah konstanta bernilai positif yang diketahui, � adalah vektor dari parameter yang bersifat tetap berukuran p x 1, m adalah jumlah area kecil dan adalah pengaruh acak yang diasumsikan menyebar normal dan berdistribusi identik dan saling bebas (iid), yakni:
� = , � = � Untuk melakukan inferensi tentang populasi berdasarkan model (1), diasumsikan bahwa penduga langsung telah ada pada model dan dituliskan sebagai:
= � + , = , … , galat penarikan contoh berdistibusi saling bebas dengan:
� | = , � | = � Jika menggabungkan Persamaan (1) dan (3) maka diperoleh model:
= �� + + , = , … , dengan asumsi bahwa ~ N , � saling bebas dengan ~ N , � . Persamaan (5) merupakan bentuk khusus dari model linier campuran.
Model Level Unit
Model level unit merupakan suatu model dengan data pendukung yang tersedia bersesuaian secara individu dengan data respon, misalnya =
, , … , � . Selanjutnya peubah perhatian dianggap berkaitan dengan
mengikuti model regresi tersarang satu tahap sebagai berikut:
4
Penduga Area Kecil
Pelaksanaan survei dilakukan untuk melakukan pendugaan parameter populasi. Pendekatan klasik untuk menduga parameter populasi didasarkan pada aplikasi model disain penarikan contoh (design-based), dan penduga yang dihasilkan dari pendekatan itu disebut penduga langsung (directestimation). Data hasil survei ini dapat digunakan untuk mendapatkan penduga yang terpercaya dari total maupun rata-rata populasi suatu area atau domain dengan jumlah contoh yang besar. Namun, ketika penduga langsung tersebut digunakan untuk suatu area yang kecil, maka akan menimbulkan galat baku yang besar (Ghosh dan Rao 1994). Selain itu, pendugaan langsung tidak dapat dilakukan pada area yang tidak terpilih sebagai contoh, karena tidak adanya data yang dapat digunakan untuk melakukan pendugaan. Suatu area dikatakan kecil jika ukuran contoh dalam domain tersebut tidak cukup memadai untuk mendukung ketelitian penduga langsung (Rao 2003b). Area kecil biasanya digunakan untuk mendefinisikan area geografi yang kecil atau domain yang memiliki ukuran contoh sangat kecil.
Penanganan masalah galat baku dalam pendugaan area kecil dilakukan dengan menambahkan informasi mengenai parameter yang sama pada area kecil lain yang memiliki karakteristik serupa, atau nilai pada waktu yang lalu, atau nilai dari peubah yang memiliki hubungan dengan peubah yang sedang diamati. Pendugaan parameter dan inferensinya yang menggunakan informasi tambahan tersebut dinamakan pendugaan tidak langsung (indirect estimation). Metode ini secara statistik memiliki sifat meminjam kekuatan (borrowing strength) dari informasi mengenai hubungan antara peubah yang diamati dengan informasi yang ditambahkan sehingga mengefektifkan jumlah contoh yang kecil. Pendugaan tidak langsung berdasarkan pada model implisit atau model eksplisit yang menyediakan suatu link yang menghubungkan area-area kecil melalui data tambahan. Dalam papernya, Petrucci dan Salvati (2004b) menuliskan bahwa penduga tak langsung ini terdiri dari dua tipe, yaitu penduga tak langsung yang berdasarkan pada model implisit, antara lain penduga sintetik (synthetic estimator) dan penduga komposit (composite estimator) serta penduga tak langsung yang berdasarkan pada model eksplisit (berbasis model) yang menggabungkan pengaruh acak antar area.
5
Prediksi Tak Bias Linier Terbaik Empiris (EBLUP)
Kurnia (2009) menyebutkan bahwa model pengaruh campuran Fay-Herriot yang dijabarkan oleh Russo et al. (2005) untuk level area adalah sebagai berikut: 1. = (x , x , … , x�), merupakan vektor data pendukung (peubah penyerta).
2. � = � + , untuk = , , … , . � merupakan parameter yang menjadi
perhatian dan diasumsikan memiliki hubungan dengan peubah penyerta pada (1).
3. � = , � = �
4. = � + , penduga langsung untuk domain ke-i yang merupakan fungsi linier dari parameter yang menjadi perhatian dan galat contoh .
5. = � + + , untuk i = 1, 2, …, m merupakan gabungan dari (2) dan
(4) yang terdiri dari pengaruh acak dan pengaruh tetap sehingga menjadi bentuk khusus dari model linier campuran dengan struktur peragam yang diagonal.
Jika terdapat model � = � + , dengan � merupakan parameter yang menjadi perhatian dan merupakan nilai penduga langsung berdasarkan rancangan survey, maka:
= � + = � + + untuk i= 1, …, m dengan = ( , , … , �) merupakan peubah penyerta pada tingkat area, � merupakan parameter yang fixed, merupakan pengaruh acak area kecil dengan ~ N , � , merupakan galat penarikan contoh dengan
~ N , � , dan saling bebas. Dengan mengasumsikan bahwa � dan �
(ragam antar area kecil) tidak diketahui, tetapi � untuk i = 1, 2, …, m diketahui. Teknik penyelesaian model pada Persamaan (13) untuk memperoleh BLUP bagi � = �� + telah dikembangkan oleh Henderson (Henderson 1948-1975 diacu dalam Kurnia 2009), dengan asumsi � diketahui. Penduga BLUP dari � berdasarkan Persamaan (13) adalah:
�̂ � � = �̂ + � ( − �̂)
�̂ � � = � + − � �̂ dengan � = � ⁄ � + � . Metode BLUP yang dikembangkan oleh Henderson
(Henderson 1948-1975 diacu dalam Kurnia 2009) mengasumsikan diketahuinya komponen ragam pengaruh acak dalam model campuran linier, padahal pada kenyataannya komponen ragam ini tidak diketahui. Sebagai akibatnya, ragam pengaruh acaknya harus diduga. Harville (Harville 1997 diacu dalam Kurnia 2009) melakukan review terhadap beberapa metode pendugaan komponen ragam, dengan menggunakan metode kemungkinan maksimum (maximum likelihood, ML) dan metode kemungkinan maksimum terkendala (restricted maximum likelihood,
REML). Pendugaan � baik dengan metode MLmaupun REMLdilakukan dengan alogaritma Fisher scoring. Dengan mengganti � dengan �̂ maka diperoleh suatu penduga baru EBLUP, sebagai berikut:
�̂ �� � = �̂ + − �̂ �̂ Penduga EBLUP yang diperoleh dengan metode ML maupun REML adalah penduga tak bias jika galat dan i berdistribusi normal dengan rataan 0.
Mean square error (MSE) dari �̂ �� � (Rao 2003b) adalah:
6
Prediksi Tak Bias Linier Terbaik Empiris Spasial (SEBLUP)
Molina et al. (2007) mendefinisikan vektor = , … , , =
, … , dan = , … , , dan matriks = , … , x dan =
� , … , . Berdasarkan definisi vektor dan matriks tersebut, maka
persamaan dalam notasi matriks adalah:
= � + + Model pada Persamaan (13) mengasumsikan bahwa terdapat pengaruh acak area, namun pengaruh tersebut saling bebas antar area. Pada kenyataannya, sangat beralasan untuk mengatakan bahwa ada korelasi antar area yang berdekatan. Korelasi tersebut akan semakin berkurang seiring dengan jarak yang bertambah. Hal ini sesuai dengan hukum pertama tentang geografi yang dikemukakan oleh Tobler (Tobler’sfirstlawofgeography) yang merupakan pilar kajian analisis data
spasial, yaitu “everything is related to everything else, but near things are more related than distant things”. Hal ini mengimplikasikan bahwa diharapkan hubungan antar objek di dalam lebih kuat dibandingkan dengan hubungan di luar dan hubungan antar peubah-peubah yang berada dalam lokasi yang dekat secara spasial lebih kuat dibandingkan dengan hubungan antar peubah di luar lokasi lainnya yang jauh.
Model dengan pengaruh spasial yang digunakan dalam model SAE ada dua model, yaitu Simultaneously Autoregressive (Simultan otoregresif, SAR) dan
Conditional Autoregressive (Otoregresif bersyarat, CAR). Model SAE dengan memasukkan korelasi spasial antar area yang diperkenalkan oleh Cressie (Cressie 1991 diacu dalam Rao 2003b), dengan mengasumsikan ketergantungan spasial mengikuti proses CAR. Model SAE ini kemudian dikembangkan lagi oleh beberapa peneliti, diantaranya Salvati (2004), Singh et al. (2005) dan Pratesi dan Salvati (2008) dengan mengasumsikan bahwa ketergantungan spasial yang dimasukkan ke dalam komponen galat dari faktor acak mengikuti proses SAR. Model SAR sendiri pertama kali diperkenalkan oleh Anselin (Anselin 1992 diacu dalam Chandra et al.
2007) dimana vektor pengaruh acak area memenuhi:
7
pengaruh acak area dan adalah vektor galat dari pengaruh acak area dengan rata-rata 0 dan ragam � � . Persamaan (14) dapat ditulis kembali sebagai berikut:
= � − � − dengan I adalah matriks identitas berukuran m x m. Dari Persamaan (15) terlihat bahwa rata-rata adalah 0 dan matriks peragam � yang merupakan matriks disperse model SAR, adalah sebagai berikut:
� = � [ � − � � − � ]− Persamaan (15) dimasukkan ke dalam Persamaan (13) menghasilkan:
= � + � − � − + Salvati 2008). Penduga Spatial BLUP tersebut diperoleh dengan memasukkan matriks peragam ke dalam penduga BLUP. Spatial BLUP akan sama dengan BLUP jika � = .
Seperti halnya dengan penduga EBLUP, penduga SEBLUP �̂ � � � , � diperoleh dari Spatial BLUP dengan mengganti nilai � , � dengan penduganya. Asumsi kenormalan dari pengaruh acak digunakan untuk menduga � dan � dengan menggunakan prosedur baik ML maupun REML dengan fungsi log-likelihood. Metode ML dalam menduga �̂ ��� �̂ , dapat diperoleh secara iteratif dengan menggunakan algoritma Nelder-Mead dan algoritma scoring (Pratesi dan Salvati 2008). Hasil pendugaan tersebut kemudian digunakan untuk melakukan pendugaan terhadap SEBLUP, dengan rumus penduga SEBLUP model SAR adalah:
�̂ �� � �̂ , �̂ = �̂ + {�̂ [ � − �̂ � − �̂ ]− }
× { � � + �̂ [ � − �̂ � − �̂ ]− }− ( − �̂)
MSE[�̂ �� � �̂ , �̂ ] untuk model Spatial EBLUP dengan pengaruh acak berdistribusi normal (Petrucci dan Salvati 2004a, 2004b) adalah:
MSE[�̂ �� � �̂ , �̂ ]
= MSE[�̂ � � � , � ] + � {[�̂ �� � �̂ , �̂ − �̂ � � � , � ] } = � i � , � + � i � , � + � i � , � Prasad & Rao (1990) menyebutkan bahwa penduga dari MSE[�̂ �� � �̂ , �̂ ] diperoleh dengan menggunakan linearisasi Taylor. Dalam aplikasi pendugaan MSE[�̂ �� � �̂ , �̂ ] mengikuti hasil dari yang dikemukakan oleh Harville dan Jeske (Harville dan Jeske 1992 diacu dalam Pratesi dan Salvati 2008) dan kemudian dikembangkan menjadi model generalized covariances oleh Zimmerman dan Cressie (1992). Petrucci dan Salvati (2004a, 2004b), Molina et al. (2007) dan Pratesi dan Salvati (2008) menyebutkan bahwa penduga tak bias bagi MSE[�̂ �� � �̂ , �̂ ] dengan mengikuti hasil pendugaan yang dikemukakan oleh Zimmerman dan Cressie (1992) adalah:
�s�[�̂ �� � �̂ , �̂ ] = �
8
Kackar dan Harville (1984) yang diacu dalam Petrucci dan Salvati (2004b) menjelaskan beberapa sifat dari penduga SEBLUP, yaitu:
1. Penduga SEBLUP merupakan penduga yang tak bias untuk �. 2. �[�̂ �� � �̂ , �̂ ] berhingga.
3. �̂ dan �̂ merupakan penduga yang invarian dari � dan �.
Review Matriks Pembobot Spasial
Matriks pembobot spasial merupakan komponen penting dalam pemodelan data-data spasial dimana pada data tersebut terdapat ketakbebasan spasial (spatial dependence). Matriks pembobot spasial W, merupakan matriks N x N tak negatif yang menspesifikasi himpunan ketetanggaan untuk setiap unit amatan spasial. Stakhovych dan Bijmolt (2008) dan Jajang (2014) membagi matriks W terbagi ke dalam tiga, yaitu: (1) memperlakukan matriks pembobot sebagai completely exogenous construct, (2) membiarkan data menentukan matriks pembobot sendiri, (3) menduga matriks pembobot.
Matriks Pembobot Berdasarkan Kedekatan Geografis
Terdapat beberapa tipe matriks pembobot spasial menurut kedekatan geografis, yaitu berdasarkan jarak, berdasarkan batas bersama atau perbatasan (boundaries) dan berdasarkan kombinasi jarak dan perbatasan (Smith 2014). Berikut beberapa ilustrasi dari tipe-tipe matriks pembobot spasial yang berdasarkan kedekatan geografis.
1. Matriks Pembobot Jarak
Matriks pembobot spasial yang didasarkan pada konsep jarak mengambil jarak sebagai jarak pusat (centroid distance) antara dua pasang unit-unit spasial
i dan j. Smith (2014) menyebutkan bahwa matriks pembobot spasial yang didasarkan konsep jarak dapat diklasifikasikan menjadi lima kategori, yaitu: a. Matriks k tetangga terdekat (k-nearest neighbor)
Setiap baris i dalam matriks pembobot spasial menurut k tetangga terdekat memiliki k buah kolom j dengan elemen 1 dan kolom selainnya bernilai 0. Mengacu pada konsep k-tetangga terdekat (k-rearest neighbor, k-NN), terdapat dua tipe matriks pembobot spasial yang dapat diperoleh yaitu matriks pembobot spasial yang tidak simetris dan matriks pembobot yang mempunyai sifat simetris. Perbedaan kedua matriks ini bergantung pada definisi elemen-elemen matriks pembobot spasial yang diambil.
Jika matriks pembobot spasial bersifat tidak simetris, maka didefinisikan sebagai:
9
sedangkan jika matriks pembobot spasial bersifat simetris maka didefinisikan sebagai:
= { ,, � � b. Matriks jarak radial
Setiap bobot atau elemen matriks pembobot spasial yang didasarkan jarak radial tergantung pada nilai batas (threshold) yang diambil. Untuk baris tertentu, semakin besar nilai threshold maka semakin banyak kolom pada baris tersebut bernilai 1 dan semakin kecil nilai threshold maka semakin sedikit kolom pada baris tersebut yang bernilai 1. Apabila dimisalkan terdapat n unit spasial dan jarak dari unit spasial i terhadap semua unit spasial j (i ≠ j) adalah serta ditentukan nilai d sebagai threshold maka matriks pembobot spasial menurut jarak radial ditentukan sebagai berikut:
= { ,, ≤ ≤ c. Matriks jarak pangkat
Matriks pembobot yang didasarkan pada jarak radial tampak bahwa unit-unit yang berada pada jarak yang tidak lebih dari nilai threshold diberi bobot 1 meskipun mempunyai nilai jarak yang berbeda. Hal yang hampis sama terjadi pula pada matriks pembobot yang didasarkan pada k-NN dimana setiap k
tetangga dari unit tertentu, katakan unit spasial i, diberi bobot 1. Semakin dekat unit j dengan unit i maka semakin mirip. Oleh karena itu, selain pemberian bobot yang hanya bernilai biner (1 dan 0) perlu dipertimbangkan nilai atau bobot jarak sebenarnya, antara lain yang disandarkan pada jarak pangkat. Berdasarkan konsep jarak pangkat setiap bobot matrik semakin kecil ketika semakin jauh dari unit spasial i. setiap elemen matriks menurut jarak pangkat didefinisiskan sebagai:
= −� dengan nilai adalah bilangan positif.
d. Matriks jarak eksponensial
Matriks pembobot spasial yang didasarkan pada jarak eksponensial pada dasarnya hamper sama dengan bobot jarak pangkat. Apabila dimisalkan adalah jarak antara unit spasial i dan uni spasial j, maka matriks pembobot spasial menurut jarak eksponensial adalah:
= �xp (− ( ) )
dengan adalah jarak dari lokasi-i ke lokasi-j dan d adalah lebar jendela, yaitu suatu nilai parameter penghalus fungsi yang nilainya selalu positif. Fungsi ini biasa disebut fungsi kernel normal (Gaussian).
e. Matriks jarak pangkat ganda
Matriks jarak pangkat ganda mempunyai prinsip yang sedikit berbeda dengan matriks jarak pangkat ataupun jarak eksponensial dimana setiap bobot atau elemen matriks, selain menggunakan fungsi pangkat juga didasarkan pada
threshold. Apabila menyatakan jarak antara unit spasial i dan unit spasial j
10
= {[ − ] , ≤ >≤
dengan nilai adalah bilangan positif. 2. Matriks Pembobot Berdasarkan Batas
Matriks pembobot yang didasarkan pada konsep jarak adalah mudah dihitung, namun dalam beberapa kasus kontibusi perbatasan (boundaries share) antar unit spasial memainkan peranan penting untuk menentukan pengaruh spasial. Dua tipe matrik pembobot yang dapat digunakan dengan memanfaatkan perbatasan, yaitu pembobot spatial contiguity (kedekatanspasial) dan bobot shared-boundaries. a. Bobot kontiguitas spasial
Elemen-elemen dari matriks pembobot spasial kontiguitas didasarkan pada hubungan ketetanggaan secara geografis. Misalkan � = { } , = , , . . , , adalah matriks kontiguitas dengan merepresentasikan elemen (nilai bobot) unit spasial i dan j. berdasarkan aturan dalam matriks kontiguitas, bernilai satu ketika antara dua unit spasial saling bertetangga atau bersebelahan dan bernilai nol ketika antara dua unit spasial tidak bertetangga atau bersebelahan serta didefinisikan pula = . Bobot spasial kontiguitas didasarkan pula pada batas bersama, artinya bahwa apabila terdapat persekutuan antara batas unit spasial i (bnd(i)) dan batas unit spasial j (bnd(j)) maka diberi bobot 1,
= { , ∩∩ ≠= Beberapa tipe matriks kontiguitas adalah rook, bishop dan queen. Sebagai ilistrasi, dimisalkan terdapat unit-unit spasial A, B, …, J (Gambar 2) dan akan ditentukan unit-unit yang bertetangga dengan F.
Unit spasial Rook Bishop Queen
A B C B A C A B C
D F G D F G F D F G
H I J I H J H I J
(a) (b) (c) (d)
Gambar 1Ilustrasimatriks kontiguitas tipe rook (b), bishop (c) dan queen (d) dari unit-unit spasial (a) yang bertetangga terhadap F
b. Bobot shared-boundaries
Bobot atau elemen matriks pembobot spasial yang didasarkan pada shared-boundaries menggunakan informasi panjang batas ( ) dari dua unit yang bersebelahan. Apabila menyatakan panjang total dari perbatasan unit i yang berbatasan dengan unit-unit spasial lain, yakni = ∑ ≠ dan adalah
11
digunakan adalah jarak pangkat −� dan panjang perbatasan , maka matriks pembobot spasial hasil kombinasi jarak dan perbatasan didefinisikan sebagai berikut:
= ∑ −�−�
≠ Selain menggunakan formula di atas, peneliti juga menggunakan konsep logika matematika dalam menentukan kombinasi jarak dan boundaries.
Matriks Pembobot Berdasarkan Prilaku Data
Berikut beberapa ilustrasi dari tipe-tipe matriks pembobot spasial yang berdasarkan prilaku data.
1. AMOEBA
Cara yang kedua dalam menentukan matriks pembobot menurut Stakhovych dan Bijimolt (2008) adalah didasarkan pada prilaku data. A Multidirectional Optimum Ecotpe-Based Algoritma (AMOEBA) merupakan salah satu ilustrasi dari matriks pembobot spasial yang didasarkan pada perilaku data. AMOEBA adalah suatu prosedur yang dirancang untuk menggerombolkan (clustering) unit-unit spasial dan mengkonstruksi matriks pembobot spasial yang menggunakan data empiris (Aldstadt dan Getis 2006). Dasar-dasar dalam prosedur AMOEBA adalah tipe statistik lokal yang digunakan untuk menguji hubungan antar unit spasial yang berdekatan. Dua statistik autokorelasi lokal yang populer adalah statistik Moran lokal � dan Getis lokal � . Misalkan , = , , … , adalah peubah yang menjadi perhatian = ��− �̅
� dan adalah elemen-elemen matriks pembobot spasial. Statistik Moran lokal � didefinisikan sebagai:
� = ∑ = , ≠ , , = , … , dengan adalah momen kedua dari peubah . Statistic Getis Lokal didefinisikan sebagai (Aldstadt dan Getis 2006).
Berikut adalah tahapan prosedur AMOEBA dalam membentuk matriks pembobot spasial. Misalkan diberikan sebuah area yang terbagi atas n wilayah (unit spasial), i, i=1,2,...,n, � adalah statistik Getis lokal dan �∗ adalah statistik Getis lokal yang dibakukan. Langkah-langkah prosedur AMOEBA adalah sebagai berikut (Aldstadt dan Getis, 2006):
12
b. Hitunglah �∗ , yaitu nilai untuk setiap daerah yang memuat unit i dan semua kombinasi dari tetangga yang berdekatan. Jika �∗ lebih atau kurang dari kombinasi yang memaksimumkan nilai mutlak �∗ maka unit-unit yang baru tersebut menjadi ecotope tinggi atau rendah yang baru. Unit-unit yang tergabung membentuk ecotope baru ini disebut sebagai unit-unit yang
ter-include. Unit spasial yang bersebelahan yang tidak termasuk dalam ecotope
dieliminasi (exclude). Ecotope adalah kumpulan unit-unit spasial berkarakteristik mirip berdasarkan statistik autokorelasi lokal hasil prosedur AMOEBA
c. Evaluasi semua kombinasi tetangga sebelah dan selanjutnya keanggotaan baru
ecotope diidentifikasi.
d. Proses ini berlanjut untuk jumlah penghubung k, k=2, 3, ..., maksimum dimana dalam kondisi ini tidak ada lagi unit-unit spasial yang dapat meningkatkan nilai mutlak �∗.
Apabila ecotope sudah terbentuk dimana tidak ada lagi unit-unit spasial yang dapat memaksimumkan nilai statistik lokal, maka dibuat matriks pembobot AMOEBA melalui prosedur berikut: penghubung antara unit i dan j meningkat. Ketika ecotope hanya mengandung satu penghubung dari unit i � � = , maka unit tersebut diberi pembobot 1. Ketika tidak ada asosiasi antara unit i dengan sembarang unit j � � = , maka baris
i dari matriks Wadalah nol. 2. Correlation
Bentuk lain dari matrik pembobot spasial berdasar prilaku data selain AMOEBA adalah matriks pembobot spasial yang dibentuk dari korelasi amatan antar area. Pada dasarnya konsep korelasi juga memperhatikan informasi ketetanggaan tiap area. Area yang bertetangga akan memberikan korelasi yang tinggi dan begitu pula dengan area yang berjauhan/tidak bertetangga akan memberikan korelasi yang rendah.
Nilai dari matriks pembobot spasial antar area i dan j berasal dari nilai korelasi data amatan antar area i dan j. Nilai korelasi amatan antar area kemungkin bernilai − ≤ ≤ , sedangkan nilai dari matriks pembobot spasial antar area adalah ≤
13
spasial. Secara umum, matriks pembobot spasial korelasi didefinisikan sebagai berikut:
= {| | ≠=
Matriks Pembobot Berdasarkan Pendugaan
Structural equation model atau model persamaan struktural (MPS) merupakan salah satu metode yang digunakan untuk memodelkan hubungan peubah laten eksogen dan peubah laten endogen. Di samping itu MPS juga dapat digunakan untuk mengkonstruksi matriks pembobot spasial. Matriks pembobot spasial merupakan fungsi dari peubah indikator dan loading dari model pengukuran terhadap peubah tak bebas. Folmer dan Oud (2008) mengkonstruksi matriks pembobot spasial dengan pendekatan peubah laten untuk memodelkan hubungan spasial. Matriks pembobot spasial (W) yang dikonstruksi oleh Folmer dan Oud (2008) merupakan fungsi peubah indikator dan loading pada persamaan pengukuran. Dalam menduga matriks W digunakan metode kemungkinan maksimum (Maksimum Likelihood), artinya bahwa sisaan model diasumsikan diketahui (Folmer dan Oud 2008, Liu et al. 2011). Folmer dan Oud (2008) dan Liu
14
3
METODE PENELITIAN
Data
Data yang digunakan dalam penelitian ini adalah data hasil simulasi dan data sekunder untuk aplikasinya. Data simulasi digunakan untuk mencari matriks pembobot spasial yang optimum yang akan digunakan dalam pendugaan pada data sekunder. Adapun data sekunder yang digunakan adalah:
1. Data yang digunakan sebagai penduga langsung, yaitu rata-rata pengeluaran per rumah tangga per bulan pada level kecamatan di Kota dan Kabupaten Bogor pada tahun 2010. Data ini dihitung dari pengeluaran per rumah tangga per bulan untuk setiap kecamatan yang terpilih sebagai contoh pada data SUSENAS tahun 2010. Selain menghitung rata-rata pengeluaran per rumah tangga per bulan pada level kecamatan, data tersebut juga digunakan untuk menghitung ragam contoh dari pengeluaran per rumah tangga per bulan untuk setiap kecamatan. Data ragam contoh digunakan untuk menduga komponen ragam dari peubah acak area.
2. Data yang digunakan sebagai auxiliary variabel (peubah penyerta) dalam masalah pengeluaran dapat ditinjau dari beberapa proksi (pendekatan) yaitu kesehatan dan pendapatan. Dari sisi kesehatan digunakan peubah jumlah keluarga yang menerima kartu JAMKESMAS/JAMKESDA dan jumlah keluarga yang tinggal di pemukiman kumuh. Dari sisi pendapatan digunakan jumlah keluarga yang ada anggota keluarganya menjadi buruh tani, jumlah keluarga yang menerima surat SKTM. Data tersebut berasal dari data Podes 2011.
Metode Analisis
Metode penelitian yang digunakan dalam penelitian ini dibagi menjadi tiga bagian, yaitu:
1. Kajian Kepustakaan
Pada bagian ini dikaji kelebihan dan kekurangan dari masing-masing metode pembentukan matriks pembobot spasial.
2. Kajian Simulasi
Kajian simulasi dilakukan dengan tujuan untuk mengetahui kualitas atau performa dari matriks pembobot spasial yang dibentuk dari masing-masing pendekatan, juga menentukan matriks pembobot spasial optimum yang akan digunakan dalam pendugaan area kecil pada data sekunder.
Desain simulasi yang dilakukan adalah sebagai berikut:
a. Membuat peta buatan berbentuk kotak yang terdiri dari m area kecil yang disusun dalam bentuk persegi n x n area. Ukuran m yang dicobakan adalah 16, 64 dan 144. Setiap area berbentuk persegi dengan ukuran 100 x 100. b. Membangkitkan data koordinat centroid tiap area berdasarkan peta yang
dibuat pada langkah (a) dan menyebar secara uniform dengan nilai maksimum dan minimum mengikuti luasan tiap area.
15
data dan berdasarkan pendugaan tidak memungkinkan untuk dibentuk dalam simulasi karena ukuran contoh untuk tiap area sangat kecil dan tidak seragam. Langkah untuk membentuk matriks pembobot spasial berdasarkan kedekatan geografis didasarkan pada desain peta area dan koordianat
centroid tiap area yang dibuat sebelumnya. Adapun matriks pembobot spasial yang dibentuk berdasarkan kedekatan geografis adalah sebagai berikut:
1) Matriks pembobot jarak
a) Matriks k tetangga terdekat (k-nearest neighbor) b) Matriks jarak radial
3) Matriks pembobot kombinasi jarak dan batas
a) Matriks kombinasi k tetangga terdekat dengan queen
b) Matriks kombinasi jarakradial dengan queen
c) Matriks kombinasi jarak pangkat dengan queen
d) Matriks kombinasi jarak eksponensial dengan queen
e) Matriks kombinasi jarak pangkat ganda dengan queen
d. Menentukan ukuran amatan di tiap area kecil.
e. Simulasi ini menggunakan satu peubah yang menjadi perhatian (y) dan satu peubah penyerta . Model yang digunakan untuk memperoleh nilai peubah yang menjadi perhatian (y) untuk area kecil ke-i dan unit ke-j adalah sebagai berikut:
= � + + , = , , … , , = , , … ,
dimana adalah peubah penyerta, adalah pengaruh acak area, dan adalah galat penarikan contoh.
1) Nilai dibangkitkan menyebar normal dengan ~ , . Nilai yang diperoleh digunakan untuk seluruh skenario pada proses simulasi. 2) Menetapkan � = , sehingga Persamaan (38) menjadi :
area kecil sebagai penduga langsung, dengan rumus: =
�∑ �
16
h. Menghitung nilai ragam dari peubah yang diperhatikan dengan rumus: = dapat dihitung nilai relative root mean squares error (RRMSE) dan average relative root mean squares error (ARRMSE) dari hasil pendugaan parameter pada setiap area dengan rumus sebagai berikut:
RRMSE i = 3. B adalah banyaknya iterasi, dalam penelitian ini B=1000.
4. Mean square error (MSE) adalah nilai harapan dari kuadrat selisih antara penduga dengan parameternya. Secara formulasi, kuadrat tengah galat mengandung dua komponen, yakni ragam penduga dan bias. Ragam penduga untuk mengukur presisi. Presisi yang dimaksudkan dalam hal ini adalah ukuran sejauh mana pengulangan suatu pendugaan akan memberikan hasil yang sama. Semakin kecil nilai dari kuadrat tengah galat maka kombinasi antara ragam penduga dan bias semakin kecil. Ragam penduga dan bias semakin kecil menunjukkan presisi dan akurasi dari suatu penduga semakin baik.
5. RRMSEi adalah relative root mean squares error pada area ke i. 6. ARRMSE adalah average relative root mean squares error.
l. Mengulangi langkah (d) sampai langkah (l) dengan menggunakan nilai
� = . , . , . , = , dan matriks pembobot spasial W yang
dibentuk pada langkah (c) kecuali langkah (c2), sehingga banyaknya skenario dalam simulasi ini adalah 132.
m. Melakukan evaluasi pada semua matriks pembobot spasial dengan membandingkan nilai ARRMSE dan kontrol pendugaan � = . untuk setiap kombinasi W, m dan �.
3. Analisis Data Sekunder
17
a. Tahap Persiapan
1. Mempersiapkan data sebagai penduga langsung. Penduga langsung dalam penelitian ini adalah pengeluaran per rumah tangga per bulan setiap kecamatan yang diperoleh dari data SUSENAS tahun 2010 dengan rumus:
= u�tuk = , , … , Keterangan:
= pengeluaran per rumah tangga kecamatan ke-i
= total pengeluaran rumah tangga sebulan di kecamatan ke-i
= banyaknya rumah tangga di kecamatan ke-i
2. Mempersiapkan data yang digunakan sebagai peubah penyerta berdasarkan kuesioner yang diperoleh dari BPS dalam mengumpulkan data PODES tahun 2011.
3. Membentuk matriks pembobot spasial menggunakan metode yang direkomendasikan pada tahapan simulasi dengan mengacu pada peta dan koordinat centroid dari kecamatan di Kabupaten dan Kota Bogor yang disajikan pada Lampiran 3 dan Lampiran 4.
4. Melakukan pengecekan ketergantungan spasial menggunakan metode
Moran’s Index (Indeks Moran).
5. Mempersiapkan data ragam dari peubah respon dengan rumus: =
�− ∑ ( − )
1
= dengan adalah ragam pengeluaran per rumah tangga pada desa ke-i. kemudian dibagi dengan untuk mendapatkan ragam contoh yang akan digunakan dalam metode SEBLUP.
b. Tahap Pendugaan
1. Melakukan pendugaan langsung, EBLUP dan SEBLUP untuk masing-masing kecamatan.
2. Melakukan pendugaan MSE untuk metode pendugaan langsung, EBUP dan SEBLUP untuk masing-masing kecamatan.
3. Mengevaluasi hasil pendugaan dengan membandingkan penduga
18
4
HASIL DAN PEMBAHASAN
Kajian Simulasi Matriks Pembobot Spasial
Secara garis besar, matriks pembobot spasial (W) yang akan dikaji dalam penelitian ini adalah matriks pembobot berdasarkan kedekatan geografis. Matriks pembobot berdasarkan kedekatan geografis yang dikaji dikelompokkan menjadi tiga, yaitu berdasarkan jarak, berdasarkan batas dan berdasarkan kombinasi jarak dan batas. Matriks pembobot spasial berdasarkan jarak terbagi menjadi lima (5) metode, yaitu matriks k tetangga terdekat, matriks jarak radial, matriks jarak pangkat, matriks jarak eksponensial dan matriks jarak pangkat ganda. Sedangkan untuk matriks berdasarkan batas, peneliti hanya menggunakan matriks bobot kontiguitas spasial tipe queen. Matriks pembobot berdasarkan kombinasi jarak dan batas diperoleh dengan menggunakan konsep logika matematika untuk fungsi
konjungsi ∧ untuk membuat kombinasi jarak dan batas. Suatu area dikatakan bertetangga menurut kombinasi jarak dan batas, jika ditinjau berdasar jarak area tersebut bertetangga dan berdasar batas juga bertetangga.
Penelitian ini menggunakan simulasi untuk mengkaji jenis matriks pembobot spasial manakah yang sesuai untuk berbagai kombinasi jumlah area dan �. Untuk menentukan matriks pembobot yang terbaik yaitu dengan melihat nilai ARRMSE dari tiap-tiap matriks pembobot setelah dilakukan pengulangan sebanyak 1000 kali. Jumlah area yang disimulasikan ada 3 jenis yaitu 16 area, 64 area dan 144 area, dengan tujuan agar jumlah area sedikit, sedang dan banyak terwakili, sedangkan untuk koefisien otoregresif spasial yang digunakan adalah 0.05, 0.25, 0.5 dan 0.75, dengan tujuan agar korelasi antar area yang sangat rendah, rendah, sedang dan tinggi terwakili.
Peneliti mengakui bahwa mensimulasikan peta cukup tidak mudah, terutama dengan kondisi riil dilapangan. Untuk itu mencoba menggambar peta yang hampir sesuai untuk mayoritas kondisi dilapangan. Peta yang dibuat sengaja berhimpitan untuk semua area karena ingin mencoba mensimulasikan matriks pembobot spasial yang pada dasarnya melihat kebertetanggaan antar area dan jauh dekatnya antara area (jarak). Peta yang dibuat dengan menggambar area yang memiliki luas 100 km x 100 km, luas sempitnya area yang digambar akan menentukan besaran lebar jendela yang akan digunakan.
Peta yang akan di cobakan ada 3 macam dengan berbagai rancangan area, sebagai berikut:
1. Peta dengan 16 area
Menggunakan Gambar 2 di atas, peneliti membentuk matriks pembobot spasial berdasar batas yaitu matriks pembobot spasial queen untuk simulasi 16 area. Sedangkan untuk matriks pembobot spasial berdasarkan jarak dan kombinasi antara
19
batas dan jarak, dengan mengacu pada Gambar 2 di atas peneliti mensimulasikan letak centroid yang akan digunakan dalam mengukur jarak antar area. Centroid tiap area dibangkitkan menyebar secara uniform dengan memperhatikan luasan tiap area dan letak tiap area. Data centroid yang dibangkitkan untuk tiap area cukup sekali dan selanjutnya akan digunakan untuk semua simulasi dengan matriks pembobot spasial yang berbeda.
Dari informasi posisi centroid untuk 16 area pada Gambar 3 di atas, maka akan didapatkan jarak antar area dengan menggunakan formula jarak euclidean, yang kemudian digunakan untuk membuat matriks pembobot spasial berdasarkan jarak dan kombinasi antara jarak dan batas. Metode pembentukan matriks pembobot spasial berdasar jarak yang digunakan adalah matriks k tetangga terdekat, matriks jarak radial, matriks jarak pangkat, matriks jarak eksponensial dan matriks jarak pangkat ganda, sedangkan metode untuk pembentukan matriks pembobot spasial kombinasi antara jarak dan batas yang digunakan adalah matriks kombinasi
k tetangga terdekat dengan queen, matriks kombinasi jarak radial dengan queen, matriks kombinasi jarak pangkat dengan queen, matriks kombinasi jarak eksponensial dengan queen dan matriks kombinasi jarak pangkat ganda dengan
queen.
2. Peta dengan 64 area 0
100 200 300 400
0 100 200 300 400
1 9 17 25 33 41 49 57 2 10 18 26 34 42 50 58 3 11 19 27 35 43 51 59 4 12 20 28 36 44 52 60 5 13 21 29 37 45 53 61 6 14 22 30 38 46 54 62 7 15 23 31 39 47 55 63 8 16 24 32 40 48 56 64
Gambar 4Peta untuk 64 area
20
Untuk simulasi dengan jumlah area sebanyak 64, peneliti menggunakan Gambar 4 di atas. Berdasarkan Gambar 4 tersebut, peneliti membentuk matriks pembobot spasial berdasar batas, yaitu matriks pembobot spasial queen untuk simulasi 64 area. Sedangkan untuk matriks pembobot spasial berdasarkan jarak dan kombinasi antara batas dan jarak, dengan mengacu pada Gambar 4 di atas peneliti mensimulasikan letak centroid yang akan digunakan dalam mengukur jarak antar area. Centroid tiap area dibangkitkan menyebar secara uniform dengan memperhatikan luasan tiap area dan letak tiap area. Data centroid yang dibangkitkan untuk tiap area cukup sekali dan selanjutnya akan digunakan untuk semua simulasi dengan matriks pembobot spasial yang berbeda.
Dari informasi posisi centroid untuk 64 area pada Gambar 5 di atas, maka akan didapatkan jarak antar area dengan menggunakan formula jarak euclidean, yang kemudian digunakan untuk membuat matriks pembobot spasial berdasarkan jarak dan kombinasi antara jarak dan batas. Metode pembentukan matriks pembobot spasial berdasar jarak yang digunakan adalah matriks k tetangga terdekat, matriks jarak radial, matriks jarak pangkat, matriks jarak eksponensial dan matriks jarak pangkat ganda, sedangkan metode untuk pembentukan matriks pembobot spasial kombinasi antara jarak dan batas yang digunakan adalah matriks kombinasi
k tetangga terdekat dengan queen, matriks kombinasi jarak radial dengan queen, matriks kombinasi jarak pangkat dengan queen, matriks kombinasi jarak eksponensial dengan queen dan matriks kombinasi jarak pangkat ganda dengan
queen. 0 100 200 300 400 500 600 700 800
0 100 200 300 400 500 600 700 800
21
3. Peta dengan 144 area
Menggunakan Gambar 6 di atas, peneliti membentuk matriks pembobot spasial berdasar batas yaitu matriks pembobot spasial queen untuk simulasi 144 area. Sedangkan untuk matriks pembobot spasial berdasarkan jarak dan kombinasi antara batas dan jarak, dengan mengacu pada Gambar 6 di atas peneliti mensimulasikan letak centroid yang akan digunakan dalam mengukur jarak antar area. Centroid tiap area dibangkitkan menyebar secara uniform dengan memperhatikan luasan tiap area dan letak tiap area. Data centroid yang dibangkitkan untuk tiap area cukup sekali dan selanjutnya akan digunakan untuk semua simulasi dengan matriks pembobot spasial yang berbeda.
0 100 200 300 400 500 600 700 800 900 1000 1100 1200
0 100 200 300 400 500 600 700 800 900 1000 1100 1200 1 13 25 37 49 61 73 85 97 109 121 133 2 14 26 38 50 62 74 86 98 110 122 134 3 15 27 39 51 63 75 87 99 111 123 135 4 16 28 40 52 64 76 88 100 112 124 136 5 17 29 41 53 65 77 89 101 113 125 137 6 28 30 42 54 66 78 90 102 114 126 138 7 19 31 43 55 67 79 91 103 115 127 139 8 20 32 44 56 68 80 92 104 116 128 140 9 21 33 45 57 69 81 93 105 117 129 141 10 22 34 46 58 70 82 94 106 118 130 142 11 23 35 47 59 71 83 95 107 119 131 143 12 24 36 48 60 72 84 96 108 120 132 144
Gambar 6Peta untuk 144 area
22
Dari informasi posisi centroid untuk 144 area pada Gambar 7 di atas, maka akan didapatkan jarak antar area dengan menggunakan formula jarak euclidean, yang kemudian digunakan untuk membuat matriks pembobot spasial berdasarkan jarak dan kombinasi antara jarak dan batas. Metode pembentukan matriks pembobot spasial berdasar jarak yang digunakan adalah matriks k tetangga terdekat, matriks jarak radial, matriks jarak pangkat, matriks jarak eksponensial dan matriks jarak pangkat ganda, sedangkan metode untuk pembentukan matriks pembobot spasial kombinasi antara jarak dan batas yang digunakan adalah matriks kombinasi
k tetangga terdekat dengan queen, matriks kombinasi jarak radial dengan queen, matriks kombinasi jarak pangkat dengan queen, matriks kombinasi jarak eksponensial dengan queen dan matriks kombinasi jarak pangkat ganda dengan
queen.
Hal yang menjadi perhatian oleh peneliti dalam membentuk matriks pembobot spasial berdasar jarak adalah metode penentuan threshold yang akan digunakan untuk menentukan suatu area dikatakan bertetangga atau tidak.
Threshold yang sangat kecil akan menyebabkan ragam menjadi semakin besar, sebaliknya nilai threshold yang besar dapat menimbulkan bias yang semakin besar pula. Penentuan threshold dalam melakukan simulasi untuk setiap jumlah area ditentukan dengan berpatokan pada lebar jendela yang digunakan untuk membentuk peta area, yaitu 200 km dan menerapkan konsep pada simulasi ini
bahwa “suatu area dianggap saling mempengaruhi jika jarak antar titik centroid
masing-masing area kurang dari atau sama dengan 200 km”.
Setelah matriks pembobot spasial pada ketiga jenis peta berbeda diperoleh (m = 16, m = 64, m = 144) selanjutnya dengan menggunakan informasi tersebut, peneliti membangkitkan data yang akan disimulasikan terhadap berbagai kombinasi besaran koefisien otoregresif spasial yang berbeda � = . , � = . , � = . ��� � = . . Data bangkitan ini yang akan dianalisis lebih lanjut menggunakan pendekatan pendugaan area kecil. Berdasarkan hasil analisis pendugaan area kecil inilah, peneliti menentukan matriks pembobot spasial mana yang terbaik berdasarkan nilai ARRMSE yang diberikan tiap matriks pembobot spasial dan kontrol pendugaan � = . .
Hasil Simulasi Matriks Pembobot Spasial
Setelah melakukan simulasi dengan 1000 kali pengulangan, didapatkan nilai ARRMSE dari kombinasi W, m, dan � berbeda.
1. Simulasi untuk m = 16 area
23
Berdasarkan nilai ARRMSE yang dihasilkan dari semua kombinasi simulasi untuk m = 16 pada Tabel 1 dapat dilihat bahwa matriks pembobot spasial yang direkomendasikan dalam pendugaan area kecil dengan memperhatikan koefisien otoregresif spasial adalah matriks pembobot spasial K-NN, matriks pembobot spasial pangkat, matriks pembobot spasial pangkat ganda, matriks pembobot spasial
queen, matriks pembobot spasial kombinasi eksponensial dan queen, matriks pembobot spasial kombinasi K-NN dan queen, matriks pembobot spasial kombinasi pangkat dan queen, matriks pembobot spasial kombinasi pangkat ganda dan queen, dan matriks pembobot spasial kombinasi radial dan queen. Sedangkan matriks pembobot spasial eksponensial dan matriks pembobot spasial radial tidak direkomendasikan dalam pendugaan area kecil untuk jumlah area yang sedikit. Hal ini berdasarkan nilai ARRMSE SEBLUP pada � = . yang digunakan sebagai kontrol dalam simulasi, nilai ARRMSE SEBLUP pada � = . haruslah tidak berbeda jauh dengan nilai ARRMSE EBLUP. Jika nilai ARRMSE SEBLUP pada
� = . berbeda jauh dengan nilai ARRMSE EBLUP, maka matriks pembobot
spasial tersebut tidak mampu melakukan pendugaan dengan baik sehingga tidak direkomendasikan dalam pendugaan area kecil.
Berdasarkan hasil pada Tabel 1, diperoleh rincian matriks pembobot spasial yang direkomendasikan dengan memperhatikan koefisien otoregresif spasial � . Pada area yang memiliki koefisien otoregresif spasial antar area yang kuat
� = . , maka matriks pembobot spasial yang direkomendasikan adalah
matriks pembobot spasial K-NN, matriks pembobot spasial pangkat ganda, matriks pembobot spasial kombinasi K-NN dan queen dan matriks pembobot spasial kombinasi pangkat ganda dan queen, untuk koefisien otoregresif spasial antar area yang sedang � = . , matriks pembobot spasial yang direkomendasikan adalah matriks pembobot spasial queen, matriks pembobot spasial kombinasi eksponensial dan queen dan matriks pembobot spasial kombinasi radial dan queen, sedangkan untuk koefisien otoregresif spasial antar area yang rendah � = . , matriks pembobot spasial yang direkomendasikan adalah matriks pembobot spasial queen,
24
matriks pembobot spasial kombinasi eksponensial dan queen, dan matriks pembobot spasial kombinasi radial dan queen.
2. Simulasi untuk m = 64 area
Berikut adalah nilai ARRMSE bagi penduga EBLUP dan penduga SEBLUP yang diperoleh dari simulasi untuk m = 64 area dengan kombinasi W dan � yang berbeda. Berdasarkan hasil yang diperoleh tersebut, selanjutnya dilakukan evaluasi kebaikan masing-masing matriks pembobot spasial dalam memberikan pendugaan area kecil yang optimum.
Berdasarkan nilai ARRMSE yang dihasilkan dari semua kombinasi simulasi untuk m = 64 pada Tabel 2 dapat dilihat bahwa matriks pembobot spasial yang direkomendasikan dalam pendugaan area kecil dengan memperhatikan koefisien otoregresif spasial adalah matriks pembobot spasial K-NN, matriks pembobot spasial pangkat, matriks pembobot spasial pangkat ganda, matriks pembobot spasial radial, matriks pembobot spasial queen, matriks pembobot spasial kombinasi eksponensial dan queen, matriks pembobot spasial kombinasi K-NN dan queen, matriks pembobot spasial kombinasi pangkat dan queen, matriks pembobot spasial kombinasi pangkat ganda dan queen, dan matriks pembobot spasial kombinasi radial dan queen. Sedangkan matriks pembobot spasial eksponensial tidak direkomendasikan dalam pendugaan area kecil untuk jumlah area yang sedikit. Hal ini berdasarkan nilai ARRMSE SEBLUP pada � = . yang digunakan sebagai kontrol dalam simulasi, nilai ARRMSE SEBLUP pada � = . haruslah tidak berbeda jauh dengan nilai ARRMSE EBLUP. Jika nilai ARRMSE SEBLUP pada
� = . berbeda jauh dengan nilai ARRMSE EBLUP, maka matriks pembobot
spasial tersebut tidak mampu melakukan pendugaan dengan baik sehingga tidak direkomendasikan dalam pendugaan area kecil.
Berdasarkan hasil pada Tabel 2, diperoleh rincian matriks pembobot spasial yang direkomendasikan dengan memperhatikan pengaruh korelasi � . Pada area yang memiliki koefisien otoregresif spasial antar area yang kuat � = . , maka matriks pembobot spasial yang direkomendasikan adalah matriks pembobot spasial K-NN, untuk koefisien otoregresif spasial antar area yang sedang � = . ,
25
matriks pembobot spasial yang direkomendasikan adalah matriks pembobot spasial kombinasi radial dan queen, sedangkan untuk koefisien otoregresif spasial antar area yang rendah � = . , matriks pembobot spasial yang direkomendasikan adalah matriks pembobot spasial pangkat.
3. Simulasi untuk m = 144 area
Berikut adalah nilai ARRMSE bagi penduga EBLUP dan penduga SEBLUP yang diperoleh dari simulasi untuk m = 144 area dengan kombinasi W dan � yang berbeda. Berdasarkan hasil yang diperoleh tersebut, selanjutnya dilakukan evaluasi kebaikan masing-masing matriks pembobot spasial dalam memberikan pendugaan area kecil yang optimum.
Berdasarkan nilai ARRMSE yang dihasilkan dari semua kombinasi simulasi untuk m = 144 pada Tabel 3 dapat dilihat bahwa matriks pembobot spasial yang direkomendasikan dalam pendugaan area kecil dengan memperhatikan koefisien otoregresif spasial adalah matriks pembobot spasial K-NN, matriks pembobot spasial pangkat, matriks pembobot spasial pangkat ganda, matriks pembobot spasial radial, matriks pembobot spasial queen, matriks pembobot spasial kombinasi eksponensial dan queen, matriks pembobot spasial kombinasi K-NN dan queen, matriks pembobot spasial kombinasi pangkat dan queen, matriks pembobot spasial kombinasi pangkat ganda dan queen, dan matriks pembobot spasial kombinasi radial dan queen. Sedangkan matriks pembobot spasial eksponensial tidak direkomendasikan dalam pendugaan area kecil untuk jumlah area yang banyak. Hal ini berdasarkan nilai ARRMSE SEBLUP pada � = . yang digunakan sebagai kontrol dalam simulasi, nilai ARRMSE SEBLUP pada � = . haruslah tidak berbeda jauh dengan nilai ARRMSE EBLUP. Jika nilai ARRMSE SEBLUP pada
� = . berbeda jauh dengan nilai ARRMSE EBLUP, maka matriks pembobot
spasial tersebut tidak mampu melakukan pendugaan dengan baik sehingga tidak direkomendasikan dalam pendugaan area kecil.
Berdasarkan hasil pada Tabel 3, diperoleh rincian matriks pembobot spasial yang direkomendasikan dengan memperhatikan koefisien otoregresif spasial � . Pada area yang memiliki koefisien otoregresif spasial antar area yang kuat