INTEGER CHANCE CONSTRAINED
DISERTASI
oleh
HOTMAN SIMBOLON NIM : 098110021
PROGRAM STUDI DOKTOR ILMU MATEMATIKA FAKULTAS MATEMATIKA DAN
ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
DISERTASI
Diajukan Sebagai Salah Satu Syarat Untuk Memperoleh Gelar Doktor
Dalam Program Studi Doktor Ilmu Matematika Pada Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Sumatera Utara oleh
HOTMAN SIMBOLON NIM : 098110021
PROGRAM STUDI DOKTOR ILMU MATEMATIKA FAKULTAS MATEMATIKA DAN
ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
Tanggal: 16 Juli 2013
==================================================================
KOMISI PENGUJI DISERTASI
Ketua : Prof. Dr. Muhammad Zarlis Anggota :
Saya menyatakan dengan sebenar-benarnya bahwa segala pernyataan dalam disertasi saya yang berjudul:
Optimisasi Persoalan Linear Integer Chance Constrained
merupakan gagasan atau hasil penelitian disertasi saya sendiri dengan pembimbingan para Komisi Pembimbing, kecuali yang dengan jelas ditunjukkan rujukannya. Disertasi ini belum pernah diajukan untuk memperoleh gelar pada program sejenis di perguruan tinggi lainnya.
Semua data dan informasi yang digunakan telah dinyatakan secara jelas dan da-pat diperiksa kebenarannya.
Medan, Juni 2013
Stochastic program related with optimization of decision making on which uncer-tainty exist in data problem from time to time. The type of this study is the random optimization problem which is outcome from random data were not revealed in a running time, and the decision itself does not have to anticipate the future outcome (non anticipate). This gives a strong connection with real time optimization seen as necessity for right and now optimal decision in an uncertain environment. As long as the information of probabilistic is available, the right model for real time optimization can be formulated as stochastic double step. The essence of this introduced is to replace the deterministic model, where the coefficient and the uncertain parameter are random with a wide spread assumption from decision variables. This dissertation examine one of the stochastic program types where the problem is linked with decision making where constraints are not conclusively met but there are a decision chance that melt the constraint for some level of confidence. Thus the model issue is called as linear chance constrained programming (LCCP) issue. This study requires that decision variables take natural number (integer) (LCCIP). LCCP issue is hard to resolved because it involves multi dimensional integration and non connectivity condition. This study submit a modification of sample average approximation (SAA) approach. The main idea of this approach is to change the LCCIP problem to be the deterministic issue. By using SAA, an equivalent deterministic issue takes the form of mixed integer nonlinear programming (MINLP). Further MINLP is solved by using the direct search method.
to solve the LCCIP issue
Keywords: linear change constraint, integer, optimization
Program stokastik berhubungan dengan optimisasi pengambilan keputusan dengan adanya ketidakpastian dalam data problema dari suatu waktu ke waktu berikutnya. Tipe objek kajian adalah problema optimisasi acak dimana hasil (outcome) dari data acak tidak terungkap pada waktu berjalan, dan keputusan yang akan dioptimalkan tidak harus mengantisipasi hasil masa datang (non-antisipasi). Hal ini memberikan kaitan erat dengan optimisasi real time yang terlihat sebagai kebutuhan untuk keputusan optimal kini dan sekarang dalam suatu lingkungan data yang tak lengkap (atau tak pasti). Asalkan informasi probabilistik tersedia, model oprasional yang sesuai untuk optimisasi real−time dapat diformulasi sebagai program stokastik tahap-ganda. Secara esensial model ini diajukan untuk menggantikan model deterministik, dimana koefisien atau parameter yang tidak diketahui merupakan acak dengan pengandaian sebaran peluang bebas dari peubah keputusan. Disertasi ini meneliti salah satu tipe dari program stokastik yang persoalannya dikaitkan dengan pengambilan keputusan dimana kendala tidak secara meyakinkan dapat terpenuhi, namun terdapat peluang keputusan yang memenuhi kendala tersebut untuk beberapa tingkat keyakinan. Model persoalan demikian ini disebut sebagai persoalan linear chance constrained
programming (LCCP). Penelitian ini mempersyaratkan bahwa peubah keputusan
mengambil bilangan cacah (integer) (LCCIP). Persoalan LCCP sulit terselesaikan karena menyangkut integrasi multi-dimensi dan kondisi non-konveksitas. Penelitian ini mengajukan modifikasi pendekatan sample average approximation (SAA). Ide
deterministik. Dengan SAA bentuk persoalan deterministik ekivalen mengambil bentuk model mixed integer nonlinear programming (MINLP). Selanjutnya MINLP diselesaikan dengan menggunakan metode pencarian langsung. Contoh komputasi diberikan. Hasil yang diperoleh memperlihatkan bahwa pendekatan demikian ini cukup menjanjikan untuk menyelesaikan persoalan LCCIP.
Kata Kunci: Linear chance constraint, integer, optimisasi.
Penulis, Hotman Simbolon dilahirkan di Rianiate tanggal 17 Nopember 1949 dari ayah Mgr. Torang Simbolon dan ibu Sanna br. Situmorang. Penulis adalah putra ke tujuh dari tujuh orang bersaudara, dan beristerikan Bunna br. Sipayung, S.Pd. Penulis memiliki empat orang anak, yaitu Pirton Hotberesman Bintatar Simbolon, S.T; Holmes Hotasiman Simbolon, S.T; Hotpascaman Simbolon, M.Psi, Psikolog dan Hotmaster-man Togap Ben Simbolon, S.T.
Pada tahun 1972 penulis lulus sebagai sarjana muda Pendidikan Ilmu Pasti di FKIP Universitas HKBP Nommensen. Pada tahun 1975 penulis lulus sarjana penuh Pen-didikan Matematika swasta. Pada Tahun 1980 penulis lulus sebagai Sarjana Penuh jurusan Matematika di IKIP Negeri Medan. Pada tahun 1988 penulis lulus sebagai Ma-gister Sains bidang Statistika Terapan di Institut Pertanian Bogor. Tahun 2009 semester genap penulis mulai mengikuti Program S3 Ilmu Matematika di Universitas Sumatera Utara. Penulis sering mengikuti seminar, konferensi, simposiun atau konvensi tingkat nasional, regional atau internasional sebagai peserta atau pemakalah.
Tahun 1970 penulis telah mengajar di SMA. Tahun 1972 penulis menjadi asis-ten dosen FKIP UHN dan tahun 1980 hingga sekarang menjadi dosen tetap di Prodi Pendidikan Matematika FKIP UHN Pematangsiantar. Selama menjadi dosen di FKIP penulis pernah menduduki jabatan struktural yaitu Ketua Jurusan dan Dekan. Selain itu penulis pernah dikaryakan menjadi Kepala SMA Kampus FKIP UHN (2004-2009).
Buku yang pernah ditulis dan diterbitkan secara nasional adalah Statistika (2006, ISBN 978-979-756-380-6), dan diterbitkan secara regional adalah Statistika Matem-atika I (2006, ISBN 979-99031-0-6)
Dengan mengucap syukur kepada Tuhan pada akhirnya disertasi ini dapat disusun sedemikian rupa sehingga diharapkan dapat menjadi salah satu landasan dalam pe-ngembangan ilmu matematika di bidang optimisasi yang diberi kendalachancedan un-sur bilangan bulat. Disertasi ini memperkenalkan suatu metode untuk pemecahan ”Op-timisasi Persoalan Linear Integer Chance Constrained”. Penulis mengucapkan banyak terimakasih kepada:
1. Prof. Dr. Syahril Pasaribu, DTM & H, CTM, Sp.A (K)., selaku Rektor Universi-tas Sumatera Utara.
2. Dr. Sutarman, M. Sc., selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Suatera Utara.
3. Prof. Dr. Herman Mawengkang, selaku Ketua Progran Studi Doktor Ilmu Matematika, sekaligus sebagai co-promotor yang tidak bosan-bosannya memberi bimbingan hingga tulisan ini terwujud. Disamping itu telah memberi dukungan dan peluang seluas-luasnya dalam mengikuti berbagai seminar Nasional maupun Internasional sehingga sangat mendukung dalam studi S3 dan isi tulisan ini. 4. Prof. Dr. Saib Suwilo, M. Sc., selaku sekretaris Prodi, dosen dan penguji yang
telah memberi ganjaran berupa bahan masukan dalam tulisan ini.
5. Prof. Dr. Muhammad Zarlis, selaku Ketua promotor yang selalu memberi moti-vasi dan masukan hingga terwujudnya tulisan ini.
6. Dr. M. D. H. Gamal, M. Sc., selaku co-promotor yang memberi masukan dan motivasi menarik terutama kesempatan waktu komunikasi yang baik langsung atau tak langsung walaupun dari Perguruan Tinggi lain.
7. Prof. Dr. Opim Salim Sitompul, selaku dosen dan penguji yang bersedia mem-berikan bantuan melalui pertanyaan dan kritik berharga yang menjadi masukan,
hatian dan motivasi menulis pengembangan dalam disertasi ini.
8. Prof. Dr. Tulus, dan Dr. Marwan Ramli, merupakan dua kawanan sejoli seba-gai unsur pimpinan IndoMS yang sering secara bersama atau terpisah memberi motivasi dan masukan sehingga meningkatkan semangat meneruskan tulisan. 9. Dr. Ir. Jongkers Tampubolon, M. Sc., selaku Rektor, dan Dr. Tagor Pangaribuan,
M.Pd, selaku Dekan FKIP, Universitas HKBP Nommensen yang berkenan mem-beri izin mengikuti kuliah S3 di USU.
10. Dr. Darwin, M. M., selaku Ketua STIE Sultan Agung Pematangsiantar yang memotivasi diri ”penulis pasti dapat menyelesaikan tulisan dan studi S3”
11. Ibu Misiani, S.Si., selaku KTU Prodi yang selalu memberi petunjuk keleng-kapan dan peringatan waktu-waktu penting terutama urusan administrasi selama mengikuti program S3.
12. Teman-teman seperkuliahan yang selalu saling memberi motivasi atas keku-rangan dan kelebihan, terutama bapak Drs. Firmansyah, M. Si., yang memberi dukungan moril maupun material yang sangat dirasakan sehari-hari.
13. Saudara Roland Sitorus, S. Pd., secara khusus sebagai teknisi, yang paling sering membantu mengatasi permasalahan komputer selama penulisan disertasi ini. 14. Istri dan semua anak-anak saya yang memberi perhatian dan terutama dukungan
doa setiap hari, juga pencarian bahan melalui internet dan sebagainya. 15. Semua pihak yang terlibat dalam pewujudan tulisan ini,
dengan harapan dapat dimanfaatkan membantu para pengguna dalam bidang terkait. Medan, Juni 2013 Penulis,
Hotman Simbolon
ABSTRACT i
ABSTRAK iii
RIWAYAT HIDUP v
KATA PENGANTAR vi
DAFTAR ISI viii
DAFTAR GAMBAR xi
DAFTAR TABEL xii
1 PENDAHULUAN 1
1. 1. Latar Belakang . . . 1
1. 2. Rumusan Masalah . . . 5
1. 3. Tujuan . . . 5
2 PROGRAM STOKASTIK 7 2. 1. Model Dasar Program Stokastik . . . 7
2. 1.1. Model Antisipatif . . . 7
2. 1.2. Model Adaptif . . . 8
2. 1.3. Model Recourse . . . 9
2. 2.1. Proses Formulasi . . . 11
2. 3. Pohon Skenario . . . 13
3 BEBERAPA APLIKASI PERSOALAN CHANCE CONSTRAINED 30 3. 1. Chance Constrained Programming Untuk Analisis Pengelolaan Portofolio 30 3. 2. OptimisasiChance ConstrainedPengelolaan Air Asin . . . 33
3. 3. Event-Driven Probabilistic Constrained Programming(EDP-CP) . . . . 38
3. 4. Model Chance Constrained Programming untuk Resiko Berbasis Ekonomi dan Analisis Kebijakan Konservasi Tanah . . . 41
4 OPTIMISASI LINEAR CHANCE CONSTRAINED PROGRAMMING 51 4. 1. Program Linear Deterministic . . . 51
4. 1.1. Contoh Model Deterministik Pada Vehicle Routing Problem (VRP) . . . 53
4. 2. Program Stokastik danChance Constrained Programming . . . 57
4. 2.1. Sumber Stokastik dengan Dua Peubah Keputusan . . . 58
4. 2.2. Generalisasi Sumber Stokastik Dengan n Peubah . . . 62
4. 2.3. Koefisien Stokastik Dengan Dua Peubah Keputusan . . . 63
4. 2.4. Generalisasi Koefisien Stokastik Dengan n Peubah Keputusan . 66 4. 2.5. Teorema . . . 67
4. 2.6. Generalisasi CCP dengan beberapa kendala . . . 73
4. 2.6.1. CCP Bersama . . . 74
4. 2.6.2. CCP Tersendiri . . . 74
4. 2.7. Bentuk Umum Linier CCP . . . 76
4. 2.8. Linear Chance Constraint Dengan ˜ai j,b˜iMenyebar Baku . . . . 80
4. 2.10. Program Integer . . . 88
4. 2.11. Aplikasi . . . 89
4. 3. Aproksimasi Rataan Sampel . . . 92
4. 3.1. Kesesuaian struktur persoalan optimasi untuk SAA . . . 94
4. 3.2. SAA sebagai pendekatan persoalanchance constrained . . . 97
4. 4. Pemecahan Sampel Aproksimasi . . . 101
4. 5. Algoritma . . . 103
5 PENGALAMAN KOMPUTASIONAL 107 5. 1. Pengenalan . . . 107
5. 2. Formulasi Persoalan Deterministik . . . 108
5. 3. Contoh numerik . . . 108
5. 4. Formulasi Persoalan dengan CCIP . . . 109
6 KESIMPULAN 111
DAFTAR PUSTAKA 113
2.1 Pohon Skenario . . . 14
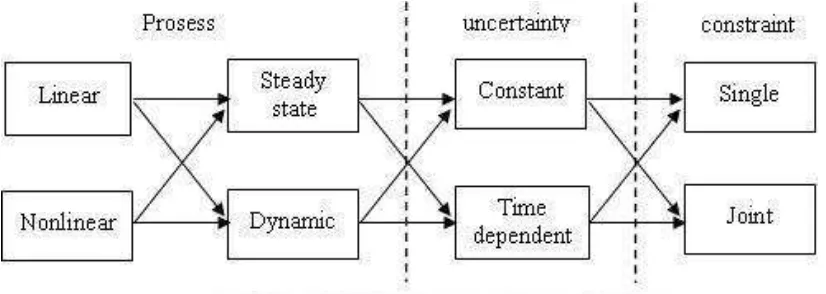
3.1 Teknik untuk persoalan model keputusan di bawah ketidakpastian (Tarim, dkk. 2009) . . . 39
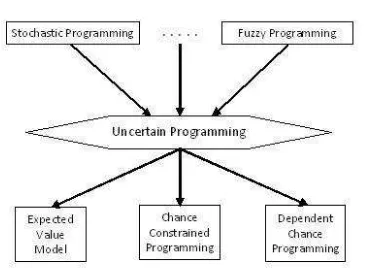
3.2 Klasifikasi persoalanchance constrained(Arellano, 2006) . . . 48
4.1 Kendala Deterministik untukeb yang berbeda . . . 59
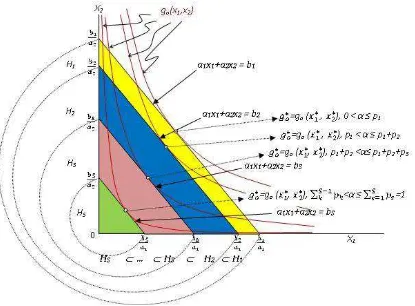
4.2 Ilustrasi solusi sesuai dengan sub-program . . . 61
4.3 Himpunan kendala deterministik untukae2yang berbeda . . . 63
4.4 Ilustrasi solusi sesuai dengan sub-program untuk peubah koefisien stokastik . . . 65
2.1 Data pengolahan tanaman padi, jagung dan kacang . . . 16
2.2 Hasil optimal dari data tabel 2.1 . . . 17
2.3 Hasil optimal data tabel 2.1 dengan skenario cuaca berbeda . . . 19
2.4 Data pengolahan tanaman padi, jagung dan kacang dengan sebaran kontinu . . . 23
4.1 Himpunan layak deterministik untuk eb . . . 60
4.2 Himpunan layak deterministikae2 . . . 64
5.1 Hasil dari Persoalan Reliabilitas . . . 110
Stochastic program related with optimization of decision making on which uncer-tainty exist in data problem from time to time. The type of this study is the random optimization problem which is outcome from random data were not revealed in a running time, and the decision itself does not have to anticipate the future outcome (non anticipate). This gives a strong connection with real time optimization seen as necessity for right and now optimal decision in an uncertain environment. As long as the information of probabilistic is available, the right model for real time optimization can be formulated as stochastic double step. The essence of this introduced is to replace the deterministic model, where the coefficient and the uncertain parameter are random with a wide spread assumption from decision variables. This dissertation examine one of the stochastic program types where the problem is linked with decision making where constraints are not conclusively met but there are a decision chance that melt the constraint for some level of confidence. Thus the model issue is called as linear chance constrained programming (LCCP) issue. This study requires that decision variables take natural number (integer) (LCCIP). LCCP issue is hard to resolved because it involves multi dimensional integration and non connectivity condition. This study submit a modification of sample average approximation (SAA) approach. The main idea of this approach is to change the LCCIP problem to be the deterministic issue. By using SAA, an equivalent deterministic issue takes the form of mixed integer nonlinear programming (MINLP). Further MINLP is solved by using the direct search method.
to solve the LCCIP issue
Keywords: linear change constraint, integer, optimization
Program stokastik berhubungan dengan optimisasi pengambilan keputusan dengan adanya ketidakpastian dalam data problema dari suatu waktu ke waktu berikutnya. Tipe objek kajian adalah problema optimisasi acak dimana hasil (outcome) dari data acak tidak terungkap pada waktu berjalan, dan keputusan yang akan dioptimalkan tidak harus mengantisipasi hasil masa datang (non-antisipasi). Hal ini memberikan kaitan erat dengan optimisasi real time yang terlihat sebagai kebutuhan untuk keputusan optimal kini dan sekarang dalam suatu lingkungan data yang tak lengkap (atau tak pasti). Asalkan informasi probabilistik tersedia, model oprasional yang sesuai untuk optimisasi real−time dapat diformulasi sebagai program stokastik tahap-ganda. Secara esensial model ini diajukan untuk menggantikan model deterministik, dimana koefisien atau parameter yang tidak diketahui merupakan acak dengan pengandaian sebaran peluang bebas dari peubah keputusan. Disertasi ini meneliti salah satu tipe dari program stokastik yang persoalannya dikaitkan dengan pengambilan keputusan dimana kendala tidak secara meyakinkan dapat terpenuhi, namun terdapat peluang keputusan yang memenuhi kendala tersebut untuk beberapa tingkat keyakinan. Model persoalan demikian ini disebut sebagai persoalan linear chance constrained
programming (LCCP). Penelitian ini mempersyaratkan bahwa peubah keputusan
mengambil bilangan cacah (integer) (LCCIP). Persoalan LCCP sulit terselesaikan karena menyangkut integrasi multi-dimensi dan kondisi non-konveksitas. Penelitian ini mengajukan modifikasi pendekatan sample average approximation (SAA). Ide
deterministik. Dengan SAA bentuk persoalan deterministik ekivalen mengambil bentuk model mixed integer nonlinear programming (MINLP). Selanjutnya MINLP diselesaikan dengan menggunakan metode pencarian langsung. Contoh komputasi diberikan. Hasil yang diperoleh memperlihatkan bahwa pendekatan demikian ini cukup menjanjikan untuk menyelesaikan persoalan LCCIP.
Kata Kunci: Linear chance constraint, integer, optimisasi.
PENDAHULUAN
1. 1. Latar Belakang
Dunia saat ini dilanda oleh adanya kondisi ketidakpastian yang tinggi, namun pengambil keputusan tetap harus menentukan keputusan walau dalam kondisi yang demikian. Persoalan keputusan sering diformulasikan sebagai persoalan optimisasi, jadi dalam berbagai situasi, pengambil keputusan ingin menyelesaikan persoalan op-timisasi yang tergantung pada parameter yang tak diketahui. Jika ketidakpastian ini tidak diperhitungkan dalam model penyelesaian, kesalahan besar dapat terjadi apabila hal ini diterapkan. Tentu saja, penyelesaian yang diperoleh dari program optimisasi adalah optimal untuk nilai tertentu dari parameter problema, namun nilai akhir atau yang sebenarnya dari parameter-parameter tak pasti tersebut yang terlibat dalam peng-ambilan keputusan dapat jauh dari optimal, atau bahkan tak layak.
Seperti halnya dalam model optimisasi matematika lainnya, persyaratan cacah dalam problema program stokastik memiliki konsekuensi serius terhadap sifat struk-tural dan rancangan algoritma.
Program stokastik berhubungan dengan optimisasi pengambilan keputusan dengan adanya ketidakpastian pada waktu ke waktu. Secara esensial model ini diajukan un-tuk menggantikan model deterministik, dimana koefisien atau paramater yang tidak diketahui merupakan acak dengan pengandaian sebaran peluang bebas dari peubah keputusan. Perkembangan dalam metode komputasi yang menggembirakan
babkan persoalan berskala besar dapat terselesaikan secara efisien dan terpercaya. Ak-ibatnya teknik program stokastik terpakai untuk menyelesaikan persoalan-persoalan dunia nyata.
Program stokastik memberikan kerangka dasar pemodelan yang mampu melibatkan fitur dunia nyata, seperti kendala pengalihan, biaya transaksi, menghindari resiko, batasan pada kumpulan aset dan pertimbangan lainnya. Begitupun model optimisasi ini menjadi ruwet jika terdapat sejumlah besar peubah, terutama untuk persoalan tahap-ganda.
Model antisipatif dan adaptif merupakan kasus khusus dari program stokastik. Kombinasi keduanya menghasilkan model rekursif yang menjadi fokus dalam peneli-tian ini. Model ini juga disebut sebagai model statis, dalam mana keputusan tidak tergantung pada pengamatan masa datang. Perencanaan yang baik harus memperhi-tungkan semua realisasi masa datang yang mungkin karena tidak akan ada kesem-patan untuk memperbaharui keputusan nantinya. Dalam model adaptif, informasi yang dikaitkan dengan ketidakpastian muncul secara parsial sebelum pengambilan ke-putusan, jadi optimisasi terjadi dalam lingkungan pembelajaran.
Model recourse menggabungkan dua model yang diutarakan terdahulu, yaitu un-tuk menenun-tukan kebijakan yang tidak hanya mengantisipasi pengamatan masa datang tapi juga memperhitungkan informasi yang ada untuk membuat keputusan rekursif. Misalnya, manajer portofolio memperhatikan gerak masa datang agar saham (antisi-pasi) tetapi juga menyeimbangkan posisi portofolio ketika harga berubah (adaptasi). Persoalan program stokastik dua tahap dengan rekursif dapat ditulis sebagai
min f(x) +E[Q(x,w)]
kendala Ax=b x∈ℜM0
+
ℜM0
+ adalah bilangan non-negatif,wvektor keputusan tahap kedua ,xadalah keputusan
antisipatif tahap pertama yang diambil sebelum peubah acak teramati, dan Q(x,w)
merupakan nilai optimalnya, untuk sembarangΩ(Ω= himpunan semua kejadian acak), dari program tak linier:
min ξ(y,w)
kendala W(w)y=h(w)−T(w)x y∈ℜM1
+
(1.2)
dengan y keputusan adaptif tahap kedua yang tergantung pada realisasi vek-tor acak tahap pertama, ξ(y,w) merupakan fungsi biaya tahap kedua, dan
{T(w),W(w),h(w)|w ∈ Ω} adalah parameter model dengan dimensi tertentu. Parameter-parameter ini merupakan fungsi dari vektor acak w dan karena itu meru-pakan parameter acak. T adalah matriks teknologi yang mengandung koefisien teknologi yang mengubah keputusan tahap pertamaxmenjadi sumber daya untuk per-soalan tahap kedua. Wadalah matriksrecoursedanhvektor sumber daya tahap kedua.
Secara umum modelrecoursedua tahap dapat diformulasikan sebagai min f(x) +E
" min y∈RM1
+
{ξ(y,w)|T(w)x+W(w)y=h(w)}
#
kendala Ax=b x∈ℜM0
+
(1.3)
Persoalan rekursif tidak dibatasi pada formulasi dua-tahap. Mungkin saja penga-matan dibuat pada T tahap berbeda dan terungkap dalam kumpulan informasi
Linear chance constrained programming (LCCP) yang diajukan oleh Charnes dan Cooper (1959), menawarkan suatu alat ampuh terhadap pemodelan keputusan stokastik dan sistem kendala, yang kemudian makin dikembangkan orang; seperti Miller dan Wagner (1964). Fokus utama LCCP ditujukan pada pemodelan optimisasi yang kendalanya tidak diketahui secara akurat namun tergantung pada realisasi vektor acak, sehingga tujuan dari model adalah memastikan bahwa kendala dapat terpenuhi dengan suatu tingkat keandalan, yaitu untuk realisasi vector acak dengan sekurang-kurangnya mengacu pada suatu nilai peluang yang ditentukan.
Secara umum model dari LCCP dapat ditulis sebagai
mincTx:x∈X,P{T xˆ ≥ξ} ≥1−ε (1.4)
dengan X ⊆ ℜd+ polyhedron, c ∈ ℜd,T matriks acakˆ m×d, ξ vector acak yang mengambil nilai dalam ℜm dan ε parameter keyakinan yang dipilih oleh pengambil keputusan, misalnya ε = 0.01 atau ε = 0,05. Dalam persamaan (1.4) terlihat bahwa tercakup hanya satu kendala peluang di semua baris yang berbeda dengan setiap baris dipersyaratkan secara bebas memenuhi nilai peluang. Bentuk kendala demikian dise-but sebagai kendala peluang gabungan (joint probability constraint), dan sesuai dalam konteks dimana pentingnya terdapat semua kendala terpenuhi secara simultan.
Apabila dalam model LCCP ini peubah keputusanxdipersyaratkan mengambil bi-langan bulat, yaitux∈Z+d, maka model sekarang disebut sebagailinear integer chance
constrained programming(LICCP)
model keandalan untuk sistem kompleks. Kemudian Agpah dan Gokcen (2007) men-gajukan LICCP untuk menyelesaikan persoalanstochastic line balancing. Dengan kata lain mereka bukan secara khusus membicrakan tentang metode penyelesaian untuk LICCP.
1. 2. Rumusan Masalah
Linear chance constrained programming merupakan persoalan yang sulit disele-saikan oleh karena dua hal (Luedtke, dkk., 2008). Kesulitan petama ialah, untuk suatu
x∈X, kuantitasP(T xˆ ≥ξ)biasanya sulit dihitung karena memerlukan integrasi multi-dimensi. Namun ada beberapa pengecualian dalam mana kuantitas ini dapat diestimasi cukup akurat apabila input acak memiliki sebaran gabungan normal ( lihat:Bukszar dan Pr ´ekopa, 2001; De ´ak, 2000; Sz ´antai ,2000). Kesulitan kedua adalah daerah layak yang diperlukan oleh kendala peluang umumnya tidak konveks. Demikian pula halnya un-tuk LICCP, di samping kedua kesulitan tesebut terdapat kesulitan lain terkait dengan persyaratan terhadapxyang harus mengambil bilangan bulat.
1. 3. Tujuan
Sesuai dengan latar belakang dan permasalan tersebut di atas, sebaran data, dae-rah yang dibatasi kendala atau konveksivitas, batasan bilangan (riel, bulat, cacah) dan fungsi tujuan mempengaruhi metode penyelesaian optimisasi. Bahasan ini dikhususkan pada optimisasi persoalanlinear integer chance constrained, walaupun dalam pemba-hasan kadang dibicarakan secara umum yang selanjutnya mengarah pada hal khusus tersebut.
Secara simbolik
maks x {c
Tx
atau sama saja dengan penulisan maks
x c Tx
kendala :P(Ax≤b)≥α (1.6)
x ≥0
x∈Zn
dengan Z adalah himpunaninteger(bilangan bulat), A adalah matriks dalam ℜm x n atau Zm x n atau Nm x n. Dengan memperhatikan dua kendala terakhirx≥0
PROGRAM STOKASTIK
2. 1. Model Dasar Program Stokastik
Model antisipatif dan adaptif merupakan kasus khusus dari program stokastik. Kombinasi keduanya menghasilkan model rekursif yang menjadi fokus dalam peneli-tian ini.
2. 1.1. Model Antisipatif
Model ini juga disebut sebagai model statis, dalam mana keputusan tidak tergan-tung pada pengamatan masa datang. Perencanaan yang baik harus memperhitergan-tungkan semua realisasi masa datang yang mungkin karena tidak akan ada kesempatan untuk memperbaharui keputusan nantinya.
Dalam model antisipatif kelayakan dinyatakan dalam kendala probabilistik. Misal-nya, tingkat keandalan α dengan 0 < α ≤ 1, dinyatakan dan kendala ditulis dalam bentuk
P{w|fj(x,w) = 0,j= 1, 2, ... ,n} ≥α
Disini x adalah vektor peubah keputusan m dimensi dan fj : ℜm×Ω → ℜ, j = 1, . . . ,n,Ωn adalah himpunan semua kejadian acak. Fungsi objektif juga dapat bertipe keandalan seperti P{w|f0(x,w)≤γ}, dimana f0:ℜm×Ω→ℜdanγkonstanta.
Model antisipatif memilih kebijakan yang memenuhi karakteristik kendala yang diinginkan dan fungsi objektif.
2. 1.2. Model Adaptif
Dalam model ini, informasi yang dikaitkan dengan ketidakpastian muncul secara parsial sebelum pengambilan keputusan, jadi optimisasi terjadi dalam lingkungan pembelajaran. Andaikan A adalah koleksi dari semua informasi relevan yang terse-dia melalui pengamatan yang merupakan sub-gelanggang dari semua kejaterse-dian yang mungkin. Keputusan xtergantung pada kejadian yang dapat diamati, danx disebutA
teradaptasi atauAterukur. Program stokastik adaptif dapat diformulasikan sebagai min E[f0(x(w),w)|A]
kendala E[fj(x(w),w)|A] =0, j=1,2, . . . ,n
x(w)∈X,hampir pasti
(2.1)
Pemetaan x:Ω→X adalah sedemikian hingga x(w) merupakan A terukur. Per-soalan ini dapat disajikan dengan menyelesaikan untuk setiapwprogram deterministik (2.2) berikut :
min E[f0(x, .)|A](w)
kendala E[fj(x, .)|A](w) =0, j=1,2, . . . ,n
x(w)∈X
(2.2)
2. 1.3. Model Recourse
Model ini menggabungkan dua model yang diutarakan terdahulu, yang akan menen-tukan kebijakan yang tidak hanya mengantisipasi pengamatan masa datang tetapi juga memperhitungkan informasi yang ada untuk membuat keputusan rekursif. Misalnya, manajer portofolio memperhatikan gerak masa datang harga saham (antisipasi), sekali-gus juga menyeimbangkan posisi portofolio ketika harga berubah (adaptasi). Persoalan program stokastik dua tahap dengan rekursif dapat ditulis sebagai
min f(x) +E[Q(x,w)]
kendala Ax=b x∈ℜM0
+
denganxadalah keputusan antisipatif tahap pertama yang diambil sebelum peubah acak teramati dan Q(x,w) merupakan nilai optimalnya, untuk sembarang Ω, dari program tak linier:
min ξ(y,w)
kendala W(w)y=h(w)−T(w)x y∈ℜM1
+
dengan y keputusan adaptif tahap kedua yang tergantung pada realisasi vek-tor acak tahap pertama, ξ(y,w) merupakan fungsi biaya tahap kedua, dan
{T(w),W(w),h(w)|w ∈ Ω} adalah parameter model dengan dimensi tertentu. Parameter-parameter ini merupakan fungsi dari vektor acak w dan karena itu meru-pakan parameter acak. T adalah matriks teknologi yang mengandung koefisien teknologi yang mengubah keputusan tahap pertama xmenjadi sumber daya untuk per-soalan tahap kedua.W adalah matriksrecoursedanhvector sumber daya tahap kedua.
min f(x) +E
" min y∈ℜM1
+
{ξ(y,w)|T(w)x+W(w)y=h(w)}
#
kendala Ax=b x∈ℜM0
+
Dari bentuk program stokastik perlu dibentuk model deterministik yang ekivalen se-hingga mudah diselesaikan.
2. 2. Formulasi Deterministik Ekivalen
Pandang model program stokastik linier berikut (Kall and Wallace, 1994) min g0(x,ξ˜)
kendala gi(x,ξ˜)≤0,i=1, . . . ,m,
x∈X ⊂ℜn,
(2.3)
dengan ˜ξ vektor acak yang bervariasi pada himpunan Ξ⊂ ℜk. Lebih tepat lagi, diandaikan bahwa keluarga (f amily) F dari “kejadian”, yaitu himpunan bagian dari
Ξ, dan sebaran peluang Ppada F diketahui. Jadi untuk setiap himpunan bagian A ⊂
Ξyang merupakan kejadian-kejadian, yaitu A∈F, peluangP(A) diketahui. Selanjut-nya, diandaikan bahwa fungsigi(x,·):Ξ→ℜ∀imerupakan peubah acak dan sebaran peluangPadalah bebas.
2. 2.1. Proses Formulasi
Pembentukan model analogi terhadap program stokastik linier denganrecourse, un-tuk problema (2.3) dilakukan dengan cara berikut. Definisikan
g+i (x,ξ) =
0 jikagi(x,ξ)≤0,
gi(x,ξ) selainnya.
Kendala keidari (2.3) dilanggar jika dan hanya jikag+i (x,ξ)>0 untuk suatu keputusan
x dan realisasi ξ dari ˜ξ. Di sini dapat diberikan untuk setiap kendala suatu recourse
atau aktivitas tahap-kedua yi(ξ), setelah mengamati realisasiξ, ( ξ dipilih) sehingga mengantisipasi pelanggaran kendala – jika ada – dengan memenuhigi(x,ξ)−yi(ξ)≤0. Usaha tambahan ini diandaikan mengakibatkan penambahan biaya atau penalti qi per unit, jadi biaya tambahan ini (disebut fungsirecourse) berjumlah
Q(x,ξ) =min y
( m
∑
i=1
qiyi(ξ)|yi(ξ)≥g+i (x,ξ),i=1,···,m )
. (2.4)
Yang menghasilkan biaya total –tahap pertamadan biayarecourse
f0(x,ξ) =g0(x,ξ) +Q(x,ξ). (2.5) Selain (2.4), dapat dipikirkan suatu program linierrecourse yang lebih umum dengan suatu vektor recourse y(ξ)∈Y ⊂ℜn¯, (Y himpunan polyhedral, seperti {y |y ≥ 0}), suatu sembarang pasti (fixed)Wmatrixm×n¯( matriksrecourse) dan vektor unit biaya
q∈ℜn¯, menghasilkan untuk (2.5) fungsirecourse Q(x,ξ) =min
y
qTy|Wy≥g+(x,ξ),y∈Y (2.6)
dengang+(x,ξ) = g+1(x,ξ),···,g+m(x,ξ)T.
perbedaan {permintaan}-{output} produki. Maka g+i (x,ξ)>0 berarti bahwa terda-pat kekurangan dalam produk i, relatif terhadap permintaan. Dengan mengandaikan bahwa pabrik komit untuk memenuhi permintaan, problema (2.4) misalnya dapat di-interpretasikan sebagai membeli kekurangan produk i di pasar. Problema (2.6) dapat dihasilkan dari program produksi tahap-kedua atauemergency, yang dilaksanakan de-ngan faktor input ydan teknologi disajikan oleh matriks W. Jika dipilih W=I, m×m
identitas matriks, (2.4) menjadi kasus khusus dari (2.6).
Akhirnya juga dapat dipikirkan program recourse nonlinier untuk mendefinisikan fungsirecourseterhadap (2.5); misalnya,Q(x,ξ)dapat dipilih sebagai
Q(x,ξ) =minq(y)|Hi(y)≥gi+(x,ξ),i=1,···,m;y∈Y ⊂ℜn¯ , denganq:ℜn¯ →ℜdanHi:ℜn¯ →ℜdiandaikan diketahui.
Dalam kasus terapan, pengambil keputusan yang ingin meminimumkan nilai ek-spektasi biaya total (yaitu, tahap pertama dan biayarecourse), cukup memandang for-mulasi deterministik ekivalen, program stokastik dua-tahap denganrecourse
min
x∈XEξ˜f0(x, ˜
ξ) =min x∈XEξ˜
n
g0(x,ξ˜) +Q(x,ξ˜) o
. (2.7)
Problema dua-tahap di atas dapat diperluas terhadap program recourse tahap-ganda
sebagai berikut: di samping dua keputusan x dan y, harus diambil di tahap 1 dan 2, sekarang problema dihadapkan dengan K+1 keputusan sekuensialx0,x1,···,xK(xτ∈
ℜn¯τ), yang harus diambil pada tahap τ=0,1,···,K. Kata “tahap” dapat, tapi tidak perlu, diartikan sebagai “periode waktu”.
Andaikan untuk penyederhanaan bahwa objektif dari (2.3) deterministik, yaitu,
g0(x,ξ) =g0(x). Pada tahap τ(τ≥1) diketahui realisasi ξ1,···,ξτ dari vektor acak ˜
gτ(x0,···,xτ,ξ1,···,ξτ≤0)
dipenuhi, yang pada tahap ini hanya dapat dicapai oleh pemilihan tepat xτ, yang di-dasarkan pada pengetahuan keputusan dan realisasi sebelumnya. Jadi, dengan men-gandaikan fungsi biayaqτ(xτ), pada tahapτ≥1 diperolah fungsirecourse
Qτ= (x0,x1, . . . ,xτ−1,ξ1, . . . ,ξτ) =min
xτ {qτ(xτ)|gτ(x0,x1, . . . ,xτ−1,ξ1, . . . ,ξτ)≤0},
yang mengidentifikasikan tindakan optimal recoursexˆτpada waktuτtergantung pada keputusan sebelumnya dan realisasi yang diamati hingga tahapτ, yaitu,
ˆ
xτ=xˆτ(x0,···,xτ−1,ξ1,···,ξτ),τ≥1
. Jadi, untuk tahap ganda, diperoleh sebagai total biaya untuk problema tahap-ganda
f0(x0,ξ1,···,ξK) =g0(x0) + K
∑
τ=1
Eξ˜
1,···,ξ˜τQτ(x0,xˆ1,···,xˆτ−1,ξ1,···,ξτ)
menghasilkan deterministik ekivalen untuk problema program stokastik tahap ganda denganrecourse
min x0∈X
"
g0(x0) + K
∑
τ=1
Eξ˜1,···,ξ˜τQτ(x0,xˆ1,···,xˆτ−1,ξ˜1,···,ξ˜τ) #
merupakan generalisasi langsung dari program stokastik dua-tahap dengan recourse (2.7).
2. 3. Pohon Skenario
yang umum untuk memilih himpunan hasil representatif yang relatif kecil yang dise-but skenario untuk menyajikan kejadian acak. Skenario dapat merupakan kuartil dari sebaran yang diketahui atau data historis, prediksi dan beberapa pohon atau dibangun dengan simulasi. Setiap skenario diberikan nilai probabilitas untuk merefleksikan ke-mungkinan kejadiannya. Untuk model tahap ganda, informasi skenario dapat diorgan-isasikan ke dalam struktur pohon.
Gambar 2.1, memberikan contoh pohon skenario untuk persoalan 4 tahap.
Gambar 2.1:Pohon Skenario
Buhul AKAR menyatakan waktu sekarang atau bagian dari data yang diketahui. Pada tahap 2, terdapat 4 kemungkinan berbeda dan setiap dari padanya mempunyai berbagai hasil berbeda yang mungkin di tahap 3 dan seterusnya. Suatu skenario terdiri dari lintasan lengkap dari buhul akar ke satu buhul daun, mendefinisikan realisasi tunggal dari himpunan peubah acak.
turunan langsung dalam waktu t dari buhul k, sedangkan notasi Dt(l.k) menyatakan turunan langsung dalam waktut dari buhulkyang terdiri darilbuhul. Misalnya dalam pohon skenario di Gambar (2.1)D3(2.1)memperlihatkan turunan langsung dari buhul 1 (paling kiri) yang terdiri 2 buhul dalam waktu 3. Untuk setiap buhul daun k dalam tahap T, andaikan Pkt merupakan probabilitas terkait dari keterjadian skenario. Untuk t=T−1, . . . ,l, pkt diberikan oleh
pkt+1=∑l∈Dt+1plt+1dengan pl= 1
Pohon keputusan memberikan kelenturan kepada pemodel untuk memilih skenario yang diperlukan untuk diperhatikan dan kepentingannya. Begitupun tidaklah praktis untuk memperhatikan terlalu banyak skenario. Ini terutama terjadi untuk persoalan dimana banyak mengandung faktor acak.
Ilustrasi Dasar
Perhatikan persoalan program linier (PL). yang formulasinya dalam notasi vektor dapat ditulis sebagai
min cTx
kendala Ax=b
x≥0
Dalam model ini nilai parameter c, A dan b tertentu (deterministik). Artinya bahwa nilai-nilai ini tidak mengandung ketidakpastian. Misalnya harga suatu peubah untuk be-berapa waktu mendatang dapat diperoleh tidak bergantung pada faktor-faktor ekonomi. Hal ini biasanya secara realita tidak tepat. Selalu saja ada pengaruh ketidakpastian. Apalagi pada kondisi dunia pada dekade ini yang dikarakterisasi oleh ketidakpastian tinggi.
Contoh 1 Petani A memiliki sebidang tanah. Ia ingin menamam padi, jagung dan kacang. Yang ingin ia tentukan adalah berapa luas tanah tersebut untuk padi, jagung dan kacang (Birge dan Loveaux, 1997)
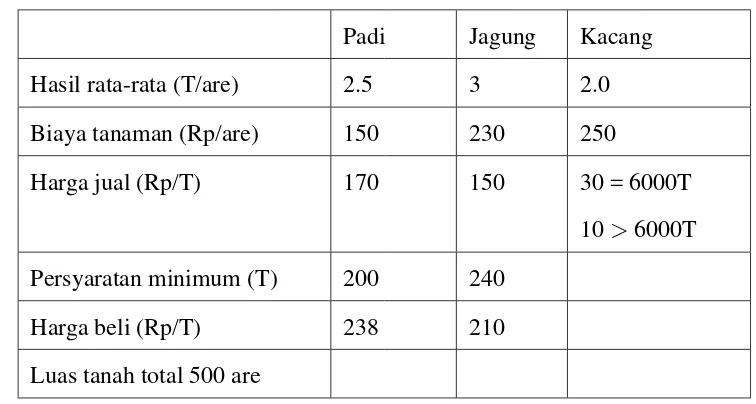
[image:37.612.128.506.223.425.2]Andaikan data untuk pengolahan tanaman tersebut seperti tabel 2.1 berikut:
Tabel 2.1: Data pengolahan tanaman padi, jagung dan kacang
Padi Jagung Kacang
Hasil rata-rata (T/are) 2.5 3 2.0
Biaya tanaman (Rp/are) 150 230 250
Harga jual (Rp/T) 170 150 30 = 6000T
10>6000T Persyaratan minimum (T) 200 240
Harga beli (Rp/T) 238 210
Luas tanah total 500 are
Dalam contoh ini simbol T menyatakan satuan berat dalam ton. Peubah keputusan
x1= luas tanah (are) untuk padi
x2= luas tanah (are) untuk jagung
x3= luas tanah (are) untuk kacang
w1= berat (ton) padi terjual
w2= berat (ton) jagung terjual
w3= berat (ton) kacang terjual pada harga yang diinginkan
w4= berat (ton) kacang terjual di bawah harga yang diinginkan
y1= berat (ton) padi yang dibeli
Problema ini dapat diformulasikan ke dalam model PL (deterministik) min 150x1+230x2+260x3+238y1+210y2−170w1−150w2−36w3−10w4 kendala x1+x2+x3≤500
2.5x1+y1−w1≥200 3x2+y2−w2≥240
w3+w4≤20x3
w3≤6000
x1,x2,x3 ≥0
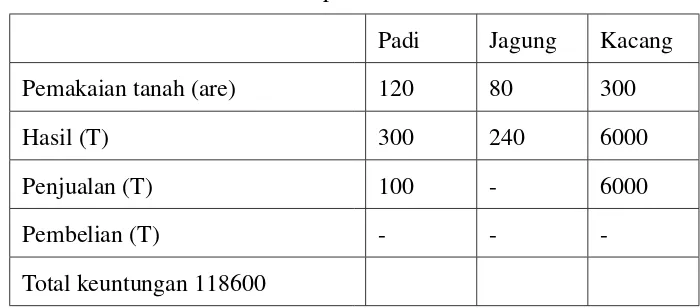
[image:38.612.143.493.370.524.2]w1,w2,w3,w4,y1,y2≥0 Hasil optimalnya adalah
Tabel 2.2: Hasil optimal dari data tabel 2.1
Padi Jagung Kacang
Pemakaian tanah (are) 120 80 300
Hasil (T) 300 240 6000
Penjualan (T) 100 - 6000
Pembelian (T) - -
-Total keuntungan 118600
Hasil demikian ini pada dasarnya telah memenuhi keinginan sang petani.
1. Memanfaatkan luas tanah sesuai dengan kuota tanaman kacangan
2. Memanfaatkan luas tanah untuk memenuhi persyaratan terhadap padi dan jagung
3. Tanam padi untuk tanah yang sisa – jual kelebihannya
1. Cuaca baik: kenaikan 20% 2. Cuaca rata-rata: tetap
3. Cuaca buruk: penurunan 20%
Masing-masing skenario memiliki peluang yang sama yaitu 1/3. Berikut model dengan adanya skenario
min 150x1+230x2+260x3
+13(238y11+210y21−170w11−150w21−36w31−10w41)
+13(238y12+210y22−170w12−150w22−36w32−10w42)
+13(238y13+210y23−170w13−150w23−36w33−10w43)
yi j := peubahyipada tahap j, wi j:= peubahwipada tahap j kendala
(I)
x1+x2+x3≤500
x1,x2,x3 ≥0
(II)
3x1+y11−w11≥200 3.6x2+y21−w21≥240
w31+w41≤24x3
w31≤6000
w11,w21,w31,w41≥0
y11,y21,y31≥0
2.5x1+y12−w12≥200 3x2+y22−w22≥240
w32+w42≤20x3
w32≤6000
w12,w22,w32,w42≥0
y12,y22,y32≥0
2x1+y13−w13≥200 2.4x2+y23−w23≥240
w33+w43≤16x3
w33≤6000
w13,w23,w33,w43≥0
y13,y23,y33≥0
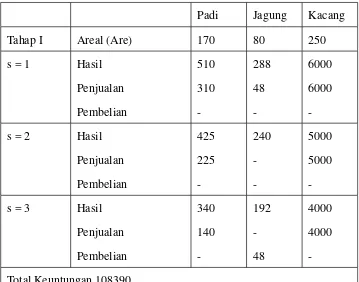
Skenario 1 Skenario 2 Skenario 3
Tabel 2.3: Hasil optimal data tabel 2.1 dengan skenario cuaca berbeda Padi Jagung Kacang
Tahap I Areal (Are) 170 80 250
s = 1 Hasil
Penjualan Pembelian 510 310 -288 48 -6000 6000
-s = 2 Hasil
Penjualan Pembelian 425 225 -240 -5000 5000
-s = 3 Hasil
Penjualan Pembelian 340 140 -192 -48 4000 4000 -Total Keuntungan 108390
Selanjutnya pandang vektor acak ξ = (ε1,ε2,ε3) dibentuk oleh tiga hasil dan ξ diambil pada tiga tiga nilai berbeda ξ1,ξ2 dan ξ3 yaitu
(ε1(1),ε2(1),ε3(1)),(ε1(2),ε2(2),ε3(2)), dan (ε1(3),ε2(3),ε3(3)) berturut-turut. Dalam hal ini ξ tergantung ε atau ξ(ε), sedangkan ε tergantung s atau ε atau ε(s), sehinggaξtergantung padasatauξ(s), dimanasmenyatakan sekenario. s=1,2,3.
Model program stokastik denganrecourse
min 150x1+230x2+260x3
+ ∑3
s=1
kendala x1+x2+x3≤500
x1,x2,x3 ≥0
ε1(s)x1+y1(s)−w1(s)≥200
ε2(s)x2+y2(s)−w2(s)≥240
w3(s) +w4(s)≤ε2(s)x3
w3(s)≤6000
y1(s),y2(s),y3(s)≥0, w1(s),w2(s),w3(s),w4(s)≥0
s= skenario,εi(s)= hasil tanamanipada skenarios
P(s) =13, s = 1,2,3
ε1(1) ε2(1) ε3(1)
ε1(2) ε2(2) ε3(2)
ε1(3) ε2(3) ε3(3) =
3.0 3.6 24 2.5 3.0 20 2.0 2.4 16
Matriks acak Jadi
min 150x1+230x2+260x3 ← bagian deterministik(tahap I)
+
3
∑
1
P(s) (238y1(s) +210y2(s)−170w1(s)−150w2(s)−36w3(s)−10w4(s))
| {z }
Bagian stokastik(tahap II)
kendala
x1+x2+x3≤500
x1,x2,x3 ≥0
ε1(s)x1+y1(s)−w1(s)≥200
ε2(s)x2+y2(s)−w2(s)≥240
w3(s) +w4(s)≤ε2(s)x3
w3(s)≤6000
y1(s),y2(s),y3(s)≥0, w1(s),w2(s),w3(s),w4(s)≥0 s=1,2,3
←kendala stokastik(tahap II)
Dari bentuk model ini dapat dituliskan fungsi recoursenya adalah
Q(x1,x2,x3,s) =min 238y1(s) +210y2(s)−170w1(s)−150w2(s)−36w3(s)−10w4(s) kendala ε1(s)x1+y1(s)−w1(s)≥200
ε2(s)x2+y2(s)−w2(s)≥240
w3(s) +w4(s)≤ε2(s)x3
w3(s)≤6000
y1(s),y2(s),y3(s)≥0, w1(s),w2(s),y3(s),y4(s)≥0 Jadi nilai ekspektasi dari fungsirecourse
Q(x) =EξQ(x,ξ) =
3
∑
i=1
P(s)Q(xi,s)
Sehingga modelrecourseberbentuk
min 150x1+230x2+260x3+EξQ(x,ξ) kendala x1+x2+x3≤500
x1,x2,x3≥0
min cTx+Q(x)
kendala Ax=b
x≥0
secara lebih umum modelrecourseini dapat berbentuk min
x f1(x) +Eξ[Q(x,ξ)] kendalaAx=b
x≥0
dimana untuk setiap realisasiwdariε
Q(x,w) =min
y f2(y,w)
kendala W(w)y=h(w)−v(w)x y≥0
nilai ekspektasi dari nilai objektif tahap kedua merupakanrecourse. Pada tahap pertama sebuah keputusan dibuat didasarkan pada data yang tersedia pada saat itu.
Ditahap kedua, untuk setiap realisasi yang mungkin dari peubah acak ε, suatu ke-putusan baru diambil yang tergantung pada keke-putusan tahap satu. Ekspektasi biaya pada kedua tahap dihitung dan keputusan tahap satu dapat direvisi untuk mencapai ke-seimbangan biaya keseluruhan yang lebih baik antara tahap 1 dan 2. Proses demikian ini diulang hingga ekspektasi biaya keseluruhan optimal.
Peubah ketidakpastian dengan sebaran kontinu
Tabel 2.4: Data pengolahan tanaman padi, jagung dan kacang dengan sebaran kontinu
Padi Jagung Kacang
Hasil (T/are) ε1 ε2 ε3
Biaya Tanam (Rp/are) 150 230 280
Harga Jual (Rp/T) 170 150 30≤6000T
10>6000T
Kebutuhan Minimum (T) 200 240
Harga Beli (Rp/T) 238 210
Luas tanah yang tersedia 500 are
1. ε1,ε2,ε3realisasi hasil vektor acakεtersebar bebas
2. ℓi ≤εi≤ui, i=1,2,3 bersebaran bebas, ℓi adalah batas bawah, dan ui adalah batas atas.
KepadatanPε(t) =
1/(ui−ℓi) ℓi≤t≤ui 0 t∈/[ℓi,ui] Formulasi Program Stokastik
min 150x1+230x2+260x3←bagian deterministik(tahap I)
+Eε1,ε2,ε3(238y1+280y2−170w1−150w2−36w3−10w4)
| {z }
Bagian stokastik(tahap II)
I
x1+x2+x3≤500
x1,x2,x3≥0
←kendala deterministik(tahap I)
II
ε1x1+y1−w1≥200
ε2x2+y2−w2≥240
w3+w4≤ε3x3
w3≤6000
y1,y2,y3≥0,w1,w2,w3,w4≥0
x1,x2,x3≥0
←kendala stokastik(tahap II)
Dekomposisi program stokastik
min 150x1+230x2+260x3+Eε1(238y1−170w1) +Eε2(210y1−150w2) +Eε3(−36w3−10w4)
Kendala:
I
x1+x2+x3≤500
x1,x2,x3≥0
Padi y Jagung y Kacang y
(II.1)
ε1x1+y1−w1≥200
y1≥0,w1≥0
(II.2)
ε2x2+y2−w2≥240
y2≥0,w2≥0
(II.3)
w3+w4≤ε3x3
w3≤6000
w3,w4≥0
dengany1danw1 hanya tergantung pada keputusanx1 dan hasil acakε1(padi),y2 dan
FungsiRecourse
Q1(x1,ε1) =min 238y1(ε1)−170w1(ε1) Kendala ε1x1+y1−w1≥200 Padi
y1(ε1)≥0,w1(ε1)≥0
Q2(x2,ε2) =min 210y2(ε2)−150w2(ε2) Jagung Kendalaε2x2+y2(ε2)−w2(ε2)≥240
y2(ε2)≥0,w2(ε2)≥0
Q3(x3,ε3) =min(−36w3(ε3)−10w4(ε3)) Kendalaw3(ε3) +w4(ε3)≤ε3x3 Kacang
w3(ε3)≤6000
w3(ε3)≥0
Bentuk eksplisit fungsirecourse
Padi
y1(ε1) =−min[ε1x1−200,0],w1(ε1) =max[ε1x1−200,0],
Q1(x1,ε1) =−238 min[ε1x1−200,0]−170 max[ε1x1−200,0] Jagung
y2(ε2) =−min[ε2x2−240,0],w1(ε1) =max[ε2x2−240,0]
Q2(x2,ε2) =−210 min[ε2x2−240,0]−150 max[ε2x2−240,0] Kacang
w3(ξ3) =min[6000,ε3x3], w4(ε3) =max[ε3x3−6000,0]
Jadi formulasirecourse
min 150x1+230x2+260x3
+Eε1Q1(x1,ε1) +Eε2Q2(x2,ε2) +Eε3Q3(x3,ε3)
kendala
x1+x2+x3≤500
Perhitungan nilai ekspektasi untuk fungsirecourse
Padi: Hasilε1bersebaran uniform
Pεε(t) =
1/(ui−ℓi) ℓi≤t≤ui 0 t∈/[ℓi,ui]
Kasus 1. Apabilau1,x1≤200,Q1(x1,ε1) =−238[x1,ε1−200],
Q1(x1) =Eε1Q1(x1,ε1) =−238
Ru1
ℓ1 (tx1−200)Pε1(t)dt =7600−238x1ε¯1
dengan ¯ε1= (u1+x1)/2 dalam nilai ekspektasi dariεi,i=1,2,3 Kasus 2. Apabilaℓ1x1≤200≤u1x1,
Q1(x1) =Eε1Q1(x1,ε1)
=−238Ru1
ℓ1 (tx1−200)Pε1(t)dt−170
Ru1
200/x1(tx1−200)Pε1(t)dt = −170(ε¯1x1−200) +34
(200−ℓ1x1)2
(u1−ℓ1)x1
Kasus 3. Apabila200≤ℓ1x1:Q1(x1,ε1) =170(x1,ε1−200),
Q1(x1) =Eε1Q1(x1,ε1) =−170
Ru1
ℓ1 (tx1−200)Pε1(t)dt =34000−170x1ε¯1
Untuk Jagung
Q2(x2) =
50400−210x2ε¯2 u2x2≤240
−150(x2ξ2−240) +30
(240−ℓ2x2)2
(u2−ℓ2)x2
ℓ2x2≤240≤u2x2 36000−150x2ε¯2 240≤ℓ2x2
Untuk Kacang
Q3(x3) =
−36x3ε¯3 u3x3≤6000
−36x3ε¯3+13
(u3x3−6000)2
(u3−ℓ3)x3
ℓ3x3≤240≤u3x3
−156000−10x3ε¯3 6000≤ℓ3x3
Jadi dapat dituliskan formulasi global dari program stokastik sebagai persoalan opti-misasi konveks
min 150x1+230x2+260x3+Q1(x1) +Q2(x2) +Q3(x3) kendalax1+x2+x3≤500
x1,x2,x3≥0
Fungsi Qi(xi)konveks, kontinu, dapat diturunkan (differentiable) yang hanya tergan-tung pada vector keputusanx. Penyelesaian persoalan global optimum dengan menggu-nakan syarat Karush-Kuhn-Tucker sebagai syarat perlu dan cukup. Dengan mengambil
Syarat Karush-Kuhn-Tucker (KKT)
xi
ci+∂∂
xi
Qi(xi) +λ
=0
ci+
∂ ∂xi
Qi(xi) +λ≥0
λ(x1+x2+x3−500) =0
x1+x2+x3≤500
x1,x2,x3≥0, λ≥0
Perhitungan derivatif
Padi
∂ ∂x1
Q1(x1) =
−238¯ε1 u1x1≤200
−34
ℓ2 1
u1−ℓ1− 5¯ε1−
40000
(u1−ℓ1)x1
ℓ1x1≤200≤u1x1 36000−150x2ε¯2 200≤ℓ1x1 Jagung
∂ ∂x2
Q2(x2) =
−210¯ε2 u2x2≤240
−30
ℓ22
u2−ℓ2− 5¯ε2−
57600
(u2−ℓ2)x2
ℓ2x2≤240≤u2x2
−150¯ε2 240≤ℓ2x2
Kacang
∂ ∂x3
Q3(x3) =
−36¯ε3 u3x3≤6000
−36¯ε3+ 13u23 u3−ℓ3−
468.106
(u3−ℓ3)x23
ℓ3x3≤6000≤u3x3
Andaikan bahwa
ℓ1=2,0, u1=3,0, ε¯1=2,5 ℓ2=2,4, u2=3,6, ε¯2=3,0 ℓ3=16, u3=24, ε¯3=20
Dengan memakai teknik enumerasi dapat ditentukan bahwa penyelesaian optimal harus memenuhi
x1≥100, 200
3 ≤x2≤100, 250≤x3≤375
Dengan menggunakan syarat KKT, diperoleh sistem persamaan
−275+λ=0
−76−1,44(10 6)
x22 +λ=0
476−5,85(10 7)
x23 +λ=0 x1+x2+x3=500
Dengan menyelesaikan sistem persamaan linier homogen di atas diperoleh nilai optimal
λ∗=275, x∗
BEBERAPA APLIKASI PERSOALAN CHANCE
CONSTRAINED
Walaupun masih terbatas, persoalan chance constraint makin berkembang, beberapa penulis membahas secara teori atau menggunakan dalam kasus-kasus tertentu. Dalam bab ini penulis hanya menyajikan beberapa ringkasan temuan atau bahasan tersebut.
3. 1. Chance Constrained Programming Untuk Analisis Pengelolaan Portofolio
Sharma, dkk (2008) mengajukan chance constrained programming untuk anali-sis pengamanan dan managemen portofolio dengan sebutan MOCCP (multi objective chance constrained programming) yang model matematikanya dapat dinyatakan seba-gai
maks n
∑
j=1
ck jxj, k=1,2, . . . ,K1 (3.1)
min n
∑
j=1
ck jxj, k=K1+1,K1+2, . . . ,K (3.2)
dengan kendala
P(
n
∑
j=1
ci jxj)≥1−αi, i=1,2, . . . ,m. (3.3)
xj≥0, j=1,2, . . . ,n, αi∈(0,1), i=1,2, . . . ,m. (3.4)
dimanaxjadalah peubah keputusan kej, ck j,ai j danbi, adalah peubah acak,αiadalah taraf signifikansi dari kendala probalistik ke i (i= 1,2, ... ,m). Fungsi tujuan dengan beberapa kendalanya mengandung peubah acak.
Pembentukan model deterministik yang setara dapat dilakukan seperti di bawah ini. Bentuk deterministiknonlinear programmingdari persamaaan (3.1)- (3.4) dapat diper-oleh seperti berikut:
K1
∑
k=1
λk+ K
∑
k=K1+1
λ′ k
dengan kendala:
E(zk− n
∑
j=1
ck jxj) +φ−1(1−βk) s
var(zk− n
∑
j=1
ck jxj)]≤λk, k=1,2, . . . .K1
E(
n
∑
j=1
ck jxj−z ′
k) +φ−1(1−β ′ k)
s
var(−
n
∑
j=1
ck jxj)z′k≤λk, k=K1+1,K1+2, . . . .K
E(
n
∑
j=1
ai jxj−bi) +φ−1(1−αi) s
var(−
n
∑
j=1
ai jxj)−bi≤0, k=1,2, . . . ,m
xj≥0, j=1,2, . . . ,n,αi∈(0,1), i=1,2, . . . ,m, λk,λ ′ k≥0 dimanazk =maks
n
∑
j=1
ck jxj, k=1,2, . . . ,K1 dan z ′
k=min n
∑
j=1
ck jxj, k=K1+1,K1+ 2, . . . ,K.
s= indeks proporsi uang diinvestasi dalam stok s∈ {1,2, . . . ,S} Xs= proporsi uang diinvestasi dalam stok s
Rs= rate tahunan perolehan dari stok, peubah acak
Ds= keuntungan saham atau hasil bunga dari stok s, peubah acak
βs= besarnya resiko berhubungan stok s, peubah acak
Us= banyaknya uang diinvestasikan pada stok s, peubah acak
Qs= indeks qualitas dari stok s
Qmin= qualitas minimum, peubah acak
PEs= rasio harga
PEmax= keuangan maksimal perusahaan, peubah acak
Rmax= rate penerimaan tahunan maksimum perusahaan
Dmax= penerimaan tahunan maksimum dari keuntungan saham
βmin= resiko stok
a,a′,a”= tingkat signifikansi rasio harga portfolio, rate analisis, dan kendala diversifikasi investasi
Fungsi tujuan dari model
• (i) Risiko portofolio: min
S
∑
s=1
βsXs, merupakan risiko sistematik dan diukur de-ngan sensivitas pengembalian stok pasar.
• (ii) Dividen tahunan: maks ∑S
s=1
DsXs, merupakanincome devidentahunan yakni bertujuan untuk memperoleh penghasilan paling tinggi dari stok.
• (iii) Perolehan tahunan: maks S
∑
s=1
Kendala dari model
(i)Rasio perolehan harga portofolio: yang diperoleh dari data yang lalu dan rataan
data yang dapat digunakan ke masa depan
P(
S
∑
s=1
PEsXs≤PEmaks)≥1−a
(ii) Uji pengamat(analyst’rating): sifatnya subjektif
P(
S
∑
s=1
QsXs≥Qmin)≥1−a′
(iii) Investasipengambil keputusan harus menggunakan total dana sehingga: S
∑
s=1
Xs=1
(iv) Diversifikasi investasi untuk meminimasi resiko, seorang investor tidak akan
menanam modal lebih dari proporsi tertentu dari uangnya pada sebarang stok tunggal, dan karena itu kendala diversivikasi investasi (investment diversification constraint) da-pat dibangun melalui suatuchance constraint sebagai berikut:
P(Xs≤Us)≥1−a”,s=1,2, . . . ,S
3. 2. OptimisasiChance ConstrainedPengelolaan Air Asin
Strack (1976) dalam Benhachmi dkk (2001) mengutarakan rumus tunggal potensial dalam nutrisi air asin berupa rumus Laplace
dalam dua dimensi yang dianggap valid untuk zona air tawar dan air asin. PotensialΦ mengikuti definisi berikut:
Untukconfined aquifer:
Φ=Bhj+
(s−1)B2
2 −sBd air tawar
Φ= 1
2(s−1[h1+ (s−1)B−sd]
2 air asin
untukunconfined aquifer:
Φ= 1
2[h 2
j−sd2] air tawar
Φ= s
2(s−1)(hj−d)
2 air asin.
hjadalahpiezometrik headair tawar,d ketinggian permukaan laut terhadap dataran,B batas ketebalan akuifer, sadalah rasio kepekatan air asin dengan air tawar. Persoalan diselesaikan sebagai masalah satu zona dengan kondisi batas yang tepat. Persoalan dapat diselesaikan dengan cara analitik atau numerik, lokasi ruang terjepitxi dihitung seperti:
ξ=
r 2φ
s−1+d−B untukconfined aquifer
ξ=
r 2φ
s(s−1) untukunconfined aquifer
Kaki pinggir air asin ditempatkan padaξ=d, sehingga persamaan menunjukkan kaki pinggir air asin ditempatkan denganΦbernilai
Φ= s−1
2 B
2 untukconfined aquifer
Φ= s(s−1)
2 d
Untuk kedua akuifer, suatu pemecahan ditemukan, lokasi kaki air asin dapat diturunkan dari persamaan tersebut di atas, sehingga lokasi kaki air asin, xtoe dapat dipecahkan dari:
Φtoe=
q Kxtoe+
n
∑
w=1
Qw 4πKln
(xtoe−xw)2+ (ytoe−yw)2
(xtoe+xw)2+ytoe−yw)2
dimana (xw,yw) adalah koordinat yang tepat, Qw besar pemompaan untuk lokasi w sejauh xw dari pantai, K adalah konduktivitas hidrolik dan qbesar kelajuan aliran air tawar
Model pengelolaan akuifer pesisir dikembangkan untuk penarikan air yang ber-kelanjutan dari akuifer untuk keperluan yang bermanfaat. Karena strategi penggu-naan memompa terdistribusi spasial, intrusi air laut terjadi dan salinitas air dipompa bervariasi dengan besarnya dan lokasi memompa dalam domain ruang dua dimensi dari akuifer. Model manajemen dikembangkan mempertimbangkan fungsi tujuan yang masuk akal dengan memperhitungkan nilai ekonomi. Pertimbangan eksplisit nilai ekonomi memerlukan definisi fungsi biaya dan manfaat yang akan termasuk dalam model. Biaya memompa diasumsikan berbanding lurus dengan produk dari tingkat pe-mompaan dan daya angkat (lift) total pada setiap sumur. Perumusan matematika dari persoalan optimisasi dapat ditulis sebagai:
MaksZ=
n
∑
i=1
BpQi−CpQi(Li−hi)
dimanaZ adalah fungsi tujuan, dengan kendala berikut:
1) Kendala lokasi kaki pantai:Xtoe<Xi,i=1,n
2) Batas-batas kapasitas praktis memompa tidak boleh melebihi:
Qi adalah laju pembuangan air sumuri, Xwi adalah jarak sumur ke i dari pantai,Xtoei adalah lokasi kaki dari pantai di depan sumuri,Qmini danQmaksi masing-masing adalah debit minimum dan maksimum dari sebuah sumur dibatasi oleh kapasitas peralatan,hi adalah kepala hidrolik pada sumur titik i, Li awal lift pada sumur i, Bp adalah keun-tungan per unit suplai air di sumur titik i, Cp adalah biaya memompa satuan volume per unit pada titik sumur i, dan n adalah jumlah sumur. Untuk sumur yang ada di lokasi tetap, peubah desain adalah tarif memompa Qi. Untuk sumur baru yang akan dipasang, peubah desain dapat mencakup sejumlah sumur, pembuangan, dan lokasi sumur dalam koordinatxdany. Kendala utama dari masalah adalah tidak ada kriteria invasi sumur. Kendala lain mungkin termasuk maksimum dan minimum tarif mem-ompa dari setiap sumur yang harus dipenuhi. Untuk memungkinkan algoritma genetika digunakan, kendala dalam persoalan maks Z = ∑n
i=1
BpQi−CpQi(Li−hi) pertama di-transformasikan menjadi sesuatu yang tanpa kendala. Hal ini dicapai dengan memak-sakan kendala dalam fungsi tujuan. Misalnya, untuk memastikan tidak ada gangguan air asin, fungsi keuntungan dapat didefinisikan sebagai:
F =
n
∑
i=1
BpQi−CpQi−CpQi(Li−hi)−r m
∑
j=1
1−Xtoej
Xwi 2
dimanar adalah faktor paksaan dan m banyak kendala pengganggu. Jika kendala di-langgar, kita asumsikan bahwa fungsi manfaat didefinisikan sebagai:
F =
n
∑
i=1
BpQi−CpQi−CpQi(Li−hi)−r n
∑
i=1
BpQmaksi −CpQmaksi (Li−hi)
Dalam hal ini maksimasi tanpa kendala (unconstrained) terselesaikan
digunakan untuk mengubah model kendala probabilistik dengan yang deterministik, karena memecahkan masalah setara deterministik jauh lebih mudah daripada persoalan probabilistik. Dengan menganggap X peubah tak bebas kaki yang dijelaskan oleh se-baran probabilitas di setiap lokasi i. Probabilitas harus lebih besar daripada beberapa reliabilitasrtoei
Pr{Xtoe<Xi} ≥rtoei
Akibatnya, kendala sisi kiri lokasi kaki adalah acak karena berisi peubah acak tarif aliran air tawar dan debit memompa pengeluaran air sumur. Pertidaksamaan terakhir tidak operasional matematis dan modifikasi lebih lanjut atau memerlukan transformasi. Untuk membuat operasional matematis, perlu akses secara statistik persamaanchance constrained. Chance constraineduntuk lokasi kaki adalah:
E[Xtoe] +N−1(rtoeiσ[Xtoei]≤Xi
E[Xtoe] adalah nilai ekspektasi lokasi kaki menyataan rataan lokasi kaki,
N−1(rtoeiσ[Xtoei] adalah komponen statistik di manaN−
1 adalah sebaran standar nor-mal kumulatf dari level spesifik rtoei, dan σ[Xtoei adalah simpangan baku lokasi kaki. Rataan dan varians dari lokasi kaki diberikan sebagai berikut:
¯
Xtoe = Xtoe+12 h
∂2X
toe
∂q2 σ2q+∂
2X
toe
∂Q2i σ 2 Q
i
+2∂2Xtoe
∂q∂QσqQ
σ2X toe = h∂ Xtoe ∂q i2 σ2 q+ h∂ Xtoe
∂Qi i2
σ2 Q+2∂
Xtoe
∂q
∂Xtoe
∂Q σqQ
Kovarian σqQ dapat diatur nol didasarkan pertimbangan fisik, dan akibatnya dapat disederhanakan.