Pemodelan Regresi Nonparametrik Dengan B – Spline Dan Mars

PEMODELAN REGRESI NONPARAMETRIK

DENGAN B – SPLINE DAN MARS

SARAH MAHDIA

090823001

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : PEMODELAN REGRESI NONPARAMETRIK DENGAN

B – SPLINE DAN MARS

Kategori : SKRIPSI

Nama : SARAH MAHDIA

Nomor Induk Mahasiswa : 090823001

Program Studi : S1 STATISTIKA EKSTENSI

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM

(FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di Medan, Juli 2011

Komisi Pembimbing:

Pembimbing 2, pembimbing 1,

Drs. Pasukat Sembiring, M.Si Prof. Suwarno Ariswoyo, M.Si

NIP. 195311319850031002 NIP. 195003211980031001

diketahui/ disetujui oleh

Departemen Matematika FMIPA USU

PERNYATAAN

PEMODELAN REGRESI NONPARAMETRIK DENGAN B – SPLINE DAN MARS.

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juli 2011

SARAH MAHDIA 090823001

PENGHARGAAN

Syukur Alhamdulillah penulis ucapkan kehadirat ALLAH SWT yang telah memberikan rahmat dan hidayah serta karunia sehingga penyusunan skripsi ini dapat diselesaikan dengan baik dan tepat waktu.

Adapun tujuan dari penulisan skripsi ini adalah merupakan salah satu syarat untuk menyelesaikan Program S1 Statistika Ekstensi pada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

Sebagai salah satu perwujudan dari proses pendidikan kemahasiswaan, penyusunan skripsi ini disajikan berdasarkan pembahasan oleh penulis.

Selama dalam penyusunan skripsi ini penulis telah banyak memperoleh bantuan dan bimbingan, untuk itu pada kesempatan ini penulis mau mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Bapak Drs. Suwarno Ariswoyo, M.Si selaku pembimbing 1 pada penulisan skripsi ini yang telah bersedia memberikan arahan, bimbingan dan petunjuk kepada penulis dalam penyelesaian skripsi ini.

2. Bapak Drs. Pasukat Sembiring, M.Si selaku pembimbing 2 pada penulisan skripsi ini yang telah bersedia memberikan arahan, bimbingan dan petunjuk kepada penulis dalam penyelesaian skripsi ini.

3. Bapak Drs. Henry Rani Sitepu, M.Si dan Bapak Drs. H. Haluddin Panjaitan selaku dosen penguji yang telah memberikan masukan dalam penyelesaian skripsi ini.

4. Bapak Dr. Sutarman, M.Sc selaku Dekan FMIPA USU.

5. Bapak Prof. Dr. Tulus, M.Si selaku Ketua Departemen Matematika FMIPA USU. 6. Bapak Drs. Pengarapan Bangun, M.Si selaku Ketua Pelaksana Jurusan Progam

S1 – Statistika Ekstensi.

7. Kepada Ayahanda Dr. H. Hamonangan Nainggolan,M.Sc dan Ibunda Hj. Jusridawati Situmeang yang telah memberikan motivasi dan kekuatan dalam menyelesaikan skripsi, serta Abangku Yasser Hudan, adik-adikku Pauzi Ibrahim, Aisyah Hudaya, dan Maulana As-salam atas dukungan yang telah diberikan.

9. Semua pihak yang terkait dalam penyelesaian skripsi ini.

Sepenuhnya penulis menyadari bahwa dalam penyusunan skripsi ini masih banyak terdapat kekurangan. Untuk itu penulis mengharapkan saran dan kritik yang bersifat membangun, dimana saran dan kritik tersebut dapat dimanfaatkan untuk kemajuan ilmu pengetahuan pada saat ini dan yang akan datang.

Semoga penulisan skripsi ini dapat memberikan manfaat dan berguna bagi pembaca dan penulis khususnya. Akhir kata penulis mengucapkan banyak terima kasih.

Medan, Juli 2011

ABSTRAK

Analisa regresi digunakan untuk melihat pengaruh variabel independen terhadap variabel dependent dengan terlebih dahulu melihat pola hubungan variabel tersebut. Hal ini dapat dilakukan dengan melalui dua pendekatan. Pendekatan yang paling umum dan seringkali digunakan adalah pendekatan parametrik. Pendekatan parametrik mengasumsikan bentuk model yang sudah ditentukan. Apalabila tidak ada informasi apapun tentang bentuk dari fungsi regresi, maka pendekatan yang digunakan adalah pendekatan nonparametrik (Hardle, 1990). Karena pendekatan tidak bergantung pada asumsi bentuk kurva tertentu, sehingga memberikan fleksibilitas yang lebih besar. Tujuan penelitian ini adalah mendapatkan model terbaik mengenai nilai ujian tengah semester (UTS) terhadap nilai ujian akhir semester (UAS) mahasiswa Jurusan Kimia Industri semester genap tahun ajaran 2009 / 2010, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara dengan analisis regresi linear sederhana, kuadratik, dan kubik, sedangkan regresi nonparametrik digunakan B – Spline dan Multivariate Adaptive Regression Splines (MARS). Secara keseluruhan, model terbaik dipilih berdasarkan koefisien determinasi terbesar. Namun demikian untuk MARS, model terbaik dipilih berdasarkan pada GCV, minimum MSA, dan koefisien determinasi terbesar.

ABSTRACT

Regression analysis is constructed for capturing the influences of independent variables to

dependent ones. It can be done by looking at the relationship between those variables. This task

of approximating the mean function can be done essentially in two ways. The quiet often use

parametric approach is to assume that the mean curve has some prespecified functional forms.

Alternatively, nonparametrik approach, .i.e., without reference to a specific form, is used when

there is no information of the regression function form (Hardle, 1990). Therefore nonparametric

approach has more flexibilities than the parametric on. The aim of this research is to find the

best fit model that captures relationship between admission test score to the GPA. The purpose

of this research is to obtain the best model abaout mark on midterm against final exam score

student majoring in industrial chemistry second 2009/2010 academic year,Faculty of

Mathematics and Natural Science northem Sumatera with a simple linear, quadratic,and cubic

regression analysis. Those two approaches were used here. In the parametric approach, we use

simple linear, quadric cubic regression, and in the nonparametric ones, we use B – Spline and

Multivariate Adaptive Regression Splines (MARS). Overall, the best model was chosen based on

the maximum determinant coefficient. However, for MARS, the best model was chosen based on

the GCV, minimum MSE, maximum determinant coefficient.

DAFTAR ISI

Halaman

Persetujuan i

Pernyataan ii

Penghargaan iii

Abstrak v

Abstract vi

Daftara Isi vii

Daftar Tabel viii

Bab I Pendahuluan 1

1.1LatarBelakang 1

1.2Perumusan Masalah 2

1.3Tinjauan Pustaka 2

1.4Tujuan Penelitian 3

1.5Kontribusi Penelitian 3

1.6Metode Penelitian 3

Bab II Landasan Teori 4

2.1 Model Regresi Nonparametrik 4

2.2 Rgresi Spline 6

2.3 Basis B - Spline 7

2.4 Multivariate Adaptive Regression Splines (MARS) 10

2.5 Memilih Persamaan Regresi Terbaik 13

Bab III Pembahasan 16

3. Data dan Pembahasan 16

3.1 Pola Hubungan Nilai UTS Terhadap UAS dengan Pemodelan B – Spline. 25

3.2 Pola Hubungan Nilai UTS Terhadap UAS dengan Pemodelan MARS. 27

Bab IV Kesimpulan dan Saran 29

4.1 Kesimpulan 29

4.2 Saran 30

Daftar Tabel

Halaman

ABSTRAK

Analisa regresi digunakan untuk melihat pengaruh variabel independen terhadap variabel dependent dengan terlebih dahulu melihat pola hubungan variabel tersebut. Hal ini dapat dilakukan dengan melalui dua pendekatan. Pendekatan yang paling umum dan seringkali digunakan adalah pendekatan parametrik. Pendekatan parametrik mengasumsikan bentuk model yang sudah ditentukan. Apalabila tidak ada informasi apapun tentang bentuk dari fungsi regresi, maka pendekatan yang digunakan adalah pendekatan nonparametrik (Hardle, 1990). Karena pendekatan tidak bergantung pada asumsi bentuk kurva tertentu, sehingga memberikan fleksibilitas yang lebih besar. Tujuan penelitian ini adalah mendapatkan model terbaik mengenai nilai ujian tengah semester (UTS) terhadap nilai ujian akhir semester (UAS) mahasiswa Jurusan Kimia Industri semester genap tahun ajaran 2009 / 2010, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara dengan analisis regresi linear sederhana, kuadratik, dan kubik, sedangkan regresi nonparametrik digunakan B – Spline dan Multivariate Adaptive Regression Splines (MARS). Secara keseluruhan, model terbaik dipilih berdasarkan koefisien determinasi terbesar. Namun demikian untuk MARS, model terbaik dipilih berdasarkan pada GCV, minimum MSA, dan koefisien determinasi terbesar.

ABSTRACT

Regression analysis is constructed for capturing the influences of independent variables to

dependent ones. It can be done by looking at the relationship between those variables. This task

of approximating the mean function can be done essentially in two ways. The quiet often use

parametric approach is to assume that the mean curve has some prespecified functional forms.

Alternatively, nonparametrik approach, .i.e., without reference to a specific form, is used when

there is no information of the regression function form (Hardle, 1990). Therefore nonparametric

approach has more flexibilities than the parametric on. The aim of this research is to find the

best fit model that captures relationship between admission test score to the GPA. The purpose

of this research is to obtain the best model abaout mark on midterm against final exam score

student majoring in industrial chemistry second 2009/2010 academic year,Faculty of

Mathematics and Natural Science northem Sumatera with a simple linear, quadratic,and cubic

regression analysis. Those two approaches were used here. In the parametric approach, we use

simple linear, quadric cubic regression, and in the nonparametric ones, we use B – Spline and

Multivariate Adaptive Regression Splines (MARS). Overall, the best model was chosen based on

the maximum determinant coefficient. However, for MARS, the best model was chosen based on

the GCV, minimum MSE, maximum determinant coefficient.

BAB 1

PENDAHULUAN

1.1Latar Belakang

Metode statistika nonparametrik atau sering disebut dengan metode statistik bebas distribusi yang menyajikan suatu cara yang berguna bagi para peneliti dan banyak mendapat perhatian yang cukup luas di kalangan ahli statistik. Ini memungkinkan karena beberapa alasan. Pertama, perhitungan yang diperlukan sederhana, murah, dan cepat. Kedua, data atau sampel dapat berupa respons kualitatif atau data ordinal. Dan ketiga, bila dalam uji parametrik sangat dipengaruhi asumsi mengenai bentuk distribusinya, baik statistik contoh maupun distribusi parameter populasinya. Oleh karena itu, dalam statistik nonparametrik terdapat suatu analisis data statistik yang sangat cocok digunakan untuk menguji data ilmu - ilmu sosial, karena asumsi - asumi yang digunakan dalam uji nonparametrik adalah pengamatan - pengamatan bebas, tidak mengikat dan lebih luas dibanding uji parametrik.

mengetahui suatu perbedaan yang tidak diketahui dalam uji nonparametrik. Akan tetapi, bila tidak memenuhi syarat – syarat dari uji parametrik seperti asumsi normalitas distribusi yang sering dijadikan asumsi utama dan tidak bisa menjamin kenormalitasan distribusi tersebut, maka dapat menggunakan pengujian nonparametrik.

Dalam pengujian nonparametrik terdapat hubungan sebab – akibat atau yang sering disebut regresi. Regresi nonparametrik itu sendiri adalah bentuk analisis regresi dimana peubah bebasnya (prediktor) tidak mengambil bentuk yang telah ditetapkan tetapi dibangun sesuai dengan informasi yang diperoleh dari sampel. Regresi nonparametrik memerlukan ukuran sampel yang lebih besar daripada regresi berdasarkan model parametrik karena data atau sampel harus memberikan struktur model serta perkiraan model.

1.2Perumusan Masalah

Masalah dalam penelitian ini adalah bagaimana pemodelan regresi B – Spline dan MARS pada model regresi nonparametrik, dan melakukan simulasi untuk membandingkan MSE B – Spline dan Spline truncated, juga penerapan B – Spline pada data riil.

1.3Tinjauan Pustaka

Bentuk umum dari model regresi nonparametrik, yaitu yi = g(xi) + εi dimana i = 1,2..,n dengan εi merupakan residual yang diasumsikan berdistribusi normal independen dengan mean nol dan variansi σ2

Dan apabila yang digunakan adalah pendekatan kurva Spline truncated maka regresi tersebut merupakan regresi nonparametrik, yang kurva regresi g dapat ditulis sebagai berikut, (Eubank, 1988) :

∑

∑

₌ − + = − _{+ −} = K j m j j m i i

it t u t g 1 1 1 1 ) ( ) ( α β ,

dengan uj, j = 1,2,..,K dengan uj<u2<…<uK adalah titik knot dan m ฀ N0 (integer non negatif). Nilai m menunjukkan derajat spline truncated. Jika kurva regresi g didekati dengan fungsi B – Spline maka g dapat ditulis menjadi :

∑

+₌ −

=m K

j m m j j t Y t g 1 , ( ) ) ( β

dengan βj-m,m merupakan basis B-Spline.

Spline adalah salah satu jenis potongan polynomial, yaitu polynomial yang memiliki sifat tersegmen. Sifat tersegmen ini memberikan fleksibilitas lebih dari polynomial biasa, sehingga memungkinkan untuk menyesuaikan diri secara lebih efektif terhadap karakteristik lokal dari suatu fungsi atau data. Secara umum, fungsi spline berorde k adalah sembarang fungsi yang dinyatakan sebagai berikut :

( )

1 1 1 0 ) ( ₊− = − − + −

=

∑

∑

k

j h j j i k i

it t u t

s α δ , dimana

    − = − = − + , 0 ) ( ) ( 1 1 k j k j u t u t j u t u t ≤ ≥ , , dengan :

α dan δ = konstanta riil

1.4Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk mendapatkan model terbaik mengenai pemodelan regresi nonparametrik dengan B – Spline dan MARS.

1.5Kontribusi Penelitian

1. Memperkaya wawasan dan literature dalam bidang statistika yang berhubungan dengan regresi nonparametrik dengan B – Spline dan MARS.

2. Mengetahui model regresi nonparametrik dengan B – Spline dan MARS.

3. Menerapkan metode regresi nonparametrik dalam ilmu sosial dalam pengambilan keputusan.

1.6Metode Penelitian

1. Menganalisis regresi nonparametrik.

2. Menganalisis kerja B – Spline pada data riil.

3. Menganalisis model terbaik untuk MARS melaui GCV, minimum MSA, dan koefisien determinasi.

BAB 2

LANDASAN TEORI

2.1Model Regresi Nonparametrik

Analisis regresi dalam sebab – akibat antara satu kecenderungan pola hubungan tersebut dengan mengestimasi kurva regresinya. Statistik nonparametrik merupakan suatu analisis data statistik yang sangat tepat digunakan untuk menguji data ilmu - ilmu sosial, karena asumsi - asumi yang digunakan dalam uji nonparametrik adalah pengamatan - pengamatan bebas, tidak mengikat dan lebih leluasa dibanding uji parametrik. Dan sampel yang telah memenuhi semua asumsi model statistik parameternya, sebaiknya dianjurkan memakai uji parametrik daripada uji nonparametrik karena di samping lebih efisien, uji parametrik dapat mengetahui suatu perbedaan yang tidak diketahui dalam uji nonparametrik.

paling berlaku untuk data dalam skala ordinal, dan berlaku juga untuk sampel dalam skala nominal. Dalam hal ini perlu pertimbangan dalam memilih suatu uji statistik untuk membuat keputusan tentang hipotesis penelitian, maka perlu kriteria berikut ini :

(a). Kekuatan uji.

(b). Penerapan model statistik di mana tes ini didasarkan pada data penelitian.

(c). Daya – efisiensi, dan

(d). Tingkat pengukuran dicapai dalam penelitian.

Untuk menyatakan bahwa uji statistik parametrik yang paling kuat dalam uji kekuatan ketika semua asumsi model statistik yang terpenuhi dan ketika variabel dalam analisis diukur dalam setidaknya skala interval. Namun, ketika semua asumsi uji parametrik tentang populasi, maka daya – efisiensi yang dengan jumlah sampel bisa menggunakan uji nonparametrik daripada uji parametrik dan mempertahankan daya yang sama untuk menolak Ho. Karena daya tes nonparametrik dapat ditingkatkan hanya dengan meningkatkan ukuran N, dan karena jarang mencapai pengukuran yang memungkinkan menggunakan tes parametrik.

Ada beberapa keuntungan dari uji statistik nonparametrik sebagai berikut :

1. Pernyataan probabilitas yang diperoleh dari sebagian uji statistik nonparametrik adalah probabilitas dalam sampel besar, dimana perkiraan baik yang tersedia, terlepas dari bentuk distribusi populasi dari mana sampel acak diambil. Keakuratan dari pernyataan probabilitas tidak bergantung pada bentuk populasi, meskipun beberapa tes nonparametrik mungkin menganggap identitas bentuk dua atau lebih distribusi populasi. Dalam kasus – kasus tertentu, tes nonparametrik berasumsi bahwa distribusi yang mendasarinya adalah kontinu, asumsi yang mereka bagi dengan tes parametrik.

2. Jika ukuran sampel yang digunakan lebih kecil dari 30, maka tidak ada alternatif untuk menggunakan uji statistik nonparametrik kecuali sifat dari distribusi populasi diketahui secara pasti.

3. Ada yang cocok dalam uji statistik nonparametrik dalam contoh pengamatan dari populasi yang berbeda. Tes nonparametrik dapat menangani data tanpa memerlukan asumsi yang tampaknya tidak realistis.

4. Uji statistik nonparametrik jauh lebih mudah untuk belajar dan menerapkan daripada tes parametrik.

Selain keuntungan uji statistik nonparametrik juga memiliki kelemahan, yaitu :

1. Jika semua asumsi dalam statistik parametrik berasal dari sampel, dan jika pengukuran adalah daya yang diperlukan, maka uji statistik nonparametrik adalah boros data. Tingkat pemborosan dinyatakan dengan efisiensi daya dari tes nonparametrik.

Regresi nonparametrik juga dikenal sebagai fungsi learing pada machine learning. Estimasi g(xi) dinotasikan ĝ(x i) dikenal sebagai penghalus (smoother). Pada penelitian ini fungsi g(xi) yang menggunakan basis B – Spline dan penghalus λ sehingga model dinamakan Cubic Spline Smoothing (CSS).

2.2Regresi Spline

Spline merupakan bentuk khusus dari potongan (piecewse) polynomial orde p yang memiliki sifat tersegmen kontinu sehingga efektif menjelaskan karakteristik lokal dari fungsi data (Eubank, 1988). Dalam spline digunakan truncated power basis dengan k sebagai titik knot, misalkan k1,k2,..,kk, yaitu : k p

p

k t k

t

t,..,( − )₊,..,( − )₊ ,

1 ₁ , dimana p menunjukkan derajat polynomial dari truncated power basis, dan untuk derajat p = 0, 1, 2, dan 3 secara umum merupakan truncated power basis konstan, linear, kuadratik, dan kubik (Takesawa, 2006). Fungsi spline

derajat p untuk model tersebut didefinisikan sebagai berikut :

(

)

p

r ij k

r r k

ij p

k k

ij t t ki

t

s ₊

=

= + −

=

∑

∑

1 1

1 1

)

( α β , j = 1,..,ni, dan i = 1,..,n. (1)

Dengan :

    − =

− +

0

) (

) (

p r ij p r ij

i i

k t k

t

i i

r ij

r ij

k t

k t

< ≥

; ;

generalized cross validation (GCV). Untuk model koefisien bervariasi, titik knot optimal dengan

metode GCV ini, dipilih secara terpisah untuk masing – masing obyek dan kemudian selanjutnya dimasukkan ke dalam model secara keseluruhan untuk mendapatkan estimasi spline secara simultan. Untuk masalah kemulusan / kekasaran kurva regresi spline nonparametrik bergantung pada pemilihan parameter penghalus λ. Pada nilai λ yang kecil maka kurvanya kasar atau sebaliknya, untuk nilai λ yang besar maka kurvanya akan menjadi mulus (smooth), dimana fungsi yang mulus akan terlihat jelas secara geometrik, ketika gradien dari kurva pada titik – titik knot tertentu tidak berubah dengan cepat (Eubank, 1988 dan Wahba, 1990).

Parameter λ merupakan pengontrol dalam melihat kurva dan keseimbangan antara kesesuaian kurva terhadap data, sehingga pemilihan parameter λ yang optimal menjadi penting,

karena berkaitan dengan perolehan estimator yang optimal.

2.3Basis B – Spline

Model regresi yi = g(ti) + ฀i : i = 1,2,..,n, merupakan residual dan g(ti) adalah kurva regresi.

Apabila digunakan pendekatan kurva spline truncated dikatakan regresi nonparametrik, maka kurva regresi g dapat ditulis sebagai berikut : (Eubank, 1988)

∑

∑

₌ −

+ =

− _{+ −}

= K

j

m j j m

i i

it t u t

g

1

1

1 1

) ( )

( α β (2)

) ( ) ( 1 , t t g K m j m m j j

∑

+₌ −

= γ β (3)

dengan Bj-m,m merupakan basis B – Spline.

Cara membangun fungsi B – Spline orde m dengan titik – titik knot a<uj <...<uK <b adalah dengan terlebih dahulu mendefinisikan knot tambahan sebanyak 2m, yaitu

m K m u u u

u_{−( −1)},..., ₋₁, ₀,.., ₊ dimana u_−(m−1) =...=u₀ =adan u_K+1 =...=u_K+m =b. Biasanya a diambil dari nilai minimum t dan b diambil dari nilai maksimum t. Fungsi B – Spline didefinisikan secara rekursif sebagai berikut : (Botella dan Shariff, 2003)

) ( )

( )

( _{1, 1}

1 1

, 1

, B t

u u t u t B u u u t t

B _{i m}

i m i m i m i i m i i m

i + −

+ + + − − + − − + − − = (4)     ≥ < ≤ < = + j j j j j u t u t u t u t B , , 0 , 1 ) ( 1 1

, (5)

dengan m adalah derajat dari B – Spline. Untuk m = 2 memberikan fungsi B – Spline linear, m = 3 memberikan fungsi B – Spline kuadratik dan m = 4 memberikan fungsi B – Spline kubik. Untuk mengestimasi koefisien γ dapat didefinisikan matrik sebagai berikut :

K m j n i i m j t B B ),.., 1 ( ,.., 1 , ( )) ( ) ( − − = = = λ (6)

atau dapat ditulis sebagai berikut :

          = − − − − − − − − ) ( ),..., ( ) ( ) ( ),..., ( ) ( ) ( , ), 2 ( ), 1 ( 1 , 1 ), 2 ( 1 ), 1 ( n m K n m m n m m m K m m m m t B t B t B t B t B t B

B λ    (7)

Jadi B(λ) adalah sebuah matrik berukuran n x (m+K).

1 dan maksimum 10, sehingga knots menjadi u₋₁ =u₀ =1,u₁ =5,u₂ =u₃ =10, maka matrik yang akan dibentuk adalah B(λ) =(B-1,2(ti),B0,2(ti),B1,2(ti)), i = 1,2,..,n yaitu sebuah matrik dengan ukuran n x 3. Dengan persamaan (4), B-1,2(ti) dapat ditulis sebagai berikut :

) ( 1 5 5 ) ( 1 1 1 )

( 1,1 0,1

2 ,

1 B t

t t B t t B − − + − − = − −

B-1,1(t) didefinisikan bernilai 0 karena u-1 = u0. (Eubank, 1988). Dan B0,1(t) akan bernilai 1 pada t bernilai u0 = 0 sampai dengan u1 = 1, dan bernilai 0 untuk yang lain, sehingga dapat ditulis seperti persamaan (5) sebagai berikut :

    − = − 0 4 5 ) ( 2 , 1 t t B 10 5 5 1 , ≤ < ≤ < t t

Sedangkan untuk basis B0,2(t) dengan menggunakan persamaan (4) dapat ditulis sebagai berikut : ) ( 5 10 10 ) ( 1 5 1 )

( 0,1 1,1

2 ,

0 B t

t t B t t B −− + − − =

dan dapat juga ditulis seperti persamaan (5) sebagai berikut :

      ≤ < − ≤ < − = 10 5 , 5 10 5 1 , 4 1 ) ( 2 , 0 t t t t t B

Untuk basis B1,2(ti) dapat menggunakan persamaan (4) dan dapat ditulis sebagai berikut :

) ( 10 10 10 ) ( 5 10 5 )

( _{1,1 2,1}

2 ,

1 B t

t t B t t B −− + − − = ( ) 5 5 )

( _1,1

2 ,

1 B t

t t

B = −

dan dapat di tulis juga seperti persamaan (5) sebagai berikut :

    − = 5 5 0 ) ( 2 ,

1 t t

Untuk kurva B – Spline kuadratik dengan 2 titik knot, misalnya pada t = 3 dan t = 7 dapat dicari dengan cara yang serupa, dengan hasil sebagai berikut :

         ≤ < ≤ <       − ≤ < − − = − 10 7 , 0 7 3 , 24 ) 7 ( 3 1 , 12 ) 3 13 )( 1 ( ) ( 2 3 , 1 t t t t t t t B

Dengan cara yang serupa, dapat dibuat kurva B – Spline dengan berbagai m dan beberapa titik knots.

2.4Multivarate Adaptive Regression Splines (MARS)

Spline adalah salah satu jenis potongan polynomial, yaitu polynomial yang memiliki sifat tersegmen. Sifat tersegmen ini memberikan fleksibilitas lebih dari polynomial biasa, sehingga memungkinkan untuk menyesuaikan diri secara lebih efektif terhadap karakteristik lokal dari suatu fungsi atau data. Secara umum, fungsi spline berorde k adalah sembarang fungsi yang dinyatakan sebagai berikut :

∑

∑

₌ − + − = + − = h j k j j k i i

it t u t S 1 1 1 0 ) ( )

( α δ dengan,

    − = − − − + 0 ) ( ) ( 1 1 k j k j u t u t j j u t u t < ≥ , , (8) dengan :

α dan δ adalah konstanta riil

uj,…,uh adalah titik – titik knot.

dengan titik – titik lompatan u1,..,uh, dan fungsi S adalah suatu polynomial dengan orde m di luar

[u1,un].

Recursive Partitioing Regression (RPR) merupakan pendekatan dari fungsi f(t) yang tidak

diketahui dengan :

∑

₌

∧

= S

j

j j t B t c

t f

1

) ( ) ( )

(

(9) dengan, Bj (t) =I[t ฀ Rj],I[.] menunjukkan fungsi indicator yang mempunyai nilai 1 (satu) jika

pernyataan benar (t ฀ Rj) dan 0 (nol) jika salah, cj(t) merupakan koefisien (konstanta) yang

ditentukan dalam subregion.

Penentuan knots pada regresi dummy atau regresi kategori dilakukan secara manual, karena memiliki dimensi data yang rendah dan hal ini tidak akan mengalami kesulitan, sedangkan untuk data yang berdimensi tinggi terdapat kesulitan. Untuk mengatasi hal tersebut digunakan model Recursive Partitiion Regression karena penentuan knots tergantung (otomatis) dari data. Namun

demikian model ini masih terdapat kelemahan yaitu model yang dihasilkan tidak kontinu pada knots, dan untu mengatasinya digunakan model MARS.

Model MARS selain penentuan knots yang dilakukan secara otamatis dari data, juga menghasilkan model yang kontinu pada knots. Pemilihan knots pada MARS menggunakan algoritma forward stepwise dan backward stepwise yang salah satunya didasarkan nilai Generalized Cross Validation (GCV) minimum. Model MARS dapat ditulis, yaitu :

[

]

∏

∑

_{= =}

∧

− +

= Km

k

km m k v km M

m

m s t u

a a

t f

1

) , ( 1

0 .( )

) (

(10) dengan :

α0 = basis fungsi induk

M = maksimum basis fungsi (nonconstant basis fungsi) Km = derajat interaksi

Skm = nilainya ± 1

tv(k,m) = variabel independen

ukm = nilai knots dari variabel independen tv(k,m)

Penjabaran dari persamaan (10) dapat disajikan sebagai berikut :

∑

₌ ∧ − + = M m m m v m

m s t u

t f 1 1 ) , 1 ( 1

0 [ .( )]

) ( α α

∑

₌ − − + M m m m v m m m v m

m s t u s t u

a 1 2 ) , 2 ( 2 1 ) , 1 (

1 .( )][ .( )]

[ )] .( [ )] .( )][ .(

[ 3 (3, ) 3

1 2 ) , 2 ( 2 1 ) , 1 (

1 m v m m

M m m m v m m m v m

m s t −u s t −u s t −u

+

∑

=α



+ (11)

dan secara umum persamaan (10) dapat dituliskan sebagai berikut :

 + + + + =

∑

∑

∑

= = = ∧ 3 2 1

0 ( ) ( , ) ( , , )

) ( m m m K k j i ijk K j i ij K i

i t f t t f t t t f

t

f α

(12) Persamaan (12), memperlihatkan bahwa penjumlahan pertama meliputi semua basis fungsi untuk satu variabel, penjumlahan kedua meliputi semua basis fungsi untuk interaksi antara dua variabel, penjumlahan ketiga meliputi semua basis fungsi untuk interaksi antara tiga variabel dan seterusnya.

Misalkan T

Kw w w) { ( ' )} ( = Λ κ

Λ adalah himpunana dari variabel yang dihubungkan dengan

∑

₌ = 1 ) ( ) ( m K i m m i

i t t

f α β

(13) fi(ti) merupakan penjumlahan semua basis fungsi untuk satu variabel xi dan merupakan spline

dengan derajat q=1 yang memrepresentasikan fungsi univariat. Setiap fungsi bivariat pada persamaan (12) dapat ditulis sebagai berikut :

∑

₌ = 2 ) , ( ) , ( Km j i m m j i

ij t t t t

f α β

(14) yang merepresentasikan penjumlahan semua basis fungsi dua variabel ti dan tj. Penambahan ini

untuk menghubungkan kontribusi univariat, yang dituliskan sebagai berikut : ) , ( ) ( ) ( ) , ( * j i ij j j i i j i

ij t t f t f t f t t

f = + +

(15) Untuk fungsi trivariat pada penjumlahan yang ketiga diperoleh dengan menjumlahkan semua basis fungsi untuk tiga variabel, yang dituliskan sebagai berikut :

∑

₌ = 3 ) , , ( ) , , ( Km k j i m m k j i

ij t t t t t t

f α β (16)

Penambahan fungsi univariate dan bivarate mempunyai kontribusi dalam bentuk : ) , , ( ) , ( ) , ( ) , ( ) ( ) ( ) ( ) , , ( * k j i ijk k j jk k i ik j i ij k k j j i i k j i

ij t t t f t f t f t f t t f t t f t t f t t t

f = + + + + + + (17)

Persamaan (12) merupakan dekomposisi dari analisis varians untuk tabel kontigensi, yang dikenal dengan dekomposisi anova dari model MARS. Interprestasi model MARS melalui dekomposisi anova adalah merepresentasikan variabel yang masuk dalam model, baik untuk satu variabel maupun interaksi antara variabel. Penambahan aditif pada persamaan (13) dapat dtunjukkan dengan membuat plot antara fi(ti) dengan ti sebagai salah satu model aditif.

Kontribusi interaksi antara dua variabel dapat divisualisasikan dengan membuat plot antara ) , ( * j i ij t t

dalam variansi dapat dibuang dengan menggunakan plot dalam beberapa variabel fixed dengan variabel komplemen.

Pada model MARS, pemilihan model menggunaan metode stepwise yang terdiri dari forward dan backward. Forward stepwise dilakukan untuk mendapatkan jumlah basis fungsi maksimum dan kriteria pemilihan basis fungsi adalah meminimumkan average sum of square residual (ASR). Untuk memenuhi kosep parsemoni dari forward stepwise dengan meminimumkan nilai generalized cross-validation (GCV). (Friedman and Silverman, 1989, Friedman, 1990, 1991).

2.5Memilih Persamaan Regresi Terbaik

Dalam memilih persamaan regresi terbaik terdapat dua kriteria yang saling bertentangan, yaitu agar persamaanya bermanfaat bagi tujuan peramalan, sebaiknya memasukkan sebanyak mungkin fungsi (Z) sehingga diperoleh nilai ramalan yang terandalkan, dan untuk memperoleh informasi dari banyak peubah serta promonitorannya serng kali memerlukan biaya tinggi, maka persamaan regresinya mencakup sedikit mungkin fungsi (Z). Kompromi antara kedua esktrem itulah biasanya disebut pemilihan persamaan regresi terbaik. Untuk mengerjakan ini tidak ada satu prosedur statistik yang khas atau unik. Sebaiknya bila mengetahui σ2

(ragam acak sesungguhnya) untuk suatu masalah, pemilihan persamaan regresi terbaik akan jauh lebih mudah.

Maka perlu diterapkan pada masalah yang sama tidak selalu menghasilkan jawaban yang sama. Oleh karena itu, perlu dilakukan prosedur – prosedur sebagai berikut :

a) Semua kemungkinan regresi dengan menggunakan tiga criteria, yaitu R2, s2, dan Cp Mellow.

c) Eliminasi langkah mundur, d) Regresi bertatar,

e) Beberapa variasi metode berikutnya, f) Regresi gulud,

g) PRESS,

h) Regresi komponen Utama, i) Regresi akar cirri, dan j) Regresi bertahap.

Secara umum, metode penentuan model terbaik dibedakan menjadi :

i. Metode tanpa seleksi variabel independen.

Metode yang memasukkan seluruh variabel independen yang diduga berpengaruh ke dalam model dan mengakomodasi adanya kolinerietas / multikolineritas. Contoh : principle component regression (regresi komponen utama), ridge regression (regresi gulud)

ii. Metode dengan seleksi

Metode yang melakukan seleksi variabel independen yang masuk ke dalam model sesuai dengan criteria / prosedurnya. Contoh : Metode backward, forward, stepwise, best subset regression.

Adapun penjelasan dari metode dengan seleksi, yaitu :

• Metode backward

Mulai dengan model lengkap, kemudian variabel independent yang dievaluasi, jika ada yang tidak signifikan dikeluarkan yang paling tidak signifikan, dilakukan terus menerus sampai tidak ada lagi variabel independent yang tidak signifikan.

Variabel independent yang pertama kali masuk ke dalam model adalah variabel yang mempunyai korelasi tertinggi dan signifikan dengan variabel dependent, variabel yang masuk kedua adalah varabel yang korelasi parsialnya dengan variabel dependet adalah tertinggi kedua dan masih signifikan, dilakukan terus menerus samapi tidak ada lagi variabel independenyang sinfikan.

• Metode Stepwise

Gabungan antara metode forward dan backward variabel yang pertama kali masuk adalah variabel yang korelasinya tertinggi dan signifikan dengan variabel dependent, variabel yang masuk kedua adalah variabel yang korelasi parsialnya tertinggi dan masih signifikan, setelah variabel tertentu masuk ke dalam model maka variabel lain yang ada di dalam model dievaluasi, jika ada variabel yang tidak signifikan maka variabel tersebut dikeluarkan.

• Metode Best Subset

Metode ini menyajikan k buah model terbaik dari setiap kelompok model regresi, berdasarkan banyaknya variabel independent, kelompok dengan 1,2,..,k variabel independent.

• Metode R2

Koefisien determinasi R2 akan selalu positif dan pengertiannya secara intuitif dapat dinyatakan sebagai berikut, yaitu R2 menyatakan proporsi varians pad Y yang dapat diterangkan oleh t. Variabel bebas Y mempunyai sejumlah varibilitas tertentu, yang didefinsikan sebagai variannya.

• Metode MSE

BAB 3

PEMBAHASAN

3. Data dan Pembahasan

Contoh kasus diambil dari Jurusan Kimia Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara. Salah satu variabel yang menentukkan seseorang lulus atau tidak lulus dalam mata kuliah kimia industri. Dasar itu dipakai karena diharapkan ada pola hubungan antara hasil ujian tengah semester (t) dan ujian akhir semester (y) pada mata kuliah kimia industri semester genap tahun ajaran 2009 / 2010, dengan jumlah mahasiswa 26 orang.

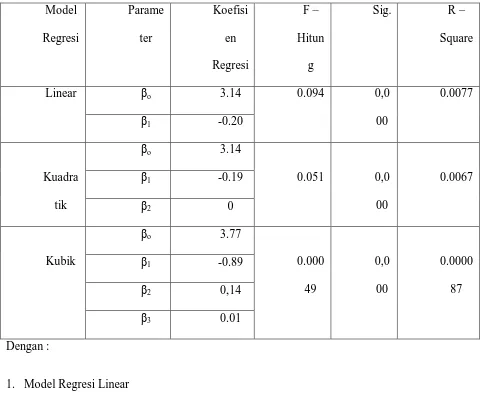
Adapun daftar nilai ujian tengah semester (t) dan ujian akhir semester (y) mata kuliah kimia industri yang dihitung dalam bentuk model regresi linear, regresi kuadratik, dan regreesi kubik, dapat dilihat pada tabel 1, tabel 2, dan tabel 3.

[image:32.612.66.548.107.506.2]

Tabel 4. Pengaruh Nilai UTS dan Nilai UAS dengan Regresi Linear Model Regresi Parame ter Koefisi en Regresi F – Hitun g

Sig. R –

Square

Linear βo 3.14 0.094 0,0

00

0.0077

β1 -0.20

Kuadra tik

βo 3.14

0.051 0,0 00

0.0067

β1 -0.19

β2 0

Kubik

βo 3.77

0.000 49 0,0 00 0.0000 87

β1 -0.89

β2 0,14

β3 0.01

Dengan :

1. Model Regresi Linear

∑

∑

∑ ∑ ∑ ∑

− −

= 2 2

2 0 ) ( t t n ty t t y β

∑

∑

∑ ∑ ∑

− −

= 2 2

1 ) ( t t n y t ty n β

( )

∑

∑

−       − = ∧ 2 2 2 y y y y R

(

)

(

n k

)

R k R Fhitung − −     = 2 2

1 =

∑

₌

n i i e n MSE 1 2 1

(

) (

) (

)

{

} (

{

) (

) (

)

}

(

) (

) (

)

{

2 4 3 2 2 3

} (

{

4

) (

3 3

) (

2 2 2

)

}

2 2 2 3 3 4 3 2 2 3 4 2 0 t t t t t n t t t t t t t t t t t n y t t t t t y t ty t t ty t y t t t t t y ∑ ∑ ∑ + ∑ ∑ + ∑ ∑ ∑ − ∑ ∑ ∑ + ∑ ∑ ∑ + ∑ ∑∑ + ∑ ∑ ∑ + ∑ ∑ ∑ − ∑ ∑ ∑ − ∑ ∑ ∑ − ∑ ∑ ∑ ∑ ∑ = β

(

) (

) (

)

{

} (

{

) (

) (

)

}

(

) (

) (

)

{

2 4 3 2 2 3

} (

{

4

) (

3 3

) (

2 2 2

)

}

2 2 2 3 3 4 3 2 2 3 4 2 1 t t t t t n t t t t t t t t t t t n y t t t t t y t ty t t ty t y t t t t t y ∑ ∑ ∑ + ∑ ∑ + ∑ ∑ ∑ − ∑ ∑ ∑ + ∑ ∑ ∑ + ∑ ∑ ∑ ∑ ∑ − ∑ ∑ ∑ − ∑ ∑ ∑ − ∑ ∑ ∑ + ∑ ∑ ∑ + ∑ ∑ ∑ = β

(

) (

) (

)

{

} (

{

) (

) (

)

}

(

) (

) (

)

{

2 4 3 2 2 3

} (

{

4

) (

3 3

) (

2 2 2

)

}

2 2 3 2 3 2 2 2 2 t t t t t n t t t t t t t t t t t n t t y t ty n y t t t t t y t ty t y t t n ∑ ∑ ∑ + ∑ ∑ + ∑ ∑ ∑ − ∑ ∑ ∑ + ∑ ∑ ∑ + ∑ ∑ ∑ + ∑ ∑ ∑ + ∑ ∑ ∑ − ∑ ∑ ∑ − ∑ ∑ − ∑ ∑ ∑ ∑ = β

( )

∑

∑

−       − = ∧ 2 2 2 y y y y R

(

)

(

n k

)

R k R Fhitung − −     = 2 2

1 =

∑

₌

n i i e n MSE 1 2 1

3. Model Regresi Kubik

            ∑ ∑ ∑ ∑ =                           ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ ∑ y t y t ty y x t t t t t t t t t t t t t t t n 3 2 3 2 1 0 6 5 4 3 5 4 3 2 4 3 2 3 2 β ββ β

( )

∑

∑

−       − = ∧ 2 2 2 y y y y R

(

)

(

n k

)

R k R Fhitung − −     = 2 2

1 =

∑

₌

n i i e n MSE 1 2 1

terbaik pada pemodelan interprestasi dan kesederhanaan model maka pola hubungan nilai ujian tengah semester (t) dengan nilai ujian akhir semester (y), yang lebih terbaik menggunakan model regresi kuadratik. Persamaan masing – masing model regresi linear adalah sebagai berikut :

1. Model Regresi Linear :

t y 3.14 0,20 ^

+

= ; t adalah nilai ujian.

2. Model Regresi Kuadratik :

2 ^

002 , 0 389 , 0 31 ,

14 t t

y=− + − ; t adalah nilai ujian

3. Model Regresi Kubik :

3 2

^

0000083 ,

0 000001 ,

0 202 , 0 957 ,

8 t t t

y=− + + − ; t adalah nilai ujian.

3.1 Pola Hubungan Nilai UTS Terhadap UAS dengan Pendekatan B – Spline

[image:35.612.67.515.133.641.2]

Tabel 5. Pengaruh Nilai UTS Terhadap UAS dengan B - Spline Model Regresi Parame ter Koefis ien Regres i F – Hitu ng Si g. M SE R – Squ are

Linear γ1 3,14 3988 0,000 0.0037 0,997

γ2 -0,1

Kuadrat ik

γ1 3,14

2640 0,000 0,0037 0,997

γ2 -0,095

γ3 0.1

Kubik

γ1 3,77

1994 0,000 0,0037 0,997 γ2 -0,445

γ3 0,046

γ4 0,02

Dengan :     − = − − + − − = = − − 0 2 3 ) ( 1 3 3 1 1 1 )

( _{1,1 0,1}

2 , 1 0 t t B t B t t B B 4 3 , 3 1 , ≤ < ≤ < t t     − − = −− + − − = = t t t B t B t t B B 4 2 1 ) ( 3 4 4 1 3 1 )

( 0,1 1,1

2 , 01 1 4 3 , 3 1 , ≤ < ≤ < t t ) ( 4 4 4 3 4 3 )

( 1,1 2,1

2 , 1

2 B t

t B t t B B −− + − − = =     − = − = 3 3 0 ) ( 3 3 )

( 1,1

2 ,

1 B t t

t t B 4 3 , 3 1 , ≤ < ≤ < t t    − = − − + − − = = − 0 3 ) ( 1 3 3 1 1 1 )

( 1,1 0,3 3 , 1 3 t t B t B t t B B 4 2 , 2 1 , ≤ < ≤ < t t

begitu juga nilai koefisien determinasi (R2) sebesar 0,997. Untuk kemudahan interprestasi dan kesederhanaan model, yang terbaik model B – Spline linear. Persamaan masing – masing model regresi linear adalah sebagai berikut :

1. Model B – Spline Linear :

1 0

*^

1 . 0 14 .

3 B B

y = +

dengan B0 = B-1,2(t), B1 = B0,2(t).

2. Model B – Spline Kuadratik :

2 1

0 *

^

1 . 0 095 . 0 14 .

3 B B B

y = − +

dengan B0 = B-2,3(t), B1 = B-1,3(t), B2 = B0,3(t).

3. Model B – Spline Kubik :

3 2

1 0

* ^

02 . 0 046 . 0 445 . 0 77 .

3 B B B B

y = − + +

dengan B0 = B-3,4(t), B1 = B-2,4(t), B2 = B-1,4(t), B3 = B0,4(t).

3.2 Pola Hubungan Nilai UTS Terhadap UAS dengan Pendekatan MARS.

[image:37.612.60.551.277.353.2]

Pola hubungan antara nilai ujian tengah semester (t) dengan nilai ujian akhir semester (y) pendekatan MARS, dengan variasi pada basis fungsi, interaksi antar variabel independen dan minimum observasi subregion secara lengkap tersaji pada tabel berikut :

Tabel 6. Pengaruh Nilai UTS Terhadap UAS dengan MARS

Model MARS

BF MO F – Hitung GCV R2 MSE

Model 1 3 16 14,874 0,041 0,996 0,0342872

Model 2 4 20 26,878 0,036 0,996 0,0348211

Model 3 3 16 14,874 0,035 0,997 0,0342796

Keterangan :

BF = Basis Fungsi

∑

₌ − = M m m m v m

m s t u

BF 1 1 ) , 1 (

1 .( )]

[ 1 α

∑

₌ − − = M m m m v m m m v m

m s t u s t u

a BF 1 2 ) , 2 ( 2 1 ) , 1 (

1 .( )][ .( )]

[ 2 )] .( [ )] .( )][ .( [

3 _{3 (3, ) 3}

1 2 ) , 2 ( 2 1 ) , 1 (

1 m v m m

M m m m v m m m v m

m s t u s t u s t u

BF =

∑

− − −

= α

MI = Maksimum Interaksi

MO = Maksimum Observasi pada setiap subregion.

paling besar yaitu 0,997. Sehingga pola hubungan nilai ujian tengah semester (t) dengan ujian akhir semester (y) pada pendekatan MARS pada persamaan sebagai berikut :

3 397 , 0 2 027 , 0 1 402 , 0 061 , 3 ^

BF BF

BF

y= − − +

dengan :

BF1 = max(0, t – 4)

BF2 = max(0, 4 – t )

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Dari hasil analisa data yang telah dilakukan, maka dapat dambil kesimpulan sebagai berikut :

1. Fungsi spline merupakan suatu gabungan fungsi polynomial, dimana penggabungan beberapa polynomial tersebut pada knot – knot dengan suatu cara menjamin sifat kontinuitas.

2. Knot pada basis B – Spline dan Mars berpengaruh sangat penting, karena apabila knot yang relatif sedikit akan memperlihatkan kesederhanaan model sedangkan knot yang relatif banyak akan memperlihatkan pola matematis yang ada pada data atau sampel. 3. Estimasi kurva regresi nonparametrik dengan pendekatan spline dalam penerapannya

cukup fleksibel dan cukup baik. Yaitu fleksibel dalam arti biarkan data yang menentukkan estimatornya, dan baik dalam arti sfat estimator ini masih linear dalam observasi sehingga memudahkan inferensinya.

4. Hasil analisis regresi linear, kuadratik, da kubik menghasilkan R2 yang cenderung sama dengan persamaan regresi kuadratik adalah sebagai berikut :

2 ^

002 , 0 389 , 0 31 ,

14 t t

5. Hasil analisis model B – Spline linear, kuadratik dan kubik mempunyai MSE yang mendekati sama. Model yang diperoleh untuk masing – masing orde adalah sebagai berikut : 2 1 0 *^ 1 . 0 095 . 0 14 .

3 B B B

y = − +

dengan :     − = − − + − − = = − − 0 2 3 ) ( 1 3 3 1 1 1 )

( 1,1 0,1

2 , 1 0 t t B t B t t B B 4 3 , 3 1 , ≤ < ≤ < t t     − − = −− + − − = = t t t B t B t t B B 4 2 1 ) ( 3 4 4 1 3 1 )

( 0,1 1,1

2 , 01 1 4 3 , 3 1 , ≤ < ≤ < t t ) ( 4 4 4 3 4 3 )

( _{1,1 2,1}

2 , 1

2 B t

t B t t B B −− + − − = =     − = − = 3 3 0 ) ( 3 3 )

( _1,1

2 ,

1 B t t

t t B 4 3 , 3 1 , ≤ < ≤ < t t

6. Dan hasil model MARS menghasilkan persamaan berikut :

3 397 , 0 2 027 , 0 1 402 , 0 061 , 3 ^ BF BF BF

y= − − +

dengan :

BF1 = max(0, t – 4) BF2 = max(0, 4 – t ) BF3 = max(0, t – 4)

4.2 Saran

DAFTAR PUSTAKA

Billier, C, and Fahrmeir, L. 2000. Bayesian varying-coefficient models using adaptive regression

Spline, Statistical Modeling.

Botella, O. and Shariff, K. 2003. B-Spline Methodes in fluid Dynamics. International Journal Of

Computational Fluid Dynamics, 17 (2),133 – 149.

Budiantara, I.N, Suryadi, F. Otok, B.W, Guritno S. 2000. Pemodelan B-Spline dan Mars Pada

Nilai Ujian Masuk terhadap IPK Mahasiswa Jurusan Disain Komunikasi Visual UK.

Petra Surabaya. hal. 1 - 12

Carter, C.K. and Silverman, B.W. 1992. A Comparison of the Reinsch and Speckman Splines.

Biometrika, 79(1), pp 81 – 91.

Draper,N.R. and H.Smith. 1992. Analisis Regresi Terapan. PT. Gramedia Pustaka Utama.

Jakarta.

Eubank, R.L. 1988. Spline Smoothing and Nonparametric Regression. New York :

Marcel Dekker.

Friedman, J.H. 1990. Estimating Function of Mixed Ordinal and Categorical Variables using

Departement, Stanford University.