PEMODELAN INDEKS HARGA SAHAM GABUNGAN DAN
PENENTUAN RANK CORRELATION DENGAN
MENGGUNAKAN COPULA
IKA SYATTWA BRAMANTYA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI KARYA ILMIAH DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*
Dengan ini saya menyatakan bahwa karya ilmiah berjudul Pemodelan Indeks Harga Saham Gabungan dan Penentuan Rank Correlation dengan Menggunakan Copula adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir karya ilmiah ini.
Dengan ini saya melimpahkan hak cipta dari karya ilmiah saya kepada Institut Pertanian Bogor.
Bogor, September 2014
Ika Syattwa Bramantya
ABSTRAK
IKA SYATTWA BRAMANTYA. Pemodelan Indeks Harga Saham Gabungan dan Penentuan Rank Correlation dengan Menggunakan Copula. Dibimbing oleh RETNO BUDIARTI dan I GUSTI PUTU PURNABA.
Indeks saham merupakan nilai dari gabungan banyak saham di mana datanya berupa financial time series yang memiliki karakteristik sebaran fat tail.
Data yang memiliki sebaran fat tail merupakan data yangtidak menyebar normal karena data tersebut memiliki ekor sebaran yang tebal. Metode rank correlation
dapat digunakan untuk menganalisis korelasi antarindeks saham yang tidak menyebar normal dan metode ini hanya bergantung pada copula. Data yang digunakan pada karya ilmiah ini berasal dari data harian indeks saham Jerman (DAX) dan Jepang (NIK) yang diambil dari tanggal 27 April 1993 sampai tanggal 20 Juni 2000. Untuk menentukan korelasinya, model terbaik perlu ditentukan dahulu dengan menggunakan ARIMA. Selanjutnya, data dimodelkan dengan GARCH untuk menghilangkan efek heteroskedastisitas. Setelah itu, data diuji dengan menggunakan metode canonical maximum likelihood untuk menentukan copula terbaik dan korelasinya dengan metode rank correlation. Model terbaik untuk indeks saham DAX adalah ARIMA(2,1,2)-GARCH(2,1) dan untuk indeks saham NIK adalah ARIMA(1,1,1)-GARCH(2,0). Copula terbaik yang didapatkan ialah copula dan untuk hasil analisis korelasi antarindeks menunjukan tingkat korelasi antarindeks di atas berkorelasi positif lemah.
Kata kunci: Indeks saham, rank correlation, ARIMA, GARCH, copula.
ABSTRACT
IKA SYATTWA BRAMANTYA. Stock Exchange Composite Index Modeling and the Determination of Rank Correlation by Using Copula. Supervised by RETNO BUDIARTI and I GUSTI PUTU PURNABA.
Stock index is a composite value of many stocks, where its data type is financial time series with fat tail distribution characteristic. Data with fat tail
distribution doesn’t normally distribute since the data has heavy distribution’s tail.
Rank correlation method, which depends on copula, can be used to analyze
correlation among stock indices which doesn’t normally distribute. Data in this
work come from daily data of Germany Stock Index (DAX) and Japan Stock Index (NIK) which taken from April 27th 1993 until June 20th 2000. In order to find out the correlation, the best model should be specified first through ARIMA.
After that, the data is modeled by using GARCH to eliminate heteroskedasticity’s
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
PEMODELAN INDEKS HARGA SAHAM GABUNGAN DAN
PENENTUAN RANK CORRELATION DENGAN
MENGGUNAKAN COPULA
IKA SYATTWA BRAMANTYA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari ini ialah copula, dengan judul Permodelan Indeks Saham Gabungan dan Penentuan Rank Correlation denganMenggunakan Copula.
Terima kasih penulis ucapkan terima kasih kepada Ibu Ir Retno Budiarti, MS dan Bapak Dr Ir I Gusti Putu Purnaba, DEA selaku pembimbing saya, serta Bapak Dr Dony Citra Lesmana, S.Si, M.Fin.Math yang telah banyak memberi saran terkait penyusunan karya ilmiah ini. Di samping itu, penghargaan penulis sampaikan kepada rekan-rekan di forum Stack-Exchange dan Matlab Central yang sudah membantu saya dalam menyusun kode-kode program yang saya pergunakan dalam karya ilmiah ini. Ungkapan terima kasih juga disampaikan kepada bapak, ibu, serta seluruh keluarga dan teman-teman, atas segala doa, kasih sayang, serta dukungan moril kepada saya.
Semoga karya ilmiah ini bermanfaat.
Bogor, September 2014
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Perumusan Masalah 2
Tujuan Penelitian 2
Manfaat Penelitian 2
TINJAUAN PUSTAKA 3
METODE 12
Alat 13
Tahapan Penelitian 14
HASIL DAN PEMBAHASAN 15
Model ARIMA 16
Model ARIMA-GARCH 19
Copula 21
SIMPULAN DAN SARAN 23
Simpulan 23
Saran 23
DAFTAR PUSTAKA 24
LAMPIRAN 26
DAFTAR TABEL
1 Hasil uji ADF 16
2 Hasil pendugaan model ARIMA pada indeks saham DAX 18 3 Hasil pendugaan model ARIMA pada indeks saham NIK 18
4 Hasil pengujian ARCH-LM 19
5 Hasil analisis model ARIMA-GARCH untuk indeks saham DAX 19 6 Hasil analisis model ARIMA-GARCH untuk indeks saham NIK 20 7 Hasil uji ARCH-LM setelah dilakukan permodelan ARIMA-GARCH 20
8 Hasil uji Jarque-Bera 21
DAFTAR GAMBAR
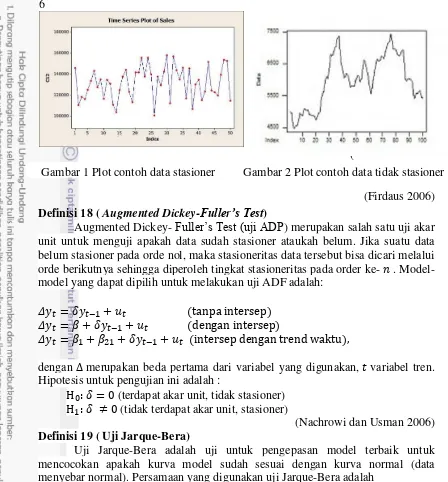
1 Plot contoh data stasioner 6
2 Plot contoh data tidak stasioner 6
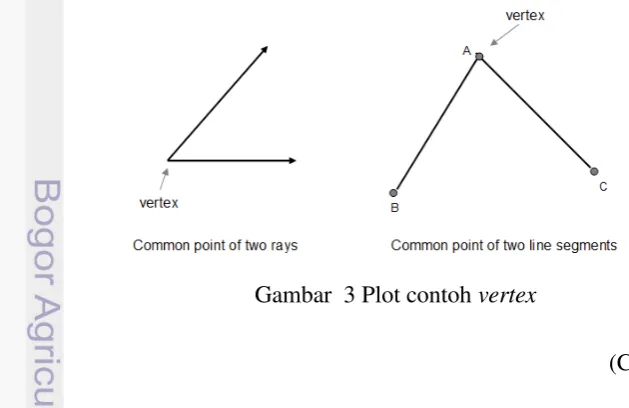
3 Plot contoh vertex 8
4 Plot nilai indeks saham DAX 15
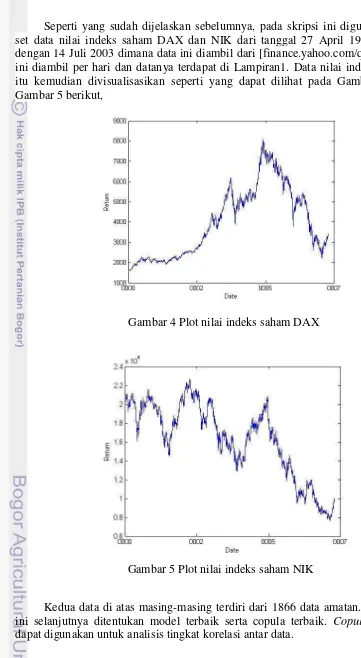
5 Plot nilai indeks saham NIK 15
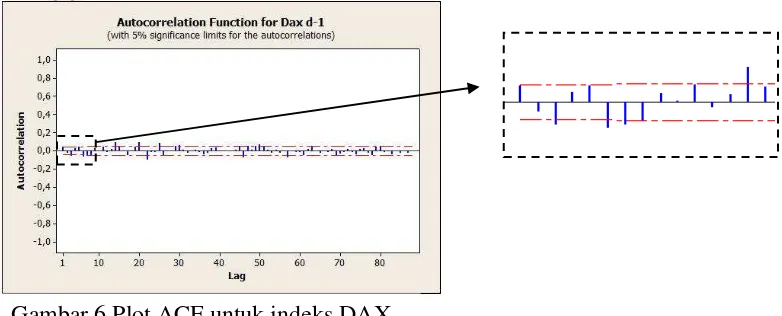
6 Plot ACF untuk indeks DAX 16
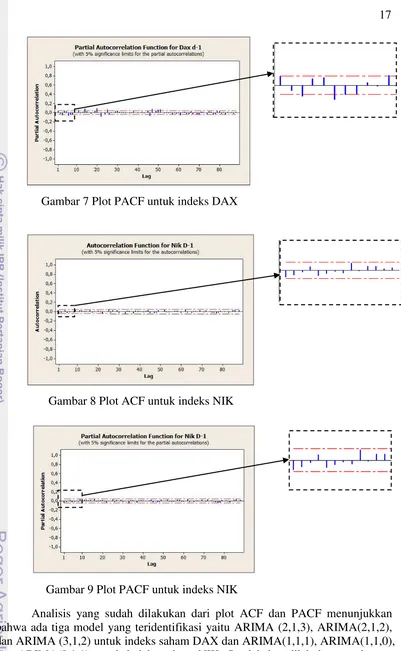
7 Plot PACF untuk indeks DAX 17
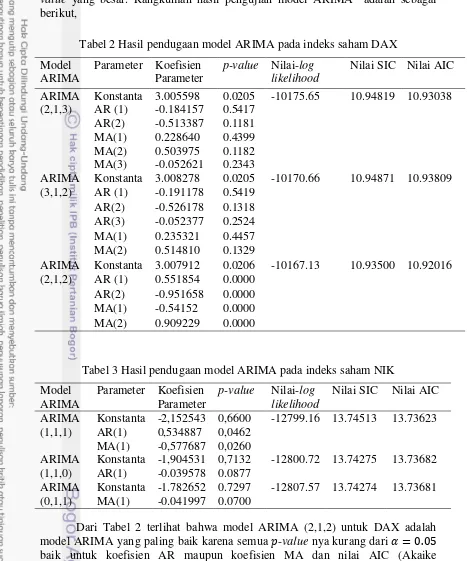
8 Plot ACF untuk indeks NIK 17
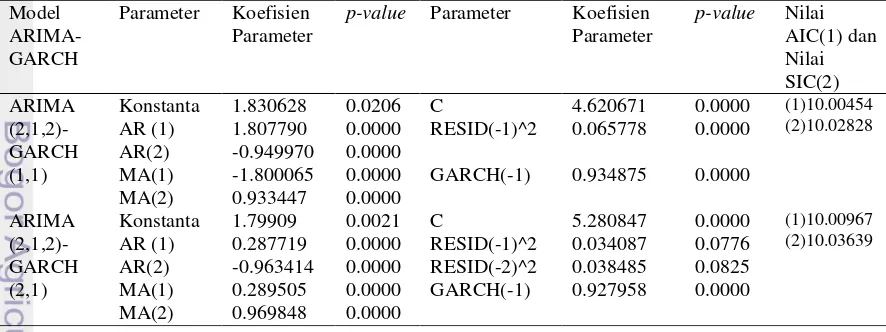
9 Plot PACF untuk indeks NIK 17
10 Plot Residual pada indeks DAX 21
11 Plot Residual pada indeks NIK 21
DAFTAR LAMPIRAN
1 Data asli indeks saham dari tanggal 27 April 1993 s.d 14 Juli 2003 26 2 Hasil uji ADF pada data asli indeks saham DAX 28 3 Hasil uji ADF pada DAX setelah pembedaan satu kali 28 4 Hasil uji ADF pada data asli indeks saham NIK 28 5 Hasil uji ADF pada NIK setelah pembedaan satu kali 28
6 Hasil model ARIMA (2,1,3) untuk indeks DAX 29
7 Hasil model ARIMA (3,1,2) untuk indeks DAX 29
8 Hasil model ARIMA (2,1,2) untuk indeks DAX 30
9 Hasil model ARIMA (1,1,0) pada indeks NIK 30
10 Hasil model ARIMA (0,1,1) pada indeks NIK 31
11 Hasil model ARIMA (1,1,1) pada indeks NIK 31
25 Hasil estimasi parameter copula 40
PENDAHULUAN
Latar Belakang
Saham adalah satu instrumen investasi yang nilai jualnya berdasarkan kinerja perusahaan penerbit saham dan diperdagangkan di bursa saham dengan imbal hasil sejumlah tertentu tergantung jenis sahamnya. Sedangkan, Indeks Harga Saham Gabungan (IHSG) adalah suatu nilai yang berfungsi sebagai pengukuran kinerja suatu saham gabungan di bursa efek (Sunariyah 2003).
Nilai indeks saham sendiri dihitung berdasarkan nilai indeks seluruh saham (metode penghitungan nilai tergantung bursa tersebut) yang diperdagangkan di bursa itu. Misalkan, Dow Jones Average adalah bursa saham yang terdiri dari 30 perusahaan besar (blue chip) dan nilai indeksnya dihitung berdasarkan indeks 30 perusahaan tersebut. Karena indeks saham merupakan kumpulan saham-saham, maka resiko yang terkandung didalam indeks saham kurang lebih sama dengan resiko pada saham itu sendiri.
Pergerakan pasar yang tidak pasti memunculkan risiko yang bisa berasal dari internal perusahaan penerbit saham seperti laporan keuntungan atau kondisi keuangan perusahaan ataupun dari eksternal pasar seperti sentimen pasar, perkembangan politik dan sosial negara, dan lain-lain. Sehingga, manajemen yang baik mutlak diperlukan dalam mengelola risiko-risiko yang mungkin muncul.
Pada ilmu studi konvensional aset-aset yang ada diasumsikan saling bebas padahal dalam kenyataannya di jaman pasar global seperti ini aset-aset tersebut tidak sepenuhnya bebas karena setiap bursa saham yang ada hampir dipastikan saling berinteraksi, baik secara langsung maupun tak langsung. Pada studi kontemporer hubungan antar satu aset dengan yang lainnya dapat dimodelkan dengan sebuah fungsi yang bernama copula.
Copula sendiri adalah sebuah fungsi yang menggabungkan dua atau lebih fungsi sebaran multivariate dimana copula mengambil fungsi marjinal dari tiap sebaran tersebut dan dijadikan sebagai sebuah fungsi marjinal satu dimensi yang normal baku (nilainya [0,1]) (McNeill et al. 2005). Dalam ilmu ekonomi fungsi marjinal merupakan fungsi yang menggambarkan risiko suatu aset, baik risiko untung maupun risiko rugi, namun biasanya para analis berfokus pada risiko rugi. Karena copula menggabungkan dua atau lebih fungsi marjinal yang ada, maka
2
Perumusan Masalah
Karya ilmiah ini menggunakan dua set data nilai indeks saham gabungan yang berasal dari bursa saham Jerman DAX (Deutscher Aktien Index) dan bursa saham Jepang NIK ( Nikkei 225) dari tanggal 27 April 1993 sampai tanggal 20 Juni 2000. Data ini kemudian dicari model yang terbaik menggunakan metode ARIMA dan metode GARCH untuk mengatasi masalah heteroskedatisitas pada model. Pada karya ilmiah ini juga ditentukan hubungan antar dua set data di atas dengan menggunakan uji mutual dependensi yang untuk selanjutnya ditentukan pula parameter-parameter dari tiap jenis copula dan copula terbaik menggunakan metode Canonical Maximum Likelihood. Copula yang diuji pada karya ilmiah ini adalah copula Gauss, Gumbel, Frank, Clayton, dan t.
Tujuan Penelitian
Tujuan utama dari penulisan karya ilmiah ini adalah:
1. Mencari model terbaik dari dua data indeks saham gabungan dengan menggunakan model ARIMA-GARCH.
2. Mencari copula terbaik yang bisa menggambarkan keterkaitan antar dua set data indeks saham.
3. Menentukan rank correlation dengan menggunakan metode copula.
Manfaat Penelitian
TINJAUAN PUSTAKA
Definisi 1 (Percobaan Acak)
Suatu percobaan yang dapat diulang dalam kondisi yang sama dan semua kemungkinan hasil yang muncul dapat diketahui tetapi hasilnya tidak dapat ditentukan dengan tepat disebut sebagai percobaan acak. bagian dari ruang contoh serta memenuhi,
1. Definisi 6 (Peubah Acak Kontinu dan Fungsi Kepekatan Peluang)
4
.
(Grimmet dan Stirzaker 1992) Definisi 8 (Fungsi Sebaran Bersama)
Misal diberikan dua peubah acak dan dimana fungsi . Maka fungsi sebaran bersama dari dua peubah acak tersebut haruslah memenuhi persamaan,
(Ghahramani 2005) Definisi 9 (Nilai Harapan untuk Peubah Acak Kontinu)
Nilai harapan untuk peubah acak kontinu dengan fungsi kepekatan peluang adalah,
Beberapa sifat nilai harapan, antara lain: 1. Jika adalah suatu konstanta, maka .
2. Jika adalah suatu konstanta dan adalah peubah acak, maka
.
3. Jika adalah konstanta dan adalah suatu peubah acak, maka
. (Hogg et al. 2005) Definisi 10 (Simpangan Baku dan Ragam Peubah Acak Kontinu)
Misalkan adalah peubah acak kontinu dengan adalah nilai
Beberapa sifat dari ragam antara lain:
5 Definisi 16 (Strict White Noise)
Proses merupakan proses strict white noise jika merupakan deret yang bebas stokastik identik, peubah acak dengan ragam berhingga. Proses
strict white noise yang dipusatkan untuk mendapatkan rata-rata 0 dengan ragam akan dinotasikan SWN(0,
(McNeil et al. 2005) Definisi 17 (Tren dan Kestasioneran Data)
6
(
(Firdaus 2006) Definisi 18 ( Augmented Dickey-Fuller’s Test)
Augmented Dickey- Fuller’s Test (uji ADP) merupakan salah satu uji akar unit untuk menguji apakah data sudah stasioner ataukah belum. Jika suatu data belum stasioner pada orde nol, maka stasioneritas data tersebut bisa dicari melalui orde berikutnya sehingga diperoleh tingkat stasioneritas pada order ke- . Model- model yang dapat dipilih untuk melakukan uji ADF adalah:
(tanpa intersep)
(dengan intersep)
(intersep dengan trend waktu),
dengan merupakan beda pertama dari variabel yang digunakan, variabel tren. Hipotesis untuk pengujian ini adalah : menyebar normal). Persamaan yang digunakan uji Jarque-Bera adalah
,
dengan n adalah jumlah data yang diuji, S adalah kesimetrisan dari sebaran sampel dan K adalah ukuran ketinggian puncak kurva (peakedness).
(Jarque dan Bera 1981) Definisi 20 (Uji ARCH-LM)
Uji ARCH-LM atau Autoregressive Conditionally Heteroscedastic – Lagrange Multiplier adalah uji untuk menentukan adanya efek ARCH (heteroskedastisitas) atau tidak. Misalkan adalah residual dari persamaan rata-rata. Barisan digunakan untuk memeriksa heteroskedastisitas bersyarat atau efek ARCH. Uji ini sama dengan statistik pada umumnya untuk menguji = 0 ( dalam regresi linear
; ,
di mana adalah jumlah sampel atau banyaknya observasi, adalah galat, bilangan bulat.
7 Hipotesis untuk pengujian adalah:
: (tidak terdapat efek ARCH) : (terdapat efek ARCH)
(Engle 1995) Definisi 21 (Canonical Maximum Likelihood)
Canonical maximum likelihood adalah sebuah metode estimasi parameter copula dengan mencari nilai maksimum menggunakan fungsi likelihood. Fungsi
likelihood nyasendiri adalah,
Model Autoregressive Integrated Moving Average (ARIMA) diperkenalkan oleh Box dan Jenkins. Pada model ini terjadi proses Autoregressive
(AR) berordo dan atau terjadi proses Moving Average (MA) berordo . Pembeda berordo d dilakukan jika data deret waktu bersifat non-stasioner, padahal model ARIMA menginginkan data yang stasioner. Model deret waktu ini
Model Autoregressive Conditionally Heteroscedastic (ARCH) diperkenalkan oleh Engle. Diberikan yang SWN(0,1), proses
Generalized Autoregressive Conditionally Heteroscedatic atau GARCH ( ) jika proses tersebut adalah strictly stationary dan memenuhi beberapa proses yang bernilai positif , persamaan nya adalah,
8 elemen di mana elemennya merupakan anggota pertama dari elemen-elemen di
ƒ adalah domain pada ƒ dan dinotasikan sebagai D(ƒ). Himpunan dari semua
elemen di mana elemennya merupakan anggota kedua dari elemen-elemen di ƒ adalah rangepada ƒ (atau himpunan nilai pada ƒ) dan dinotasikan sebagai R(ƒ).
(Bartle dan Sherbert 2011)
Dalam teori graf, vertex adalah titik atau pojok dimana dua garis lurus atau lebih bertemu. Contoh ilustrasi dari vertex adalah sebagai berikut,
9 Lema 3 (Sifat Copula Archimedean)
Diberikan sebagai copula Archimedean dengan pembangkit , maka 1. simetris yang berarti di
Persamaan umum dari copula Clayton adalah sebagai berikut { } , di mana .
(Schmidt 2006) Definisi 34 (Copula Frank)
Persamaan umum dari copula Frank adalah sebagai berikut
10
.
(Schmidt 2006) Definisi 36 (Copula Student’s )
Persamaan Copula- 2 dimensi adalah copula yang memenuhi persamaan berikut,
Peubah acak kontinu X dan Y dikatakan independen atau saling bebas jika dan hanya jika, measures yang bernilai real dan berkorespondensi dengan setiap pasangan peubah acak dan bila memenuhi, dikatakan strictly monotonic jika salah satu kondisi berikut terpenuhi,
1. maka (strictly increasing) 2. , maka (strictly decreasing) untuk
(Aliprantis dan Burkinshaw 1990) Definisi 40 (Comonotonicity dan Countermonotonicity)
Diberikan peubah acak disebut comonotonic jika dan hanya jika,
,
untuk peubah acak Z dan fungsi naik . Sedangkan peubah acak disebut countermonotonic jika dan hanya jika,
,
untuk peubah acak Z dengan fungsi naik dan fungsi turun vice versa.
11
Definisi 41 (Equality in Distribution)
Diberikan peubah acak dan dimana dan dikatakan equal in distribution ( jika,
(Castaneda et.al 2012) Definisi 42 (Pearson’sLinear Correlation)
Pearson’s linear correlation merupakan dependence yang paling umum digunakan karena uji nya yang sederhana. Uji ini menentukan derajat dan arah hubungan antara satu variabel dengan variabel lainnya secara linier. Misal, diberikan peubah acak tak turun X dan Y, maka koefisien linear correlation nya
Tingkat korelasi atau rank correlation merupakan dependence measure
skalar sederhana yang hanya bergantung dengan sebaran copula bivariate dan tidak bergantung pada sebaran marjinalnya. Untuk mencari tingkat korelasi ada dua cara yang bisa digunakan yaitu dengan mencari Kendall’s tau atau dengan Spearman’s rho. Kelebihan rank correlation dibandingkan dengan Pearson’s linear correlation ialah:
1. Rank correlation mampu mendeteksi zero dependence sedangkan Pearson linear correlation tidak karena kebebasan antar variabel berimplikasi korelasi bernilai nol sedangkan korelasi bernilai nol belum tentu antar variabel saling bebas (independent).
2. Pearson linear correlation hanya mampu mendeteksi dependence pada variabel yang menyebar normal karena linear correlation tidak bisa menentukan kapan variance dari peubah acak X atau Y terbatas atau tak terbatas.
3. Rank correlation mampu mendeteksi dependence pada sebaran yang memiliki fat tail sedangkan Pearson linear correlation tidak karena karakteristik sebaran tersebut dimiliki oleh sebaran selain sebaran normal dan sehingga linear correlation tidak cocok untuk dijadikan uji pada data-data financial time series.
( McNeil et al. 2005) Definisi 44 (Concordant dan Discordant)
Diberikan pasangan peubah acak dan disebut concordant
jika dan atau jika dan , sedangkan dan
disebut discordant jika dan atau jika dan . (Nelsen 2005) Definisi 45 (Kendall’s TauRank Correlation)
Kendall’s rank correlation adalah uji yang mencari selisih antara peluang
12
∫ ∫ ,
di mana merupakan copulabivariate dari fungsi sebaran X dan Y.
(Cherubini et al. 2004) Definisi 46 (Spearman’s RhoRank Correlation)
Spearman’s rho yang dinotasikan dengan ρ adalah uji dengan mencari selisih proposional antara peluang concordant dengan peluang discordant peubah acak ( dan yang memiliki marjinal yang sama tapi variabel pertama memiliki fungsi sebaran bersama dan peubah acak lainnya independen :
∫ ∫
di mana merupakan copulabivariate dari fungsi sebaran X dan Y.
(Cherubini et al. 2004)
METODE
Data dan Analisis
Pada penelitian ini data yang digunakan merupakan data sekunder dari nilai indeks saham gabungan dua bursa saham yang berbeda. Data yang pertama diperdagangkan di pasar saham Tokyo. Pengambilan data tidak menggunakan data yang termutakhir karena pada selang waktu itu sedang terjadi krisis moneter di seluruh dunia yang juga Indonesia terkena dampaknya sehingga menurut penulis data ini sangat ideal untuk dijadikan sampel menguji korelasi antar pasar saham walaupun pasar saham itu tidak berasal dari negara yang sama bahkan berbeda regional dan benua.
13 digunakan. Langkah terakhir, menentukan nilai korelasi dengan menggunakan metode rank correlation.
Alat
14
Tahapan Penelitian
Pengujian data (apakah sudah stasioner atau belum)
Mencari ACF dan PACF sebagai perkiraan indeks
AR dan MA
Menentukan model pada data dengan menggunakan
metode ARIMA Menguji adanya efek
heteroskedastisitas pada data
Menghilangkan efek heteroskedastisitas dengan
metode GARCH
Pengujian mutual dependensi pada data untuk
melihat korelasi antarindeks
Penentuan copula terbaik dengan menggunakan metode
Canonical Maximum Likelihood
Penentuan tingkat korelasi dengan metode
Spearman's rho dan
15
HASIL DAN PEMBAHASAN
Seperti yang sudah dijelaskan sebelumnya, pada skripsi ini digunakan dua set data nilai indeks saham DAX dan NIK dari tanggal 27 April 1993 sampai dengan 14 Juli 2003 dimana data ini diambil dari [finance.yahoo.com/q/hp]. Data ini diambil per hari dan datanya terdapat di Lampiran1. Data nilai indeks saham itu kemudian divisualisasikan seperti yang dapat dilihat pada Gambar 4 dan Gambar 5 berikut,
Kedua data di atas masing-masing terdiri dari 1866 data amatan. Data-data ini selanjutnya ditentukan model terbaik serta copula terbaik. Copula yang di dapat digunakan untuk analisis tingkat korelasi antar data.
Gambar 4 Plot nilai indeks saham DAX
16
Model ARIMA
Model Autoregressive Integrated Moving Average (ARIMA) merupakan metode yang biasa digunakan untuk peramalan data deret waktu. Model umum
= sisaan acak pada waktu ke-t yang diasumsikan menyebar normal bebas stokastik
= operator backshift
.
Model umum ARIMA ) menyatakan bahwa data periode sekarang dipengaruhi oleh data periode sebelumnya. Untuk melakukan permodelan ARIMA dibutuhkan data yang stasioner. Untuk melihat kestasioneran data, data diuji dengan uji Augmented Dickey-Fuller. Secara singkat, hasil uji ADF pada data adalah sebagai berikut,
Tabel 1 Hasil uji ADF
Pada Tabel 1, nilai p-value pada kedua set data sebelum beda ke 1 bernilai lebih besar dari yang artinya menurut uji ADF kedua data di atas tidak stasioner. Ketika sudah dilakukan beda pertama, p-value lebih kecil dari yang berarti kedua data di atas stasioner. Setelah data stasioner, tahap selanjutnya mengindentifikasi plot ACF dan PACF setelah dilakukan beda pertama sebelumnya. Hasil plot ACF dan PACF nilai indeks saham DAX dan NIK adalah sebagai berikut,
p-value DAX p-value NIK
Sebelum beda ke 1 0.6142 0.2235
Setelah beda ke 1 0.001 0.001
17
Analisis yang sudah dilakukan dari plot ACF dan PACF menunjukkan bahwa ada tiga model yang teridentifikasi yaitu ARIMA (2,1,3), ARIMA(2,1,2), dan ARIMA (3,1,2) untuk indeks saham DAX dan ARIMA(1,1,1), ARIMA(1,1,0), dan ARIMA(0,1,1) untuk indeks saham NIK. Setelah itu, dilakukan pendugaan
parameter dengan metode “coba-coba” yaitu dengan memperkecil ordo p atau yang memiliki -value yang kecil atau menambah ordo p atau yang memiliki t
-Gambar 8 Plot ACF untuk indeks NIK Gambar 7 Plot PACF untuk indeks DAX
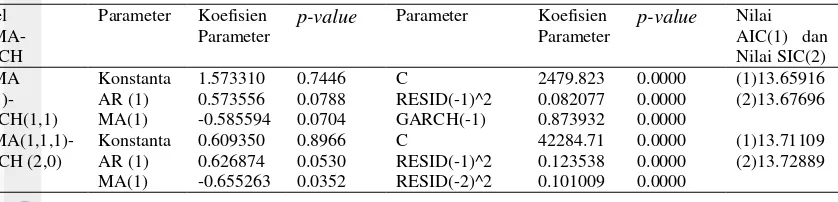
18
value yang besar. Rangkuman hasil pengujian model ARIMA adalah sebagai berikut,
Tabel 2 Hasil pendugaan model ARIMA pada indeks saham DAX Model
Konstanta 3.005598 0.0205 -10175.65 10.94819 10.93038 AR (1) -0.184157 0.5417
Konstanta 3.008278 0.0205 -10170.66 10.94871 10.93809 AR (1) -0.191178 0.5419
Konstanta 3.007912 0.0206 -10167.13 10.93500 10.92016 AR (1) 0.551854 0.0000
AR(2) -0.951658 0.0000 MA(1) -0.54152 0.0000 MA(2) 0.909229 0.0000
Tabel 3 Hasil pendugaan model ARIMA pada indeks saham NIK Model
Konstanta -2,152543 0,6600 -12799.16 13.74513 13.73623 AR(1) 0,534887 0,0462
MA(1) -0,577687 0,0260 ARIMA
(1,1,0)
Konstanta -1,904531 0,7132 -12800.72 13.74275 13.73682 AR(1) -0.039578 0.0877
ARIMA (0,1,1)
Konstanta -1.782652 0.7297 -12807.57 13.74274 13.73681 MA(1) -0.041997 0.0700
Dari Tabel 2 terlihat bahwa model ARIMA (2,1,2) untuk DAX adalah model ARIMA yang paling baik karena semua -value nya kurang dari baik untuk koefisien AR maupun koefisien MA dan nilai AIC (Akaike
19 ada efek heteroskedastisitas pada model. Hipotesis untuk pengujian ARCH-LM sendiri ialah sebagai berikut,
data tidak memiliki efek heteroskedastisitas.
data memiliki efek heteroskedastisitas.
Untuk hasil ujinya ialah sebagai berikut,
Tabel 4 Hasil pengujian ARCH-LM
p-value pada DAX p-value pada NIK
0.0000 0.0002
Pada Tabel 4 hasil pengujian pada kedua nilai indeks saham menunjukkan bahwa p-value kurang dari sehingga ditolak yang artinya pada kedua model ARIMA masih terdapat efek heteroskedastisitas, sehingga tahap selanjutnya adalah memodelkan model ARIMA dengan metode GARCH.
Model ARIMA-GARCH
Permodelan ragam sisaan GARCH adalah permodelan yang bertujuan untuk menstasionerkan ragam pada model sehingga model yang sudah didapatkan tidak memiliki efek heteroskedastisitas. Pada model sebelumnya dilakukan uji ARCH-LM yang hasilnya pada kedua model ARIMA masih terdapat efek heteroskedastisitas, sehingga pada tahap ini ditentukan model ARIMA-GARCH yang paling baik. Hasil analisis menunjukkan setidaknya terdapat dua model yang kemungkinan merupakan model terbaik untuk masing-masing nilai indeks saham yaitu, ARIMA(2,1,2)-GARCH(1,1) dan ARIMA(2,1,2)-GARCH(2,1) untuk DAX dan ARIMA(1,1,1)-GARCH(1,1) dan ARIMA(1,1,1)-GARCH(2,0) untuk NIK. Secara ringkas hasil pengujiannya dapat dilihat pada Tabel 5 dan 6 berikut,
Tabel 5 Hasil analisis model ARIMA-GARCH untuk indeks saham DAX
Model ARIMA-GARCH
Parameter Koefisien Parameter
20
Tabel 6 Hasil analisis model ARIMA-GARCH untuk indeks saham NIK
Model ARIMA-GARCH
Parameter Koefisien
Parameter
p-value Parameter Koefisien Parameter
Konstanta 1.573310 0.7446 C 2479.823 0.0000 (1)13.65916
(2)13.67696
AR (1) 0.573556 0.0788 RESID(-1)^2 0.082077 0.0000
MA(1) -0.585594 0.0704 GARCH(-1) 0.873932 0.0000
ARIMA(1,1,1)- GARCH (2,0)
Konstanta 0.609350 0.8966 C 42284.71 0.0000 (1)13.71109
(2)13.72889
AR (1) 0.626874 0.0530 RESID(-1)^2 0.123538 0.0000
MA(1) -0.655263 0.0352 RESID(-2)^2 0.101009 0.0000
Pada Tabel 5 terlihat bahwa p-value dari koefisien AR dan MA sudah baik karena semua koefisennya kurang dari . Namun, untuk persamaan ragamnya model ARIMA(2,1,2)-GARCH(2,1) masih belum signifikan karena nilai p-value nya lebih besar dari Sehingga, model ARIMA(2,1,2)-GARCH(1,1) dipilih menjadi model yang terbaik untuk indeks DAX. Pada Tabel 6 terlihat bahwa p-value dari persamaan ragamnya sudah baik karena semua p-value nya kurang dari Namun, untuk p-value pada koefisien AR dan MA pada model ARIMA(1,1,1)-GARCH(1,1) masih belum signifikan karena nilai p-value
nya lebih dari . Sedangkan, pada model ARIMA(1,1,1)-GARCH(2,0) nilai p-value pada koefisien AR sebesar 0.0530 atau kelebihan sebesar 0.003 dari
masing-21
Copula
Langkah selanjutnya setelah mendapatkan model ARIMA-GARCH adalah melakukan uji normalitas pada residualnya dengan menggunakan uji Jarque-Bera. Hipotesis untuk pengujian Jarque-Bera ini adalah
data menyebar normal.
data tidak menyebar normal. Hasil ujinya sendiri disajikan pada tabel berikut,
Tabel 8 Hasil uji Jarque-Bera
p-value indeks DAX p-value indeks NIK
0.001 0.001
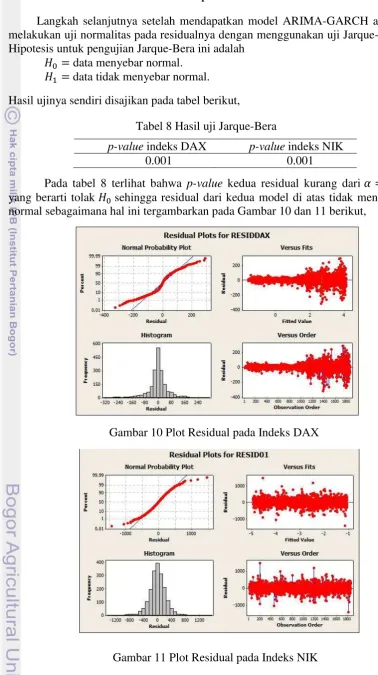
Pada tabel 8 terlihat bahwa p-value kedua residual kurang dari yang berarti tolak sehingga residual dari kedua model di atas tidak menyebar normal sebagaimana hal ini tergambarkan pada Gambar 10 dan 11 berikut,
Gambar 10 Plot Residual pada Indeks DAX
22
Setelah diketahui bahwa residual tidak menyebar normal maka dicari distribusi masing-masing data dan hasilnya tergambarkan di Tabel 9 berikut,
Tabel 9 Hasil uji distribusi
Indeks Saham Jenis Distribusi AIC BIC Log-likelihood value
DAX location scale 19645 19661 9819.4 NIK location scale 25468 25485 12731
Selanjutnya, dilakukan uji mutual dependensi pada kedua data indeks saham. Hipotesis untuk pengujian mutual depedensi ini adalah,
Tidak ada mutual dependensi diantara indeks saham. Ada mutual dependensi diantara indeks saham.
Tabel 10 Hasil Uji mutual dependensi
Pada Tabel 10 terlihat bahwa value hasil pengujian lebih kecil dari
yang berarti tolak sehingga ada mutual dependensi antara indeks saham DAX dengan indeks saham NIK. Karena adanya mutual dependensi antarindeks saham dan residual yang didapatkan tidak menyebar normal, maka fungsi copula dapat mengkorelasikan kedua indeks saham tersebut. Selanjutnya, parameter copula diestimasi dengan menggunakan copula Clayton, Frank, Gumbel, Gaussian, dan Hasil estimasi parameter copula ialah sebagai berikut,
Tabel 11 Hasil Estimasi Parameter Copula
Berdasarkan Tabel 11, copula memiliki nilai maximum likelihood
23 Pada tabel di halaman sebelumnya terlihat bahwa nilai tingkat korelasi pada kedua residual data dengan menggunakan metode Kendall’s tau adalah sebesar 0.1491 atau 14.91% dan jika menggunakan Spearman’s rho sebesar 0.2221 atau 22.21%. Hal ini menunjukkan bahwa kedua indeks saham gabungan yang digunakan berkorelasi positif meskipun bernilai relatif kecil. Metode rank correlation adalah metode penentuan tingkat korelasi ekor sebaran yang hanya berdasarkan pada jenis copula yang digunakan. Sehingga, ketika indeks saham DAX mengalami penurunan nilai maka kejadian itu berkorelasi lemah dengan penurunan nilai yang terjadi pada indeks saham NIK. Korelasi diatas dikatakan lemah karena berdasarkan rule of thumb yang dikemukakan Hinkle et.al
(1998:120) menyatakan, “... nilai koefisien korelasi yang berkisar dari 0.1 sampai 0.3 atau -0.3 sampai -0.1 dikategorikan berkorelasi lemah...”. Karena nilai korelasi yang didapatkan semua nya di antara 0.1 sampai 0.3 maka kedua indeks berkorelasi positif lemah.
SIMPULAN DAN SARAN
Simpulan
Skripsi ini berhasil mencari model terbaik dari data nilai indeks saham DAX dan NIK serta menentukan rank correlation menggunakan metode Spearman’s
rho dan Kendall’s tau. Dari hasil yang sudah didapatkan, model terbaik untuk data indeks saham DAX adalah ARIMA(2,1,2)-GARCH(2,1) dan untuk data indeks saham NIK adalah ARIMA(1,1,1)-GARCH(2,0). Copula terbaik yang didapatkan pada skripsi ini adalah copula dengan parameter sebesar 0.2321. Untuk nilai koefisien korelasi yang didapatkan dengan metode Kendall’s tau adalah sebesar 0.1491 dan jika dengan metode Spearman’s rho hasilnya sebesar 0.2221.
Saran
Pada skripsi ini dependence measures yang digunakan hanya Spearman’s
rho dan Kendall’s tau. Sebenarnya selain rank correlation, terdapat berbagai macam jenis dependence measures lain yang lebih relevan dan akurat ketimbang
rank correlation yang mengintepretasikan korelasi berdasarkan nilai skalar seperti,
tail depedence, pengukuran berdasarkan Ginni’s coefficient, dan lain-lain. Sehingga, untuk penelitian selanjutnya metode yang lain bisa digunakan untuk mendapatkan hasil yang lebih akurat dan realistis. Copula yang digunakan pada skripsi ini merupakan copula dua dimensi (bivariate) karena skripsi ini hanya menganalisis dua variabel peubah acak. Copula ini kurang cocok untuk menggambarkan investasi atau portofolio yang dimiliki baik oleh individu maupun kelompok yang pada umumnya berjumlah sebanyak jenis investasi atau portofolio. Sehingga, kedepannya penelitian ini perlu diperluas ke permodelan dimensi banyak (multivariate) dan tentunya menggunakan copula multivariate
24
DAFTAR PUSTAKA
Aliprantis CD, Burkinshaw O. 1990. Principle of Real Analysis. Ed ke-2. California (US): Academic Press.
Bartle RG, Shebert DR. 2011. Introduction to Real Analysis. Ed ke-4. New Jersey (AS): John Wiley and Sons, Inc.
Castaneda L, Arunachalam V, Dharmaraja S. 2012. Introduction to Probability and Stochastic Processes with Applications. West Sussex (GB): Wiley, Ltd Chartrand G. 1985. Introductory Graph Theory. New York (US): Dover
Publications.
Cherubini W, Luciano W, Vecchiato W. 2004. Copula Methods In Finance. West Sussex (GB): John Wiley and Sons, Ltd.
Cryer JD. 1986. Time Series Analysis. Boston (US): Duxburry Press.
Embrechts P, McNeil AJ, Straumann D. 2001. Correlation and depedency in risk management: properties and pitfalls. Cambridge (GB): Cambridge University Press.
Engle RF. 1995. ARCH: Selected Readings. Oxford (GB): Oxford University Press.
Firdaus M. 2006. Analisis Deret Waktu Satu Ragam. Bogor (ID): IPB Press. Ghahramani S. 2005. Fundamentals of Probability. New Jersey (US): Pearson
Hinkle DE, Wiersma W, Jurs SG. 1998. Applied Statistics for the Behavioral Sciences. Ed ke-4. Boston (US): Houghton Mifflin Company.
Hogg RV, McKean JW, Craig AT. 2005. Introduction to Mathematical Statistics.
Ed ke-6.New Jersey (US): Pearson Education, Inc.
Jarque CM, Bera AK. 1981. Efficient test for normality test, homoscedasticity, and serial independence. Economic Letters. 7(4):313-318.doi:10.1016/0165-1765(81)90035-5.
Kay R. 2007. Statistical Thinking for Non Staticians in Drug Regulation. West Sussex (GB): John Wiley and Sons Ltd.
McNeil AJ, Rudger F, Embrechts P. 2005. Quantitative Risk Management.
Princeton (US): Princeton University Press
Nachrowi DN, Usman H. 2006. Pendekatan Populer dan Praktis Ekonometrika untuk Analisis Ekonomi dan Keuangan. Jakarta (ID): UI Press.
Nelsen RB. 2005. An Introduction to Copulas. Oregon (US): Springer Science and Business Media,Inc.
Ross SM. 2003. A First Course Linear Statistical Models. Burlington (CA): Elsevier, Inc.
Roussas GG. 2004. An Introduction to Measure-theoretic Probability. California (US): Academic Press.
25 Schmidt T. 2006. Copulas from theory to application in France. IJTAF,
28
Lampiran 2 Hasil uji ADF pada data asli indeks saham DAX
Lampiran 3 Hasil uji ADF pada DAX setelah pembedaan satu kali
Lampiran 4 Hasil uji ADF pada data asli indeks saham NIK
29 Lampiran 6 Hasil model ARIMA (2,1,3) untuk indeks DAX
30
Lampiran 8 Hasil model ARIMA (2,1,2) untuk indeks DAX
31
32
34
36
37 Lampiran 18 Hasil dari uji ARCH-LM ARIMA (1,1,1) pada NIK
38
Lampiran 20 Hasil uji Jarque-Bera ARIMA(2,1,2)-GARCH(1,1) pada DAX
39 Lampiran 22 Hasil uji distribusi ARIMA(2,1,2)-GARCH(1,1) pada DAX
Lampiran 23 Hasil uji distribusi ARIMA(1,1,1)-GARCH(2,0) pada NIK
40
Lampiran 25 Hasil estimasi parameter copula
41
RIWAYAT HIDUP
Penulis dilahirkan di Gisting pada tanggal 1 November 1992 dari pasangan Budhy Syattwa Indraputra dan Rosmalina. Penulis berkewarganegaraan Indonesia dan beragama Islam. Penulis adalah putra pertama dari empat bersaudara. Tahun 2004 penulis lulus dari SD Al-Kautsar Bandar Lampung, tahun 2007 penulis lulus dari SMP Negeri 1 Bandar Lampung dan tahun 2010 penulis lulus dari SMA Al-Kautsar Bandar Lampung. Pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor (IPB) melalui jalur undangan seleksi masuk IPB dan di terima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.