( Skripsi )
Oleh Dwi Ratnasari
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
MODEL PERTUMBUHAN PREMI ASURANSI JIWA BERJANGKA DENGANTINGKAT SUKU BUNGA KONSTAN UNTUK KASUS
ABSTRAK
MODEL PERTUMBUHAN PREMI ASURANSI JIWA BERJANGKA DENGAN TINGKAT SUKU BUNGA UNTUK KASUS KONTINU DAN
DISKRIT
Oleh
DWI RATNASARI
Dalam asuransi,terdapat istilah yang disebut asuransi jiwa dimana dalam asuransi tersebut yang dipertanggungjawabkan adalah kematian. Asuransi jiwa pun terdapat berbagai jenis produk, salah satunya yaitu asuransi jiwa berjangka. Jika seseorang (tertanggung) menandatangani kontrak polis asuransi maka harus membayarkan premi untuk tiap bulannya sebagai kewajiban atas keikutsertaannya pada asuransi. Premi itu sendiri dapat menaik ataupun menurun untuk tiap tahunnya. Pada pembayaran premi terdapat benefit yang akan diberikan kepada si tertanggung meninggal, jika pemberian benefit dilakukan pada saat tertanggung meninggal disebut dengan kasus kontinu sedangkan jika benefit dibayarkan pada akhir tahun meninggalnya si tertanggung maka disebut dengan kasus diskrit. Dengan menentukan benefit yang akan diberikan tiap tahunnya untuk kasus kontinu maupun diskrit sehingga dapat mendapatkan model pertumbuhan premi.Penelitian ini bertujuan untuk memodelkan pertumbuhan premi asuransi jiwa berjangka dengan tingkat suku bunga konstan (sama tiap tahunnya) untuk kasus kontiu dan diskrit.
ABSTRACT
PREMIUM GROWTH MODEL TERM LIFE INSURANCE WITH RATE OF INTEREST IS CONSTANT FOR KONTINU DAN DISKRIT CASE’S
By
DWI RATNASARI
In insurance,available the so called life assurance terminology where in that insurance one is laided at the door is death. Life assurance even exists various product type, one of it which is life assurance gets meter. If someone (the insured) sign contracts insurance policy therefore have pay premium for every month it as liabilities on its participation on insurance. That premium is alone gets to ascend or menurun even for per annum it. On premium payment exists benefit who will be given unto the the insured dies, if benefit's application is done at the moment deceased the insured is called with kontinu's case whereas if benefit pay on year-end its deceased the the insured therefore so-called with diskrit's case. By determining benefit what do will be given per annum it for kontinu's case and also diskrit so gets to get premium growth model. This research intent to model life assurance premium growth gets meter with level constant rate of interest (with per annum it) for kontinu's case and diskrit.
MODEL PERTUMBUHAN PREMI ASURANSI JIWA BERJANGKA DENGAN TINGKAT SUKU BUNGA KONSTAN UNTUK KASUS
KONTINU DAN DISKRIT
Oleh
DWI RATNASARI
Skripsi
Sebagai Salah Satu Syarat untuk Memperoleh Gelar SARJANA SAINS
Pada
Jurusan Matematika
Fakultas Matematika dan Ilmu Pengetahuan Alam
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG
BANDAR LAMPUNG 2017
RIWAYAT HIDUP
Penulis dilahirkan di Rumbia pada tanggal 07Januari 1996. Penulis merupakan anak ketujuh dari pasangan Bapak Surip dan Ibu Rasminten sertaadik dari Sumaji, Sulastri, Suyono, Bambang Wicaksono, Dodi Wahyudi, dan Ari Wibowo.
Penulis memulai pendidikan dari Pendidikan sekolah dasar di SD Negeri 6 Rukti Basukipada tahun 2001. Pendidikan sekolah menengah pertama di SMP Negeri 1Rumbia pada tahun 2007. Pendidikan sekolah menengah atas di SMA Negeri 1Rumbia pada tahun 2011.
Penulis melanjutkan pendidikan di perguruan tinggi dan terdaftar sebagai mahasiswa Jurusan Matematika dan Ilmu Pengetahuan Alam Universitas Lampung melalui jalur SNMPTN pada tahun 2013. Pada periode tahun 2013/2014 penulis terdaftar sebagai anggota Biro Dana dan Usaha Himpunan Mahasiswa Matematika Unila juga sebagai anggota Natural dan Rohani Islam (ROIS) .
Sebagai bentuk aplikasi bidang ilmu kepada masyarakat, penulis telah menyelesaikan Kerja Praktik (KP) di Kantor Dinas Pendapatan UPTD Pendapatan Wilayah I Bandar Lampung dan ditempatkan di bagian seksiPenagihan Dan Pendanaan selama kurang lebih satu bulan. Penulis juga telah melakukan Kuliah Kerja Nyata (KKN) Tematik pada tahun 2016 selama 40 hari di Desa Purwodadi Kecamatan Bangun Rejo, Lampung Tengah.
PERSEMBAHAN
Puji dan syukur kepada Allah SWT berkat rahmat dan hidayah-Nya sebuah
karya sederhana namun penuh perjuangan telah terselesaikan
Kupersembahkan Skripsi ini untuk :
Kedua orang tuaku tercinta
Ayahanda Surip & Ibunda Rasminten
Serta Kakak- kakakku tersayang
Sumaji, Suyono, Sulastri, Bambang Wicaksono, Dodi Wahyudi,
Dan Ari Wibowo
MOTTO
Learn from yesterday, live for today, hope for tomorrow
(Albert Einstein)
Man jadda wajadda, man shabara zhafira, man sara ala darbi washala
(Animo)
Kesabaran, kegigihan, dan kerja keras menciptakan sebuah kombinasi
yang tidak terkalahkan untuk kesuksesan
(Napoleon Hill)
Selalu ada harapan bagi mereka yang sering berdoa, selalu ada jalan
bagi mereka yang sering berusaha
SANWACANA
Puji syukur kehadirat Allah SWT berkat rahmat dan hidayahnya, sehingga penulis dapat menyelesaikan skripsi ini dengan baik. Shalawat serta salam senantiasa tercurah kepada junjungan kita Nabi Muhammad SAW, suri tauladan terbaik sepanjang masa.
Pada proses penyusunan skripsi, penulis memperoleh banyak bantuan, dukungan, bimbingan serta kritik dan saran yang membangun sehingga skripsi ini mampu terselesaikan. Oleh karena itu, dalam kesempatan ini penulis ingin mengucapkan terima kasih kepada :
1. Bapak Drs. Rudi Ruswandi, M.Si., selaku dosen pembimbing utama yang telah membimbing penulis dengan setulus hati, menyumbangkan ilmunya, memberikan motivasi serta telah banyak meluangkan waktu ditengah kesibukannya untuk membimbing hingga skripsi ini terselesaikan.
2. Bapak Dr. Muslim Ansori, S.Si., M.Si., selaku dosen pembimbing pembantu yang telah banyak membantu, memberi masukan serta dengan sabar memberikan pengarahan dalamproses penyusunan skripsi ini.
5. Ibu Dra. Wamiliana, M.A.,Ph.D., selaku Ketua Jurusan Matematika FMIPA Universitas Lampung.
6. Bapak Prof. Warsito, S.Si., D.E.A, Ph.D selaku dekan FMIPA Universitas Lampung.
7. Dosen, staf dan karyawan Jurusan Matematika FMIPA UNILA yang telah memberikan ilmu pengetahuan dan segala bentuk bantuan kepada penulis.
8. Orang tuaku tercinta dan kakak - kakakku tersayang, serta seluruh keluarga yang senantiasa memberikan kasih sayang yang tiadaterkira, selalu menjadi penyemangat disaat lemah, selalu memotivasi penulis untuk memberikan yang terbaik, serta tak henti-hentinya mendoakan untuk keberhasilan penulis.
9. Teman-teman satu bimbingan, vinny, Cinkia, Aiman, Retno, Shintia yang telah banyak membantu, memberikan perhatian dan dukungan mental kepada penulis.
10. Untuk sahabat KKN, Disti, Melia, Shiska, Vyna, Indra, Yona, Gagah, Mydori terimakasih telah mendengarkan keluh kesah dan memberikan semangat.
11. Teman-teman satu bimbingan akademik, Dita, Efrizal, dan Dimas yang selalu membantu penulis, berjuang bersama serta saling mendukung dalam menyelesaikan skripsi ini.
12. Muhammad Adi Yusuf yang rela meluangkan waktunya untuk menemani, membantu dan memberikan perhatian yang menjadi semangat tersendiri bagi penulis.
13. Keluarga besar HIMATIKAterimakasihataspengalaman yang luarbiasa.
14. Teman-teman seperjuangan Matematika 2013 yang tidak bisa penulis sebutkan satu persatu, terimakasih atas empat tahun kebersamaan yang bermakna dan kisah-kisah indah yang takkan terlupakan.
15. Seluruh pihak yang telah membantu penulis yang tidak dapat disebutkan satu persatu atas peran dan dukungannya dalam menyusun skripsi ini.
Bandarlampung, 10 Oktober 2017 Penulis,
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... iii
DAFTAR SIMBOL ... iv
DAFTAR TABEL ... vi
I. PENDAHULUAN 1.1 Latar Belakang dan Masalah ... 1
1.2 Tujuan Penelitian ... 3
1.3 Manfaat Penelitian ... 3
1.4 Batasan Masalah ... 3
II. TINJAUAN PUSTAKA 2.1 Asuransi ... 4
2.2 Asuransi Jiwa ... 5
2.3 Jenis–Jenis Asuransi Jiwa ... 6
2.4 Fungsi Kelangsungan Hidup (Survival Function) ... 8
2.5 Peluang Waktu Sisa Hidup (Curtate-Future-Lifetime) ... 8
2.6 Laju Tingkat Kematian (Force Of Mortality) ... 12
2.7 Tabel Mortalitas ... 15
2.8 Bunga ... 19
2.9 Laju Tingkat Suku Bunga (Force Of Interest) ... 20
2.10 Premi Tunggal ... 21
2.11 Premi Tunggal Asuransi Jiwa Berjangka ... 22
2.12 Fungsi Bilangan Bulat Terbesar ... 25
2.13 Hubungan Antara Kasus Diskrit Dan Kasus Kontinu Pada Asuransi Jiwa ... 25
2.14 Premi Asuransi Jiwa Berjangka Menaik (Increasing) Untuk Kasus Kontinu ... 27
2.15 Premi Asuransi Jiwa Berjangka Menurun (Decreasing) Untuk Kasus Kontinu ... 28
Halaman 2.16 Premi Asuransi Jiwa Berjangka Menaik (Increasing)
Untuk Kasus Diskrit ... 29 2.17 Premi Asuransi Jiwa berjangka Menurun (Decreasing)
Untuk Kasus Diskrit ... 31
III. METODOLOGI PENELITIAN
3.1 Waktu dan Tempat Penelitian ... 32 3.2 Data Penelitian ... 32 3.3 Metode Penelitian ... 32
IV. HASIL DAN PEMBAHASAN
4.1 Menentukan besarnya benefit tiap tahun yang akan diberikan
kepada tertanggung sesaat ketika meninggal (kontinu) ... 39 4.2 Menghitung Nilaitpx... 42
4.3 Memodelkan pertumbuhan premi (menaik dan menurun)
untuk kasus kontinu ... 42 4.4 Menentukan besarnya benefit tiap tahun yang akan diberikan
kepada tertanggung pada saat akhir tahun meninggalnya
si tertanggung (diskrit) ... 51 4.5 Menghitung nilaik|qx dan v... 55
4.6 Memodelkan pertumbuhan premi (menaik dan menurun)
untuk kasus diskrit ... 56
V. KESIMPULAN
5.1 Kesimpulan ... 62
DAFTAR PUSTAKA
DAFTAR SIMBOL
Simbol Pengertian
T(x) Sisa umur bagi x
FT(x) Peluang seseorang berusia x tahun akan meninggal sebelum berusia x+t
tahun
st(x)(t) Peluang orang berusia x tahun akan hidup mencapai usia x+t tahun tqx Peluang meninggal seseorang berusia x
tpx Peluang hidup seseorang berusia x
t|uqx Peluang seseorang berusia x akan meninggal antara umur x+t tahun dan
x+t+u
( ) Laju tingkat kematian seseorang berusia x
lx Jumlah orang yang diharapkan masih hidup sampai usia x tahun
l0 Banyaknya bayi yang dilahirkan
L(x) Banyaknya bayi yang hidup sampai dengan usia x Ij Indikator untuk bayi yang bertahan hidup dari j
dx Banyaknya orang berusia x tahun akan meninggal sebelum mencapai usia
x+t tahun
nDx Banyaknya bayi yang meninggal antara usia x sampai dengan usia x+n tahun ndx Banyaknya orang yang berusia x tahun akan meninggal sebelum mencapai
usia x+n tahun
i(m) Dana yang dibungakan lebih dari satu kali dalam setahun dengan m tahun Laju tingkat suku bunga (force of interest)
I Tingkat suku bunga
vt Faktor diskon (discount factor) bt Fungsi benefit/santunan
Simbol Pengertian
: | Premi yang harus dibayarkan oleh seseorang berusia x dengan jangka waktun tahun untuk kasus kontinu : | Premi yang harus dibayarkan oleh seseorang berusia x dengan jangka waktu
n tahun untuk kasus diskrit
vk+1 Fungsi diskon pada kasus diskrit bk+1 Fungsi benefit pada kasus diskrit ⌊ ⌋ Fungsi bilangan bulat terbesar
bt=⌊ + 1⌋
Besarnya benefit yang akan didapatkan oleh seorang tertanggung pada premi menaik yaitu sebesar t+1 satuan
: |
Premi yang harus dibayarkan oleh seseorang berusia x akan menaik tiap tahunnya dalam jangka waktu n tahun
: |
Premi yang harus dibayarkan oleh seseorang berusia x akan menurun tiap tahunnya dalam jangka waktu n tahun
k|qx Peluang meninggal seseorang berusia x
DAFTAR TABEL
Tabel Halaman
1. Life table united states 2002 ... 38
2. Nilaitpx... 42
3. Model premi menaik asuransi jiwa berjangka (kontinu) ... 45
4. Premi menaik tiap tahun untuk kasus kontinu ... 46
5. Model premi menurun asuransi jiwa berjangka (kontinu) ... 49
6. Premi menurun tiap tahun untuk kasus kontinu ... 50
7. Nilaik|qxdan v... 55
8. Model premi menaik untuk kasus diskrit ... 57
9. Premi per tahun menaik untuk kasus diskrit ... 57
10. Model premi menaik untuk kasus diskrit ... 59
DAFTAR GAMBAR
Gambar Halaman
1. Sistem pembayaran benefit pada asuransi jiwa berjangka ... 22
2. Kenaikan premi untuk kasus kontinu ... 46
3. Penurunan premi untuk kasus kontinu ... 51
4. Kenaikan premi untuk kasus diskrit ... 58
I. PENDAHULUAN
1.1 Latar Belakang Dan Masalah
Pada kehidupan saat ini, manusia tidak hanya membutuhkan tiga kebutuhan ( sandang,pangan, dan papan ) saja namun hal lain juga ingin dipenuhi seperti halnya kebutuhan di hari tua maka manusia sudah menyiapkan dana pensiun untuk masa yang akan datang serta anak-anak yang belum sekolah sudah disiapkan dana mulai tingkat dasar hingga perguruan tinggi. Problem yang ditakuti manusia adalah kemungkinan kematian yang terjadi terlalu dini. Kematian ini merupakan hal yang pasti namun masalah waktu atau kapan kematian itu datang adalah suatu hal yang tidak dapat ditentukan oleh manusia. Salah satu cara untuk mengurangi risiko tersebut yaitu dengan mengalihkan atau melimpahkan risiko tersebut kepada pihak atau badan usaha lain. Yang dimaksud pihak atau badan usaha lain ialah suatu lembaga yang menjamin sekiranya timbul suatu peristiwa yang tidak diinginkan, lembaga ini dikenal dengan apa yang disebut asuransi.
Salah satu jenis asuransi yang dikenal sekarang ini adalah asuransi jiwa. Asuransi jiwa merupakan alat sosial ekonomi, yang merupakan cara dari sekelompok orang untuk dapat bekerjasama meratakan beban kerugian karena kematian sebelum waktunya dari anggota-anggota kelompok tersebut. Pada asuransi jiwa yang
2
dipertanggungjawabkan ialah disebabkan oleh kematian (death). Terdapat beberapa jenis asuransi jiwa yang sering ditawarkan oleh perusahaan asuransi antara lain yaitu asuransi jiwa seumur hidup (whole life insurance), asuransi jiwa berjangka ( term insurance), asuransi jiwa endowment murni (pure endowmet), dan asuransi jiwa dwiguna (endowment). Pada saat seseorang menandatangani kotrak polis asuransi maka akan dibebankan sejumlah premi yang harus dibayarkan oleh orang tersebut. Premi merupakan sejumlah uang yang mesti dibayarkan pada setiap bulannya sebagai suatu kewajiban dari yang tertanggung atas keikutsertaannya pada asuransi.
Nilai besarnya premi dari keikutsertaannya pada asuransi yang mesti dibayarkan sudah ditetapkan oleh para perusahaa asuransi dengan dapat memperhatikan segala kondisi dari yang tertanggung. Premi yang dibayarkan bisa menaik ataupun menurun untuk tiap tahunnya, pertumbuhan premi tersebut dapat dikategorikan dalam dua kasus yaitu untuk kasus kontinu dan kasus diskrit. Pembayaran premi dikatakan kasus kontinu ketika perusahaan asuransi memberikan benefit pada saat tertanggung meninggal sedangkan dikatakan kasus diskrit ketika perusahaan asuransi memberikan benefit pada saat akhir tahun meninggal si tertanggung. Pada premi asuransi jiwa berjangka, pertumbuhan premi baik premi menaik ataupun premi menurun memiliki perumusan tersendiri. Besarnya premi
3
membuat model pertumbuhan premi asuransi jiwa berjangka dengan tingkat suku bunga konstan untuk kasus diskrit dan kontinu. Keuntungan dari pembentukan model ini sendiri yaitu mempersingkat rumus utama premi menaik/menurun sehingga mempermudah perhitungan premi tiap tahunnya, sedangkan kelemahannya yaitu karna bentuk/model berasal dari penjabaran rumus utama premi menaik/menurun sehingga perhitungan premi harus dilakukan bertahap.
1.2 Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah sebagai berikut :
1. Membuat model pertumbuhan premi asuransi jiwa berjangka dengan tingkat suku bunga konstan untuk kasus kontinu dan diskrit
2. Mengetahui pertumbuhan premi menaik dan menurun pada asuransi jiwa berjangka
1.3 Manfaat Penelitian
Adapun manfaat dari penelitian ini adalah :
1. Dapat memberikan informasi tentang pertumbuhan premi
2. Dapat memberikan informasi tentang model pertumbuhan premi asuransi jiwa berjangka dengan tingkat suku bunga konstan untuk kasus kontinu dan diskrit
1.4 Batasan Masalah
Penelitian ini dibatasi hanya pada pertumbuhan premi tunggal asuransi jiwa berjangka secara umum.
II. TINJAUAN PUSTAKA
2.1 Asuransi
Untuk memenuhi kebutuhan yang belum pasti di masa yang akan datang tersebut maka sebagian manusia memerlukan asuransi. Karena asuransi merupakan salah satu buah peradaban manusia dan merupakan suatu hasil evaluasi kebutuhan manusia yang sangat hakiki ialah kebutuhan akan rasa aman dana terlindung, terhadap kemungkinan menderita kerugian. Asuransi merupakan buah pikiran dan akal budi manusia untuk mencapai suatu keadaan yang dapat memenuhi kebutuhannya, terutama sekali untuk kebutuhan – kebutuhannya yang hakiki sifatnya antara lain rasa aman dan terlindung ( Hartono, 1992).
Disadari bahwa asuransi mempunyai beberapa manfaat antara lain pertama, membantu masyarakat dalam rangka mengatasi segala masalah risiko yang dihadapinya. Hal itu akan memberikan ketenangan dan kepercayaan diri yang lebih tinggi kepada yang bersangkutan. Kedua, asuransi merupakan sarana
5
metode yang paling banyak dipakai. Karena asuransi menjanjikan perlindungan kepada pihak tertanggung terhadap risiko yang dihadapi perorangan maupun risiko yang dihadapi oleh perusahaan (Sastrawidjaja, 1993).
Karena dipandang begitu pentingnya asuransi bagi sebagian masyarakat maka kebutuhan akan jasa perasuransian makin dirasakan, baik oleh perorangan maupun dunia usaha di Indonesia. Asuransi merupakan sarana finansial dalam dalam tata kehidupan rumah tangga, baik dalam mengahadapi risiko mendasar seperti risiko kematian, atau dalam menghadapi risiko atas harta benda yang dimiliki. Demikian pula dunia usaha dalam menjalankan kegiatannya menghadapi berbagai risiko yang mungkin dapat mengganggu kesinambungan usahanya (Darmawi, 2006).
2.2 Asuransi Jiwa
Asuransi jiwa merupakan alat sosial ekonomi, yang merupakan cara dari sekelompok orang untuk dapat bekerja sama meratakan beban kerugian karena kematian sebelum waktunya dari anggota - anggota kelompok tersebut. Pada asuransi jiwa yang dipertanggungkan ialah yang disebabkan oleh kematian (death). Kematian tersebut mengakibatkan hilangnya pendapatan seseorang atau suatu keluarga tertentu. Risiko yang mungkin timbul pada asuransi jiwa terutama
terletak pada “unsur waktu (time), oleh karena sulit untuk mengetahui kapan
seseorang meninggal dunia. Untuk memperkecil risiko tersebut, maka sebaiknya diadakan pertanggungan jiwa ( Darmawi, 2006).
6
Pada dasarnya yang dimaksud dengan asuransi jiwa adalah suatu asuransi yang bertujuan untuk memberikan proteksi terhadap orang perindividu dan atau perkelompok (keluarga) atas kerugian financial tak terduga, maksud dari kerugian financial tak terduga adalah karena terjadi kematian yang mendadak (terlalu cepat), cacat tetap total, atau sudah tidak produktif (terlalu tua – terlalu lama hidup) atas seseorang yang mengakibatkan hilangnya penghasilan. Jadi, asuransi jiwa akan memproteksi keluarga tertanggung jika sewaktu-waktu tertanggung meninggal dunia atau sudah tidak produktif (karena terlalu tua) lagi, disini diasumsikan tertanggung adalah tulang punggung keluarga, sehingga jika tertanggung sudah tidak dapat memperoleh penghasilan lagi, asuransi jiwa akan memberikan pertanggungan/santunan kepada keluarga yang tertanggung tinggalkan tersebut (Darmawi, 2006).
2.3 Jenis–Jenis Asuransi Jiwa
Adapun jenis asuransi jiwa yang sering ditawarkan kepada konsumen oleh pihak asuransi yang disesuaikan dengan kontrak asuransi konsumen, jenisnya sebagai berikut :
1. Asuransi Jiwa Seumur Hidup
7
tentu premi yang lebih tinggi, walaupun nanti ada uang tunai yang diterima dari pembayaran premi,namun jumlahnyatidaklah terlalu tinggi, apalagi nanti jika mendapat pengurangan dari pajak, akan semakin kecil uang yang akan diterima.
2. Asuransi Jiwa Berjangka
Asuransi jiwa berjangka adalah asuransi jiwa dengan sistem pertangggungan berjangka waktu tertentu, artinya ada masa habisnya. Jangka waktu yang dimaksud bervariasi, bisa 5 tahun, 10, 15, 20, dan seterusnya. Kelemahan asuransi jiwa ini adalah jika tertanggung meninggal atau tidak produktif setelah jangka waktunya habis, maka keluarga tidak mendapat pertanggungan. Sedangkan keunggulannya adalah premi yang rendah, asuransi jiwa term life adalah asuransi yang paling rendah preminya (paling murah). Walaupun disebut sebagai asuransi jiwa yang paling murah, namun pertanggungannya cukup tinggi yaitu mencapai miliaran rupiah.
3. Asuransi Jiwa Dwiguna (Endowment)
Asuransi jiwa dwiguna adalah asuransi dengan dua fungsi, fungsi pertama adalah sebagai asuransi jiwa berjangka, dan fungsi kedua adalah sebagai tabungan. Sebagai tabungan artinya tertanggung dapat menarik polis asuransi jika suatu saat tertanggung memiliki kebutuhan yang mendesak, hal ini bisa dilakukan dalam jangka waktu beberapa tahun sekali sesuai dengan perjanjian kepada perusahaan asuransi, selain itu tertanggung juga akan mendapatkan uang tunai seperti halnya pada asuransi whole life, namun persentasenya lebih tinggi.
8
2.4 Fungsi Kelangsungan Hidup (Survival Function)
Misalkan ( ) adalah seseorang yang berusia tahun pada saat polis asuransi ditanda tangani dan sedangkan jarak waktu antara ( ) sampai meninggal dunia
( ) akan disebut sisa umur bagi ( ), sehingga terdapat peubah acak ( ), yaitu
( ) = − untuk ≥ 0. ( ) menyatakan sisa umur bagi ( ). Fungsi
distribusi dari ( ) dinyatakan dengan ( ) dan didefinisikan (Bowers, dkk., 1997) dengan :
( ) = ( ( ) ≤ ), ≥ 0 (2.4.1)
( ) menyatakan peluang seseorang seseorang yang berusia tahun akan meninggal sebelum berusia + tahun. Secara umum fungsi kelangsungan hidup dapat dinyatakan dengan :
( )( ) = 1 − ( ) = ( ( ) > ) ; > 0 (2.4.2)
( )( ) adalah peluang orang berusia x tahun akan hidup mencapai usia + tahun.
9
= 1 − = ( ( ) > ) (2.5.2)
Sehingga fungsi distribusi dari ( )nya adalah :
( )( ) = ( ( ) ≤ | > ) = ( − ≤ | > ) = ( ≤ ≤ + | > ) = ( + ) − ( )1 − ( ) = (1 − ( + ) − (1 − ( ))( ) = ( ) − ( + )( ) = ( )( ) − ( + )( ) = 1 − ( + )( ) = (2.5.3) Maka ( ( ) > ) = 1 − ( ( ) ≤ ) = 1 − = 1 − 1 − ( + ) ( )
10
= ( + )
( )
= (2.5.4)
Simbol tqx dapat diinterpretasikan sebagai probabilitas (peluang) bahwa (x) akan
meninggal dalam t tahun, tqx adalah fungsi distribusi pada T(x). Sebaliknya, tpxdapat diinterpretasikan sebagai peluang bahwa (x) akan hidup sampa umur x+t, tpx merupakan fungsi survival untuk (x). Dalam kasus tertentu untuk umur hidup
0, maka T(0) = X dan
tp0= s(x) x≥ 0 (2.5.5)
Jika t = 1, maka
qx= Pr[(x) akan meninggal diantara 1 tahun]
px= Pr[(x) akan hidup sampai umur x+1]
Berikut simbol khusus untuk kejadian yang lebih umum bahwa (x) akan hidup selama t tahun dan meninggal diantara u tahun, (x) akan meninggal antara umur
x + t dan x + t + u
t|uqx= Pr[t < T(x)≤ t + u]
11
Diasumsikan bahwa observasi dari survival saat umur x akan menghasilkan untuk survival sebagai perkiraan bahwa seorang bayi akan hidup pada umur x , kemudian
tpx= = (( )) (2.5.7)
tqx= 1 - (( )) (2.5.8)
dengan pendekatan ini, dan banyak kasus spesial, dapat dituliskan sebagai berikut
t|uqx= ( ) ( ) ( ) = ( ) ( ) ( ) ( ) ( ) =tpx uqx+t (2.5.9)
Peluang waktu sisa hidup (x) dinotasikan dengan K(x). Karena K(x) adalah bilangan bulat terbesar dalam T(x), sehingga fungsi probabilitasnya menjadi
Pr[K(x) = k] = Pr[k≤ T(x) < k+1] = Pr[k < T(x)≤ k+1] =kpx–k+1px =kpxqx+k =k|qx ; k = 0, 1, 2, ... (2.5.10) (Bowers,dkk., 1997).
12
2.6 Laju Tingkat Kematian (Force Of Mortality)
Laju kematian dari seseorang yang baru lahir dan akan meninggal antara usia x
dan x + Δx dengan syarat hidup pada usia x dapat dinyatakan dengan :
( < < + Δx| > ) = ( + Δx) − ( )1 − ( ) (2.6.1)
Karena ( + Δx) − ( )dapat dinyatakan sebagai fungsi limit, maka :
lim→ ( + Δx) − F(x)1 − ( ) = lim→ lim( + Δx) − F(x). ΔxΔx
→ 1 − ( ) = lim→ ( + Δx) − F(x) Δx . Δx lim→ 1 − ( ) = 1 − ( )( )Δx ≌ 1 − ( )( ) (2.6.2)
Untuk setiap usia , laju tingkat kematian dari seseorang yang berusia tahun dapatdinyatakan dengan
13
Dengan μ( + ) adalah probabilitas (peluang) sisa umur hidup seseorang yang berusia tahun antara + tahun dengan syarat ia masih hidup pada usia sampai + tahun.
Karena ( ) = 1 − ( )atau ( ) = 1 − ( ),maka :
( ) = ( ) = − ( ) (2.6.5)
Sehingga diperoleh nilai laju kematian pada usia x adalah :
μ( ) = − ′( )( ) = −1( ) . ( ( ))( )
= − ln ( )( ) . ( ( ))( )
= − ln ( )( )
μ( ) = − ln ( ) (2.6.6)
Dengan mengganti menjadi , maka diperoleh :
μ( ) = − ln ( ) (2.6.7)
dan dengan menggunakan intergral tertetu pada batas sampai + maka
diperoleh ∫ μ( ) = − ∫ ln ( )
= − ln ( )|
= −{ln ( + ) − ln ( )}
14
= − ln
= ∫ ( ) (2.6.8)
Jika nilai laju kematiannya konstan (μ( + ) = μ)untuk semua ≥ 0, artinya besarnya nilai dari force of mortality (laju tingkat kematian) adalah sama untuk semua usia nasabah yang hidup, yang artinya
( ) = = ∫ ( ) = ∫ = (2.6.9)
Diketahui sebelumnya bahwa adalah fungsi distribusi dari ( ), sehingga fungsi densitas dari ( )adalah :
( )( ) = = 1 − = 1 − ( + )( ) = − ( + )( ) = − ( + )( ) ( + ) ′( + )
15
2.7 Tabel Mortalitas
Pada tabel mortalitas terdapat variabel dan , menyatakan jumlah orang yang diharapkan masih hidup sampai usia tahun dari sekelompok orang yang jumlahnya ketika baru lahir. Dalam hal ini, yang menyatakan banyaknya bayi yang baru dilahirkan diasumsikan mempunyanyi fungsi survival sama dengan ( ).
Misalkan = 100.000, lalu diberi indeks = 1, 2, 3, . . . , (orang ke-1, ke-2, . . ., ke- ), dan ℒ( ) menyatakan banyaknya bayi yang hidup sampai dengan usia , sehingga diperoleh persamaan sebagai berikut :
ℒ( ) = (2.7.1)
dimana adalah indikator untuk bayi yang bertahan hidup dari , dan dapat pula dinyatakan dengan :
= 1 ,0, ℎ
karena adalah random variabel, dan berdasarkan asumsi bahwa mempunyai fungsi survival yang sama dengan ( ), maka akan diperoleh nilai peluangnya sebagai berikut :
= 1 = ( ) (2.7.2)
16
Dari persamaan (2.7.2) dan (2.7.3), diperoleh nilai harapan dari sebagai berikut :
= 1. ( ) + 0. 1 − ( ) = ( )
Sehingga nilai ekspetasi dariℒ( )dapat dinyatakan dengan :
[ℒ( )] = = = ( ) + ( )+ . . . + ( ) = . ( ) (2.7.4) = . = . exp μ (2.7.5)
Selanjutnya, variabel menyatakan banyaknya orang berusia tahun akan meninggal sebelum mencapat usia + 1tahun.
17
Selanjutnya indikator yang berlaku adalah sebagai berikut :
= 1,0, + ℎ
Karena adalah random variabel, maka akan diperoleh nilai peluangnya sebagai berikut :
= 1 = ( ) − ( + ) (2.7.6)
= 0 = 1 − { ( ) − ( + )} ( 2.7.7)
Dari persamaan (2.7.6) dan (2.7.7) diperoleh nilai harapan dari sebagai berikut :
=
=
= . { ( ) − ( + )}
= . ( ) − . ( + )
= − (2.7.8)
dimana menyatakan banyaknya orang yang berusia tahun yang meninggal sebelum mencapai usia + tahun.
Berdasarkan persamaan (2.7.4) dan (2.7.8) diperoleh persamaan sebagai berikut :
18
= (2.7.9)
dan
= 1 − = 1 − = − = (2.7.10)
Sehingga peluang ( ) akan meninggal sebelum mencapai usia + tahun dapat dinyatakan dengan :
= 1 − = 1 −
= −
= (2.7.11)
dan sebuah peluang meninggal yang ditangguhkan atau kondisi yang menyatakan bahwa akan berlangsung hidup sampai tahun dan meninggal dalam tahun, didefinisikan sebagai berikut :
| = 1 − | (2.7.12)
19
2.8 Bunga
Bunga merupakan pembayaran yang dilakukan oleh peminjam sebagai balas jasa atas pemakaian uang yang dipinjam. Secara umum perhitungan bunga dibagi menjadi dua, yaitu bunga sederhana dan bunga majemuk.
1. Bunga Sederhana (Simple Interest)
Bunga tunggal atau bunga sederhana adalah besarnya bunga dihitung dari nilai pokok awal dikalikan dengan tingkat bunga dan waktu . Besarnya bunga sederhana dapat dihitung dengan menggunakan rumus :
= . . (2.8.1)
dengan :
: interest value (nilai bunga)
: Pokok investasi
: rate of interest annually, tingkat suku bunga
: time, jangka waktu (lama) investasi (tahun) 2. Bunga Majemuk (Compound Interest)
Bunga majemuk adalah perhitungan bunga dimana besar pokok janga investasi selanjutnya adalah besar pokok sebelumnya di tambah dengan besar bunga yang diperoleh . Besar bunga majemuk dapat dihitung dengan menggunakan rumus :
20
dengan :
: interest value (nilai bunga)
: Pokok investasi
: rate of interest annuality, tingkat suku bunga
: time, jangka waktu (lama) investasi (tahun)
2.9 Laju Tingkat Suku Bunga (Force Of Interest )
Definisikan bahwa i(m) merupakan nominal interest rate atau yang biasa disebut dana yang dibungakan lebih dari satu kali dalam setahun dengan m tahun
(Gerber, 1990) . Sehingga dapat dituliskan
1 + ( ) = 1 + (2.9.1)
Sehingga
( )= (1 + ) − 1 (2.9.2)
Kemudian dilimitkan dengan →∞, diperoleh
21
Kemudian dituliskan kembali
( )=(1 + ) − (1 + )
1/ (2.9.4)
Terlihat bahwa merupakan derivative function dari (1+i)x pada saat x = 0. Jadi didapatkan
= ln(1 + ) atau
= 1 +
Sehingga jika untuk t tahun maka diperoleh persamaan
(1 + ) = (2.9.5)
Diketahui bahwa discount factor untuk periode atau waktu yang sama adalah
= (2.9.6)
2.10 Premi Tunggal
Pada asuransi dengan perhitungan kontinu, pembayaran benefit kepada ahli waris nasabah dilakukan sesaat setelah nasabah meninggal dunia. Jumlah dan waktu pembayaran benefit pada asuransi jiwa tergantung pada panjang interval dari dikeluarkannya polis sampai tertanggung meninggal dunia. Berdasarkan uraian tersebut, asuransi jiwa terdiri dari fungsi benefit atau santunan ( )dan .Fungsi adalah nilai sekarang dari pembayaran dan adalah panjang interval pada saat polis dikeluarkan sampai dengan( )meninggal dunia.Keduanya membentuk
22
suatu peubah acak yang dilambangkan dengan yang didefinisikan sebagai berikut :
= .
Karena ( ) adalah peubah acak dari sisa waktu hidup nasabah atau waktu dari dikeluarkannya polis sampai waktu meninggalnya nasabah, maka adalah fungsi peubah acak (Actuarial Present Value) pembayaran benefit pada saat polis asuransi dikeluarkan (Bowers, dkk., 1997).
2.11 Premi Tunggal Asuransi Jiwa Berjangka
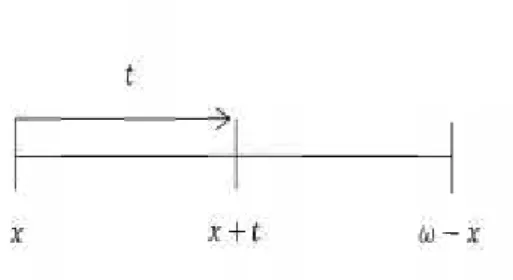
Asuransi jiwa berjangka adalah suatu asuransi yang membayarkan benefit atau santunan kepada ahli waris nasabah apabila si nasabah meninggal dunia selama dalam jangka waktu polis asuransi yang telah ditentukan.
Gambar 1. Sistem pembayaran benefit pada asuransi jiwa berjangka
23 bt= 1 ≤ 0 > vt= vt t≥ 0 z = ≤ 0 >
Definisi ini menggunakan tiga syarat. Pertama, future lifetime merupakan variabel non-negatif, didefinisikan bt, vt, and z hanya pada nilai non negatif. Kedua, untuk
nilai t dimana bt bernilai 0, nilai vttidak relevan. Ketiga, kecuali jika, laju tingkat
suku bunga ( force of interest ) diasumsikan konstan. APV ( actuarial present
value ) untuk asuransi jiwa berjangka dengan satu unit pembayaran pada saat
meninggal (x), E[Z], dinotasikan dengan ̅x1: n|. Kemudian dapat dihitung dengan
mengenali Z sebagai fungsi T jadi E[Z] = E[zT]. Kemudian gunakan p.d.f pada T
untuk peroleh ̅x1 : n|= E[Z] = E[zT] =∫ ( ) =∫ ( ) =∫ ( ) =∫ ∫ ( ) ( ) ( konstan) =∫ = ∫ ( ) = (1 − ( ) )
24
Pada asuransi jiwa berjangka dengan pembayaran benefit pada saat akhir tahun meninggal fungsi benefit dinotasikan dengan bk+1, dan fungsi diskon vk+1,
sejumlah benefit kan dibayarkan dan faktor diskon diperlukan untuk periode dari waktu pembayaran saat kejadian polis ketika curtate-future-lifetime tertanggung adalah k, ketika tertanggung meninggal pada tahun k+1 masa asuransi. Present value pada kejadian polis dengan pembayaran benefit dinotasikan dengan zk+1
z
k+1=b
k+1v
k+1Untuk asuransi jiwa berjangka menyediakan satu unit jumlah benefit yang akan dibayarkan pada akhir tahun meninggal si tertanggung, diperoleh
bk+1= 10 = 0, 1, … , − 1
vk+1= vk+1
z = = 0, 1, … , − 1
0
Actuarial Present Value (APV) dari asuransi jiwa berjangka diberikan sebagai berikut
̅
25
2.12 Fungsi Bilangan Bulat Terbesar
Di antara fungsi-fungsi yang akan sering digunakan sebagai contoh terdapat dua fungsi yang sangat khusus yaitu : fungsi nilai mutlak, | |, dan fungsi bilangan bulat terbesar⌊ ⌋. Fungsi–fungsi ini didefinisikan oleh :
| x | = ≥ 0
– < 0
dan
⌊ ⌋= bilangan bulat terbesar yang lebih kecil atau sama dengan x.
Jadi, |-3,1| = |3,1|, sedangkan ⌊−3,1⌋ = -4 dan ⌊3,1⌋ = 3. Fungsi nilai mutlak adalah genap, karena | -x | = | x | sedangkan fungsi bilangan bulat terbesar bukan fungsi genap atau ganjil (Purcell, dkk., 2003).
2.13 Hubungan Antara Kasus Diskrit Dan Kasus Kontinu Pada Asuransi Jiwa
Disini akan dibahas hubungan dengan analisis actuarial present value untuk asuransi jiwa seumur hidup dengan pembayaran benefit sebesar satu unit pada saat tertanggung meninggal, didapatkan
̅
x=∫ ( )
∞
=∫ ( ) +∫∞ ( ) (2.13.1) Ubah variabel dengan s = t-1 pada integral kedua sehingga
̅x=∫ ( ) + ∫ ( + 1)
∞
26
Kemudian, dengan basis mortalita
( + 1) = ( + + 1) (2.13.3)
Pada (2.13.2) akan menjadi ̅ . Pada basis mortalitas kedua akan menjadi [ ] ̅[ ] . Kembali menggunakan (2.13.2) dan menggunakan notasi sebelumnya,
diperoleh
̅x=∫ ( ) + ̅ = ̅ + ̅ (2.13.4)
Dibawah asumsi bahwa umur kematian tiap tahun berdistribusi uniform,
( ) = (2.13.5)
Kemudian,
̅ = ∫ + ̅
= + ̅ (2.13.6)
Domain untuk hubungan ini adalah x = 0, 1, ..., - 1, dan nilai awal ̅ = 0. Jika ditambahkkan kedua sisi formula (a) dengan , maka didapatkan
= + (2.13.7)
Dengan (a) dan (2.13.6) memiliki bentuk yang sama dan domain sama serta nilai awal 0 pada saat , adalah solusi untu (2.13.6), dan
27
sama dengan pada akhir tahun meninggal. Formula (2.13.8) dapat diperoleh menggunakan random variabel future-lifetime dengan asumsi berdistribusi uniform pada usia kematian tiap tahun sehingga dapat dituliskan T = K+S.K dan S saling bebas dan S berdistribusi uniform diseluruh unit interval. K + 1 dan 1–S
juga saling bebas, dan 1 – S berdistribusi uniform pada seluruh unit interval.
Kemudian
̅ = [ ] = [ (1 + ) ] (2.13.9)
Sehingga dapat digunakan hubungan saling bebas K + 1 dan 1–S untuk
menghitung
[ (1 + ) ] = [ ] [(1 + ) (2.13.10)
Faktor pertama berada pada sisi kanan berada pada . Sudah diketahui bahwa 1-S berdistribusi uniform di seluruh unit intervalnya, faktor kedua yaitu
[(1 + ) ] = ∫ (1 + ) 1 = (2.13.11)
Sehingga diperoleh kembali ̅ = ( ) dibawah asumsi usia kematian pada tiap tahun berdistribusi uniform (Bowers, dkk.,1997).
2.14 Premi Asuransi Jiwa Berjangka Menaik (Increasing) Untuk Kasus Kontinu
Kenaikan benefit pada asuransi jiwa berjangka akan berpengaruh dengan kenaikan premi, jika diasumsikan tertanggung akan mendapatkan benefit sebesar 1 unit,
28
maka tahun kedua akan mendapatkan benefit sebesar 2 unit dan seterusnya, sehingga bt= ⌊ + 1⌋ ≤ 0 > vt= vt Z = ⌊ + 1⌋ ≤ 0 >
Maka APV nya
(I )x1: n|= E [Z] =∫ ⌊ + 1⌋vttpxµx(t) dt (2.14.1)
(Bowers, dkk., 1997).
2.15 Premi Asuransi Jiwa Berjangka Menurun (Decreasing) Untuk Kasus Kontinu
Melengkapi kenaikan asuransi jiwa berjangka adalah setiap tahun penurunan asuransi jiwa berjangka menyediakan benefit sebesar n pada saat meninggal selama tahun pertama, n-1 pada saat meninggal selama tahun kedua, dan seterusnya, dengan cakupan berakhir pada n tahun. Berikut fungsi dari asuransi tersebut :
29
Sehingga diperoleh APV (Newton, dkk., 1997) sebagai berikut
(D ̅)x1:n|=∫ ( − ⌊ ⌋) tpxµx(t) dt (2.15.1)
2.16 Premi Asuransi Jiwa Berjangka Menaik (Increasing) Untuk Kasus Diskrit
Increasing premi asuransi jiwa berjangka dengan pembayaran pada saat tertanggung meninggal di akhir tahun disebut dengan kasus diskrit , pada premi menaik dalam kasus diskrit ini memiliki beberapa fungsi sebagai berikut :
bk+1= 0+ 1 = 0, 1, … , − 1= , + 1, … … .
vk+1= vk+1
zk+1= ( + 1 ) = 0, 1, … , − 1
0 = , + 1, … … .
Sehingga memiliki Actuarial Present Value sebagai berikut :
(IA)x1: n|=∑ ( + 1) kpxqx+k (2.16.1)
Dalam kasus lain, setiap tahun kenaikan asuransi jiwa berjangka yang dibayarkan pada saat meninggal. Untuk asuransi ini memiliki present-value sebagai berikut :
Z = ⌊ + 1⌋ <
30
Dimana ⌊ + 1⌋= K + 1 , kita dapat menggunakan hubungan T = K +S untuk mengisi
Z = ( + 1 ) <
0 ≥ (2.16.3)
Jika W merupakan present-value random variable untuk setiap tahun kenaikan asuransi berjangka n tahun yang dibayarkan pada akhir tahun meninggal,
W = ( + 1 ) = 0, 1, . . , − 1
0 = , + 1, … … … … . (2.16.4)
Kemudian
Z = W (1+i)1-S (2.16.5)
Dan
E[Z] = E[W (1+i)1-S] (2.16.6)
Dimana W adalah fungsi dari K + 1 sendiri dan K+1 dan 1-S saling bebas ,
E[Z] = E[W] E [ (1+i)1-S]
= (IA)x. ∫ (1 + ) . 1
31
̅= Ax (2.16.8)
Dan
(I ̅)x1: n|= (IA)x1:n| (2.16.9)
(Bowers, dkk.,1997).
2.17 Premi Asuransi Jiwa berjangka Menurun (Decreasing) Untuk Kasus Diskrit
Setiap tahun peurunan benefit asuransi jiwa berjangka selama periode n tahun menyediakan benefit pada akhir tahun meninggal dalam jumlah sama untuk n-k dimana k jumlah tahun lengkap hidup oleh tertanggung karena masalah.
Fungsinya : bk+1= 0− = 0, 1, … , − 1= , + 1, … . vk+1= vk+1 k=0, 1,... zk+1= ( − ) = 0,1, … , − 1 0 = , + 1, … . . Dengan APV (DA)x1: n|=∑ ( − ) kpxqx+k (Bowers, dkk., 1997).
III. METODOLOGI PENELITIAN
3.1 Tempat Dan Waktu Penelitian
Penelitian ini dilakukan di Jurusan Matematika Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Lampung pada semester genap tahun akademik 2016/2017.
3.2 Data Penelitian
Data yang digunakan pada penelitian ini merupakan data yang diambil dari life
table for the total population: United States, 2002(terlampir). Data yang akan
digunakan yaitu tertanggung yang berusia 25 tahun dengan kontrak asuransi selama 10 tahun (n = 10). Dengan tingkat suku bunga (i) premi tiap tahunnya (konstan) sebesar 6% atau 0,06, maka akan diperoleh laju tingkat suku bunga ( ) sebesar 0,058. Dengan perhitungan dibantu dengan Ms.Excel.
33
1. Menentukan besarnya benefit tiap tahun yang akan diberikan kepada tertanggung sesaat ketika meninggal (kontinu)
Diketahui bahwa untuk premi menaik memiliki fungsi benefit sebagai berikut :
bt= ⌊ + 1⌋ ; ≤
0 ; >
dengan t = 0, 1, 2, 3, ..., n-1, sehingga ketika tertanggung meninggal pada tahun ke-t maka akan mendapatkan benefit sebesar t + 1, jika tertanggung meninggal setelah n tahun (masa waktu berlakunya polis asuransi) maka tertanggung ataupun keluarga tertanggung tidak akan mendapatkan benefit.
Kemudian untuk premi menurun asuransi jiwa berjangka memiliki fungsi benefit sebagai berikut :
bt= − ⌊ ⌋ ; ≤
0 ; >
dengan t = 0, 1, 2, 3, ..., n-1, ketika tertanggung meninggal pada saat tahun ke-t maka akan mendapatkan benefit sebesar n – t , jika tertanggung
meninggal setelah n tahun maka tertanggung maupun keluarga tertanggung tidak akan mendapatkan benefit.
2. Menghitung nilaitpx
Pada rumus premi menaik/menurun, besarnya premi juga dipengaruhi oleh peluang hidup seseorang berusia x (tpx). Nilaitpxdapat diperoleh dari
34
=
3. Memodelkan pertumbuhan premi (menaik dan menurun) untuk kasus kontinu
Diketahui bahwa rumus dari premi asuransi jiwa berjangka menaik dapat dituliskan sebagai berikut :
bt= 0⌊ + 1⌋ ; ≤; >
vt= vt
Z = ⌊ + 1⌋ ; ≤
0 ; >
( Dimana⌊ ⌋merupakan fungsi bilangan bulat terbesar )
Sehingga premi tunggal untuk premi menaik sebagai berikut :
(I )x1: n|= E [z] =∫ ⌊ + 1⌋vttpxµx(t) dt
Kemudian untuk premi menurun dapat dituliskan :
bt= − ⌊ ⌋ ; ≤
0 ; >
vt= vt ; t > 0
Z = ( − ⌊ ⌋) ; ≤
35
4. Menentukan besarnya benefit tiap tahun yang akan diberikan kepada tertanggung pada saat akhir tahun meninggalnya si tertanggung (diskrit)
Diketahui bahwa untuk premi menaik memiliki fungsi benefit sebagai berikut :
bk+1= 0+ 1 ; = 0, 1, … , − 1; = , + 1, … … .
Jika tertanggung meninggal pada tahun ke-k+1 maka tertanggung akan mendapatkan benefit sebesar k+1, sedangkan jika tertanggung meninggal melebihi masa kontrak asuransi maka tertanggun maupun keluarga tertanggung tidak akan mendapatkan benefit.
Kemudian untuk premi menurun memiliki fungsi sebagai berikut :
bk+1= 0− ; = 0, 1, … , − 1; = , + 1, … .
Jika tertanggung meninggal pada saat tahun ke-k+1 maka akan mendapatkan benefit sebesar n-k jika meninggal sebelum masa kontrak asuransi, namun jika meninggal setelah kontrak akan tertanggung tidak akan mendapat benefit.
5. Menghitung nilai | dan v
Dalam perhitungan premi menaik/menurun dipengaruhi dengan nilai | dan
v, sehinggaakan dihitungnilai | dengan :
| =
Kemudian akan dihitung nilai v :
36
6. Memodelkan pertumbuhan premi (menaik dan menurun) untuk kasus diskrit
Diketahui bahwa rumus untuk premi menaik sebagai berikut :
bk+1= 0+ 1 ; = 0, 1, … , − 1; = , + 1, … … .
vk+1= vk+1
zk+1= ( + 1 ) ; = 0, 1, … , − 1
0 ; = , + 1, … … .
Sehingga memiliki Actuarial Present Value untuk premi menaik sebagai berikut :
(IA)x1: n|=∑ ( + 1) kpxqx+k
Kemudian untuk premi menurun memiliki rumus sebagai berikut :
bk+1= −0 ; = , + 1, … .; = 0, 1, … , − 1
vk+1= vk+1 ;k=0, 1,...
zk+1= ( − ) ; = 0,1, … , − 1
0 ; = , + 1, … . .
sehingga memiliki Actuarial Present Value untuk premi menurun sebagai berikut :
37
Diketahui bahwa kpxqx+k=k|qx, sehingga dapat disubtitusikan ke rumus premi
menaik dan premi menurun, dapat dituliskan sebagai berikut :
(IA)x1: n|=∑ ( + 1) k|qx
Dan
V. KESIMPULAN
5.1 Kesimpulan
Berdasarkan hasil penelitian, maka dapat disimpulkan bahwa :
1. Dari model premi menaik asuransi berjangka untuk kasus kontinu ( ̅) : | =E [Z] =∫ ⌊ + 1⌋vttpxµx(t) dt
dengan bertambahnya waktu (t) dimana t ≤ n dengan n = 10 serta
meningkatnya benefit tiap tahun sebesar 1 satuan maka premi yang dibayarkan akan menaik tiap tahunnya dengan besar kenaikan berbeda tiap tahunnya.
2. Dari model premi menurun asuransi jiwa berjangka untuk kasus kontinu (D ̅)x1:n|=∫ ( − ⌊ ⌋) tpxµx(t) dt
dengan bertambahnya waktu (t) dimana t ≤ n dengan n = 10 namun benefit
tiap tahun menurun 1 satuan, maka premi yang akan dibayarkan tiap tahun juga menurun dengan besar penurunan berbeda tiap tahunnya.
63
dibayarkan akan menaik tiap tahunnya dengan besar kenaikan berbeda tiap tahunnya.
4. Dari model premi menaik asuransi jiwa berjangka untuk kasus diskrit
(DA)x1: n|=∑ ( − ) kpxqx+k
dengan bertambahnya k dimana k=0,1,…,n-1 dengan n =10,serta menurunnya benefit sebesar 1 satuan tiap tahunnya, maka premi yang akan dibayarkan akan menurun tiap tahunnya dengan besar penurunan berbeda tiap tahunnya.
5. Pada pensubtitusian data ke dalam model premi menaik dan menurun untuk kasus diskrit dan kontinu, premi yang harus dibayarkan tiap tahun untuk kasus kontinu lebih besar dibandingkan dengan premi yang harus dibayarkan pada kasus diskrit.
DAFTAR PUSTAKA
Bowers, N. L., dkk. 1997. Actuarial Mathematics. The Society Of Actuaries.
Darmawi, Herman. 2006. Manajemen Asuransi. Jakarta, Bumi Aksara. Hal 1.
Gerber, Hans U. 1990. Life Insurance Mathematics. Springer-Verlag Berlin Heidelberg, New York. First Edition.
Hartono, Sri Rejeki. 1992. Hukum Asuransi Dan Perusahaan Asuransi. Jakarta, Sinar Grafika
Purcell, Edwin L., dkk. 2003. Calculus 8thEdition.Prentice Hall. Edisi 8.
Rotar, Vladimir I. Actuarial Models :The Mathematics Of Insurance. New York : Taylor &bFrancis Group. Second Edition