Analisis titik ekuilibrium dan solusi model interaksi pemangsa mangsa menggunakan metode dekomposisi adomian.

(1)

vii

ABSTRAK

Yulius Wahyu Putranto, 2017. Analisis Titik Ekuilibrium dan Solusi Model Interaksi Pemangsa-Mangsa Menggunakan Metode Dekomposisi Adomian.

Tesis.

Program Studi Magister Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.

Tesis ini bertujuan untuk meneliti tentang sistem dinamika dua populasi dengan satu populasi memangsa populasi yang lain. Populasi disebut populasi pemangsa dan populasi disebut populasi mangsa. Setiap spesies dari diasumsikan hanya mendapat makanan dari sedangkan bertumbuh secara alami. Dengan demikian terjadi suatu sistem dinamika pemangsa- mangsa. Aspek pemanenan ditambahkan pada kedua populasi tersebut untuk mengetahui dampak yang terjadi pada titik ekuilibrium ketika kedua populasi atau salah satu dilakukan pemanenan. Model yang dimodifikasi ada tiga macam yaitu model mangsa dengan aspek pemanenan pada mangsa, model pemangsa-mangsa dengan aspek pemanenan pada pepemangsa-mangsa dan model pepemangsa-mangsa-pemangsa-mangsa dengan aspek pemanenan pada keduanya. Masing-masing model telah dianalisis kestabilan titik ekuilibriumnya. Peneliti mencari solusi sistem dinamika dua populasi secara umum dengan metode dekomposisi Adomian. Pada analisis solusi sistem, dilakukan perhitungan dengan tiga parameter yang berbeda, sehingga menghasilkan tiga macam interaksi yang berbeda. Interaksi yang muncul dengan parameter yang telah ditentukan adalah mutualisme, parasitisme dan kompetisi.

(2)

viii

ABSTRACT

Yulius Wahyu Putranto, 2017. Analysis of Equilibrium Points and Solution of Predator-Prey Interaction Model Using Adomian Decomposition Method.

Thesis.

Study Program of Master of Mathematics Education, Department of Mathematics and Science Education, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.

This thesis aims to examine the dynamical system of two populations with one population prey on other populations. Population is called predator population and population is called prey population. Each species of is assumed to only get food from while grows naturally. Thus there is dynamical systems of predaror-prey. Harvesting aspects are added to both populations to determine the impacts that occur at the equilibrium point when the two populations or one is harvested. There were three kinds pf models that were modified: predator-prey models with harvesting aspects of prey, predator-prey models with harvesting aspects of predators and predatory models with harvesting aspects in both. Each model has analyzed the stability of the equilibrium point. We seek a general solution for dynamical systems in general with Adomian decomposition method. In the analysis of system solutions have been calculated with three different parameters, so as to produce three kinds of different interactions. Interactions that arise with predetermined parameters are mutualism, parasitism and competition.

(3)

i

ANALISIS TITIK EKUILIBRIUM DAN SOLUSI MODEL

INTERAKSI PEMANGSA-MANGSA MENGGUNAKAN

METODE DEKOMPOSISI ADOMIAN

TESIS

diajukan untuk memenuhi salah satu syarat memperoleh gelar Magister Pendidikan

Disusun oleh: Yulius Wahyu Putranto

NIM: 151442001

PROGRAM STUDI MAGISTER PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(4)

(5)

(6)

iv

HALAMAN MOTTO

(7)

v

HALAMAN PERSEMBAHAN

Tesis ini kupersembahkan untuk:

Ibuku Emiliana Yuniasih,

Bapaku Ignatius Bowo Hariyanto,

dan segenap keluarga yang mendukung dengan perhatian

dan Doa.

(8)

(9)

vii

ABSTRAK

Yulius Wahyu Putranto, 2017. Analisis Titik Ekuilibrium dan Solusi Model Interaksi Pemangsa-Mangsa Menggunakan Metode Dekomposisi Adomian.

Tesis.

Program Studi Magister Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.

Tesis ini bertujuan untuk meneliti tentang sistem dinamika dua populasi dengan satu populasi memangsa populasi yang lain. Populasi disebut populasi pemangsa dan populasi disebut populasi mangsa. Setiap spesies dari diasumsikan hanya mendapat makanan dari sedangkan bertumbuh secara alami. Dengan demikian terjadi suatu sistem dinamika pemangsa- mangsa. Aspek pemanenan ditambahkan pada kedua populasi tersebut untuk mengetahui dampak yang terjadi pada titik ekuilibrium ketika kedua populasi atau salah satu dilakukan pemanenan. Model yang dimodifikasi ada tiga macam yaitu model mangsa dengan aspek pemanenan pada mangsa, model pemangsa-mangsa dengan aspek pemanenan pada pepemangsa-mangsa dan model pepemangsa-mangsa-pemangsa-mangsa dengan aspek pemanenan pada keduanya. Masing-masing model telah dianalisis kestabilan titik ekuilibriumnya. Peneliti mencari solusi sistem dinamika dua populasi secara umum dengan metode dekomposisi Adomian. Pada analisis solusi sistem, dilakukan perhitungan dengan tiga parameter yang berbeda, sehingga menghasilkan tiga macam interaksi yang berbeda. Interaksi yang muncul dengan parameter yang telah ditentukan adalah mutualisme, parasitisme dan kompetisi.

(10)

viii

ABSTRACT

Yulius Wahyu Putranto, 2017. Analysis of Equilibrium Points and Solution of Predator-Prey Interaction Model Using Adomian Decomposition Method.

Thesis.

Study Program of Master of Mathematics Education, Department of Mathematics and Science Education, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.

This thesis aims to examine the dynamical system of two populations with one population prey on other populations. Population is called predator population and population is called prey population. Each species of is assumed to only get food from while grows naturally. Thus there is dynamical systems of predaror-prey. Harvesting aspects are added to both populations to determine the impacts that occur at the equilibrium point when the two populations or one is harvested. There were three kinds pf models that were modified: predator-prey models with harvesting aspects of prey, predator-prey models with harvesting aspects of predators and predatory models with harvesting aspects in both. Each model has analyzed the stability of the equilibrium point. We seek a general solution for dynamical systems in general with Adomian decomposition method. In the analysis of system solutions have been calculated with three different parameters, so as to produce three kinds of different interactions. Interactions that arise with predetermined parameters are mutualism, parasitism and competition.

(11)

(12)

x

DAFTAR PUBLIKASI HASIL PENELITIAN TESIS

Sebagian hasil dari tesis ini telah dipresentasikan dalam konferensi internasional dan/atau dipublikasikan dalam jurnal internasional sebagai berikut:

Y.W. Putranto dan S. Mungkasi, “Adomian decomposition method for solving the population dynamics model of two species”, Journal of Physics:

Conference Series, Volume 795, Nomor 1, Artikel 012045, Tahun 2017

(terideks Scopus), Link Artikel:

http://doi.org/10.1088/1742-6596/795/1/012045

(13)

xi

KATA PENGANTAR

Sungguh sebuah mimpi yang menjadi kenyataan bagi penulis ketika tesis yang berjudul Analisis Titik Ekuilibrium dan Solusi Model Interaksi Pemangsa-Mangsa Menggunakan Metode Dekomposisi Adomian telah selesai dengan baik dan tepat waktu. Puji dan syukur penulis haturkan kepada Tuhan Yang Maha Kuasa, karena telah mengabulkan doa penulis selama menyusun tesis ini dan senantiasa mendampingi dalam setiap tulisan yang dibuat oleh penulis.

Menjadi bagian dari keluarga Magister Pendidikan Matematika Sanata dharma memang tidak terbayangkan oleh penulis mengingat sulitnya kerja keras ketika menulis skripsi pada jenjang S1. Rencana Tuhan memang luar biasa karena penulis diberi kesempatan untuk mengikuti kembali dunia kampus yang telah ditinggalkan biarpun belum lama. Penulis berterima kasih kepada Suster Vianney, S.SpS karena telah mendorong penulis untuk menempuh kembali kuliah S2 Pendidikan Matematika demi bekal di masa depan. Semangat itulah yang penulis pegang selama mengikuti perkuliahan di S2 Pendidikan Matematika ini. Tentunya keberhasilan menulis Tesis ini tidak luput dari para dosen dan teman-teman yang penulis temui ketika menjadi bagian kembali di Kampus Sanata Dharma ini. Pada kesempatan ini penulis ingin mengucapkan rasa terima kasih kepada:

1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku dosen pembimbing yang sudah meluangkan waktu dan dengan sabar membimbing penulis, sehingga tesis ini dapat diselesaikan dengan baik dan tepat waktu.

(14)

xii

dan memfasilitasi mahasiswa dalam berkonsultasi baik tentang perkuliahan maupun tentang dunia luar perkuliahan sejak pertama kali masuk kuliah. 3. Bapak Dr. rer. nat. Herry Pribawanto Suryawan yang telah membimbing

pada awal penulisan tesis ini. Terima kasih sudah membimbing kami untuk memulai masuk ke dalam dunia sistem dinamika.

4. Segenap dosen JPMIPA yang telah membantu dan memberikan dukungan selama penulis menempuh kuliah, sehingga akhirnya penulis dapat menyelesaikan tesis dengan baik dan tepat waktu dan segenap staf Sekretariat JPMIPA yang telah membantu dalam hal administrasi kampus selama penulis melaksanakan studi di sini.

5. Teman seperjuangan tesis yaitu Meta, Mas Beni dan Mas Tatak yang telah mau saling memberi semangat dan meluangkan waktu untuk bersama-sama untuk menyelesaikan tesis serta teman-teman dari Program Studi Magister Pendidikan Matematika angkatan 2015-2016 yang memberikan dukungan kepada penulis selama studi di S2 pendidikan matematika.

6. Semua pihak yang tidak dapat disebutkan satu per satu, yang telah membantu sehingga penulis dapat menyelesaikan tesis ini.

Penulis menyadari tesis ini masih jauh dari sempurna, tetapi penulis meyakini bahwa penulisan tesis ini memiliki kontribusi yang cukup bagi kampus dan para pembaca yang ingin mengembangkan tesis ini. Terima kasih.

Penulis,

(15)

xiii

DAFTAR ISI

Halaman Judul ... i

Halaman Persetujuan Pembimbing ... ii

Halaman Pengesahan ... iii

Halaman Motto ... iv

Halaman Persembahan ... v

Pernyataan Keaslian Karya ... vi

Abstrak ... vii

Abstract ... viii

Pernyataan Persetujuan Publikasi Karya Ilmiah ... ix

Daftar Publikasi Karya Ilmiah ... x

Kata Pengantar ... xi

Daftar Isi ... xiii

BAB I PENDAHULUAN... 1

A. Latar Belakang ... 1

B. Tinjauan Pustaka ... 2

C. Perumusan Masalah ... 4

D. Batasan Masalah ... 4

E. Tujuan Penelitian ... 5

F. Kebaruan Penelitian ... 5

G. Manfaat Penelitian ... 6

H. Sistematika Penulisan ... 6

I. Metode Penelitian ... 9

BAB II LANDASAN TEORI ... 10

A. Pemodelan Matematika... 10

B. Model Pertumbuhan Populasi ... 11

C. Aspek Pemanenan ... 15

D. Aspek Kompetisi... 16

E. Sistem Persamaan Diferensial... 17

(16)

xiv

G. Kerangka Berpikir... 38

BAB III ANALISIS KESTABILAN MODEL SISTEM DINAMIKA ... 39

A. Model Pemangsa-Mangsa dengan Aspek Pemanenan pada mangsa ... 40

B. Model Pemangsa-Mangsa dengan Aspek Pemanenan pada pemangsa . 47 C. Model dengan Aspek Pemanenan pada mangsa dan pemangsa ... 54

BAB IV SOLUSI SISTEM DINAMIKA DENGAN METODE DEKOMPOSISI ADOMIAN ... 62

A. Mutualisme ... 63

B. Parasitisme ... 67

C. Kompetisi ... 70

BAB V ASPEK KEPENDIDIKAN... 75

A. Pembelajaran di Sekolah Menengah ... 75

B. Pembelajaran di S1 ... 79

C. Refleksi ... 80

BAB VI PENUTUP ... 86

A. Kesimpulan ... 86

B. Saran ... 87

(17)

1

BAB I

PENDAHULUAN

A. Latar Belakang

Model dinamika populasi sudah banyak dikembangkan dalam bidang matematika biologi. Banyaknya individu akan selalu bertambah atau pun berkurang setiap waktu tergantung pada laju pertumbuhan individu tersebut, sehingga dari data jumlah individu pada suatu populasi tiap waktu dapat ditentukan pola atau model matematika. Pada awal diperkenalkan, model pertumbuhan populasi berupa model eksponensial. Model eksponensial memperlihatkan bahwa populasi suatu individu bertumbuh menurut grafik fungsi eksponen. Seiring berjalannya waktu, model pertumbuhan populasi diperbaiki dengan memperhatikan beberapa faktor seperti tempat tinggal, ketersediaan makanan, ancaman bahaya, dan lain sebagainya. Model baru yang diberikan dapat dikembangkan lebih realistis sesuai kondisi suatu populasi berasal. Suatu populasi pastinya berinteraksi dengan populasi yang lain sehingga menimbulkan suatu sistem dinamika.

(18)

terdapat aspek pemanenan. Solusi dari sistem secara umum akan dicari menggunakan metode dekomposisi Adomian.

B. Tinjauan Pustaka

Sistem dinamika sudah banyak dibahas dalam berbagai buku dan jurnal yang telah diterbitkan. Pada tesis ini beberapa artikel dan jurnal yang dijadikan acuan adalah sebagai berikut:

1. Penelitian yang dilakukan oleh Rao (2011). A study on series solution of two

species lotka volterra equations by adomian decomposition and homotopy pertubation methods. Pada penelitian tersebut Rao membandingkan dua metode

untuk menyelesaikan persamaan Lotka Voltera dua spesies.

2. Penelitian yang dilakukan oleh Zhou (2003) dengan judul The stability of

predator-prey systems subject to the Allee effects. Pada penelitian tersebut

diberikan model interaksi pemangsa-mangsa dengan dikenai efek Allee pada pemangsa maupun mangsa. Allee effects adalah suatu batas bawah dari populasi dengan batas tersebut membuat populasi tidak akan punah. Analisis grafik serta titik ekuilibrium dilakukan untuk mengetahui efek yang ditimbulkan jika dibandingkan dengan model yang aslinya.

(19)

model pertumbuhan logistik pada interaksi pemangsa-mangsa. Pada sistem ini peneliti menambahkan aspek pemanenan baik pada mangsa maupun pemangsa. Solusi secara umum model sistem dinamika akan dicari menggunakan pendekatan Metode Dekomposisi Adomian.

Berdasarkan tinjauan pustaka, letak penelitian ini dapat digambarkan dengan diagram berikut berikut:

Keterangan diagram:

: Hal yang dibahas pada penelitian ini.

: Hubungan antara penelitian yang sudah dilakukan. : Penelitian yang telah dilakukan sebelumnya.

Diagram 1.1. Letak penulisan tesis ditinjau dari beberapa penelitian yang telah dilakukan.

ANALISIS TITIK EKUILIBRIUM DAN SOLUSI MODEL INTERAKSI PEMANGSA-MANGSA MENGGUNAKAN METODE DEKOMPOSISI

ADOMIAN Zhou (2003). The stability of

predator-prey systems subject to the Alle effects

Rao (2011). A study on Series Solution of

two Species Lotka Volterra Equations by Adomian Decomposition and Homotopy

Pertubation Methods.

Putranto dan Mungkasi (2017). Adomian

(20)

C. Rumusan Masalah

Berdasarkan latar belakang masalah yang telah dipaparkan maka rumusan masalah dalam penelitian ini adalah:

1. Bagaimana modifikasi model sistem dinamika interaksi dua populasi pemangsa-mangsa dengan aspek pemanenan pada pemangsa dan mangsa? 2. Bagaimana analisis sifat-sifat kestabilan titik ekuilibrium model sistem

dinamika interaksi dua populasi dengan aspek pemanenan pada pemangsa dan mangsa?

3. Bagaimana solusi secara umum sistem dinamika dengan metode dekomposisi Adomian?

D. Batasan Masalah

(21)

E. Tujuan Penelitian

Berdasarkan rumusan masalah di atas maka tujuan penelitian ini adalah:

1. Untuk modifikasi model sistem dinamika interaksi dua populasi pemangsa-mangsa dengan aspek pemanenan pada pepemangsa-mangsa dan pemangsa-mangsa.

2. Untuk analisis sifat-sifat kestabilan titik ekuilibrium model sistem dinamika interaksi dua populasi dengan aspek pemanenan pada pemangsa dan mangsa. 3. Untuk mengetahui solusi secara umum sistem dinamika dengan metode

dekomposisi Adomian.

F. Kebaruan Penelitian

(22)

G. Manfaat Penelitian

Manfaat penelitian ini adalah:

1. Menambah pengetahuan dalam analisis kestabilan model sistem dinamika populasi pemangsa-mangsa dengan pemanenan pada pemangsa dan mangsa. 2. Mengetahui yang terjadi pada kedua populasi jika berinteraksi dalam jangka

panjang.

3. mengetahui salah satu metode untuk menyelesaikan sebuah sistem persamaan diferensial

4. Memberikan informasi bagi peneliti selanjutnya untuk menganalisis kasus yang lebih kompleks.

5. Memberi pengetahuan kepada guru dan siswa Sekolah Menengah Atas tentang kegunaan persamaan diferensial.

H. Sistematika Penulisan

Sistematika penulisan akan dibagi menjadi lima bagian, yaitu: BAB I: Pendahuluan

(23)

sistem yang mengakibatkan setiap populasi akan mempengaruhi populasi yang lain. Solusi dari sebuah sistem tersebut sulit untuk didapatkan secara eksak tetapi dapat dilakuan dengan metode pendekatan salah satunya Metode Dekomposisi Adomian. BAB II: Landasan Teori

Pada bab ini dijelaskan mengenai teori-teori yang terkait dengan penelitian antara lain: pemodelan matematika, persamaan diferensial, sistem persamaan diferensial nonlinear, model pertumbuhan logistik, model pertumbuhan logistik populasi dua spesies dengan interaksi pemangsa-mangsa, dan analisis titik ekuilibrium.

BAB III: Analisis Kestabilan Sistem Dinamika

Bab ini membahas tentang analisis kestabilan tiap titik ekuilibrium dari model sistem dinamika pemangsa-mangsa yang telah dimodifikasi. Model dimodifikasi dengan menambahkan aspek pemanenan baik pada pemangsa saja,atau mangsa saja maupun keduanya. Hal ini mengacu pada rumusan masalah pada Bab I di mana peneliti membuat modifikasi model dengan aspek pemanenan dan analisis kestabilan titik ekuilibriumnya.

BAB IV: Solusi Model dengan Metode Dekomposisi Adomian

Pada bab ini akan dipaparkan hasil serta pembahasan mengenai solusi dari model pertumbuhan logistik populasi dua spesies secara umum. Nilai parameter yang diberikan ada tiga jenis sehinga mengakibatkan tiga macam interaksi yaitu interaksi mutualisme, parasitisme dan kompetisi. Masing-masing model dicari solusinya dengan mengitung menggunakan Metode Dekomposisi Adomian.

(24)

persamaan diferensial dan menggambar grafik dari perilaku model populasi yang dapat dianalisis perilaku jangka panjang.

BAB V : Aspek Kependidikan

Pada bab ini akan dibahas tentang berbagai aspek kependidikan yang terkait dengan materi tesis. Aspek kependidikan yang dibahas adalah kependidikan adalah aplikasi tentang sistem dinamika pada pada jenjang Sekolah Menengah dan tingkat S1. Pada jenang sekolah menengah dibuat dengan membuat soal cerita dengan sistem dinamika, sedangkan untuk jenjang S1 sudah ada mata kuliah tentang pemodelan matematika yang membahas masalah sistem dinamika populasi secara lebih detail. Selain itu terdapat refleksi dari peneliti tentang penulisan tesis matematika murni.

BAB VI: Penutup

(25)

I. Metode Penelitian

(26)

10

BAB II

LANDASAN TEORI

A. Pemodelan Matematika

Pemodelan matematika merupakan suatu proses matematisasi dari dunia nyata menuju dunia matematika, artinya permasalahan yang ada pada dunia nyata diterjemahkan ke dalam bahasa matematika. Pertumbuhan populasi merupakan salah satu dari berbagai permasalahan di dunia nyata yang dapat dibawa ke dalam dunia matematika menggunakan teori-teori yang sesuai. Pada perkembangannya, model yang sudah dibentuk dapat dikembangkan lagi dengan menambah aspek-aspek yang lain yang sekiranya mempengaruhi. Menurut Lovitt (1991) pemodelan matematika ditandai oleh dua ciri utama, yaitu:

1. Pemodelan bermula dan berakhir dengan dunia nyata 2. Pemodelan membentuk suatu siklus

Pada prosesnya pemodelan memiliki beberapa tahap yang saling berhubungan satu dengan yang lainnya. Proses pemodelan dapat digambarkan seperti sebuah siklus yang terus mengalami perbaikan. Berikut ini merupakan gambar dari siklus pemodelan matematika:

Perumusan Perbaikan

Interpretasi

Gambar 2.1. Pemodelan matematika menurut Lovitt

Dunia nyata Model

(27)

B. Model Pertumbuhan Populasi

Model pertumbuhan populasi pertama kali diperkenalkan oleh Malthus dengan model pertumbuhan eksponensial. Model ini memperlihatkan bahwa pertumbuhan individu pada populasi mengikuti grafik eksponensial, sehingga model awal dari pertumbuhan eksponensial yang diperlihatkan dalam Murray (2001:2) adalah:

= ,

dengan konstanta > 0 merupakan laju pertumbuhan populasi dan (0) = . Dengan demikian menurut Murray (2001:2), laju pertumbuhan eksponen dapat dicari solusinya. Shonkwiler (2009:15) mengemukakan hal yang sama sehingga nilai setiap waktu dapat dicari dengan fungsi sebagai berikut:

= ,

ln = + ,

( ) = ,

( ) = .

substitusikan (0) = ,sehingga diperoleh persamaan: (0) = ,

= ,

(28)

dengan

: jumlah populasi,

: laju pertumbuhan populasi, : waktu.

Model Malthus masih memiliki banyak kekurangan. Pada tahun 1838 Verhulst mengemukakan sebuah model pertumbuhan populasi baru yang merupakan perbaikan dari model Malthus. Model tersebut biasa disebut model logistik. Model ini memperhatikan berbagai aspek-aspek yang tidak ada pada model sebelumnya seperti daya dukung alam. Daya dukung alam merupakan kemampuan alam sekitar dalam mendukung kelangsungan hidup suatu populasi baik dari segi makanan, lahan untuk tinggal dan sebagainya. Model logistik dirumuskan sebagai berikut seperti dalam Murray (2001:3):

= 1 − .

Model pertumbuhan logistik tersebut bertumbuh dengan laju dan memiliki daya dukung alam . Konstanta dan merupakan konstanta positif dari model tersebut. Model ini memiliki solusi yang berasal dari model yang diberikan. Model logistik yang diberikan dilakukan pengintegralan untuk mendapatkan solusi. Murray (2001:3) menuliskan solusi dari model logistik sebagai berikut:

= 1 − ,

(29)

Kedua ruas diintegralkan sehingga didapat penyelesaian sebagai berikut:

1 − = + .

Dengan menggunakan teknik pengintegralan fungsi rasional, maka dapat dicari hasil integral pada ruas kiri sebagai berikut:

1 − = + 1 − ,

Hasil integral tersebut membentuk persamaan menjadi:

(30)

ln

− = + ,

− = .

Misalkan = maka persamaan di atas akan menjadi:

=

− 1.

Populasi awal untuk (0) = , sehingga dengan mensubstitusi ke variabel maka didapat:

(31)

dengan

: jumlah populasi,

: laju pertumbuhan populasi,

: daya dukung alam terhadap populasi, : waktu.

Secara umum model pertumbuhan populasi tunggal dalam Murray (2001:5) memiliki model sebagai berikut:

= ( ),

dengan ( ) merupakan fungsi nonlinear dari kemudian solusi ekuilibrium ∗ merupakan solusi dari ( ) = 0 dan secara umum stabil untuk gangguan kecil jika ’ ( ∗ ) < 0dan tidak stabil jika ’ ( ∗ ) > 0.

C. Aspek Pemanenan

Model pertumbuhan dengan aspek pemanenan diperkenalkan pertama kali oleh Rotenberg tahun 1987 dalam Murray (2001:31). Pada model ini, aspek pemanenan ditambahkan pada model pertumbuhan logistik. Model yang baru dalam Murray (2001:31) adalah:

= 1 − − ,

dengan

: jumlah populasi,

(32)

: daya dukung alam terhadap populasi, : laju pemanenan.

Konstanta , dan adalah konstanta positif dan merupakan banyaknya pemanenan tiap satu waktu dengan adalah besaran dari pemanenan.

D. Aspek Kompetisi

Kompetisi pada individu merupakan hal yang biasa terjadi. Setiap populasi yang hidup bersama tentunya akan saling berkompetisi satu sama lain karena yang diinginkan adalah hal yang sama. Murray (2001:94) menuliskan model dengan aspek kompetisi dari masing-masing individu. Model berikut berdasarkan model kompetisi dua spesies Lotka-Volterra dengan spesies dan yang bertumbuh secara logistik dan berinteraksi satu sama lain. Model tersebut adalah:

= 1 − − ,

dengan

: jumlah populasi pertama,

: jumlah populasi kedua,

: laju pertumbuhan populasi,

(33)

: laju pertumbuhan populasi pertama ketika berkompetisi dengan populasi kedua,

: laju pertumbuhan populasi kedua ketika berkompetisi dengan populasi pertama.

E. Sistem Persamaan Diferensial

Persamaan diferensial merupakan persamaan yang menghubungkan nilai fungsi tersebut dengan turunannya. Bentuk dari persamaan diferensial biasanya berupa laju perubahan. Dalam penelitian ini laju perubahan atau pertumbuhan sebuah populasi digambarkan dalam bentuk persamaan diferensial. Setiap populasi yang ada akan berkumpul dan hidup membentuk ekosistem. Interaksi antar populasi ini yang akan menjadi interpretasi dari sebuah sistem persamaan diferensial.

(34)

1. Model dasar interaksi pemangsa-mangsa

Model dasar yang diperkenalkan adalah model yang pertumbuhan populasi secara eksponensial. Kedua populasi bertumbuh secara eksponen dan saling berinteraksi satu sama lain. Populasi yang bertumbuh akan berkurang ketika berinteraksi dengan P dikarenakan merupakan makanan dari . Populasi akan semakin bertambah ketika berinteraksi dengan dikarenakan tersedianya makanan. Dengan demikian, model interaksi dua populasi dapat dirumuskan sebagai berikut:

= − ,

= − + ,

dengan , , , > 0dan

: jumlah populasi mangsa,

: laju pertumbuhan populasi mangsa,

: laju pertumbuhan mangsa ketika berinteraksi dengan pemangsa, : jumlah populasi pemangsa,

: laju pertumbuhan pemangsa,

: laju pertumbuhan pemangsa ketika berinteraksi dengan mangsa.

a. Titik ekuilibrium

(35)

ekulibrium maka fungsi tersebut akan bernilai 0 (nol) sedemikian hingga mengakibatkan = = 0. Selanjutnya akan diperoleh dua persamaan nonlinear sebagai berikut:

− = 0,

− + = 0.

Dari sistem persamaan nonlinear tersebut diperoleh titik ekuilibrium yaitu (0,0) dan , .

b. Linearisasi

Linearisasi merupakan proses membawa suatu sistem nonlinear menjadi sistem linear. Menurut Perko (2001:102) Linearisasi bertujuan untuk memperoleh aproksimasi sederhana dengan menggunakan deret Taylor untuk mencari suatu hampiran solusi di sekitar titik ekuilibrium.

= = − −

− + .

Dengan mensubstitusikan titik dan pada matriks Jacobi tersebut maka diperoleh:

= 0

0 − dan =

0

0 .

(36)

yang didapatkan akan digunakan untuk menentukan jenis titik ekuilibrium tersebut dan jenis kestabilan.

c. Analisis Kestabilan Titik Ekuillibrium

Berdasarkan matriks Jacobi yang telah dicari maka analisis kestabilan pada titik ekuilibrium dapat ditentukan dengan mencari nilai eigen dari masing-masing matriks jacobi. Nilai eigen dapat dicari ketika memenuhi persamaan det( − ) = 0, dimana merupakan nilai eigen dari matriks Jacobi. Adapun kriteria kestabilan menurut Boyce dan DiPrima (2012 : 504) adalah sebagai berikut:

Tabel 2.1. Kriteria jenis titik kritis dan kestabilan No Nilai Eigen Jenis titik kritis Kestabilan

1 > > 0 Simpul Tidak stabil

2 < < 0 Simpul Stabil Asimtotik 3 < 0 < Titik Sadel Tidak stabil 4 = > 0 Simpul sejati

7 < 0 Stabil asimtotik

8 = ,

= −

Pusat Stabil

(37)

eigen yang telah dicari setelah mensubtitusi masing-masing titik ekuilibrium pada matriks jacobi:

1) Titik ekuilibrium (0,0) dengan matriks = 0

0 − .

Diperoleh nilai eigen ( ) sebagai berikut: =

= −

Dikarenakan < 0 < maka titik tersebut merupakan titik sadel sehingga titik ekuilibrium pada bersifat tidak stabil.

2) Titik ekuilibrium , dengan matriks = 0

0 .

Diperoleh nilai eigen ( ) sebagai berikut: = − √

= √

Dikarenakan = , = − maka titik tersebut merupakan titik pusat sehingga titik ekuilibrium pada bersifat stabil.

(38)

1) Titik simpul.

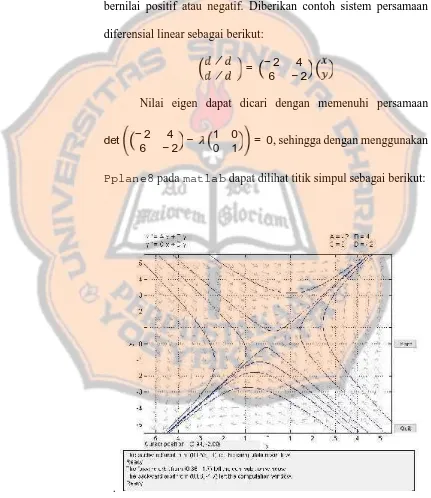
Titik simpul akan terjadi ketika nilai eigen dan seluruhnya bernilai positif atau negatif. Diberikan contoh sistem persamaan diferensial linear sebagai berikut:

⁄

⁄ =

− 2 1 1 − 2

Nilai eigen dapat dicari dengan memenuhi persamaan

det − 2 1 1 − 2 −

1 0

0 1 = 0, sehingga dengan menggunakan

Pplane8padamatlabdapat dilihat titik simpul sebagai berikut:

Gambar 2.2. Grafik jenis titik simpul

(39)

2) Titik simpul sejati.

Titik simpul sejati atau tidak sejati akan terjadi ketika nilai eigen dan bernilai sama baik seluruhnya berupa bilangan positif atau negatif. Diberikan contoh sistem persamaan diferensial linear sebagai berikut:

⁄

⁄ =

4 0

0 4

det 4 0

0 4 −

1 0

Gambar 2.3. Grafik jenis titik simpul sejati

(40)

membelok sehingga terlihat seperti garis lurus yang langsung menuju ke suatu titik.

3) Titik sadel.

Titik sadel akan terjadi ketika nilai eigen dan salah satu bernilai positif atau negatif. Diberikan contoh sistem persamaan diferensial linear sebagai berikut:

⁄

⁄ =

− 2 4 6 − 2

det − 2 4 6 − 2 −

1 0

.

(41)

Pada titik sadel tersebut garis-garis yang berasal dari berbagai titik akan dibelokan menjauhi titik tersebut. Pada awalnya garis tersebut akan mendekati titik sadel tersebut, tetapi setelah mendekati akan dibelokkan menjauhi titik tersebut.

4) Spiral.

Titik spiral akan terjadi ketika nilai bagian real dari eigen dan yang merupakan bilangan kompleks seluruhnya bernilai positif atau negatif. Diberikan contoh sistem persamaan diferensial linear sebagai berikut:

⁄

⁄ =

− 2 3 2 − 2

det − 2 3 2 − 2 −

1 0

(42)

Gambar 2.5. Grafik jenis titik spiral

Nilai yang diambil dari berbagai arah akan menuju ke suatu titik seolah-olah akan mengelilingi titik tersebut.

5) Titik Pusat.

Titik pusat akan terjadi ketika nilai bagian imajiner dari eigen dan yang merupakan bilangan kompleks salah satu bernilai positif atau negatif.. Diberikan contoh sistem persamaan diferensial linear sebagai berikut:

⁄

⁄ =

0 − 8

8 0

det 0 − 8

8 0 −

1 0

(43)

Gambar 2.6. Grafik jenis titik pusat

Grafik pada titik pusat membuat nilai yang diambil dari berbagai arah hanya mengelilingi titik tersebut tanpa adanya upaya untuk mendekati maupun menjauhi.

d. Grafik interaksi pemangsa-mangsa

Pada sistem persamaan pemangsa-mangsa diberikan nilai untuk tiap parameter yang ada yaitu = 0.4, = 0.3, = 0.01, dan =

(44)

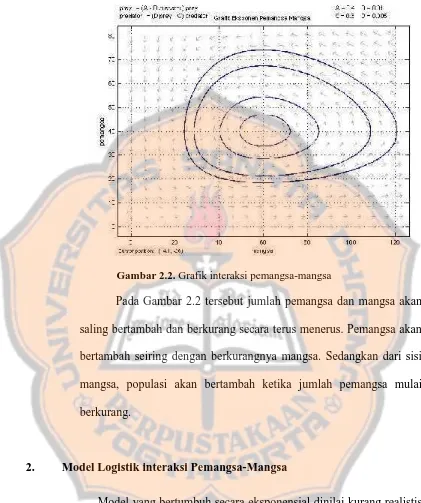
Gambar 2.2. Grafik interaksi pemangsa-mangsa

Pada Gambar 2.2 tersebut jumlah pemangsa dan mangsa akan saling bertambah dan berkurang secara terus menerus. Pemangsa akan bertambah seiring dengan berkurangnya mangsa. Sedangkan dari sisi mangsa, populasi akan bertambah ketika jumlah pemangsa mulai berkurang.

2. Model Logistik interaksi Pemangsa-Mangsa

(45)

pertama ( ) dan populasi kedua ( ) dibentuk ulang menjadi bertumbuh secara logistik dengan memperhatikan aspek daya dukung alam, sehingga tidak akan mungkin populasi tumbuh terus menerus sampai tak hingga. Dengan demikian model yang baru yang dibentuk menjadi:

= 1 − − ,

= − 1 − + ,

dengan , , , , , > 0dan

: laju pertumbuhan mangsa ketika berinteraksi dengan pemangsa, : daya dukung alam sekitar pada populasi mangsa,

: jumlah populasi pemangsa, : laju pertumbuhan pemangsa,

: laju pertumbuhan pemangsa ketika berinteraksi dengan mangsa, : daya dukung alam sekitar pada populasi pemangsa.

a. Titik Ekuilibrium

(46)

1 − − = 0,

− 1 − + = 0,

Berdasarkan sistem persamaan nonlinear tersebut diperoleh titik

ekuilibrium (0,0), ( ,0), (0, ) dan , ( ) .

b. Konstruksi Matriks Jacobi

Perko (2001:63) menuliskan cara untuk mengkonstruksi matriks Jacobi. Hal tersebut dapat dilakukan dengan cara berikut dalam linearisasi dari sistem persamaan nonlinear:

= = − 2 / − ) −

− + 2 / + .

Dengan mensubstitusikan titik , , dan pada matriks Jacobi tersebut maka diperoleh:

c. Analisis Kestabilan Titik Ekuillibrium

(47)

eigen. Boyce dan DiPrima (2012:504) menuliskan syarat untuk menjaci nilai eigen adalah dengan memenuhi persamaan det( − ) = 0, dimana merupakan nilai eigen dari matriks Jacobi. Berdasarkan Tabel 2.1, maka kriteria kestabilan Model Logistik pemangsa-mangsa adalah: 1) Titik ekuilibrium (0,0) dengan matriks = 0

0 − .

Diperoleh nilai eigen ( ) sebagai berikut: =

= −

Dikarenakan < 0 < maka titik tersebut merupakan titik sadel sehingga titik ekuilibrium pada bersifat tidak stabil.

2) Titik ekuilibrium ( , 0) dengan matriks

= − 2 −

0 − + .

Diperoleh nilai eigen ( ) sebagai berikut: = − (negatif)

= − +

a) jika =− + bernilai positif, < maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil. b) jika =− + bernilai negatif, > maka titik tersebut berupa titik simpul sehingga titik ekuilibrium bersifat stabil. 3) Titik ekuilibrium (0, )dengan matriks = − 0 .

(48)

= −

= (positif)

a) jika = − bernilai positif, > maka titik tersebut berupa titik simpul sehingga titik ekuilibrium bersifat stabil. b) jika = − bernilai negatif, < maka titik tersebut

berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil. 4) Titik ekuilibrium , ( ) dengan matriks

=

Andaikan nilai dari masing-masing elemen dimisalkan menjadi , , dan , maka matriks Jacobi akan menjadi sebagai berikut:

=

Diperoleh nilai eigen ( ) dengan kemungkinan sebagai berikut:

, = ( + ) ± ( − ) + 4

2 .

(49)

a) Jika + dan ( − ) + 4 bernilai positif, maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil.

b) Jika + bernilai negatif,( − ) + 4 bernilai positif, dan | + | <( − ) + 4 maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil.

c) Jika A bernilai negatif, ( − ) + 4 bernilai positif, dan | + | > ( − ) + 4 maka titik tersebut berupa titik simpul sehingga titik ekuilibrium bersifat stabil asimtotik. d) Jika( − ) + 4 bernilai negatif dan + bernilai positif

maka titik tersebut berupa titik spiral dengan sifat tak stabil. e) Jika( − ) + 4 bernilai negatif dan + bernilai negatif

maka titik tersebut berupa titik spiral dengan sifat stabil asimtotik.

d. Grafik Interaksi Pemangsa-Mangsa yang bertumbuh secara Logistik

Pada sistem persamaan pemangsa-mangsa logistik diberikan nilai untuk tiap parameter yang ada yaitu = 0.4, = 0.3, =

(50)

Gambar 2.3. Grafik interaksi pemangsa-mangsa yang bertumbuh secara

logistik

Pada Gambar 2.3. terlihat bahwa ketika pemangsa dan mangsa berinteraksi terus menerus dalam jangka waktu panjang maka perilaku kedua populasi akan berada disekitar suatu titik kesetimbangan.

F. Metode Dekomposisi Adomian

(51)

Adomian memang bukan yang paling sempurna tetapi metode ini cukup mudah dan efektif ketika digunakan dalam menyelesaikan persamaan diferensial.

Metode dekomposisi Adomian dapat digunakan untuk menyelesaikan sebuah persamaan diferensial maupun suatu sistem persamaan diferensial. Berikut ini merupakan contoh penggunaan metode dekomposisi Adomian pada sebuah sistem persamaan nonlinear. Persamaan diambil dari Batiha dkk (2016:903):

= + + ,

= + + . (2.1)

Dengan mengubah = sesuai dengan Wazwaz (2009:22), maka bentuk dari sistem (2.1) menjadi:

= + + ,

= + + , (2.2)

dan mengoperasikan = ∫ (. ) pada kedua ruas dari sistem nonlinear tersebut sedemikian hingga sistem dari persamaan nonlinear menjadi:

= + + ,

= + + . (3.2)

(52)

( ) = , ( ) = ,

(4.2)

dan untuk komponen yang nonlinear seperti , dan y akan diubah menjadi

= , = , = .

(5.2)

Jumlahan dari komponen nonlinear dapat dilihat sebagai berikut:

= , = , = ,

(6.2)

sehingga dapat ditentukan polinomial Adomian untuk , dan :

=

= +

= + +

= + + +

...

(7.2)

=

= +

= + +

= + + +

(53)

...

Sistem persamaan diferensial nonlinear dari (3.2) dapat ditulis dengan mensubstitusikan (4.2), (5.2) dan (6.2) seperti pada Rao (2011), sehingga

Nilai awal (0) = , (0) = , sehingga solusi dari sistem dapat dicari. Iterasi yang dilakukan yaitu mensubstitusikan (7.2), (7.3) dan (7.4) pada (11.2) sedemikian hingga iterasi dapat ditentukan sebagai berikut:

= (0) =

= + +

(54)

= (0) =

= + +

(13.2)

Secara umum solusi dari sistem adalah jumlahan dari seluruh iterasi yang didapat sampai tak hingga, tetapi peneliti dapat menentukan banyaknya iterasi sesuai kebutuhan. Contoh ketika solusi dicari dengan jumlahan sampai iterasi ketujuh adalah sebagai berikut:

= + + + + + + + , (14.2)

= + + + + + + + . (15.2)

G. Kerangka Berpikir

(55)

39

BAB III

ANALISIS KESTABILAN MODEL SISTEM DINAMIKA

Model pertumbuhan logistik dinilai lebih realistis dari pada model

eksponensial yang merupakan model terdahulu dikarenakan model pertumbuhan logistik mempertimbangkan aspek daya dukung alam. Pada interaksi spesies pertama ( )dan spesies kedua ( )di suatu ekosistem akan diterapkan beberapa kondisi tambahan seperti pemanenan pada salah satu spesies maupun keduanya. Sebelum membuat model-model matematika, ada beberapa asumsi yang perlu diperhatikan dalam pengembangan model ini.

Beberapa asumsi yang diberikan oleh peneliti adalah sebagai berikut: 1. Interaksi dua spesies berada pada sistem yang tertutup.

2. Spesies pertama merupakan satu-satunya makanan dari spesies kedua. 3. Spesies pertama akan bertumbuh meski tidak ada spesies kedua.

4. Spesies kedua akan mengalami penurunan jumlah populasi jika tidak ada spesies pertama.

5. Tidak ada migrasi.

(56)

A. Model Logistik Pemangsa-Mangsa dengan Aspek Pemanenan pada Mangsa

Pada model ini, aspek pemanenan diterapkan pada populasi spesies pertama, sehingga dapat dianalisis perilaku spesies kedua ketika spesies pertama mengalami pemanenan. Dengan demikian model akan menjadi:

= 1 − − − ,

= − 1 − + ,

dengan , , , , , , merupakan konstanta positif dan

: jumlah populasi pemangsa, : laju pertumbuhan pemangsa,

: laju pertumbuhan pemangsa ketika berinteraksi dengan mangsa, : daya dukung alam sekitar pada populasi pemangsa,

: laju pemanenan mangsa.

1. Titik Ekuilibrium

(57)

1 − − − ₁ = 0,

− 1 − + = 0,

atau ( − + − 1 ) = 0,

( − + ) = 0.

Dengan demikian, sistem persamaan tersebut memiliki empat titik ekuilibrium, yakni (0,0), (0, ), ( ) , 0 , dan

( )_, ( ) _.

2. Konstruksi Matriks Jacobi

Konstruksi matriks Jacobi dapat dilakukan dengan cara linearisasi dari sistem persamaan nonlinear:

= = − − − 1 −

− + + .

(58)

3. Analisis Kestabilan Titik Ekuilibrium

Berdasarkan matriks Jacobi yang telah dicari maka analisis kestabilan pada titik ekuilibrium dapat ditentukan dengan mencari nilai eigen. Nilai eigen dapat dicari ketika memenuhi det( − ) = 0, di mana merupakan nilai eigen dari matriks Jacobi. Berdasarkan Tabel 2.1 maka kriteria kestabilannya adalah:

a. Titik ekuilibrium (0,0)dengan matriks = − 0

0 − .

Diperoleh nilai eigen ( ) sebagai berikut:

= − ,

= − .

Dikarenakan < 0 < dan > maka titik tersebut merupakan titik sadel sehingga titik ekuilibrium pada bersifat tidak stabil. Titik ekuilibrium pada merupakan titik simpul dan akan bersifat stabil asimtotik ketika < , sehingga < < 0.

b. Titik ekuilibrium (0, ) dengan matriks = − − 0 .

Diperoleh nilai eigen ( ) sebagai berikut: = (positif),

(59)

1) Jika = − − bernilai positif, + < maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil. 2) Jika = − − bernilai negatif, + > maka titik tersebut

berupa titik simpul sehingga titik ekuilibrium bersifat tidak stabil.

c. Titik ekuilibrium ( ) , 0 dengan matriks =

−3 1+ 3 ( 1 )

0 − + ( 1 ) .

Diperoleh nilai eigen ( ) sebagai berikut: = 3( − ),

=− + ( − ).

1) Jika < maka bernilai positif dan bernilai negatif, sehingga titik tersebut berupa titik sadel dan titik ekuilibrium bersifat tak stabil. 2) Jika > dan,

a) > ( 1 ) maka dan bernilai negatif, sehingga titik tersebut berupa titik simpul dan titik ekuilibrium bersifat stabil.

b) < ( 1 ) maka bernilai negatif dan bernilai positif, sehingga titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil.

d. Titik ekuilibrium ( ), ( ) dengan matriks =

( ) ( )

(60)

Misalkan matriks = , maka diperoleh nilai eigen ( ) sebagai berikut:

= −( + ) + +₂ − 6 − 4 ,

=−( + ) − +₂ − 6 − 4 .

1) Jika + − 6 − 4 bernilai positif, maka ada beberapa kemungkinan sebagai berikut:

a) Jika bernilai positif dan bernilai positif maka titik tersebut berupa titik simpul sehingga titik ekuilibrium bersifat tak stabil. b) Jika bernilai positif dan bernilai negatif maka titik tersebut

berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil. c) Jika bernilai negatif dan bernilai positif maka titik tersebut

berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil. d) Jika bernilai negatif dan bernilai negatif maka titik tersebut

berupa titik simpul sehingga titik ekuilibrium bersifat stabil asimtotik.

2) Jika + − 6 − 4 bernilai negatif dan:

a) + bernilai negatif maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat stabil asimtotik.

(61)

4. Grafik Interaksi Pemangsa-Mangsa yang Bertumbuh secara Logistik Dengan Aspek Pemanenan pada Mangsa

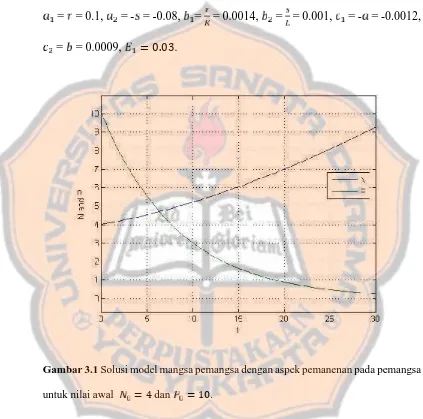
Nilai awal dan parameter yang dimasukan adalah = 4dan = 10, = = 0.1, = - = -0.08, = = 0.0014, = = 0.001, = - = -0.0012, = = 0.0009, = 0.03.

Gambar 3.1 Solusi model mangsa pemangsa dengan aspek pemanenan pada pemangsa

untuk nilai awal = 4dan = 10.

(62)

Gambar 3.2 Lapangan arah untuk model mangsa pemangsa dengan aspek pemanenan

pada mangsa.

(63)

B. Model Logistik Pemangsa-Mangsa dengan Aspek Pemanenan pada Pemangsa

Pada model ini pemangsa akan diberi aspek kompetisi dikarenakan spesies kedua sebagai pemangsa memakan makanan yang sama dan hanya ada satu-satunya. Dalam model ini pada spesies pertama tidak ada pemanenan. Sehingga dapat disimpulkan bahwa spesies pertama hanya bertumbuh saja. Dengan demikian model yang dibuat menjadi:

= 1 − − ,

= − 1 − + − ,

dengan , , , , , , , > 0 dan

: jumlah populasi pemangsa, s : laju pertumbuhan pemangsa,

(64)

Analisis kestabilan titik ekuilibrium interaksi pemangsa-mangsa dengan aspek kompetisi pada pemangsa dapat dimulai dengan syarat titik ekuilibrium yaitu = = 0, sehingga diperoleh:

1 − − = 0,

− 1 − + − = 0,

atau ( − − ) = 0,

( − + − ₂ ) = 0.

Sedemikian hingga terdapat empat titik ekuilibrium, yakni (0,0),

0,( ) , ( , 0)dan ( ),( ) .

Konstruksi matriks Jacobi dapat dilakukan dengan cara berikut dalam linearisasi dari sistem persamaan nonlinear:

= = −

2

− −

+2 + − 2

.

Dengan mensubstitusikan titik , , dan pada matriks Jacobi tersebut maka diperoleh:

= _{0 − −}0

(65)

=

Berdasarkan matriks Jacobi yang telah dicari maka analisis kestabilan pada titik ekuilibrium dapat ditentukan dengan mencari nilai eigen. Nilai eigen dapat dicari ketika memenuhi det( − ) = 0, di mana merupakan nilai eigen dari matriks Jacobi. Berdasarkan Tabel 2.1 maka kriteria kestabilannya adalah:

a. Titik ekuilibrium (0,0)dengan matriks = _{0 − −}0 .

= ,

=− − .

(66)

b. Titik ekuilibrium 0,( ) dengan matriks tersebut berupa titik simpul sehingga titik ekuilibrium bersifat tak stabil.

2) Jika = − ( ₂+ ) bernilai negatif, < ( + ) maka titik tersebut berupa titik simpul sehingga titik ekuilibrium bersifat stabil. c. Titik ekuilibrium ( , 0)dengan matriks = − −

0 − + .

Diperoleh nilai eigen ( ) sebagai berikut: = − (negatif),

= − + .

1) Jika =− + bernilai positif, < maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil.

(67)

d. Titik ekuilibrium ( ),( ) dengan matriks =

( ) ₋ ( )

( ) ( ) .

Misalkan matriks = , maka diperoleh nilai eigen ( ) sebagai berikut:

= −( + ) + +₂ − 6 − 4 ,

=−( + ) − +₂ − 6 − 4 .

(68)

2) Jika + − 6 − 4 bernilai negatif, maka beberapa kemungkinan yang muncul adalah:

a) Jika + bernilai negatif maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat stabil asimtotik.

b) Jika + bernilai posistif maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tidak stabil.

4. Grafik Interaksi Pemangsa-Mangsa yang Bertumbuh secara Logistik dengan Pemanenan pada Pemangsa

Nilai awal dan parameter yang dimasukan adalah = 4dan = 10, = = 0.1, = − = −0.08, = = 0.0014, = = 0.001, = − = −0.0012, = = 0.0009, = 0.005.

(69)

Dengan menggunakan programPplane8, grafik mangsa pemangsa dapat terlihat titik ekuilibriumnya seperti pada Gambar 3.3 dan Gambar 3.4:

pada pemangsa.

(70)

C. Model Logistik Pemangsa-Mangsa dengan Aspek Pemanenan pada Mangsa dan Pemangsa

Model terakhir yang dibentuk adalah model pertumbuhan logistik dengan pemanenan pada spesies pertama dan kedua. Model ini merupakan gabungan dari model sebelumnya. Sehingga analisis yang dibuat menggambarkan perilaku spesies kedua yang dipanen dan makanan mereka (spesies pertama) juga mengalami pemanenan. Model yang diberikan sebagai berikut:

= 1 − − − ,

= − 1 − + − ,

dengan , , , , , , , > 0dan : jumlah populasi mangsa,

: jumlah populasi pemangsa, s : laju pertumbuhan pemangsa,

(71)

Analisis kestabilan titik ekuilibrium interaksi pemangsa-mangsa dengan aspek pemanenan pada mangsa dan kompetisi pada pemangsa dapat dimulai dengan syarat titik ekuilibrium yaitu = = 0, sehingga diperoleh:

1 − − − 1 = 0,

− 1 − + − ₂ = 0, atau

( − + − ₁ ) = 0,

( − + − 2 ) = 0.

Terdapat empat titik ekuilibrium, yakni (0,0), 0, ( ) , ( ) , 0 ,dan

( )_, ( )

.

Konstruksi matriks Jacobi dapat dilakukan dengan cara berikut dalam linearisasi dari sistem persamaan nonlinear:

= = −

2

− − 1 −

− +2 + − 2

.

(72)

= − 2 − 2 1− 1

Berdasarkan matriks Jacobi yang telah dicari maka analisis kestabilan pada titik ekuilibrium dapat ditentukan dengan mencari nilai eigen. Dengan mencaridet( − ) = 0, di mana merupakan nilai eigen dari matriks Jacobi, maka kestabilan dapat ditentukan berdasarkan Tabel 2.1, maka kriteria kestabilannya adalah:

a. Titik ekuilibrium (0,0)dengan matriks = − 0

0 − − .

= − ,

= − − .

(73)

b. Titik ekuilibrium 0, ( ) dengan matriks

= − + ( + ),

=− −2 ( + )− .

1) Jika = − + ( + ) bernilai positif dan =− −2 ( + )− bernilai negatif maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil.

2) Jika = − + ( + ) bernilai negatif dan =− −2 ( + )− bernilai negatif maka titik tersebut berupa titik simpul sehingga titik ekuilibrium bersifat stabil asimotik.

c. Titik ekuilibrium ( ) , 0 dengan matriks =

− 2 − 2 ₁− ₁ ( 1)

0 − +( 1) ₋

2 .

Diperoleh nilai eigen ( ) sebagai berikut :

= − 2 − 2 − ,

(74)

1) Jika = − 2 − 2 − bernilai positif dan =− +( − ) − bernilai positif maka titik tersebut berupa titik simpul sehingga titik ekuilibrium bersifat tak stabil.

2) Jika = − 2 − 2 − bernilai positif dan =− +( − ) − bernilai negatif maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil.

3) Jika = − 2 − 2 ₁− ₁bernilai negatif dan =− +( − ) − bernilai positif maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tak stabil.

4) Jika = − 2 − 2 − bernilai negatif dan =− +( 1) −

2bernilai negatif maka titik tersebut berupa titik simpul sehingga titik

(75)

berupa titik simpul sehingga titik ekuilibrium bersifat stabil asimtotik.

2) Jika + − 6 − 4 bernilai negatif, maka beberapa kemungkinan yang muncul adalah:

a) Jika + bernilai negatif maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat stabil asimtotik.

b) Jika + bernilai posistif maka titik tersebut berupa titik sadel sehingga titik ekuilibrium bersifat tidak stabil.

4. Grafik Interaksi Pemangsa-Mangsa yang Bertumbuh Secara Logistik dengan Aspek Pemanenan pada Mangsa dan Pemangsa

(76)

dan mangsa untuk nilai awal = 4dan = 10.

Dengan menggunakan program Pplane8, grafik mangsa pemangsa dapat terlihat titik ekuilibriumnya seperti tampak pada Gambar 3.5 dan Gambar 3.6:

(77)

(78)

62

BAB IV

SOLUSI SISTEM DINAMIKA DUA SPESIES DENGAN

METODE DEKOMPOSISI ADOMIAN

Pada bab ini akan dibahas tentang solusi dari sistem dinamika dua populasi dengan metode dekomposisi Adomian. Model sistem dinamika populasi dibuat lebih sederhana berdasarkan Batiha dkk (2016:903), sehingga model sistem menjadi:

= ( + + )

(4.1)

dimana dan adalah populasi pada waktu , , , , , , adalah konstanta positif dan

: populasi pertama,

: laju pertumbuhan populasi pertama, : kapasitas batas populasi pertama,

: laju pertumbuhan populasi pertama ketika berinteraksi dengan populasi kedua,

: populasi kedua,

: laju pertubuhan populasi kedua, : kapasitas batas populasi kedua,

(79)

Nilai awal dari masing-masing populasi didapat dari Batiha dkk (2016:903) yaitu untuk nilai = 4 dan = 10. Jenis-jenis interaksi dari kedua populasi dapat ditentukan dengan memanipulasi nilai parameter. Nilai parameter berdasarkanBatiha dkk (2016:903)yaitu = 0.1, = 0.08, = 0.0014, = 0.001, = 0.0012, = 0.0009. Dengan demikian, jika nilai parameter diubah, maka akan mendapat tiga macam jenis interaksi yang berasal dari sebuah model secara umum. Untuk setiap nilai awal yang berbeda, jenis interaksi pada sistem dinamika tersebut berubah menjadi mutualisme, parasitisme dan kompetisi.

A. Mutualisme

Subtitusikan nilai = 0.1, = 0.08, =−0.0014, = −0.001, =

0.0012, = 0.0009, = 4 dan = 10 pada sistem persamaan (4.1) sehingga sistem akan menjadi:

= (0.1 − 0.0014 + 0.0012 ),

= (0.08 − 0.001 + 0.0009 ).

(4.2)

(80)

= 0.0005198410667

= 0.00002377241892 = 0.00000715508705

= 4.762365706 ∗ 10^(−7) = 1.122902100 ∗ 10^(−7)

= 4.92081361 ∗ 10^(−9) = 3.924828700 ∗ 10^(−9) = −9.99735783 ∗ 10^(−11)

= 1.355344556 ∗ 10^(−10)

Solusi sistem persamaan (4.2) merupakan jumlahan dari hasil iterasi pada (4.3). Misalkan jumlahan adalah 1dan jumlahan adalah 1, maka solusi dari sistem persamaan (4.2) adalah:

1 = 4 + 0.4256000000 ∗ + 0.02321664000 ∗ ^2 + 0.0008613579093 ∗ ^3 + 0.00002377241892 ∗ ^4 + 4.762365706

∗ 10^(−7) ∗ ^5 + 4.92081361 ∗ 10^(−9) ∗ ^6 − 9.99735783 ∗ 10^(−11) ∗ ^7,

1 = 10 + 0.7360000000 ∗ + 0.02532000000 ∗ ^2

(81)

Dengan menggunakan programMaple, grafik solusi dari sistem persamaan (4.2) telah ditunjukan pada gambar berikut:

4.1a. Grafik populasi 4.1b.Grafik populasi

(82)

Merupakan grafik populasi

Gambar 4.2. Grafik populasi yang berinteraksi secara Mutualisme

(83)

B. Parasitisme

Subtitusikan nilai = 0.1, =0.08, =−0.0014, =−0.001, =

0.0012, =−0.0009, = 4dan = 10pada sistem persamaan (4.1) sehingga sistem akan menjadi:

= (0.1 − 0.0014 + 0.0012 ),

= (0.08 − 0.001 − 0.0009 ).

(4.4)

Perhitungan solusi dari sistem (4.4) dengan metode dekomposisi Adomian dilakukan menggunakan programmapledan memperoleh hasil sebagai berikut:

(84)

2 = 4 + 0.4256000000 ∗ + 0.02304384000 ∗ ^2 + 0.0008296779093

∗ ^3 + 0.00002079741808 ∗ ^4 + 2.877838352 ∗ 10^(−7) ∗ ^5 − 3.968167659 ∗ 10^(−9) ∗ ^6

− 4.223308270 ∗ 10^(−10) ∗ ^7 2 = 10 + 0.6640000000 ∗ + 0.01680960000 ∗ ^2

+ 0.0000151441067 ∗ ^3 − 0.00001228646758 ∗ ^4 − 4.066091675 ∗ 10^(−7) ∗ ^5 − 5.050637136 ∗ 10^(−9)

∗ ^6 + 8.804344521 ∗ 10^(−11) ∗ ^7

Dengan menggunakan programMaple, grafik solusi dari sistem persamaan (4.4) telah diilustrasikan pada gambar berikut:

4.3a. Grafik populasi 4.3b. Grafik populasi

(85)

Grafik gambar 4.3 dapat digambarkan pada sebuah diagram cartesius sehingga perilaku keduanya dapat terlihat. Berikut gambar grafik populasi dengan interaksi Parasitisme ketika digambarkan dalam satu diagram cartesius.

Merupakan grafik populasi

Gambar 4.4. Grafik populasi yang berinteraksi secara Parasitisme

(86)

C. Kompetisi

Perhitungan solusi dari sistem (4.6) dengan metode dekomposisi Adomian dilakukan menggunakan programmapledan memperoleh hasil sebagai berikut:

(87)

3 = 4 + 0.3296000000 ∗ + 0.01106304000 ∗ ^2 +

0.0001173886293 ∗ ^3 − 0.000004301207450 ∗ ^4 − 1.851824568 ∗ 10^(−7) ∗ ^5 − 1.635576185 ∗ 10^(−9) ∗ ^6 + 8.190722735 ∗

10^(−11) ∗ ^7,

3 = 10 + 0.6640000000 ∗ + 0.01724160000 ∗ ^2 +

0.0000783313067 ∗ ^3 − 0.000007815319423 ∗ ^4 − 2.136855195 ∗ 10^(−7) ∗ ^5 − 7.0058057 ∗ 10^(−11) ∗ ^6 + 1.240343622 ∗

10^(−10) ∗ ^7.

Dengan menggunakan program Maple, grafik solusi dari sistem persamaan (4.6) telah diilustrasikan pada gambar berikut:

(88)

Grafik gambar 4.5 dapat digambarkan pada sebuah diagram cartesius sehingga perilaku keduanya dapat terlihat. Berikut gambar grafik sistem dinamika populasi dengan jenis interaksi Kompetisi ketika digambarkan dalam satu diagram cartesius.

Merupakan grafik populasi Merupakan grafik populasi

Gambar 4.6. Grafik populasi yang berinteraksi secara Kompetisi

(89)

gambar 4.6 populasi akan mendominasi sedangkan populasi cenderung turun dan bahkan akan habis karena berkompetisi dengan populasi .

Perbedaan dari ketiga macam sistem yaitu pada sistem persamaan (4.2), (4.4) dan (4.6) dapat dilihat pada Tabel 4.1 berikut:

Tabel 4.1. Perbandingan berhitungan dengan metode dekomposisi Adomian pada tiga

interaksi berbeda.

t Mutualisme Parasitisme kompetisi

X1 Y1 X2 Y2 X3 Y3

0 4 10 4 10 4 10

0.1 4.04279 10.07385 4.042791 10.06657 4.033071 10.06657 0.2 4.08606 10.14822 4.086048 10.13347 4.066363 10.13349 0.3 4.12979 10.22309 4.129777 10.20071 4.099879 10.20075 0.4 4.17401 10.29848 4.173981 10.26829 4.133617 10.26836 0.5 4.21871 10.37440 4.218666 10.33620 4.167580 10.33632 0.6 4.26391 10.45083 4.263838 10.40445 4.201767 10.40462 0.7 4.30960 10.52779 4.309501 10.47304 4.236180 10.47327 0.8 4.35579 10.60527 4.355661 10.54196 4.270819 10.54227 0.9 4.40249 10.68329 4.402324 10.61122 4.305684 10.61162 1 4.44970 10.76185 4.449495 10.68081 4.340776 10.68131

(90)

Tabel 4.2. Hasil numerik dari metode iterasi variasional berdasarkan contoh yang

diberikan.

Model Mutualisme Model Parasitisme Model Kompetisi

( ) ( ) ( ) ( ) ( ) ( )

0.0 4 10 4 10 4 10

(91)

75

BAB V

ASPEK KEPENDIDIKAN

A. Aspek Kependidikan di Sekolah Menengah

Sekolah Menengah di Indonesia terbagi menjadi dua yaitu Sekolah Menengah Pertama (SMP) dan Sekolah Menengah Atas (SMA). Pada materi SMP tentunya sudah diajari materi tentang menghitung kecepatan benda yang bergerak. Konsep matematika diajarkan langsung kepada kegunaan dan tuntutan materi yang harus diselesaikan sehingga mengabaikan asal usul dari materi yang dipelajari. Pada materi matematika sendiri, konsep turunan belum diajarkan pada Sekolah Menengah Pertama. Materi turunan baru diajarkan pada kelas XI Sekolah Menengah Atas. Pada buku-buku terbaru sudah mulai digambarkan tentang penerapan turunan didunia nyata, bahkan untuk memulai pembelajaran tentang materi turunan tersebut. Bahasa yang digunakan tidaklah formal dan harus sederhana agar siswa-siswa sekolah menengah atas dapat menerima dengan baik. Selain pengantar yang menggunakan cerita, soal-soal awal juga sebaiknya diawali dengan alur cerita yang logis dan mengarah pada konsep turunan.

(92)

terkadang terkesan unik jika harus dikaitkan langsung dengan aplikasi materi yang dipelajari, namun jika hal tersebut dapat menjadi gambaran bagi para siswa tentunya tidak masalah. Sebagai contoh, terdapat permasalahan yang disajikan dari buku SMA kelas XI kurikulum 2013. Sebelum memasuki konsep turunan, siswa terlebih dahulu mendalami konsep garis secan dan garis tangen dengan permasalahan berikut:

Masalah 11.1

Seorang pemain ski meluncur kencang di permukaan es yang bergelombang. Dia meluncur turun kemudian naik mengikuti lekukan permukaan es sehingga disuatu saat, dia melayang ke udara dan turun kembali ke permukaan.

Setelah disajikan cerita tersebut siswa diberi permasalahan yaitu secara analitik, misalkan bahwa bukit es disketsa pada bidang (dimensi dua) dengan sudut pandang tegak lurus ke depan sehingga terdapat garis dan papan ski adalah sebuah garis lurus. Kemudian siswa diberi pertanyaan dapatkah kamu tunjukan hubungan kedua garis tersebut? Permasalahan selanjutnya tidak pernah menyinggung lagi tentang orang yang bermain ski tersebut karena cerita tersebut hanya sebagai awalan dan memberikan gambaran bagi siswa.

(93)

Tabel 5.1. Prakiraan Tabel yang dibuat oleh siswa

Pada Tabel 5.1 tersebut siswa mencari jumlah populasi dari waktu ke waktu berdasarkan laju pertumbuhan yang ada. Siswa tentu saja dapat memahami hal tersebut dan menggambarkan grafik pertumbuhan kambing tiap waktu dengan

excel.

(94)

Siswa SMP dan SMA pun dapat melihat bahwa tabel yang dihasilkan dari pertumbuhan kambing tersebut ada akan menghasilkan suatu grafik yang teratur. Dengan menggunakan grafik tersebut siswa dapat dibawa untuk melangkah lebih jauh lagi pada materi yang akan dipelajari.

Buku matematika elektronik lain kelas XI karya Djumanta dan Sudrajat (2008) menjelaskan konsep turunan langsung dengan diagram seperti beberapa penjelasan aplikasi turunan yaitu untuk menentukan laju perubahan fungsi, menentukan gradien, menentukan titik balik dan titik belok, dan lain-lain. Pada pembahasan fungsi dari turunan sebagai laju perubahan, cerita yang disajikan masih seputar kecepatan pada bidang fisika seperti laju kendaraan bermotor. Laju perubahan tidak hanya pada jarak saja tetapi dapat juga terhadap waktu. Laju pertumbuhan populasi juga dapat dijadikan contoh untuk konsep turunan sehingga siswa tidak terfokus konsep turunan hanya untuk bidang-bidang fisika saja.

(95)

B. Aspek Kependidikan di Strata 1

Pada bangku kuliah tentunya mahasiswa sudah dapat lebih mendalami tentang konsep turunan dan aplikasinya. Mata kuliah khusus untuk mendalami pemodelan sempat dialami peneliti sewaktu kuliah S1. Mata kuliah Pemodelan Matematika pada waktu S1 membahas tentang pertumbuhan populasi dan analisis kesetimbangannya. Pada tingkat kuliah tentu materi yang dipelajari lebih mendalam dari pada saat masih di bangku Sekolah Menengah Atas di mana materi yang dipelajari sangat banyak dan dapat dibilang cukup luas.

Mata kuliah Pemodelan Matematika merupakan salah satu mata kuliah yang membahas secara khusus tentang penerapan salah satu konsep turunan. Konsep turunan sendiri dibahas pada mata kuliah Kalkulus Diferensial yang berbicara turunan secara umum dan beberapa aplikasinya. Pemodelan Matematika sendiri juga mencakup berbagai bidang seperti fisika dan biologi. Pada waktu peneliti mengambil mata kuliah pemodelan ini, hal yang dibahas adalah bidang biologi dengan materi tentang pertumbuhan populasi dengan buku Mathematical models in

biology: An introduction karya Allman dan Rhodes. Allman dan Rhodes (2004)

menuliskan tentang model pertumbuhan populasi beserta cara-cara untuk menganalisis kestabilannya. Model yang dipakai dalam buku tersebut merumakan model populasi yang bersifat diskrit. Materi pada buku sangat banyak sehingga tidak semua bagian dari buku dipelajari semua dalam satu semester.

(96)

ketika menjadi sebuah sistem persamaan diferensial salah satunya dengan cara linearisasi yang dilakukan pada penelitian ini. Pada mata kuliah lain pun dapat langsung dikaitkan dengan materi ini seperti mata kuliah kalkulus diferensial. Mata kuliah tersebut merupakan dasar teori dari mata kuliah Pemodelan Matematika sehingga penting untuk mengetahui masalah-masalah di dunia nyata yang dapat diselesaikan menggunakan persamaan diferensial atau pun ketika membentuk sistem.

Jika ditelusuri lebih jauh lagi setiap teori dari limit hingga metode penyelesaian persamaan diferensial memang saling berhubungan. Hal tersebut dapat dibuat peta konsep bagi mahasiswa untuk mempelajari setiap materi yang ada. Peta konsep yang berhubungan akan membantu mahasiswa dalam melihat hubungan dari masing-masing konsep yang dipelajari sehingga apa yang dipelajari tidak terkesan saling beridiri sendiri-sendiri. Mahasiswa juga akan lebih melihat tujuan dari teori yang dipelajari akan mengarakan mereka ke bidang apa dan salah satunya adalah bidang pemodelan matematika biologi.

C. Refleksi