M01220

(1)

14 José da Costa /Analisis Numerik untuk Gerak Osilasi Bergandeng pada Air Track dengan Metode Runge-Kutta

Prosiding Pertemuan Ilmiah XXVIII HFI Jateng & DIY, Yogyakarta, 26 April 2014 ISSN: 0853-0823

Analisis Numerik untuk Gerak Osilasi Bergandeng pada

Air Track

dengan Metode Runge-Kutta

José Da Costa1,2,*, Suryasatriya Trihandaru1,2, Made Rai Suci Santi1,2

Program Studi Pendidikan Fisika dan Fisika, Universitas Kristen Satya Wacana Email: yosephtls@yahoo.com

Abstrak _– _{Ilmu pengetahuan banyak memberikan landasan teori bagi perkembangan suatu teknologi, salah satunya}

adalah matematika. Untuk mengembangkan ilmu pengetahuan dan teknologi, sistem osilasi bergandeng pada air track, merupakan pengembangan iptek. Permasalahannya adalah bagaimana memodelkan dan mensimulasikan sistem osilasi bergandeng dua dengan metode numerik. Sistem dua derajat kebebasan atau sistem osilasi bergandeng dua (two degree of freedom systems) adalah suatu partikel yang dapat bergerak secara bebas secara dua arah dalam suatu ruang tertentu. Dalam penelitian ini, dua massa yang diikatkan pada tiga (3) buah pegas. Persamaan dari sistem dua derajat kebebasan dapat diselesaikan dengan menggunakan mekanika Lagrange, dan diselesaikan dengan menggunakan metode Runge-Kutta orde empat (RK4). Simulasi numerik dan hasil percobaan ditunjukkan saling berkorelasi dengan baik.

Kata kunci:osilasi bergandeng, Langragian, Runge-Kutta, Matlab/Simulink.

Abstract – Science gives a lot of theoretical review for the progress of technology. One of the progresses is mathematics. To develop science and the technology, coupled oscillation system on an air track is a developing science and technology. The problem is how to model and simulate couple oscillation system with numeric method. Two degree of freedom system or coupled oscillation system is a particle which can move freely into two ways in a certain space. In this research, two masses are bound to tree springs. The equation of two degree of freedom system can be solved by Lagrangian mechanics and it is solved by the fourth order Runge-Kutta Method (RK4). Numeric system and the result of experiment correlate well.

Key words: coupled oscillation, Langrangian, Runge-Kutta, Matlab/Simulink.

I. PENDAHULUAN

Getaran merupakan salah satu bentuk gerak benda yang cukup banyak dijumpai dalam kehidupan sehari-hari, misalnya bagaimana getaran yang terjadi jika sebuah beban dikaitkan atau digantungkan pada sebuah pegas. Contoh yang lain adalah bandul jam yang berayun kekanan dan kekiri, perahu kecil yang berayun naik turun dan lain-lain. Berdasarkan contoh tersebut di atas dapat diketahui bahwa getaran dapat terjadi jika suatu sistem diganggu dari posisi kesetimbangan stabilnya. Getaran ini akan terjadi secara terus menerus dan berulang-ulang selama sistem mendapatkan gaya. Gerak getaran benda yang berulang dengan waktu yang tetap biasanya disebut sebagai gerak periodik [1].

Gerak getaran benda yang terjadi secara terus menerus dan tidak terdapat faktor hambatan atau redaman biasanya disebut sebagai gerak harmonik sederhana. Karakteristik gerak harmonik sederhana adalah memiliki amplitudo dengan nilai tetap Amplitudo merupakan simpangan maksimum dari posisi kesetimbangan [2]. Untuk sistem osilasi pada air track yang selama ini kita pelajari yaitu hanya melalui teorinya saja serta penyelesaian persamaannya secara matematika, tetapi kita tidak mengetahui bagaimana bentuk gelombang yang dihasilkan dari sistem osilasi bergandeng tersebut. Oleh karena itu penulis ingin memanfaatkan simulasi numerik melalui pemrogaman matlab ini untuk

mengamati dan

menganalisis bentuk pola gelombang yang dihasilkan oleh sistem osilasi bergandeng pada air track.

A. Metode Numerik

Metode numerik disebut juga sebagai metode alternatif dari metode analitik, yang merupakan metode penyelesaian persoalan matematika dengan rumus-rumus aljabar yang sudah baku atau lazim. Disebut demikian, karena persoalan matematik sulit diselesaikan atau bahkan tidak dapat diselesaikan secara analitik sehingga dapat dikatakan bahwa persoalan matematik tersebut tidak mempunyai solusi analitik. Sehingga sebagai alternatifnya, persoalan matematik tersebut diselesaikan dengan metode numerik.

B. Gerak Getaran Pegas

Getaran dapat didefinisikan sebagai gerak bolak balik suatu benda yang terjadi secara periodik atau berkala yaitu gerak benda tersebut berulang pada selang waktu yang tetap[3]. Gerak benda yang terjadi secara periodik biasanya disebut sebagai gerak harmonik[4]. Pada Gambar 1 di tunjukkan bahwa ada dua buah massa m1 dan m2 yang dihubungkan dengan tiga buah pegas yaitu

k1, k2, dan k3 yang bergerak secara bebas pada sumbu horizontal, di mana X1danX2akan digerakan oleh massa

(2)

José da Costa /Analisis Numerik untuk Gerak Osilasi Bergandeng pada Air Track dengan Metode Runge-Kutta 15

[image:2.595.68.287.60.127.2]

Gambar 1. Sistem pegas dengan 2 derajat kebebasan [6].

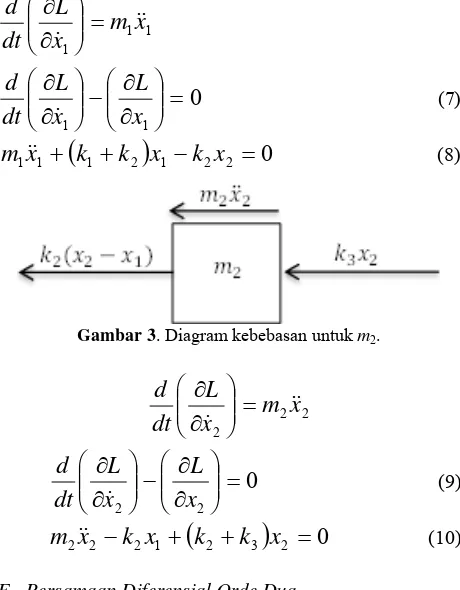
Pada Gambar 1, jika diagram free-body, x2

diasumsikan lebih besar dari x1 sehingga pegas k2

mengalami tarikan, seperti pada Gambar 3, dan gaya tariknya sebesar . Dengan perkataan lain, jika x1 diberi nilai lebih besar dari x2, pegas k2 akan

[image:2.595.322.552.107.402.2]

mengalami gaya tekanan, dengan gaya tekan pegas ditulis sebagai seperti pada Gambar 2.

Gambar 2. Diagram kebebasan untuk m1.

Jika salah satu massa dipindahkan kekanan ataupun kekiri yang berarti merentangkan pegas, jika massa tersebut di lepaskan maka pegas akan memberikan gaya pada kedua massa untuk berosilasi dan lama kelamaan kedua massa itu akan kembali pada posisi setimbangnya. Gaya ini disebut gaya pemulih [7].

Untuk mendeskripsikan gerak osilator dari kedua massa dalam sistem ini digunakan metoda Lagrangian yang merupakan selisih dari energi kinetik dan energi potensialnya [8].

Energi kinetik T dan Energi potensial V[9]adalah (1)

(2)

C. Langrange

Persamaan Lagrange adalah sebagai selisih antara energi kinetik T dan energi potensial V [10], dengan persamaannya adalah sebagai berikut :

(3) Jadi,

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ ₋ ₊ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ = 2 2 3 2 2 1 2 2 1 1 2 2 2 2 1 1 2 1 2 1 2 1 2 1 2 1 x k x x k x k x m x m

L & &

(4) Persamaan Lagrangian jika diturungkan terhadap x1 dan x2 adalah sebagai berikut:

2 1 1 1

k

x

k

x

L

+

−

=

∂

(5)

(

2 3

)

2

1 2 2

x

k

x

k

x

L

+

−

=

∂

(6) D. Euler-Lagrange

Persamaan Euler-Lagrange untuk sistem osilasi diturunkan terhadap massa m1dan massa m2 [11] yaitu sebagai berikut: 1 1 1

x

m

x

L

dt

d

&

⎟⎟

⎠

=

⎞

⎜⎜

⎝

⎛

∂

0

1 1

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

x

L

x

L

dt

d

&

(7)

(

₁ ₂

)

₁ ₂ ₂

0

1

x

+

k

+

k

x

−

k

x

=

m

&

(8)

Gambar 3. Diagram kebebasan untuk m2.

2 2 2

x

m

x

L

dt

d

&

⎟⎟

⎠

=

⎞

⎜⎜

⎝

⎛

∂

0

2 2

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

x

L

x

L

dt

d

&

(9)

(

₂ ₃

)

₂

0

1 2 2

2

x

−

k

x

+

k

+

k

x

=

m

&

(10)

E. Persamaan Diferensial Orde Dua

Pada Persamaan (7) dan (9) masih berupa persamaan diferensial biasa orde 2, sedangkan metoda numerik yang dipakai (yaitu Runge-Kutta) memerlukan persamaan diferensial orde 1, maka untuk mendapatkan sistem persamsaan diferensial orde pertama, maka persamaannya didefinisikan

1

v

dt

dx

=

(11)

2

v

dt

dx

=

(12)

1 1

x

dt

dv

&

=

(13)

2 2

x

dt

dv

&

=

(14)

Dalam persamaan (11) sampai persamaan (14) digunakan sistem persamaan diferensial biasa dan diringkas dengan menggunakan notasi vektor

[

x

1

v

1

x

2

v

2

]

u

r

=

. (15)

Maka diperoleh persamaan yaitu sebagai berikut:

( )

t

u

f

dt

u

d

r

,

[image:2.595.66.293.155.313.2]

(3)

16 José da Costa /Analisis Numerik untuk Gerak Osilasi Bergandeng pada Air Track dengan Metode Runge-Kutta

[

v

1

x

1

v

2

x

2

]

f

&

r

=

(17)

F. Metode Runge-Kutta Orde Empat (RK4)

Metode Runge-Kutta orde 4 adalah suatu metode yang digunakan untuk menyelesaikan persamaan diferensial secara numerik atau pendekatan sehingga mendapatkan penyelesaian yang lebih signifikan atau handal dari pada penyelesaian secara eksat atau analitik [12]. Dengan menggunakan metode Runge-Kutta orde 4 maka persamaannya yaitu sebagai berikut [13].

( )

t

u

f

S

r

₁

=

,

r

( )

⎟

⎠

⎞

⎜

⎝

⎛

+

=

₁

2

,

2

S

h

t

u

h

t

f

S

r

( )

⎟

⎠

⎞

⎜

⎝

⎛

+

=

₂

3

2

,

2

S

h

t

u

h

t

f

S

r

( )

⎟

⎠

⎞

⎜

⎝

⎛

+

=

₃

4

,

2

u

t

h

S

h

t

f

S

r

(

) ( )

(

)

6

2

₂ ₃ ₄

1

S

h

t

u

h

t

u

r

+

=

+

(18)

Parameter-parameter ini dapat dicari dengan optimasi Nelder-Mead [14]. Nelder-Mead adalah metode simplex untuk menemukan fungsi minimum dari fungsi ralat yang didefinisikan sebagai:

(

)

N

xd

xt

E

i i i

2

−

∑

=

(19)

III. METODE PENELITIAN/EKSPERIMEN

[image:3.595.44.272.186.343.2]

Dalam penelitian ini, bahan yang digunakan adalah seperti pada susunan gambar di bawah ini :

Gambar 4. Perncangan alat percobaan.

Dengan menghidupkan tabung udara, udara mengalir ke rel udara kemudian memberi sedikit gaya pada salah massa dari kedua massa tersebut, dengan cara menarik massa ke kiri atau pun ke kanan dan kemudian dilepaskan. Tujuan memberikan gaya kepada ke dua massa agar kedua massa berosilasi dengan maksimal. Kemudian merekam kedua massa yang saling berosilasi pada air track dengan menggunakan Camera Digital. Waktu yang dibutuhkan dalam rekaman hanya 9-10 detik saja. Setelah selesai merekam maka hasil rekaman atau video tersebut di import ke dalam Macromedia Flash MX 20004 untuk mengedit video dari hasil rekaman tersebut. Program Matlab R2009a, untuk mencari koordinat dari hasil data yang diekstrak, sesuai dengan program function cari koordinat 2.

IV. HASIL DAN PEMBAHASAN

Pada penelitian ini akan dipaparkan penyelesaian secara numerik model getaran pegas (sistem oasilasi bergandeng dua). Pada awalnya, model getaran tersebut yang termasuk persamaan deferensial linear orde dua dan diubah menjadi sistem persamaan diferensial linear orde satu. Kemudian sistem persamaan diferensial linear orde satu tersebut diselesaikan dengan menggunakan metode Runge-Kutta orde empat (RK4). Pada bagian ini diambil beberapa asumsi untuk sebagai parameter yaitu k1, k2, dan k3 (konstanta pegas), m1 dan m2 (massa beban), maka hasil pendekatan numerik terhadap sistem osilasi bergandeng secara lengkap maka grafik hasil komputasi numerik adalah Hasil dari input (grafik biru), data kemudian didekati dengan solusi analitik yang ditulis dalam bentuk Runge-Kutta (grafik merah), yang sesuai dengan Gambar 5

Gambar 5. _{Hasil grafik pada sistem osilasi bergandeng pada air}

track.

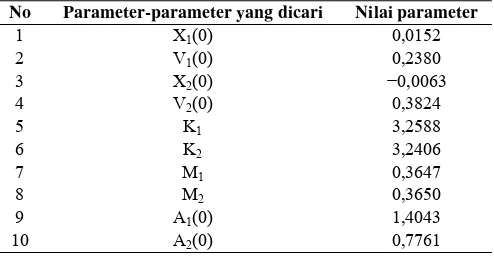
Tabel 1. Pencocokan nilai dari grafik pada Gambar 5.

No Parameter-parameter yang dicari Nilai parameter

1 X1(0) 0,0152

2 V1(0) 0,2380

3 X2(0) −0,0063

4 V2(0) 0,3824

5 K1 3,2588

6 K2 3,2406

7 M1 0,3647

8 M2 0,3650

9 A1(0) 1,4043

10 A2(0) 0,7761

V. KESIMPULAN

Dari hasil simulasi osilator atau osilasi bergandeng pada air track, diperoleh kesimpulan yaitu : dengan memasukkan nilai berupa konstanta pegas dan massa maka bentuk pola gelombang yang dihasilkan oleh sistem osilasi bergandeng pada air track berupa grafik waktu terhadap posisi m1 dan posisi m2 seperti pada Gambar 5.

[image:3.595.312.520.287.417.2] [image:3.595.297.544.466.595.2]

(4)

José da Costa /Analisis Numerik untuk Gerak Osilasi Bergandeng pada Air Track dengan Metode Runge-Kutta 17

bergandeng pada air track dapat disimulasikan dengan cepat dan akurat. Dan dengan metode pemodelan ini, kita dapat mengetahui bahwa ternyata semua benda yang berosilasi juga mempunyai bentuk pola gelombang yang dihasilkan.

UCAPAN TERIMA KASIH

Dengan terlaksananya penelitian ini, penulis tak lupa mengucapkan limpah terima kasih kepada Kedutaan Besar Negara Rupublik Demokratik Timor-Leste di Jakarta yang telah memberikan bantuan kepada peneliti.

PUSTAKA

[1] P. A. Tipler, Fisika untuk Sains dan Teknik Jilid 1,

Penerbit Erlangga, Jakarta, 1998.

[2] D. C. Giancoli, Ilmu-ilmu Murni Cetakan ke 4, Edisi 1,

Penerbit Erlangga, Jakarta, 1997.

[3] P. Soedojo, ”Fisika Dasar”, Penerbit Yogyakarta,

Indonesia, 1999.

[4] D. Halliday, ”Fisika”, Penerbit Erlangga, Jakarta, 1985.

[5] R. N. Jazar, Advanced Vibration A Modern Approach,

Springer, 2013.

[6] W. W. Pratt. “Introduction to Classical Mechanics”.

[7] Giancoli, Douglas C., Fisika (terjemahan), Penerbit

Erlangga, Jakarta, 1998.

[8] Gregory, Douglas R, Classical Mechanics, Cambridge

University Press, 2006.

[9] M. Webster, Essentials of higher physics, London, 1987.

[10] Y. Yamamoto, Nxtway-gs model-Based design-control of

self-balancing two-wheeled robot built with Lego mind

storms next, University of Rhode Island, Amerika

Serikat, 2009.

[11] C. Fox, An introduction to the calculus of variations.

Courier Dover Publications, 1987.

[12] J. H. Mathews andK. D. Fink, Numerical Methods Using

Matlab Third Edition, 1999.

[13] A. Klein and A. Godunov, Introductory Computational

Physics.

[14] L. Honeycutt, Communication and Design Course, 1998.

Website: http://dcr.rpi.edu/commdesign/class1.html, diakses tanggal 3 Maret 2011.

TANYA JAWAB

Budi S., UNAS

? Persamaan diferensial apa yang anda gunakan dalam menganalisis paper (sistem osilasi bergandeng dua pada air track) ?

JoseDa Costa (UKSW)

@ Persamaan yang digunakan yaitu dengan metode diferensial orde ke satu karena metode yang dibutuhkan adalah orde satu. Jadi persamaan diferensial orde dua harus diubah ke dalam persamaan diferensial orde satu

Fahrudin N., UGM

? Bagaiman dengan menggunakan metode lain selain menggunakan untuk menganalisis osilasi bergandeng dua pada air track?

JoseDa Costa (UKSW)

@ Sementara metode yang saya gunakan dalam menganalisis system osilasi bergandeng dua dengan metode orde 4. Mungkin selain dari itu juga bisa menggunakan metode yang lain Reynolds yang biasa ditemui dalam kasus fluida cairan dalam skala besar misalnya selat atau laut. Hasil-hasil penelitian bisa menunjukkan kesesuaian yang baik dengan temuan langsung dan simulasi numerik

Anonim

? Bagaimana hasil akuisisi data dari kamera diproses sampai pada proses komputasi dengan metode RK-4 di Matlab?

JoseDa Costa (UKSW)