bb8b7 bab ii relasi

(1)

Matematika Diskrit Liduina Asih Primandari

9

BAB II

RELASI

1. Produk Cartesian Definisi 1

Perkalian kartesian dari himpunan A dan B adalah himpunan yang elemennya semua pasangan berurutan (ordered pairs) yang dibentuk dari komponen pertama dari himpunan A dan komponen kedua dari himpunan B.

Notasi: | Contoh:

Jika C = {1,2,3} dan D = {a,b}, maka C x D = {(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)} D x C = {(a,1),(a,2),(a,3),(b,1),(b,2),(b,3)}

Catatan:

a) Jika A dan B merupakan himpunan berhingga, maka | | | | | | b)Pasangan berurutan a b berbeda dengan b a denga kata lain a b ≠ b a

c) Perkalian kartesian tidak komutatif yaitu A x B ≠ B x A dengan syarat A dan B bukan himpunan kosong

d)Jika dan , maka 2. Relasi

Definisi 2

Relasi antara A dan B disebut relasi biner. Relasi biner R antara A dan B adalah himpunan bagian dari A x B

Notasi:

Jika (a,b) R, maka a R b artinya a dihubungkan dengan b oleh R dan jika (a,b) R maka a R b yang artinya a tidak dihubungkan dengan b oleh R. Himpunan A disebut daerah asal (domain) dari R dan himpunan B disebut daerah hasil (range / codomain) dari R.

Contoh:

Jika P = {2,3,4} dan Q = {2,4,8,9,15} dan difenisikan relasi R dari P ke Q dengan jika p habis membagi q, maka diperoleh:

R = {(2,2), (2,4), (2,8), (3,9), (3,15), (4,4), (4,8)}

(2)

10

Definisi 3

Relasi pada himpunan A adalah A x A

Dengan kata lain, relasi pada himpunan A adalah himpunan bagian dari A x A.

Contoh:

Jika R adalah relasi pada A = {2,3,4,8,9} yang didefinisikan oleh jika x adalah faktor prima dari y. Maka diperoleh

R = {(2,2), (2,4), (2,8), (3,3), (3,9)}

3. Bentuk Penyajian Relasi

Sebuah relasi dapat disajikan dalam beberapa bentuk, antara lain: a. Pendaftaran

Contoh:

R = {(2,2), (2,4), (2,8), (3,3), (3,9)}

R = {(2,2), (2,4), (2,8), (3,9), (3,15), (4,4), (4,8)} b. Pencirian

Contoh:

R = {(x,y) | x adalah faktor prima dari y dan x,y A} c. Diagram

d. Matriks

Misalkan R adalah relasi dari A = {a1,a2,a3 … am} dan B = {b1,b2,b3 … bn}, relasi R dapat disajikan dalam Matriks M = [Mij].

…

[

…

]

Di mana:

{ ( ₍ ) ₎ Contoh:

Jika R adalah relasi pada A = {2,3,4,8,9} yang didefinisikan oleh jika x adalah faktor prima dari y. Maka diperoleh

R = {(2,2), (2,4), (2,8), (3,3), (3,9)} 2

3 4

(3)

11

Apabila disajikan dalam bentuk matriks:

[

]

4. Invers dari Relasi Definisi 4

Misalkan R adalah relasi dari himpunan A ke himpunan B. Inversi dari relasi R dilambangkan dengan R-1_{adalah relasi dari himpunan B ke himpunan A yang didefinisikan oleh:}

_|

Jika R adalah relasi pada himpunan orang – orang di mana (a,b) R. Jika a adalah ayah dari b, maka dapat dibuat kebalikannya yaitu (b,a) yang menyatakan bahwa b adalah anak dari a.

Contoh:

Misalkan P = {2,3,4} dan Q = {2,4,8,9,15}. Jika didefinisikan relasi R dari P ke Q dengan (p,q) R jika p habis membagi q

Maka diperoleh

R = {(2,2),(2,4),(2,8),(3,9),(3,15),(4,4),(4,8)} R-1 _{adalah invers dari relasi R, yaitu relasi dari Q ke P, maka}

R-1 _{={(2,2),(4,2),(8,2),(9,3),(15,3),(4,4),(8,4)}} Dengan hubungan

(q,p) R-1 _{jika q adalah kelipatan dari p}

5. Kombinasi Relasi

Relasi biner adalah himpunan pasangan terurut, maka operasi himpunan seperti irisan, gabungan, selisih dan beda setangkup antara dua relasi atau lebih juga berlaku.

Contoh:

Misalkan A = {a,b,c} dan B = {a,b,c,d}. Relasi R1 = {(a,a),(b,b),(c,c)} dan relasi R2 = {(a,a),(a,b),(a.c),(a,d)} adalah relasi dari A ke B. Maka kombinasi kedua buah relasi tersebut:

(4)

12

6. Komposisi Relasi

Definisi 5

Misalkan R adalah relasi dari himpunan A ke himpunan B dan S adalah relasi dari himpunan B ke C. Komposisi R dan S, dinotasikan dengan adalah relasi dari A ke C yang didefinisikan oleh:

|

Contoh:

Misalkan R = {(1,2),(1,6),(2,4),(3,4),(3,6),(3,8)} adalah relasi dari himpunan {1,2,3} ke himpunan {2,4,6,8} dan S = {(2,u),(4,s),(4,t),(6,t),(8,u)} adalah relasi dari himpunan {2,4,6,8} ke {s,t,u}. Maka komposisi relasi R dan S adalah

Simbol Rn digunakan untuk mendefinisikan komposisi relasi dengan dirinya sendiri sebanyak n kali

… (sebanyak n kali) 7. Relasi n – ary

Definisi 6

Misalkan … adalah himpunan. Relasi n – ary pada himpunan tersebut adalah himpunan bagian dari … atau dinotasikan dengan notasi … .

… adalah daerah asal (domain) relasi dan n disebut derajat. Contoh:

NIM = {1551001, 1551002, 1551003,1551004,1551005} Nama = {Adi, Budi, Candra, Doni, Ega}

Mata Kuliah = {Matematika, Bahasa Indonesia, Agama, Fisika} Nilai = {A,B,C,D}

Relasi MHS dinotasikan dengan Relasi MHS yang disajikan dalam bentuk pendaftaran:

MHS = {(1551001,Adi,Matematika,A),(1551001,Adi,Bahasa Indonesia,B),

(1551002,Budi,Matematika,C),(1551002,Budi,Agama,B),(1551003,Candra,Bahasa

Indonesia,C),(1551003,Candra,Agama,D),(1551003,Candra,Fisika,A),(1551004,Doni,Matema tika,B),(1551004,Doni,Agama,B),(1551005,Ega,Agama,C)}

1 2 3

2 4 6 8

(5)

13

Relasi MHS dapat disajikan dalam bentuk tabel:

NIM Nama Mata Kuliah Nilai

Ada beberapa operasi yang dapat digunakan: Seleksi

Operasi seleksi memilih baris tertentu dari suatu tabel yang memenuhi persyaratan tertentu. Operator:

Contoh:

Untuk relasi MHS, ingin ditampilkan daftar mahasiswa yang mengambil mata kuliah Agama. Operasi seleksinya adalah:

Yang menghasilkan (1551002,Budi,Agama,B), (1551003,Candra,Agama,D), (1551004,Doni,Agama,B) dan (1551005,Ega,Agama,C)

Proyeksi

Operasi proyeksi memilih kolom tertentu dari suatu tabel. Jika ada beberapa baris yang sama nilainya, diambil salah satu.

Operator:

Contoh:

Untuk relasi MHS, ingin ditampilkan kolom Nama, Mata Kuliah dan Nilai. Operasi proyeksinya adalah:

(6)

14

Untuk relasi MHS, ingin ditampilkan kolom NIM dan Nama

Operasi proyeksinya adalah:

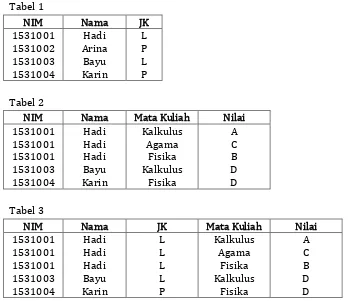
Maka, operasi Join:

Akan menghasilkan Tabel 3.