PENYELESAIAN TEORI PERMAINAN MENGGUNAKAN METODE SIMPLEKS ALTERNATIF

(1)

Rini Hidayattillah, Penyelesaian Teori Permainan Menggunakan Metode Simpleks Alternatif

PENYELESAIAN TEORI PERMAINAN MENGGUNAKAN METODE SIMPLEKS ALTERNATIF

Rini Hidayattillah, Pardi Affandi, Akhmad Yusuf

Program Studi Matematika Fakultas MIPA Universitas Lambung Mangkurat Jln. A. Yani KM. 36, Banjarbaru 70714, Kalimantan Selatan

Email: rini.h0706@gmail.com

ABSTRAK

Teori permainan diawali oleh penemuan teorema pertama pada permainan catur oleh E. Zermelo pada tahun 1913. Kemudian teori permainan dikenal kembali setelah munculnya karya dari John Von Neumann dan V. Morgenstern pada tahun 1944. Salah satu cara penyelesaian teori permainan adalah program linier. Metode simpleks alternatif merupakan salah satu teknik penyelesaian dalam program linier yang digunakan untuk mencari solusi optimal, proses perhitungan metode ini dengan melakukan iterasi hingga tercapai hasil optimal. Metode simpleks alternatif merupakan sebuah algoritma yang sama dengan metode simpleks, satu-satunya perbedaan adalah dalam menentukan elemen kunci/angka kunci yang menjadi dasar untuk melakukan proses iterasi. Tujuan dari penelitian ini untuk menjelaskan proses pembentukan dari masalah teori permainan ke dalam bentuk program linier dan menyelesaikan teori permainan menggunakan metode simpleks alternatif. Dengan menggunakan metode simpleks alternatif persoalan program linier pada teori permainan dapat digunakan untuk memperoleh solusi optimal. Metode simpleks alternatif dapat menyelesaikan permainan dengan mendapatkan strategi optimal dan nilai permainan optimal bagi setiap pemain.

Kata Kunci: Teori Permainan, Program linier, dan Metode Simpleks Alternatif. ABSTRACT

Game theory is begun from the first theorem at chess game at 1913 by E. Zermelo. After that, game theory made its comeback at 1944 with the masterpiece of John Von Neumann and V. Morgenstern. Game theory have many way to solve problem which is in Linear Program. Simplex alternative method is of accomplishment techniques in linear program to find on optimal solution, the process of calculating this method by conducting repeated iteration to achieve an optimal result. This method has the same algorithm with simplex method. The only difference is in determining key element or numeral key as a basic to do iterations process. The purpose of this study was to explain the process of game theory problem formation into linear program and to accomplish game theory by using alternative simplex method. With the alternative simplex method problems of linear programing on game theory can be used to obtain the optimal solution. This method can solve the game by getting the optimal strategy and optimal value of the game for each player.

Keywords : Game theory, linear program, and alternative simplex method. 1. PENDAHULUAN

Teori permainan adalah model matematika yang digunakan dalam keadaan konflik atau persaingan dari berbagai kepentingan yang saling berhadapan sebagai

(2)

pesaing [1]. Model matematika yang sudah dibentuk selanjutnya akan dianalisa dan dicari penyelesaian optimalnya [2]. Metode untuk menyelesaikan teori permainanstrategi campuran adalah salah satunya dengan menggunakan program linier. Metode simpleks adalah teknik penyelesaian dalam program linier yang digunkan untuk mencari nilai optimal yang melibatkan banyak pembatas (constraint) dan banyak variabel, proses perhitungan metode ini dengan melakukan iterasi hingga diperoleh hasil yang optimal [3]. Berdasarkan pemaparan di atas, maka penulis mempelajari bentuk persoalan program linierpada teori permainan menggunakan metode simpleks alternatif.

2. TINJAUAN PUSTAKA 2.1 Teori Permainan

Penyelesaian dari pertentangan antara dua belah pihak yang bersaing adalah inti dari teori permainan. Dengan kata lain berarti juga pengambilan keputusan dalam suatu pertentangan umumnya disebut sebagai teori permainan. Jadi teori permainan melibatkan dua pihak yang bertentangan, pihak I memilih strategi setelah melihat strategi yang dipilih oleh pihak II. Demikian juga dengan pihak II memilih strategi setelah memperkirakan strategi yang dipilih oleh pihak I [4].

2.1.1 Permainan Dua Orang dan Permainan Jumlah Nol (Two-Person Zero-sum Game)

Bentuk strategi atau bentuk normal dari permainan two-peson zero-sum[5] adalah 𝐻(𝑋, 𝑌) dimana:

1. 𝑋 adalah himpunan tak kosong, himpunan strategi pemain I 2. 𝑌 adalah himpunan tak kosong, himpunan strategi pemain II

3. 𝐺 adalah fungsi harga nyata yang didefinisikan pada 𝑋 × 𝑌 sedemikian sehingga 𝐺(𝑝, 𝑞) adalah angka nyata untuk setiap 𝑝 𝜖 𝑋 dan 𝑞 𝜖 𝑌.

Dengan interprestasi pemain I memiliki 𝑝 𝜖 𝑋dan pemain II memiliki 𝑞 𝜖 𝑌, masing-masing menyadari pilihan strategi pemain lain. Jika H adalah positif maka pemain I menang sebanyak 𝐺(𝑝, 𝑞) dan jika 𝐺 negatif, maka pemain I membayar nilai mutlak dari jumlahnya ke pemain II.

2.1.2 Memilih Strategi

Ada dua jenis persoalan pada teori permainan[6]jenis pertama yaitu permainan strategi murni (pure strategy game) dimana para pemain menggunakan hanya satu yaitu strategi tunggal, dan jenis kedua yaitu permainan strategi campuran (mixed strategy game). Dalam permainan strategi murni, pemain baris mengidentifikasi strategi optimalnya degan melihat kriteria maksimin (maksimum di antara minimum baris), sedang pemain kolom menggunakan kriteria minimaks (minimum di antara maksimum kolom).

2.1.3 Permainan dengan Strategi Campuran

Definisi permainan dengan strategi campuran [5]Vektor 𝑋 = [𝑥𝑝]

ukuran𝑚 × 1 dengan 𝑝 = 1,2, … , 𝑚 dari bilangan tak negatif 𝑥_𝑝 sedemikian sehingga ∑𝑚_𝑝=1𝑥_𝑝 = 1 didefinisikan sebagai strategi campuran pemain I (𝑃₁). Dan Vektor 𝑌 = [𝑦𝑞] ukuran 1 × 𝑛dengan 𝑞 = 1,2, … , 𝑛 dari bilangan tak negatif

(3)

𝑦𝑞sedemikian sehingga ∑𝑛𝑞=1𝑦𝑞 = 1 didefinisikan sebagai strategi campuran pemain

II (𝑃₂).

Tabel 1. Tabel matriks permainan dengan strategi campuran 𝑃2 𝑃₁ (𝑦1) (𝑦2) … (𝑦𝑛) (𝑥1) 𝐺( 1,1) 𝐺(1,2) … 𝐺(1, 𝑛) (𝑥2) 𝐺(2,1) 𝐺(2,2) … 𝐺(2, 𝑛) ⋮ ⋮ ⋮ ⋱ ⋮ (𝑥_𝑚) 𝐺(𝑚, 1) 𝐺(𝑚, 2) … 𝐺(𝑚, 𝑛) Keterangan:

𝑥_𝑝 : Probabilitas pemain 𝑃₁ menggunakan strategi ke 𝑝. 𝑦_𝑞 : Probabilitas pemain 𝑃₂ menggunakan strategi ke 𝑞.

𝐺(𝑝, 𝑞): Nilai pembayaran yang bersesuaian dengan strategi ke 𝑝 untuk 𝑃1 dan

strategi ke 𝑞 untuk 𝑃2.

Secara matematis, kriteria untuk kasus strategi campuran berdasarkan [7]adalahseperti berikut ini.

a. Bagi pemain I (𝑃₁)

𝑃1memilih 𝑥𝑝, (𝑥𝑝 ≥ 0, ∑𝑚𝑝=1𝑥𝑝 = 1) yang akan menghasilkan

𝑉 = 𝑚𝑎𝑥_𝑥_𝑝{𝑚𝑖𝑛(∑𝑚_𝑝=1𝐺(𝑝, 1)𝑥_𝑝, ∑𝑚_𝑝=1𝐺(𝑝, 2)𝑥_𝑝, … , ∑𝑚_𝑝=1𝐺(𝑝, 𝑛)𝑥_𝑝)...(2.1) b. Bagi pemain II (𝑃2)

𝑃₂memilih 𝑦_𝑞, (𝑦_𝑞 ≥ 0, ∑𝑛_𝑞=1𝑦_𝑞 = 1) yang akan menghasilkan 𝑉 = 𝑚𝑖𝑛_𝑦_𝑞{𝑚𝑎𝑥(_∑ _{𝐺(1, 𝑞)𝑦}

𝑞 𝑛

𝑞=1 , ∑𝑛𝑞=1𝐺(2, 𝑞)𝑦𝑞, … , ∑𝑛𝑞=1𝐺(𝑚, 𝑞)𝑦𝑞)...(2.2)

Minmaks ekspektasi payoff ≥ maksmin harapan payoff atau 𝑉≥ 𝑉Jika xp dan yp

berkorespondensi pada solusi optimalnya, maka 𝑉= 𝑉 di mana nilai yang diperoleh akan sama dengan nilai harapan optimal dari permainan.

2.1.4 Bentuk Program Linier pada Teori Permainan

Setiap permainan dengan strategi campuran dapat diselesaikan dengan mengubah masalah menjadi masalah program linier. Transformasi ini menggunakan kriteria nilai maksimin 𝑉 dan nilai minimaks 𝑉pada [8] didefinisikan sebagai berikut:

a. Bagi pemain I (𝑃₁) Minimumkan 𝑋 = 𝑋1+ 𝑋2 + ⋯ + 𝑋𝑚atau 1 𝑉 ...(2.3) Dengan batasan: 𝐺(1,1)𝑋1+ 𝐺(2,1)𝑋2 + ⋯ + 𝐺(𝑚, 1)𝑋𝑚 ≥ 1 𝐺(1,2)𝑋1+ 𝐺(2,2)𝑋2 + ⋯ + 𝐺(𝑚, 2)𝑋𝑚 ≥ 1 ⋮ 𝐺(1, 𝑛)𝑋₁+ 𝐺(2, 𝑛)𝑋₂+ ⋯ + 𝐺(𝑚, 𝑛)𝑋_𝑚 ≥ 1 …(2.4) 𝑋1+ 𝑋2+ ⋯ + 𝑋𝑚 ≥ 0 b. Bagi pemain II (𝑃₂)

(4)

Rini Hidayattillah, Penyelesaian Teori Permainan Menggunakan Metode Simpleks Alternatif Maksimumkan 𝑌 = 𝑌₁+ 𝑌₂ + ⋯ + 𝑌_𝑛atau 1 𝑉 …(2.5) Dengan batasan: 𝐺(1,1)𝑌1+ 𝐺(1,2)𝑌2+ ⋯ + 𝐺(1, 𝑛)𝑌𝑛 ≤ 1 𝐺(2,1)𝑌₁+ 𝐺(2,2)𝑌₂+ ⋯ + 𝐺(2, 𝑛)𝑌_𝑛 ≤ 1 ⋮ 𝐺(𝑚, 1)𝑌₁+ 𝐺(𝑚, 2)𝑌₂+ ⋯ + 𝐺(𝑚, 𝑛)𝑌_𝑛 ≤ 1 …(2.6) 𝑌1+ 𝑌2+ ⋯ + 𝑌𝑛 ≥ 0

Jadi solusi optimal dari satu masalah secara otomatis menghasilkan solusi optimal untuk masalah lainnya. Masalah pemain II (P2) dapat diselesaikan dengan

metode simpleks alternatif dan masalah pemain I (P1) dapat diselesaikan dengan

metode simpleks dual alternatif.

2.2 Program Linier

Dapat dirumuskan model matematis bentuk umum model program linier [9] adalah sebagai berikut:

Fungsi Tujuan:

Memaksimumkan atau meminimumkan

𝑍 = 𝑐1𝑥1+ 𝑐2𝑥2 + ⋯ + 𝑐𝑛𝑥𝑛 ...(2.7) Fungsi kendala 𝑎₁₁𝑥₁+ 𝑎₁₂𝑥₂+ ⋯ + 𝑎_1𝑛𝑥_𝑛(=, ≤, ≥)𝑏₁ 𝑎₂₁𝑥₁+ 𝑎₂₂𝑥₂+ ⋯ + 𝑎_2𝑛𝑥_𝑛(=, ≤, ≥)𝑏₂ ⋮ 𝑎_𝑚1𝑥₁ + 𝑎_𝑚2𝑥₂ + ⋯ + 𝑎_𝑚𝑛𝑥_𝑛(=, ≤, ≥)𝑏_𝑚 ...(2.8) 𝑥1, 𝑥2, … , 𝑥𝑛 ≥ 0 Keterangan : 𝑍 : Fungsi tujuan

𝑐_𝑗 : Koefisien tujuan, dengan j = 1,2, . . .,n 𝑥_𝑗 : Variabel bebas, dengan j = 1,2, . . .,n

𝑎𝑖𝑗 : Koefisien fungsi kendala, dengan j = 1,2, . . .,n dan i = 1,2,. . .,m

𝑏𝑖 : Batasan fungsi kendala, dengan i = 1,2, . . .,m

2.2.1 Bentuk Standar Model Program Linier

Sebelum mengaplikasikan metode simpleks dalam menyelesaikan masalah persoalan program linier perlu dipelajari cara mengubah bentuk program linier menjadi bentuk standarnya [1] yaitu pada langkah pertama beberapa aturan bentuk program linier standar:

1. Semua kendala berupa bentukpersamaan dengan konstanta non-negatif. 2. Semua variabel non-negatif.

3. Fungsi tujuan dapat memaksimumkan dan meminimumkan.

Persamaan (2.7) dan (2.8) adalah model standar program linier dengan mengkonversikan pertidaksamaan pada fungsi-fungsi kendala menjadi persamaan:

a. Untuk batasan bernotasi (≤) dapat dimodifikasi ke dalam bentuk persamaan dengan menambahkan variabel slack pada ruas kiri kendala.

b. Untuk batasan bernotasi (≥) dapat dimodifikasi ke dalam bentuk persamaan dengan mengurangkan ruas kiri kendala tersebut dengan variabel surplus. Langkah-langkah perhitungan dalam algoritma metode simpleks [9] adalah:

(5)

1. Langkah Awal: Masukkan variabel slack dalam bentuk standar sebagaimana diasumsikan sebelumnya. Dengan variabel-variabel asli menjadi variabel tidak dasar (artinya sama dengan nol) dan variabel-variabel slack menjadi variabel dasar (artinya sama dengan nilai ruas kanan NK).

2. Langkah Iterasi:

a. Bagian 1: Menentukan variabel dasar masuk (entering variable), dengan memilih dengan koefisien negatif terbesar untuk kasus maksimum dan koefisien positifterbesar untuk kasus minimum pada variabel tidak dasar. b. Bagian 2: Menentukan variabel dasar keluar (leaving variable), dengan

memilih nilai rasio positif terkecil pada variabel dasar. Rasio diperoleh dari pembagian antara niai kanan dengan kolom kunci.

c. Bagian 3: Melakukan operasi baris elementer (OBE) untuk membuat untuk membuat elemen kunci (angka kunci) menjadi berharga 1 dan berharga 0 pada baris-baris lainnya pada kolom kunci.

3. Uji Optimalitas: Menentukan apaka penyelesaian optimal. Memeriksa koefisien pada tabel fungsi tujuan 𝑍 jika tidak ada yang bernilai negatif untuk kasus maksimasi dan tidak ada yang bernilai positif untuk kasus minimasi berarti optimasi telah tercapai. Namun apabila masih bernilai negatif untuk kasus maksimasi dan bernilai positif untuk kasus minimasi maka kembali pada langkah iterasi.

2.2.2 Kasus Khusus dalam Penggunaan Algoritma Simpleks

Di dalam menyelesaikan persoalan program linier dengan menggunakan algoritma metode simpleks terdapat persoalan yang mempunyai kasus khusus [9] seperti:

1. Keadaan Seri bagi Variabel dasar masuk (entering variable)

Untuk melakukan proses iterasi pada metode simpleks, sebelumnya akan memilih variabel masuk dengan menentukan koefisien negatif dengan nilai yang paling besar dalam persamaan awal fungsi tujuan sama dengan (0). Jika variabel memiliki koefisien negatif terbesar adalah seri atau sama maka jawabnya adalah pemilihan akan dilakukan secara sembarang.

2. Keadaan Seri bagi Variabel dasar keluar (leaving variable) - Degenerasi

Kasus ini terjadi jika terdapat rasio minimum memiliki kesempatan yang sama untuk meninggalkan basis. Oleh karena itu terdapat kemungkinan pertama variabel dasar secara simultan menjadi nol dan kedua iterasi simpleks selanjutnya akan berputar-putar.

3. METODE PENELITIAN

Pada penelitian ini digunakan referensi pendukung dari buku dan jurnal yang berkaitan dengan teori permainan, program linier, dan metode simpleks. Langkah yang dilakukan pada penelitian ini yaitu menjelaskan pembentukan model matematika untuk permasalahan teori permainan ke dalam program linier. Serta menentukan solusi optimal dari permasalahan program linier teori permainan menggunakan metode simpleks alternatif.

4. HASIL DAN PEMBAHASAN 4.1 Deskripsi Permasalahan

(6)

Teori permainan pada umumnya digunakan untuk menganalisa proses pengambilan keputusan dari situasi persaingan yang berbeda dan melibatkan dua atau lebih kepentingan. Dalam permasalahan ini, strategi yang digunakan masing-masing pesaing (competitor), atau dalam teori permainan yang disebut sebagai pemain, akan dibandingkan dengan pengaruh tindakan pemain lainnya dengan kepentingan yang sama untuk memilih keputusan-keputusan yang memaksimumkan atau meminimum-kan.Dalam memilih strategi optimal, beberapa asumsi ditetapkan terlebih dahulu, yaitu:

1). Setiap pemain terdapat sejumlah pilihan yang disebut strategi. 2). Setiap pemain diasumsikan memliki kecerdasan yang sama. 3). Setiap pemain mengetahui strategi lawan.

4). Setiap pemain mengetahui jumlah perolehan sendiri dan pemain lain.

4.2 Transformasi Permainan 𝑚 × 𝑛 ke Bentuk Program Linier

Untuk menyelesaikan permainan-permainan strategi campuran yang berdimensi 𝑚×𝑛, dapat menggunakan program linier dengan mentransformasikan persamaan minimaks dan maksmin ke bentuk program linier.

Tabel 2. Tabel matriks perolehan untuk permainan m × n 𝑃2 𝑃₁ (𝑦1) (𝑦2) … (𝑦𝑛) (𝑥1) 𝐺( 1,1) 𝐺(1,2) … 𝐺(1, 𝑛) (𝑥2) 𝐺(2,1) 𝐺(2,2) … 𝐺(2, 𝑛) ⋮ ⋮ ⋮ ⋱ ⋮ (𝑥_𝑚) 𝐺(𝑚, 1) 𝐺(𝑚, 2) … 𝐺(𝑚, 𝑛) Misalkan: 𝒱 = nilai permainan

𝑥_𝑝 =Probabilitas pemain 𝑃₁ menggunakan strategi ke 𝑝 𝑦_𝑞=Probabilitas pemain 𝑃₂ menggunakan strategi ke 𝑞

4.2.1 Proses Pembentukan Program Linier Pada Pemain I

Pertama akan dibahas program linier pada permainan dari sudut pandang pemain I. 𝑃1 yang merupakan pemain baris (maximizing player), maka dapat

dinyatakan harapan menang 𝑃₁ dalam tanda pertidaksamaan lebih besar. Artinya 𝑃₁ mungkin mendapat kemenangan lebih dari 𝒱 bila 𝑃₂ menggunakan strategi yang lemah. Jadi nilai harapan menang 𝑃₁ adalah:

∑ 𝐺(𝑝, 1)𝑥_𝑝≥ 𝑚 𝑝=1 𝒱 ∑ 𝐺(𝑝, 2)𝑥_𝑝≥ 𝑚 𝑝=1 𝒱 ∑ 𝐺(𝑝, 𝑛)𝑥_𝑝 ≥ 𝑚 𝑝=1 𝒱 … (4.1)

(7)

Rini Hidayattillah, Penyelesaian Teori Permainan Menggunakan Metode Simpleks Alternatif dan ∑ 𝑥_𝑝 = 𝑚 𝑝=1 1 … (4.2) 𝑥𝑝 ≥ 0, untuk semua 𝑝 = 1,2, … , 𝑚.

Dengan membagi pertidaksamaan (4.1) dan persamaan (4.2) dengan 𝒱, dalam pembentukan perumusan program linier diasumsikan bahwa 𝑉 ≥ 0, untuk menghindari resiko nilai 𝑉 ≤ 0, maka semua nilai elemen pada matriks permainan ditambah dengan nilai mutlak terbesar dari konstanta permainan, maka diperoleh:

∑𝐺(𝑝, 1)𝑥𝑝 𝒱 ≥ 𝑚 𝑝=1 1 ∑𝐺(𝑝, 2)𝑥𝑝 𝒱 ≥ 𝑚 𝑝=1 1 ∑𝐺(𝑝, 𝑛)𝑥𝑝 𝒱 𝑚 𝑝=1 ≥ 1 … (4.3) dan ∑𝑥𝑝 𝒱 = 𝑚 𝑝=1 1 𝒱 … (4.4) 𝑥𝑝 ≥ 0, untuk semua 𝑝 = 1,2, … , 𝑚. Misalkan: 𝑋_𝑝 =𝑥𝑝 𝒱 , 𝑝 = 1,2, … , 𝑚 … (4.5) Maka diperoleh: ∑ 𝐺(𝑝, 1)𝑋_𝑝 ≥ 1 ∑ 𝐺(𝑝, 2)𝑋_𝑝 ≥ 1 ∑ 𝐺(𝑝, 𝑛)𝑋_𝑝 ≥ 1 … (4.6) dan ∑ 𝑋_𝑝 = 𝑚 𝑝=1 1 𝒱 … (4.7) 𝑋𝑝 ≥ 0, untuk semua 𝑝 = 1,2, … , 𝑚.

Karena 𝑃1 adalah maximizing player maka fungsi tujuan adalah

memaksimumkan nilai 𝒱 atau sama dengan meminimumkan 1

𝒱, maka dapat

(8)

Rini Hidayattillah, Penyelesaian Teori Permainan Menggunakan Metode Simpleks Alternatif 𝑀𝑎𝑘𝑠 𝒱 = 𝑀𝑖𝑛 1 𝒱 = 𝑀𝑖𝑛 ∑ 𝑥_𝑝 𝒱 = 𝑀𝑖𝑛 ∑ 𝑋𝑝 … (4.8) 𝑚 𝑝=1 𝑚 𝑝=1

Diketahui pada persamaan (4.7) bahwa: 𝑋₁+ 𝑋₂+ ⋯ + 𝑋_𝑚

= 1

𝒱 … (4.9) Jadi bentuk umum program linier untuk pemain I adalah:

𝑀𝑖𝑛 𝑓₀ = 𝑋 = 𝑋₁+ 𝑋₂ + ⋯ + 𝑋_𝑚 … (4.10) Dengan batasan: 𝐺(1,1)𝑋1+ 𝐺(2,1)𝑋2+ ⋯ + 𝐺(𝑚, 1)𝑋𝑚 ≥ 1 𝐺(1,2)𝑋1+ 𝐺(2,2)𝑋2+ ⋯ + 𝐺(𝑚, 2)𝑋𝑚 ≥ 1 ⋮ 𝐺(1, 𝑛)𝑋1+ 𝐺(2, 𝑛)𝑋2+ ⋯ + 𝐺(𝑚, 𝑛)𝑋𝑚≥ 1 …(4.11) 𝑋𝑝 ≥ 0, untuk semua 𝑝 = 1,2, … , 𝑚. Di mana: 𝑓₀ = 1 𝒱 … (4.12) dan 𝑋𝑝 = 𝑥_𝑝 𝒱 , 𝑝 = 1,2, … , 𝑚. … (4.13)

4.2.2 Proses Pembentukan Program Linier Pada Pemain II

Dengan cara yang sama permasalahan pemain II dapat dibawa ke bentuk program linier. Pemain 𝑃2 yang merupakan pemain kolom (minimizing player), maka

dapat dinyatakan harapan menang 𝑃2 dalam tanda pertidaksamaan lebih kecil.

Artinya 𝑃2 mungkin mengalami kekalahan kurang dari 𝒱 bila 𝑃1 menggunakan

strategi yang lemah. Jadi nilai harapan kekalahan 𝑃2 adalah:

∑ 𝐺(𝑞, 1)𝑦_𝑞 ≤ 𝑛 𝑞=1 𝒱 ∑ 𝐺(𝑞, 2)𝑦_𝑞 ≤ 𝑛 𝑞=1 𝒱 ∑ 𝐺(𝑞, 𝑚)𝑦_𝑞≤ 𝑛 𝑞=1 𝒱 … (4.14) dan ∑ 𝑦_𝑞= 𝑛 𝑞=1 1 … (4.15) 𝑦_𝑞≥ 0, untuk semua 𝑞 = 1,2, … , 𝑛.

Dengan membagi pertidaksamaan (4.15) dan persamaan (4.16) dengan 𝒱, maka diperoleh:

(9)

Rini Hidayattillah, Penyelesaian Teori Permainan Menggunakan Metode Simpleks Alternatif ∑𝐺(𝑞, 1)𝑦𝑞 𝒱 ≤ 𝑛 𝑞=1 1 ∑𝐺(𝑞, 2)𝑦𝑞 𝒱 ≤ 𝑛 𝑞=1 1 ∑𝐺(𝑞, 𝑚)𝑦𝑞 𝒱 𝑛 𝑞=1 ≤ 1 … (4.16) dan ∑𝑦𝑞 𝒱 = 𝑛 𝑞=1 1 𝒱 … (4.17) 𝑦_𝑞≥ 0, untuk semua 𝑞 = 1,2, … , 𝑛. Misalkan: 𝑌𝑞 = 𝑦_𝑞 𝒱 , 𝑞 = 1,2, … , 𝑛 … (4.18) Maka diperoleh: ∑ 𝐺(𝑞, 1)𝑌_𝑞 ≤ 1 ∑ 𝐺(𝑞, 2)𝑌_𝑞 ≤ 1 ∑ 𝐺(𝑞, 𝑚)𝑌_𝑞 ≤ 1 … (4.19) dan ∑ 𝑌_𝑞 = 𝑛 𝑞=1 1 𝒱 … (4.20) 𝑌𝑞 ≥ 0, untuk semua 𝑞 = 1,2, … , 𝑛.

Untuk 𝑃2 yang merupakan minimizing player, maka fungsi tujuannya adalah

meminimumkan 𝒱 atau sama dengan memaksimalkan 1

𝒱, maka dapat dirumuskan

program linier untuk 𝑃₂ sebagai berikut:

𝑀𝑖𝑛 𝒱 = 𝑀𝑎𝑘𝑠 1 𝒱 = 𝑀𝑎𝑘𝑠 ∑ 𝑦_𝑞 𝒱 = 𝑀𝑎𝑘𝑠 ∑ 𝑌𝑞 … (4.21) 𝑛 𝑞=1 𝑛 𝑞=1

Diketahui pada persamaan (4.20) bahwa: 𝑌1+ 𝑌2+ ⋯ + 𝑌𝑛

= 1

𝒱 … (4.22) Jadi bentuk umum program linier untuk pemain II adalah:

𝑀𝑎𝑘𝑠 𝑔0 = 𝑌 = 𝑌1+ 𝑌2+ ⋯ + 𝑌𝑛 … (4.23)

Dengan batasan:

𝐺(1,1)𝑌1+ 𝐺(1,2)𝑌2+ ⋯ + 𝐺(𝑛, 1)𝑌𝑛≤ 1

𝐺(2,1)𝑌1+ 𝐺(2,2)𝑌2+ ⋯ + 𝐺(𝑛, 2)𝑌𝑛≤ 1

(10)

Rini Hidayattillah, Penyelesaian Teori Permainan Menggunakan Metode Simpleks Alternatif 𝐺(1, 𝑚)𝑌1+ 𝐺(2, 𝑚)𝑌2+ ⋯ + 𝐺(𝑛, 𝑚)𝑌𝑛 ≤ 1…(4.24) 𝑌𝑞 ≥ 0, untuk semua 𝑞 = 1,2, … , 𝑛. Di mana: 𝑔0 = 1 𝒱 … (4.25) dan 𝑌_𝑞= 𝑦𝑞 𝒱 , 𝑞 = 1,2, … , 𝑛. … (4.26) Rumusan program linier pada pemain 𝑃₁ merupakan dual dari pemain 𝑃₂ dan sebaliknya. Oleh karena itu, strategi optimal pada 𝑃1 menjadi strategi optimal bagi

𝑃2. Untuk menyelesaikan problema program linier ini dapat menggunakan metode

simpleks alternatif.

4.3 Langkah–Langkah Penyelesaian Program Linier dengan Metode Simpleks Alternatif

Langkah-langkah metode simpleks alternatif yang harus dilakukan:

Langkah 1.

Pada langkah pertama permasalahan program linier akan dibawa ke dalam bentuk standar program linier, sesuai aturan bentuk program linier standar pada bab II.

Langkah 2.

Setelah permasalahan program linier diubah ke dalam bentuk standar program linier, data disusun ke dalam tabel dalam bentuk simbol seperti tabel 3.

Tabel 3. Tabel simpleks awal dalam bentuk simbol

Variabel Dasar 𝑥₁ 𝑥₂ … 𝑥_𝑛 𝑠₁ 𝑠₂ … 𝑠_𝑛 NK 𝑠₁ a11 a12 … a1n 1 0 … 0 b1 𝑠₂ a21 a22 … a2n 0 1 … 0 b2 … … … … 𝑠_𝑚 am1 am2 … amn 0 0 … 1 bm 𝑍 −𝑐1 −𝑐2 … −𝑐𝑛 0 0 … 0 0 Langkah 3.

Pada langkah selanjutnya akan dicari elemen kunci dari elemen terbesar pada variabel keputusan. Jika koefisien negatif terbesar seri (unik) dalam menentukan kolom kunci, maka menggunakan metode simpleks alternatif menentukan elemen kunci (angka kunci).

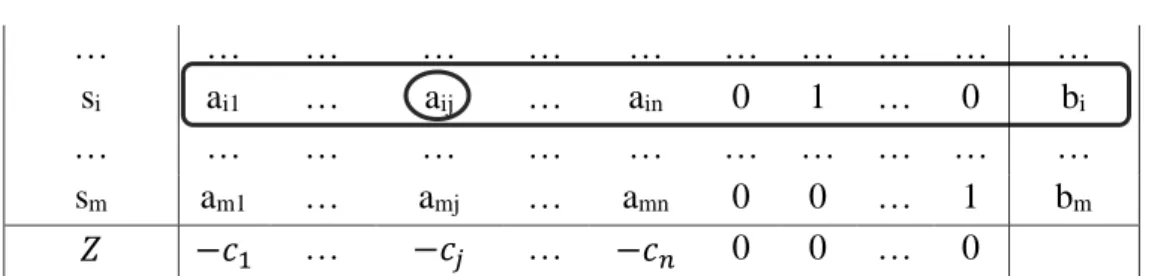
Tabel 4. Tabel elemen kunci, baris kunci dan kolom kunci

Variabel Dasar

𝑥₁ … 𝑥_𝑗 … 𝑥_𝑛 s1 s2 … sn NK

(11)

Rini Hidayattillah, Penyelesaian Teori Permainan Menggunakan Metode Simpleks Alternatif … … … … si ai1 … aij … ain 0 1 … 0 bi … … … … sm am1 … amj … amn 0 0 … 1 bm 𝑍 −𝑐1 … −𝑐𝑗 … −𝑐𝑛 0 0 … 0

Pada tabel tersebut aij sebagai elemen kunci, perpotongan dari elemen kunci

tersebut menjadi baris kunci dan kolom kunci.

Langkah 4.

Lanjutkan langkah berikutnya seperti metode simpleks biasa, dengan melakukan operasi baris elementer (ERO) untuk membuat elemen kunci menjadi berharga 1 dan berharga 0 pada baris-baris lainnya.

Langkah 5

Label pada sebelah kiri elemen kunci diganti dengan label pada atas elemen kunci, dan sebaliknya. Terjadi perubahan yang menjadi variabel dasar dengan adanya variabel masuk (entering variable) dan variabel keluar (leaving variable).Pada tabel tersebut siakan bertukar tempat dengan xj dengan poros aij (dilingkari sebagai elemen

kunci).

Tabel 5. Tabel perubahan variabel

Langkah 6

Lanjutkan dengan kembali pada langkah 3 jika solusi belum optimal.

Langkah 7

Setelah didapatkan solusi optimal, akan dicari strategi optimal pemain I dan Pemain II sebagai berikut:

a. Penyelesaian untuk pemain I (𝑃₁): 𝑓₀ = 𝑋 = 𝑋₁+ 𝑋₂+ ⋯ + 𝑋_𝑚 atau 𝑓₀ = 1

𝒱sehinggga diperoleh 𝑉 = 1 𝑓₀

dan untuk pemain II (𝑃₂): 𝑔₀= 𝑌₁+ 𝑌₂+ ⋯ + 𝑌_𝑛 atau 𝑔₀ = 1

𝒱 sehinggga

diperoleh 𝑉 = _𝑔1

0.

b. Strategi optimal pemain I Karena 𝑋𝑝 =

𝑥𝑝

𝒱, maka 𝑥𝑝 = 𝑋𝑝× 𝑉, 𝑢𝑛𝑡𝑢𝑘 𝑝 = 1,2, … , 𝑚.

c. Strategi optimal pemain II Karena 𝑌_𝑞 = 𝑦𝑞 𝒱, maka 𝑦𝑞 = 𝑌𝑞× 𝑉, 𝑢𝑛𝑡𝑢𝑘 𝑞 = 1,2, … , 𝑛. 5. KESIMPULAN 𝑥₁ … 𝑥_𝑗 … 𝑥_𝑛 s1 a11 … a1j … a1n … … … … si ai1 … aij … ain … … … … sm am1 … amj … amn 𝑥1 … si … 𝑥_𝑛 s1 a11 … a1j … a1n … … … … 𝑥𝑗 ai1 … aij … ain … … … … sm am1 … amj … amn

(12)

Kesimpulan dari penelitian ini berdasarkan hasil dan pembahasan adalah bentuk persoalan teori permainan dapat dibawa kedalam bentuk program linier kemudianmetode simpleks alternatif dapat digunakan untuk menyelesaikan program linier untuk kasus teori permainan tersebut, sehingga nantinya akan didapatkan solusi optimal dan strategi optimal permainan.

DAFTAR PUSTAKA

[1]Aminudin. 2005. Prinsip-prinsip Riset Operasi. Erlangga, Jakarta.

[2]Affandi, P. 2011. Penerapan Program Linier pada Permainan Non-Koperatif. Jurnal Matematika Murni dan Terapan vol.5 No.2 (1-12).

[3]Mulyono, S. 2007, Riset Operasi. Lembaga Penerbit Fakultas Ekonomi Universitas Indonesia, Jakarta.

[4]Siagian. 1987. Penelitian Operasional :teori dan praktek. (UI-Press), Jakarta.

[5]Ferguson, T. S. 2008. Game Theory. University of California, Los Angeles.

[6]Taha, H. A. 1997. Riset Operasi. Departement of indrustrial Engineering university of Arkans, Fayettevile.

[7]Dimyati, T., dan Dimyati, A. 2004. Operations Research: Model-model Pengambilan Keputusan. Sinar Baru Algensindo, Bandung.

[8]K. P. Ghadle., dan T. S. Pawar. 2014. Game theory problems by an alternatie simplex method. International Journal of Research in Engineering and Technology vol.03 (900-905).

[9]Hillier, G., dan Lieberman, J. 1990. Introduction To Operations Research, McGraw-Hill, Inc.