PEMODELAN SISTEM PENDULUM TERBALIK DENGAN
LINTASAN MIRING DAN KARAKTERISASI PARAMETER
PADA MASALAH TRACKING ERROR OPTIMAL
BAMBANG EDISUSANTO
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
BOGOR
2008
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis Pemodelan Sistem Pendulum
Terbalik dengan Lintasan Miring dan Karakterisasi Parameter pada Masalah Tracking
Error Optimal adalah karya saya dengan arahan dari komisi pembimbing dan belum
diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi
yang berasal atau dikutip dari karya yang diterbitkan dari penulis lain telah
disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis
ini.
Bogor, Juli 2008
Bambang Edisusanto
ABSTRACT
BAMBANG EDISUSANTO
.Modeling of Inverted Pendulum System with
Oblique Track and Parameter Characterization on Optimal Tracking Error
Problem. Under direction of TONI BAKHTIAR and ALI KUSNANTO
Inverted pendulum is an important device in education and research for control
engineering. Many results of research are reached through study to pendulum system.
The primary objective of this thesis is to characterize the inverted pendulum system
with oblique track on the optimal tracking error problem in terms of the system of
parameters. We first derive the equations of motion for the pendulum system with flat
track and then extend it to the system with oblique track. We then derive the
analytical expressions of the optimal tracking error problem for both systems. It is
shown that the expressions are completely determined by the pendulum’s parameters.
Furthermore, its is shown that the lowest possible tracking error can be attained as
long as the ratio between pendulum and motor masses is equal to a certain constant,
regardless the material of the pendulum.
RINGKASAN
BAMBANG EDISUSANTO. Pemodelan Sistem Pendulum Terbalik dengan Lintasan
Miring dan Karakterisasi Parameter pada Masalah Tracking Error Optimal.
Dibimbing oleh TONI BAKHTIAR, dan ALI KUSNANTO.
Pendulum adalah sebuah bandul. Ada dua jenis pendulum yaitu pendulum
biasa (direct pendulum) dan pendulum terbalik (inverted pendulum). Dewasa ini
pendulum biasa maupun pendulum terbalik merupakan alat yang sangat penting
dalam pendidikan dan penelitian di bidang teknik pengendalian (control engineering).
Banyak hasil penelitian dicapai melalui studi terhadap sistem pendulum. Di bidang
teknik, pendulum biasa dan terbalik dipakai untuk memantau pergerakan fondasi
bendungan, jembatan, dermaga dan struktur bangunan lainnya. Alat pengangkat peti
kemas (cranes) bekerja atas dasar pendulum biasa. Selain itu pendulum terbalik dapat
dimanfaatkan untuk mendeteksi usikan gelombang seismik dalam tanah yang
disebabkan oleh aktifitas seismik-makro, oseanik, dan atmosferik. Di bidang fisiologi
dan ilmu olah raga, prinsip kerja pendulum terbalik banyak digunakan untuk
mengkaji keseimbangan gerak manusia.
Berdasarkan dari hal tersebut maka penelitian ini bertujuan menentukan model
sistem pendulum terbalik dengan lintasan miring dan menentukan karakterisasi
parameter sistem pendulum terbalik dengan lintasan miring pada masalah tracking
error optimal.Langkah pertama adalah menurunkan model sistem pendulum terbalik
dengan lintasan datar dan lintasan miring. Model tersebut berbentuk persamaan
taklinear, sehingga harus dilinearkan terlebih dahulu dengan bantuan deret Taylor.
Selanjutnya dengan tranformasi Laplace ditentukan fungsi transfer P
x(s) dan P
?(s), di
mana
P s merupakan fungsi transfer antara input kendali u dengan posisi motor x
x( )
dan
P s merupakan fungsi transfer antara input kendali u dengan sudut pendulum
( )
. Kemudian dicari pole dan zero dari fungsi transfer dengan mengasumsikan tidak
ada friksi antara motor dan pendulum serta tidak ada friksi antara motor dan lintasan,
yaitu
0 . Dari P
x(s) dan P
?(s), dapat ditentukan pole takstabil dan non
minimum phase zero. Selanjutnya diturunkan ekspresi analitik bagi J yang dapat
meminimumkan tracking error. Dengan menyelesaikan
dJ 0dl
, maka panjang
pendulum optimal dapat ditentukan. Selanjutnya dilakukan simulasi antara ekspresi
analitik bagi J
dan panjang pendulum optimal, dari simulasi ini dapat dilihat bahwa
ketika panjang pendulum sangat pendek maka nilai J sangat besar. Jika panjang
pendulum diperpanjang, maka nilai J semakin kecil. Kejadian ini berlaku sampai
pada satu titik minimum, setelah itu akan berubah panjang pendulum semakin
panjang maka nilai J
semakin besar. Titik minimum dipengaruhi oleh sudut
kemiringan lintasan. Sudut kemiringan lintasan semakin besar maka titik
minimumnya juga semakin besar. Sedangkan hasil simulasi antara sudut kemiringan
lintasan dan panjang pendulum optimal menunjukkan bahwa untuk mendapatkan
kestabilan panjang pendulum optimal sangat dipengaruhi oleh sudut kemiringan
lintasan. Sudut kemiringan lintasan semakin besar maka panjang pendulum optimal
semakin pendek.
Dari hasil penelitian ini dapat disimpulkan bahwa nilai tracking error minimal
dipengaruhi oleh sudut kemiringan lintasan. Jika sudut kemiringan lintasan semakin
besar, maka nilai tracking errornya juga semakin besar. Panjang pendulum minimal
dipengaruhi oleh sudut kemiringan lintasan. Hubungan antara panjang pendulum
minimal dan sudut kemiringan lintasan berbanding terbalik. Sudut kemiringan
lintasan semakin besar maka panjang pendulum minimal semakin pendek. Karena
diasumsikan bahwa rasio antara massa pendulum dan massa motor adalah konstan,
maka dapat ditunjukkan bahwa tracking error optimal dapat dicapai sepanjang rasio
antara massa pendulum dan massa motor adalah konstan tanpa memandang bahan
dari pendulum.
© Hak cipta milik IPB, tahun 2008
Hak cipta dilindungi Undang-undang
1 Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan
atau menyebut sumber.
a Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya
ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.
b Pengutipan tidak merugikan kepentingan yang wajar IPB.
2 Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis
dalam bentuk apapun tanpa izin IPB
PEMODELAN SISTEM PENDULUM TERBALIK DENGAN
LINTASAN MIRING DAN KARAKTERISASI PARAMETER
PADA MASALAH TRACKING ERROR OPTIMAL
BAMBANG EDISUSANTO
Tesis
sebagai salah satu syarat untuk memperoleh gelar
Magister Sains pada
Departemen Matematika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
BOGOR
2008
Judul Tesis
: Pemodelan Sistem Pendulum Terbalik dengan Lintasan Miring dan
Karakterisasi Parameter pada Masalah Tracking Error Optimal
Nama
: Bambang Edisusanto
NIM
: G551060171
Disetujui
Komisi Pembimbing
Dr. Toni Bakhtiar, M.Sc.
Drs. Ali Kusnanto, M.Si.
Ketua
Anggota
Diketahui
Ketua Program Studi
Dekan Sekolah Pascasarjana
Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M.S.
Prof. Dr. Ir. Khairil A. Notodiputro, M.S.
Tanggal Lulus:
Tanggal Ujian: 10 Juli 2008
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya
sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian
yang dilaksanakan sejak bulan Nopember 2007 ini ialah masalah tracking error
optimal pada sistem pendulum, dengan judul Pemodelan Sistem Pendulum Terbalik
dengan Lintasan Miring dan Karakterisasi Parameter pada Masalah Tracking Error
Optimal.
Terima kasih penulis ucapkan kepada Bapak Dr. Toni Bakhtiar, M.Sc dan
Bapak Drs. Ali Kusnanto, M.Si selaku pembimbing, serta Ibu Dr. Ir. Endar H.
Nugrahani, M.S. yang telah banyak memberikan saran selaku penguji luar komisi dan
selaku ketua Program Studi Matematika Terapan. Tak lupa ucapan terima kasih
penulis sampaikan pada Departemen Agama Republik Indonesia yang telah
memberikan fasilitas. Ungkapan terima kasih juga disampaikan kepada istri dan anak
serta seluruh keluarga, atas segala doa dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat
Bogor, Juli 2008
Bambang Edisusanto
RIWAYAT HIDUP
Penulis dilahirkan di Purworejo pada tanggal 27 Agustus 1966 dari ayah
Witosedono dan ibu Astuti. Penulis merupakan putra kedua dari empat bersaudara.
Tahun 1986 penulis lulus dari STM Negeri Purworejo jurusan Teknik
Bangunan dan pada tahun yang sama lulus seleksi masuk IKIP Muhammadiyah
Yogyakarta. Penulis memilih Jurusan Pendidikan Matematika pada Fakultas
Pendidikan Matematika dan Ilmu Pengetahuan Alam dan selesai pada tahun 1990.
Tahun 1991 penulis menjadi staf pengajar di SMU Muhammadiyah 7
Yogyakarta. Pada tahun 1997 masuk PNS dan mengajar di MTs Negeri Sidoharjo
Samigaluh Kulon Progo. Setahun kemudian pindah tugas mengajar di MTs Negeri
Pakem. Pada tahun 2006 penulis lulus seleksi masuk Program Magister Program
Studi Matematika Terapan di Institut Pertanian Bogor lewat jalur Beasiswa Utusan
Daerah Departemen Agama Republik Indonesia.
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... xiii
DAFTAR LAMPIRAN ... xiv
I PENDAHULUAN ...
1
1.1 Latar Belakang ... 1
1.2 Tujuan Penelitihan ...
2
II LANDASAN TEORI ... 3
2.1 Sistem Pendulum Terbalik ... 3
2.2 Transformasi Laplace ...
4
2.3 Deret Taylor ... 5
2.4 Persamaan Ruang Keadaan ...
6
2.5 Fungsi Transfer ...
7
2.6 Pole dan Zero ... 8
2.7 Kestabilan ... 9
2.8 Sistem Umpanbalik ... 10
2.9 Masalah Tracking Error ... 11
III PEMODELAN SISTEM PENDULUM TERBALIK ... 13
3.1 Sistem Pendulum Terbalik dengan Lintasan Datar ... 13
3.2 Sistem Pendulum Terbalik dengan Lintasan Miring ... 16
3.3 Pole dan Zero ... 19
IV KARAKTERISASI PARAMETER PADA MASALAH TRACKING ERROR
OPTIMAL ... 23
4.1 Ekspresi Analitik ... 23
4.2 Tracking Error Optimal ... 24
V SIMULASI ... 28
DAFTAR PUSTAKA ... 33
DAFTAR GAMBAR
Halaman
1. Sistem pendulum terbalik dengan lintasan datar ...
3
2. Diagram blok hubungan antara input dan output ... 8
3. Sistem pengendalian dengan umpanbalik ... 10
4. Sistem pengendalian dengan umpan balik pada masalah tracking error ... 11
5. Sistem pendulum terbalik dengan lintasan datar ... 13
6. Sistem pendulum terbalik dengan lintasan miring ... 16
7. Grafik masalah tracking error ... 29
DAFTAR LAMPIRAN
Halaman
1. Bukti sifat-sifat Transformasi Laplace ... 35
2. Pole dan Zero pendulum terbalik dengan lintasan datar ... 38
3. Bukti Teorema 1 ... 41
4. Bukti Teorema 2 ... 44
5. Contoh penggunaan Deret Taylor ... 46
6. Pelinearan model sistem pendulum terbalik dengan lintasan miring ... 47
7. Karakterisasi parameter sistem pendulum terbalik dengan lintasan datar ... 49
8. Karakterisasi parameter sistem pendulum terbalik dengan lintasan miring ... 54
9. Tabel panjang pendulum dan ekspresi analitik ... 61
10. Tabel panjang pendulum dan kemiringan lintasan ... 62
This document was created with Win2PDF available at http://www.daneprairie.com. The unregistered version of Win2PDF is for evaluation or non-commercial use only.
BAB I
PENDAHULUAN
1.1 Latar Belakang
Pada kehidupan sehari-hari sering terlihat anak-anak bermain dengan berusaha menegakkan dan menyeimbangkan sebuah tongkat di ujung jari. Secara terus-menerus mereka berusaha menyesuaikan posisi tangan agar tongkat tersebut tetap tegak. Tongkat yang terletak di atas jari anak tersebut merupakan contoh pendulum terbalik (inverted pendulum) yang pada dasarnya memiliki konsep yang sama dengan hal tersebut. Hanya saja pendulum terbalik bergerak dalam satu dimensi, sementara tangan dapat bergerak bebas ke atas, ke bawah, dan ke samping.
Ada dua jenis pendulum yaitu pendulum biasa (direct pendulum) dan pendulum terbalik (inverted pendulum). Dewasa ini pendulum biasa maupun pendulum terbalik merupakan alat yang sangat penting dalam pendidikan dan penelitian di bidang teknik pengendalian (control engineering) (Ogata 1990). Sistem pendulum memiliki karakteristik sebagai berikut :
1. Taklinear dan takstabil.
2. Dapat dilinearkan di sekitar titik kesetimbangan.
3. Kompleksitasnya dapat ditingkatkan melalui penambahan pendulum atau modifikasi lainnya.
4. Mudah diterapkan dalam sistem aktual
Karena karakteristik di atas berbagai teori pengendalian (control theory) banyak dievaluasi dan dibandingkan melalui pengujian sistem pendulum (Microrobot 2007). Banyak hasil penelitian dicapai melalui studi terhadap sistem pendulum. Di bidang teknik, pendulum biasa dan terbalik dipakai untuk memantau pergerakan fondasi bendungan, jembatan, dermaga dan struktur bangunan lainnya. Alat pengangkat peti kemas (cranes) bekerja atas dasar pendulum biasa. Selain itu pendulum terbalik dapat dimanfaatkan untuk mendeteksi usikan gelombang seismik dalam tanah yang disebabkan oleh aktifitas seismik-makro, oseanik, dan atmosferik (Taurasi 2005). Di bidang fisiologi dan ilmu olah raga, prinsip kerja pendulum terbalik banyak digunakan untuk mengkaji
2
keseimbangan gerak manusia (Loram et al. 2001; Loram & Lakie 2002; Loram et al. 2006).
Kajian terhadap aspek teoritis sistem pendulum pun banyak dilakukan. Sebagai contoh, di (Atay 1999) dipelajari masalah kestabilan asimtotik dengan menggunakan umpanbalik posisi, sedangkan di (Woodyatt et al. 1997) dikaji kendala-kendala fundamental dalam pengendalian sistem pendulum terbalik dengan dua-input dan dua-output. Sedangkan di (Chen et al. 2003) dibahas sistem pengendalian dengan umpan balik pada masalah tracking error yang mampu menstabilkan sistem dan sekaligus meminimumkan tracking error.
1.2 Tujuan Penelitian
Berdasarkan latar belakang tersebut di atas maka penelitian ini bertujuan untuk : 1.2.1 Memodelkan sistem pendulum terbalik dengan lintasan miring.
1.2.2 Melakukan karakterisasi terhadap parameter pendulum terbalik dengan lintasan miring pada masalah tracking error optimal.
BAB II
LANDASAN TEORI
2.1 Sistem Pendulum Terbalik
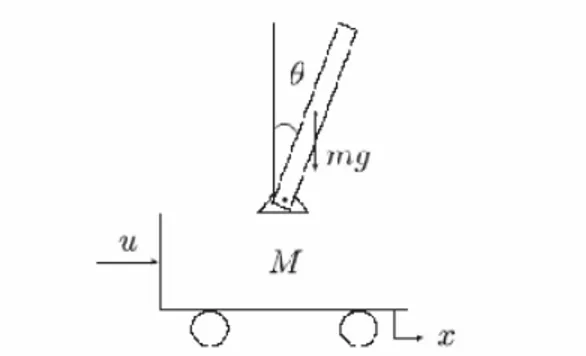
Dalam penelitian ini diperhatikan sistem pendulum terbalik seperti pada Gambar 1 di mana sebuah pendulum terbalik dimuat dalam motor yang bisa digerakkan. Diasumsikan motor bergerak dalam satu dimensi, yaitu maju atau mundur dalam satu garis lurus, sedangkan pendulum diasumsikan hanya bergerak dalam bidang vertikal yang datar.
Gambar 1: Sistem Pendulum Terbalik dengan Lintasan Datar
Berat motor dinotasikan dengan M dan berat pendulum dengan m, satuannya dalam kilogram. Panjang pendulum dilambangkan dengan 2l dan satuannya dalam meter. Pendulum diasumsikan seragam (uniform) sehingga inersianya diberikan oleh I = 1 2
3ml . Diasumsikan friksi antara pendulum dengan
motor sebesar dan friksi antara motor dengan lintasan sebesar . Diasumsikan bahwa sudut yang dibentuk oleh pendulum adalah cukup kecil.
Persamaan gerak antara input kendali u, yang merupakan gaya yang bekerja pada motor, dengan posisi motor x terhadap titik awal dan sudut pendulum
diberikan oleh persamaan-persamaan berikut :
(M m x) ml x u (2.1)
2
4
0
4
2.2Tranformasi Laplace
Transformasi Laplace adalah suatu metode operasional yang dapat digunakan untuk menyelesaikan persamaan diferensial linear. Dengan menggunakan transformasi Laplace, persamaan diferensial linear dapat diubah ke dalam persamaan aljabar dalam peubah kompleks.
Definisi 1. Transformasi Laplace dari fungsi f(t) adalah
£f(t) 0 st
e
f t dt
F s
f(t)
fungsi waktu t s
peubah kompleks £
simbol operasi yang mengidikasikan bahwa persamaan
diubah dengan menggunakan integral Laplace
0 ( )
st
e f t dt
F(s) transformasi Laplace dari f(t),
dengan syarat f t kontinu bagian demi bagian pada t 0 dan berorde eksponensial saat t menuju takhingga, yaitu ada konstanta real positif sedemikian sehingga lim t 0
t e f t (Ogata 1990).
Sifat – sifat transformasi Laplace :
Misalkan £ f t F s dan £ g t G s , maka: 1. Sifat penjumlahan
£ f t( ) g t( ) F s( ) G s( ) 2. Sifat perkalian
Jika a R , maka: £af(t) a F(s) 3. Sifat turunan pertama
£
df t
sF s
f
0
dt
4. Sifat turunan kedua
£ 2 2
( )
( )
(0)
(0)
d f t
s F s
f
sf
dt
5 5. Sifat eksponensial £
1
ate
s a
Bukti dari sifat-sifat di atas dapat dilihat di Lampiran 1.
2.3 Deret Taylor
Suatu sistem taklinear dapat dilinear menggunakan deret Taylor dengan mengasumsikan variabel mengalami deviasi yang kecil terhadap titik kesetimbangannya.
Definisi 2. Deret Taylor Satu Peubah
Andaikan f dan semua turunannya, f ',f'', f''', …, kontinu di dalam selang [a,b]. Misalkan x0 [ , ]a b , maka untuk nilai-nilai x di sekitar x0 dan x0 [ , ]a b , f(x) dapat diekspansi ke dalam deret Taylor sebagai berikut (Ogata 1990):
2 ( ) 0 0 0 0 0 0 0 ( ) ( ) ( ) ( ) ( ) '( ) ''( ) ... ( ) ... 1! 2! ! m m x x x x x x f x f x f x f x f x m .
Definisi 3. Deret Taylor Dua Peubah
Deret Taylor dua peubah merupakan fungsi dari dua buah masukanx1 dan x . 2 Sehingga nilai x1 dan x di sekitar 2 x1 dan x2 merupakan deret Taylor dua peubah sebagai berikut (Ogata 1990):
1 2 1 2 1 1 2 2 1 2 ( , ) ( , ) f ( ) f ( ) f x x f x x x x x x x x
2 2 2 2 2 1 1 1 1 2 2 2 2 2 2 1 1 2 2 1 ( ) 2 ( )( ) ( ) ... 2! f f f x x x x x x x x x x x x
di mana turunan-turunan parsialnya dihitung pada x1 x x1, 2 x . Di sekitar titik 2 kerja normal, bentuk-bentuk orde tinggi dapat diabaikan. Model matematika linear dari sistem taklinear ini di sekitar kondisi kerja normal selanjutnya diberikan oleh
1 2 1 2 1 1 1 2 2 2
( , ) ( , ) ( ) ( )
f x x f x x K x x K x x
6
1 1 2 2 1 1 x x x, x f K x , 1 1 2 2 2 2 x x x, x f K x .
2.4 Persamaan Ruang Keadaan
Bentuk standar persamaan ruang keadaan merupakan bentuk persamaan diferensial biasa berorde satu berdimensi n, dan persamaan keluaran (out put) dengan dimensi m, didefenesikan sebagai berikut (Ogata 1990):
Defnisi 4.
Diberikan sistem persamaan ruang keadaan dan persamaan keluaran berturut-turut sebagai berikut: , , , x t f x u t
(2.3) , , y t g x u t . (2.4)
Jika vektor fungsi f, g bergantung terhadap peubah t, maka persamaan (2.3) dan (2.4) disebut sistem parameter-berubah (time-varying). Jika sistem tersebut dilinierkan, maka persamaan linear ruang keadaan dan persamaan keluarannya dapat ditulis sebagai berikut:
x t A t x t B t u t , (2.5)
y t C t x t D t u t , (2.6)
dengan A t ,B t C t, ,D t merupakan matriks-matriks yang bergantung pada peubah t, sedangkan x adalah vektor peubah keadaan (variable state) dan y adalah keluaran (output)sistem serta u merupakan input kendali.
Jika vektor fungsi f, g tidak bergantung terhadap peubah t, maka persamaan (2.3) dan (2.4) disebut sistem parameter-konstan (time-invariant). Di dalam kasus ini persamaan (2.3) dan (2.4) dituliskan sebagai berikut:
, x t f x u ,
, y t g x u .
Jika sistem tersebut dilinearkan,maka persamaan linear ruang keadaan dan persamaan keluarannya adalah:
( ) ( ) ( )
x t Ax t Bu t , (2.7)
( ) ( ) ( )
7
dengan A,B,C,D adalah matriks-matriks bernilai real, x adalah vektor peubah keadaan (state variable), y adalah keluaran (output) sistem, dan u adalah input kendali.
Sistem pada persamaan (2.7) dan (2.8) dapat ditulis dalam bentuk , , ,
A B C D , untuk A Rn n,B Rn m,C Rr n, dan D Rr m
2.5 Fungsi Transfer
Fungsi transfer adalah suatu fungsi yang menghubungkan antara output sistem dengan input sistem.
Hasil transformasi Laplace dari (2.7) dan (2.8) adalah: sX(s) = AX(s) + BU(s),
Y (s) = CX(s) + DU(s).
Dengan demikian diperoleh fungsi transfer:
1 ( ) ( ) ( ) ( ) Y s P s C sI A B D U s
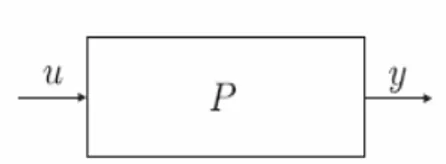
(2.9) Selanjutnya, interaksi antara u dan y dapat diungkapkan melalui diagram blok seperti pada Gambar 2.
Gambar 2: Diagram blok hubungan antara input dan output.
2.6 Pole dan Zero
Dari fungsi transfer seperti pada persamaan (2.9) dapat dituliskan dalam bentuk fungsi rasional sebagai berikut:
1 1 1 0 1 1 1 0 ... ( ) ( ) ( ) ... m m m m n n n b s b s b s b N s P s D s s a s a s a , (2.10) dengan pembilang N(s) dan penyebut D(s) adalah koprima. Pole dari sistem P didefinisikan sebagai akar dari persamaan D(s) = 0. Zero dari sistem P
8
didefinisikan sebagai akar dari persamaan N(s) = 0. Jika n > m maka sistem P memiliki sejumlah zero di takhingga.
Misalkan p dan z berturut-turut adalah pole dan zero dari P s , pole p disebut sebagai pole takstabil jika Re p 0, selain itu disebut pole stabil. Zero z disebut sebagai non minimum phase zero Re z 0, selain itu disebut zero stabil. Dapat dilihat bahwa dari persamaan (2.1) dan (2.2) dapat diperoleh
2 2 3 2 3 2 1 0 ( ) 4 3 3 ( ) : ( ) ( ) x X s s ml s gml P s U s s a s a s a s a , (2.11) 3 2 3 2 1 0 ( ) 3 ( ) : ( ) s mls P s U s a s a s a s a , (2.12) dengan 2 3 (4 ), a ml M m 2 2 3 ( ) 4 a M m ml , 1 3 3 ( ), a mgl M m 0 3 a mgl .
Di sini P s merupakan fungsi transfer antara input kendali u dengan posisi x( ) motor x dan P s merupakan fungsi transfer antara input kendali u dengan posisi ( ) sudut pendulum .
Jika diasumsikan tidak ada friksi antara motor dan pendulum serta tidak ada friksi antara motor dan lintasan, yaitu 0 , maka P s dan x( ) P s( ) memiliki pole takstabil di 3 ( ) (4 ) g M m p l M m (2.13) dan P s memiliki zero takstabil di x( )
3 , 4 g z z l . (2.14) Penurunan pole dan zero sistem pendulum terbalik dengan lintasan datar secara lengkap dapat dilihat pada Lampiran 2.
9
2.7 Kestabilan Definisi 3
Sistem = (A,B,C,D) seperti pada (2.7) dan (2.8) dikatakan 1. stabil jika lim sup ( )
x x t untuk setiap solusi x(t) dari
persamaan ( )x t Ax t ;
2. stabil asimtotik jika lim sup ( ) 0
x x t untuk setiap solusi x(t) dari persamaan
( ) ( ); x t Ax t
3. takstabil jika ia tidak stabil.
Dapat dilihat bahwa kestabilan tidak terkait dengan bagian manapun dari sistem selain dengan matriks A. Oleh karena itu, kestabilan dapat ditentukan dari spektrum matriks A (Lewis 2004).
Teorema 1
Diberikan sistem = (A,B,C,D) dengan A matriks berukuran n n yang memiliki akarciri 1, 2,..., n. Pernyatataan-pernyataan berikut berlaku:
1. Sistem stabil jika dan hanya jika Re i 0 untuk semua i = 1,2....,n 2. Sistem stabil asimtotik jika dan hanya jika Re i 0 untuk semua i = 1,2,…, n.
3. Sistem takstabil jika dan hanya jika Re i 0 untuk suatu i = 1,2,...,n (Lewis 2004).
Bukti: lihat Lampiran 3.
Teorema 2
Diberikan sistem P(s) yang memiliki pole p p1, 2,...,pn Pernyataan-pernyataan berikut berlaku:
1. Sistem P(s) stabil jika dan hanya jika Re pi 0 untuk semua i = 1,...,n.
2. Sistem P(s) stabil asimtotik jika dan hanya jika Re pi < 0 untuk semua i = 1,...,n
3. Sistem P(s) takstabil jika dan hanya jika Re pi > 0 untuk suatu i = 1,..., n
10
Bukti: lihat Lampiran 4.
2.8 Sistem Umpanbalik
Istilah umpanbalik digunakan untuk menjelaskan sebuah situasi di mana dua atau lebih sistem dinamik saling terhubung sedemikian sehingga setiap sistem mempengaruhi sistem lainnya. Umpanbalik memiliki banyak sifat menarik. Salah satunya adalah mampu membuat sistem taksensitif terhadap usikan dari luar.
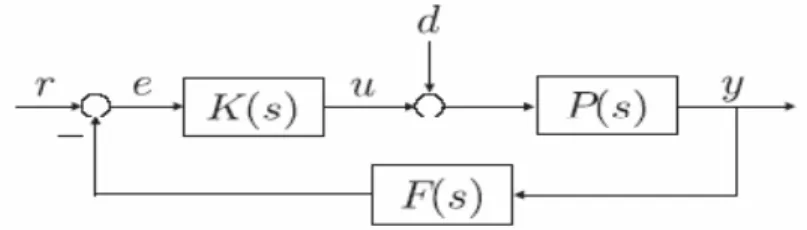
Gambar 3: Sistem pengendalian dengan umpanbalik.
Sistem umpanbalik paling sederhana melibatkan tiga komponen, yaitu plant atau sistem P yang akan dikendalikan, controller atau pengendali K yang harus didesain sehingga menghasilkan input kendali tertentu, dan sensor F yang mencatat output sistem sebagai umpanbalik. Pada Gambar 3, r merupakan fungsi referensi bagi peubah yang akan dikendalikan, e merupakan galat (error) antara input referensi dan output sistem, yaitu e r Fy , dan d merupakan usikan yang bersifat eksogen.
Masalah utama dalam sistem umpanbalik adalah mendesain pengendali K sedemikian sehingga sistem menjadi stabil. Bentuk paling sederhana bagi umpanbalik u adalah
u Kx , (2.15) yaitu u merupakan kombinasi linear dari peubah keadaan x. Dengan menyubstitusikan (2.15) ke (2.3) diperoleh x (A BK x) . Dengan demikian K dipilih sehingga A BK memiliki akarciri seperti yang diinginkan. Masalah ini dikenal sebagai pole placement. Jika state x tidak tersedia maka dipilih umpanbalik u sebagai kombinasi linear dari output y, yaitu
u Ky , (2.16) sehingga diperoleh x (A BK I( DK)1C x)
11
2.9 Masalah Tracking Error
Perhatikan sistem umpanbalik seperti pada Gambar 4 di mana ditetapkan d(t) = 0, F(s) = 1, dan r merupakan fungsi tangga satuan (step function), yaitu :
( ) 1, 0
0, 0. t r t
t (2.18)
Gambar 4: Sistem pengendalian dengan umpanbalik pada masalah tracking error.
Masalah tracking error bertujuan untuk mendesain pengendali K yang menstabilkan sistem dan sekaligus meminimumkan tracking error, yaitu:
2 2
0 0
: ( ) [ ( ) ( )]
J e t dt r t y t dt (2.19) Dalam karya ilmiah ini, yang menjadi pokok perhatian bukanlah pada pendesainan pengendali optimal K melainkan pada ekspresi analitik pada J , * yaitu inf
K
BAB III
PEMODELAN SISTEM PENDULUM TERBALIK
3.1 Sistem Pendulum Terbalik dengan Lintasan DatarPada penelitian ini pertama kali yang dilakukan adalah menurunkan model sistem pendulum terbalik dengan lintasan datar seperti pada Gambar 5. Pendulum diasumsikan seragam (uniform) sehingga inersianya diberikan oleh I = 1 2
3ml .
Diasumsikan friksi antara pendulum dengan motor sebesar dan friksi antara motor dan lintasan sebesar .
Gambar 5: Sistem Pendulum Terbalik dengan Lintasan Datar
Persamaan gerak antara input kendali u, yang merupakan gaya yang bekerja pada motor, dengan posisi motor x terhadap titik awal, sudut pendulum maka model dapat diturunkan sebagai berikut :
1 Energi Kinetik
Energi kinetik pada motor:
2 1 . 2 m K Mx
Energi kinetik pada pendulum:
2 2 2 1 2 cos 2 3 p K mx mx ml .
Total energi kinetik:
m p K K K . 2 2 2 1 2 ( ) cos 2 3 K M m x mlx ml .
14 2 Energi Potensial
Energi potensial pada motor: 0
m
P .
Energi potensial pada pendulum: cos
p
P mgl .
Total energi potensial: cos
m p
P P P mgl .
3 Energi yang Hilang
Energi yang hilang pada motor:
2 1
1 2
D x .
Energi yang hilang pada pendulum:
2 2
1 2
D .
Total energi yang hilang:
2 2 1 2 1 ( ) 2 D D D x 4 Fungsi Lagrange L 1( ) 2 cos 2 2 2 cos 2 3 K P M m x mlx ml mgl
5 Persamaan Euler Lagrange
Misal q = (q1,q2) di mana q1 = x , 1 1 dq q dt dan q2 = ? , 2 2 dq q dt . Diperoleh: 1 ( ) cos L M m x ml q , 2 1 ( ) cos sin d L M m x ml ml dt q , 1 0 L q , 1 D x q ,
15
2 2 4 cos 3 L ml mlx q , 2 2 4 cos sin 3 d L ml mlx mlx dt q , 2 sin sin L mlx mgl q , 2 D q , 1 1 1 d L L D u dt q q q , 2 2 2 0 d L L D dt q q q .
Dengan menyubstitusikan suku-suku yang bersesuaian pada dua persamaan terakhir diperoleh: 2 (M m x) ml cos ml sin x u , (3.1) 2 4 cos sin 0 3ml mxl mgl . (3.2)
Karena model persamaan (3.1) dan (3.2) tersebut taklinear maka dilinearkan terlebih dahulu. Diasumsikan bahwa sudut yang dibentuk oleh pendulum adalah cukup kecil, sehingga sin , cos 1 dan 2 0 .
(lihat Lampiran 5)
Dengan demikian bentuk linear dari persamaan (3.1) dan (3.2) adalah sebagai berikut: (M m x) ml x u , (3.3) 2 4 0 3ml mlx mlg . (3.4)
3.2 Sistem Pendulum Terbalik dengan Lintasan Miring
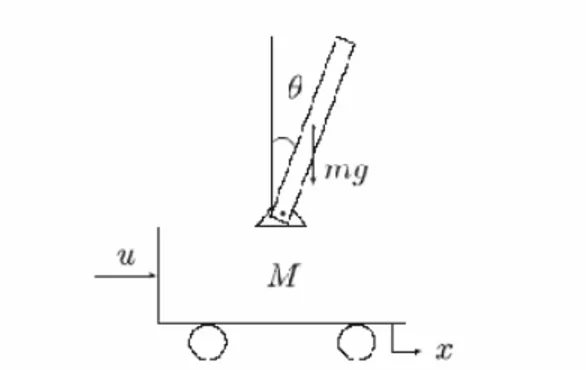
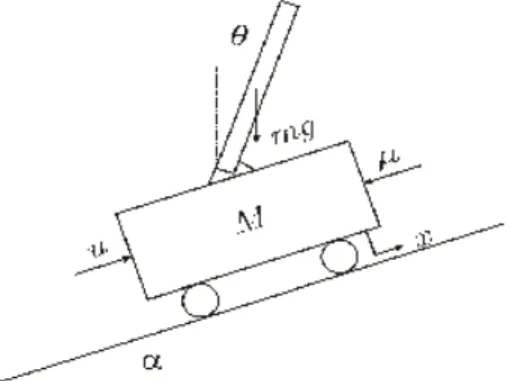
Di bagian ini akan diturunkan model sistem pendulum terbalik dengan lintasan miring seperti pada Gambar 6, di mana lintasan pendulum membentuk sudut sebesar dari sumbu datar. Pendulum diasumsikan seragam (uniform)
16 sehingga inersianya diberikan oleh I = 1 2
3ml . Diasumsikan friksi antara pendulum
dengan motor sebesar dan friksi antara motor dan lintasan sebesar .
Gambar 6 : Sistem Pendulum terbalik dengan lintasan miring M = berat motor
m = berat pendulum ? = sudut pendulum a = sudut kemiringan jalan u = input kendali
Persamaan gerak antara input kendali u, yang merupakan gaya yang bekerja pada motor, dengan posisi motor x terhadap titik awal, sudut pendulum dan sudut kemiringan lintasan a dapat diturunkan sebagai berikut:
1 Energi Kinetik
Energi kinetik pada motor:
2
1 2
m
K Mx .
Energi kinetik pada pendulum:
2 2 1 2 cos( ) 2 3 p K mx mx ml .
Total energi kinetik:
m p K K K . 2 2 2 1 2 ( ) cos( ) 2 3 K M m x mlx ml . 2 Energi Potensial
Energi potensial pada motor:
µ = koefisien gesek antara motor dengan jalan
? = koefisen gesek antara motor dengan pendulum
g = koefisien gravitasi
17
0 m P .
Energi potensial pada pendulum:
cos( )
p
P mgl .
Total energi potensial:
cos( )
m p
P P P mgl .
3 Energi yang Hilang
Energi yang hilang pada motor:
2 1
1 2
D x .
Energi yang hilang pada pendulum:
2 2
1 2
D .
Total energi yang hilang:
2 2 1 2 1 ( ) 2 D D D x . 4 Fungsi Lagrange L 1( ) 2 cos( ) 2 2 2 cos( ) 2 3 K P M m x mlx ml mgl
5 Persamaan Euler Lagrange
Misal q = (q1,q2) dimana q1 = x , 1 1 dq q dt dan q2 = ? , 2 2 dq q dt
1 ( ) cos( ) L M m x ml q , 2 1 ( ) cos( ) sin( ) d L M m x ml ml dt q , 1 0 L q , 1 D x q , 2 2 4 cos( ) 3 L ml mlx q ,
18
2 2 4 cos( ) sin( ) 3 d L ml mlx mlx dt q , 2 sin( ) sin( ) L mlx mgl q , 2 D q , 1 1 1 ( ) sin d L L D u M m g dt q q q , 2 2 2 0 d L L D dt q q q .
Dengan menyubstitusikan suku-suku yang bersesuaian pada dua persamaan terakhir diperoleh:
2
(M m x) ml cos( ) ml sin( ) x u (M m g) sin , (3.5)
4 2
cos( ) sin( ) 0
3ml mxl mgl . (3.6)
Karena model persamaan (3.5) dan (3.6) tersebut taklinear maka dilinearkan terlebih dahulu. Diasumsikan bahwa sudut yang dibentuk oleh pendulum adalah cukup kecil, dengan demikian maka sin , cos 1, 2 0
danx 0 (lihat Lampiran 5). Diasumsikan juga bahwa x 0 0, x 0 0, 0 0 , 0 yang artinya berturut-turut adalah posisi awal motor ada di titik 0, motor bergerak dari keadaan diam, posisi awal pendulum adalah tegak lurus dengan bidang datar, dan pendulum bergerak dari keadaan diam.
Bentuk linear dari persamaan (3.5) dan (3.6) sebagai berikut:
(M m x) ml cos x u (M m g) sin , (3.7)
2
4
cos cos sin 0
3ml mlx mlg mlg . (3.8) Penurunan lengkap dari bentuk linear persamaan (3.7) dan (3.8) dapat dilihat di Lampiran 6.
Persamaan (3.7) dan (3.8) merupakan persamaan gerak antara input kendali u, yang merupakan gaya yang bekerja pada motor, dengan posisi motor x terhadap titik awal, sudut pendulum dan sudut kemiringan jalan a. Langkah selanjutnya
19 akan akan dicari pole dan zero dari persamaan gerak sistem pendulum terbalik dengan lintasan miring.
3.3 Pole dan Zero
Karena persamaan (3.7) dan (3.8) merupakan bentuk persamaan diferensial, maka untuk mempermudah penyelesaian persamaan tersebut diubah ke dalam bentuk persamaan aljabar dengan menggunakan transformasi Laplace.
Transformasi Laplace dari persamaan (3.7) dan (3.8) adalah:
2 2
(M m s X s) ( ) mls cos ( )s sX s( ) U s( ) (M m g) sin (3.9)
2 2 2
4
( ) ( ) cos ( ) cos ( ) sin
3ml s s s s mls X s mgl s mgl
(3.10)
Persamaan (3.19) dan (3.20) dapat ditulis dalam bentuk matriks sebagai berikut:
2 2 2 4 2 2 3 ( ) ( ) ( ) sin ( ) cos ( ) sin cos cos X s U s M m g M m s s mls s mgl mls ml s s mgl
1 2 2 2 4 2 2 3 ( ) ( ) cos ( ) ( ) sin
( ) cos cos sin
X s M m s s mls U s M m g s mls ml s s mgl mgl
2 2 2 4 3 2 2
( ) 1 cos cos ( ) ( ) sin
( ) cos ( ) sin X s ml s s mgl mls U s M m g s mls M m s s mgl
dengan 3 2 3 2 1 0 ( ) s a s a s a s a
di mana 4 2 2 2 2 3 3( ) cos a M m ml m l
2 4 2 3 ( ) a ml M m
1 ( ) cos a M m mgl
0 cos a mgl
Bentuk persamaan matriks di atas dapat dituliskan dalam bentuk persamaan matrik sebagai berikut:
2 2 2
4 3
2 2
( ) 1 cos cos ( ) ( ) sin
( ) cos ( ) 0 sin
X s ml s s mgl mls U s M m g
20 2 2 2 4 3 2 2 ( ) 1 cos cos ( ) ( ) cos ( ) 0 X s ml s s mgl mls U s s mls M m s s 2 2 2 4 3 2 2 ( ) sin cos cos 1 sin cos ( ) M m g ml s s mgl mls mgl mls M m s s
Selanjutnya dapat diperoleh:
2 2 2 4 3 2 2 ( ) 1 cos cos ( ) ( ) cos ( ) 0 X s ml s s mgl mls U s s mls M m s s 2 2 4 3 2 ( ) 1 cos ( ) ( ) cos X s ml s s mgl U s s mls Dengan demikian, 2 2 4 3 3 2 3 2 1 0 cos ( ) ( ) : ( ) ( ) x ml s s mgl X s P s U s s a s a s a s a
2 3 2 3 2 1 0 ( ) cos ( ) : ( ) ( ) s mls P s U s s a s a s a s a
Diasumsikan tidak ada friksi antara motor dan pendulum serta tidak ada friksi antara motor dan lintasan, yaitu 0 , maka Px(s) dan P?(s) memiliki pole
takstabil di 2 2 4 3 2 4 2 2 2 2 2 3 cos ( ) [ ( ) cos ] ( ) cos x ml s mgl P s s M m ml m l s M m mgl , (3.11) 2 2 2 2 2 4 3 cos ( ) [ ( ) cos ] ( ) cos ml P s M m ml m l s M m mgl . (3.12)
Dapat dilihat dengan mudah bahwa jika 0 , maka bentuk persamaan (3.11) dan (3.12) akan tereduksi menjadi:
2 2 3 2 3 2 1 0 ( ) 4 3 3 ( ) : ( ) ( ) x X s s ml s gml P s U s s a s a s a s a , 3 2 3 2 1 0 ( ) 3 ( ) : ( ) s mls P s U s a s a s a s a , seperti pada persamaan (2.11) dan (2.12) pada kasus sistem pendulum terbalik dengan lintasan datar.
21
Menentukan Zero
Pada bagian ini akan ditentukan zero dari fungsi transfer P s dan x( ) P s pada ( ) persamaan (3.11) dan (3.14) a. Zero dari P sx( )
2 2 4 cos 0 3ml s mgl
2 2 4ml s 3mglcos
2 2 3 cos 4 mgl s ml
2 3 cos 4 g s l 3 cos 4 g s l
Jadi non minimum phase zero dariP s adalah: x( ) 3 cos 4 g z l
(3.13) Jika 0 maka bentuk persamaan (3.13) akan tereduksi menjadi:
3 4 g z
l seperti pada persamaan (2.14) b. Zero dari P s( ) cos 0 ml
0 s
Jadi P s tidak mempunyai non minimum phase zero ( )
Menentukan Pole
Selanjutnya akan ditentukan pole dari fungsi transfer P s dan x( ) P s( )
2 4 2 2 2 2 2 ( ) cos cos 0 3 s M m ml m l s M m mgl 2 2 2 2 2 2 4( ) 3 cos 3 cos 0 s M m ml m l s M m mgl 2 0
22 2 2 2 3( ) cos 4( ) 3 cos M m mgl s M m m ml 2 3 ( ) cos 4( ) 3 cos g M m s l M m m
Jadi pole tak stabil dari P s danx( ) P s adalah: ( )
2 3 ( ) cos 4( ) 3 cos g M m p l M m m
(3.14)
Jika 0 maka bentuk persamaan (3.14) akan tereduksi menjadi:
3 ( )
(4 )
g M m p
BAB IV
KARAKTERISASI PARAMETER PADA MASALAH
TRACKING ERROR OPTIMAL
4.1 Ekspresi Analitik
Pada bagian ini akan dibahas karakterisasi parameter pada masalah tracking error optimal. Pengendalian posisi motor x dan ekspresi analitik dari J yang akan menjadi pusat perhatian dalam karya ilmiah ini. Ekspresi analitik dari J diberikan oleh Teorema 3 berikut ini:
Teorema 3
Misalkan sistem P(s) memiliki pole takstabil pk (k = 1, ... , np) dan zero takstabil zi
(i = 1, ... , nz). Ekspresi analitik bagi
* 2 0 inf ( ) K J e t dt diberikan oleh * 2 1 , 1 2 Re 4 Re Re ( ) p z n n i k l k l k i i k l k l k l l z p p J p p p p b b z di mana 1; 1 : l k; 2 k l p p p k p p p l k n b n
1 : 1 z i k i k n z p k z p i
Bukti : lihat Chen et al. 2003.
Akibat 1
( )
x
P s pada kasus ini hanya memiliki satu pole takstabil p dan satu non minimum phase zero z, maka :
2 2 2 2 4 2 p J z pp 2 2 2 z p
(4.1) dengan 1 z p z p
24
2 2 2 4 ( ) p z p
Sehingga dengan menyubstitusi 2 ke dalam persamaan (4.1) didapat
2 2 2 2 2 4 2 p J z p z zp p
2 2 2( ) ( ) z p J z z p
(4.2) Akibat 2
Jika P s memiliki dua pole takstabil p p1, 2 dan satu non minimum phase zero z, maka : 2 2 1 1 2 2 2 2 1 1 1 2 1 2 2 2 2 2 8 2 J z p b p p b b p b
(4.3) dengan 2 1 1 2 1 p p b p p , 2 2 1 2 1 2 2 1 p p b p p , 1 2 2 1 2 p p b p p , 2 1 2 2 2 2 1 2 p p b p p , 1 1 1 1 z p z p , 2 2 1 1 2 1 4 p z p , 2 2 2 1 z p z p , 2 2 2 2 2 2 4 p z p . Dengan menyubstitusi 2 2 2 2 1, 2, 1, 2, 1, 2, 1, 2 b b b b ke dalam persamaan (4.3) di dapat: 2 2 1 2 1 1 2 1 2 2 1 2 2 2 2 2 2 1 1 2 1 2 2 1 1 1 2 2 8 16 8 2 p p p p p p p p p p J z p p z p p p p p z p z p p p z p
4.2Tracking Error Optimal
Sudah ditunjukkan bahwa sistem pendulum terbalik dengan lintasan miring memiliki satu pole takstabil dan satu non minimum phase zero seperti diberikan
25
oleh persamaan (3.13) dan (3.14), maka berdasarkan akibat 1 tracking error optimal diberikan oleh:
2 2 2 2 3 cos 3 ( ) cos 2 4 4( ) 3 cos
3 cos 3 cos 3 ( ) cos
4 4 4( ) 3 cos g g M m l l M m m J g g g M m l l l M m m (4.4)
Dari persamaan (4.4) dapat disederhanakan menjadi:
2 2 3 4 2 3 4 cos 4 3 cos cos M m m M m l J g M m m M m (4.5) Selanjutnya diasumsikan m m l
l dengan m massa pendulum, l panjang pendulum dan ”massa jenis pendulum”. Persamaan (4.5) menjadi:
2 2 3 4 2 3 4 cos 4 3 cos cos M l l M l l J g M l l M l . (4.6) Bentuk berikut: 2 3 4 2 3 4 cos cos M l l M l M l l M l
dapat dirasionalkan penyebutnya sehingga menjadi:
2 2 3 4 2 3 4 cos cos M l l M l l Sehingga persamaan (4.6) menjadi:
2 2 2 3 4 2 3 4 cos 4 3 cos cos M l l M l l J g l
dan dapat disederhanakan menjadi:
3 2 9 2 4 2 3 4 2 64 cos 9 3 cos l J M l l M l g . (4.7)
Selanjutnya akan dicari l dengan menyelesaikan persamaan dJ 0 dl
26 Misalkan 3 2 9 2 2 64 9 3 cos l w g maka 5 9 2 2 2 32 ' 3 3 cos w g l
4 2 3 4 cos v M l l M l maka 2 3 2 3 4 2 3 4 4 3cos ' 4 cos 2 8 cos v M l l M l M l M l l 5 9 2 2 4 2 3 4 2 32 cos 3 3 cos M l l M l dJ dl g l 3 9 2 2 3 2 3 2 4 2 3 2 4 256 cos 4 3cos 2 9 3 cos 8 cos M l l M l M l g l M l l
Dengan demikian berakibat:
5 9 2 2 4 2 3 4 2 32 cos 3 3 cos M l l M l g l 3 9 2 2 3 2 3 2 4 2 3 2 4 256 cos 4 3cos 2 9 3 cos 8 cos M l l M l M l g l M l l
yang selanjutnya dapat disederhanakan menjadi:
2 2 2 2 2
4 3cos l 8 3cos lM 60M 0.
Penyelesaian bagi l adalah:
2
2 2 2 2 2 2 2
1,2 2 2
8 3cos 8 3cos 240 4 3cos
2 4 3cos
M M M
l
2 2 4
1,2 2
8 3cos 1024 768 cos 9 cos
8 6 cos
M M
l
2 2 4
1 2
8 3cos 1024 768 cos 9 cos
8 6 cos
M l
27
2 2 4
2 2
8 3cos 1024 768 cos 9 cos
8 6 cos
M l
Jadi panjang pendulum minimal adalah
2 2 4
2
8 3cos 1024 768 cos 9 cos
8 6 cos
M
l
2 2 4
2
8 3cos 1024 768 cos 9 cos
8 6 cos m
M
(4.8) Penurunan secara lengkap dapat dilihat pada Lampiran 8.
Dapat dilihat bahwa jika 0 , maka ekspresi akan tereduksi menjadi: 265 5 2 m M
(4.9) Persamaan (4.8) menunjukkan bahwa rasio antara massa pendulum dan massa motor adalah konstan. Sehingga tracking error optimal dapat dicapai sepanjang rasio antara massa pendulum dan massa motor adalah konstan, tanpa memandang bahan dari pendulum.
BAB V
SIMULASI
Pada karya ilmiah ini bahan pendulum yang digunakan adalah platina. Bahan platina dipilih karena platina mempunyai massa jenis yang cukup besar bila dibandingkan dengan bahan yang lain, yaitu sebesar 21450 kg/m3 (Kittel 2005).
Dengan asumsi pendulum berbentuk silinder berjari-jari (0,5 .10-2) meter dan panjang pendulum 2l, maka volum pendulum:
2 2 V r l
3 2 (5 10 ) 2 V l
6 2 25 10 V l
5 5 10 V l .
Selanjutnya akan dicari nilai dari sebagai berikut: m V
5 5 5 10 5 10 m m l l
Jadi nilai adalah :
5
5 10
di mana
= massa jenis pendulum m = massa pendulum V = volum pendulum
Jika pendulum terbuat dari platina yang mempunyai massa jenis 21450 kg/m3, maka 107250 .10 . Dengan mengambil 5 3,14 maka nilai
3, 3677 .
Dengan mengambil M = 1 maka dapat ditentukan panjang pendulum minimal untuk sistem pendulum terbalik dengan lintasan datar yaitu 1, 675 meter. Sedangkan untuk sistem pendulum terbalik dengan lintasan miring 450 diperoleh
2 0 2 0 4 0
2 0
8 3cos 45 1024 768 cos 45 9 cos 45 1 8 6 cos 45 3, 3677
29 2 2 4 2 8 3(0, 7071) 1024 768(0, 7071) 9(0, 7071) 8 6(0, 7071) 3, 3677 l l = 1,119 meter.
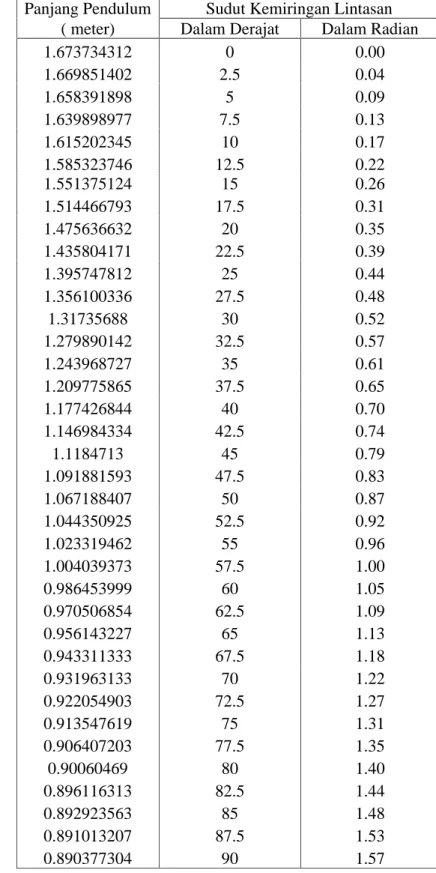
Secara lengkap perbandingan sudut kemiringan lintasan dan panjang pendulum minimal yang diperlukan l dapat dilihat Gambar 7.
Pada Gambar 7 disimulasikan nilai tracking error optimal J dan panjang pendulum minimal l pada lintasan yang besar sudut kemiringannya berbeda-beda.
Hasil dari simulasi antara nilai tracking error optimal J dan panjang pendulum optimal l pada lintasan yang besar sudut kemiringannya berbeda-beda dapat dilihat pada Gambar 7 sebagai berikut:
TRACKING ERROR 0 50 100 150 200 250 300 350 400 450 500 0.1 0.4 0.7 1 1.3 1.6 1.9 2.2 2.5 2.8
panjang pendulum optimal (l)
tr a ck in g er ro r o p ti m a l (J ) Jd J45 J30 J15 J12
Gambar 7: Grafik masalah tracking error Dari gambar di atas dapat dilihat:
1. Pada lintasan datar panjang pendulum minimal 1,7 meter dengan J = 15,5085 2. Pada lintasan miring dengan sudut kemiringan 100 panjang pendulum minimal
1,6 meter dengan J = 17,27245
3. Pada lintasan miring dengan sudut kemiringan 150 panjang pendulum minimal
30 4. Pada lintasan miring dengan sudut kemiringan 300 panjang pendulum minimal
0,7 meter dengan J = 96,19386
5. Pada lintasan miring dengan sudut kemiringan 450 panjang pendulum minimal
1,1 meter dengan J = 120,7843
Hasil secara lengkap simulasi dapat dilihat pada Lampiran 9.
Jadi jika pendulum sangat pendek maka nilai J sangat besar. Jika panjang pendulum diperpanjang, maka nilai J semakin kecil. Kejadian ini berlaku sampai pada satu titik minimum. Setelah itu akan berubah, yaitu jika pendulum semakin panjang maka nilai J semakin besar. Tracking error optimal juga dipengaruhi oleh sudut kemiringan lintasan. Jika sudut kemiringan lintasan semakin besar maka nilai optimumnya juga semakin besar. Ini berarti bahwa semakin miring lintasan, maka semakin sulit sistem untuk dikendalikan dan distabilkan.
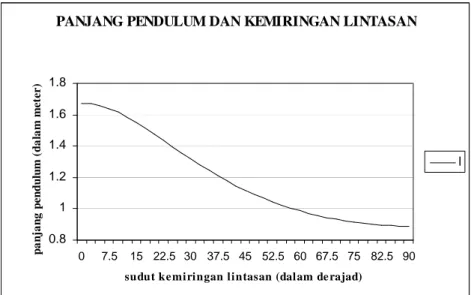
Selain itu juga disimulasikan panjang pendulum optimal l dan lintasan yang besar sudut kemiringannya berbeda-beda lihat Gambar 8.
Hasil dari simulasi antara panjang pendulum optimal l dan lintasan yang besar sudut kemiringannya berbeda-beda dapat dilihat pada Gambar 8 berikut:
PANJANG PENDULUM DAN KEMIRINGAN LINTASAN
0.8 1 1.2 1.4 1.6 1.8 0 7.5 15 22.5 30 37.5 45 52.5 60 67.5 75 82.5 90
sudut ke miringan lintasan (dalam de rajad)
p a n ja n g p e n d u lu m (d a la m m e te r ) l
Gambar 8: Grafik panjang pendulum optimal dan sudut kemiringan lintasan
Dari Gambar 8 di atas dapat dilihat bahwa panjang pendulum minimal yang diperlukan sangat dipengaruhi oleh besar sudut kemiringan lintasan. Apabila sudut kemiringan lintasan semakin besar, maka panjang pendulum semakin kecil.
BAB VI
SIMPULAN
Dari penelitian ini dapat disimpulkan sebagai berikut :
1. Diturunkan model sistem pendulum terbalik dengan lintasan datar dan model sistem pendulum terbalik dengan lintasan miring. Kedua model tersebut merupakan persamaan gerak antara input kendali u, yang merupakan gaya yang bekerja pada motor dengan posisi motor x terhadap titik awal dan sudut pendulum .
2. Tracking error optimal dipengaruhi oleh sudut kemiringan lintasan. Jika sudut kemiringan lintasan semakin besar, maka tracking errornya juga semakin besar.
3. Panjang pendulum optimal dipengaruhi oleh sudut kemiringan lintasan. Hubungan antara panjang pendulum optimal dan sudut kemiringan lintasan berbanding terbalik. Sudut kemiringan lintasan semakin besar maka panjang pendulum optimal semakin pendek.
4. Tracking error optimal dapat dicapai sepanjang rasio antara massa pendulum dan massa motor adalah konstan, tanpa memandang bahan dari pendulum.
DAFTAR PUSTAKA
Atay FM, Balancing the inverted pendulum using position feedback, App. Math. Lett., vol. 12, pp. 51–56;1999.
Chen J, Hara S, and Chen G , ”Best tracking and regulation performance under control energy constraint,” IEEE T. Automat. Contr., vol. 48, no. 8, pp. 1320– 1336; 2003.
Hara S dan Kogure C , ”Relationship between H2 control performance limits and RHP pole/zero locations,” Proc. 2003 SICE Annual Conference, Fukui, Japan, pp. 12421246; 2003
Kittel C. Introduction to Solid State Physics. Eighth Edition. John Wiley & Sons, Inc; 2005.
Lewis AD. A Mathematical Approach to Classical Control, Canada: Departement of Mathematics and Statistics Queen’s University Kingston; 2004.
Loram ID dan Lakie M , ”Human balancing of an inverted pendulum:
position control by small, ballistic-like, throw and catch movements,”J. Physiol., 540.3, pp. 1111-1124; 2002.
Loram ID, Gawthrop PJ, dan Lakie M , ”The frequency of human, manual adjustments in balancing an inverted pendulum is constrained by intrinsic physiological factors,” J. Physiol., 577.1, pp. 417-432; 2006.
Loram ID, Kelly SM, dan Lakie M , ”Human balancing of an inverted pendulum: is sway size controlled by ankle impedance?” J. Physiol., 532.3, pp. 879-891; 2001.
Microrobot Co.L.td,” MP-2000 ( MR-010 )Inverted Pendulum System Manual”, , http//www.active-robots.com/produck/inverted-pendulum/ip-manual.pdf, [21 Des 2007]
Ogata K. Modern Control Engineering, Second Edition. Minnesota: University of Minnesota; 1990.
Ogata K. Teknik Kontrol Automatik. Jilid 1,2. Edi Laksono, penerjemah; Bandung: ITB; 1985. Terjemahan dari:” Modern Control Engineering”. Taurasi I, Inverted Pendulum Studies for Seismic Attenuation, SURF Final Report
LIGO T060048-00-R, California Institute of Technology, USA; 2005.
Woodyatt AR, Middleton RH, and Freudenberg JS, Fundamental Constraints for the Inverted Pendulum Problem, Technical Report EE9716, Department of Electrical and Computer Engineering, the University of Newcastle, Australia; 1997
35
Lampiran 1
Bukti Sifat-sifat Transformasi Laplace
Sifat – sifat transformasi Laplace :
Misalkan £ f t F s dan £ g t G s , maka: 1. Sifat penjumlahan £ f t( ) g t( ) F s( ) G s( ) Bukti: £ 0 st
f t
g t
e
f t
g t dt
0 0 st st e f t dt e g t dt
£f(t) + £g(t) F(s) + G(s) 2. Sifat perkalian Jika a R , maka: £af(t) a F(s) Bukti: £ af(t) 0 st e af t dt
0 st a e f t dt
a£ f(t) a F(s) 3. Sifat turunan pertama
£
0
df t
sF s
f
dt
Bukti: £ 0 0( )
( )
( )
lim
b st st bdf t
df t
df t
e
dt
e
dt
dt
dt
dt
Misalkan fungsi f t dan turunannya adalah kontinu di dalam selang terbatas, maka :
Misal u e st
st
36
df t dv dt
v f t maka dengan integral parsial diperoleh:
0 0 0
( )
( )
( )
b stdf t
st b b ste
dt
e
f t
s
e
f t dt
dt
0 0 st sb s e f t dt f e f b Akan ditunjukkan lim sb 0
b e f b
Karena f t eksponensial berorder e , maka ada konstanta M dan T yang t memenuhi: t t Me f t Me
atau st t st st t e Me e f t e Me
s t st s t Me e f t Me untuk t T
Karena T cukup besar t T , fungsi e stf t terbatas diantara dua fungsi untuk s mendekati 0 ketika t . Sehingga e stf t juga mendekati 0 ketika t , jadi lim sb 0
b e f b
£ df t sF s f 0 0 dt
( ) (0) sF s f 4. Sifat turunan kedua
£ 2 2
( )
( )
(0)
(0)
d f t
s F s
f
sf
dt
Bukti: £ 2 2 0( )
st( )
d f t
d f t
e
dt
dt
dt
0 0
( )
( )
stdf t
stdf t
e
s
e
dt
dt
dt
(0)f s £ df t( ) dt
37
2 ( ) (0) (0) s F s f sf
5. Sifat eksponensial £
1
ate
s a
Bukti: £ 0 at st ate
e e dt
( ) 0 s a te
dt
( ) 0 1 s a t e s a
0 1 e e s a
1 0 1 s a
1 s a
35
Lampiran 1
Bukti Sifat-sifat Transformasi Laplace
Sifat – sifat transformasi Laplace :
Misalkan £ f t F s dan £ g t G s , maka: 1. Sifat penjumlahan £ f t( ) g t( ) F s( ) G s( ) Bukti: £ 0 st
f t
g t
e
f t
g t dt
0 0 st st e f t dt e g t dt
£f(t) + £g(t) F(s) + G(s) 2. Sifat perkalian Jika a R , maka: £af(t) a F(s) Bukti: £ af(t) 0 st e af t dt
0 st a e f t dt
a£ f(t) a F(s) 3. Sifat turunan pertama
£
0
df t
sF s
f
dt
Bukti: £ 0 0( )
( )
( )
lim
b st st bdf t
df t
df t
e
dt
e
dt
dt
dt
dt
Misalkan fungsi f t dan turunannya adalah kontinu di dalam selang terbatas, maka :
Misal u e st
st
36
df t dv dt
v f t maka dengan integral parsial diperoleh:
0 0 0
( )
( )
( )
b stdf t
st b b ste
dt
e
f t
s
e
f t dt
dt
0 0 st sb s e f t dt f e f b Akan ditunjukkan lim sb 0
b e f b
Karena f t eksponensial berorder e , maka ada konstanta M dan T yang t memenuhi: t t Me f t Me
atau st t st st t e Me e f t e Me
s t st s t Me e f t Me untuk t T
Karena T cukup besar t T , fungsi e stf t terbatas diantara dua fungsi untuk s mendekati 0 ketika t . Sehingga e stf t juga mendekati 0 ketika t , jadi lim sb 0
b e f b
£ df t sF s f 0 0 dt
( ) (0) sF s f 4. Sifat turunan kedua
£ 2 2
( )
( )
(0)
(0)
d f t
s F s
f
sf
dt
Bukti: £ 2 2 0( )
st( )
d f t
d f t
e
dt
dt
dt
0 0
( )
( )
stdf t
stdf t
e
s
e
dt
dt
dt
(0)f s £ df t( ) dt
37