Makalah Perpindahan Kalor Radiasi Bahan

(1)

Makalah Perpindahan Kalor

Pemicu V – Perpindahan Kalor Radiasi

Disusun oleh: Kelompok 1 Angela Susanti / 1206247303 Rexy Darmawan / 1206202103 Reza Syandika / 1206240013 Seva Juneva / 1206241152 Wildan Nurasad / 1206202160

DEPARTEMEN TEKNIK KIMIA

FAKULTAS TEKNIK UNIVERSITAS INDONESIA DEPOK

(2)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |i

DAFTAR ISI

Daftar Isi...i

BAB I : PENDAHULUAN

I.1 Problem Statement...1

I.2 Rumusan Masalah...2

I.3 Informasi – Informasi yang Diperlukan...2

BAB II : ISI

II.1 Tugas...3

II.2 Perhitungan...21

BAB III : PENUTUP

III.1 Kesimpulan...26

Daftar Pustaka...28 Lampiran

(3)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |1 BAB I

PENDAHULUAN I.1 Problem Statement

Radiasi termal adalah proses di mana permukaan benda memancarkan energi panas dalam bentuk gelombang elektromagnetik. Contoh radiasi termal di antaranya adalah : radiasi infra merah dari radiator rumah tangga biasa atau pemanas listrik, serta panas dan cahaya yang dikeluarkan oleh sebuah bola lampu pijar bercahaya.

Radiasi termal dihasilkan ketika panas dari pegerakan partikel bermuatan dalam atom diubah menjadi radiasi elektromagnetik. Gelombang frekuensi yang dipancarkan dari radiasi termal merupakan distribusi probabilitas tergantung hanya pada suhu.

I. 2 Rumusan Masalah

 Apa yang dimaksud dengan radiasi termal?

 Apa perbedaan antara perpindahan kalor secara radiasi dengan berbagai mode perpindahan kalor lainnya?

 Bagaimana mekanisme fisis dan sifat – sifat dari radiasi termal?

 Hukum – hukum atau asas – asas apa saja yang terlibat dalam perpindahan kalor radiasi?

 Bagaimana proses perpindahan kalor pada benda hitam dan benda tak-hitam?

 Apa yang dimaksud dengan koefiisen perpindahan kalor radiasi?

 Bagaimana cara menentukan faktor bentuk radiasi?

 Bagaimana mekanisme proses radiasi antara dua permukaan?

 Bagaimana proses perpindahan kalor secara radiasi yang terjadi pada gas?

 Bagaimana proses perpindahan kalor secara radiasi yang terjadi antara gas dan permukaan yang mengelilinginya?

I. 3 Informasi – Informasi yang Diperlukan

 Prinsip radiasi termal

 Perbedaan antara radiasi dan konveksi

 Mekanisme fisis proses radiasi

 Sifat – sifat proses radiasi

 Hukum Stefan-Boltzman

 Hukum Kirchoff

 Asas Planck

(4)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |2

 Perpindahan kalor secara radiasi pada benda hitam dan benda tak – hitam

 Koefisien perpindahan kalor radiasi

 Faktor – faktor yang mempengaruhi koefisien perpindahan kalor radiasi

 Pengertian faktor bentuk radiasi

 Cara menentukan faktor bentuk radiasi

 Hubungan antara berbagai faktor bentuk radiasi

 Radiasi antara dua permukaan

 Radiasi pada gas

(5)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |3 BAB II

ISI II.1 Tugas

1. Apa yang anda ketahui tentang radiasi termal? Bagaimana perbedaannya dengan proses konveksi?

Radiasi termal merupakan proses di mana energi diemisikan oleh suatu benda pada temperatur tak-nol. Emisi tak hanya terjadi pada permukaan solid, tetapi juga dapat timbul dari liquid maupun gas. Energi pada medan radiasi dipindahkan oleh gelombang elektromagnetik (atau secara alternatif, oleh foton). Apabila perpindahan kalor secara konveksi dan konduksi membutuhkan medium perantara, perpindahan kalor secara radiasi tidak membutuhkan medium. Pada kenyataannya, perpindahan secara radiasi dapat terjadi paling efektif dalam kondisi vakum.

Gambar 1. Perpindahan Kalor Konduksi, Konveksi, dan Radiasi(Sumber :

Fundamentals of Heat and Mass Transfer, 7th Edition, Incropera, 2011)

Beberapa perbedaan antara perpindahan kalor secara radiasi (radiasi termal) dan konveksi ditunjukkan dalam tabel di bawah ini.

Tabel 1. Perbandingan Beberapa Karakteristik antara Perpindahan Kalor Radiasi dan Konveksi

Perpindahan Kalor Radiasi Perpindahan Kalor Konveksi

 Pertukaran kalor terjadi antara dua atau  Pertukaran kalor terjadi antara permukaan solid dan fluida bergerak yang berada pada lebih benda (permukaannya)

temperatur yang berebeda

 Perpindahan kalor dapat terjadi tanpa  Perpindahan kalor dapat terjadi dengan

menggunakan medium perantara medium perantara

 = =− = ( 4 − 4 )  = ( − )

∞

(6)

(7)

Radiasi selalu merambat dengan kecepatan cahaya 3 × 1010_{cm/s. Kecepatan cahaya setara}

dengan hasil perkalian antara panjang gelombang dengan frekuensi radiasi yang dapat dituliskan secara matematis sebagai berikut.

= (1.1)

Perambatan radiasi berlangsung dalam bentuk kuantum-kuantum yang diskrit. Setiap kuantum tersebut memiliki energi sebesar:

= (1.2)

dengan nilai h sebesar 6.625 x 10-34 J.s (konstanta Planck). Kuantum dapat dianggap sebagai partikel yang mengandung energi

Radiasi dapat digambarkan sebagai “gas foton” (“photon gas”) yang dapat mengalir dari satu tempat ke tempat yang lain. Dengan menggunakan hubungan relativitas antara massa dan energi, dapat diturunkan sebuah persamaan untuk massa dan energi “partikel” tersebut, yaitu:

= 2₌ (1.3)

(1.4) = 2

(1.5)

Momentum = 2 =

Persamaan densitas energi radiasi per satuan volume dan per satuan panjang-gelombang dapat ditentukan dengan menerapkan prinsip termodinamika statistik-kuantum, yaitu :

= 8 −5

(1.6) − 1

di mana k merupakan konstanta Boltzmann sebesar 1,38066 × 10-23 J/molekul.K. Bila densitas energi diintegrasikan sepanjang seluruh panjang-gelombang untuk benda hitam, maka energi total yang dipancarkan sebanding dengan pangkat empat suhu absolut.

Sifat - Sifat Radiasi Termal

Ketika energi radiasi menimpa permukaan suatu bahan, maka sebagian dari radiasi itu akan dipantulkan (refleksi), sebagian lainnya akan diserap (absorpsi), dan sebagian lagi akan diteruskan (transmisi). Fraksi yang dipantulkan disebut sebagai reflektivitas ρ, fraksi yang diserap disebut sebagai absorptivitas α, dan fraksi yang diteruskan disebut sebagai transmisivitas τ. Ketiga komponen ini terhubung secara matematis dalam persamaan :

+ + = 1 (1.7)

di mana ketiganya akan mempengaruhi sifat-sifat radiasi sebagai berikut.

a. Absorpsi. Radiasi yang jatuh akan diserap oleh bahan, tergantung pada benda itu sendiri (hitam, kelabu, atau putih).

(8)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |5 b. Refleksi. Radiasi yang jatuh pada bahan akan dipantulkan. Dua fenomena refleksi yang dapat diamati adalah refleksi spekular dan refleksi baur. Pada refleksi spekular, sudut jatuh sama dengan sudut pantul radiasi sedangkan pada refleksi baur, radiasi yang jatuh tersebar merata ke segala arah.

c. Transmisi. Radiasi yang jatuh akan diteruskan oleh bahan. Akan tetapi, tidak banyak benda yang mampu meneruskan radiasi (biasanya diserap).

Besar radiasi dapat dinyatakan dalam :

Daya emisi (E) yaitu energi yang dipancarkan suatu benda per satuan luas

waktu. Jika terdapat suatu benda hitam sempurna dalam keadaan vakum maka lama kelamaan suhu benda tersebut akan turun dan sama dengan suhu lingkungan akibat dari permukaan yang memancarkan emisi radiasi termal, sampai pada suatu saat keadaan setimbang. Pada saat ini, berlaku hubungan:

= (1.8)

di mana A adalah luas permukaan sedangkan qi adalah fluks radiasi dalam W/m2.

Emisivitas ( ) yaitu perbandingan emisi suatu benda dengan daya emisi benda

hitam pada suhu yang sama. Secara matematis, emisivitas dapat dinyatakan sebagai :

= (1.9)

dengan E dan Eb adalah daya emisi benda dan benda hitam.

3. Apa yang anda ketahui tentang hukum Stefan-Boltzman, Hukum Kirchoff, dan Asas Planck?

Hukum Stefan - Boltzman

Hukum Stefan – Boltzman menyatakan bahwa “Jika suatu benda hitam memancarkan

kalor, maka intensitas pemancaran kalor tersebut sebanding – laras dengan pangkat empat dari temperatur absolut”. Pernyataan tersebut dapat dituliskan secara matematis sebagai :

= 4 (1.10)

di mana merupakan konstanta Stefan Boltzman sebesar 5,6697 x 10-8 W/(m2 K4).

Umumnya setiap permukaan memancarkan jumlah energi yang berbeda pada panjang gelombang yang tidak sama. Apabila melambangkan daya emisi monokromatik pada panjang gelombang , maka daya emisi total dapat dituliskan sebagai berikut :

∞

= (1.11)

(9)

(10)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |

6

∞

= λ (1.12)

0

Dari hukum Stefan Boltzman tersebut, terlihat bahwa :

Efek radiasi pada umumnya tidak signifikan pada temperatur yang relatif rendah karena nilai konstanta sangat rendah.

Pada temperatur kamar, kira – kira 300 K,bernilai 460 (W/m2).

Pada T rendah, efek radiasi sering diabaikan, sedangkan pada temperatur tinggi, efek radiasi perlu diperhatikan bahkan sering menjadi faktor yang dominan, karena E sebanding dengan T4.

Asas Planck

Teori Max Planck mencoba menjelaskan konsep radiasi karakteristik yang dipancarkan oleh benda mampat. Radiasi inilah yang menunjukkan sifat partikel dari gelombang. Radiasi yang dipancarkan sertiap benda terjadi secara tidak kontinu dan dipancarkan dalam satuan kecil yang disebut kuanta (energi kuantum). Asas Planck menyatakan kuanta berbanding lurus dengan frekuensi tertentu dari cahaya (Persamaan 1.2)

Asas Planck menyatakan bahwa “Cahaya yang terdiri dari partikel – partikel yang bergerak disebut foton mempunyai energi sebesar hv.”. Energi yang dipancarkan pada panjang gelombang dari benda hitam dengan temperatur T dapat dinyatakan sebagai berikut.

( ) = 1 2 −1 (1.13) 5

di mana melambangkan daya emisi radiasi monokromatik benda hitam pada temperatur T (W/m3_),

1 melambangkan konstanta radiasi pertama (3,7418 x 10-16 W/m2), dan 2

melambangkan konstanta radiasi kedua (1,4388 x 10-2_{m K).}

Daya emisi akan mencapai nilai maksimum pada panjang gelombang yang menurun bersamaan dengan temperatur permukaan yang bertambah. Nilai dari saat maksimum dapat ditentukan dengan menggunakan Asas Planck dengan turunan pertama sebesar 0.

= 1 (1.14) 5 2−1 Hukum Kirchoff

Berdasarkan Hukum Kirchoff, pada saat kesetimbangan termal α dari body memiliki nilai yang sama besar dengan ɛ. Hasilnya tidak berlaku apabila body tidak berada dalam kesetimbangan termal dengan lingkungannya. Dalam kesetimbangan termal berlaku :

(11)

7

1 = 1 (1.15)

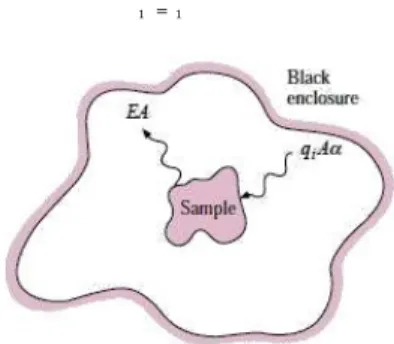
Gambar 2. Model yang Digunakan untuk Penurunan Hukum Kirchoff

(Sumber : Heat Transfer, 10th Edition, Holman, 2010)

Berdasarkan persamaan 1.15, apabila suatu benda dengan properti T, α, dan ɛ berada di dalam selubung isotermal dengan temperatur T, maka dalam keadaan kesetimbangan berlaku kondisi “Energi yang diserap sama dengan energi yang dikeluarkan”. Apabila benda diganti dengan benda hitam, maka akan berlaku :

2 = 2 = (1.16)

Dengan demikian berlaku :

1 = 1

(1.17)

2

Karena benda hitam memiliki nilai absorptivitas 1, persamaan di atas dapat direduksi menjadi

=1 (1.18)

1

Sesuai dengan definisi 1, persamaan di atas dapat diubah kembali ke dalam bentuk berikut.

= =4 _(1.19)

sehingga diperoleh bentuk Hukum Kirchoff , yaitu 1 = 1.

4. Apa yang dimaksud Benda Hitam dan Benda Tak-Hitam? Bagaimanakah proses perpindahan kalor yang terjadi pada benda tersebut?

Pengertian Benda Hitam

Benda hitam adalah objek yang dapat mengabsorb seluruh radiasi elektomagnetik yang jatuh kepadanya tanpa memperhatikan panjang gelombang dan arahnya. Pada suhu dan panjang gelombang tertentu, tidak ada permukaan yang dapat memancarkan energi lebih besar dari benda hitam. Radiasi yang dipancarkan oleh benda hitam merupakan fungsi dari panjang gelombang dan suhu, tetapi tidak bergantung kepada arah. Akan tetapi pada kenyataannya, tidak ada benda yang hitam sempurna. Setiap permukaan selalu memantulkan radiasi yang datang, betapapun kecilnya. Meskipun demikian, konsep benda hitam ini sangat diperlukan untuk menyederhanakan proses perhitungan perpindahan kalor radiasi.

(12)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |8 Pengertian Benda-Tak-Hitam

Benda tak hitam adalah benda yang tidak menyerap seluruh energi yang jatuh pada permukaannya. Sebagian dari energi yang jatuh padanya akan dipantulkan kembali ke permukaan perpindahan kalor lainnya sedangkan sebagian lainnya akan dipantulkan ke luar sistem.

Perpindahan Kalor Benda Hitam

Daya emisi (emissive power), E dari suatu benda ialah energi yang dipancarkan benda itu per satuan luas per satuan waktu. Hukum Kirchhoff (1859) menunjukkan bahwa berdasarkan hukum kedua termodinamika, radiasi di dalam rongga benda hitam bersifat isotropik, yaitu fluks radiasi bebas dari arah, dan juga bersifat homogen yaitu fluks radiasi sama di setiap titik dan sama dalam semua rongga pada suhu yang sama, untuk setiap panjang gelombang. Relasi antara daya emisi yang dikaitkan dengan rapat energi u(λ, T) di dalam rongga adalah :

, =4 , (1.20)

Wien (1894) menunjukkan bahwa rapat energi dapat dinyatakan dalam bentuk berikut.

(13)

dengan f yang merupakan sebuah fungsi maka persamaan dapat dituliskan kembali

(14)

, = , = ( , ) (1.22)

2

Berdasarkan persamaan tersebut, hukum Wien dapat dinyatakan dalam bentuk :

, = 3₍ ₎ (1.23)

Implikasi dari hukum ini adalah :

 Distribusi spektrum radiasi benda hitam untuk sembarang temperatur dapat kita cari dengan persamaan di atas.

 Bila fungsi g(x) mempunyai nilai maksimum untuk x > 0 maka berlaku= , dengan b

tetapan universal. Untuk fungsi g(x), Wien menggunakan model berikut = −

v

Dengan model ini maka data eksperimen untuk frekuensi tinggi dapat diverifikasi dengan sangat baik. Pada tahun 1900, Rayleigh menurunkan sebuah formula, yaitu :

8 2

(1.24)

, = 3

(15)

dengan k senilai 1,38 x 10 erg/derajat dan c adalah kecepatan cahaya. Rumus ini diturunkan berdasarkan dua hal, yaitu :

(16)

1. Hukum klasik ekipartisi energi menyatakan bahwa rata-rata energi per derajat kebebasan untuk sistem dinamik yang berada dalam keadaan kesetimbangan adalah kT.

2. Perhitungan jumlah modus (yaitu derajat kebebasan) untuk radiasi elektromagnetik dengan frekuensi dalam interval (ν,ν+dν), yang dikungkung oleh rongga.

Benda - benda nyata memancarkan radiasi yang lebih sedikit dari permukaan hitam sempurna. Pada kenyataannya, emisivitas bahan berubah menurut suhu dan panjang-gelombang radiasi. Emisivitas merupakan sifat karakteristik permukaan yang menggambarkan seberapa efektif permukaan beradiasi dibandingkan dengan black body. Black body merupakan permukaan ideal yang menerima emisi radiasi termal maksimum pada temperatur yang diberikan.

Perpindahan Kalor Benda-Tak-Hitam

Perhitungan perpindahan kalor untuk benda-tak-hitam (non-blackbodies) lebih rumit dibandingkan benda hitam, karena tidak seluruh energi yang jatuh di permukaan itu akan diserap. Sebagian energi yang jatuh pada permukaan tersebt akan dipantulkan kembali ke permukaan perpindahan-kalor lainnya, dan sebagian dipantulkan ke luar sistem. Energi radiasi mungkin dipantulkan bolak-balik berkali-kali di antara permukaan-permukaan perpindahan-kalor. Untuk mempermudah analisis, diasumsikan bahwa semua permukaan yang ada dalam analisis bersifat baur, mempunyai suhu seragam, dan sifat-sifat refleksi dan emisinya konstan di seluruh permukaan. Berdasarkan asumsi yang dibuat, akan diperkenalkan dua istilah baru yaitu:

G (Irradiation), yaitu total radiasi yang menimpa suatu permukaan per satuan waktu per satuan luas.

J (Radiocity), yaitu total radiasi yang meninggalkan suatu permukaan per satüan waktu per satuan luas

Iradiasi dan radiositas dapat diasumsikan seragam pada setiap permukaan dalam analisis. Radiositas dapat dinyatakan sebagai

=+ (1.25)

di mana E adalah emisivitas dan Eb merupakan daya emisi benda-hitam. Karena transmisivitas diasumsikan bernilai nol, maka refleksivitas dapat dinyatakan sebagai :

= 1 − = 1 − (1.26)

sehingga

=+ 1 − (1.27)

Energi netto yang meninggalkan permukaan merupakan selisih antara radiositas dan iradiasi yang dapat dinyatakan sebagai :

(17)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |10 = 1 − − = ( − ) (1.28) 1 − /

Jika pertukaran energi radiasi ditinjau di antara dua permukaan A1 dan A2, maka dari seluruh radiasi yang meninggalkan permukaan 1, jumlah yang mencapai permukaan 2 ialah

J1A1F12. Dari seluruh energi yang meninggalkan permukaan 2, yang sampai di permukaan 1

ialah J2A2F21. Besar pertukaran netto antara kedua permukaan itu ialah :

1−2 =₁−_{2 1 12}=₁−_{2 2 21} (1.29)

Dalam penyusunan jaringan suatu sistem perpindahan-kalor radiasi, hanya dibutuhkan

hubungan antara tahanan-permukaan ke setiap permukaan, dan tahanan-ruang antara

potensial radiositas. Dua permukaan yang hanya saling bertukar kalor saja dapat digambarkan dengan jaringan berikut.

Gambar 3. Jaringan Radiasi untuk Dua Permukaan yang Saling Melihat dan Tidak Melihat

Permukaan Lain

(Sumber: Heat Trasnfer, 10th Edition, Holman, 2010)

Dalam hal ini, perpindahan-kalor netto dapat dinyatakan sebagai beda potensial menyeluruh dibagi dengan jumlah semua tahanan, sehingga :

− ( 4 − 4) = 1 2 = 1 2 (1.30) 1 1 1 − 1 + + 1 − 2 1 − 1 + + 1 − 2 2 2 1 1 1 12 2 1 1 1 12 2

Sistem tiga-benda dapat ditunjukkan melalui jaringan berikut

(18)

(19)

Gambar 4. Jaringan Radiasi Tiga Permukaan yang Saling Melihat Satu Sama Lain dan Tidak Melihat Permukaan Lain

(20)

Dalam hal ini masing-masing benda itu mengalami pertukaran kalor dengan dua permukaan lain. Pertukaran kalor antara benda 1 dan benda 2 dapat dinyatakan sebagai :

= 1 − 2 (1.31)

1−2

1/ 1 12

Pertukaran kalor antara benda 1 dan benda 3 dapat dinyatakan sebagai :

= 1 − 3 (1.32)

1−3

1/ 1 13

Untuk menentukan perpindahan kalor dalam kondisi seperti ini, nilai-nilai radiositas harus dihitung. Hal ini dapat dicapai dengan melakukan metode analisis standar yang digunakan dalam teori rangkaian arus searah. Metode yang paling mudah ialah dengan menerapkan hukum arus Kirchoff pada rangkaian tersebut, yang menyatakan bahwa jumlah semua arus yang memasuki suatu node ialah nol. Suatu sistem yang dapat diselesaikan dengan mudah dengan metode jaringan ialah sistem dengan dua permukaan rata yang saling bertukar kalor, tetapi berhubungan dengan permukaan ketiga yang tidak menukar kalor; artinya, permukaan ketiga ini diisolasi sempuma. Namun, permukaan ketiga ini mempengaruhi proses perpindahan-kalor, karena ia menyerap dan meradiasikan kembali energi ke kedua permukaan yang saling bertukar kalor. Jaringan untuk sistem ini ditunjukkan pada gambar berikut

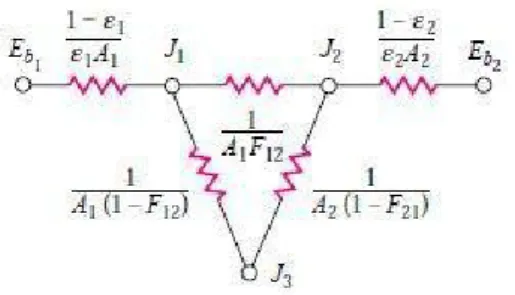
Gambar 5. Jaringan Radiasi untuk Dua Permukaan yang Melingkungi Permukaan Ketiga yang

Tidak Melakukan Konduksi tetapi Melakukan Radiasi Kembali. (Sumber: Heat Transfer, 10th Edition, Holman, 2010)

Node J3 tidak dihubungkan dengan tahanan-permukaan radiasi karena permukaan 3 tidak bertukaran energi. Nilai tahanan ruang memiliki hubungan berupa :

13 = 1 − 12 (1.33)

23 = 1 − 21 (1.34)

Hubungan tersebut diperoleh karena permukaan 3 melingkupi kedua permukaan lain sepenuhnya. Jaringan pada gambar di atas merupakan suatu jaringan seri-paralel yang sederhana, dan dapat diselesaikan untuk perpindahan-kalor sebagai berikut :

( 4 − 4) = 1 1 2 (1.35) 1 + 2 − 2 1 12 + 1 − 1 + 1 1 − 1 − 2 2 2 1 12 1 2

(21)

Jaringan ini, dan jaringan-jaringan berikutnya, mengandaikan bahwa pertukaran kalor terjadi semata-mata dengan radiasi, tanpa disertai dengan konduksi dan konveksi.

5. Bagaimana pula cara menentukan Koefisien Perpindahan Kalor Radiasi? Faktor – faktor apa saja yang mempengaruhi nilai koefisien ini?

Secara umum, penentuan koefisien perpindahan kalor radiasi dimulai dengan menuliskan persamaan untuk laju perpindahan kalor radiasi, yaitu :

= ( 1 − 2) (1.36)

di mana melambangkan koefisien perpindahan kalor radiasi (W/m2K). Langkah selanjutnya

yang dilakukan adalah menuliskan bentuk lain dari persamaan perpindahan kalor radiasi dengan menggunakan nilai emisivitas, yaitu :

=4 _{− 4} (1.37)

1 2

Modifikasi kedua persamaan (1.36 dan 1.37) dapat menghasilkan persamaan baru yaitu :

=4 ₋4 _{= (} _{− )} 1 2 1 2 =4 − 4 _{= ( − )} 1 2 1 2 2 + 2 + − = ( − ) 1 2 1 2 1 2 1 2 = 2 + 2 ₊ (1.38) 1 2 1 2 dengan keterangan :  = Laju Perpindahan Kalor Radiasi (W)  1 = Suhu Benda 1 (K)

 2 = Suhu Benda 2 atau Suhu Lingkungan (K)  = Konstanta Boltzman (5,673 x 10-8_{W m}-2_K-4₎  = Luas Permukaan Benda 1 (m2₎  = Emisivitas Benda 1

Penentuan nilai bergantung pada sistem, tetapi prinsip yang digunakan sama seperti di atas, yaitu membagi nilai laju aliran kalor dengan ₍₁₋₂₎, di mana persamaan untuk laju aliran kalor dapat diperoleh dari tabel yang ada pada referensi, misalnya tabel yang terdapat pada buku Cengel berikut :

(22)

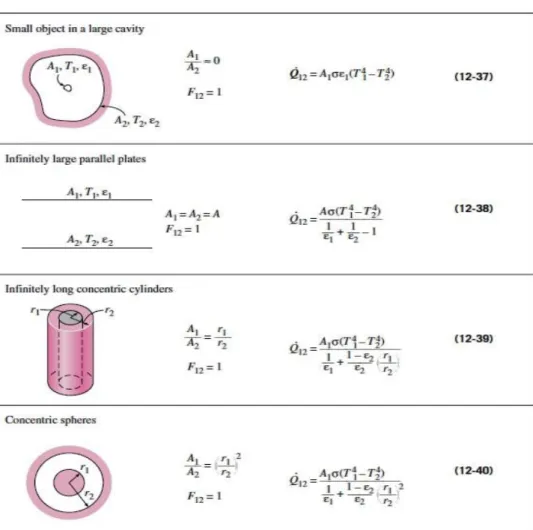
Tabel 2. Persamaan Laju Aliran Kalor untuk Beberapa Jenis Sistem.

(Sumber : Heat Transfer : A Practical Approach, Cengel 2002)

Dari persamaan-persamaan di atas, jelaslah bahwa koefisien perpindahan kalor radiasi merupakan sebuah fungsi yang sangat tergantung pada suhu. Selain itu, koefisien perpindahan kalor radiasi juga dipengaruhi oleh :

 Emisivitas

Emisivitas merupakan sifat karakteristik permukaan yang menggambarkan seberapa efektif permukaan memancarkan radiasi dibandingkan dengan black body. Black body merupakan permukaan ideal yang memancarkan radiasi termal secara sempurna. Semakin besar emisivitas suatu benda, nilai hr akan semakin besar.

 Luas Permukaan Benda

Semakin besar perbandingan antara luas permukaan benda 1 dengan benda 2 pada sistem, nilai hr akan semakin kecil.

6. Apa yang dimaksud dengan Faktor Bentuk Radiasi? Bagaimana cara menentukannya? Jelaskan hubungan antara berbagai faktor bentuk!

(23)

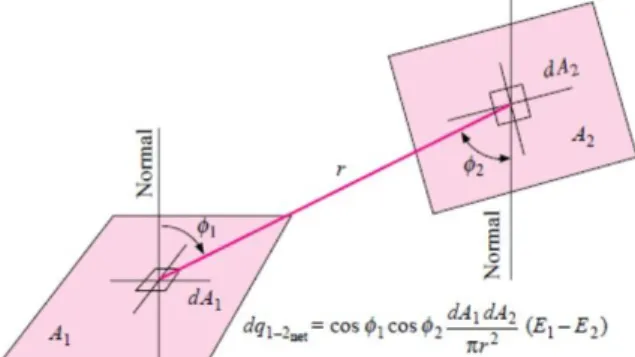
Gambar 6. Sketsa Area Elemen untuk Menurunkan Faktor Bentuk Konduksi

Gambar di atas menunjukkan dua permukaan hitam A1 dan A2. Persamaan umum yang menggambarkan pertukaran kalor antara keduanya pada temperatur yang sama dapat ditentukan apabila besar energi yang meninggalkan permukaan satu dan diterima oleh permukaan lain dapat diketahui. Dalam hal ini, faktor bentuk konduksi didefinisikan sebagai :

F1-2= fraksi energi yang meninggalkan permukaan 1 dan diterima permukaan 2

F2-1= fraksi energi yang meninggalkan permukaan 2 dan diterima permukaan 1

Fi-j = fraksi energi yang meninggalkan permukaan i dan diterima permukaan j Besarnya energi yang meninggalkan permukaan 1 dan sampai pada permukaan 2 adalah

Eb1A1F12sedangkan besar energi yang meninggalkan permukaan 2 dan sampai pada permukaan

1 adalah Eb2A2F21. Karena kedua permukaan adalah black surfaces, maka besar pertukaran energi antara keduanya adalah :

1 1 12 −_{2 2 21}=₁₋₂ (1.39)

Jika suhu kedua permukaan sama (T1 = T2), tidak terjadi pertukaran panas sehingga nilai Q

adalah nol dan Eb1 = Eb2 sehingga A1F12 = A2F21. Dengan demikian laju bersih pertukaran energi dituliskan sebagai :

1−2 =_{1 12 1}−₂=_{2 21}(₁−₂) (1.40)

Persamaan (1.40) dikenal sebagai reciprocity relation, yang berlaku secara umum untuk dua permukaan bebas i dan j.

= (1.41)

Untuk menentukan persamaan umum untuk F1-2 dan F2-1, kedua permukaan pada Gambar 6 diamati. Sudut 1dan 2merupakan sudut yang

diukur antara sumbu normal terhadap permukaan dan garis yang menghubungkan kedua area r. Proyeksi dA1 pada garis antar permukaan

adalah dA11. Dalam analisis ini, diasumsikan permukaan bersifat diffuse sehingga intensitas radiasi bernilai seragam untuk seluruh arah.

(24)

ditentukan. Dengan demikian, energi yang diemisikan elemen dengan luas dA1 pada arah tertentu adalah :

1 cos 1 (1.42)

di mana Ib menyatakan intensitas benda hitam. Radiasi yang diterima oleh elemen dengan luas

dAndengan jarak r dari A1adalah :

1 cos 1

(1.43) 2

di mana dAn dibuat normal terhadap vektor radius. Nilai dAn/r2 menggambarkan solid angle

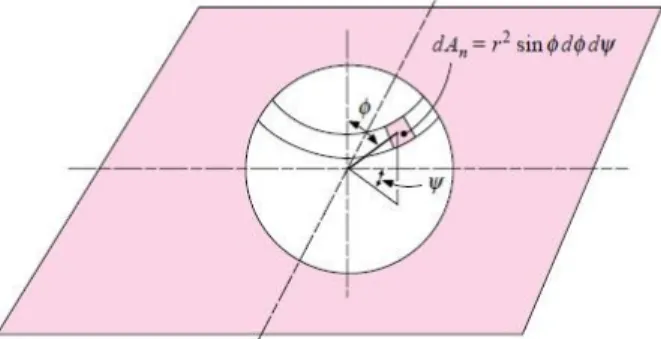
subtended oleh area dAn. Intensitas dapat diperoleh dalam bentuk daya emisi dengan cara mengintegralkan persamaan 1.43 sepanjang wilayah berbentuk setengah bola (hemisphere) yang melingkupi elemen dengan area dA1. Dalam koordinat bola, sistem dapat direpresentasikan melalui gambar berikut.

Gambar 7. Sistem Koordinat Bola untuk Faktor Bentuk Relasi

(Sumber : Heat Transfer, 10th Edition, Holman, 2010) Maka 2 2 1 =1 (1.44) sin cos=1 0 0

Dengan demikian diperoleh hubungan Eb = πIb. Kembali pada masalah pertukaran energi yang tampak pada Gambar 6, luas area

elemen dAn dapat dinyatakan sebagai cos2dA2. Sehingga energi yang meninggalkan permukaan dA1 menuju permukaan dA2 adalah : 1 2 1−2 = 1 cos 1 cos 2 2

Besar energi yang meninggalkan dA2 menuju dA1 adalah :

1 2 2−1 = 2 cos 2 cos 1 2

Maka pertukaran energi bersih antara kedua permukaan adalah :

1−2 = ( 1 − 2) _cos₁_cos₂ 1 2 2 2 1 (1.45) (1.46) (1.47)

(25)

Untuk mengevaluasi integral di atas, bentuk geometri dari kedua permukaan harus diketahui. Perhitungan faktor bentuk dapat dilakukan untuk geometri yang lebih kompleks. Hubungan analitis untuk berbagai bentuk geometri diberikan pada Tabel 8-2 halaman 396 buku Heat Transfer 10thEdition karangan J.P. Holman.

Hubungan antara Berbagai Faktor Bentuk

Salah satu contoh bentuk persamaan yang menghubungkan faktor – faktor bentuk dapat diperoleh dengan mengamati Gambar 8.

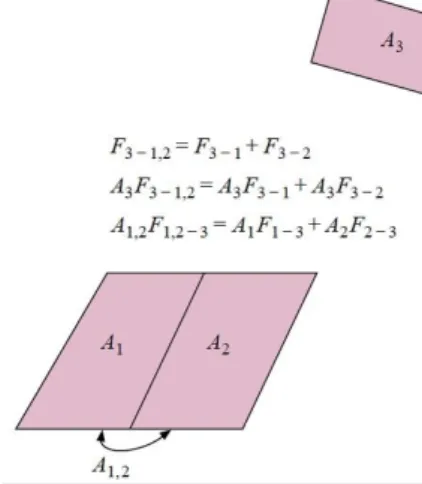
Gambar 8. Relasi antara Beberapa Faktor Bentuk

Faktor bentuk radiasi dari bidang A3 menuju bidang gabungan A12 adalah

3−1,2 =₃₋₁+₃₋₂ _(1.48)

Faktor bentuk total pada dasarnya merupakan hasil penjumlahan dari berbagai faktor bentuknya penyusunnya. Berdasarkan hubungan resiprositas berlaku :

1,2 1,2−3 =_{1 1−3}+_{2 2−3} (1.49)

Berdasarkan persamaan di atas, tampak bahwa besar radiasi total yang sampai pada permukaan 3 merupakan hasil penjumlahan radiasi dari permukaan 1 dan 2.

7. Jelaskan mekanisme proses perpindahan kalor secara radiasi antara dua permukaan!

(26)

Gambar 9. Skema Laju Perpindahan Panas Radiasi Pada 2 Permukaan Benda Hitam (Sumber: Heat Transfer, 2nd Edition, Cengel, 2002)

(27)

Gambar 9 menunjukkan 2 permukaan benda hitam dengan bentuk tertentu yang mempunyai suhu

permukaan sebesar T1 dan T2 secara merata. Pada sistem seperti ini, faktor bentuk radiasi (F1-2) harus

diperhitungkan, yaitu bagian radiasi yang meninggalkan permukaan 1 dan mengenai permukaan 2.

Seperti yang telah diketahui, radiasi per unit luas area dari benda hitam adalah ₌ 4 sehingga laju

perpindahan panas total secara radiasi dari permukaan 1 ke permukaan 2 dapat diekspresikan sebagai :

1 −2 = ₁ ₋ ₂ (1.50)

2 1

1 −2 =_{1 1 1−2}−_{2 2 2−1}

(1.51)

Lalu dengan mengaplikasikan hubungan resiprositas yaitu 1 1−2= 2 2−1, maka

persamaan 1.51 diubah menjadi:

= 4 ₋4 (1.52)

1−2 1 1−2 1 2

Nilai 1−2 yang negatif menunjukkan laju perpindahan panas secara radiasi terjadi dari permukaan 2 ke permukaan 1.

Untuk sistem benda hitam tertutup dengan N permukaan yang memiliki suhu permukaan tertentu dan dijaga konstan, maka laju perpindahan panas secara radiasi dari permukaan i ke seluruh permukaan lainnya dinyatakan sebagai :

= = 4 − 4 (1.53)

− −

=1 =1

Nilai yang negatif menunjukkan bahwa permukaan i justru mendapat energi radiasi dari permukaan di sekitarnya, atau dengan kata lain tidak kehilangan energi.

(28)

(29)

Gambar 10. Analogi Radiasi pada Dua Permukaan Benda Abu-Abu (Sumber: Heat Transfer, 2nd Edition, Cengel, 2002)

(30)

Gambar di atas menunjukan radiasi yang terjadi antara dua benda abu-abu berbentuk lingkaran. Variabel J merepresentasikan radiositas, yaitu laju radiasi yang meninggalkan permukaan tiap satuan luas permukaan. Variabel Fi-j merepresentasikan faktor bentuk radiasi, yaitu bagian radiasi yang meninggalkan permukaan i dan mengenai permukaan j. Laju radiasi yang terjadi dari permukaan i ke permukaan j dapat diekspresikan sebagai :

− = −

− = − − −

Dengan mengaplikasikan hubungan resiprositas, maka persamaan diatas menjadi :

− = − _{( −}( − ) ₎

− =

− 1

di mana ₋setara dengan

− .

(1.54) (1.55)

(1.56) (1.57)

Variabel ₋ menunjukan resistansi radiasi. Perhitungan kuantitas ₋ mirip seperti perbedaan potensial, dan nilai laju perpindahan radiasi yang terjadi analoginya seperti arus listrik.

Radiasi pada Dua Permukaan Tertutup

Gambar 11. Skema Perpindahan Panas Radiasi pada Dua Permukaan Tertutup

(Sumber: Heat Transfer, 2nd Edition, Cengel, 2002)

Gambar di atas menunjukan suatu sistem permukaan tertutup di mana terdapat perpindahan panas radiasi di dalamnya. Sistem ini terdiri dari 2 permukaan, yaitu permukaan 1 dengan

1, 1, 1 dan permukaan 2 dengan 2, 2, 2. Oleh karena itu, laju radiasi yang terjadi dapat dituliskan sebagai berikut.

12 = 1 = − 2 (1.58)

Perpindahan panas secara radiasi yang terjadi pada sistem ini melibatkan dua resistansi permukaan dan satu resistansi ruang. Apabila kita gunakan analogi aliran listrik maka sistem pada Gambar 11 serupa dengan rangkaian seri, sehingga laju radiasi yang terjadi :

(31)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi | 19 12 = 1 −₂ = 1 = − 2 _(1.59) 1 + 12 + 2 ( 4 − 4) 12 = 1 2 (1.60) 1− 1 + 1 + 1 − 2 1 1 1 12 2 2

Untuk berbagai bentuk sistem dua permukaan tertutup, persamaan 1.60 akan berubah, tergantung pada geometrinya. Tabel 12-3 pada buku Heat Transfer 2nd Edition Cengel hal. 628 telah memuat berbagai rumus laju radiasi untuk berbagai bentuk geometri yang berbeda-beda.

8. Bagaimana proses perpindahan kalor secara radiasi yang terjadi pada gas serta antara gas dengan permukaan yang mengelilinginya?

Radiasi yang terjadi antara permukaan suatu benda dengan gas jauh lebih kompleks dibanding pada zat padat. Absorpsi suatu radiasi di lapisan gas dapat di ilustrasikan sebagai berikut.

Gambar 12. Absorpsi Pada Suatu Lapisan Gas

Gambar 12 menunjukkan suatu sinar monokromatis radiasi dengan intensitas yang ditembakkan ke lapisan gas dengan ketebalan dx. Penurunan intensitas akibat peristiwa absobrsi sebanding dengan ketebalan lapisan gas dan intensitas radiasi pada titik tersebut.

= − (1.61)

0

Persamaan 1.61 dikenal sebagai Hukum Beer, dan transmisivitas monokromatisnya dirumuskan

= − (1.62)

Untuk gas yang tidak memantulkan berlaku persamaan :

= 1 − − (1.63)

Persamaan 1.61 dan 1.63 mendeskripsikan variasi intensitas dan absorptivitas untuk lapisan gas dengan ketebalan x. Emisivitas gas CO2 dan uap air dapat dilihat pada Gambar 12-36 buku

Heat Transfer 2ndEdition Cengel pada hal. 643. Selain itu, emisivitas gas juga dipengaruhi oleh tekanan. Apabila gas tidak berada pada tekanan 1 atm maka diperlukan faktor koreksi untuk menghitung nilai emisivitasnya. Faktor koreksi ini dapat dilihat melalui Gambar 12-37 pada buku Heat Transfer 2nd Edition Cengel pada hal. 643. Nilai emisivitas gas juga bergantung pada panjang sinar rata-rata (Le), yang dirumuskan sebagai :

(32)

20

= 3,6 (1.64)

dengan V volume gas dan A luas permukaan total benda yang mengadakan kontak dengan gas.

Radiasi pada Gas di Benda Hitam Tertutup

Gambar 13. Radiasi pada Gas di Dalam Benda Hitam

(Sumber: Heat Transfer, 2nd Edition, Cengel, 2002)

Gambar 13 menunjukan suatu balok tertutup yang mempunyai karakteristik seperti benda hitam dan mempunyai suhu permukaan yang merata sebesar Tw. Di dalam balok tersebut terdapat gas dengan suhu Tg. Laju perpindahan panas radiasi tiap satuan luas permukaan dari gas ke permukaan balok tersebut dirumuskan sebagai :

= − (1.65)

= 4₋ 4 (1.66)

Maksud dari variabeldan berturut-turut adalah emisivitas gas pada suhu Tg dan

absorptivitas gas pada suhu Tw.

Apabila gas pada sistem terdiri dari campuran (misalnya CO2 dan uap air) maka persamaan

danmenjadi: = + − ∆ (1.67) = + − ∆ (1.68) dengan 0,65 0,45 = ′ dan = ′ (1.69)

Selain itu juga diketahui bahwa ∆ =∆ .

Untuk sistem dua plat hitam sejajar dengan suhu plat masing-masing T1 dan T2 dan di antaranya terdapat gas, maka laju energi radiasi yang didapat oleh masing-masing plat adalah:

Plat 1 → 1 = 1 1 −1 1 (1.70) Plat 2 → 2 = 2 2 − 2 2 (1.71) dengan 1 1 =1 +_{2 21} 2 2 (1.72)

(33)

21

2 2 =2 + 1 12 1 1 (1.73)

2 = 1 −2 (1.74)

Radiasi pada Gas di Benda Abu-Abu Tertutup

Laju perpindahan panas total secara radiasi pada benda abu-abu lebih kompleks dari benda hitam, namun Hottel telah menemukan korelasinya dengan laju radiasi di benda hitam tertutup yaitu:

− ₌ + 1 (1.75)

2

II. 2 Perhitungan

1. Hitunglah perpindahan kalor secara radiasi antara kedua tutup sebuah silinder yang berdiameter 12 in dan panjang 3 in. Suhu pada kedua bidang itu berturut – turut

1940ºF dan 140ºF. Bahan tutup silinder terbuat dari Cr-Ni alloy dengan ε = 0,7.

Dinding silinder dianggap tidak dapat menghantarkan panas tetapi dapat memantulkan semua panas yang diterimanya.

Diketahui:

-Sebuah silinder dengan diameter 12 inch

-Panjang silinder 3 inch

-Suhu kedua tutup silinder bertutur-turut adalah 19400F dan 1400F

-Bahan kedua tutup silinder terbuat dari Cr-Ni alloy ( = 0,7)

T2 = 1400F

(34)

12

(35)

T1 = 19400F

Asumsi:

- Dinding silinder dapat memantulkan semua panas yang diterimanya secara sempurna ( = 0)

Jawab:

Langkah 1: Menghitung luas kedua tutup silinder

(36)

(37)

3 1 =6= 0,5

2₌6

3 = 2

Dengan menggunakan gambar 8-16 pada buku Heat Transfer 10th Edition karya J.P.Holman hal. 396 dapat diperoleh faktor bentuk radiasi antar kedua tutup silinder (F1-2).

1−2 = 0,62

Langkah 3: Menghitung laju perpindahan kalor secara radiasi antar kedua tutup silinder

1 = 19400 = 1333,15 2 = 1400 = 333,15 ( 4 − 4) 12 = 1 2 1 − 1 + 1 + 1 − 2 1 1 1 12 2 2 12 = 5,7 × 10−8 2 4 (1333,154_{− 333,15}4₎4 =, 1 − 0,7 1 1 − 0,7 + + 0,07293 2_{× 0,7} _0,072932_{× 0,62} _0,072932_{× 0,7}

Jadi laju perpindahan kalor secara radiasi antar kedua tutup silinder (dari permukaan 1 ke permukaan 2) adalah sebesar 5296,7 W.

2. Gas hasil pembakaran terdiri atas 10,3% (mol) H2O, 11,4% CO2 dan sisanya inert,

pada tekanan 1 atm. Gas tersebut mengalir melalui pipa yang berdiameter 6 in dan mengalami perpindahan kalor secara radiasi dnegan udara luar.

Suhu gas masuk 2000ºF dengan suhu permukaan ujung pipa 800ºF, sedangkan suhu

gas keluar 1000ºF dengan suhu permukaan ujung pipa 600ºF. Jika massa gas x Cp

gas (= m.Cp) gas dianggap tetap sebesar 90Btu/J.ºF, hitunglah panjang pipa yang

dibutuhkan agar perpindahan kalor terjadi sempurna.

Berikut adalah sketsa sistem yang disebutkan pada soal.

Diketahui :

Komposisi gas = 10,3% H2O dan 11,4% CO2, sisanya gas inert.

Tekanan total = 1 atm.

(38)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |23 Ditanya :

Panjang pipa yang dibutuhkan agar perpindahan kalor terjadi secara sempurna.

Jawab :

Karena diketahui kondisi sistem pada kedua ujung, maka dapat dibentuk persamaan di mana perbedaan kalor yang diserap pada kedua ujung merupakan akibat dari adanya kalor yang keluar ke udara dan menyebabkan suhu gas menurun, selain karena adanya perpindahan kalor radiasi sepanjang L. Dengan demikian persamaan yang digunakan menjadi

− = ∆ (2.1) 1 2 dengan A = 2πrL, dan = 4₋ ₍ ₎4 (2.2) Untuk Kondisi 1 : 1 4 = 5,669 10−8 / 2 4. (700 4) = 13.611,27 / 2 4 = 5,669 10−8 / 2 4. (1366 4) = 197.382,78 / 2 1

Diasumsikan pipa berbentuk silinder dengan panjang tak hingga dan radiasinya adalah ke permukaan cembung, sehingga dari Tabel 8-2 (Holman) dapat diketahui panjang ekuivalen rata-rata Le yaitu 0,95D.

Panjang berkas ekuivalen adalah

= 0,5 0,95 = 0,475 = 0,14478

Tekanan parsial komponen-komponen gas ( = ) :

pCO2= 0,114 atm = (0,114)(1,0132 x 105) = 11,55 kPa = 1,593 psia pH2O = 0,103 atm = (0,103)(1,0132 x 105) = 10,435 kPa = 1,834 psia Maka

pCO2Le = (0,114 atm) (0,475 ft ) = 0,054 atm.ft pH2OLe = (0,103 atm) (0,475 ft ) =

0,049 atm.ft pCO2Le + pH2OLe = 0,054 + 0,049

= 0,103 atm.ft (½)(P + pH2O) = (0,5)(1 + 0,103) = 0,552 atm 2 = 0,103 = 0,475 + 0,114 + 0,103 2 2

Sehingga pada Tg = 2460 R = 1366 K, dari grafik diperoleh data sebagai berikut :

2 = 0,051 (Gambar 8.34 buku J. P. Holman)

(39)

Karena tekanan total 1 atm maka tidak ada faktor koreksi. Sehingga dari persamaan 8-52 (J. P. Holman) : = 0,051 + 0,023 − 0,001 = 0,073 Pada Tw = 800oF = 700 K diperoleh : = 0,054 700 _{= 0,0276 atm ft} 1366 2 = 0,049 700 _{= 0,0251 atm ft} 1366 2

Dari grafik diperoleh :

= 0,048 (Gambar 8.34 buku J. P. Holman)

2 Sehingga : 0.65 1366 0.65 2 = ′ = 0,048 = 0,074 700 2 0.65 1366 0.65 2 = ′ 2 = 0,033 700 = 0,051 = +− Δ = 0,051 + 0,074 − 0,001 = 0,124 2 2

Nilai q/A dapat dicari dengan melakukan substitusi nilai-nilai yang sudah didapat ke persamaan 2.2, yaitu : = 0,073 (197.382,78 2) − (0,124)(13.611,27 2 ) = 12.721,15 = 12,72 1 2 2 Untuk Kondisi 2 : (Tg)2 = 1000oF = 1460 R = 811 K (Tw)2 = 600oF = 1060 R = 589 K Maka 24 = 5,669 10−8 / 2 4. (811 4) = 24.523,92 / 2 24 = 5,669 10−8 / 2 4. (589 4) = 8.822,89 / 2 Pada Tg = 1460 R = 811 K :

∆ = 0,001 = 0,063 + 0,059 − 0,001 = 0,121

(40)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |25 Sehingga pada Tw = 589 K = 1060,8 R : = 0,054 589 _{= 0,039 atm ft} 811 2 = 0,049 589 _{= 0,036 atm f} 811 2

Dari grafik diperoleh :

2 = 0,054 2 = 0,046

Dari persamaan 8-55 dan 8-56 buku J. P. Holman diperoleh :

0.65 811 0.65 2 = ′ = 0,054 = 0,066 589 2 0.65 811 0.65 2 = ′ 2 = 0,046 589 = 0,057 =+− Δ = 0,066 + 0,057 − 0,001 = 0,122 2 2

Nilai-nilai ini disubstitusi ke persamaan 2.2 untuk memperoleh q/A.

= 0,121 (24.523,92 2) − (0,122)(8.822,89 2)

= 1.891,00 = 1,89

2 2 2

Kemudian, nilai-nilai ini dimasukkan ke persamaan 2.1 menjadi :

12,72 − 1,89 = (90 / ℉)(1000℉) 2 2 (0,026 ℉ )(1000℉) = 12,49 2 − 1,85 2 = 2,4 2_{(= 2} ₎ 2,4 2=_{2 (0,072 )} = ,

(41)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |26 BAB III

PENUTUP III. 1 Kesimpulan

 Radiasi termal merupakan proses di mana energi diemisikan oleh suatu benda pada temperatur tak-nol melalui gelombang elektromagnetik.

 Perbedaan utama antara radiasi termal dan konveksi adalah ada tidaknya medium perantara yang terlibat selama proses perpindahan kalor.

 Radiasi yang dipancarkan sertiap benda terjadi secara tidak kontinu dan dipancarkan dalam satuan kecil yang disebut kuanta (energi kuantum).

 Proses perpindahan kalor radiasi dapat diartikan sebagai suatu bentuk pancaran energi dari suatu benda yang secara matematis dinyatakan sebagai :

Q = eσAT4

 Benda hitam adalah suatu benda dengan permukaan ideal yang mempunyai sifat-sifat sebagai berikut:

o Mengabsorbsi seluruh radiasi elektomegnetik yang jatuh kepadanya tanpa memperhatikan panjang gelombang dan arahnya.

o Pada suhu dan panjang gelombang tertentu, tidak ada permukaan yang dapat memancarkan energi lebih besar dari benda hitam.

o Walaupun radiasi yang dipancarkan oleh benda hitam merupakan fungsi dari panjang

gelombang dan suhu, tetapi tidak bergantung kepada arah.

 Konsep benda hitam sebetulnya merupakan suatu idealisasi, artinya benda hitam sempurna tidak ada – setiap permukaan selalu memantulkan, betapa pun kecilnya.

 Benda-tak-hitam adalah benda yang tidak seratus persen menyerap energi yang dipancarkan

 Penentuan nilai bergantung pada sistem. Prinsip penentuan yang digunakan adalah membagi nilai laju aliran kalor dengan ₍₁₋₂₎, di mana persamaan untuk laju aliran kalor dapat diperoleh dari tabel yang ada pada referensi.

 Koefisien perpindahan kalor radiasi merupakan sebuah fungsi yang sangat tergantung pada suhu. Selain itu, koefisien perpindahan kalor radiasi juga dipengaruhi oleh emisivitas dan luas permukaan benda.

 Faktor bentuk radiasi dapat menunjukkan besarnya fraksi energi yang meninggalkan sebuah permukaan i dan diterima oleh permukaan lain, yaitu permukaan j.

(42)

1−2 = 1 1−2 14−24

 Laju perpindahan panas secara radiasi antar dua permukaan benda

abu-abu adalah ( 4₋4₎ 12 = 1 2 1 − 1 + 1 + 1 − 2 1 1 1 12 2 2

 Nilai negatif pada laju perpindahan panas secara radiasi menunjukkan bahwa laju perpindahan panas yang terjadi dalam arah sebaliknya

 Laju perpindahan panas secara radiasi per unit luas area pada gas di benda hitam tertutup adalah :

= 4 ₋ 4

 Korelasi antara laju perpindahan panas secara radiasi pada gas di benda abu-abu tertutup dengan benda hitam adalah

− = + 1

(43)

Makalah Perpindahan Kalor : Perpindahan Kalor Radiasi |28 DAFTAR PUSTAKA

Cengel, Y. 2006. Heat Transfer, 2nd Edition. USA: Mc Graw-Hill.

Holman, J.P. 1986. Heat Transfer, 6th Edition. Singapore: McGraw-Hill Book Company. Holman, J.P. 2009. Heat Transfer, 10th Edition. New York: McGraw-Hill.

Incropera, F.P., et.al. 2011. Fundamentals of Heat and Mass Transfer, 7th Edition. NJ : John Wiley & Sons, Inc.

(44)