Eksponen Lokal Masuk Dua Cycle Dwiwarna Dengan Panjang Selisih 2

Pada bab ini akan dijelaskan teori-teori dasar tentang digraph yang meliputi de-finisi dua cycle, primitifitas dari digraph, eksponen, dan lokal eksponen. Dengan demikian, akan mempermudah peneliti dalam menjelaskan teori digraph dwiwar-na pada bab berikutnya.

2.1. Dua Cycle

Digraph atau graph berarah adalah sekumpulan titik-titik atau verteks yang di-hubungkan oleh busur berarah atau arc. Berikut ini definisi yang diungkapkan oleh Suwilo (2001).

Definisi 2.1. Sebuah graph berarah (directed graph) atau digraph Dadalah him-punan hingga dan tak kosong V = {1,2, . . . , n} yang unsur-unsurnya disebut dengan verteks, bersama dengan himpunanEyang merupakan pasangan-pasangan verteks di D yang unsur-unsurnya disebut dengan arc.

Representasi dari sebuah digraph D dapat dilihat pada contoh berikut.

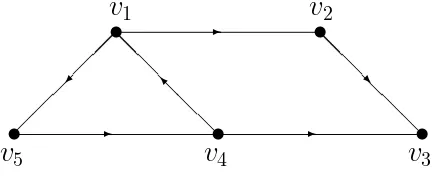
Contoh 2.1. Representasi dari digraph dengan 5 buah verteks.

v

1

v

2

v

₃

v

₄

v

₅

•

•

•

❅

•

•

❅ ❅ ❅ ❅ ❅

❅ ❅ ❅ ❅ ❅ ❅ ✲

✠ ❘

■

✲ ✲

Gambar 2.1 Representasi digraph

Dari Gambar 2.1 terdapat himpunanV yakniV ={v₁, v₂, v₃, v₄, v₅}dan terdapat himpunan busur E yakniE ={(1,2),(1,5),(2,3),(4,1),(4,3),(5,4)}.

Andaikan digraph D terdiri atas n verteks vj = v1, v2, . . . , n, didefinisikan

derajat masuk (In Degree) yaitu banyaknya busur berarah yang menujuvj

berarah yang keluar dari vj dinotasikan sebagai od(vj). Pada Contoh 2.1 terlihat

yang memiliki derajat masuk yaitu v₂, v₃, v₄, v₅, id(v₂) = 1 karena hanya terda-pat satu busur berarah yang menuju v2, id(v3) = 2, id(v4) = 2, dan id(v5) = 1.

Serta yang memiliki derajat keluar yaituv1, v2, v4, v5, od(v1) = 3 karena terdapat

tiga busur berarah yang keluar (meninggalkan) v1, od(v2) = 1, od(v4) = 1, dan

od(v₅) = 1.

Pada digraph D terdapat path, cycle dan walk. Sebuah path atau lintasan sederhana dari verteksuke verteksv adalah sebuah lintasan dimana tidak terjadi pengulangan satu atau lebih verteks dari u ke v. Sebuah lintasan dari verteks u ke verteks v disebut cycle apabila verteks awal dan ujungnya sama atau dapat ditulis u = v. sebuah lintasan dari verteks u ke verteks v disebut walk apabila terdapat pengulangan satu atau beberapa verteks dari u kev.

Suatu jalan w merupakan jalan yang menghubungkan dua buah verteksu dan v di digraph D. Panjang jalan w dinotasikan dengan ℓ(w) yaitu banyaknya arc atau busur berarah yang dilalui bila bergerak dari verteks u ke verteks v. Dalam hal ini jalan dapat berupa path, cycle ataupun walk.

Pada Contoh 2.1 dapat ditemukan beberapa path, cycle, dan walk yaitu:

1. Terdapat dua buah path dari verteks 1 ke verteks 3, yaitu v1 → v2 → v3

dengan panjang ℓ(v1, v3) = 2 dan v1 → v5 → v4 → v3 dengan panjang ℓ(v1, v3) = 3.

2. Terdapat sebuah path dari verteks 1 ke verteks 2, yaitu v₁ → v₂ dengan panjang ℓ(v₁, v₂) = 1.

3. Terdapat sebuah path dari verteks 1 ke verteks 4, yaituv1 →v5→v4dengan

panjang ℓ(v1, v4) = 2.

4. Terdapat cycle dari verteks 1 ke verteks 1, v1 → v5 → v4 → v1 dengan

panjang ℓ(v₁, v₁) = 3.

5. Terdapat walk dari verteks 1 ke verteks 3, v₁ → v₅ → v₄ → v₁ → v₂ → v₃ dengan panjang 5.

cycle yang bersinggungan dapat bersinggungan pada sebuah busur berarah atau pada salah satu verteks di D. Representasi duacycle dapat dilihat pada Contoh 2.2.

Contoh 2.2. Representasi dari dua cycle

(a) (b) (c)

v

₁

v

₂

v

₃

v

₄

v

₁

v

₂

v

₃

v

₄

v

₅

v

₁

v

₂

v

₃

v

₄

v

₅

v

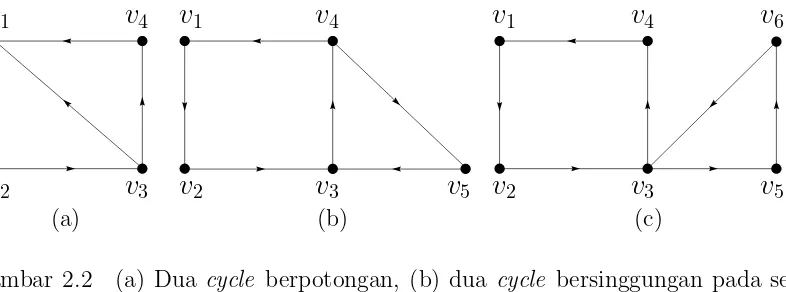
₆

Gambar 2.2 (a) Dua cycle berpotongan, (b) dua cycle bersinggungan pada se-buah busur berarah, dan (c) dua cycle bersinggungan pada satu verteks

Pada Gambar 2.2 (a) melukiskan dua cycle yaitu dari v1 → v2 → v3 → v1

dengan panjang 3 dan dari v1 →v2 →v3 →v4 →v1 dengan panjang 4. Gambar

2.2 (b) melukiskan dua cycle yaitu dari v3 → v4 → v5 → v3 dengan panjang 3

dan dari v₁ →v₂ →v₃ →v₄ →v₁ dengan panjang 4. Gambar 2.2 (c) melukiskan dua cycle yaitu dari v₃ →v₅ → v₆ →v₃ dengan panjang 3 dan dari v₁ → v₂ → v3 →v4 →v1 dengan panjang 4.

2.2. Primitifitas

Sebuah digraph dikatakan terhubung kuat (strongly connected) bila untuk setiap pasangan verteks (u, v) di D terdapat jalan dari verteks u ke v dan dari v keu. Sebaliknya, sebuah digraph dikatakan tidak terhubung kuat bila untuk beberapa pasangan verteks (u, v) di D tidak terdapat jalan dari u ke v atau dari v ke u. Untuk lebih memahami digraph terhubung kuat dan tidak terhubung kuat

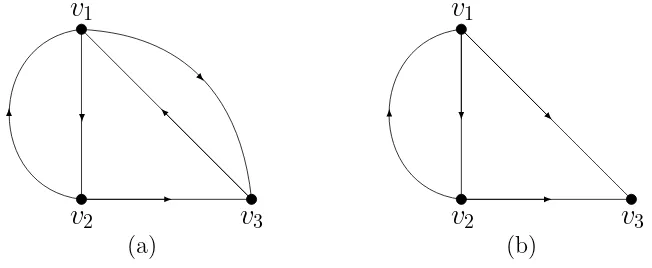
adanya jalan dari verteks 1 ke verteks 3 yaitu 1→3, namun tidak terdapat jalan dari verteks 3 ke verteks 1, sehingga merupakan digraph yang tidak terhubung kuat. Proposisi berikut memperlihatkan hubungan antara terhubung kuat dengan verteks-verteks pada cycle.

(a) (b)

v

₁

v

₂

v

₃

❄ ✻

❘

v

₁

v

₂

v

₃

Gambar 2.3 (a) Digraph terhubung kuat, dan (b) digraph tak terhubung kuat

Proposisi 2.2. Andaikan D adalah suatu digraph terhubung kuat maka setiap verteks terletak pada cycle.

Bukti. Andaikan digraphDterdiri atasnverteks{v1, v2, . . . , vn}. Ambil sebarang

verteks u dan v di D, karena D terhubung kuat, maka terdapat sebuah lintasan sederhana (path) dari verteks u ke verteks v dan dari verteks v ke verteks u. Sehingga gabungan dua buah path tersebutu→ · · · →v → · · · →umembentuk sebuah cycle di D. Akibatnya, verteksudan v terletak padacycle.

Suatu digraph D yang terhubung kuat dikatakan primitif apabila untuk dua buah verteks u dan v di D terdapat jalan dari u ke v dan dari v ke u dengan panjang k. Nilai k digunakan untuk perhitungan eksponen dari digraph D. Bilangan bulat positif terkecilk disebut eksponen dari digraph D dan ditulis

dengan exp(D).

AndaikanDadalah digraph yang terhubung kuat. Misalkan terdapat sebuah verteks tertentu x di D. Untuk dua buah verteks u dan v di D terdapat jalan

wxu yaitu jalan dari verteksx ke verteksu dan jalan wxv yaitu jalan dari verteks x ke verteks v. Jika ℓ(wxu) = ℓ(wxv), maka verteks u dan v dikatakan ekivalen

diilustrasikan sebagai:

y →w xwxu

→ u

dan jalan wyv yaitu jalan dari verteks y ke verteks v, wyv dapat diilustrasikan

sebagai:

y→w xwxv

→ v.

Karenau dan v ekivalen, ini berakibat jalan dariy ke udan dari y kev memiliki panjang yang sama dimana w merupakan jalan dari y kex.

Andaikan C = {C1, C2, . . . , Cr} adalah himpunan semua cycle-cycle di D.

Misalkan ℓ(C) adalah matriks baris dengan kolom ke-idimanai= 1,2, . . . ,r, dan entri-entri dari ℓ(C) adalah panjang cycle Ci (ℓ(Ci)), yakni

ℓ(C) ={ℓ(C1), ℓ(C2), . . . , ℓ(Cr)}

dan misalkanm= gcd(ℓ(C1), ℓ(C2), . . . , ℓ(Cr)). Definisikan H sebagai sebuah

sub-grup dari sub-grup bilangan bulatZ, dimanaH dibangun oleh himpunanℓ(C). Yakni H =hℓ(C₁), ℓ(C₂), . . . , ℓ(Cr)i. KarenaZadalah sebuah grup siklik, demikian juga

halnya dengan H. AkibatnyaH dibangun oleh sebuah bilangan bulat, dalam hal iniH = gcd(ℓ(C1), ℓ(C2), . . . , ℓ(Cr)).

AndaikanDadalah digraph imprimitif dengan indeks imprimitifitask, maka k = gcd(ℓ(C₁), ℓ(C₂), . . . , ℓ(Cr)). Suatu digraph adalah primitif jika k = 1 dan

imprimitif jika k > 1. Teorema berikut menjelaskan tentang imprimitifitas dari digraph D.

Teorema 2.3. Andaikan D adalah sebuah digraph terhubung kuat. D adalah primitif jika dan hanya jika pembagi persekutuan terbesar dari panjang cycle-cycle di D adalah 1.

Bukti. Andaikan digraphDadalah primitif. Maka untuk setiap pasangan verteks

u dan v di D, u ∼ v, Karena ℓ(wuv) ∈ H untuk setiap pasangan verteks u dan v di D dan setiap jalan (wuv) dari u ke v maka u ∼ v. Di ambil jalan dengan

panjang 1, maka 1 ∈ H, karena H = hgcd(ℓ(c₁), ℓ(c₂), . . . , ℓ(ct)i maka pembagi

persekutuan terbesar dari panjang cycle-cycle di D adalah 1.

D dan setiap jalan wuv dari u kev diD diperolehℓ(wuv)∈H. Sehingga

masing-masing pasangan verteks di D adalah ekivalen. Akibatnya digraph D adalah primitif.

Contoh 2.3. Pada Gambar 2.3 (a), sebuah dua cycle dengan panjang 3 dari v1 → v2 → v3 → v1 dan dengan panjang 4 dari v1 → v2 → v3 → v4 → v1.

Gcd(3,4) = 1, sehingga duacycle tersebut adalah primitif.

2.3. Matriks Ketetanggaan

Andaikan D(2) adalah sebuah digraph atas n verteks {v1, v2, . . . , vn}. Sebuah

matriks ketetanggaan A = (aij) dari D adalah sebuah sebuah matriks

bujur-sangkar berordo n yang didefinisikan sebagai berikut.

aij =

(

1, jika terdapat busur berarah dari verteks i ke verteksj,

0, jika sebaliknya

dimana i, j = 1,2, . . . , n.

Berikut ini diberikan contoh matriks ketetanggaan dari sebuah digraph.

Contoh 2.4. Dari Gambar 2.3 (a) dan (b), matriks ketetanggaannya adalah

A=

Sebuah matriks ketetanggaan A dari sebuah digraph D dikatakan primitif, jika terdapat bilangan bulat positif k sehingga seluruh entri dari Ak adalah posi-tif. Hal ini sesuai dengan pendapat Wielandt (Schneider, 2002), yaitu sebuah matriks tak negatif A dikatakan primitif jika Ak >0. Pada Contoh 2.3, matriks ketetanggaan A adalah matriks ketetanggaan dari digraph primitif, hal ini dapat dilihat bahwa

Dengan mengambil bilangan bulat positifk yang lebih dari 1 diperoleh

Untuk nilai k > 5, Ak _{>0. Sehingga disimpulkan seluruh entri pada A}k _dengan k ≥4 adalah positif.

Matriks B adalah matriks dari digraph yang tak terhubung kuat sehingga tidak primitif. Andaikan B adalah primitif maka untuk bilangan bulat positif k,

Bk > 0. Bila primitif, maka untuk nilai k yang besar, seluruh entri Bk adalah positif. Diambilk = 30 sehingga diperoleh

B30= 

 

1 0 1

0 1 1

0 0 0 

 .

Untuk bilangan bulat positif k > 30, entri dari Bk _{hanya berada pada interval}

[0,1]. Karena masih terdapat entri yang bernilai 0, mengakibatkan digraph D dengan matriks ketetanggaan B tidak primitif.

2.4. Eksponen

Eksponen dari digraph D didefinisikan sebagai bilangan bulat positif terkecil k sehingga untuk setiap pasangan verteksudanvdiDterdapat jalan dariukevdan dariv keudengan panjangk. Eksponen dari digraph tersebut dinotasikan dengan exp(D). Dalam hal ini, eksponen hanya ada bila digraphD adalah primitif.

Contoh 2.5. Dari Gambar 2.3 (a), akan diperlihatkan bahwa nilai eksponennya adalah 4 yaitu dengan memperlihatkan semua kemungkinan jalan dengan panjang 1, jalan dengan panjang 2, jalan dengan panjang 3, dan jalan dengan panjang 4.

1. Jalan dengan panjang 1,yaitu

v1 →v2, v1 →v3, v2 →v1, v2→v3, v3 →v1

Karena tidak terdapat jalan yang panjangnya 1 dari v₁ ke v₁, v₂ ke v₂, v₃ ke v2, dan v3 ke v3 maka 1 bukanlah eksponennya.

2. Jalan dengan panjang 2, yaitu

v1 →v2 →v3 v2→ v1 →v2 v3 →v1 →v3 v₁ →v₂ →v₁ v₂→ v₁ →v₃

v₂ →v₃ →v₁ v₃→ v₁ →v₂

Karena tidak terdapat jalan yang panjangnya 2 dari v1 ke v2, dan v3 ke v1

3. Jalan dengan panjang 3, yaitu

v1 →v2 →v3→ v1 v2 →v3 →v1 →v2 v3 →v1 →v2 →v1 v1 →v3 →v1→ v2 v2 →v3 →v1 →v3 v3 →v1 →v2 →v3 v₁ →v₂ →v₁→ v₃ v₂ →v₁ →v₂ →v₁

Karena tidak terdapat jalan yang panjangnya 3 dariv3 kev2 maka 3

bukan-lah eksponennya.

4. Jalan dengan panjang 4, yaitu

v₁ →v₂ →v₁→ v₂ →v₁ v₂ →v₁ →v₂ →v₁ →v₃ v1 →v2 →v3→ v1 →v2 v3 →v1 →v2 →v3 →v1 v1 →v2 →v3→ v1 →v3 v3 →v1 →v2 →v1 →v2 v₂ →v₃ →v₁→ v₂ →v₁ v₃ →v₁ →v₂ →v₁ →v₃ v₂ →v₁ →v₃→ v₁ →v₂

Karena terdapat jalan yang panjangnya 4 dari setiap pasangan verteks (u, v) maka eksponen dari digraph tersebut adalah 4.

Eksponen suatu digraphDdapat dicari dengan menggunakan perpangkatan dari matriks ketetanggaanA. Brualdi dan Ryser (1991), menyatakan bahwa entri (i, j) dari Ak _{merupakan banyaknya jalan dari verteksv}

i kevj dengan panjang k.

Berikut ini diperlihatkan hubungan antara suatu digraph dengan matriks kete-tanggaannya.

Proposisi 2.4. Andaikan A adalah suatu matriks ketetanggaan dari digraph D. Entri (i, j)dari Ak _{menyatakan banyaknya jalan dari v}

i ke vj yang panjangnya k

di D.

Bukti. Akan dibuktikan dengan induksi pada k. Jika k = 1 maka setiap entri a1

ij dari A1 menyatakan banyaknya jalan dari vi ke vj yang panjangnya satu.

Asumsikan setiap entri ak

ij dari Ak menyatakan banyaknya jalan dari vi ke vj

yang panjangnya adalah k diD, untuk k ≥1.

Akan diperlihatkan ak+1_ij adalah banyaknya jalan dari vi ke vj yang

pan-jangnya k+ 1, untuk k ≥ 1. Perhatikan setiap jalan dari vi ke vj di D dengan

panjang k untukℓ = 1,2, . . . , n dan dilanjutkan dengan busur berarah darivℓ ke vj, sehingga akiℓaℓj menyatakan jalan dengan panjang k + 1 dari vi ke vj di D.

Andaikan tidak terdapat jalan yang panjang k dari vi ke vℓ di D, maka akiℓ = 0

sedemikian sehingga ak

iℓaℓj = 0. Ini berarti tidak terdapat jalan dengan panjang k+ 1 dari vi kevj yang melaluivℓ diDsehingga banyaknya jalan dengan panjang k+ 1 dari vi ke vj di Dadalah:

KarenaAk+1 =Ak_{A diperolehlah}

ak+1_ij =

n

X

ℓ=1

ak_iℓaℓj.

Hal ini berakibat ak+1_ij adalah benar menyatakan banyaknya jalan dari vi ke vj

dengan panjangk+1 diD. Jadi, setiap entri (i, j) dari Ak_{menyatakan banyaknya}

jalan dengan panjang k dari vi kevj.

Dengan menggunakan Proposisi 2.4 akan dicari eksponen dari Contoh 2.3 (a). Dari subbab 2.3 sebelumnya telah diketahui bahwa matriks ketetanggaan

A =

entri dariAk_{>0 dipenuhi olehk ≥4 dan dari definisi eksponen adalah bilangan}

positif terkecilk sehingga eksponen dari digraph tersebut adalah 4.

2.5. Eksponen Lokal Digraph

Andaikan D adalah sebuah digraph primitif atas n verteks V ={v₁, v₂, . . . , vn}.

Untuk vi ∈ V di D, eksponen lokal dari verteks vi di D adalah bilangan bulat

positif terkecilℓ sehingga untuk setiap verteksvj dimanaj = 1,2, . . . , nterdapat

jalan dari verteksvi ke verteks vj di D dengan panjang ℓ. Eksponen verteks vi

disebut juga sebagai eksponen lokal keluar dari verteksvi dan dinotasikan dengan

expout(vi, D).

AndaikanDadalah digraph primitif yang terdiri darinverteks. Jika verteks-verteks di Dadalah (v1, v2, . . . , vn) sedemikian hingga

Contoh 2.6. Dari Gambar 2.3 (a), akan dicari eksponen lokal dari setiap verteks di D berdasarkan Proposisi 2.4 yaitu dengan melihat entri ak

ij dari Ak, dimana

semua entri pada baris ke-i harus bernilai positif.

Matriks ketetanggaan dari Gambar 2.3 (a) adalah

A= 

 

0 1 1

1 0 1

1 0 0 

 .

Nilai dariA2₌



 

2 0 1

1 1 1

0 1 1 



, padaA

2 _{terlihat baris ke-2 memiliki entri yang positif,}

sehingga expout(v2, D) = 2. Untuk A3 =



 

1 2 2

2 1 2

2 0 1 



, pada A

3 _{terlihat baris ke-1}

dan ke-2 memiliki entri-entri yang positif, maka expout(v1, D) = 3. Selanjutnya

A4 = 

 

4 1 3

3 2 3

1 2 2 



, pada A

4 _{terlihat setiap baris memiliki entri-entri yang positif,}

sehingga expout(v₃, D) = 4.