Chapter 1 The Nature and Organization of Optimization Problems

8

Chapter 1

The Nature and Organization of

Optimization Problems

Ch

apt

er

9

Ch

apt

er

1

WHY OPTIMIZE?

1. Improved yields, reduced pollutants

2. Reduced energy consumption

3. Higher processing rates

4. Reduced maintenance, fewer shutdowns

5. Better understanding of process (simulation)

10

11

12

Ch

apt

er

1

OPTIMIZATION

• Interdisciplinary Field

Max Profit

Min Cost

Max Efficiency

• Requires

1. Critical analysis of process

13

14

15

16

Ch

apt

er

1

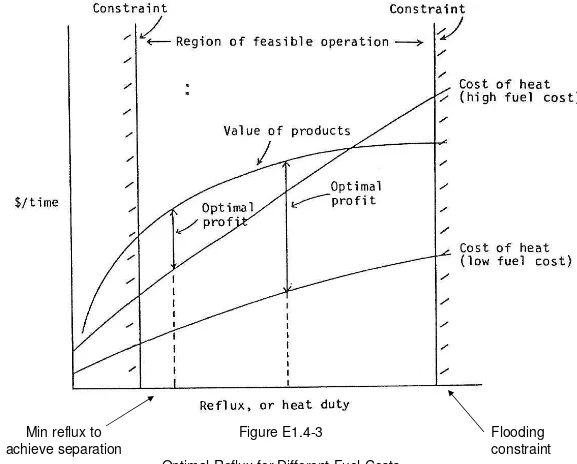
Figure E1.4-3

Optimal Reflux for Different Fuel Costs

Flooding constraint Min reflux to

17

18

19

20

21

Ch

apt

er

1

22

Ch

apt

er

1

Least squares solution:

2 1

)

(

min

i

i B

P

i

C

A

m

m

m







_

opt. m_A is the “average” value

23

24

Ch

apt

er

1

THREE INGREDIENTS IN OPTIMIZATION PROBLEM

1. Objective function economic model 2. Equality Constraints

Process model 3. Inequality Constraints

  

nx1 1 2

1. min f(x) x 2. subject to h( ) 0 (m ) 3. g( ) 0 (m )

2

(feasible region :)

3

dependent variables

independent variables

 

  

  

x x

1 2

25

26

Ch

apt

er

1

TABLE 1

THE SIX STEPS USED TO SOLVE OPTIMIZATION PROBLEMS

1. Analyze the process itself so that the process variables and specific characteristics of interest are defined, i.e.,

make a list of all of the variables.

2. Determine the criterion for optimization and specify the objective function in terms of the above variables together with coefficients. This step provides the

27

Ch

apt

er

1

3. Develop via mathematical expressions a valid process or equipment model that relates the input-output variables of the process and associated coefficients. Include both equality and inequality constraints. Use well-known

physical principles (mass balances, energy balances), empirical relations, implicit concepts, and external

28

Ch

apt

er

1

4. If the problem formulation is too large in scope: (A)Break it up into manageable parts and/or

(B)Simplify the objective function

5. Apply a suitable optimization technique to the mathematical statement of the problem.

29

Ch

apt

er

1

EXAMPLES – SIX STEPS OF OPTIMIZATION

specialty chemical

100,000 bbl/yr.

2 costs inventory (carrying) or storage, production cost >

how many bbl produced per run?

Step 1

define variables

Q = total # bbl produced/yr (100,000) D = # bbl produced per run

30

Ch

apt

er

1

Step 2

develop objective function

inventory, storage cost = k₁D

production cost = k₂ + k₃ D

per run (set up operating

cost) cost per unit

(could be nonlinear)

Q k D

Q k D

k C

D Q n

D k k

n D

k C

3 2

1

3 2

1 ( )

 

 

 

31

Ch

apt

er

1

Step 3

evaluate constraints

continuous

integer

n

D>0

Step 4

32

computation of the optimum

analytical vs. numerical solution

33

34

Sensitivity of the optimum

36

Ch

apt

er

1

RELATIVE SENSITIVITY (Percentage change)

37

Ch

apt

er

1

PIPELINE PROBLEM

variables parameters

V

p

f L

Re m

D pipe cost

 



electricity cost

#operating days/yr

38

Ch

apt

er

1

Equality Constraints

2

2

0.2

4

Re

/

2

.046 Re







 







 



D

v

m

Dv

L

p

v

f

39

40

Ch

apt

er

1

min (C_oper + C_inv.)

subject to equality constraints

2

2 v

D L f

p  



need analytical formula for f

tubes smooth

f  .046 Re0.2

pump power cost    o

p C m

2

mass flow rate

4

  D 

m v

substituting for ∆p,

) (

5 . 1 1

0 . 2 8 . 2 2 . 0 8 . 4

a nnua lized D

C C

m D

C C

inv

o oper





41

Ch

apt

er

1

5 . 1 1 8

. 4 8

. 2 2 2

. 0

TC

cost

Total





C

_o









m



D





C

D

(constraint eliminated by substitution)

6.3 0.2 2 2.8

1 0.16

.32 .45 .03

1

opt

2

( )

0 necessary condition for a minimum

solving,

( )

( )

opt velocity V

4 (sensitivity analysis)







 



 

 _ _

 



 

 

 _

opt o

opt o

opt

d TC dD

C

D m

C

C

D m

C

m

42

Ch

apt

er

1

optimum velocity

non-viscous liquids 3 to 6 ft/sec.

gases (effect of ρ) 30 to 60 ft/sec.

at higher pressure, need to use different constraint (isothermal)

1

2 2

1

1 1

1 2

1 1

ln 2

.323

24

upstream velocity or use Weymouth equation

p p

p fL

p S V

p p D

S



gV

 _{   } 

 _{   } 

  _{ }  _{ }

 _{  } _

 

 

 

for large L, ln ( ) can be neglected

43

Ch

apt

er

1

Heat Exchanger Variables

1. heat transfer area 2. heat duty

3. flow rates (shell, tube) 4. no. passes (shell, tube) 5. baffle spacing

6. length

7. diam. of shell, tubes 8. approach temperature

9. fluid A (shell or tube, co-current or countercurrent) 10.tube pitch, no. tubes

11.velocity (shell, tube) 12.∆p (shell, tube)

13.heat transfer coeffs (shell, tube) 14.exchanger type (fins?)

15.material of construction

(given flow rate of one fluid, inlet