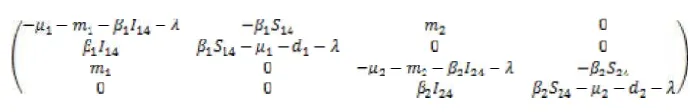KATA PENGANTAR
Jurnal Matematika merupakan jurnal yang memuat hasil penelitian mahasiswa, dosen atau penelit dalam bidang matematika dan statistika atau yang berhubungan dengan kedua bidang tersebut. Jurnal Matematika terbit setahun dua kali dan desember 2012 merupakan terbitan pertama. Pada penerbitan yang pertama,kedua dan ketiga ini, jurnal matematika memuat artikel mahasiswa yang merupakan bagian dari skripsi mahasiswa. Oleh karena itu, pada penerbitan selanjutnya redaksi mengharapkan dapat menerima artikel dari hasil penelitian dosen dan peneliti.
Dewan Redaksi
.
Ketua Dewan Redaksi : Dr. Miswanto,M.Si
2.Wakil Dewan Redaksi : Drs. Eko Tjahjono,M.Si
3.Anggota
: Dr. Fatmawati,M.Si
DAFTAR ISI
Achmad Romansyah, Moh. Imam Utoyo, Inna Kuswandari
PENYELESAIAN SISTEM LINIER FRAKSIONAL WAKTU KONTINU
1-5
Anisa Muthiatul Husnah, Suliyanto,
Toha Saifudin
Pemodelan Demam BerdarahDenguedi Surabaya dengan
PendekatanMixed Geographically Weighted Poisson Regression
6-15
Febri K.D.K.W, Liliek Susilowati, Inna Kuswandari, Hazrul Iswadi DimensiMetrikdanBilanganPembedaTerhubungdari GrafPiramidadan Graf PiramidaTerpancung
16-25
Friska Panggabean, Suliyanto,
Toha Saifudin
Estimasi Model Regresi Panel Poisson denganConditional Maximum Likelihood
26-42
Maulida Syarifah, Fatmawati, Yayuk Wahyuni
Model Matematika Penyebaran HIV/AIDS dalam Tubuh Manusia
dengan Faktor Respon Imun
43-53
Ratnaning Palupi, Liliek Susilowati, Nenik Estuningsih, Hazrul Iswadi
Bilangan Dominasi Lokasi Metrik pada Graf Kisi
54-61
Rizky Eka Abdullah, Fatmawati,
Windarto
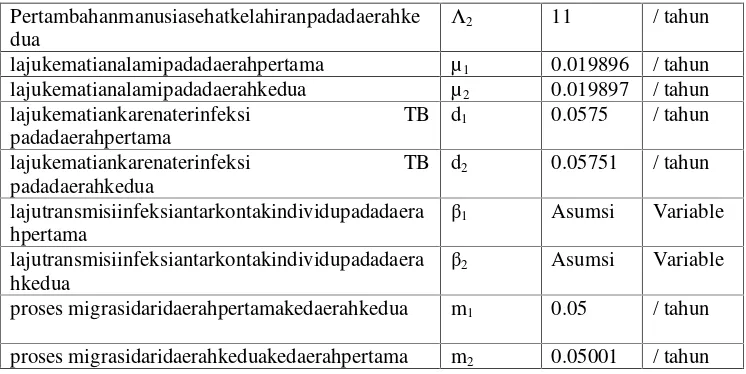
MODEL MATEMATIKA PENYEBARAN PENYAKIT
TUBERKULOSIS DENGAN PENGARUH MIGRASI
62-72
Yuniati Mahmudah,
Fatmawati, Yayuk Wahyuni
Analisis Model Matematika Penyebaran Penyakit HIV dengan Koinfeksi Kolera
73-80
Eko Prasetyo, Liliek Susilowati, Nenik Estuningsih, Hazrul Iswadi, Miswanto DimensiMetrikdanDimensiPartisi Graf BukuBertumpuk81-89
Welly Agus Budiono, Herry Suprajitno, Miswanto
PENYELESAIAN AIRLINE CREW SCHEDULING
PROBLEM BIKRITERIA MENGGUNAKAN FIREFLY ALGORITHM
PENYELESAIAN SISTEM LINIER FRAKSIONAL WAKTU
KONTINU
Achmad Romansyah1, Moh. Imam Utoyo2, dan Inna Kuswandari3
1 [email protected] 2 [email protected] 3 [email protected] DepartemenMatematika FakultasSainsdanTeknologi UniversitasAirlangga
Abstract.The objective of this final project is to determine the solution of the continuous-time fractional linear system by applying the Laplace transform of fractional derivatives and convolution properties can be obtained by applying the Laplace transform of fractional derivatives and convolution properties.
Keywords : Fractional continuous-time linear systems, Laplace transform, Fractional derivatives.
1 Pendahuluan
Dalam ilmu matematika analisa sistem linier waktu kontinu dapat diselesaikan dengan dua metode, yaitu dengan metode langsung dan metode tak langsung. Metode tak langsung ini sering dijumpai dalam sistem persamaan diferensial. Beberapa model sistem persamaan diferensial yang sering dibahas adalah sistem persamaan diferensial dengan orde , dengan adalah bilangan asli. Tetapi pada perkembangan selanjutnya orde persamaan diferensial tersebut tidak hanya untuk bilangan asli saja, melainkan untuk bilangan real yang biasa disebut sebagai
kalkulus fraksional(Podlubny [8]). Hal ini menyebabkan adanya sub-sub bahasan yang perlu dikaji lebih dalam lagi.
2 MetodePenelitian
Metode yang digunakan dalam penulisan ini adalah metode studi literatur.
3 HasildanPembahasan
Menurut Kaczorek [5], salah satu contoh sistem linier waktu kontinu dengan masukan dapat disajikan dengan model sebagai berikut :
dengan adalah variabel state (keadaan), variabel
masukan, variabel keluaran dan , , ,
.
Teorema 1.Bentuk umum selesaian persamaan (1) adalah:
dengan
Bukti. Dengan menerapkan transformasi Laplace pada persamaan (1) dan adalah nilai awal dari maka akan diperoleh:
Karena
maka persamaan (4) dapat diubah menjadi:
dengan
Contoh 1 : Carilah selesaian dari persamaan (1) jika:
dan
Dengan menggunakan persamaan (3) maka akan diperoleh:
Dan misalkan nilai dari ada yaitu maka dengan
4 Kesimpulandan Saran
Berdasarkan hasil dan pembahasan, diperoleh kesimpulan bahwa penyelesaian dari sistem linier fraksional waktu kontinu diperoleh dari penerapan transformasi Laplace pada turunan fraksional dan sifat konvolusi pada persamaan (1) (Teorema 1). Dalam melakukan penelitian ini, penulis hanya melakukan dengan batasan untuk yaitu . Sedangkan untuk penulis belum melakukan penelitian, sehingga masih menjadi open problem bagi pembaca yang tertarik untuk meneliti lebih lanjut.
DaftarPustaka
[1] Bronson, R., dan Costa, G. B., 2007,Differential Equations,The Mc Grow-Hill Companies, Inc., New Jersey.
[2] Chen, C. T., 1984, Linear System Theory and Design. New York: CBS College Publishing.
[3] Fahcruddin, I., 2011, Positifitas dan Ketercapaian Sistem Linier Fractional Waktu Kontinu, Jurnal CAUCHY-ISSN: 2086-0382, Vol. 2, No. 1 November 2011. [4] Graham, A., dan Gurghes, D.N., 1980, Introduction to Control Theory Including
Optimal Control, Halsted Press, New York.
[5] Kaczorek, T., (2008), Fractional Positive Continuous-Time Linear Systems and Their Reachability. Int. J. Appl. Math. Comput. Sci., 2008, Vol. 18, No. 2, 223-228. DOI : 10.2478/v10006-008-0020-0.
[6] Kimeu, J. M., 2009, Fractional Calculus: Definition and Applications.
Masters Thesis & Specialist Projets, Paper 115.
[7] Leon, S.J., 1998,Linear Algebra with Applications. Fifth Edition, Prentice-Hall, Inc.
Pemodelan Demam Berdarah
Dengue
di Surabaya dengan
Pendekatan
Mixed Geographically Weighted Poisson Regression
Anisa Muthiatul Husnah, Suliyanto & Toha Saifudin Departemen Matematika Fakultas Sains dan Teknologi
Universitas Airlangga
Abstract.Mixed Geographically Weighted Poisson Regression (Mixed GWPR) model is an expansion of GWPR. Mixed GWPR model has locally influential predictor variable and globally predictor variable influential. Generally, Mixed GWPR model is: ; i = 1, 2, … , n. The local parameter estimation of Mixed GWPR model using estimation method of GWPR model : and using estimation of global poisson regression to estimate global parameter : . The data used in the application of the model Mixed GWPR is data on the number of dengue hemorrhagic fever patients in 23 sub-district in Surabaya on 2011 as a response variable. While predictor variable are population density, the number of population aged less than 16 years, the population of at least high school education, the percentage of households living clean and healthy behavior, wiggler free numbers , the number of health facilities and the percentage of healthy. Based on data analysis, six locally influential predictor variables and one globally influential predictor variables are obtained. From that matter, it can be concluded that the number of health facilities not-significantly influenced. This might occur due to the high number of health facilities but not matched by the number of adequate health facilities. While the percentage of households living clean and healthy behavior non-significantly in one sub-district in Surabaya, population density, the number of population aged less than 16 years, the population of at least high school education, wiggler free numbers and the percentage of healthy significantly in 23 sub-district in Surabaya.
Keywords:mixed geographically weighted poisson regressiondan .
PENDAHULUAN
Demam Berdarah Dengue (DBD) adalah salah satu penyakit yang ditakuti masyarakat Indonesia sampai saat ini. Berdasarkan data Dinkes Kota Surabaya, sepanjang 2011 lalu terdapat 1.008 penderita DBD. Dari jumlah tersebut sebanyak 7 diantaranya meninggal dunia. Jumlah tersebut memang menurun dibandingkan tahun 2010, dimana terdapat 3.379 pasien dan 13 diantaranya meninggal dunia (Bachtiar, D., 2012). Seiring dengan masih tingginya angka kasus DBD maka diperlukan upaya penanggulangan faktor-faktor yang memicu berkembangnya penyakit tersebut salah satunya adalah melalui pendugaan model.
mungkin masalah DBD dipengaruhi oleh faktor lokal maupun global sehingga penulis tertarik untuk membahas pemodelan jumlah penderita DBD di Surabaya menggunakan pendekatanMixed GWPR.
Dalam artikel ini penulis membahas estimasi model GWPR danMixed GWPRkemudian menginferensi dan membandingkan kedua model menggunakan kriteria Akaike’s
Information Criterion Corrected ( ). Dari model terbaik kemudian akan diterapkan pada data jumlah penderita DBD di Surabaya dengan bantuansoftwareGWR 4.0. Artikel ini bersumber dari jurnal Nakaya,et. al.(2005) dengan judul “Geographically Weighted Poisson Regression for Disease Association Mapping”.
METODE PENELITIAN
Adapun langkah-langkah yang digunakan dalam menyelesaikan artikel ini sebagai berikut :
• Mengestimasi model Mixed GWPR menggunakan Metode Maksimum Likelihood.
• Melakukan inferensi dan perbandingan model GWPR dan modelMixed GWPR dengan kriteria .
• Menerapkan modelMixed GWPR pada data jumlah penderita penyakit DBD di kota Surabaya menggunakansoftwareGWR4.0
HASIL DAN PEMBAHASAN
Estimasi ModelMixedGWPR
Pada modelMixed GWPRvariabel respon diduga oleh variabel prediktor
yang bersifat lokal dengan parameter lokasi yang disimbolkan dimana lokasi
letak lintang dan bujur diperhatikan serta variabel prediktor yang bersifat global
dengan parameter yang tidak bergantung pada lokasi. Model Mixed GWPR dapat
ditulis sebagai berikut :
(1)
dengan lokasi kei dan .
ModelMixed GWPRpada (1) dapat dinyatakan dalam bentuk
(2)
dengan
=
=
Untuk mengestimasi model Mixed GWPR dari persamaan (2) diperoleh sehingga
(3)
Estimasi parameter lokal pada (3) dilakukan dengan iterasi menggunakan metode
estimasi GWPR dan mengganti variabel respon adjusted dengan , sehingga
diperoleh
(4)
dengan
Selanjutnya mengestimasi parameter global menggunakan metode estimasi regresi
poisson global. Dari modelMixed GWPR(2) diperoleh sehingga
=
(5)
Estimasi parameter global pada (5) dilakukan dengan iterasi menggunakan metode
estimasi model regresi poisson global dengan mengganti variabel respon adjusted
dengan , sehingga diperoleh
(6)
Pada saat persamaan (4) dan (6) konvergen maka indeks iterasi dapat dihilangkan sehingga diperoleh
(7)
dan
(8)
Substitusikan persamaan (7) ke persamaan (8) maka diperoleh
(9)
Persamaan (9) dapat digunakan untuk perhitungan cepat dengan prosedur iterasi
(10)
Inferensi dan Perbandingan ModelMixed GWPR
Untuk membandingkan model GWPR danMixed GWPRdigunakan kriteria
(11)
dengan
dengan langkah-langkah sebagai berikut :
Langkah 1.
Mengestimasi model GWPR menggunakan kriteria nilai terkecil.
Langkah 2.
Mengestimasi modelMixed GWPRdilakukan dengan langkah-langkah sebagai berikut :
(1) Menyeleksi variabel lokal dan variabel global pada model GWPR menggunakan hipotesis :
Variabel prediktor dikatakan variabel global jika tidak signifikan di semua
lokasi. Sebaliknya, variabel prediktor dikatakan variabel lokal jika signifikan
minimal satu lokasi tertentu sehingga merupakan variabel lokal.
(2) Mengelompokkan variabel global dan variabel lokal.
(3) Menghitung estimator prediktor linier model Mixed GWPR dengan mensubstitusikan (7) ke (8) sehingga diperoleh estimator prediktor linier yang dapat ditulis sebagai perkalian antara matriks smoother dengan vektor adjusted dari variabel respon :
(12) dengan
(4) Mengestimasi model Mixed GWPR menggunakan kriteria terkecil dengan mengganti sehingga diperoleh
(13)
dengan
adalah jumlah parameter yang efektif.
Nilai terkecil yang diperoleh menghasilkanbandwidth terbaik untuk estimasi parameter lokal dalam modelMixed GWPR.
Langkah 3.
Memilih model terbaik antara model GWPR danMixed GWPRmenggunakan pada persamaan (11) dan (13). Model terbaik dipilih berdasarkan nilai terkecil .
Selanjutnya melakukan inferensi berdasarkan model terbaik yang dipilih, yaitu model Mixed GWPR. Inferensi dilakukan dengan melakukan uji parsial parameter variabel lokal pada modelMixed GWPR.
Uji Parsial Parameter Variabel Lokal ModelMixed GWPR
Pengujian ini dilakukan untuk mengetahui variabel lokal yang berpengaruh signifikan terhadap variabel respon pada model Mixed GWPR. Untuk menguji parsial parameter variabel lokal pada model Mixed GWPR perlu dihitung covarians dari estimator parameternya. Jika persamaan (8) disubstitusikan ke persamaan (7) maka diperoleh :
(14)
dengan
Matriks dan pada persamaan (14) dihitung ketika estimasi parameter konvergen.
Dari (14) diperoleh matriks varians-covarians dari secara asimtotis adalah
(16) Dari (15) dan (16) diperoleh matriks varians-covarians dari adalah
= (17)
dengan
Untuk menguji secara parsial variabel lokal ( ) menggunakan hipotesis sebagai berikut :
, ,
dengan statistika uji :
(18)
dengan .
Nilai adalah elemen diagonal utama ke dari matriks
Daerah kritis untuk uji tersebut adalah tolak jika .
Penerapan ModelMixed GWPR
Sumber Data
Data yang digunakan dalam penerapan model Mixed GWPR ini adalah data sekunder tahun 2011 yang berupa data jumlah penderita Demam Berdarah Dengue
(DBD), data angka bebas jentik, prosentase rumah tangga ber PHBS, prosentase rumah sehat di 23 kecamatan di Surabaya yang diperoleh dari Dinas Kesehatan kota Surabaya, data prosentase penduduk miskin, jumlah fasilitas kesehatan, jumlah penduduk umur kurang dari 16 tahun, jumlah penduduk pendidikan minimal SMA, dan kepadatan penduduk yang diperoleh dari Badan Pusat Statistik (BPS) kota Surabaya (Badan Pusat Statistik, 2012), data letak astronomis lintang dan bujur yang diperoleh dari Badan Pusat Statistik (BPS) Jawa Timur, serta peta administrasi kota Surabaya diperoleh dari Teknik Geomatika ITS Surabaya.
Analisis Data
Gambar 1 Peta Persebaran Jumlah Penderita DBD di Surabaya Tahun 2011 Gambar 1 menunjukkan bahwa lokasi kecamatan dalam satu kelompok memperlihatkan pola yang cukup menyebar. Selain itu pula diketahui bahwa jumlah penderita DBD sangat tinggi berada di kecamatan Tandes yaitu sebanyak 62 hingga 100 penderita. Sedangkan Pakal, Lakarsantri, Gayungan, Bulak, Dukuh Pakis, Asemrowo, Genteng, Karangpilang, Jambangan, Rungkut, dan Gunung Anyar merupakan daerah dengan jumlah penderita DBD yang sangat rendah yaitu sebesar 9 hingga 22 penderita. Daerah dengan jumlah penderita DBD tertinggi di kecamatan Tandes dan terendah di kecamatan Bulak.
Estimasi model GWPR menggunakan software GWR4.0 dengan pembobot
kernel Gaussian diperolehbest bandwidth = 552.205 yang diperoleh dari hasil iterasi, serta diperoleh nilai minimal = 93.546. Mengingat kecamatan yang memiliki jumlah penderita DBD tertinggi adalah kecamatan Tandes dan disusul kecamatan Kenjeran (Gambar 1), maka berikut hanya ditampilkan hasil estimasi yang diperoleh dari
softwareGWR4.0.
Estimasi parameter model GWPR untuk kecamatan Tandes diperoleh :
Estimasi parameter model GWPR untuk kecamatan Kenjeran diperoleh :
Untuk mengestimasi model Mixed GWPR, pertama kali yang dilakukan adalah menyeleksi variabel prediktor, apakah berpengaruh secara lokal atau global dengan menggunakan hipotesis sebagai berikut :
sekurang-kurangnya ada satu
dengan menggunakan GWR4.0 untuk nilai = 5% didapat t(0,025; 14.305888) = 2.140 maka keputusan diambil dengan menolak jika nilai > . Variabel prediktor dikatakan variabel global jika tidak signifikan di semua lokasi. Sebaliknya, variabel prediktor dikatakan variabel lokal jika minimal signifikan di satu lokasi tertentu sehingga merupakan variabel lokal. Dengan menggunakan program seleksi variabel dalam software S-Plus 2000 diperoleh variabel prediktor yang berpengaruh secara global adalah dan variabel prediktor yang berpengaruh secara lokal adalah dan . Hasil estimasi untuk parameter variabel global dan parameter variabel lokal diperoleh hasil untuk kecamatan Tandes dan kecamatan Kenjeran sebagai berikut :
Estimasi parameter modelMixed GWPRuntuk kecamatan Tandes diperoleh :
Estimasi parameter modelMixed GWPRuntuk kecamatan Kenjeran diperoleh :
Pemilihan model terbaik dilakukan dengan menggunakan nilai kriteria .
Berikut nilai minimal model GWPR dan Mixed GWPR yang didapatkan dari
[image:17.612.161.475.126.166.2]softwareGWR4.0 dengan menggunakan pembobot fungsi kernelgaussian. Tabel 1. Perbandingan Model
Model minimal
GWPR 93.546
Mixed GWPR 93.314
Tabel 1. menunjukkan bahwa nilai minimal model Mixed GWPR lebih kecil dari pada nilai minimal model GWPR sehingga model Mixed GWPRmerupakan model terbaik untuk pemodelan DBD di Surabaya tahun 2011.
Setelah dipilih model terbaik selanjutnya dilakukan uji signifikasi variabel prediktor lokal yang signifikan mempengaruhi variabel responnya dengan = 5% maka variabel prediktor lokal yang berpengaruh secara signifikan apabila t(0,025;14.353628) = 2.1398 < . DengansoftwareGWR4.0 didapatkan beserta koefisien variabel prediktor lokal modelMixed GWPR pada semua lokasi. Variabel-variabel lokal yang signifikan pada 23 kecamatan di Surabaya adalah variabel prediktor rumah tangga ber PHBS ( ) tidak signifikan di kecamatan Benowo. Sedangkan variabel prediktor kepadatan penduduk ( ), jumlah penduduk umur kurang dari 16 tahun ( ), jumlah penduduk pendidikan minimal SMA ( ), angka bebas jentik ( ), dan prosentase rumah sehat ( ) signifikan di 23 kecamatan di Surabaya.
Dari hasil analisis disoftwareGWR.4.0 dapat diketahui koefisien masing-masing variabel prediktor yang signifikan mempengaruhi variabel respon, variabel prediktor rumah tangga ber PHBS ( ) dan angka bebas jentik ( ) berpengaruh negatif terhadap jumlah penderita DBD di 23 kecamatan. Ini menunjukkan bahwa makin tinggi prosentase rumah tangga ber PHBS dan angka bebas jentik, maka semakin rendah jumlah penderita DBD. Sedangkan variabel prediktor kepadatan penduduk ( ), jumlah penduduk umur kurang dari 16 tahun ( ), jumlah penduduk pendidikan minimal SMA ( ), dan prosentase rumah sehat ( ) berpengaruh positif terhadap jumlah penderita DBD. Ini menunjukkan makin tinggi kepadatan penduduk dan jumlah penduduk umur kurang dari 16 tahun, maka jumlah penderita DBD makin tinggi pula. Sedangkan jumlah penduduk pendidikan minimal SMA dan prosentase rumah sehat berpengaruh positif terhadap jumlah penderita DBD. Uji validasi dengan bantuansoftwareS-Plus 2000 diperoleh nilai MSE = 160.4288.
KESIMPULAN DAN SARAN Kesimpulan
Dari hasil dan pembahasan pada bab sebelumnya, maka dapat diambil kesimpulan bahwa :
1. Estimasi model Mixed GWPR menggunakan persamaan iterasi berdasarkan metode estimasi parameter model GWPR untuk mengestimasi parameter lokal dan menggunakan persamaan iterasi berdasarkan estimasi parameter model regresi poisson global.
Persamaan iterasi estimasi parameter model GWPR adalah
Sedangkan persamaan iterasi estimasi parameter model regresi poisson global adalah
a. Mengestimasi model GWPR dengan menggunakan kriteria
b. Mengestimasi modelMixed GWPRdengan langkah-langkah :
(1) Menyeleksi variabel lokal dan variabel global pada model GWPR menggunakan statistik uji ~
(2) Mengelompokkan variabel global dan variabel lokal.
(3) Mengestimasi modelMixed GWPRmenggunakan kriteria
c. Memilih model terbaik berdasarkan nilai terkecil antara model GWPR dan
Mixed GWPR
d. Menguji secara parsial variabel global pada model Mixed GWPR dengan menggunakan statistik uji dan daerah kritis adalah tolak jika
e. Menguji secara parsial variabel lokal pada model Mixed GWPR dengan
menggunakan statistik uji daerah kritis adalah tolak jika
3. Hasil penerapan data menggunakan software GWR4.0 estimasi model GWPR diperoleh minimal = 93.546. Variabel prediktor yang berpengaruh secara global adalah dan variabel prediktor yang berpengaruh secara lokal adalah
dan . Dari hasil estimasi modelMixed GWPRdiperoleh nilai minimal = 93.314. Pemilihan model terbaik dipilih berdasarkan nilai terkecil. Nilai minimal model Mixed GWPR lebih kecil dari pada nilai minimal model GWPR. Sehingga dapat disimpulkan bahwa model Mixed GWPRmerupakan model terbaik untuk pemodelan DBD di Surabaya tahun 2011. Uji signifikansi parameter lokal bahwa variabel prediktor rumah tangga ber PHBS ( ) tidak signifikan di kecamatan Benowo. Sedangkan variabel prediktor kepadatan penduduk ( ), jumlah penduduk umur kurang dari 16 tahun ( ), jumlah penduduk pendidikan minimal SMA ( ), angka bebas jentik ( ), dan prosentase rumah sehat ( ) signifikan di 23 kecamatan di Surabaya. Uji validasi dilakukan dengan bantuan softwareS-Plus 2000 dan diperoleh nilai MSE = 160.4288.
Saran
disarankan agar menggunakan semua kecamatan di Surabaya sehingga model yang didapatkan lebih valid.
DAFTAR PUSTAKA
[1] Amrullah, A. 2011. Kesehatan Masyarakat Demam Berdarah. http://www.kesmas.tk/2010/11/ dbd-demam-berdarah-dengue.html [diakses tanggal, 22 Maret 2013, pukul18:010]
[2] Aradea, 2011. Gejala Demam Berdarah Obat Alami Demam Berdarah. http://obat-alami.com/tag/gejala-demam-berdarah [diakses tanggal, 23 Maret 2013, pukul 14:15]
[3] Badan Pusat Statistik, 2012. Surabaya Dalam Angka 2011. Surabaya.
[4] Charlton, M., Fotheringham, A.S., and Brunsdon, C., 2003. GWR 3 Software for Geographically Weighted Regression, Departement of Geography University of Newcastle, England.
[5] Nakaya, T., Fotheringham, A.S., Brunsdon, C. and Charlton, M., 2005. Geographically Weighted Poisson Regression for Disease Association Mapping, Statistics in Medicine, Volume 24 Issue 17, pages 2695-2717.
DimensiMetrikdanBilanganPembedaTerhubungdari Graf
Piramidadan Graf PiramidaTerpancung
Febri K.D.K.W1, Liliek Susilowati1, Inna Kuswandari1&Hazrul Iswadi2
1
DepartemenMatematika, FakultasSainsdanTeknologi UniversitasAirlangga
2
Departemen MIPA, Gedung TG Lantai 6 Universitas Surabaya
Abstract.Let is connected graph and The representation a vertex ) with respect to is the ordered k-tuple where represents the distance between vertices and . The set is called a resolving set for if every vertex of has a distinct representation. A resolving set containing a minimum number of vertices is called basis for . The metric dimension of denoted , is the number of vertices in a basis of . A resolving set of is connected if the subgraph induced by is a connected subgraph of . The connected resolving number is the minimum cardinality of a connected resolving set in a graph denoted by ). In this paper, determined metric dimension and connected resolving set number of pyramid graph and truncated pyramid graph. The pyramid graph is form by snake graph, denoted by and truncated pyramid graph is form by deleting vertex of vertices pyramid graph. The result from this paper are
, , for , for
, , , and .
Keywords:basis; metric dimension; connected resolving set number; pyramid graph
1. Pendahuluan
Graf G didefinisikan sebagai himpunantitik tak kosong dan himpunansisi yang menghubungkanduatitiktak terurut pada . Kardinalitas , dinotasikan dengan disebut ordo dari graf . Graf dikatakan terhubung jika setiap dua titik dan di graf selalu dihubungkandengansuatu lintasan.Jarak antara dua titik dan dinotasikan di suatu graf terhubung adalah panjang lintasan terpendek dari ke di .[3]
Misalkan graf terhubung dan himpunan . Representasititik , terhadap adalah pasangan terurut -tuple . Himpunan disebut himpunan pembeda dari graf jika representasi setiap titik di terhadap himpunan berbeda. Himpunan pembeda darigraf yang mempunyai kardinalitas minimum disebut basis dari graf dan kardinalitas basis disebut dimensi metrik dari graf yang dinotasikan dengan .
Himpunanpembeda dari terhubung jika subgraf yang terinduksi oleh merupakan
suatusubgrafterhubungdari . Kardinalitas minimum
darihimpunanpembedaterhubungdisebutbilanganpembedaterhubungdarigraf dan dinotasikan dengan [1].
dandimensimetriksuatugrafmendapatkanbanyakperhatiandariahligrafteori. Padapenelitianini,
ditentukandimensimetrikdanbilanganpembedaterhubungdarigrafpiramidadangrafpiramida terpancung.
2. Pembahasan
Pengubinanadalahrangkaiandarisegibanyak yang digunakanuntukmenutupisuatubidangdatartertentutanpatumpangtindihdantanpaadanyaper potongan.
Subgrafberhinggadarihasilpengubinandisebutdengangrafubin[4].Misalkanterdapatsuatupe ngubinanpadabidangdatarmenggunakansegitigasamasisi yang kongruen, duasegitigadikatakanterhubungjikaduasegitigatersebutbersekutupadasatusisi. Misalkan T adalahkumpulansegitiga-segitiga yang terhubung, maka T adalahgrafterhubungdengansikelterpendektigadanmasing-masingsegitiga paling sedikitterdapatsatusisi yang bersekutudengansisisegitiga yang lainnya. Kumpulan segitigaterhubungdisebuttriomino. T disebut -triominojika T merupakan buah graf ubin. Graf ular, graf piramida, dan graf piramida terpancung terbentuk dari satu buah graf ubin sehingga ketiga graf tersebut merupakan 1-triomino. [6]
Definisi 2.2.1 Graf ulardenganpanjang yang dinotasikan dengan merupakan 1-triomino yang dibentuk dari segitiga samasisi dengan cara berikut:
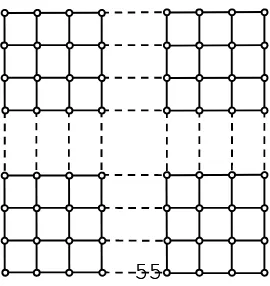
Definisi 2.2.2 Graf piramidadengantinggi ditulis merupakan 1-triomino, yang dibentuk dengan cara berikut:
terdiri dari , dengan ordo dari adalah 3.
terdiri dari , , dan , dengan ordo dari adalah 10.
Graf piramida dengan = { 1,2,3, , dan } dan
= { 1,2,3, , +1 1,2,3, , dan
}. terdiri dari , , , .
. ., dandan , dengan ordo dari adalah .
Graf piramidaterpancungadalahgraf yang dibentukdaripenghapusantitikpadapuncaksegitiga dan dinotasikan , dengan
adalah tinggi graf piramida terpancung. Graf piramida disajikan pada gambar
berikutini:
Graf
piramidaterpancung dengan { +1 +2 +1dan }d an ={ +1, +2, +3,…, +1 1,2,3,…, dan +1,
+1, +1, }. Ordo dari graf adalah +2 +2 +1 .
Lemma 1Misalkan adalah graf terhubung dengan ordo . Graf mempunyai dimensi metrik 1 jika dan hanya jika graf adalah . [2]
Lemma 2Misalkan graf terhubungdan . Jika memuat sebuah himpunan pembeda pada sebagai himpunan bagiannya, maka juga merupakan himpunan pembeda. [5]
Berikutiniadalahhasildari dan ) yang
disajikandalambentukteorema.
Teorema 2.1
Bukti: Dipilihhimpunanterurut dantitik-titikpada tersebut membangun subgraf terhubung dari . Representasisetiaptitik terhadap himpunan adalah:
bukan merupakan graf lintasan maka sehinggahimpunan merupakan himpunan pembeda minimal. Jadi merupakan basis dari dan terbukti bahwa
=2.▀
Teorema 2.2
Bukti: Dipilihhimpunanterurut
dantitik-titikpada tersebut membangun subgraf terhubung dari . Representasisetiaptitik terhadaphimpunan adalah:
Karenarepresentasisetiaptitik di terhadap himpunan berbeda maka merupakan himpunan pembeda dari . Berdasarkan Lemma 2.3.3, karenagrafpiramidaterpancung bukan merupakan graf lintasan maka
sehinggahimpunan merupakan himpunan pembeda minimal. Jadi merupakan basis dari graf piramida terpancung dan terbukti bahwa =2.▀
Setelahmenentukandimensimetrikdarigrafpiramida dan graf piramida terpancung , selanjutnya ditentukan bilangan pembeda terhubung dari graf piramida dan graf piramida terpancung . Berikut ini disajikan beberapa lemma untuk mendukung penentuan bilangan pembeda terhubung dari grafpiramida dan graf piramida terpancung .
Lemma 2.3Misalkan , jika anggota himpunan terdiri dari tepatsatutitikujungdantitik-titiksegarisdengantitikujungtersebutmaka
bukan merupakan himpunan pembeda.
Bukti: Misalkandiambilsebarang yang anggotadari terdiri dari titik-titik segaris tanpa titik-titik ujung, maka terdapat 2 titik-titik di yang mempunyai representasi yang sama terhadap himpunan . Himpunan tersebut adalah:
Tanpamengurangikeumumanbukti,
dipilihhimpunan mengakibatkan
. Karena maka
himpunan tersebut bukan merupakanhimpunanpembedadari .▀
Lemma 2.4Misalkan , jika anggota himpunan terdiri dari titik-titik segaris tanpa memuat titik ujung maka bukan merupakan himpunan pembeda.
Bukti: Diambilsebarang yang anggota dari terdiri dari titik-titik segaris tanpa titik ujung dan titik-titik pada tersebut membangun subgraf terhubung dari . Himpunan = . Tanpa mengurangi keumuman bukti, misalkan dipilih himpunan
mengakibatkan . Karena maka himpunan
tersebut bukan himpunan pembeda dari .▀
Bukti: Dipilihhimpunan dantitik-titikpada tersebut membangun subgraf terhubung dari . Representasi setiap titik di terhadap himpunan sebagai berikut:
Karenarepresentasisetiaptitik di terhadap himpunan tersebut berbeda maka himpunan tersebut merupakan himpunan pembeda terhubung dari . Berdasarkan Lemma 1, karena bukan merupakan graf lintasan maka sehingga himpunan tersebut merupakan himpunan pembedaterhubung minimal dari dan terbukti bahwa .▀
Lemma 2.6
Bukti: Dipilihhimpunan dantitik-titikpada
tersebut membangun subgraf terhubung dari . Representasi setiap titik di terhadap himpunan sebagai berikut:
Representasisetiaptitik di terhadap himpunan berbeda sehingga himpunan merupakan himpunan pembeda terhubung dari graf . Selanjutnya dibuktikan untuk himpunan dengan . Berdasarkan Lemma 2.3dan Lemma 2.4, himpunan dengan bukan merupakan himpunanpembedaterhubungdarigraf . Representasi setiap titik di terhadap himpunan dengan disajikan pada Lampiran 1. Karena himpunan merupakan himpunan pembeda terhubung dan semua himpunan dengan bukan merupakan himpunan pembeda terhubung dari maka himpunan merupakan himpunan pembeda terhubung minimal dari graf dan terbukti bahwa .▀
Lemma 2.7
Bukti: Dipilihhimpunan dantitik-titikpada tersebut membangun subgraf terhubung dari . Representasisetiaptitik di terhadap himpunan diberikan pada Lampiran 4. Karena representasi setiap titik di terhadap himpunan berbeda maka himpunan merupakan himpunan pembeda terhubung dari graf . Selanjutnya dibuktikan untuk himpunan
dengan . Berdasarkan Lemma 2.3dan Lemma 2.4, himpunan dengan bukan merupakan himpunan pembeda terhubung dari graf . Representasi setiap titik di terhadap himpunan dengan disajikanpadaLampiran 2. Karenahimpunan merupakan himpunan pembeda terhubung dan semua himpunan dengan bukan merupakan himpunan pembeda terhubung dari maka himpunan merupakan himpunan pembeda terhubung minimal dari graf dan terbukti bahwa .▀
Lemma 2.8
Bukti: Dipilihhimpunan dantitik-titikpada
Sehingga himpunan dengan bukan merupakan himpunan pembeda terhubung dari graf . TerbuktibahwaW merupakan himpunan pembeda terhubung minimal dari graf dan .▀
Lemma 2.9
Bukti: Dipilihhimpunan dantitik-titikpada
tersebut membangun subgraf terhubung dari . Representasisetiaptitik di terhadap himpunan diberikan pada Lampiran 4. Karena representasi setiap titik di
terhadap himpunan berbeda maka himpunan merupakan himpunan pembeda terhubung darigraf . Selanjutnyadibuktikanuntukhimpunan dengan . Semua himpunan dengan mempunyai karakterisasi yang sama seperti himpunan dengan . Karena himpunan dengan bukan merupakan himpunan pembeda terhubungdari maka himpunan dengan juga bukan merupakan himpunan pembeda terhubung dari graf . Jaditerbuktibahwahimpunan merupakan himpunan pembeda terhubung minimal dari graf dan .▀
Lemma 2.10
Bukti: Dipilihhimpunan
dantitik-titikpada tersebut membangun subgraf terhubung dari . Representasisetiaptitik di terhadap himpunan diberikan pada Lampiran 4. Karena representasi setiap titik di terhadap himpunan berbedamakahimpunan
merupakan himpunan pembeda terhubungdarigraf . Selanjutnya dibuktikan untuk himpunan , dengan . Berdasarkan Lampiran 3, semua himpunan dengan bukanmerupakanhimpunanpembedakarenaselaluterdapat 2 titikpadagraf yang mempunyai representasi sama terhadap himpunan tersebut. Sehingga himpunan dengan bukan merupakan himpunan pembeda terhubung dari graf . Jadi terbukti bahwahimpunan merupakanhimpunanpembedater hubung minimal darigraf dan terbukti bahwa ▀
Lemma 2.11
Bukti: Dipilihhimpunan
dantitik-titikpada tersebut membangun subgraf terhubung dari . Representasisetiaptitik di terhadap himpunan diberikan pada Lampiran 4. Karena representasi setiap titik di terhadap himpunan berbeda maka himpunan
merupakan himpunan pembeda terhubung dari graf . Selanjutnya dibuktikan untuk himpunan , dengan . Semua himpunan dengan mempunyai karakterisasi yang samasepertihimpunan dengan . Karena himpunan dengan bukan merupakan himpunan pembeda terhubung dari maka himpunan dengan juga bukan merupakan himpunan pembeda terhubung dari graf . Jaditerbuktibahwahimpunan merupakan himpunan pembeda terhubung minimal dari graf dan .▀
Selanjutnyadidapatkankonjekturbilanganpembedaterhubungdarigrafpiramida untuk , yaitu:
Konjektur 2.12Bilanganpembedaterhubungdarigrafpiramida dengan adalah,
denganhimpunanpembedaterhubungminimalnyaadalah,
Setelahmenentukan , untuk , selanjutnya disajikan beberapa lemma untuk bilangan pembeda terhubung dari graf piramida terpancung .
Lemma 2.13
Bukti: Dipilihhimpunan dantitik-titikpada
tersebut membangun subgraf terhubung dari . Representasi setiap titik di terhadap himpunan sebagai berikut:
Karenarepresentasisetiaptitik di terhadap himpunan tersebut berbeda dan subgraf dari yang terinduksi oleh adalah subgraf terhubung maka himpunan tersebut merupakan himpunan pembeda terhubung dari . Berdasarkan Lemma 2.3.3, himpunan tersebut merupakan himpunan pembeda terhubung minimal dari dan terbukti bahwa .▀
Lemma 2.14 .
Bukti: Dipilihhimpunan dan titik-titik pada
Karenarepresentasisetiaptitik di terhadap himpunan tersebut berbeda dan subgraf dari yang terinduksi oleh adalah subgraf terhubung maka himpunan tersebutmerupakanhimpunanpembedaterhubungdari . Berdasarkan Lemma 2.3.3, karena bukan merupakan graf lintasan maka himpunan tersebut merupakan himpunan pembeda terhubung minimal dari dan terbukti bahwa .▀
Lemma 2.15 .
Bukti: Dipilihhimpunan dan titik-titik pada
tersebut membangun subgraf terhubung dari . Karena , berdasarkan Lemma 4.3.4, maka merupakan hipunan pembeda terhubungdari . Diambil sebaranghimpunan dengan dan titik-titik pada tersebut membangun subgraf terhubung dari . Semua kombinasi himpunan tersebut selalu beranggotakan tepat satu titik ujung dan titik-titik segaris dengannya atautitik-titiksegaris yang tidakmemuattitikujung. Berdasarkan Lemma 4.3.1 dan Lemma 4.3.2, himpunan merupakan himpunan pembeda terhubung minimal dari graf dan terbukti bahwa .▀
Dari Lemma 2.13, Lemma 2.14, dan Lemma 2.15dapatdisimpulkanbahwabilanganpembedaterhubungdarigrafpiramidaterpancung
untuk adalah,
Selanjutnyadidapatkankonjekturbilanganpembedaterhubungdarigrafpiramidaterpanc ung untuk , yaitu:
Konjektur
2.16Bilanganpembedaterhubungdarigrafpiramidagrafpiramidaterpa ncung adalah,
denganhimpunanpembedaterhubungnya,
1. Graf piramida dengan = { 1,2,3, , +1dan } dan
= { 1,2,3, , +1 1,2,3, ,
dan }. Dimensi metrik dari
grafpiramida adalah 2danbasisnyaadalah .
2. Graf piramidaterpancung dengan
{ +1 +2 +1dan }dan =
{ +1, +2, +3, , +1 1,2,3, , dan +1, +1,
+1, }. Dimensi metrik dari grafpiramidaterpancung adalah
2danbasisnyaadalah .
3. Bilanganpembedaterhubungdarigrafpiramida dengan adalah,
4. Bilanganpembedaterhubungdarigrafpiramidaterpancung untuk adalah,
4. DaftarPustaka
[1] Baskoroputro,
Herolistra., DimensiMetrikdanBilanganPembedaTerhubungdariAmalgamasi-SisiSiklus. Matematika, InstitutTeknologi Bandung, Bandung, 2009.
[2] Chartrand, G., Eroh, L., Johnson M.A., danOellermann, O.R., Resolvability in graphs and the metric dimension of a graph, Discrete Appl. Math., 105: 5 – 7, 2000.
[3] Chartrand, G. danLesniak, L., Graphs and Digraph, 3rd ed., Chapman & Hall, Florida, pp. 1-16, 2000.
[4] Grunbaum, B. danShephard, G.C., Tilings and Patterns, W. H. Freeman and Company, Newyork, pp. 58-64, 2007.
[5] Iswadi, H., Baskoro, E.T., Salman, A.N.M., danSimanjutak, R., The Resolving Graph of Amalgamation of Cycles, An International Journal of Discrete and Combinatorial Mathematics. UtilitasMathematica,83, 2010.
[6] Low, R.M. dan Lee, S.M., On the integer-magic spectra of tessellation graphs, Australian Journal of Combinatorics, 34: 195-210, 2004.
Estimasi Model Regresi Panel Poisson
dengan
Conditional Maximum Likelihood
Friska Panggabean, Suliyanto & Toha Saifudin Departemen Matematika Fakultas Sains dan Teknologi
Universitas Airlangga [email protected]
Abstrct. Panel Poisson Regression Model using Conditional Maximum Likelihood is a combination of cross-section data and time series data, that is applied to data that individual effects have highly significant correlation to the predictor variable from a large population, stated as the following below:
.
The purpose of this final project is to obtain estimates of the panel poisson regression model using the Conditional Maximum Likelihood method and to test the suitability of the model. To estimate the model parameters can be obtained by solving the equation form below
Parameter estimation of the panel Poisson regression model is gotten in a implicit form, so that it is solved using numerical iteration, which is the Newton-Raphson algorithm. After obtaining the parameter estimates, carried out several tests: to test the parameter estimation twice: simultaneously usingLikelihood Ratio Test(LRT) and individually using test statistics . After that, continued to test the suitability of the model usingdeviancetest statistic.
Keywords : Conditional Maximum Likelihood, Deviance, Newton-Raphson, Panel Poisson Regression Model
1. PENDAHULUAN
Hubungan fungsional variabel respon dengan variabel prediktor dapat digambarkan oleh model regresi. Data panel merupakan gabungan dari datatime seriesdan datacross section. Ekonometrika secara sederhana dijelaskan sebagai ilmu yang memperlajari suatu aplikasi dalam metode statistika pada ekonomi, yang tidak hanya terfokus pada data statistik saja namun merupakan gabungan dari teori ekonomi, matematika dan statistika. Data panel merupakan gabungan dari data time series dan data cross section. Dengan demikian pada data panel terdapat unit individu yang masing-masing diamati dalam interval waktu . Data panel adalah jenis data yang paling banyak digunakan dalam ekonometrika melalui model regresi panel.
estimator CML memiliki keuntungan membuat data dapat dianalisis dengan mudah, namun diperlukan asumsi bahwa variabel prediktornya bersifat sangat mempengaruhi variabel responnya sehingga pada model regresinya variabel responnya hanya bergantung pada variabel prediktornya. Pada kasus data panel dengan tetap dan besar, maka akan diperoleh masalah parameter yang terjadi secara isidentil (tak terduga) dan estimator maksimum likelihood menjadi tidak konsisten, sehingga digunakan pendekatan CML dengan jumlah variabel respon sebagai syarat.
Berdasarkan uraian di atas dalam skripsi ini penulis tertarik untuk membahas estimasi model regresi panel Poisson menggunakan CML dengan bantuan algoritma Newton Raphson karena algoritma ini akan memberikan hasil yang lebih akurat dan merupakan penyelesaian CML ketika diperoleh bentuk implisit. Setelah memperoleh nilai estimator parameter selanjutnya akan dilakukan uji parameter secara serentak dan individu serta melakukan uji kesesuaian model regresi panel poisson, dan menerapkan model tersebut pada data riil.
2. METODE PENELITIAN
2.1 Estimasi Model Regresi Panel Poisson
Untuk mengestimasi Model Regresi Panel Poisson digunakan langkah-langkah sebagai berikut :
Langkah 1
Mengasumsikan data panel yang memenuhi
model regresi poisson yaitu
dengan
adalah variabel respon pada unitcross-section dan waktu ke-adalah sebuah vektor berdimensi
adalah vektor parameter berdimensi
Langkah 2
Mengasumsikan variabel respon pada langkah 1 mempunyai fkp yaitu
Langkah 3
Menentukan fkp bersama dari dengan syarat yang dapat dituliskan sebagai
Langkah 4
Menentukkan fungsilikelihooddari langkah 3, yaitu:
Langkah 5
Menentukkan fungsi log-likelihooddari langkah 4, yaitu:
Mengestimasi parameter , dimulai dengan mendiferensialkan hasil log-likelihooddari langkah 5 terhadap parameter .
Langkah 7
Hasil dari diferensial pada langkah 6 disamakan dengan nol sebagai syarat perlu untuk memaksimumkan fungsi log-likelihooddan diselesaikan.
Langkah 8
Melakukan pendekatan iterasi, dengan menggunakan algoritma Newton-Raphsonkarena pada langkah 7 masih diperoleh persamaan yang berbentuk implisit. Langkah-langkah algoritmaNewton-Raphsonyaitu:
(1) Menentukan , dan nilai awal estimator parameter (2) Menghitung dan dengan
dan
(3) Menghitung
(4) Jika nilai maksimum , dengan memilih , maka
perhitungan dilanjutkan langkah (5), tetapi jika nilai maksimum , maka ulangi langkah (3) dengan mengganti
.
(5) Mendapatkan estimator
(6) Mengestimasi model regresi panel poisson
2.2Uji Kesesuaian Model
Setelah mendapatkan estimasi parameter, dilakukan beberapa uji terhadap parameter diantaranya uji serentak menggunakan uji Likelihood Ratio Test
a. Untuk menguji pengaruh variabel prediktor terhadap variabel respon secara serentak menggunakan statistik uji LRT dilakukan langkah-langkah sebagai berikut.
Langkah 1
Merumuskan hipotesis
Langkah 2
Menghitung nilai maksimum fungsi log-likelihoodmasing-masing di bawah benar dan benar yaitu
dan .
Langkah 3
Menghitung nilai statistik LRT yaitu
Langkah 4
Menentukkan daerah kritis dengan tingkat signifikansi , yaitu tolak jika diperoleh .
b. Untuk menguji pengaruh variabel prediktor terhadap variabel respon secara individu menggunakan statistik uji uji normal baku atau statistik uji Wald dengan langkah-langkah sebagai berikut.
Langkah 1
Merumuskan hipotesis vs
Langkah 2
Menghitung nilai statistik uji normal baku, yaitu
Langkah 3
Menentukkan daerah kritis dengan tingkat signifikansi , yaitu tolak jika diperoleh .
c. Untuk menguji kesesuaian model dugaan dibandingkan dengan model sebenarnya menggunakan statistik ujideviancedilakukan langkah-langkah sebagai berikut. Langkah 1
Merumuskan hipotesis
: Model regresi panel poisson sesuai.
: Model regresi panel dengan poisson tidak sesuai..
Langkah 2
Menghitung nilaideviance,yaitu
Langkah 3
3. HASIL DAN PEMBAHASAN 3.1 Estimasi Model Panel Poisson
Diasumsikan data panel yang
memenuhi model regresi poisson yaitu:
(1)
dengan
adalah variabel respon pada unitcross-section dan waktu ke-adalah sebuah vektor berdimensi
adalah vektor parameter berdimensi
Variabel respon pada mempunyai fungsi kepadatan peluang (fkp) yaitu:
(2)
Pada kasus data panel dengan tetap dan besar, maka akan diperoleh estimator maksimum likelihood yang tidak konsisten, sehingga digunakan pendekatan CML dengan jumlah variabel respon sebagai syarat.
Karena distribusi Poisson adalah anggota dari keluarga eksponensial, maka terdapat statistik cukup untuk dan . Dengan demikian
berdistribusi poisson dengan parameter sehingga CML dapat diterapkan. Selanjutnya menentukan pdf bersama dari dengan syarat yaitu
(3)
dengan
Dari diperoleh fungsilikelihood
(4)
Fungsi log-likelihooddari adalah , sehingga diperoleh
Syarat perlu agar fungsi log-likelihood pada persamaan (5) mencapai nilai maksimum adalah
dan akhirnya diperoleh persamaan secara umum sebagai berikut
(6)
Persamaan (6) merupakan persamaan berbentuk implisit sehingga tidak dapat diselesaikan secara analitik. Untuk mengetimasi vektor parameter pada persamaan (6) digunakan metode iterasiNewton Raphson.Didefinisikan vektor gradien sebagai berikut.
(6a)
maka diperoleh bentuk umum yaitu:
(7)
Turunan kedua dari fungsi log-likelihood terhadap dan untuk dengan adalah
(8)
Dari persamanaan (7) dan (8) diperoleh matriks Hessian sebagai berikut:
(9)
Syarat perlu agar fungsi log-likelihood pada persamaan (5) mencapai nilai maksimum adalah matriks Hessian pada persamaan (9) harus definit negatif.
Langkah-langkah untuk menyelesaikan persamaan (6) dengan menggunakan algoritma
Newton-Raphsonadalah sebagai berikut.
Langkah 1.
Menentukkan nilai awal estimator parameter dengan memilih Nilai dapat dihitung menggunakan metode kuadrat terkecil seperti yang diusulkan Draper dan Smith (1992) sebagai berikut:
(10) Untuk mengestimasi parameter pada persamaan (10) dapat didekati dengan model regresi linier berganda sehingga diperoleh bentuk matriks sebagai berikut.
, dengan (12)
, dengan (13)
, dengan dan
Esimasi parameter pada persamaan (11) digunakan sebagai nilai awal iterasi menggunakan metode kuadrat terkecil yaitu
. Langkah 2.
Menghitung dengan mengunakan persamaan (6a) dan menghitung dengan menggunakan persamaan (9).
Langkah 3.
Menghitung
Langkah 4.
Jika nilai maks , dengan memilih maka lanjutkan ke langkah 5, tetapi jika nilai maks , maka ulangi langkah 3 dengan mengganti .
Langkah 5.
Mendapatkan estimator
Langkah 6.
Mengestimasi model regresi panel poisson .
3.2 Uji Kesesuaian Model Regresi Panel Poisson
Setelah mendapatkan estimasi parameter, dilakukan beberapa uji.
Untuk menguji parameter model regresi panel poisson secara serentak digunakan hipotesis
Himpunan parameter di bawah adalah . Himpunan parameter di bawah adalah .
Dari persamaan (5) diperoleh nilai maksimum fungsi log-likelihood di bawah benar adalah
Akhirnya diperoleh statistik LRT sebagai berikut:
(14)
Secara asimptotik statistik uji berdistribusi . Daerah untuk menguji hipotesis parameter secara serentak dengan tingkat signifikansi adalah tolak
jika .
Sedangkan uji individu dilakukan untuk menguji signifikansi parameter secara individu pada model regresi panel poisson dengan menggunakan hipotesis
dengan adalah banyaknya parameter dengan menggunakan statistik uji normal yaitu:
(15)
dengan adalah simpangan baku dari estimator . Statistik uji berdistribusi normal asimtotik dengan mean 0 dan varians 1. Daerah kritis untuk menguji hipotesis tersebut dengan tingkat signifikansi adalah H0ditolak jika .
Hipotesis yang digunakan untuk menguji kesesuaian model regresi panel Poisson adalah sebagai berikut
H0 : Model regresi panel Poisson sesuai H1 : Model regresi panel Poisson tidak sesuai
Untuk menguji hipotesis tersebut digunakan statistik ujideviancesebagai berikut
(16)
Daerah kritis untuk menguji kesesuaian model regresi panel poisson adalah tolak H0jika
3.1 Penerapan Estimasi Model Regresi Panel Poisson pada Data
Data yang digunakan untuk penerapan model adalah data sekunder yang diperoleh dari Badan Pusat Statistik (BPS) provinsi Jawa Timur. Data yang dijadikan unit penelitian adalah kabupaten / kota diseluruh provinsi Jawa Timur yang terdiri dari 38 kabupaten / kota. Variabel-variabel yang digunakan dalam penulisan skripsi ini meliputi variabel respon dan variabel prediktor. Sebagai variabel respon adalah jumlah penganggur di
tiap kabupaten/kota di provinsi Jawa Timur tahun 2007-2011 dan sebagai variabel prediktornya adalah ingkat partisipasi angkatan kerja , tingkat partisipasi sekolah
usia 13-15 tahun , tingkat pengangguran terbuka , tingkat kesempatan kerja
, indeks pembangunan manusia , laju pertumbuhan ekonomi . Selain itu
juga digunakan data bangkitan dari program software S-PLUS sebagai simulasi bahwa model telah valid. Kedua data tersebut akan estimasi dengan menggunakan bantuan program S-PLUS 2000. Algoritma untuk membuat data bangkitan pada S-PLUS 2000 adalah:
Langkah 1.
Menginputkan banyak individu dari data yang ingin dibangkitkan.
Langkah 2.
Langkah 3.
Menentukkan variabel respon yang memiliki hubungan eksponensial terhadap semua variabel presdiktor yang telah dibangkitkan.
Langkah 4.
Menggabungkan variabel respon dan variabel prediktor dalam bentuk matriks.
Langkah 5.
Memanggil data bangkitan.
Banyaknya variable prediktor yang akan dibangkitkan ditentukan sama seperti banyaknya variabel prediktor pada data riil yaitu sebanyak 6 buah, masing-masing variabel prediktor mewakili variabel prediktor yang ada pada data riil.
Analisa Data 1. Data Riil
Berdasarkan tabel data jumlah penganggur di setiap kabupaten / kota di provinsi Jawa Timur tahun 2007-2011, maka dapat dibuat model regresi panel poisson sebagai berikut:
dengan .
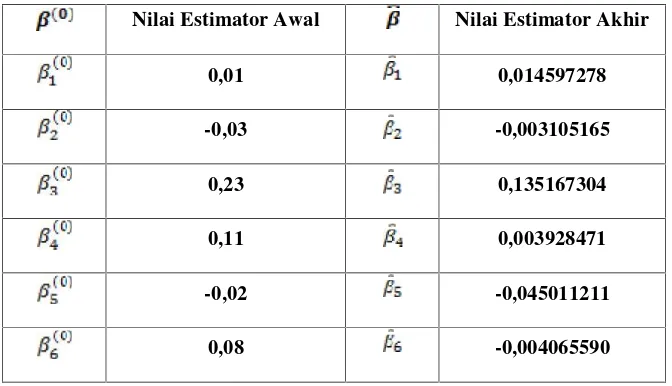
[image:39.612.152.488.454.647.2]Proses analisa data dalam contoh kasus data jumlah penganggur di setiap kabupaten / kota di provinsi Jawa Timur tahun 2007-2011 dilakukan dengan menggunakan program yang dibuat dalam software S-PLUS 2000. Berdasarkan hasil penerapan program pada data diperoleh nilai estimator awal seperti pada tabel 1 berikut.
Tabel 1. Nilai estimator awal parameter dan Nilai estimator akhir dari data jumlah penganggur di setiap kabupaten/kota di Provinsi Jawa Timur tahun
2007-2011
Nilai Estimator Awal Nilai Estimator Akhir
0,01 0,014597278
-0,03 -0,003105165
0,23 0,135167304
0,11 0,003928471
-0,02 -0,045011211
0,08 -0,004065590
dengan menyatakan banyaknya unit eksperimen yaitu kabupaten / kota di provinsi Jawa Timur. Berdasarkan persamaan model regresi panel poisson di atas dijelaskan bahwa variabel prediktor yang paling dominan berpengaruh dalam model regresi panel poisson di atas adalah yang menyatakan prosentase tingkat pengangguran terbuka dan dapat juga dilihat secara keseluruhan berdasarkan model di atas bahwa dengan semakin bertambahnya prosentase tingkat partisipasi angkatan kerja , prosentase tingkat pengangguran terbuka , dan tingkat kesempatan kerja maka akan meningkatkan jumlah penganggur di provinsi Jawa Timur tahun 2007-2011. Sebaliknya, semakin bertambahnya prosentase angka partisipasi sekolah usia 13-15 tahun , indeks pembangunan manusia dan prosentase laju pertumbuhan ekonomi maka akan menurunkan jumlah penganggur di provinsi Jawa Timur.
Uji serentak digunakan untuk mengetahui pengaruh variabel prediktor secara bersama-sama terhadap variabel respon, sedangkan uji individu dilakukan untuk mengetahui apakah masing-masing variabel prediktor tersebut berpengaruh signifikan terhadap variabel respon. Hasil analisis selengkapnya dapat dijelaskan sebagai berikut. Hipotesis yang digunakan untuk menguji parameter secera serentak adalah
Berdasarkan hasil yang didapat pada lampiran 7, terlihat bahwa keenam variabel prediktor yaitu: prosentase tingkat partisipasi angkatan kerja, prosentase angka partisipasi sekolah usia 13-15 tahun, prosentase tingkat pengagguran terbuka, prosentase tingkat kesempatan kerja, indeks pembangunan manusia dan laju pertumbuhan ekonomi secara serentak berpengaruh signifikan terhadap jumlah penganggur di setiap kabupaten / kota di provinsi Jawa Timur tahun 2007-2011. Hal ini ditunjukkan oleh nilai statistik uji dengan menggunakan tingkat signifikan diperoleh nilai (program dapat dilihat pada lampiran 4 dan output dapat dilihat pada lampiran 7). Oleh karena maka diperoleh keputusan tolak sehingga dapat disimpulkan bahwa semua variabel prediktor berpengaruh pada variabel respon. Hipotesis yang digunakan untuk menguji parameter secara individu adalah
Berdasarkan hasil yang didapat pada lampiran 7, terlihat bahwa variabel signifikan karena nilai statistik uji , variabel signifikan karena nilai statistik uji , variabel signifikan karena nilai statistik uji , variabel tidak signifikan karena nilai statistik uji , variabel signifikan karena nilai statistik uji , dan variabel signifikan karena nilai statistik uji
.
Nilai statistik ujideviance yang diperoleh adalah dan dengan menggunakan tingkat signifikan diperoleh nilai (program dapat dilihat pada lampiran 4 dan output dapat dilihat
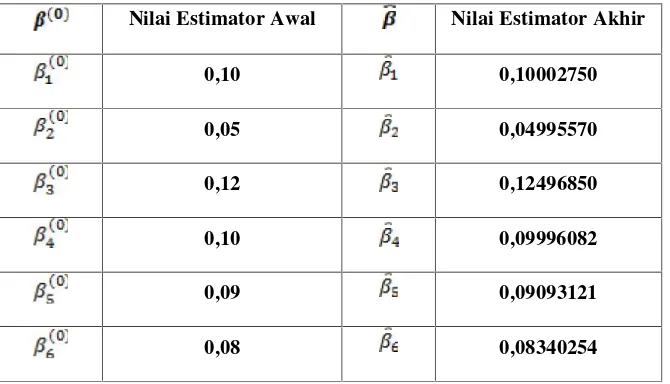
2. Data bangkitan
Tabel 2. Nilai estimator awal parameter dan Nilai estimator akhir dari
data Bangkitan S-PLUS
Nilai Estimator Awal Nilai Estimator Akhir
0,10 0,10002750
0,05 0,04995570
0,12 0,12496850
0,10 0,09996082
0,09 0,09093121
0,08 0,08340254
Berdasarkan tabel 2 maka diperoleh bentuk umum model regresi panel poisson untuk data bangkitan yang mewakili data jumlah penganggur di tiap kabupaten/kota di provinsi Jawa Timur tahun 2007-2011 sebagai berikut:
dengan menyatakan banyaknya unit eksperimen. Berdasarkan persamaan model regresi di atas variabel prediktor yang paling berpengaruh dominan dalam model regresi panel poisson di atas adalah dan berturut-turut diikuti oleh variabel prediktor , , , dan . Berdasarkan persamaan model regresi panel poisson di atas dijelaskan bahwa semua variabel prediktor berpengaruh positif variabel respon. Artinya semakin besar semua variabel prediktor maka variabel respon semakin besar.
Hipotesis yang digunakan untuk menguji parameter secera serentak adalah
Berdasarkan hasil yang didapat pada lampiran 11, terlihat bahwa keenam variabel prediktor secara serentak berpengaruh signifikan terhadap variabel respon. Hal ini ditunjukkan oleh nilai statistik uji dengan menggunakan tingkat signifikan diperoleh nilai (program dapat dilihat pada lampiran 8 dan output dapat dilihat pada lampiran 11). Oleh karena maka diperoleh keputusan tolak sehingga dapat disimpulkan bahwa semua variabel prediktor berpengaruh pada variabel respon.
Berdasarkan hasil yang didapat pada lampiran 11, terlihat bahwa variabel signifikan karena nilai statistik uji , variabel signifikan karena nilai statistik uji , variabel signifikan karena nilai statistik uji , variabel signifikan karena nilai statistik uji , variabel signifikan karena nilai statistik uji , dan variabel signifikan karena nilai statistik
uji .
Nilai statistik uji deviance yang diperoleh adalah dan dengan menggunakan tingkat signifikan diperoleh nilai (program dapat dilihat pada lampiran 8 dan output dapat dilihat
pada lampiran 11). Oleh karena maka diperoleh keputusan terima sehingga dapat disimpulkan bahwa model dugaan sesuai.
4. KESIMPULAN DAN SARAN 4.1 Kesimpulan
Dari hasil dan pembahasan pada bab sebelumnya, maka dapat diambil kesimpulan bahwa :
Berdasarkan pada Bab IV Hasil dan Pembahasan, maka dapat disimpulkan bahwa :
1. Estimator parameter model regresi panel poisson dapat diperoleh dengan menggunakan sistem persamaan sebagai berikut :
yang dapat diselesaikan dengan menggunakan algoritmaNewton Raphson. 2. Uji parameter model regresi panel poisson secara serentak dengan
menggunakan statistik uji LRT, yaitu:
dengan daerah kritisnya adalah tolak jika .
Uji parameter model regresi panel poisson secara individu dengan statistik uji normal asimtotik, yaitu:
dengan daerah kritisnya adalah tolak H0jika .
dengan daerah kritisnya adalah tolak H0jika
3.1 Hasil penerapan program estimasi model regresi panel poisson pada data jumlah penganggur di setiap kabupaten / kota di provinsi Jawa Timur tahun 2007-2011 diperoleh model dugaan sebagai berikut :
Berdasarkan model dugaan tersebut dapat disimpulkan bahwa semakin meningkatnya jumlah penganggur dikarenakan prosentase untuk masing-masing tingkat partisipasi angkatan kerja, tingkat pengangguran terbuka dan tingkat kesempatan kerja semakin bertambah. Sedangkan jumlah penganggur di provinsi Jawa Timur semakin berkurang jika prosentase angka partisipasi sekolah usia 13-15 tahun, indeks pembangunan manusia dan laju pertumbuhan ekonomi semakin tinggi. Karena prosentase angka partisipasi sekolah usia 13-15 tahun dan indeks pembangunan manusia yang semakin tinggi menandakan sumber daya manusia yang semakin berkualitas untuk bekerja atau untuk menciptakan lapangan pekerjaan, dan semakin meningkatnya laju pertumbuhan ekonomi berarti tenaga kerja yang dilibatkan semakin banyak sekaligus menurunkan jumlah penganggur. Adapun hasil penerapan program uji kesesuain model regresi panel poisson pada data jumlah penganggur di setiap kabupaten / kota di provinsi Jawa Timur tahun 2007 - 2011 diperoleh nilai dan .
Oleh karena nilai < maka diperoleh keputusan terima H0pada
tingkat kepercayaan 95%, sehingga dapat disimpulkan bahwa model dugaan sesuai.
Berdasarkan persamaan model regresi di atas variabel prediktor yang paling berpengaruh dominan dalam model regresi panel poisson di atas adalah dan
berturut-turut diikuti oleh variabel prediktor , , , dan .
Berdasarkan persamaan model regresi panel poisson di atas dijelaskan bahwa semua variabel prediktor berpengaruh positif variabel respon. Artinya semakin besar semua variabel prediktor maka variabel respon semakin besar Pada hasil penerapan program uji kesesuain model regresi panel poisson pada data bangkitan diperoleh nilai
dan . Oleh karena nilai <
maka diperoleh keputusan terima H0 pada tingkat kepercayaan 95%,
sehingga dapat disimpulkan bahwa model dugaan telah sesuai.
4.2 Saran
Saran yang dapat diberikan untuk penulisan selanjutnya adalah menggunakan data yang lebih memenuhi asumsi distribusi poisson untuk penerapan data estimasi model regresi panel poisson untuk mendapatkan hasil yang lebih baik.
5. DAFTAR PUSTAKA
[1] Gujarati, D., 2004, Basic Econometrics , 4th edition, McGraw-Hill, New York
[2] Hall, B.H., Hausman, J., dan Griliches, Z., (1984),”Econometric Models for Count Data with an Application to the Patents-R and D Relationship”, Journal of Econometrica, Vol.52, No. 4, page 909-938
Model Matematika Penyebaran HIV/AIDS dalam Tubuh Manusia
dengan Faktor Respon Imun
Maulida Syarifah, Fatmawati, Yayuk Wahyuni Departemen Matematika, Fakultas Sains dan Teknologi
Universitas Airlangga [email protected]
Abstract. Human Immunodeficiency Virus(HIV) is retrovirus which infects cells of human immune system causesAcquired Immunodeficiency Syndrome(AIDS). The purpose of this paper is to analyze the mathematical model of HIV/AIDS spreading in human body with immune response factor and constantly dynamical quantity of HIV. Based on analyze HIV/AIDS model with constantly dynamical quantity of HIV obtain three equilibrium point, those are free-infection equilibrium point will be exist and asymptotic locally stable for the immune-absence equilibrium point will be exist and asymptotic locally stable for and and the immune-presence equilibrium point will be exist and asymptotic locally stable for . The interpretation of that model got a standart classification for infection phase, based on parameter spread of HIV/AIDS . In a long term, the patient can be classified in free infection HIV phase when
infection HIV phase when , asymptomatic phase when and AIDS phase when . The result of simulation show that HIV/AIDS model with constanly dynamical quantity of HIV tend to constant osilated.
Keywords:HIV/AIDS model, , immune response of CTL, routh-hurwitz criterion
4. PENDAHULUAN
5. PENYEBARAN HIV DAN RESPON IMUN SEL CTL
Sel CD4 adalah salah satu jenis dari sel T, yakni sejenis sel darah putih yang
merupakan bagian penting dari sistem imun tubuh. Sel CD4 sendiri adalah target utama
dari HIV. Virus HIV cenderung memilih target sel CD4 karena pada permukaan sel CD4
terdapat gp120 (surface glycoprotein 120) yang merupakan pasangan ideal bagi
permukaan luar HIV. Virus HIV yang masuk ke dalam tubuh segera berusaha
menginfeksi sel CD4. Keberhasilan replikasi HIV berdampak pada kenaikan jumlah sel
CD4 yang terinfeksi. Keadaan ini mendorong terjadinya penurunan jumlah CD4 sehat
berarti pula terjadi penurunan sistem imun tubuh sehingga mudah terkena penyakit.
Munculnya berbagai penyakit karena rendahnya jumlah sel CD4 oleh pengaruh HIV,
disebut sebagaiinfeksi opportunistik. Hal inilah yang memicu munculnya AIDS.
Komponen jenis lain dari sel T adalah sel CD8 atau CTL (Cytotoxic T cell) yang berfungsi untuk membunuh sel yang terinfeksi oleh virus, dan seringkali juga dapat membunuh virus yang masuk. Berdasarkan [4], cara kerja CTL ini adalah dengan merilis Cytotoxins yang mengakibatkan virus mengalami apoptosis. Apoptosis merupakan bentuk kematian sel yang ditandai dengan perubahan struktur seperti penyusutan volume. Aktivasi CTL bergantung pada jumlah sel CD4 sehat maupun terinfeksi sebagai stimulus dan adanya interaksi atau kontak antara permukaan sel CD4 dengan permukaan sel CD4 yang terinfeksi. Sekali diaktifkan, CTL akan mulai mem-proliferasi atau menaikkan jumlah CTL yang spesifik terhadap virus yang akan dibunuh secara cepat. Ketika proses tersebut telah selesai, beberapa sel CTL yang aktif ini akan mati.
6. MODEL PENYEBARAN HIV
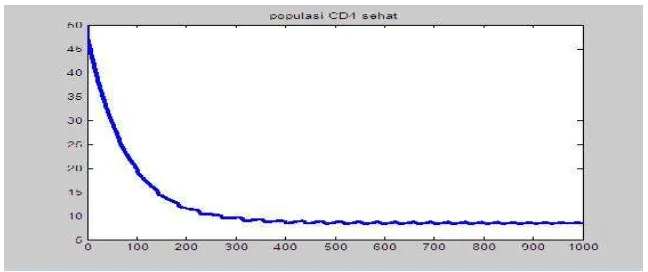
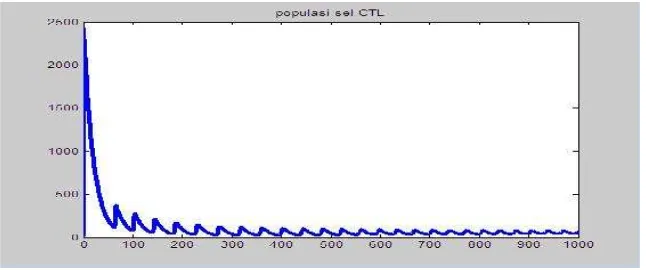
Berikut ini adalah model HIV/AIDS dengan perubahan jumlah virus konstan yang terdiri dari tiga kompartemen yakni populasi sel CD4 sehat , populasi sel CD4 terinfeksi dan populasi sel CTL :
(1)
1. Infeksi HIV terjadi secara internal yaitu didalam tubuh manusia. 2. Tidak ada virus lain yang menyerang tubuh selain virus HIV. 3. Laju produksi sel CD4 sehat dalam tubuh konstan.
4. HIV hanya menginfeksi sel CD4 sehat. 5. Sel CTL hanya membunuh sel CD4 terinfeksi.
6. Aktivasi dan proliferasi sel CTL bergantung pada jumlah sel CD4 sehat, sel CD4 terinfeksi dan sel CTL sendiri.
7. Perubahan jumlah virus HIV dalam tubuh konstan .
7. ANALISIS KESTABILAN
Untuk menganalisis kestabilan dari suatu model matematika yang berbentuk nonlinier, maka langkah awal yang dilakukan adalah mencari titik setimbang dari model tersebut. Berdasarkan [2] titik setimbang dapat diperoleh dengan menggunakan dengan adalah titik setimbang dan adalah
persamaan diferensial yang autonomous. Setelah didapatkan titik setimbang, selanjutnya dilakukan analisis kestabilan dengan cara membentuk matriks Jacobian dari titik setimbang tersebut dan didapatkan persamaan karakteristik sehingga diperoleh nilai eigen. Sebelum dilakukan analisis model perlu dikenalkan suatu bilangan reproduksi dasar dan . Bilangan reproduksi dasar dari sel CD4 terinfeksi didefinisikan sebagai yakni bilangan yang menyatakan rata-rata jumlah sel-sel CD4 terinfeksi yang muncul akibat masuknya virus HIV di dalam lingkungan sel-sel-sel-sel CD4 sehat. Sedangkan didefinisikan sebagai bilangan reproduksi dasar dari respon imun sel CTL yakni bilangan yang menyatakan rata-rata jumlah sel-sel CTL yang diproduksi oleh satu sel CTL di dalam sistem yang didalamnya terdapat sel-sel CD4 sehat dan terinfeksi.
Pada permasalahan tertentu kestabilan dari titik setimbang tidak dapat diamati karena tanda bagian real dari nilai eigen tidak mudah ditentukan. Untuk matriks yang berukuran dengan 2 tanda bagian real dari nilai eigen dapat ditentukan dengan menggunakan kriteria kestabilan Routh-Hurwitz. Berdasarkan [1], analisis kestabilan dengan menggunakan Kriteria Routh-Hurwitz, dapat dilakukan sebagai berikut:
Diberikan persamaan karakteristik:
(2)
, , ,
untuk gasal dan
untuk genap.
dengan saat . Akar-akar persamaan karakteristik (2) akan negatif atau mempunyai bagian real negatif jika dan hanya jika .
8. HASIL DAN PEMBAHASAN
8.1. Analisis Kestabilan Model HIV/AIDS dengan Perubahan Jumlah Virus Konstan
Dengan menggunakan [2], model HIV/AIDS dengan perubahan jumlah virus konstan mempunyai tiga titik setimbang yaitu titik setimbang bebas penyakit = ( , titik
setimbangimmune-absence = yang dijamin ada jika
(3)
dan titik setimbang immune-presence dijamin
ada jika dan . Perhatikan pertidaksamaan berikut:
.
Berdasarkan pertidaksamaan tersebut sama halnya dengan mengatakan bahwa titik setimbang dijamin ada jika
(4) Selanjutnya akan dianalisis kestabilan pada setiap titik setimbang tersebut dengan menggunakan kriteria Kestabilan Routh-Hurwitz. Untuk titik setimbang didapatkan matriks Jacobian
merupakan hasil pelinieran dari model HIV/AIDS perubahan jumlah virus konstan pada titik setimbang . Dari matriks Jacobian tersebut, dengan menggunakan
,diperoleh persamaan karakteristik
Berdasarkan kriteria kestabilan Routh-Hurwitz, titik setimbang akan stabil
asimtotis lokal jika .
Untuk titik setimbang didapatkan matriks Jacobian
.
dan diperoleh persamaan karakteristik
Berdasarkan (3) dan kriteria kestabilan Routh-Hurwitz, titik setimbang akan
ada dan stabil asimtotis lokal jika dan .
Sedangkan untuk titik setimbang didapatkan matriks jacobian dan persamaan karakteristik berikut:
Berdasarkan (4) dan kriteria kestabilan Routh-Hurwitz, titik setimbang akan
ada dan stabil asimtotis lokal jika .
8.2. Interpr
etasi Model HIV/AIDS dengan Perubahan Jumlah Virus HIV Konstan
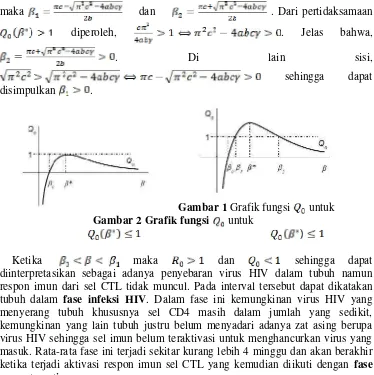
Perhatikan kembali bentuk dan berikut ini:
dan . (5)
sedangkan merupakan fungsi nonlinier dalam . Dengan mensubstitusikan
nilai ke fungsi diperoleh, . Karena adaah
fungsi linier naik jelas bahwa untuk mengakibatkan artinya titik setimbang bebas penyakit stabil lebih jauh lagi tidak terjadi infeksi HIV dalam tubuh. Sedangkan untuk mengakibatkan yang berarti telah terjadi penyebaran virus HIV dalam tubuh.
Selanjutnya akan diuraikan nilai yang dapat memaksimumkan , maka dilakukan langkah berikut:
, karena maka atau
. Selanjutnya akan ditentukan syarat agar yang didapat
mengakibatkan maksimum,
.
Didefinisikan , ketika maka akan mencapai nilai maksimum
dengan syarat . Hal ini berarti, respon imun yang dihasilkan oleh sel CTL merupakan respon maksimalnya. Dengan mensubstitusikan ke , berikut adalah nilai maksimum dari yakni,
. (4)
Berdasarkan syarat kestabilan titik setimbang immune-absence
dan immune-presence maka nilai maksimum dari dapat dibagi
menjadi dua kasus yakni dan .
Untuk , berdasarkan (4) diperoleh,
Interpretasinya, rasio aktivasi produksi sel CTL dengan kematian sel CTL lebih rendah dibanding rasio matinya sel CD4 terinfeksi dan sel CD4 sehat terhadap jumlah produksi sel CD4 sehat. Individu yang berada dalam kondisi tersebut dapat dikatakan mengalami primary immunodeficiency syndrome, yakni sindrom awal penurunan sistem imun tubuh.