BAB 2 LATAR BELAKANG MATEMATIK TRANSFORMASI LAPLACE. Dalam mempelajari sistem kendali sangat bergantung pada penggunaan

1. PENDAHULUAN

Dalam mempelajari sistem kendali sangat bergantung pada penggunaan matematika terapan. Satu dari tujuan utama mempelajari sistem kendali adalah untuk mengembangkan alat bantu analitis sehingga perancang meng-hasilkan perancangan yang dapat diprediksi dan dapat dipercaya tanpa tergantung sepenuhnya pada percobaan atau simulasi komputer.

Untuk mempelajari teori kendali klasik, yang diuraikan dalam buku ini, latar belakang matematis yang perlu adalah masalah teori variabel kompleks, persamaan diferensial dan diferensi, transformasi Laplace dan transformasi z, dan sebagainya. Sedangkan teori kendali modern, mensyaratkan latar belakang matematis yang lebih lengkap. Sebagai tambahan dari masalah di atas, teori kendali modern didasarkan pada dasar teori matriks, teori himpunan, transformasi dan aljabar linear, kalkulus variasi, pemrograman matematis, teori probabilitas, dan matematika lanjut lainnya.

Pada bab ini akan diuraikan bahan-bahan yang menjadi latar belakang, yang dibutuhkan untuk masalah sistem kendali. Karena keterbatasan tempat dan sebenarnya kebanyakan pokok masalah tersebut harus dikaji ulang sendiri oleh pembaca, masalah matematis ini tidak akan diuraikan dengan lengkap. Bagi

pembaca yang ingin mendalami masalah ini harus menelaah lebih lanjut buku-buku yang berhubungan dengan masalah tersebut.

Konsep Variabel Kompleks

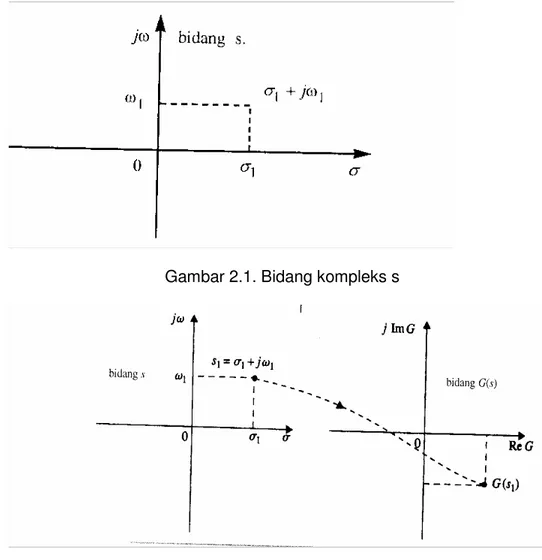
Suatu variabel kompleks s mempunyai dua komponen: komponen nyata s dan komponen khayal ω. Secara grafis komponen nyata s dinyatakan dengan sumbu s pada arah horizontal, dan komponen khayal diukur sepanjang sumbu vertical jω, pada bidang kompleks s. Gambar 2-1 menggambarkan bidang kompleks s, yang pada titik sembarang s=s1 ditentukan oleh koordinat

σ

=

σ

₁ ^atau

ω

=

ω

1

atau secara sederhana

^s

₁ =

σ

₁+

^j ω

₁^.

Fungsi Variabel Kompleks

Fungsi G(s) dikatakan merupakan fungsi variabel kompleks s, jika untuk setiap nilai s terdapat satu atau lebih nilai G(s) Karena s mempunyai bagian nyata dan khayal, fungsi G(s) juga dinyatakan dengan bagian nyata dan khayal, yaitu

dengan Re G(s) menyatakan bagian nyata dan Im G(s) menyatakan bagian khayal dari G(s). Fungsi G(s) juga dinyatakan dengan bidang kompleks G(s), dengan Re G(s) sebagai sumbu nyata dan Im G(s) sebagai sumbu khayal. Jika untuk setiap nilai s hanya terdapat satu nilai G(s) pada bidang G(s), G(s) dikatakan merupakan fungsi nilai tunggal, dan pemetaan dari satu titik pada bidang-s ke titik pada bidang G(s) dikatakan sebagai nilai tunggal (Gambar 2-2). Jika pemetaan dari bidang G(s) ke bidang-s juga merupakan nilai tunggal, pemetaan tersebut dikatakan pemetaan satu-satu. Walaupun bergitu, banyak fungsi untuk pemetaan

dari bidang fungsi ke bidang variabel kompleks yang bukan bernilai tunggal.

Misalnya fungsi

terlihat jelas bahwa untuk setiap nilai s, hanya terdapat satu nilai unik G(s).

Tetapi untuk pemetaan sebaliknya tidak demikian; misalnya titik G(s) = ∞ dipetakan pada dua titik pada bidang s, yaitu s = 0 dan s= -1.

Gambar 2.1. Bidang kompleks s

Gambar 2.2. Pemetaan nilai tunggal dari bidang s ke bidang G(s)

Fungsi Analitik

Suatu fungsi G(s) dari variabel kompleks s disebut fungsi analitik dalam daerah s jika fungsi tersebut dan turunanannya berada pada daerah tersebut

2.2 TRANSFORMASI LAPLACE Marilah kita definisikan

/(/) = fungsi waktu t sedemikian rupa sehingga fit) = 0 untuk t < 0 s = variabel kompleks

= simbol operasional yang menunjukkan bahwa besaran yang didahuluinya

ditransformasi dengan integral Laplace ^∞

∫

⁻

0

dt e

^st

F(s) = transformasi Laplace dari f(t)

Selanjutnya transformasi Laplace dari/(f) didefinisikan oleh

Transformasi Laplace suatu fungsi fit) ada jika fit) secara sepotong-sepotong kon- tinyu pada setiap selang-terhingga (finite interval) dalam daerah t > 0 dan jika fungsi tersebut mempunyai orde eksponensial dengan membesarnya t menuju tak

terhingga. Dengan kata lain, integral Laplace harus konvergen. Suatu fungsi f(f) mempunyai orde eksponensial jika ada suatu konstanta nyata positif , a sedemikian rupa sehingga fungsi

mendekati nol jika t mendekati tak terhingga.

Teorema Transformasi Laplace

Penggunaan transformasi Laplace dalam berbagai hal disederhanakan dengan memanfaatkan sifat-sifat trans-j formasi. Sifat-sifat ini dinyatakan dengan teorema berikut, dengan tidak memberikan bukti.

Teorema 1. Perkalian dengan suatu Konstanta

Misal k adalah suatu konstanta dan F(s) adalah transformasi Laplace dari f(f).

Kemudian ,

Teorema 2. Penjumlahan dan Pengurangan

Misal F}(s) dan F0(s) adalah transformasi Laplace dari f}(i) dan /2(0 . Kemudian

Teorema 3. Diferensiasi

Misal F(s) adalah transformasi Laplace dari f(t) dan f(O) adalah limit dari f(t) dengan t mendekati 0. Tra formasi Laplace dari turunan f(t) terhadap waktu adalah

Bentuk umum untuk turunan berorde lebih tinggi dari f(t),

Teorema 4. Integrasi

Transformasi Laplace dari intergral pertama f(t) terhadap waktu adalah transformasi Laplace dari f(f) dibagi dengan s; yaitu,

Untuk integrasi orde ke n,

[

n

]

_n

t t t

s s dt F

dt dt d f

n ( )

...

) (

... _{1 2 1}

0 0 0

2 1

− =

∫

∫

∫

^{τ τ}

Teorema 5. Pergeseran terhadap Waktu

Transformasi Laplace dari f(f) yang ditunda dengan waktu T adalah sama dengan transformasi Lapace f(f) dikalikan dengan e^-Ts; yaitu

[ ^f

⁽

^{t T}

⁾

^u

s⁽

^{t T}

⁾

] ^e

^Ts

^F

⁽

^s

⁾

= −

−

−

Dengan us(t-T) menyatakan fungsi undak satuan yang digeser terhadap waktu ke kanan sebesar T.

Teorema 6. Teorema nilai awal

Jika transformasi laplace f(t) adalah F(s), kemudian lim ( ) lim ( )

0 f t sF s

s

t→ = →∞ jika limitnya ada.

Teorema 7. Teorema nilai akhir.

Jika transformasi (t) adalah F(s), dan sF(s) analitis pada sumbu khayal dan berada pada bagian kanan bidang s, kemudian

) ( lim ) ( lim

0sF s t

f

s

t→∞ = →

Teorema nilai akhir sangat berguna untuk analisis dan merancang sistem kendali, karena memberikan nilai akhir dari fungsi waktu dengan mengetahui perilaku transformasi Laplace-nya pada s = 0. Teorema nilai akhir tidak berlaku jika sF(s) mempunyai pole yang bagian nyatanya nol atau positif, yaitu ekivalen dengan per-

syaratan analitis dari sF(s) pada bidang sebelah kanan seperti yang telah dinyatakan pada teorema. Contoh berikut mengilustrasikan perhatian khusus pada penggunaan teorema.

Teorema 8. Pergeseran Kompleks

Transformasi Laplace dari f(t) yang dikalikan dengan e^±ar, dengan a merupakan suatu konstanta, akan sama dengan transformasi Laplace, dengan s diganti oleh s

± a; yaitu

Teorema 9. Konvolusi Nyata (Perkalian Kompleks)

Misal F1(s) dan F2(s) adalah transformasi Laplace dari /j(t) dan/2(f), dan /1(t) = 0, /2(t) = 0, untuk t < 0 kemudian,

F1(s) F2(s) = [/2(t)* /1(t)]

= =



 





∫

^{t f f t}− ^d

0

2

1(

τ

) (

τ

)

τ 



 



 ∫

^t

^{f f t} − ^d

0

1

2

( τ ) ( τ ) τ

dengan simbol "*" menyatakan konvolusi dalam domain waktu.

Persamaan diatas menunjukkan bahwa perkalian dari dua fungsi yang ditransformasikan dalan domain-skompleks sama dengan konvolusi dari dua fungsi nyata t dalam domain-f. Suatu fakta penting untuk diingat adalah transformasi Laplace balik dari hasil kali dua fungsi pada domain-s tidak sama dengan hasil kali dari dua fungsi nyata dalam domain t.

[e ^±atf(t)] = F(s ± α)

Aplikasi Transformasi Laplace terhadap Solusi Persamaan Diferensial Linear Biasa

Persamaan diferensial linear biasa dapat diselesaikan oleh metode transformasi Laplace dengan bantuan teore-ma transformasi Laplace yang telah diberikan, uraian pecahan parsial, dan tabel transformasi Laplace. Prosedurnya adalah sebagai berikut:

1. Transformasikan persamaan diferensial ke domain-.? dengan transformasi Laplace dengan menggunakan tabel transformasi Laplace.

2. Manipulasi persamaan aljabar yang telah ditransformasi dan cari variabel keluaran.

3. Bentuklah uraian pecahan parsial ke persamaan aljabar yang telah ditransformasi.

4. Dapatkan transformasi Laplace balik dari tabel transformasi Laplace

2.3. TRANSFORMASI LAPLACE BALIK

Proses matematik dalam mengubah ekspresi variabel kompleks menjadi ekspresi waktu disebut transformasi balik. Notasi transformasi balik adalah ,sehingga

Dalam menyelesaikan soal dengan menggunakan metoda transformasi Laplace, kita dihadapkan pada suatu pertanyaan tentang cara mencari f(t) dari F(s). Secara mate-matisf(t) diperoleh dari F(s) dengan ekspresi sebagai berikut:

di mana c, adalah absis konvergensi, yang^merupakan konstanta nyata yang dipilih sede-mikian rupa sehingga lebih besar dari semua titik singuler dari F(s). Jadi lintasan integrasi sejajar dengan sumbu j

ω

dan digeser sejauh c dari sumbu khayal. Lintasan ini ber-ada di sebelah kanan semua titik singuler.

Proses integrasi di atas kelihatannya sukar dilakukan. Untunglah, ada beberapa metoda yang lebih sederhana untuk mencarif(t) dari F(s) daripada dengan meng- hitung integral tersebut secara langsung. Suatu metoda yang mudah untuk mendapatkan transformasi .Laplace balik adalah dengan menggunakan tabel transformasi Laplace. Dalam hal ini, transformasi Laplace harus dalam bentuk yang segera dapat dikenal dengan tabel semacam itu. Seringkali fungsi yang ditanyakan tidak ada pada tabel transformasi Laplace yang tersedia pada seorang insinyur.

Apabila suatu transformasi Laplace F(s) tidak ditemukan dalam label, maka kita dapat menguraikannya menjadi suatu pecahan parsial dan menuliskan F(s) dalam bentuk fungsi s yang sederhana sehingga secara cepat transformasi Laplace balik dari F(s) segera diperoleh.

Perhatikan bahwa metoda yang lebih sederhana untuk mencari transformasi

Laplace balik ini adalah didasarkan pada kenyataan bahwa berlaku hubungan yang unik antara fungsi waktu dan transformasi Laplace balik, untuk setiap fungsi waktu yang kontinyu.

Tabel transformasi Laplace

f(t) F(s)

1 Impulsa satuan δ(t) ¹

2 tangga satuan 1(t)

s 1

3 t 1₂

s

4

e

^−at

a s+

1

5

te

^−at

)2

( 1

a s+

6 ^sinωt

2 2 ωω

+ s

7 ^cos

ω t

2 2+ω s

s

8 tⁿ (n=1, 2, 3, ….)

1

!

+

s

n

n

9

t

ⁿ

e

^−at (n=1, 2, 3, ….)

)

1

(

! + a

ⁿ+

s n

10 1 ( _{at bt})

e a e

b

−

− −

− ( )( )

1 b s a

s+ +

11 1 ( _{bt at})

ae a be

b

−

− −

− (s a)(s b)

s + + 12



 



 −

+ −1 ( ⁻ )

1 1 _{at bt}

ae b be

a

ab ( )( )

1 b s a s

s + +

13

e

^−at

^sin ω t

_{2 2}

)

(

ω ω

+ +a s

14

e

^{− at}

si ω t

_{2 2}

)

( + +

ω

+ a s

a s

15 1 ( 1 )

2

eat

a at− +

) (

1

2 s a

s +

16 ⁿ e ^nt _n ²t

2 sin 1

1

ω ζ

ζ

ω

ζω −

−

−

2 2

2

2 _{n n}

n

s

s ζω ω

ω

+ +

17

ζ θ ζ

θ ζ ζ ω

ζω

2 1

2 2

tan 1

) 1

sin(

1 1

= −

−

− −

−

− t

e ^nt _n

2

2 2 _ns _n

s

s

ω ζω

+ +

18

ζ θ ζ

θ ζ ζ ω

ζω

2 1

2 2

tan 1

) 1

sin(

1 1 1

= −

+

− −

−

−

− t

e ^nt _n

) 2

( ^{2 2}

2

n n n

s s

s ζω ω ω

+ +