1 BAB I PENDAHULUAN A. Latar Belakang Penelitian
Middle East Respiratory Syndrome-Corona Virus atau biasa disingkat MERS-CoV adalah penyakit sindrom pernapasan yang disebabkan oleh Virus-Corona yang menyerang saluran pernapasan mulai dari yang ringan sampai yang berat. Gejalanya adalah demam, batuk dan sesak nafas, bersifat akut, dan biasanya pasien memiliki penyakit ko-morbid (penyakit penyerta). Virus MERS-CoV baru dikenali pertama kali pada tahun 2012 di Negara Arab Saudi. Virus tersebut yang menyebabkan SARS (Severe Acute Respiratory Syndrom) pada tahun 2002 hingga 2003, virus tersebut sangat berbahaya dan sudah mewabah hingga 8273 kasus dan 775 meninggal dunia (Elshinta, 2015).
2
Selain itu, sekelompok peneliti dari Universitas Bonn, Jerman, dan Universitas Erasmus, Belanda, setelah meneliti ratusan hewan di Timur Tengah, termasuk sapi, kuda, kambing, domba, dan unta, menduga bahwa penyebaran virus MERS-CoV berasal dari unta. Dari penelitian yang dipaparkan dalam jurnal ilmiah Emerging Infectious Diseases, terungkap bahwa 90% unta terinfeksi pada usia dua tahun dan penularan virus MERS-CoV lebih sering ditemukan pada anak unta dibandingkan unta dewasa (Jonathan Ball, 2015).
Dari data WHO mengatakan bahwa, sejak September 2012 sampai dengan Maret 2016, telah ditemukan 1.698 kasus konfirmasi MERS-CoV dengan 609 orang mengalami kematian. Selain itu, WHO juga mengatakan bahwa sekitar 36% pasien yang dilaporkan terkena virus MERS-CoV meninggal dunia dan lebih dari 85% kasus penyakit menular MERS-CoV ini berasal dari Arab Saudi.
Banyak warga negara Indonesia yang berada di Arab Saudi terutama sebagai jama’ah umrah/haji, sehingga memungkinkan terjadinya penyebaran penyakit ini
3
yang diambil adalah meningkatkan kekebalan tubuh manusia yakni dengan pemberian vaksin. Adapun permasalahan yang terjadi adalah terdapat populasi rentan dan terinfeksi dalam suatu wilayah, sehingga untuk meningkatkan kekebalan tubuh perlu tindakan vaksinasi. Oleh karena itu, muncul populasi vaksinasi (populasi rentan yang telah diberi vaksin).
Salah satu pendekatan untuk menjelaskan solusi dari permasalahan yang terjadi dalam dunia nyata adalah memodelkan atau merumuskan permasalahan nyata ke dalam bahasa matematika, maka untuk dapat mengetahui penyebaran penyakit MERS-CoV, perlu dibuat suatu pemodelan matematika sehingga diharapkan dapat digunakan untuk membantu mencari solusi terkait dengan penyebaran penyakit tersebut.
Penyebaran penyakit menular diantara wilayah yang berbeda adalah fenomena yang melibatkan banyak kompartemen (kelas) yang berbeda. Untuk mengontrol penyebaran penyakit menular, kita harus memahami bagaimana pengaruh pertumbuhan dan penyebaran penyakit menular tersebut. Banyak faktor yang mempengaruhi dinamika populasi akibat penyakit menular, misalkan perpindahan populasi, gaya hidup, dan meningkatnya perjalanan internasional. Untuk penyakit menular seperti SARS dan MERS-CoV, faktor perpindahan populasi menjadi faktor penting yang mempengaruhi penyebaran penyakit diantara wilayah yang berbeda (Benny Yong dan Livia Owen, 2015).
4
5 B. Identifikasi Masalah
Berdasarkan latarbelakang masalah di atas, masalah dapat diidentifikasi sebagai berikut:
1. Perpindahan populasi rentan menjadi faktor utama penyebaran penyakit MERS-CoV antar dua wilayah
2. Penyakit MERS-CoV dapat menjadi wabah dalam suatu wilayah karena sifat penularannya yang begitu cepat
C. Pembatasan Masalah
Skripsi ini hanya membahas tentang penyebaran penyakit MERS-CoV yang terjadi antar dua wilayah yaitu Indonesia dan Arab Saudi, dengan pertimbangan yang diberi vaksin hanya orang Indonesia yang akan bepergian ke Arab Saudi sebagai calon haji/umrah dan analisis penyebaran penyakit ini hanya untuk kasus bebas penyakit.
D. Perumusan Masalah
Berdasarkan latar belakang masalah, maka dapat dirumuskan masalah sebagai berikut:
6
2. Bagaimana analisis kestabilan titik ekuilibrium model penyebaran penyakit menular MERS-CoV antar wilayah Indonesia dan Arab Saudi dengan pengaruh vaksinasi?
3. Bagaimana simulasi model penyebaran penyakit menular MERS-CoV antar wilayah Indonesia dan Arab Saudi dengan pengaruh pemberian vaksin Meningitis terhadap individu rentan yang ada di Indonesia?
E. Tujuan Penelitian
Berdasarkan rumusan masalah di atas, tujuan dari penulisan tugas akhir ini adalah:
a. Menjelaskan pemodelan matematika penyebaran penyakit menular MERS-CoV antar wilayah Indonesia dan Arab Saudi dengan pengaruh pemberian vaksinasi terhadap calon jama’ah haji/umrah dari Indonesia b. Menjelaskan analisis kestabilan titik ekuilibrium model penyebaran
penyakit menular MERS-CoV antar wilayah Indonesia dan Arab Saudi dengan pengaruh vaksinasi
c. Menjelaskan simulasi model penyebaran penyakit menular MERS-CoV antar wilayah Indonesia dan Arab Saudi dengan pengaruh pemberian vaksin Meningitis terhadap individu rentan yang ada di Indonesia.
F. Manfaat Penelitian
Manfaat dalam analisis model penyebaran penyakit menular MERS-CoV antar wilayah Indonesia dan Arab Saudi antara lain:
7
a. Diharapkan dapat menambah kekayaan ilmu matematika khususnya permodelan epidemik penyakit
b. Diharapkan dapat menjadi referensi baru dalam pengembangan ilmu matematika di bidang pemodelan epidemik.
2. Bagi Institusi Kesehatan
i
ANALISIS KESTABILAN MODEL PENYEBARAN
PENYAKIT MENULAR MIDDLE EAST RESPIRATORY SYNDROME-CORONA VIRUS (MERS-CoV) ANTAR WILAYAH INDONESIA (INA)
DAN ARAB SAUDI (KSA)
SKRIPSI
Diajukan Kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta
untuk Memenuhi Sebagian Persyaratan guna Memperoleh Gelar Sarjana Sains
Oleh
MUHAMMAD SYARIFUDIN 12305144035
PROGRAM STUDI MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA
iv PERNYATAAN
Yang bertanda tangan di bawah ini saya: Nama : Muhammad Syarifudin NIM : 12305144035
Prodi : Matematika
Jurusan : Pendidikan Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam
Judul : ANALISIS KESTABILAN MODEL PENYEBARAN
PENYAKIT MENULAR MIDDLE EAST
RESPIRATORY SYNDROME-CORONA VIRUS
(MERS-CoV) ANTAR WILAYAH INDONESIA (INA) DAN ARAB SAUDI (KSA)
Dengan ini saya menyatakan bahwa skripsi ini benar-benar karya saya sendiri. Sepanjang pengetahuan saya tidak terdapat karya atau pendapat yang ditulis atau diterbitkan orang lain kecuali sebagai acuan atau kutipan dengan mengikuti kata penulisan karya ilmiah yang telah lazim. Apabila terbukti bahwa pernyataan ini tidak benar maka sepenuhnya menjadi tanggungjawab saya dan saya bersedia menerima sanksi sesuai peraturan yang berlaku.
Yogyakarta, 26 Januari 2017 Yang Menyatakan,
v MOTTO
“Sesungguhnya bersama kesulitan ada kemudahan. Maka apabila engkau telah selesai (dari suatu urusan), tetaplah bekerja keras (untuk urusan yang lain)”
(Q.S Al Insyirah: 6-7)
“Hidup adalah perjuangan”
“life is a struggle”
“Jadikanlah ilmu berguna bagi diri sendiri dan orang lain”
“Segala yang indah belum tentu baik, namun segala yang baik sudah tentu indah”
"Develop success from failures. Discouragement and failure are two of the surest stepping stones to success"
(Dale Carnegie)
“Barang siapa menginginkan kebahagiaan di dunia maka haruslah dengan ilmu, barang siapa yang menginginkan kebahagiaan di akhirat haruslah dengan ilmu, dan barang siapa yang menginginkan kebahagiaan pada keduanya maka haruslah dengan
ilmu”
vi
PERSEMBAHAN
Alhamdulillah ... segala puji bagi Allah SWT ... dengan memanjatkan puja-puji syukur atas kehadirat-Nya, karya yang sederhana ini saya persembahkan kepada:
Alm. Ayahku tercinta, Bapak Ngizudin.... yang selama hidupnya telah mendidik, selalu memberikan nasihat, memberikan kasih sayang yang tak pernah henti dan selalu medoakan dengan tulus disetiap harinya untuk kebaikan dan kesuksesan bagiku, semoga Allah SWT membalas semua kebaikan-kebaikannya dengan memberikan tempat yang paling mulia di sisi-Nya.... Aamiin Yaa Robbal Aalamiin.
Ibunda tercinta, Ibu Salami.... yang selalu memberikan kasih sayang tak terbatas, dan do anya yang tulus yang selalu menyertaiku. Jasa-jasamu sungguh mulia bahkan takkan mampu diriku
tuk membalasnya, yang bisa kulakukan hanyalah berdo a, Semoga Ibunda selalu dalam lindungan Allah SWT, Aamiin Yaa Robbal Aalamiin.
Kakak”ku dan keponakan”ku yang tercinta, Mbak Siti, Mbak Qib, Mas Ilham, Rona, Zaki, Farich, dan Licha... terimakasih atas perhatian, dukungan dan do a kalian semua, kalian adalah tempatku berbagi kebahagian, tempatku melepas kesedihan dan kesulitan yang kalian ubah itu menjadi keindahan dengan canda tawa kalian, I love you all... semoga kalian semua selalu dalam lindungan-Nya... Aamiin.
My second mother, Ibu Hj. Harini Tjaswadi. Terimakasih banyak Ibu... yang telah memberikanku banyak ilmu selain yang diajarkan di kampus. Terima kasih telah berkenan menyediakan tempat tinggal dan memenuhi segala kebutuhan hidupku selama di jogja. Engkau selalu memberikan
nasihat, memberikan masukan, dukungan dan selalu mendo akanku untuk menjadi yang lebih
baik. Maafkan segala kesalahan saya dan maaf tidak bisa membalas semua kebaikan Ibu, saya
hanya bisa mendo akan semoga kebaikan-kebaikan Ibu memperoleh balasan yang lebih baik dari Allah SWT dan semoga Ibu selalu dalam lindungan-Nya. Aamiin.
vii
ANALISIS KESTABILAN MODEL PENYEBARAN
PENYAKIT MENULAR MIDDLE EAST RESPIRATORY SYNDROME-CORONA VIRUS (MERS-CoV) ANTAR WILAYAH INDONESIA (INA)
DAN ARAB SAUDI (KSA) Oleh
Muhammad Syarifudin NIM. 12305144035
ABSTRAK
Middle East Respiratory Syndrome-Corona Virus (MERS-CoV) merupakan penyakit sindrom pernapasan yang disebabkan oleh Virus-Corona yang menyerang saluran pernapasan mulai dari yang ringan sampai yang berat. Penyakit ini dapat menjadi wabah dalam suatu wilayah karena sifat menularnya yang begitu cepat. Oleh karena itu, diberikan program vaksinasi sebagai upaya pencegahan penyebaran penyakit MERS-CoV. Skripsi ini mengkaji tentang model matematika pada penyebaran penyakit MERS-CoV dengan vaksinasi. Model matematika yang digunakan yaitu model SIV (Susceptible-Infected-Vaccinated) dengan individu tervaksinasi hanya dari Indonesia. Penelitian ini bertujuan untuk mengetahui pengaruh tingkat vaksinasi terhadap penyebaran penyakit MERS-CoV dalam populasi antar dua wilayah.
Analisis model SIV yang dilakukan pada penyebaran penyakit MERS-CoV dalam pembahasan ini terdapat 5 tahapan. Pertama, membentuk model SIV; kedua, mencari titik ekuilibrium; ketiga, menentukan bilangan reproduksi dasar ; kemudian yang keempat, menganalisis kestabilan di sekitar titik ekuilibrium dan yang terakhir yaitu melakukan simulasi menggunakan software Maple 18.
Model SIV pada penyebaran penyakit MERS-CoV memiliki lima kelas populasi yaitu kelas Susceptible Indonesia ��� , kelas Susceptible Arab Saudi ��� , kelas Vaccinated Indonesia ���� , kelas Infected Indonesia ��� dan kelas Infected Arab Saudi ��� . Pemodelan matematika yang didapatkan berupa sistem persamaan diferensial nonlinear. Berdasarkan simulasi, untuk pengaruh pemberian vaksin
Meningitis terhadap calon jama’ah haji/umrah asal Indonesia diperoleh bahwa
semakin tinggi tingkat vaksinasi yang diberikan, menyebabkan banyaknya individu yang terinfeksi semakin menurun. Hal ini menunjukkan bahwa program vaksinasi dapat digunakan untuk menekan banyaknya individu terinfeksi yang diakibatkan oleh penyebaran penyakit menular MERS-CoV yang terjadi antar dua wilayah yang berbeda.
viii
KATA PENGANTAR
Assalamu’alaikum Wr. Wb.
Puji syukur penulis panjatkan kehadirat Allah SWT, yang telah melimpahkan segala karunia, rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan
penuliasan skripsi dengan judul “Analisis Kestabilan Model Penyebaran Penyakit
Menular Middle East Respiratory Syndrome Corona Virus (MERS-CoV) Antar Wilayah Indonesia (INA) dan Arab Saudi (KSA)”. Tugas Akhir Skripsi ini dibuat sebagai salah satu syarat untuk menyelesaian Studi Sarjana Sains (S.Si). Sejak awal kuliah hingga terselesainya tugas akhir ini, penulis mendapat dukungan dan bantuan dari berbagai pihak. Pada kesempatan ini, penulis mengucapkan terima kasih kepada pihak-pihak yang telah membantu dan memberikan dukungan kepada penulis, yaitu:
1. Bapak Dr. Hartono selaku Dekan FMIPA Universitas Negeri Yogyakarta 2. Bapak Dr. Ali Mahmudi selaku Ketua Jurusan Pendidikan Matematika 3. Bapak Dr. Agus Maman Abadi selaku Ketua Prodi Matematika
4. Ibu Dwi Lestari M.Sc. dan Ibu Husna Arifah M.Sc. selaku dosen pembimbing skripsi yang telah memberikan pengarahan, saran, bimbingan dan masukan sehingga penulis dapat menyelesaikan penulisan Tugas Akhir Skripsi ini
5. Bapak Ibu Dosen Jurusan Pendidikan Matematikda yang telah memberikan ilmu kepada penulis secara langsung maupun tidak langsung
ix
7. Ibu Hj. Harini Tjaswadi selaku orang tua asuh yang telah memberikan nasihat,
dukungan serta do’a demi kelancaran penulis dalam menyelesaikan tugas akhir
8. Seluruh Mahasiswa Matematika Angkatan 2012 dan semua pihak yang telah memberikan motivasi dan membantu secara langsung maupun tidak langsung sehingga dapat memperlancar proses penyusunan tugas akhir ini.
Semoga tugas akhir ini dapat berkah dan bermanfaat untuk setiap orang yang membacanya, Aamiin.
Wassalamu’alaikum Wr. Wb.
Yogyakarta, 26 Januari 2017 Penulis
x
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN ... ii
HALAMAN PENGESAHAN ... iii
B. Identifikasi Masalah ... 5
C.Pembatasan Masalah... 5
D.Perumusan Masalah ... 5
E. Tujuan Penelitian ... 6
F. Manfaat Penelitian ... 6
BAB II LANDASAN TEORI ... 8
xi
B. Persamaan Diferensial ... 11
C. Solusi Persamaan Diferensial ... 12
D. Sistem Persamaan Diferensial ... 13
E. Nilai Eigen dan Vektor Eigen ... 18
F. Titik Ekuilibrium ... 21
G. Linearisasi ... 22
H. Kestabilan ... 30
I. Bilangan Reproduksi Dasar ... 38
BAB III PEMBAHASAN ... 42
A. Permasalahan Nyata ... 42
B. Formulasi Model ... 43
C. Transformasi Model ... 55
D. Titik Ekuilibrium ... 62
E. Bilangan Reproduksi Dasar ... 66
F. Kestabilan Lokal di sekitar Titik Ekuibrium ... 72
G. Simulasi Model Penyebaran Penyakit MERS-CoV ... 79
BAB IV PENUTUP ... 88
A. Kesimpulan ... 88
B. Saran ... 90
DAFTAR PUSTAKA ... 92
xii
DAFTAR TABEL
xiii
DAFTAR GAMBAR
Gambar 2.1 Proses Pemodelan Matematika... 8
Gambar 2.2 Ilustrasi Kestabilan ... 31
Gambar 3.1 Diagram Kompartemen Model Penyebaran Penyakit Menular MERS-CoV antar Wilayah INA dan KSA ... 45
Gambar 3.2 Simulasi Sistem (3.20) dengan � = ... 82
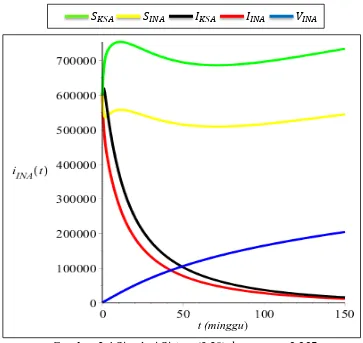
Gambar 3.3 Simulasi Sistem (3.20) dengan � = . 5 ... 83
Gambar 3.4 Simulasi Sistem (3.20) dengan � = . 5... 84
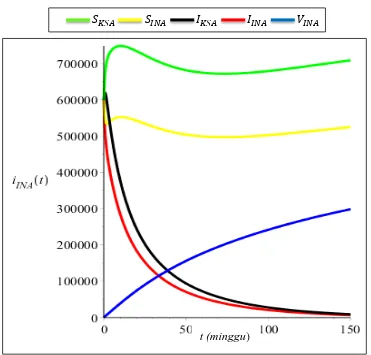
Gambar 3.5 Simulasi Sistem (3.20) dengan � = . 75 ... 85
xiv
DAFTAR LAMPIRAN
Lampiran 1 Program Maple untuk model matematika penyebaran penyakit MERS-CoV tanpa pengaruh vaksinasi atau = ...95 Lampiran 2 Program Maple untuk model matematika penyebaran penyakit
xv
DAFTAR SIMBOL
���� Jumlah total populasi dari Indonesia (INA) ���� Jumlah total populasi dari Arab Saudi (KSA) ��� Populasi kelas Susceptible INA pada saat t ��� Populasi kelas Susceptible KSA pada saat t ��� Populasi kelas Infected INA pada saat t ��� Populasi kelas Infected KSA pada saat t ���� Populasi kelas Vaccinated INA pada saat t
��� Proporsi kelas Susceptible INA pada saat t ��� Proporsi kelas Susceptible KSA pada saat t ���� Proporsi kelas Infected INA pada saat t ���� Proporsi kelas Infected KSA pada saat t ���� Proporsi kelas Vaccinated INA pada saat t
Himpunan bilangan real dimensi n ̇ Turunan pertama ̇ terhadap t ̇ Nilai awal atau kondisi awal
̇ Titik ekuilibrium Himpunan terbuka
′ Himpunan semua fungsi yang mempunyai turunan pertama yang kontinu di E
� Banyaknya calon jamaah haji/umrah dari Indonesia � Banyaknya calon jamaah haji/umrah dari Arab Saudi
Laju perpindahan individu rentan dan terinfeksi dari wilayah Indonesia ke wilayah Arab Saudi
xvi
µ Laju individu rentan yang meninggal secara alami µ Laju individu terinfeksi yang meninggal karena penyakit
� Laju perpindahan individu rentan yang ada di Indonesia yang diberi vaksinasi dari kelompok ��� ke kelompok ����
� Laju individu terinfeksi yang pulih
� Laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang berbeda
Laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang sama
Proporsi banyaknya calon jamaah haji/umrah dari Indonesia Proporsi banyaknya calon jamaah haji/umrah dari Arab Saudi ℱ� Laju kemunculan infeksi baru pada kompartemen ke-i
8 BAB II
LANDASAN TEORI
Pada bab ini akan diuraikan beberapa teori-teori yang digunakan sebagai acuan dalam penulisan skripsi ini. Teori-teori yang digunakan berupa definisi-definisi serta teorema-teorema yaitu sebagai berikut:
A. Pemodelan Matematika
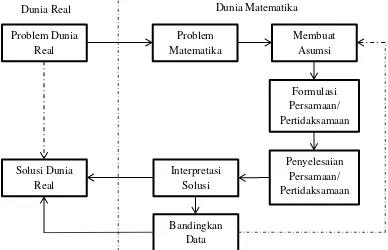
Pemodelan matematika merupakan bidang matematika yang digunakan untuk merepresentasikan dan menjelaskan sistem-sistem fisik atau masalah-masalah pada dunia nyata dalam pernyataan matematik (Widowati dan Sutimin, 2007:1). Beberapa tahap dalam menyusun model matematika dapat dinyatakan dalam Gambar 2.1:
9
Representasi matematika yang dihasilkan dari proses pemodelan dinamakan model matematika. Model matematika dapat dimanfaatkan dalam berbagai bidang studi yang berbeda.
Berdasarkan Gambar 2.1, langkah-langkah untuk proses pemodelan matematika sebagai berikut
1. Menyatakan problem dunia nyata ke dalam pengertian matematika
Untuk mempermudah mencari penyelesaian masalah yang ada di dunia nyata yaitu dengan memodelkan masalah tersebut ke dalam bahasa matematis karena terkadang penyelesaian masalah dunia nyata secara langsung sulit dilakukan. Adapun dalam langkah pertama ini yaitu menentukan variabel-variabel yang terdapat dalam masalah nyata dan membentuk beberapa hubungan variabel-variabel yang diperoleh tersebut menjadi suatu sistem model.
2. Mengkontruksi kerangka dasar model
Dalam langkah ini, hal yang dilakukan yaitu membuat asumsi-asumsi model dari masalah di dunia nyata. Asumsi yang terbentuk pada dasarnya mencerminkan bagaimana proses berfikir sehingga model dapat berjalan. Asumsi-asumsi tersebut dibuat agar model yang dihasilkan dapat menggambarkan masalah dunia nyata secara tepat.
3. Membuat formulasi persamaan/pertidaksamaan
10
Langkah ini merupakan langkah yang paling penting dan sulit. Terkadang diperlukan adanya pengujian kembali asumsi-asumsi agar proses formulasi persamaan sesuai, sehingga dapat diselesaikan dan realistik.
4. Menyelesaikan persamaan/pertidaksamaan
Setelah terbentuk persamaan atau pertidaksamaan, dalam langkah ini yang dilakukan yaitu mencari penyelesaiaannya untuk memperoleh solusi dari model matematika dengan penyelesaian secara matematis. Namun tidak semua model matematika dapat dengan mudah dicari solusinya. Persamaan model matematika mungkin saja tidak memiliki solusi atau bahkan mempunyai lebih dari satu solusi. Oleh karena itu, pada langkah ini dapat dilakukan analisis sifat atau perilaku dari solusi model matematika tersebut.
5. Interpretasi hasil atau solusi
11 B. Persamaan Diferensial
Pemodelan matematika penyebaran penyakit menular MERS-CoV berbentuk persamaan diferensial. Oleh karena itu, pada subbab ini akan dikaji tentang persamaan diferensial.
Definisi 2.1 (Ross, 2004:3)
Persamaan diferensial adalah suatu persamaan yang memuat turunan dari satu atau lebih variabel tak bebas terhadap satu atau lebih variabel bebas.
Contoh 2.1
Berikut adalah contoh-contoh persamaan diferensial:
Berdasarkan jumlah variabel bebas yang terlibat, persamaan diferensial diklasifikasikan menjadi dua bentuk persamaan yaitu persamaan diferensial biasa dan persamaan diferensial parsial.
1. Persamaan Diferensial Biasa Definisi 2.2 (Ross, 2004:4)
Persamaan diferensial biasa adalah suatu persamaan diferensial yang melibatkan turunan dari satu atau lebih variabel tak bebas terhadap satu variabel bebas.
12 2. Persamaan Diferensial Parsial
Definisi 2.3 (Ross, 2004:4)
Persamaan diferensial parsial adalah suatu persamaan diferensial yang melibatkan turunan dari satu atau lebih variabel tak bebas terhadap lebih dari satu variabel bebas.
Pada Contoh . dan . merupakan persamaan diferensial biasa karena terdapat satu variabel bebas yaitu variabel sedangkan pada Contoh . dan . merupakan persamaan diferensial parsial karena terdapat dua variabel bebas yaitu variabel dan untuk Persamaan . dan variabel dan untuk Persamaan
. .
C. Solusi Persamaan Diferensial Definisi 2.4 (Ross, 2004: 8)
Diberikan suatu persamaan diferensial orde-n berikut:
(2.2) dengan F adalah fungsi real.
1. Misalkan f adalah fungsi bilangan real yang terdefinisi untuk semua x dalam interval I dan mempunyai turunan ke-n untuk semua . Fungsi f disebut solusi eksplisit dari (2.2) dalam interval I jika fungsi f memenuhi syarat berikut: a. = [ ], terdefinisi
b. = [ ] = ,
13
Hal ini berarti bahwa substitusi dan variasi turunan y dan turunannya yang berkorespondensi ke (2.2) akan membuat (2.2) menjadi suatu identitas di interval I.
2. Suatu relasi = disebut solusi implisit dari Persamaan (2.2) jika relasi ini mendefinisikan sedikitnya satu fungsi bilangan real f dengan variabel x di interval I.
3. Solusi eksplisit dan solusi implisit biasa disebut sebagai solusi sederhana. Contoh 2.2
Carilah solusi dari persamaan diferensial berikut:
Jadi, solusi dari persamaan diferensial
= adalah = + .
D. Sistem Persamaan diferensial
14
adalah himpunan terbuka dari . Fungsi dengan = dan . adalah himpunan semua fungsi yang mempunyai turunan pertama yang kontinu di . Jika =
menyatakan turunan pertama terhadap ,
maka sistem persamaan diferensial dapat dituliskan menjadi, =
=
=
= .
Sistem (2.3) dapat dituliskan menjadi,
(2.4) Berdasarkan kelinearannya sistem persamaan diferensial dibedakan menjadi dua yaitu sistem persamaan diferensial linear dan sistem persamaan diferensial nonlinear. 1. Sistem Persamaan Diferensial Linear
Sistem persamaan diferensial linear orde satu dapat muncul dalam masalah yang melibatkan beberapa variabel tak bebas dan variabel bebas . Secara umum, sistem persamaan diferensial linear orde satu dinyatakan dalam bentuk sebagai berikut:
= + + + +
= .
15
= + + + +
= + + + +
Jika setiap nilai , adalah nol, maka Sistem Persamaan (2.5) disebut sistem persamaan diferensial linear homogen, sedangkan jika tidak bernilai nol, maka Sistem Persamaan (2.5) disebut sistem persamaan diferensial nonhomogen. Notasi matriks Sistem Persamaan (2.5) dapat ditulis sebagai berikut:
[
atau dapat dinyatakan dalam persamaan berikut:
(2.6)
Persamaan diferensial dikatakan nonlinear jika persamaan diferensial tersebut memenuhi paling sedikit satu dari kriteria berikut ini (Ross, 2004:5):
a. Memuat variabel tak bebas dan/atau turunan-turunannya berpangkat selain satu.
� = � �+ �
16
b. Terdapat perkalian pada variabel tak bebas dan/atau turunan-turunannya c. Terdapat fungsi transendental dari variabel tak bebas dan turunan-turunannya. Contoh 2.3
Berikut diberikan contoh sistem persamaan diferensial linear.
(2.7)
Sistem Persamaan Diferensial (2.7) merupakan persamaan diferensial linear homogen.
2. Sistem Persamaan Diferensial Non Linear Definisi 2.5 (Ross, 2004: 5)
Persamaan diferensial nonlinear adalah persamaan diferensial biasa yang tidak linear.
Contoh 2.4
Berikut contoh-contoh persamaaan diferensial nonlinear:
17
Persamaan (2.8a) memuat variabel tak bebas yang berpangkat tiga
dan
turunannya yang berpangkat dua
sehingga persamaan tersebut merupakan
persamaan diferensial nonlinear. Persamaan (2.8b) memuat perkalian variabel tak bebas dan turunannya
sehingga persamaan tersebut merupakan persamaan
diferensial nonlinear, dan Persamaan (2.8c) memuat fungsi transenden , maka pada persamaan tersebut juga merupakan persamaan diferensial nonlinear.
Sistem persamaan diferensial dikatakan nonlinear, jika persamaan diferensial yang membentuknya merupakan persamaan diferensial nonlinear.
Contoh 2.5
Diberikan sistem persamaan diferensial nonlinear sebagai berikut:
(2.9a)
Sistem Persamaan (2.9) merupakan sistem persamaan diferensial nonlinear dengan variabel bebas dan variabel tak bebas dan , karena memuat persamaan diferensial nonlinear yaitu pada Persamaan (2.9a) terdapat perkalian dari variabel tak bebasnya dan pada Persamaan (2.9b) terdapat variabel tak bebasnya yang berpangkat dua.
= +
18
Analisis dari sistem persamaan diferensial nonlinear ini akan lebih mudah dilakukan jika sistem persamaan diferensial nonlinear diubah ke dalam bentuk sistem persamaan diferensial linear.
E. Nilai Eigen dan Vektor Eigen
Nilai Eigen adalah suatu nilai yang digunakan untuk mengetahui kestabilan suatu sistem. Adapun definisi dari nilai eigen adalah sebagai berikut
Definisi 2.6 (Anton, 2010:277)
Jika A adalah matriks , maka vektor taknol x di dalam dinamakan vektor eigen (eigenvector) dari A jika Ax adalah kelipatan skalar dari x yakni,
(2.10) untuk suatu skalar λ, skalar λ dinamakan nilai eigen (eigenvector) dari dan
dikatakan vektor eigen yang bersesuaian dengan .
Untuk mencari nilai eigen matriks A yang berukuran , maka dituliskan kembali Persamaan (2.10) sebagai
(2.11) atau secara ekivalen
(2.12) Menurut Howard (2010:278), Supaya menjadi nilai eigen, maka harus ada pemecahan taknol dari Persamaan (2.12). Persamaan (2.12) akan mempunyai pemecahan taknol (solusi non trivial) jika dan hanya jika,
(2.13)
� =
−� = .
� =
19
Persamaan (2.13) dinamakan persamaan karakteristik dan skalar yang memenuhi Persamaan (2.13) adalah nilai eigen dari .
− = + + + +
sehingga karakteristik dari menjadi,
+ + + + =
dengan = . Contoh 2.6
Diberikan matriks = − −9 . Akan ditentukan nilai eigen dan vektor eigen dari .
Penyelesaian:
Akan dicari nilai eigen dari matriks ,
− =
| − − −9 | =
| + − | =9
+ − = .
Jadi diperoleh nilai eigen dari matriks adalah = − dan = . Akan dicari vektor eigen dari matriks yang bersesuaian dengan nilai eigen dari matriks . Untuk = − ,
− =
− + −9
20
21 F. Titik Ekuilibrium
Suatu langkah terbaik dalam memulai menganalisis sistem nonlinear untuk Sistem Persamaan (2.4) adalah menentukan titik ekuilibrium dari Sistem Persamaan (2.4) dan menjelaskan perilaku (2.4) disekitar titik ekuilibrium. Titik ekuilibrium atau titik kesetimbangan merupakan solusi dari Sistem Persamaa (2.4) yang tidak mengalami perubahan terhadap waktu. Definisi tentang titik ekuilibrium akan dijelaskan pada Definisi 2.7 berikut ini,
Definisi 2.7 (Perko, 2000:102)
Titik disebut titik ekuilibrium atau titik kritis dari Sistem Persamaan (2.4) jika =
Contoh 2.7
Akan dicari titik ekuilibrium dari sistem berikut ini:
22
Subtitusikan ̅ = ke Persamaan (2.16) sehingga diperoleh ̅ = . Jika ̅ = − disubtitusikan ke Persamaan (2.16) sehingga diperoleh:
− + ̅ =
̅ = − .
Jadi Sistem (2.14) memiliki titik ekuilibrium yaitu − − .
G. Linearisasi
Proses linearisasi perlu dilakukan pada model matematika penyebaran MERS-CoV karena persamaan yang diperoleh dari model tersebut berupa persamaan nonlinear. Linearisasi adalah proses mengubah suatu sistem persamaan diferensial nonlinear menjadi sistem persamaan diferensial linear. Proses ini dilakukan dengan linearisasi di sekitar titik ekuilibrium. Namun sebelum membahas proses linearisasi tersebut akan dibahas terlebih dahulu mengenai matriks jacobian yang akan dijelaskan pada Teorema 2.1 berikut:
Teorema 2.1 ( Perko,2000:67 )
Jika terdiferensial di maka turunan parsial
, i,j=1,2,3,…,n, di
ada untuk semua dan
= ∑
23 akan ditunjukkan proses linearisasi dari sistem persamaan diferensial nonlinear ke dalam sistem persamaan diferensial linear.
24
= ̅ ̅ ̅ ̅ + ̅ ̅ ̅ ̅ − ̅
+ ̅ ̅ ̅ ̅ − ̅ +
+ ̅ ̅ ̅ ̅ − ̅ +
= ̅ ̅ ̅ ̅ + ̅ ̅ ̅ ̅ − ̅
+ ̅ ̅ ̅ ̅ − ̅ +
+ ̅ ̅ ̅ ̅ − ̅ +
= ̅ ̅ ̅ ̅ + ̅ ̅ ̅ ̅ − ̅
+ ̅ ̅ ̅ ̅ − ̅ +
25
karena nilainya mendekati nol sehingga dapat diabaikan. dan karena ̅ ̅ ̅ ̅ titik ekuilibrium dari Sistem (2.4), maka
= = = =
= , sehingga diperoleh:
= ̅ ̅ ̅ ̅ − ̅ + ̅ ̅ ̅ ̅ − ̅ +
+ ̅ ̅ ̅ ̅ − ̅
= ̅ ̅ ̅ ̅ − ̅ + ̅ ̅ ̅ ̅ − ̅ +
+ ̅ ̅ ̅ ̅ − ̅ .
= ̅ ̅ ̅ ̅ − ̅ + ̅ ̅ ̅ ̅ − ̅ +
+
̅ ̅ ̅ ̅ − ̅
= ̅ ̅ ̅ ̅ − ̅ + ̅ ̅ ̅ ̅ − ̅ +
+ ̅ ̅ ̅ ̅ − ̅ .
26
Matriks jacobian dari Persaman (2.18) adalah
=
jika matriks jacobian memiliki nilai eigen yang tidak nol pada bagian realnya, maka sifat kestabilan sistem dapat dilihat dari,
(2.19)
27 Definisi 2.8 (Perko, 2000:102)
Diberikan matrik jacobian . Sistem Linear = disebut
linearisasi dari Sistem Persamaan (2.4) di .
Setelah dilakukannya linearisasi, maka dapat dilihat perilaku kestabilan dari sistem persamaan diferensial nonlinear disekitar titik ekuilibrium. Kestabilan Sistem (2.4) disekitar titik ekuilibrium dapat dilihat dari kestabilan hasil linearisasinya jika hiperbolik. Diberikan definisi untuk titik ekuilibrium hiperbolik yang dijelaskan pada Definisi 2.9 berikut ini:
Definisi 2.9 (Perko, 2000:102)
Titik ekuilibrium disebut titik ekuilibrium hiperbolik dari Sistem (2.4) jika
tidak ada nilai eigen dari matriks yang mempunyai bagian real nol.
Contoh 2.8
Diberikan sistem persamaan diferensial nonlinear sebagai berikut:
(2.20)
Sistem (2.20) memiliki titik ekuilibrium yaitu ̅ = ̅ = ̅ = . Akan dicari matriks jacobian di titik-titik ekuilibrium serta akan diidentifikasikan untuk masing-masing titik ekuilibrium tersebut.
Matriks jacobian dari Sistem (2.20) adalah
= −
29
| − | =
| − −− − | =
| + + | =
+ + =
= − + = − + .
Bagian real dari nilai eigen tidak nol sehingga titik ekuilibrium ̅ = merupakan titik ekuilibrium hiperbolik.
Untuk ̅ = [ − −
− − ]
= − −
nilai eigen untuk yaitu
| − | =
| − − − | =
| | =
30
+ − =
= − + = + .
Bagian real dari nilai eigen tidak nol sehingga titik ekuilibrium ̅ = merupakan titik ekuilibrium hiperbolik.
H. Kestabilan
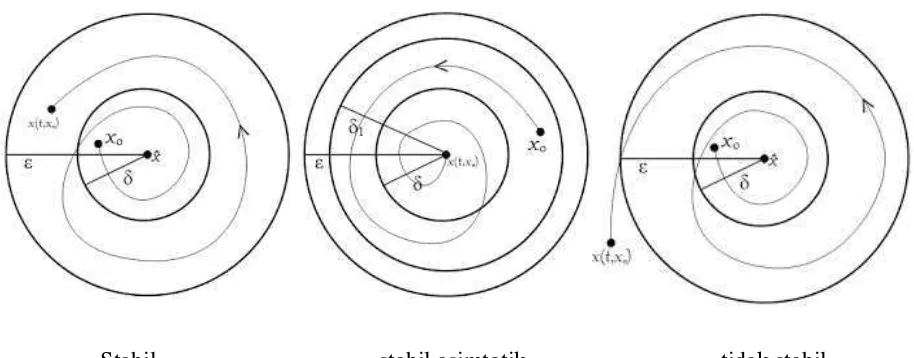
Kestabilan di titik ekuilibrium secara umum dibagi menjadi tiga jenis yaitu stabil, stabil asimtotik dan tidak stabil. Kestabilan titik ekuilibrium dari suatu sistem persamaan diferensial baik linear maupun nonlinear akan dijelaskan pada Definisi 2.10 dan Teorema 2.2 berikut:
Definisi 2.10 (Olsder, 2004: 57)
Diberikan persamaan diferensial orde satu = ̅ dan adalah solusi persamaan = ̅ pada saat dengan kondisi awal = .
1. Vektor ̅ memenuhi ̅ = disebut sebagai titik ekuilibrium.
2. Titik ekuilibrium ̅ dikatakan stabil jika untuk setiap terdapat sedemikian sehingga jika − ̅ , maka − ̅ untuk setiap .
31
4. Titik ekuilibrium ̅ dikatakan tidak stabil jika titik ekuilibrium ̅ tidak memenuhi (2).
Ilustrasi dari Definisi 2.10 disajikan pada Gambar 2.2 berikut:
Stabil stabil asimtotik tidak stabil
Gambar 2.2. Ilustrasi Kestabilan
Menganalisis kestabilan pada sistem persamaan diferensial di titik sekitar titik ekuilibrium tidak mudah dilakukan. Oleh karena itu, diberikan penjelasan mengenai sifat-sifat kestabilan suatu sistem yang ditinjau dari nilai eigen untuk mempermudah menganalisis kestabilan sistem di sekitar titik ekuilibrium. Penjelasan tersebut dijelaskan dalam Teorema 2.2 berikut:
Teorema 2.2 (Olsder, 2004: 58)
32
1. Titik ekuilibrium ̅ = adalah stabil asimtotik jika dan hanya jika untuk semua = .
2. Titik ekuilibrium ̅ = adalah stabil jika dan hanya jika , untuk semua = dan untuk setiap nilai eigen pada sumbu imajiner dengan = yang multiplisitas aljabar dan multiplisitas geometri untuk nilai eigen sama.
3. Titik ekuilibrium ̅ = adalah tidak stabil jika dan hanya jika untuk beberapa = atau terdapat nilai eigen pada sumbu imajiner dengan = yang multiplisitas aljabar lebih besar daripada multiplisitas geometri untuk nilai eigen.
Bukti:
1. Akan dibuktikan bahwa titik ekuilibrium ̅ = adalah stabil asimtotik jika dan hanya jika untuk semua = .
Jika titik ekuilibrium ̅ = adalah stabil asimtotik maka untuk semua = .
Menurut Definisi 2.10, titik ekuilibrium ̅ = dikatakan stabil asimtotik jika − ̅ = . Sehingga untuk , menuju ̅ = .
33 (⇐)
Jika untuk semua = , maka titik ekuilibrium ̅ = stabil asimtotik.
Solusi selalu memuat . Jika maka untuk ,
akan menuju ̅ = . Berdasarkan Definisi 2.10, titik ekuilibrium ̅ =
stabil asimtotik.
2. Akan dibuktikan bahwa titik ekuilibrium ̅ = adalah stabil jika dan hanya jika untuk semua = dan untuk setiap nilai eigen pada sumbu imajiner dengan yang multiplisitas aljabar dan multiplisitas geometri untuk nilai eigen harus sama.
( )
Jika titik ekuilibrium ̅ = stabil maka untuk semua = .
Andai , maka solusi persamaan diferensial yang selalu memuat akan menuju (menjauh dari titik ekuilibrium ̅ = ). Untuk , sehingga sistem tidak stabil. Hal ini terjadi kontraposisi dengan pernyataan jika titik ekuilibrium ̅ = stabil, maka untuk semua = . Jadi terbukti bahwa jika titik ekuilibrium ̅ = stabil, maka maka untuk semua = .
34
Jika untuk semua = maka titik ekuilibrium ̅ = stabil dan jika ada = maka multiplisitas aljabar dan multiplisitas geometri untuk nilai eigen harus sama.
adalah solusi dari Sistem Persamaan (2.8) maka yang selalu memuat . Jika maka akan menuju ̅ = yang artinya stabil asimtotik. Titik ekuilibrium yang stabil asimtotik pasti stabil. Jika = maka nilai eigen berupa bilangan kompleks murni. Menurut Luenberger (1979: 85), multiplisitas aljabar berhubungan dengan nilai eigen dan multiplisitas geometri berhubungan dengan vektor eigen. Oleh karena itu, akan dibuktikan bahwa banyak nilai eigen dan vektor eigen adalah sama. Ambil sebarang sistem di yang mempunyai nilai eigen bilangan kompleks murni. Diambil sistem sebagai berikut:
(2.21) a. Akan ditentukan nilai eigen dari Sistem (2.21),
| − | =
| − − | =
| − | =
+ = .
Akar-akar Persamaan (2.21) adalah
= √− = √ = √
35 sehingga = √ dan = −√ .
Vektor eigen yang bersesuaian dengan = √ , [√
− √ ] =
maka,
[√
− √ | ]
[ − √
√ | ] −
[ −√
√
| ] − √
[ −√ | ]
setelah itu diubah ke bentuk seperti pada persamaan awal sehingga menjadi,
[ − √ ] =
diperoleh,
− √ =
= √ .
36 = [ √ ] = [
√ ]
ambil = , maka diperoleh vektor eigen yang bersesuaian dengan = √
yaitu = √ .
Vektor eigen yang bersesuaian dengan = −√ , [−√
− −√ ] =
maka,
[−√
− −√ | ]
[ − −√
−√ | ] −
[ √
−√ | ] + √
[ √ | ]
setelah itu diubah ke bentuk seperti pada persamaan awal sehingga menjadi,
[ √ ] =
diperoleh,
37
= − √
Misal = , maka = − √ . Sehingga diperoleh,
= [− √ ] = [− √
]
ambil = , maka diperoleh vektor eigen yang bersesuaian dengan = −√
yaitu = − √ .
Jadi terbukti bahwa banyaknya nilai eigen sama dengan banyaknya vektor eigen. 3. Akan dibuktikan bahwa titik ekuilibrium ̅ = adalah tidak stabil jika dan hanya
jika untuk beberapa = atau terdapat nilai eigen pada sumbu imajiner = dengan yang multiplisitas aljabar lebih besar daripada multiplisitas geometri untuk nilai eigen.
( )
Jika titik ekuilibrium ̅ = tidak stabil maka , untuk beberapa = . Titik ekuilibrium tidak stabil apabila , menuju . Hal tersebut terjadi apabila .
(⇐)
38
= � −� =
= � =
Disimpulkan bahwa untuk melihat kestabilan Sistem (2.4) digunakan linearisasi agar Sistem (2.4) menjadi sistem linear = dimana = ̅ adalah matriks Jacobian. Kestabilan yang dimaksud adalah kestabilan lokal. Titik ekuilibrium ̅ dikatakan stabil asimtotik lokal jika semua nilai eigen matriks Jacobian mempunyai bilangan real negatif.
I. Bilangan Reproduksi Dasar
Bilangan reproduksi dasar, dinotasikan R0 adalah angka harapan banyaknya
kasus baru (sekunder) yang dihasilkan dalam suatu populasi rentan oleh individu yang terinfeksi (kasus primer). Jika R0 < 1, maka rata-rata individu yang terinfeksi
menghasilkan kurang dari satu individu yang terinfeksi baru selama periode menular dan infeksi tidak bisa tumbuh. Sebaliknya, jika R0 > 1, maka setiap individu yang
terinfeksi menghasilkan rata-rata lebih dari satu infeksi baru sehingga penyakit dapat menyerang populasi.
Dalam model kompartemen untuk penularan penyakit, suatu kompartemen (kelas) disebut kompartemen penyakit jika individu-individu didalamnya terinfeksi penyakit. Misalkan terdapat n kelas terinfeksi dan m kelas tidak terinfeksi. Dimisalkan menyatakan subpopulasi kelas terinfeksi dan menyatakansubpopulasi kelas tidak terinfeksi dengan dan untuk . Model kompartemen (kelas) dapat dituliskan dalam bentuk berikut:
39
merupakan matriks dari laju individu baru terinfeksi penyakit yang menambah kelas terinfeksi dan merupakan matriks laju perkembanganpenyakit, kematian dan kesembuhan yang mengurangi kelas terinfeksi.
Penentuan bilangan reproduksi dasar berdasarkan linearisasi dari Sistem (2.22) pada titik ekuilibrium bebas penyakit. Persamaan kompartemenkelas terinfeksi yang telah dilinearisasi pada titik ekuilibrium bebas penyakit adalah sebagai berikut,
= −
dimana merupakan titik ekuilibrium bebas penyakit.
Selanjutnya didefinisikan matriks K sebagai berikut:
(2.23)
disebut next generation matrix. Penentuan bilangan reproduksi dasar (R0) ini
akan diperoleh dengan mencari nilai eigen terbesar dari next generation matrix (P. Van Den Driessche dan J. Watmough, 2002) ditulis,
(2.24)
dengan,
= ��
40
= − −
= − −
= − .
: menunjukkan radius spektral dari matriks K
: laju kemunculan infeksi baru pada kompartemen ke-i di titik E0
: laju perpindahan individu yang keluar dari kompartemen ke-i di titik E0
Contoh 2.9
Diberikan sistem persamaan diferensial sebagai berikut:
(2.25)
S menyatakan populasi individu rentan terhadap penyakit pada saat t, I menyatakan populasi terinfeksi pada saat t dan R menyatakan populasi individu pulih pada saat t. Sistem (2.25) mempunyai titik ekuilibrium bebas penyakit . Pada Sistem (2.25) kelas terinfeksi adalah I. Next generation matrix dapat diperoleh dari kelas I sehingga kelas I dapat dituliskan sebagai berikut:
= −
= [ ] dan = [ + ]. Hasil linearisasi dari dan masing-masing adalah
41 =��
= [ ] [ + ] = + = = + = + .
Sehingga diperoleh next generation matrix berikut:
. (2.26)
Selanjutnya, substitusikan titik ekuilibrium bebas penyakit = ke Persamaan (2.26) maka diperoleh,
= + .
Bilangan reproduksi dasar diperoleh dari nilai eigen terbesar dari matriks K. Jadi, nilai bilangan reproduksi dasar dari Sistem (2.26) adalah
42 BAB III PEMBAHASAN
A. Permasalahan Nyata
Penyakit MERS-CoV masih menjadi salah satu penyakit yang banyak memakan korban dan faktor penting yang mempengaruhi penyebaran penyakit tersebut adalah faktor perpindahan populasi. Dalam dua wilayah antar Indonesia dan Arab Saudi terjadi perpindahan populasi, dimana dalam populasi tersebut terdapat individu rentan dan individu terinfeksi, sehingga memungkinkan terjadinya penyebaran penyakit terutama penyakit MERS-CoV. Penyakit ini sangat cepat menular terutama pada individu rentan dengan sistem kekebalan tubuh yang lemah. Oleh karena itu perlu dilakukan suatu tindakan berupa pemberian vaksinasi terhadap individu rentan untuk menekan laju penyebaran penyakit tersebut, sehingga muncul individu rentan tervaksinasi. Salah satu cara untuk menurunkan laju penyebaran penyakit tersebut adalah dengan mengetahui pola penyebaran penyakit MERS-CoV. Oleh karena itu, ilmu matematika dapat dimanfaatkan untuk mengetahui pola penyebaran penyakit MERS-CoV yaitu dengan memanfaatkan model matematika SIV.
43
(SINA), banyaknya populasi rentan yang ada di Arab Saudi (SKSA), banyaknya populasi
terinfeksi yang ada di Indonesia (IINA), banyaknya populasi terinfeksi yang ada di
Arab Saudi (IKSA), dan banyaknya populasi rentan yang ada di Indonesia yang telah
diberi vaksinasi (VINA).
B. Formulasi Model
Skripsi ini menerapkan beberapa asumsi. Asumsi tersebut digunakan untuk mempermudah dalam perhitungan dan pemodelan. Diasumsikan laju perpindahan individu rentan dan terinfeksi dari wilayah Indonesia ke wilayah Arab Saudi lebih besar dibandingkan laju perpindahan individu rentan dan terinfeksi dari wilayah Arab Saudi ke wilayah Indonesia. Hal ini dikarenakan lebih banyak warga negara Indonesia yang pergi ke Arab Saudi untuk melaksanakan Haji/Umrah. Selain asumsi tersebut asumsi-asumsi lain yang digunakan adalah:
1. Terdapat individu rentan dan terinfeksi pada kedua wilayah
2. Terdapat individu rentan tervaksinasi hanya dari Indonesia dan individu yang diberi vaksin Meningitis tidak terkena penyakit
3. Terdapat individu rentan yang meninggal secara alami dan laju individu rentan meninggal secara alami sama untuk kedua wilayah
4. Individu terinfeksi dapat pulih dan kembali menjadi individu rentan
44
6. Pada saat individu rentan berada dalam perjalanan, tidak terjadi kelahiran maupun kematian
7. Pada saat individu terinfeksi berada dalam perjalanan, tidak terjadi pemulihan pada individu tersebut
8. Semua populasi dapat berpindah dari satu wilayah ke wilayah lain.
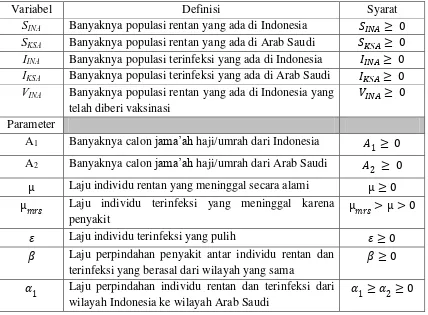
Karena masa inkubasi virus MERS-CoV adalah 5-6 hari (Benny Yong dan Livia Owen, 2015), maka satuan waktu (t) dihitung dalam minggu. Adapun variabel dan parameter yang digunakan dalam pemodelan ini adalah
Tabel 3.1 Variabel dan Parameter
Variabel Definisi Syarat
SINA Banyaknya populasi rentan yang ada di Indonesia
SKSA Banyaknya populasi rentan yang ada di Arab Saudi
IINA Banyaknya populasi terinfeksi yang ada di Indonesia
IKSA Banyaknya populasi terinfeksi yang ada di Arab Saudi
VINA Banyaknya populasi rentan yang ada di Indonesia yang
telah diberi vaksinasi
Parameter
A1 Banyaknya calon jama’ah haji/umrah dari Indonesia �
1 A2 Banyaknya calon jama’ah haji/umrah dari Arab Saudi �
2
Laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang sama
1 Laju perpindahan individu rentan dan terinfeksi dari
45
2 Laju perpindahan individu rentan dan terinfeksi dari
wilayah Arab Saudi ke wilayah Indonesia 1 2
Laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang berbeda
Laju perpindahan individu rentan yang ada di Indonesia yang diberi vaksinasi dari kelompok ke kelompok
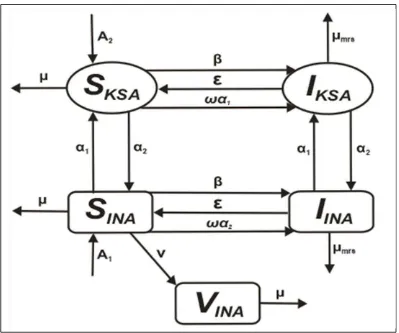
Berdasarkan data pada Tabel 3.1 dan asumsi-asumsi yang telah digunakan, maka dapat digambarkan diagram kompartemen model penyebaran penyakit menular MERS-CoV yang ditunjukkan pada Gambar 3.1 berikut:
46
Berdasarkan Gambar 3.1 dapat ditentukan hal-hal yang mempengaruhi proses penyebaran penyakit menular MERS-CoV antar kedua wilayah tersebut. Selanjutnya akan dijelaskan proses pembentukan model penyebaran penyakit menular MERS-CoV antar wilayah Indonesia (INA) dan Arab Saudi (KSA) dengan pertimbangan yang divaksinasi calon jama’ah haji/umrah yang berasal dari Indonesia untuk tiap-tiap kelas.
a) Perubahan banyaknya individu rentan Indonesia (INA) terhadap waktu (t).
Misalkan SINA ( ) menyatakan banyaknya individu rentan INA pada saat t maka
pada selang waktu � akan terjadi perubahan banyak individu rentan INA yang dipengaruhi oleh:
i. Jika banyaknya pertambahan individu rentan INA sebesar A1 maka
akan bertambah sebesar � � .
ii. Jika laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang sama menjadi individu terinfeksi INA sebesar β, maka akan berkurang sebesar
�
iii. Jika laju kematian alami dari individu rentan INA per satuan waktu sebesar �, laju perpindahan individu rentan dari wilayah Indonesia ke wilayah Arab Saudi sebesar dan banyaknya individu rentan INA yang divaksinasi sebesar v, maka akan berkurang sebesar � .
47
v. Jika laju individu terinfeksi INA yang pulih dan kembali menjadi individu rentan sebesar � maka akan bertambah sebesar � � .
vi. Jika laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang berbeda (dari Arab Saudi ke Indonesia) sebesar sedangkan laju perpindahan individu rentan dan terinfeksi dari wilayah Arab Saudi ke wilayah Indonesia sebesar , maka akan berkurang sebesar
� .
Sehingga model matematis dari perubahan banyaknya individu rentan INA terhadap waktu (t) adalah sebagai berikut:
48
b) Perubahan banyaknya individu terinfeksi yang di Indonesia terhadap waktu (t). Misalkan IINA ( ) menyatakan banyaknya individu terinfeksi INA pada saat t
maka pada selang waktu � akan terjadi perubahan banyak individu terinfeksi INA yang dipengaruhi oleh :
i. Jika laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang sama menjadi individu terinfeksi INA sebesar β, maka akan bertambah sebesar
�
ii. Jika laju kematian karena penyakit MERS-CoV dari individu terinfeksi INA per satuan waktu sebesar µ� , laju perpindahan individu terinfeksi dari wilayah Indonesia ke wilayah Arab Saudi sebesar dan laju individu terinfeksi INA yang pulih dan kembali menjadi individu rentan sebesar �, maka akan berkurang sebesar � �
iii.Jika laju perpindahan individu terinfeksi dari wilayah Arab Saudi ke wilayah Indonesia sebesar , maka akan bertambah sebesar �
49
Arab Saudi ke wilayah Indonesia sebesar , maka akan bertambah sebesar
�
Sehingga model matematis dari perubahan banyaknya individu terinfeksi INA terhadap waktu (t) adalah sebagai berikut:
� � � � �
c) Perubahan banyaknya individu tervaksinasi asal Indonesia terhadap waktu (t). Misalkan VINA ( ) menyatakan banyaknya individu tervaksinasi INA pada saat t
50
i. Jika banyaknya individu rentan INA yang divaksinasi sebesar v maka VINA ( )
akan bertambah sebesar vSINA ( ).
ii. Jika laju kematian alami dari individu tervaksinasi INA per satuan waktu sebesar �, maka VINA ( ) akan berkurang sebesar �SINA ( ).
Sehingga model matematis dari perubahan banyaknya individu tervaksinasi INA terhadap waktu (t) adalah sebagai berikut:
d) Perubahan banyaknya individu rentan yamg di Arab Saudi terhadap waktu (t). Misalkan SKSA ( ) menyatakan banyaknya individu rentan KSA pada saat t maka
pada selang waktu � akan terjadi perubahan banyak individu rentan KSA yang dipengaruhi oleh:
i. Jika banyaknya pertambahan individu rentan KSA sebesar A2 maka
51
ii. Jika laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang sama menjadi individu terinfeksi asal KSA sebesar β, maka akan berkurang sebesar
� .
iii. Jika laju kematian alami dari individu rentan KSA per satuan waktu sebesar � dan laju perpindahan individu rentan dari wilayah Arab Saudi ke wilayah Indonesia sebesar , maka akan berkurang sebesar � . iv. Jika laju perpindahan individu rentan dari wilayah Indonesia ke wilayah Arab
Saudi sebesar , maka akan bertambah sebesar � .
v. Jika laju individu terinfeksi KSA yang pulih dan kembali menjadi individu rentan sebesar � maka akan bertambah sebesar � � .
vi. Jika laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang berbeda (dari Indonesia ke Arab Saudi) sebesar sedangkan laju perpindahan individu rentan dan terinfeksi dari wilayah Indonesia ke wilayah Arab Saudi sebesar , maka akan berkurang sebesar
� .
Sehingga model matematis dari perubahan banyaknya individu rentan KSA terhadap waktu (t) adalah sebagai berikut:
� � �
� � �
52
e) Perubahan banyaknya individu terinfeksi yang di Arab Saudi terhadap waktu (t) Misalkan IKSA ( ) menyatakan banyaknya individu terinfeksi KSA pada saat t
maka pada selang waktu � akan terjadi perubahan banyak individu terinfeksi KSA yang dipengaruhi oleh:
i. Jika laju perpindahan penyakit antar individu rentan dan terinfeksi yang berasal dari wilayah yang sama menjadi individu terinfeksi asal KSA sebesar β, maka akan bertambah sebesar
� .
53
terinfeksi KSA yang pulih dan kembali menjadi individu rentan sebesar �, maka akan berkurang sebesar � � .
iii. Jika laju perpindahan individu terinfeksi dari wilayah Indonesia ke wilayah Arab Saudi sebesar , maka akan bertambah sebesar � . iv. Jika laju perpindahan penyakit antar individu rentan dan terinfeksi yang
berasal dari wilayah yang berbeda (dari Indonesia ke Arab Saudi) sebesar sedangkan laju perpindahan individu rentan dan terinfeksi dari wilayah Indonesia ke wilayah Arab Saudi sebesar , maka akan bertambah sebesar
� .
Sehingga model matematis dari perubahan banyaknya individu terinfeksi KSA terhadap waktu (t) adalah sebagai berikut:
54 penyebaran penyakit MERS-CoV sebagai berikut:
dengan daerah asal dari variabel-variabel pada model adalah
55 C. Transformasi Model
Untuk memudahkan dalam mencari titik ekuilibrium endemik dan analisis yang akan dilakukan, maka pada Sistem Persamaan (3.6) perlu dilakukan penyederhanaan dengan cara pengskalaan yaitu dengan mengubah Sistem Persamaan (3.6) menjadi bentuk proporsi antara banyaknya individu dalam suatu subpopulasi dengan banyaknya populasi total. Didefinisikan variabel baru yaitu proporsi banyaknya individu pada masing-masing kelas adalah sebagai berikut :
� �
57
61 dibentuk transformasi dari Sistem Persamaan yaitu:
62
63
ii. Jika , maka Sistem Persamaan (3.6) memiliki titik ekuilibrium endemik yaitu
Bukti :
i. Sistem Persamaan (3.6) akan mencapai titik ekuilibrium jika,
Maka Sistem Persamaan (3.6) dapat ditulis :
64
. (3.15)
Karena maka dari Persamaan (3.6.4) diperoleh
�
� (3.16)
(3.17)
Dari Persamaan (3.14) dan (3.17) diperoleh:
� (� )
� �
� �
� � �
� � �
� � � � � �
Dari Persamaan (3.15) dan (3.16) diperoleh :
65
� �
� �
� �
� �
� � � �
Jika , maka dari Persamaan (3.6.3) diperoleh,
[ � � � ]
Diperoleh titik ekuilibrium bebas penyakit atau disease free, .
66
Bilangan reproduksi dasar digunakan untuk mengetahui besarnya angka tingkat penyebaran penyakit. Dari Sistem Persamaan (3.6) diperoleh :
67
69
Karena pada titik tidak terdapat kelas yang terinfeksi, maka dan sehingga diperoleh :
� � � �
kemudian akan dicari invers dari :
70
Akan dicari nilai eigen dari sebagai berikut :
71
Nilai eigen terbesar dari next generation matrix adalah
√
� �
Dengan menggunakan Persamaan (2.24), maka diperoleh :
72
F. Kestabilan Lokal di sekitar Titik Ekilibrium
Pada subbab ini akan dianalisis kestabilan lokal di sekitar titik ekuilibrium bebas penyakit. Berdasarkan Teorema 3.1 telah diperoleh titik ekuilibrium bebas penyakit yaitu:
dengan
,
dan
.
Selanjutnya analisis kestabilan di sekitar titik ekuilibrium ini dinyatakan dalam teorema berikut:
Teorema 3.2
(i) Jika maka titik ekuilibrium bebas penyakit stabil asimtotik lokal
(ii) Jika maka titik ekuilibrium bebas penyakit tidak stabil.
Bukti
Sistem Persamaan (3.13) didefinisikan sebagai:
73
Maka matriks jacobian dari Sistem Persamaan (3.18) adalah
75
78 ) ( ) ) (
) ] ( ) [( ( ) ( )
( ) ) ( )]}
� ( ) ( ) (
� ) ( �
� ) ( ) (
) ( ) ( ) (
� ) ( �
� ) [ ( �
� )] [ (
� )] ( �
� ) ( � ) (
) ( ) ( )
79
� ) ( �
� ) ( ) (3.19)
dengan,
[ ]
Secara implisit diperoleh nilai eigen yang merupakan solusi dari Persamaan (3.19). Jika nilai-nilai eigen tersebut negatif atau , maka dapat disimpulkan bahwa titik ekuilibrium bebas penyakit dari Sistem Persamaan (3.6) stabil asimtotik. Selanjutnya untuk memudahkan analisa penyebaran penyakit MERS-CoV digunakan simulasi model dengan parameter yang diambil dari data Kementerian Agama Republik Indonesia, data haji Internasional dan Jurnal Model Penyebaran Penyakit Menular MERS-CoV.
G. Simulasi Model Penyebaran Penyakit MERS-CoV
80
Simulasi ini dilakukan untuk memberikan gambaran geometris mengenai pola penyebaran penyakit MERS-CoV sesuai dengan kondisi bilangan reproduksi dasar dan dengan pengaruh pemberian vaksin Meningitis terhadap calon jama’ah haji/umrah dari Indonesia. Bilangan reproduksi dasar dapat digunakan untuk mengetahui penyakit tersebut menghilang atau endemik dalam populasi.
Saat artinya setiap individu yang terinfeksi dapat menularkan penyakit MERS-CoV kepada rata-rata kurang dari satu individu rentan, sehingga dalam jangka waktu tertentu penyakit dapat menghilang dari populasi. Namun, untuk artinya setiap individu terinfeksi dapat menularkan penyakit MERS-CoV kepada rata-rata lebih dari satu individu rentan, sehingga dalam jangka waktu tertentu penyakit akan menyebar dalam populasi.
81
Kemudian untuk parameter menyatakan parameter tingkat vaksinasi. Nilai dari parameter ini dapat bervariasi sesuai dengan kondisi nilai . Diberikan nilai awal untuk masing-masing individu rentan yang ada di Indonesia, individu rentan yang ada di Arab Saudi, individu rentan asal Indonesia yang tervaksinasi, individu terinfeksi yang ada di Indonesia dan individu terinfeksi yang ada di Arab Saudi adalah
dan . Berdasarkan
nilai-nilai parameter dan nilai awal yang diberikan, selanjutnya akan dilakukan simulasi numerik untuk pemodelan matematika penyebaran penyakit menular MERS-CoV dengan pengaruh vaksinasi untuk individu rentan yang ada di Indonesia. Dari simulasi tersebut akan dilihat pengaruh vaksinasi untuk penyebaran penyakit menular MERS-CoV dalam suatu populasi antar dua wilayah.
82
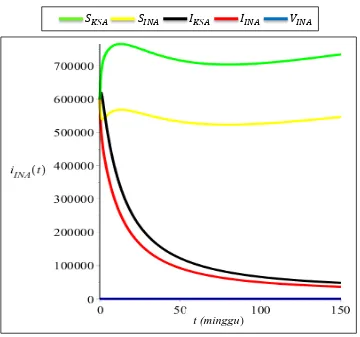
1. Simulasi Model Matematika pada Penyebaran Penyakit Menular MERS-CoV tanpa Pengaruh Vaksinasi atau
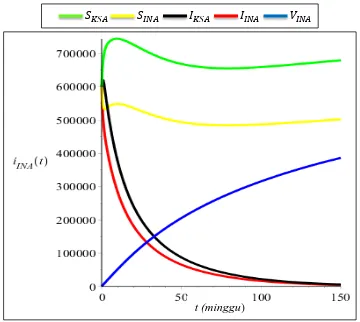
Berikut diberikan simulasi untuk Sistem (3.20) dengan mengambil nilai parameter . Simulasi disajikan pada Gambar 3.2 berikut ini:
Gambar 3.2 Simulasi Sistem (3.20) dengan
Pada Gambar 3.2, untuk atau dengan kata lain pada simulasi ini tanpa pengaruh vaksinasi, ditunjukkan bahwa banyaknya individu terinfeksi yang ada di Indonesia dan Arab Saudi menurun namun tidak menuju nol sehingga pada waktu
t (minggu)
���� ���� ���� ���� ����
83
tertentu penyakit MERS-CoV akan selalu ada dalam populasi sampai waktu yang tak terbatas.
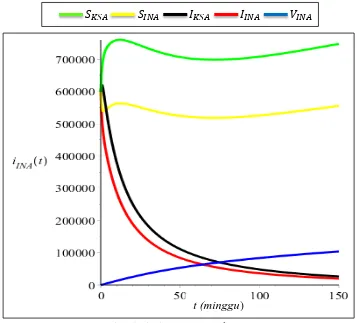
2. Simulasi Model Matematika pada Penyebaran Penyakit Menular MERS-CoV dengan Pengaruh Vaksinasi untuk
Berikut diberikan simulasi untuk Sistem (3.20) dengan mengambil nilai parameter . Simulasi disajikan pada Gambar 3.3 berikut ini:
Gambar 3.3 Simulasi Sistem (3.20) dengan
Gambar 3.3 menunjukkan pada saat tingkat pemberian vaksinasi sebesar , terlihat bahwa banyaknya individu terinfeksi yang ada di Indonesia dan
���� ���� ���� ���� ����