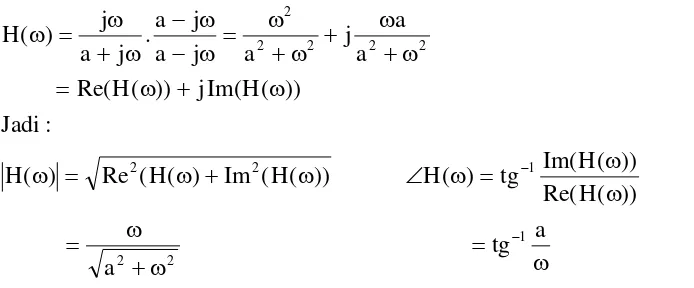2Rangkaian RC seri.pdf

(1)

Rangkaian RC seri

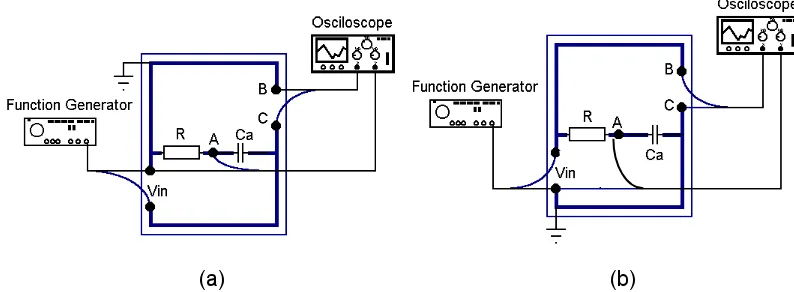
Dengan melihat Gambar 1 dapat diketahui dua macam rangkaian RC seri. Respon

frekuensi dari masing-masing rangkaian dapat dijelaskan sebagai berikut.

Gambar 1. Rangkaian RC seri

a. Rangkaian RC dengan tegangan kapasitor sebagai tegangan output

Dengan H.K tegangan di peroleh:

V1 = VR1 + VC1 (RCS.1)

V1(ω) = I(ω).R1 + I(ω)/jωC1

Sehingga arus dalam rangkaian dapat diketahui,

 

1 1 1

C

j

1

R

V

I











(RCS.2)

Tegangan output rangkaian, VC, adalah:

VC(ω) = I(ω)/jωC1 (RCS.3)

)

(

V

.

a

j

a

.C

R

1

j

1

.

.C

R

)

(

V

1

.C

.R

j

)

(

V

)

(

V

1 1 1 1 1 1 1 1 1 C























dimana a = 1/R1.C1, Tranfer function, H(ω), dapat diperoleh:

a

j

a

)

(

V

)

(

V

)

(

H

1 C













(RCS.4)

(2)

Mata Praktikum R.L. II Rangkaian RC seri

a

tg

a

))

(

H

Re(

))

(

H

Im(

tg

)

(

H

))

(

H

(

Im

)

(

H

(

Re

)

(

H

:

Jadi

))

(

H

Im(

j

))

(

H

Re(

a

j

a

j

a

j

a

.

j

a

)

(

H

1 2 2 1 2 2 2 2 2 2 2



































































  (RCS.5)

Tabel berikut menunjukkan magnituda dan fasa bila ω diubah-ubah.

Tabel 1. Perubahan |H(ω)| dan



H

(



)

dari rangkaian (a) akibat perubahan ω.

ω |H(ω)| ω ∟H(ω)°

0 1 0 0

a 0,707 a -45

10a ≈ 0,1 10a -84

100a ≈ 0,01 100a -89,4

b. Rangkaian RC dengan tegangan resistor sebagai tegangan output

Arus yang mengalir dalam rangkaian (a) sama dengan arus dalam rangkaian (b),

sehinga dengan menggunakan (RSC.2), tegangan pada resistor adalah:

VR(ω) = I(ω).R1 (RCS.6)

 

               1 1 1 1 1 1 1 1 R V . a j j V . C R 1 j j C j 1 R R . V V

dimana a = 1/R1.C1, Tranfer function, H(ω), dapat diperoleh:

a

j

)

(

V

)

(

V

)

(

H

1 R













(RCS.7)

(3)







































































 

a

tg

a

))

(

H

Re(

))

(

H

Im(

tg

)

(

H

))

(

H

(

Im

)

(

H

(

Re

)

(

H

:

Jadi

))

(

H

Im(

j

))

(

H

Re(

a

j

a

j

a

j

a

.

j

a

j

)

(

H

1 2 2 1 2 2 2 2 2 2 2 (RCS.8)

Tabel berikut menunjukkan magnituda dan fasa bila ω diubah-ubah.

Tabel 1. Perubahan |H(ω)| dan



H

(



)

dari rangkaian (b) akibat perubahan ω.

ω |H(ω)| ω ∟H(ω)°

0 0 0 ≈ 90

a 0,707 a 45

10a 0,995 10a 5,71

100a 1 100a 0,57

Saat ω = a diperoleh |H(ω)| = 1/√2 = 0,707 ini adalah frekuensi yang menyebabkan

daya output menjadi separuh dari nilai daya output maksimum. Oleh karena itu

dikenal dengan frekuensi setengah daya. Hal ini dijelaskan sebagai berikut.

Z

v

p

2 o out



Untuk rangkaian (a),

p

_out



v

2_o

.

s

.

C

₁. Bila amplitudo puncak vinput = 1 volt, saat ω = 0

diperoleh vo = 1 volt, sehingga pout = s.C1. saat ω = a, dengan amplitudo vinput yang

sama, diperoleh pout = 0,5.s.C1. Pada rangkaian (b), 1 2 o out

v

/

R

p



. Bila amplitudo

puncak vinput = 1 volt, saat ω >> a diperoleh vo = 1 volt, sehingga pout = 1/R1. saat ω =

a, dengan amplitudo vinput yang sama, diperoleh pout = 0,5.R-1.

Frekuensi saat ω = a disebut juga sebagai frekuensi cut-off, fc. Suatu frekuensi batas

yang menyatakan sinyal input diteruskan atau tidak diteruskan ke terminal output.

Gambar berikut adalah hasil simulasi rangkaian RC seri dengan R1=1kΩ dan

C1=1uF, sehingga a = 1000, dan saat ω = a nilai fc hasil perhitungan adalah

(4)

Mata Praktikum R.L. II Rangkaian RC seri

Gambar 2. Respon frekuensi, magnitudo, fasa, dan daya.

Gambar 3. Beda fasa antara Vinput dan Voutput.

Tujuan Percobaan:

1. Mengetahui respon frekuensi rangkaian resistif kapasitif yang terhubung seri

2. Menganalisa tegangan pada simpul rangkaian RC seri

(5)

Mata Praktikum R.L. II Rangkaian RC seri

Alat dan bahan

 Papan percobaan rangkaian RC seri

 Kabel penghubung

 Sinyal Generator

 Frequency counter

 Osciloscope dual trace

Langkah Percobaan

1. Siapkan rangkaian percobaan seperti ditunjukkan pada Gambar 4.a.

(a) (b)

Gambar 4. a. Percobaan I, pengukuran VR. b. Percobaan II, pengukuran VC

2. Hitunglah frekuensi cut-off dari rangkaian tersebut dan catatlah hasilnya.

a =



RC

1

……….. ωc = a = ……… rad/det

fc =   

. 2

c

……… Hz

3. Lengkapi kolom f dari Tabel 3.

4. Siapkan sinyal sinus dengan amplitudo 2 vpp dan frekuensi seperti ditunjukkan

dalam Tabel 3.

5. Gunakan osciloscope untuk melakukan pengukuran amplitudo tegangan resistor,

VR. Amati VR puncak dan VR saat Vin = 0. Catatlah hasil pengukuran pada Tabel

3.

6. Matikan catu daya, kemudian ubahlah rangkaian percobaan seperti Gambar 4.b.

(6)

Mata Praktikum R.L. II Rangkaian RC seri

Data Hasil Percobaan

Tabel 3. Hasil pengukuran percobaan I. Tegangan resitor dengan Vin = 2 vpp.

f (Hz) VR puncak (volt) VR saat Vin = 0 (volt) |VR | θR

0,1.fc = X = X =

0,5.fc = X = X =

fc = X = X =

2.fc = X = X =

10.fc = X = X =

Tabel 4. Hasil pengukuran percobaan II. Tegangan kapasitor dengan Vin = 2 vpp .

f (Hz) VC puncak (volt) VC saat Vin = 0 (volt) |VC | θC

0,1.fc = X = X =

0,5.fc = X = X =

fc = X = X =

2.fc = X = X =

10.fc = X = X =

Gambar 5. Contoh pengukuran tegangan input dan output saat frekuensi f = …… Hz.

Perhitungan Data Hasil Pengukuran

Isilah kolom |VR | θR dan |VC | θC pada Tabel 3 dan Tabel 4.



 

puncak R

vin saat R R

v

0

1 puncak R R

sin

v

V

(7)

Mata Praktikum R.L. II Rangkaian RC seri



 

puncak C

vin saat C C

v

₀

1 puncak C C

sin

v

V



Dengan Vin = 2 vpp maka Vin puncak = 1 Vp; Vin digunakan sebagai acuan fasa, maka

nilai |H(ω)| = VR dan beda fasa tegangan output terhadap tegangan input adalah θR.

Oleh karena itu dari Table 3 dapat dibuat sketsa kurva respon frekuensi, H = Vo/Vi.

Gambar 6. Perubahan magnitudo sebagai pengaruh perubahan frekuensi

Gambar 7. Perubahan fasa sebagai pengaruh perubahan frekuensi

Perhitungan Teoritis

Vc dapat dihitung dengan persamaan berikut:

)

(

/

1

/

1

)

(



in

C

xV

RC

j

RC

V





=

Selisih hasil pengukuran terhadapa hasil perhitungan = hasil ukur – hasil hitung

(8)

Catat hasilnya pada Tabel 5. Perhitungan diulangi untuk nilai  lainnya.

VR dapat dihitung dengan persamaan berikut:

)

(

/

1

)

(



_in

R

xV

RC

j

V





=

Selisih hasil pengukuran terhadapa hasil perhitungan = hasil ukur – hasil hitung

Selisih dalam persentase = selisih / hasil ukur x 100 %

Catat hasilnya pada Tabel 6. Perhitungan diulangi untuk nilai  lainnya.

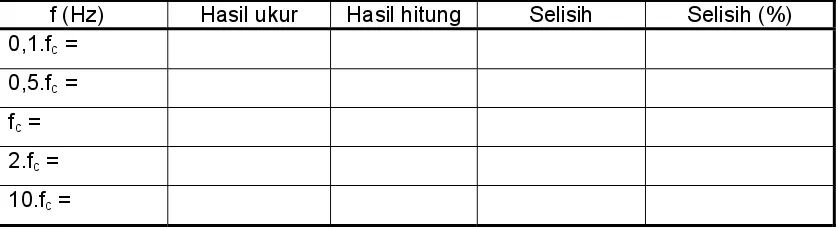
Tabel 5. Perbandingan hasil pengukuran dan hasil perhitungan tegangan resistor dengan Vin = 2 Vpp

f (Hz) Hasil ukur Hasil hitung Selisih Selisih (%) 0,1.fc =

0,5.fc =

fc =

2.fc =

10.fc =

Tabel 6. Perbandingan hasil pengukuran dan hasil perhitungan tegangan kapasitor dengan Vin = 2 Vpp

f (Hz) Hasil ukur Hasil hitung Selisih Selisih (%) 0,1.fc =

0,5.fc =

fc =

2.fc =

10.fc =

Gambarkan kurva hasil perhitungan pada Tabel 5 dan Tabel 6. Amatilah tabel

tersebut dan catat hasil pengamatan.

Tugas

Buatlah rangkaian LPF dan HPF yang masing-masing mempunyai frekuensi cut-off

pada 10 kHz dan 1kHz. Buktikan rancangan tersebut dengan menggunakan

(9)