DIKTAT PERKULIAHAN
MATEMATIKA I
UNTUK MAHASISWA TEKNIK TELEKOMUNIKASI SEMESTER SATU
JURUSAN TEKNIK ELEKTRO
POLITEKNIK NEGERI JAKARTA
1 Oleh: Ir. Sutanto,MT. NIP.195911201989031002
Dibiayai Dengan : Dana DIPA Penyusunan Naskah Bahan Ajar Nomor Kontrak : 021/K7.A/UP2AI/2010 Politeknik Negeri Jakarta Tahun Anggaran 2009
rR R
r R 1/2h
Z = a +jb
DESEMBER, 2010
PRAKATAPenulisan diktat ini bertujuan untuk memudahkan dan membantu mahasiswa program studi Teknik Telekomunikasi semester satu dalam mempelajari, memahami dan mengaplikasikan matakuliah matematika dalam bidang teknik telekomunikasi. Selain dari pada itu diktat ini juga sangat bermanfaat dalam memberikan bekal pada para mahasiswa sebagai bahan penunjang mata kuliah lain dan sebagai sarana pembantu dalam menyelesaikan persoalan keteknikan yang membutuhkan matematika tingkat tinggi. Sebagaimana diketahui bahwa dalam bidang teknik telekomunikasi sangat banyak persoalan yang penyelasaiannya sangat membutuhkan bantuan matematika. Sebagai contoh perhitungan medan listrik, medan magnet, rangkaian listrik, pengolahan sinyal, otomatisasi system dan sebagainya. Berdasarkan penelusuran diperpustakaan dan informasi dari dosen pengasuh masing-masing materi tersebut ternyata antara 70% – 90 % penyelesaian persoalan hitungan sangat membutuhkan bantuan matematika.
Materi yang akan dibahas dalam diktat ini antara lain diferensial, integral, penerapan diferensial, penerapan integral, akar, pangkat, persamaan kuadrat, persamaan linier, bilangan kompleks, penerapan bilangan kompleks dan penerapan persamaan linier.
Pada kesempatan ini penulis sebelumnya mengucapkan terimakasih kepada:
1. Kepala UP2AI PNJ yang telah menyediakan pendanaan untuk penulisan diktat
2. Ketua Jurusan Teknik Elektro dan Ketua Program Studi Teknik Telekomuniksi PNJ yang telah memberi kepercayaan pada penulisan diktat ini.
Depok, 29 Desember 2010 Penulis diktat
Ir. Sutanto,MT
DAFTAR ISI
Tugas / latihan soal-soal ... 13
Daftar Pustaka ... 13
Bab II. Diferensial ………...……….... 14
Pendahuluan ………... 14
Prinsip dasar diferensial ... 14
Penerapan diferensial ... 28
Tugas / latihan soal-soal ... 33
Daftar Pustaka ... 33
Bab V. Persamaan non linier ... 49
Pendahuluan ... 49
Persamaan kuadrat ... 49
Penerapan (aplikasi) persamaan non linier... 73
Tugas / latihan soal-soal ... 83
Daftar Pustaka ... 85
Bab VI. Persamaan linier ... 86
Pendahuluan ... 86
Bentuk umum bilangan kompleks ... 100
Penerapan bilangan kompleks ... 109 Tugas/latihan soal-soal... 112 Daftar Pustaka ... 113
PENDAHULUAN
1.1. Gambaran Umum Materi Kuliah
Materi yang akan dibahas dalam diktat Matematika I ini terdiri atas diferensial, integral, penerapan diferensial, penerapan integral, akar, pangkat, persamaan kuadrat, persamaan linier, bilangan kompleks, penerapan bilangan kompleks dan penerapan persamaan linier. Dalam setiap materi yang akan diajarkan pada mahasiswa selalu diberikan gambaran umum tentang isi materi yang akan dipelajari dan manfaat dari materi tersebut dalam kaitannya dengan mata kuliah lain maupun pada saat mahasiswa tersebut bekerja di masyarakat umum atau industri.
1.2. Tujuan Pembelajaran Umum
Supaya Mahasiswa Teknik Telekomunikasi Semester I mampu menerapkan dasar matematika pada Teknik Telekomunikasi
1.3. Gambaran Umum Isi Diktat
Secara umum diktat terdiri atas kata pengantar, pendahuluan, topik bahasan, uraian topik bahasan (meliputi pendahuluan , penjelasan masing-masing topik, contoh soal, latihan soal- soal dan tugas) dan daftar pustaka
1.4. Proses Pembelajaran
Proses pembelajaran yang akan dilakukan terdiri atas: a. memberikan penjelasan kepada mahasiswa
b. memberikan informasi, uraian dan contoh c. memberikan latihan dan tugas
d. memeriksa latihan dan tugas yang telah diselesaikan oleh mahasiswa
e. memberikan bimbingan berdasarkan umpan balik dari latihan atau tugas yang telah dikerjakan mahasiswa
f. memberikan penilaian pada setiap mahasiswa berdasarkan tugas/latihan, tes harian dan UTS dan UAS
BAB I. INTEGRAL
Integral merupakan kebalikan dari hitungan diferensial. Artinya jika hasil integral didiferensialkan, maka hasilnya harus sama dengan soal yang diintegralkan tersebut. Pembagian integral berdasarkan batas integral dibedakan menjadi integral tertentu dan tak tentu. Integral tertentu artinya batas bawah dan batas atas telah ditentukan nilainya, sedangkan integral tak tentu nilai batas bawah dan atas belum ditentukan. Berdasarkan tingkat integrasinya, maka integral dibedakan menjadi itegral tunggal, integral rangkap dua,integral rangkap tiga dan seterusnya. Tetapi dalam pembahasan integral ini hanya dibatasi sampai integral rangkap tiga saja. Dalam aplikasinya integral rangkap dua antara lain digunakan untuk menghitung luas bidang, sedangkan integral rangkap tiga antara lain digunakan untuk menghitung volume dalam ruang tertutup.
I.2. Integral tunggal tak tentu Contoh
1. ʃ x dx = ½ x2 + C
2. ʃ (1/x)dx = ln x + ln C
3. ʃ ex dx = ex + C
4. ʃ e2x dx = ½ e2x + C
5. ʃ Sinx dx = - Cosx + C
6. ʃ Cosx dx = Sinx + C
7. ʃ tgx dx = ln(Sec x) + C
8. ʃ Cotx dx = ln(Sinx) + C
9. ʃ Secx dx = ln(Sec x + tg x) + C
10. ʃ Cosec x dx = ln(Cosec x – Cot x) + C
11. ʃ Sin2x dx = ½ (x) -1/4 (Sin 2x) + C
12. ʃ Cos2x dx = ½ (x) +1/4 (Sin 2x) + C
13. ʃ tg 2x dx = tg x – x + C
14. ʃ cot 2x dx = -cot x – x + C
15. ʃ ax dx = (ax/lna)+ C
16. ʃ lnx dx = x ln x –x + C
17. ʃ (1/x lnx) dx = ln (lnx) + C
18. ʃ Sinhx dx = Cosh x + C
19. ʃ Cosh x dx = Sinh x + C
20. ʃ tghxdx = ln (Cosh x) + C
21. ʃ Cothxdx = ln (Sinh x) + C
22. ʃ Sech xdx = arc tg (Sinh x) + C
23. ʃ Cosech xdx = ln [tgh(1/2 x)] + C
24. ʃ Sinh2 xdx = ¼ Sinh 2x – ½ x + C
25. ʃ Cosh2xdx = ¼ Sinh 2x + ½ x + C
26. ʃ tgh2xdx = x – tgh x + C
27. ʃ Cotgh2xdx = x – Cotgh x + C
I.3. Bentuk umum integral tunggal tak tentu
1. ʃ x dx/(a + bx) = 1/(b2) [ a + bx – a ln(a +bx)] + C, dengan a dan b adalah tetapan ≠ 0
2. ʃ x2dx/(a +bx) = 1/(b3) [1/2( a + bx)2 – 2a(a +bx) + a2 ln (a +bx)] + C, dengan a dan b
adalah tetapan ≠ 0
3. ʃ xdx/(a +bx)2 = 1/(b2) [ a/(a + bx) + ln(a +bx)] + C
4. ʃ x2dx/(a +bx)2 = 1/(b3) [ a + bx – a2/(a +bx) - 2aln (a +bx)] + C
5. ʃ x √(a + bx) dx = 2/(15b3)(3 bu -2a)( a + bu)3/2 + C
7. ʃ x dx/( √a + bx) = [2/(3b2)][ bu -2a) √ a +bx + C
Sin θ = x/3 x = 3 Sin Ѳ
dx/d θ = 3 Cos Ѳ dx = 3 Cos Ѳ dѲ x 3 Cos θ = 1/3 √4 – x2
3 √9 – x2 = 3 Cos θ
√ 9 – x2 (9 – x2)1/2 = 3 Cos Ѳ
√9 – x2
1/[xʃ 2√ (9 – x2)]dx
Latihan
Dengan subsitusi trigonometri selesaikan integral berikut:
I.4.2. Metoda integral sebagian Contoh:
1. Tentukan :ʃ arc Cos 2 x dx
Jawab:
dv = dx v = x
ʃ arc Cos 2 x dx = ʃ udv = uv - ʃ vdu
Menentukan:
Misalkan: 1 - 4x2 = m atau m = 1 - 4x2
dm/dx = - 8 x
dm = - 8 xdx 2x dx = - 1/4 dm
Sehingga:
= -1/4 (2 m1/2) = - 1/2 m1/2
= - 1/2√ 1- 4 x2
Jadi:
ʃ arc Cos 2 x dx = x arc Cos 2x - 1/2√ 1- 4 x2 + C
2. Tentukan: ʃ x2√1 – x dx
Jawab:
Misal: u = x2 du/dx = 2x atau du = 2x dx
dv = √1 – x dx = (1-x)1/2 dx v = - 2/3 (1-x)3/2
ʃ x2√1 – x dx = ʃ udv
= uv - ʃ vdu = -2/3 x2 (1-x)3/2 + 2/3 2x (1-x)ʃ 3/2 dx
= - 2/3 x2 (1-x)3/2 + 4/3 x (1-x)ʃ 3/2 dx
Menentukan : ʃ x (1-x)3/2 dx
Misal: u = x du/dx = 1 atau du = dx
dv = (1-x)3/2 dx v = -2/5 (1 - x)5/2
Sehingga:
ʃ x√1 – x dx = ʃ udv = uv - ʃ vdu
= -2/5(x)(1 - x)5/2 – ʃ -2/5 (1 - x)5/2dx
= -2/5(x)(1 - x)5/2 + 2/5 ʃ(1 - x)5/2dx
= -2/5(x)(1 - x)5/2 + (2/5)(-2/7) (1 - x)7/2
= -2/5(x)(1 - x)5/2 - 4/35 (1 - x)7/2
Jadi:
ʃ x2√1 – x dx = - 2/3 x2 (1-x)3/2 + 4/3ʃ x (1-x)3/2 dx
= - 2/3 x2 (1-x)3/2 + 4/3[-2/5(x)(1 - x)5/2 - 4/35 (1 - x)7/2] + C
= - 2/3 x2 (1-x)3/2 -8/15(x)(1 - x)5/2 - 16/105 (1 - x)7/2] + C
I.4.3. Metoda pecahan sebagian Contoh:
1. Tentukan :
Jawab:
Misal:
1 = x (A+B) +3(A-B) Bila dilakukan evaluasi koefisien pada x0 dan x1
Ruas kiri Ruas kanan
x0 1 3(A-B)
x1 0 A + B
Diperoleh persamaan:
3(A-B) = 1 ...(1) A + B = 0 ...(2) Dari persamaan (1) dan (2) didapat harga A = 1/6 dan B = -1/6 Sehingga:
= 1/6 ln (x-3) - 1/6 ln (x+3) + ln C
2. Tentukan:
Jawab: Misal:
Terlihat bahwa:
x3+ x2 + x +3 = (A+C) x3+ (B+D) x2 +(3A+C) x + (3B+D)
Berdasarkan evaluasi koefisien pada x3, x2 , x, x0diperoleh persamaan:
A + C = 1 ...(1)
B + D = 1 ...(2)
3A + C = 1 ...(3)
3B + D = 3 ...(4)
Dari persamaan (1) s/d (4) diperoleh harga: A= 0, B=1, C = 1, D = 0
= arc tg x + ½ ln (x2+3) + C
Catatan: Menentukan :
Misal:
u= x2+3 du/dx = 2x atau du = 2x dx xdx = ½ du
Latihan
1. ʃ x arc tg x dx
2. ʃ Sin x Sin 3x dx
I.5. Integral rangkap dua tak tentu
Prinsip penyelesaian integral rangkap dua: f(x) f(y) dy dx
ʃ ʃ
integral dalam integral luar
Penyelesaian dapat dimulai dari integral dalam terlebih dahulu dilanjutkan integral luar atau sebaliknya.
Contoh:
1. Selesaikan: ʃ ʃ x y dy dx
Jawab:
a. Penyelesaian dimulai dari integral dalam (dy)
ʃ ʃ x y dy dx = ʃ ½ y2 x dx = (½ y2)( (½ x2) + C = ¼ y2 x2 + C
b. Penyelesaian dimulai dari integral luar (dx)
ʃ ʃ x y dy dx = ʃ ½ x2 y dy = (½ x2)( (½ y2) + C = ¼ y2 x2 + C
c. Penyelesaian dengan cara memisahkan masing-masing integral (hanya berlaku untuk bentuk perkalian):
ʃ x y dy dx =[ ʃ y dy][ ʃ x dx] = (½ y2)( (½ x2) + C = ¼ y2 x2 + C
2. Selesaikan: ʃ ʃ (x2 + y2) dy dx
Jawab:
a. Penyelesaian dimulai dari integral dalam (dy)
ʃ ʃ (x2 + y2) dy dx = ʃ (y x2 + 1/3 y3) dx
= y(1/3 x3) + 1/3 y3(x) + C = 1/3 y x3+1/3 y3x + C
b. Penyelesaian dimulai dari integral dalam (dx)
ʃ ʃ (x2 + y2) dy dx = ʃ (1/3 x2 + y2 x) dy
= (1/3 x2)(y) + 1/3 y3(x) + C = 1/3 y x2 + 1/3 y3x + C
I.6. Integral rangkap tiga tak tentu Contoh:
1. ʃ ʃ ʃ x2 y z2 dy dx dz
Jawab:
ʃ ʃ ʃ x2 y z2 dy dx dz
a. Penyelesaian dimulai dari integral dalam (dy)
ʃ ʃ ʃ x2 y z2 dy dx dz = ʃ ʃ (x2)(1/2 y2)( z2)dx dz
= ʃ (1/3x3)(1/2 y2)( z2) dz
= (1/3x3)(1/2 y2)( 1/3z3)
= 1/18 (x3y2z3) + C
b. Penyelesaian dimulai dari integral tengah (dx)
ʃ ʃ ʃ x2 y z2 dy dx dz = ʃ ʃ (1/3 x3)( y2)( z2)dy dz
= ʃ (1/3x3)(1/2 y2)( z2) dz
= (1/3x3)(1/2 y2)( 1/3z3)
= 1/18 (x3y2z3) + C
c. Penyelesaian dimulai dari integral luar(dz)
ʃ ʃ ʃ x2 y z2 dy dx dz = ʃ ʃ (x3)( y2)( 1/3z2)dy dx
= ʃ (x3)(1/2 y2)( z2) dy
= 1/18 (x3y2z3) + C
d. Penyelesaian dilakukan dengan memisahkan masing-masing integral
ʃ ʃ ʃ x2 y z2 dy dx dz = [ ʃ x2 dx][ ʃ ydy][ ʃ z2dz]
= (1/3x3)(1/2 y2)( 1/3z3)
= 1/18 (x3y2z3) + C
2. Tentukan : ʃ ʃ ʃ (x2 + y + z2) dy dx dz
Jawab:
Pilihan memulai penyelesaian bebas. Bila dipilih integral luar, maka hasil integral: ʃ ʃ ʃ (x2 + y + z2) dy dx dz = ʃ ʃ (zx2 + zy + 1/3z3) dy dx
= ʃ (1/3 zx3 + zyx + 1/3z3 x) dy
= 1/3zx3y + ½ zy2x + 1/3z3xy + C
Bila dipilih integral tengah, maka hasil integral:
ʃ ʃ ʃ (x2 + y + z2) dy dx dz = ʃ ʃ ( 1/3 x3 + yx + xz2) dy dz
= ʃ (1/3zx3 + zyx + 1/3z3 x) dy
= 1/3zx3y + ½ zy2x + 1/3z3xy + C
Catatan:
Untuk integral yang memiliki variabel dalam bentuk penjumlahan atau pengurangan, maka penyelesaian integral tidak bisa dipisahkan kedalam integral masing-masing variabel. Tetapi untuk bentuk perkalian, maka penyelesaian integral bisa dipisahkan kedalam masing-masing integral.
I.7. Integral tertentu Contoh:
Selesaikan integral berikut:
Jawab:
Misal : u = 1- x du/dx = -1
du = - dx atau dx = - du
=2/3[1-x]3/2 1/2
0
= 2/3 [(1 - ½)3/2 – (1-0)3/2]
= 2/3 [(½)3/2 – (1)3/2] = 2/3 [0,353553 -1]= -0,43096
Jawab:
Latihan
Selesaikan:
Kreyzig, E., 1979. Advenced Engineering Mathematics. 4nd, John Willey and Sons, New York. pp. 249-468,509-560,563-590
Mundit,A.K., 1984. Soal- Penyelesaian Kalkulus Deferensial dan Integral.Jilid I, Armico, Bandung. hal. 37-238, 305-433
BAB II. DIFERENSIAL II.1. Pendahuluan
Pada bagian ini akan dibahas prinsip dasar cara penyelesaian diferensial total dan parsial dari suatu fungsi. Selanjutnya dari prinsip dasar yang telah dilakukan tersebut akan dibuat suatu rumusan umum yang berkaitan dengan tata cara penurunanan atau diferensiasi dari berbagai bentuk fungsi. Tujuan utama dari bahasan ini adalah untuk mempelajari cara mendiferensialkan berbagai bentuk fungsi baik secara total maupun secara parsial.
II.2. Prinsip dasar diferensial total
Pada prinsipnya diferensial atau turunan dari suatu fungsi x atau y = f(x) dapat dihitung dengan menggunakan dasar persamaan:
Atau dapat juga dituliskan sebagai:
II.2.1. Prinsip dasar diferensial fungsi aljabar
Fungsi aljabar mempunyai bentuk yang sangat beragam, sehingga hasil diferensialnya juga sangat beragam.
II.2.1.1. Bentuk Polinomial Contoh:
Dengan menggunakan prinsip bahwa:
1. Tentukan dy/dx dari y = x2 +1
Jawab:
y +∆y = (x+∆x)2 + 1
= x2 + 2 x ∆x+ (∆x)2 +1
∆y = y +∆y - y
= [x2 + 2 x ∆x+ (∆x)2 +1] –[x2 +1]
= 2 x ∆x+ ( ∆x )2
2. Tentukan dy/dx dari :
Jawab:
∆y = y +∆y - y
Latihan
Dengan menggunakan prinsip bahwa :
Tentukan dy/dx dari: 1. y = 2x2 + 2x
2. y = x/(x+1)
3. y = (x2 +1)/(2x +2)
4. y = x2.x3
II.2.1.2. Bentuk Esponensial Contoh:
Dengan menggunakan prinsip bahwa:
1. Tentukan y’ dari : y = e x
Jawab:
Dengan acuan turunan polinomial, maka: y’ = 0 +1 +2x/2! + 3x2/3! + 4x3/4!
y’ = 1 + x + x2/2! + x3/3! = e x
2. Tentukan y’ dari : y = e2x
Jawab:
y = 1 +2x +4x2/2!+ 8 x3/3! + 16 x4/4! + ...
Dengan acuan turunan polinomial, maka:
y’ = 0 +2 +8x/2! + 24x2/3! + 64x3/4! + ... = 2(1+4x/2! + 12x2/3! + 32x3/4! + ...)
y’= 2[1+2x + (2x)2/2! + (2x)3/3! + ...] = 2 e2x
Bentuk umum turunan eksponensial: y = e f(x) y’= f ’
(x) e f(x)
II.2.1.3.Bentuk logaritma
Hubungan antara log dengan ln adalah : log x = 1/2,3[ lnx] 1. Tentukan y’ dari : y = ln x
Jawab
y = ln x ey = x
x = ey x’ = dx/dy = ey
y’= dy/dx = 1/ ey = 1/x
2. Tentukan y’ dari : y = ln x2
Jawab: y = ln x2
x2 = ey 2x dx/dy = ey
dx/dy = ey/2x
dy/dx = 2x / ey = 2x/x2 y’ = 2x/x2
3. Tentukan y’ dari : y = logx2
Jawab :
y = logx2 =1/2,3[ln x2]
y’= 1/2,3[2x/x2]
Bentuk umum turunan fungsi logaritma y = ln[f(x)] y’= f ’(x) / f(x)
Latihan
Tentukan y’ ataua dy/dx dari: 1. y = log (2x3 + x2 + x +3)
2. y = log (3x4 + 3x2+ 2x +4)4
3. y = ln(x4 + 3x3+ 2x2 +4x+2 )3
4. y = ln(x4 + 3x3+ 2x2 +4x+2 )1/2
5. y = e(5x+4)
II.2.2. Prinsip dasar diferensial fungsi Trigonometri
Ada beberapa fungsi trigonometri yang sering dijumpai pada pemakaian sehari-hari. fungsi tersebut antara lain: Sin x, Cos x, tg x dan sebagainya.
Contoh:
Dengan menggunakan prinsip bahwa:
1. Tentukan dy/dx dari : y = Sin x Jawab:
y + ∆y = y + ∆y = Sin (x +∆x) ∆y = y + ∆y – y
= Sin (x +∆x) - Sin x
2. Tentukan dy/dx dari : y = Cos x Jawab:
y + ∆y = Cos (x +∆x) ∆y = y + ∆y –y
= Cos (x +∆x) – Cos x
Latihan
Dengan menggunakan prinsip bahwa :
2. y = Cot x 3. y = Sec x 4. y = Cosec x
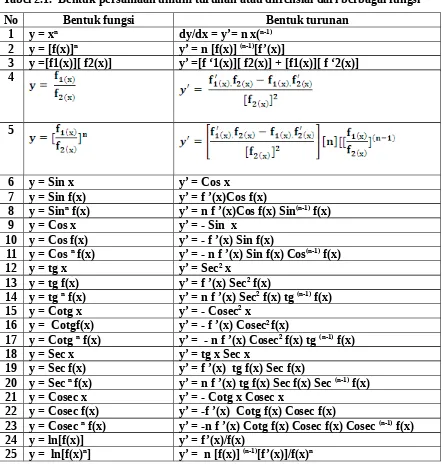
II.3. Bentuk umum diferensial fungsi aljabar dan trigonometri Dengan menggunakan prinsip bahwa :
maka bentuk diferensial dari berbagai fungsi dapat dilihat seperti pada tabel 2.1 berikut: Tabel 2.1. Bentuk persamaan umum turunan atau difrensial dari berbagai fungsi
26 y = ef(x) y’= f’(x) ef(x)
27 y = log [f(x)]=[1/2,3][lnf(x)] y’ =[1/2,3][ f’(x)/f(x)] Contoh penggunaan tabel 2.1
Tentukan y’ atau dy/dx dari: 1. y = x3
Jawab: y’ = 3 x2
2. y = (2x2 +3x +2)3
Jawab: n =3
f(x) = 2x2 +3x +2 f ’(x)= 4x +3
y’ = n [f(x)] (n-1)[f’(x)]
= 3 (2x2 +3x +2)2 (4x +3)
= (12x +9) (2x2 +3x +2)2
3. y = Sin4 (2x2 +3x +2)3 y = Sinn f(x) y’ = n f ’(x)Cos f(x) Sin(n-1) f(x)
Jawab: n =4
f(x) = (2x2 +3x +2 )3
y = [f(x)]n y’ = n [f(x)] (n-1)[f’(x)]
y = (2x2 +3x +2 )3 f(x)= 2x2 +3x +2 f ’(x)= 4x +3
f ’(x) = 3 (2x2 +3x +2)2 (4x +3) = (12x +9) (2x2 +3x +2)2
y’ = n f ’(x)Cos f(x) Sin(n-1) f(x)
= 4(12x +9) (2x2 +3x +2)2 Cos(2x2 +3x +2)3 Sin3(2x2 +3x +2)3
= (48x +36) (2x2 +3x +2)2 Cos(2x2 +3x +2)3 Sin3(2x2 +3x +2)3
4. y = e(3x +4)
f(x) = 3x +4 f ’(x)= 3
5. y = ln [(2x2 +3x +2 )3]
f(x)= [2x2 +3x +2]3 f ’(x)= 3 (2x2 +3x +2)2 (4x +3) = (12x +9) (2x2 +3x +2)2
y’ = f’(x)/f(x) = [(12x +9) (2x2 +3x +2)2 ] / [ 2x2 +3x +2]3
6. y = log [(2x2 +3x +2 )3] = [1/2,3] ln [(2x2 +3x +2 )3]
y’ = f’(x)/f(x) = [1/2,3] [(12x +9) (2x2 +3x +2)2 ] / [ 2x2 +3x +2]3
7. y = [Sin4 (2x2 +3x +2)3][ln [(2x2 +3x +2 )3]
f1(x) = Sin4 (2x2 +3x +2)3
f ‘
1(x) = 4(12x +9) (2x2 +3x +2)2 Cos(2x2 +3x +2)3 Sin3(2x2 +3x +2)3
f 2(x) = ln [(2x2 +3x +2 )3
f ‘
2(x) = [(12x +9) (2x2 +3x +2)2 ] / [ 2x2 +3x +2]3
y’ =[f ‘1(x)][ f2(x)] + [f1(x)][ f ‘2(x)]
=[4(12x +9) (2x2 +3x +2)2 Cos(2x2 +3x +2)3 Sin3(2x2 +3x +2)3][ln [(2x2 +3x +2 )3]
+ [Sin4 (2x2 +3x +2)3][(12x +9) (2x2 +3x +2)2 ] / [ 2x2 +3x +2]3
8. y = [ e(3x +4)]/[ (2x2 +3x +2)3]
f1(x) = e(3x +4) f1 ‘(x) = 3e(3x +4)
f2(x) = (2x2 +3x +2)3 f2 ‘(x) = 3(2x2 +3x +2)2 (4x +3)
=[{3e(3x +4)}{(2x2 +3x +2)3}- {e(3x +4)}{3(2x2 +3x +2)2 (4x +3)}]/[(2x2 +3x +2)3]2
=[{3e(3x +4)}{(2x2 +3x +2)3}- {e(3x +4)}{3(2x2 +3x +2)2 (4x +3)}]/[(2x2 +3x +2)6]
Latihan
Dengan menggunakan tabel 2.1, tentukan y’ dari:
2. y = (x2- 4x +3) tg(2x+4)
3. y = Cos[(x2- 4x +3)/{ 2x2 +3x +2)3}]
Petunjuk soal no 3: f1(x) =(x2- 4x +3)
f2(x) = (2x2 +3x +2)3
II.4. Diferensial fungsi invers trigonometri Contoh:
1. Tentukan diferensial (turunan) dari y = arc Sin 2x Jawab:
y = arc Sin 2x 2x = Sin y
x = ½ Sin y
dx/dy = ½ Cos y dy/dx = 2/Cos y
Cos y = √1 – 4x2
1 1 dy/dx = 2/Cos y = 2/√1 – 4x2
2x Bentuk umum:
y = arc Sin f(x) dy/dx = f’(x)/√1 – [f(x)]2
√ 1 – 4x2
2. Tentukan diferensial (turunan) dari y = arc Cos 2x Jawab:
y = arc Cos 2x 2x = Cos y
x = ½ Cos y
dx/dy = - ½ Sin y dy/dx = -2/Sin y
Sin y = √1 – 4x2
√ 1 - 4x2 1 1 dy/dx = - 2/Sin y = - 2/√1 – 4x2
Bentuk umum:
y = arc Cos f(x) dy/dx = - f’(x)/√1 – [f(x)]2
y
2x
3. Tentukan diferensial (turunan) dari y = arc tg 2x Jawab:
y = arc tg 2x 2x = tg y
x = ½ tg y
dx/dy = ½ Sec2 y dy/dx = 2/Sec2 y = 2 Cos2 y
Cos y = 1/√1 + 4x2 Cos2 y = 1/(1 + 4x2)
2x √1 + 4x2 dy/dx = 2 Cos2 y = 2/(1 + 4x2)
Bentuk umum:
y = arc tg f(x) dy/dx = f’(x)/[1 + f(x)2]
1
Latihan
Tentukan dy/dx dari: 1. y = arc Cotg 3x 2. y = arc Sec 4x 3. y = arc Cosec 5x
II.5. Prinsip diferensial parsial
Diferensial parsial biasanya dipakai untuk menurunkan atau mendiferensialkan suatu fungsi yang mempunyai perubah bebas minimum 2. Dalam hal ini variabel yang tidak didiferensialkan dianggap tetap sehingga dapat dikeluakan dari tanda diferensial.
Misal:
m = f(x,y,z), dengan variabel bebas x,y,z
maka bentuk diferensial dari fungsi tersebut dapat dituliskan sebagai berikut:
II.5.1.Diferensial parsial fungsi aljabar Contoh:
m = x y2 z3, tentukan harga dari:
Jawab:
II.5.2. Diferensial parsial fungsi trigonometri m = y2 Sin x Cosz, tentukan harga dari:
Jawab:
II.6. Turunan fungsi implisit
Perbedaan cara penulisan antara fungsi implisist dan eksplisit:
y = 2x +4 Fungsi eksplisit
2xy +y+ x2y = 4x Fungsi implisit
Contoh:
1. Tentukan dy/dx atau y’ dari : 2xy +y+ x2y = 4x
Jawab:
d/dx{2xy +y+ x2y }=d/dx( 4x)
y d/dx (2x) + 2x d/dx(y) + d/dx(y) + y d/dx ( x2) + x2d/dx (y) = 4
y (2) + 2x dy/dx + dy/dx + 2xy + x2dy/dx = 4
dy/dx[ 2x + 1 + x2] = 4 – 2y - 2xy
dy/dx = [4 – 2y - 2xy] /[ 2x + 1 + x2]
2. Tentukan dy/dx atau y’ dari : 2x + y3 + xy2 = x2
Jawab:
d/dx [2x + y3 + xy2 ]= d/dx[x2]
d/dx (2x) + d/dx(y3) + d/dx(xy2)= d/dx[x2]
2 + d/dx(y2.y) + y2d/dx (x) + x d/dx (y2) = 2x
2 + y2 d/dx(y) + yd/dx(y2) + y2d/dx (x) + x d/dx (y.y) = 2x
2 + y2 dy/dx + yd/dx(y.y) + y2 + x [yd/dx (y) + yd/dx (y)] = 2x
2 + y2 dy/dx + y[y d/dx(y) + y d/dx(y) ] + y2 + x [ 2ydy/dx ] = 2x
2 + y2 dy/dx + 2y2 dy/dx + y2 + 2x ydy/dx = 2x
2 + 3y2 dy/dx + y2 + 2x ydy/dx = 2x
dy/dx [ 3y2 + 2xy ] = 2x -2 - y2
dy/dx = [2x -2 - y2] / [ 3y2 + 2xy ]
Catatan:
d( yn) /dx = n y(n-1)dy/dx
Latihan
Tentukan y’ atau dy/dx dari: 1. 2xy + x3y3 + x2 y2 = x2
2. x4 + y4 + 4xy2 = x2 y4
II.7. Tugas
A. Tentukan y’ dari:
1. y = [ tg( x4+4)5] /[Cosec(x2- 4x +3)
2. y = Sin2( 3x+2) Cotg(x4+ 3x2+3x+3)
4. y = [ ln( x4+4)5] /[log(x2- 4x +3)
Untuk menentukan harga variabel bebas dalam suatu fungsi , maka harga turunan pertama dari fungsi tersebut harus berharga nol (0). Untuk menguji sutu fungsi apakah fungsi tersebut berharga maksimum atau minimum, maka harus dilihat pada harga turunan kedunya pada saat variabel yang diperoleh dari turunan pertma dimasukkan ke dalam turunan kedua dari funhsi tersebut. Ada dua kemungkinan yang terjadi pada saat harga variabel tersebut dimasukkkan dalam turunan kedua, yaitu:
a. Jika harga turunan adalah negatip atau kurang dari nol (0), maka fungsi mempunyai harga maksimum
b. Jika harga turunan adalah positip atau lebih dari nol (0), maka fungsi mempunyai harga minimum
Contoh
1. Sebuah bejana berbentuk kotak persegi bagian atas terbuka dan bagian bawah tertutup.
Bejana diisi penuh dengan cairan sebanyak 216 m3. Alas bejana berbentuk bujur sangkar
dan dinding berbentuk persegi panjang. Biaya pembuatan alas Rp 5000; per m2 dan
dinding Rp2.500; per m2.Tentukan ukuran bejana yang paling ekonomis, sehingga
maksud pembuatan tercapai sesuai rencana. Jawab:
31
Volume bejana = V = Luas alas x tinggi 216 = (x)(x)(y)
216 = x2y
y =216/x2 ...(1)
Biaya alas = 5.000(x)(x)= 5000 x2
Biaya total dinding = 4(x)(y)(2.500) = 10.000xy Biaya total pembuatan bejana= 5000 x2+10.000xy
H = 5000 x2+10.000xy ... (2)
x .
H = 5000 x2+10.000xy
= 5000x2+10.000x(216/x2)
=5000x2 + 2.160.000 /x ...(3)
dH/dx = 10.000 x - 2.160.000 /x2
dH/dx = 0 10.000 x - 2.160.000 /x2 = 0
10.000 x = 2.160.000 /x2 x3 = 216
x = 6 dan y =216/x2 = 216/36 = 6
d 2H/dx2 = d/dx (10.000 x - 2.160.000 /x2) =10.000 +4.320.000/x3
= 10.000 +4.320.000/x3 = 10.000 +4.320.000/216 = 10.000+20.000 = 30.000
Dengn demikian d 2H/dx2 > 0 memenuhi syarat minimasi
Jadi x = y = 6 bejana berbentuk kubus dengan panjang sisi-sisi 6 m
6cm
6 cm
2. Tentukan ukuran dari silinder lingkaran tegak dengan luas selimut maksimum yang dapat dilukis pada sebuah bola dengan jari-jari 20 cm
Jawab:
Artinya d2A/dr2 = 0 tidak bisa dipakai untuk evaluasi harga maksimum atau
minimum fungsi. Untuk mengatasi persoalan tersebut, maka diasumsikan bahwa harga h dianggap konstan atau tetap.
Dengan demikian: dA/dr = -8IIr2/h + 2IIh
d2A/dr2 = - 16IIr/h
= -16II(h/2)/h = - 8 II
Artinya d2A/dr2 < 0 atau d2A/dr2 berharga negatip (memenuhi syarat untuk harga
maksimum).
Dari persamaan (1): 400 = ¼ h2 + r2
¼ h2 + r2 = 400
¼ h2 + [(1/2)h]2 = 400
¼ h2 + ¼ h2 = 400
½(h2) = 400
h2 = 800
h = 20√2 cm dan r = ½(h) = 10√2 cm
Latihan
1. Tentukan jari-jari R dari kerucut ingkaran tegak dengan volume maksimum yang dapat dilukiskan dalam sebuh bola dengan jari-jari r (kunci R= 2/3 (r√2).
2. Sebuah silinder lingkaran tegak dilukiskan di dalam sebuah kerucut lingkaran tegak dengan jari-jari r. Bila volume silinder maksimum, maka tentukan jari-jari R silinder [kunci R = 2/3(r)]
3. Sebuah bejana (tabung) yang tertutup rapat berisi cairan setengahnya.Bentuk tabung adalah silinder tegak dengan biaya pembuatan dinding Rp 10.000; per m2 dan tutup Rp
5.000; per m2. Bila dikehendaki tabung tersebut diisi penuh dapat menampung cairan
1000 m3, maka tentukan ukuran ekonomis tabung tersebut.
II.9. Aplikasi turunan (diferensial) parsial Contoh:
Bila D = xy2 z5 a
x + x3 y2 z5 ay + x3 y2 z5 az
Tentukan ρv pada A (1,2,3)
Jawab: Dx = x y2 z5
Dy =x3 y2 z5
Dz =x3 y2 z5
= y2 z5
= 2 y x3 z5
= 5z4 x3 y2
= y2 z5 + 2 y x3 z5 + 5z4 x3 y2
= (22)(35) + 2(2)(1)( 35) +5 (34)(1)(22) = 3564 [C/m3]
Persamaan untuk medan listrik ( E ) dinyatakan sebagai: E= - V, dengan:Tentukan medan listrik pada A(1,2,3), jika diketahui bahwa medan potensial (V) dinyatakan sebagai V = 50 x2yz + 20 y2 [Volt]
Jawab:
∂V/∂x = ∂/∂x (50 x2yz + 20 y2) = 50 yz d/dx (x2) + 20 y2d/dx (1)= 100xyz + 0
= 100xyz
∂V/∂y= ∂/∂y (50 x2yz + 20 y2) = 50 x2z dy/dy + 20d(y2)/dy = 50 x2z + 40 y
∂V/∂y= ∂/∂y (50 x2yz + 20 y2) = 50 x2y dz/dz + 20 y2 d(1)/dz = 50 x2y
E = - (100xyz ax + (50 x2z + 40 y) ay + 50 x2y) az
EA = -[100(1)(2)(3) ax + [50(12)(3) + 40(2)] ay + 50 (12)(2)] az
= - 600 ax - 230 ay - 100 az [V/m]
Latihan
1. Kerapatan muatan ruang dinyatakan sebagai:
Bila D = xy2 ln(z5 ) a
x + e3x y2 z5 ay + x2 y3 z4 az
Tentukan ρv pada A (2,4,6)
Persamaan untuk medan listrik ( E ) dinyatakan sebagai: E= - V, dengan:Tentukan medan listrik pada A(1,2,3), jika diketahui bahwa medan potensial (V) dinyatakan sebagai V = 50 ln(x2 ) y z + 20 x z3 y2 [Volt]
II.10. Daftar Pustaka
Kreyzig, E., 1979. Advenced Engineering Mathematics. 4nd, John Willey and Sons, New York. pp. 249-468,509-560,563-590
Mundit,A.K., 1984. Soal- Penyelesaian Kalkulus Deferensial dan Integral.Jilid I, Armico, Bandung. hal. 37-238, 305-433
BAB III. PANGKAT
III.1. PendahuluanDalam kehidupan sehari-hari sering kita berhadapan dengan suatu angka yang nilainya sangat besar. Misal tabungan seseorang dalam suatau bank nilainya 1 milyar rupiah atau kalau dituliskan dengan angka, maka nialainya adalah Rp1.000.000.000;. Dalam bidang matematika atau keteknikan cara penulisan seperti ini cukup panjang, menyulitkan dan banyak memakan tempat. Untuk menghindari kesulitan-kesulitan tersebut dibutuhkan alaternatif lain. Salah satu cara penulisan yang cukup sederhana adalah dengan menuliskan dalam bentuk pangkat. Angka 1.000.000.000 tersebut dalam bentuk pangkat dapat dituliskan sebagai 10 9. Dalam hal ini 10 disebut bilangan pokok, sedangkan 9
disebut bilangan pangkat. Karena pangkatnya bilangan bulat, maka disebut bilangan berpangkat bilangan bulat. Pada bab III ini akan dibahas secara rinci tentang bentuk-bentuk pangkat dan cara penghitungannya.
III.2. Pengelompokan pangkat
Berdasarkan tanda operasionalnya pangkat dapat dikelompokkan menjadi pangkat positip dan negatip. Sedangkan berdasarkan nilainya pangkat dikelompokkan menjadi pangkat bulat, pecah , nol dan tak tentu (∞)
III. 2.1. Pangkat bulat
III. 2.1.1. Pangkat bulat dan positip
Dalam kehidupan sehari-hari kita sering menemui perkalian bilangan-bilangan dengan faktor-faktor yang sama. Misalkan kita temui perkalian bilangan-bilangan sebagai berikut:
a. 2 x 2 x 2 = 8
b. 3 x 3 x 3 x 3 x 3 = 243
c. 4 x 4 x 4 x 4 x 4 x 4 = 4.096
Perkalian bilangan-bilangan dengan faktor-faktor yang sama seperti di atas, disebut sebagai perkalian berulang. Setiap perkalian berulang dapat dituliskan secara ringkas dengan menggunakan notasi bilangan berpangkat. Perkalian bilangan-bilangan di atas dapat kita tuliskan dengan:
a. 2 x 2 x 2 = 23
b. 3 x 3 x 3 x 3 x3 = 35
c. 4 x 4 x 4 x 4 x 4 x 4 = 46
Bilangan 23, 35, 46 disebut bilangan berpangkat sebenarnya (riil) karena
bilangan-bilangan tersebut dapat dinyatakan dalam bentuk perkalian berulang. Bilangan berpangkat an dengan n bilangan bulat positif didefinisikan sebagai berikut:
an = a x a x a...x a ...(1)
Berdasarkan persamaan (1) tersebut dapat diturunkan berbagai rumusan atau formulasi sebagai berikut:
an am = a n +.m ... (2)
(an)m = a n . m ... (3)
(a.b)n = an .bn ... (4)
(a/b)n = an / bn,dengan b≠0 ... (5)
(am/an) = am–n,denga m > n dan a ≠ 0 ... (6)
Contoh
1. 22 .23 = 4 . 8 = 32 atau 22 23 = 25 = 32
2. (22 )3 = 43 = 64 atau (22 )3 = 26 = 64
3. (2.2)3 = 43 = 64 atau (2.2)3 = 23 .2 3 = 8.8 = 64
4. (4/2)3 = (2)3 = 8 atau (43/23) = 64/8 = 8
5. (23/22)= (8/4) = 2 atau (23/22)= 2(3 – 2) = 2
1. 32 .63 4. (8/5)3 6. (3.4)4
2. (92 )3 5. (43/32) 7. (-34/ 43)
III. 2.1.2. Pangkat bulat dan negatip Dari bentuk perkalian :
a. 2 x 2 x 2 = 8
b. 3 x 3 x 3 x 3 x 3 = 243
c. 4 x 4 x 4 x 4 x 4 x 4 = 4.096
Dikembangkan menjadi bentuk pangkat negatip sebagai berikut :
a. 2-1 x 2-1 x 2-1 = ½ x ½ x ½ = 1/(23)= 1/8
b. 3-1 x 3-1 x 3-1 x 3-1 x 3-1 = 1/3x1/3x1/3x1/3x1/3 = 1/(35) = 1/243
c. 4-1 x 4-1 x 4-1 x 4-1 x 4-1 x 4-1 = 1/4x1/4x1/4x1/4x1/4x1/4=1/(46) =1/4096
Atau kalau menggunakan persamaan (2), maka dapat dituliskan sebagai:
a. 2-1 x 2-1 x 2-1 = 2 (-1-1-1) = 2 -3 = 1/8
b. 3-1 x 3-1 x 3-1 x 3-1 x 3-1 = 3 -5 = 1/243
c.4-1 x 4-1 x 4-1 x 4-1 x 4-1 x 4-1 = 4- 6 =1/4096
Berdasarkan dari uraian tersebut dapat disimpulkan bahwa:
1/(23) = 2 -3
1/(35) = 3 -5
1/(46) = 4- 6
Bila dinyatakan secara umum,maka bentuk pangkat bulat dan negatip dapat dituliskan sebagai:
(1/an ) = a – n , dengan a ≠ 0 …..………(7)
Latihan
Tentukan harga:
1. 1/( 34) 4. 5(-3)
2. 1/( -34) 5. -34/ (4 -3)
3. (-5) -5 6. (3.4)-5
Berdasarkan persamaan (7) tersebut dapat diturunkan berbagai rumusan atau formulasi sebagai berikut:
a-n .a-m = a - (n +.m) ... (8)
a-n .a m = a (- n +.m) ... (9)
an a-m = a (n -.m) ... (10)
(an) -m = a[(n)(- m)] ... (11)
(a-n) -m = a[(-n)(- m)] ... (12)
(a-n) m = a[(-n)( m)] ... .. (13)
(a.b)-n = a-n .b-n ... (14)
(a/b) -n = a-n / b-n,dengan b ≠ 0 ... (15)
(a-m/an) = a(-m–n),dengan a ≠ 0 ... (16)
(a-m/a-n) = a(-m + n),dengan a ≠ 0 ... (17)
Contoh
1. 2-2 2-3 = 1/4 .1/ 8 =1/ 32 atau 2-2 2-3 = 2 -5 = 1/32
2. (22 ) -3 = 4-3 = 1/64 atau (22 )-3 = 2 - 6 = 1/64
3. (2.2)-3 = 4-3 = 1/64 atau (2.2) -3 = (2-3 )(2 -3 ) = (1/8)(1/8) = 1/64
4. (4/2) -3 = (2) -3 = 1/8 atau (4 -3/2 -3) = (1/64) / (1/8) = 8/64 =1/8
5. (2 -3/2 -2)= (1/8) / (1/4) = 4/8 =1/2 atau (2 -3/2 -2)= 2(-3 + 2) = 2-1=1/2
III. 2.2. Pangkat pecah
III. 2.2.1. Pangkat pecah positip Dari bentuk perkalian :
a. 4 x 4 x 4 = 64
c. 16 x 16 x 16 x 16 x 16 = 1.048.576
Dikembangkan menjadi bentuk pangkat pecahan sebagai berikut:
a. 41/ 2 x 4 1/ 2 x 4 1/ 2 = √4 x √4 x √4 = 2 x 2 x 2= 8
b. 91/2 x 91/2 x 91/2 x 91/2 = √9 x √9 x √9 x √9 = 3 x 3 x 3 x3 =81
c. 161/2 x 161/2 x 161/2 x 161/2 x 161/2 = √16 x √16 x √16 x √16 x √16 =
4 x 4 x 4 x 4 x 4 = 1024
Atau dapat dituliskan pula sebagai:
a. 41/ 2 x 4 1/ 2 x 4 1/ 2 = 4(1/ 2+1/2+1/2) = 4 3/ 2 =√43 = √64 = 8
b. 91/2 x 91/2 x 91/2 x 91/2 = 9(1/ 2+1/2+1/2 +1/2) = 92 = 81
c. 161/2 x 161/2 x 161/2 x 161/2 x 161/2 = 16(1/ 2+1/2+1/2+1/2+1/2) =165/2 =√165 = 1024
Dengan demikian dapat dikatakan bahwa:
a. 41/ 2 x 4 1/ 2 x 4 1/ 2 = 4 3/ 2 = √43 = 8
b. 91/2 x 91/2 x 91/2 x 91/2 = 94/2 = 92 =81
c. 161/2 x 161/2 x 161/2 x 161/2 x 161/2 = 165/2 = √165 = 1024
Dapat disimpulkan bahwa :
Latihan
Tentukan harga dari 1. 41/ 2 x 9 1/4 x 31/ 3
2. 4 2 x 9 1/2 x 62/ 3
3. 8 2/3 x 10 1/2 x 52/ 3
4. 9 2 x 6 1/2 x 162/ 3
III. 2.2.2. Pangkat pecah negatip Dari bentuk perkalian :
a. 4 x 4 x 4 = 64
b. 9 x 9 x 9 x 9 = 6.561
c. 16 x 16 x 16 x 16 x 16 = 1.048.576
Dikembangkan menjadi bentuk:
a. 4-1/ 2 x 4 -1/ 2 x 4 -1/ 2 = 1/41/ 2 x 1/ 4 -1/ 2 x 1/4 -1/ 2 =1/√4 x 1/√4 x 1/√4 =
1/2 x 1/2 x 1/2 = 1/8
b. 9-1/2 x 9-1/2 x 9-1/2 x 9-1/2 = 1/91/2 x 1/91/2 x 1/91/2 x 1/91/2 =
1/√9 x 1/√9 x 1/√9 x 1/√9 = 1/3 x 1/3 x 1/3 x 1/3 = 1/81
c. 16-1/2 x 16-1/2 x 16-1/2 x 16-1/2 x 16-1/2 =
1/161/2 x 1/161/2 x 1/161/2 x 1/161/2 x 1/161/2 =
1/√16 x 1/√16 x 1/√16 x 1/√16 x 1/√16 =
1/4 x 1/4 x 1/4 x 1/4 x 1/4 = 1/1024
Atau dapat dituliskan pula sebagai:
a. 4-1/ 2 x 4 -1/ 2 x 4 -1/ 2 = 4(-1/ 2-1/2-1/2) = 4 -3/ 2 =1/√43 = 1/√64 = 1/8
b. 9-1/2 x 9-1/2 x 9-1/2 x 9-1/2 = 9 (-1/ 2-1/2-1/2 -1/2) = 1/92 = 1/81
c. 16-1/2 x 16-1/2 x 16-1/2 x 16-1/2 x 16-1/2 = 16 (-1/ 2-1/2-1/2-1/2-1/2) =16-5/2 =1/√165 = 1/1024
Dengan demikian dapat dikatakan bahwa:
a. 4-1/ 2 x 4 -1/ 2 x 4 -1/ 2 41/ 2 x 4 1/ 2 x 4 1/ 2 = 4 -3/ 2 =1/√43 = 1/√64 =1/84 3/ 2 = 1/√43 =1/ 8
b. 9-1/2 x 9-1/2 x 9-1/2 x 9-1/2 = 9 (-1/ 2-1/2-1/2 -1/2) = 1/92 = 1/81
c. 16-1/2 x 16-1/2 x 16-1/2 x 16-1/2 x 16-1/2 = 16 (-1/ 2-1/2-1/2-1/2-1/2) =16-5/2 = 1/165/2
= 1/√165 = 1/ 1024
Latihan
Tentukana harga dari:
1. 4-1/ 2 x 9 -1/4 x 3-1/ 3
2. 4 - 2 x 9 1/2 x 6 -2/ 3
3. 8 - 2/3 x 10 1/2 x 5 -2/ 3
III. 2.3. Pangkat nol
III. 2.3.1. Pangkat nol positip Dari bentuk perkalian :
a. 4 x 4 x 4 = 64
b. 9 x 9 x 9 x 9 = 6.561
c. 16 x 16 x 16 x 16 x 16 = 1.048.576
Dikembangkan menjadi bentuk:
a. 4 0 x 4 0 x 4 0 = 1 x 1 x 1=1
b. 9 0 x 9 0 x 9 0 x 9 0 = 1 x 1 x 1 x 1 = 1
c. 16 0 x 16 0 x 16 0 x 16 0 x 16 0 = 1 x 1 x 1 x 1 x 1 = 1
III. 2.3.2. Pangkat nol negatip Dari bentuk perkalian :
a. 4 x 4 x 4 = 64
b. 9 x 9 x 9 x 9 = 6.561
c. 16 x 16 x 16 x 16 x 16 = 1.048.576
Dikembangkan menjadi bentuk:
a. 4 - 0 x 4 - 0 x 4 - 0 = 1/40 x 1/40 x 1/40 =1/1 x 1/1 x 1/1 =1
b. 9 - 0 x 9 - 0 x 9 - 0 x 9 - 0 = 1/90 x 1/90 x 1/90 x 1/90 =1/1 x 1/1 x 1/1x1/1 =1
c. 16 - 0 x 16 - 0 x 16 - 0 x 16 - 0 x 16 - 0 = 1/160 x 1/160 x 1/160 x 1/160 x 1/16
= 1 x 1 x 1 x 1 x 1 = 1
Kesimpulan:
a 0 = a – 0 = 1 ...(22)
III. 2.4. Pangkat tak terhingga (tak tentu )
III. 2.4.1. Pangkat tak terhingga (tak tentu ) positip ( + ∞ )
Harga + ∞ berarti harga tersebut sangat besar sekali dan positip. Dari bentuk perkalian :
a. 2+∞ = 2 x 2 x 2 x ... x 2 = besar sekali = ∞
b. 9 +∞ x 9 +∞ = ∞ x ∞ = ∞
Tetapi untuk 1+∞ = 1x1x1x ….x1= 1
Dapat disimpulkan bahwa :
a∞ = ∞, dengan a ≠ 0 dan a >1 ………(23)
Jika -1< a < 1 dan a ≠ 0, maka :
a∞ = kecil atau kecil sekali, sehingga a∞ = 0,00000…….≈ 0 …………(24)
Jika a < -1, maka :
│a∞│= besar atau besar sekali, sehingga a∞ ≈ ∞ ………(25)
III. 2.4.2. Pangkat tak terhingga (tak tentu ) negatip ( - ∞ ) Harga - ∞ berarti harga tersebut besar sekali dan negatip. Dari bentuk perkalian :
a. 2 - ∞ = 1/2∞ = 1/2 x 1/2 x ... x 1/2 = 0,0000000... = kecil sekali ≈0
b. 2 -∞ x 2 - ∞ = 0 x 0 = 0
Tetapi untuk 1- ∞ = 1x1x1x ….x1= 1
a-∞ = 0, dengan a ≠ 1 ………(26)
Jika -1< a < 1, maka :
│ a- ∞│= kecil atau kecil sekali, sehingga boleh didekati ≈ 0 …………(27)
Contoh soal komprehensip:
1. Tentukan harga dari: 3-3 x 1/ 8-3 x 92/3
Jawab:
2. Tentukan harga dari : 4-1/3 x 1/ 8-3/2 x 9-3/4
Jawab:
0.19245 = 6,92
3. Tentukan harga dari: 8-1/3 x 1/6 -3/2 x 5 -2/3
Jawab:
0.37 x 108 x0,34 = 13,59
4. Tentukan harga dari : 4- ∞ x 1/ 8- ∞ x 9-3/4
Jawab:
4- ∞ x 1/ 8 - ∞ x 9-3/4 = 1/4∞ x 8 ∞ x 1/ 93/4
= 0 x ∞ x 1/ 93/4 = 0
5. Tentukan harga dari : 1- ∞ x 1/ 8- ∞ x 9-3/4
Jawab:
1- ∞ x 1/ 8 - ∞ x 9-3/4 = 1/ 1 ∞ x x 8 ∞ x 1/ 93/4 = 1 x ∞ x 9-3/4 = ∞
Tugas
Tentukan harga dari : 1. 8-1/3 x 1/ 2-3/2 x 100 -5/4
2. 8-1/3 x 1/6 -3/2 x 5 -2/3
3. 3- ∞ x 8 ∞ x 9-3/4
4. 6 ∞ x 1/ 8 - ∞ x 4-3/4
5. 16 1/3 x 1/(4 -3/2 ) x 9 -2/3
6. 16 1/3 x 1/4 - 0 x 9 0
7. 3- 0 x 8 ∞ x 9-3/4
8. (2 -3/2 -2) x (2.2)-3x (4/2) -3
Kunci jawaban 1. 0.004472 2. 2.513141 3. 0
4. ∞
5. 4.659095812
6. 16 1/3
7. ∞
8. 0.000977
Daftar Pustaka:
BAB IV. AKAR
IV.1. Pendahuluan
Akar merupakan pernyataan lain dari pangkat dalam bentuk pecahan baik positip atau negatip dari suatu bilangan, dimana bilangan tersebut harus berharga positip dan tidak boleh berharga nol. Bila bilangan tersebut berharga nol, maka hasil pengakaran adalah nol juga. Sedangkan kalau bilangan tersebut berharga negatip, maka akan dihasilkan bilangan khayal atau imajiner yang membutuhkan pembahasan khusus atau tersendiri. Oleh karena itu pada bagian pembahasan akar ini hanya akan dibatasi dulu pada hasil yang nyata atau riil saja. Dengan demikian sebenarnya hasil perhitungan menggunakan pangkat pecahan dan akar bisa saling bertukar tempat, karena hasil perhitungan baik dengan menggunakan bentuk akar atau bentuk pangkat pecahan dari suatau bilangan akan menghsilkan suatu harga yang sama saja.
IV.2. Pernyataan bentuk akar
Secara umum bentuk akar dapat dinyatakan sebagai:
... (1)
dengan:
n = indeks atau ordo dan berharga positip dan untuk n=2 biasanya tidak pernah dituliskan
a= bilangan yang diakar dan berharga positip
Hubungan antara akar dengan bentuk pangkat pecahan dapat dinyatakan sebagai berikut
= ...(2)
Contoh:
1. Tentukan harga dari:
Jawab : = 3
Dengan perhitungan secara manual menggunakan alat hitung didapat bahwa 91/2 = 3
Oleh karena itu = 91/2 = 3
2. Tentukan harga dari:
Jawab:
= 2.666667 (dihitung dengan kalkulator)
Dengan menggunakan alat hitung (komputer) didapat bahwa:
8
1/2= 2.666667
Oleh karena itu
=
8
1/2=
2.666667
IV.3. Sifat - sifat akar
Beberapa sifat akar antara lain:
a.
b.
c.
d.
=
e.
=
Contoh:
1.
Tentukan harga dari : Jawab:Bila dihitung dengan kalkulator harga dari : = ( 1.587401)3 = 4
Dengan demikian : = 43/3
= 41 = (1.587401)3 = 4
2.
Tentukan harga dari :Jawab:
(1.44225)( 1.587401) = 2.289429
Atau dengan cara lain :
3.
Tentukan harga dari :Jawab:Dengan menggunakan cara lain dapat pula dihitung sebagai berikut:
0.829827
4.
Tentukan harga dari :Jawab
Atau dengan cara lain dapat pula dihitung sebagai berikut:
5.
Tentukan harga dari : Jawab:Dengan cara lain dapat pula dihitung sebagai berikut:
6.
Tentukan harga dari :1,090508
Dengan cara lain dapat pula diselesaikan sebagai berikut:
1,090508
Latihan
Tentukan harga dari:
a.
b.
c.
d. e.
IV.4. Akar dari bilangan negatip
Untuk menyelesaikan akar dari suatu bilangan negatip bisa digunakan sifat dari akar
seperti yang ditunjukkan dalam bentuk
Contoh
Catatan:
pada perhitungan rangkaian listrik arus bolak-balik (AC). Contoh pernytaan bilanag kompleks adalah Z = 2 + 3j atau Z = 2 + 3i.
Latihan
Tentukan hasil dari : dan
Catatan:
Tugas
Tentukan harga dari
a. +
b.
c.
d.
+
+
Kunci jawaban a. 1.84917 b. 0.210731 c. 26.62187 d. 9.103802
e. 1.84917 + 2.828427 j
Daftar Pustaka:
…….., 1982. Aljabar Semester 1 dan 2. Edisi pertama, Departemen Elekteronik Politeknik, TEDC, Bandung. Hal. 22-29
BAB V. PERSAMAAN NON LINIER
V.1. PendahuluanPersamaan nojn linier adalah suatu persamaan polynomial dengan orde dua atau lebih. Jika orde tersebut berharga dua, maka disebut persaman kuadrat. Sedangkan menurut jenisnya persamaan non linier dapat dikelompokkan menjadi persamaan kuadrat, persamaan eksponensial dan sebaginya.
V.2. Persamaan kuadrat
Persamaan kuadrat adalah suatu persamaan polinomial berorde dua. Bentuk umum dari persamaan kuadrat adalah
……….(1)
dengan:
Huruf-huruf a, b dan c disebut sebagai koefisien. Dalam hal ini koefisien kuadrat a adalah
koefisien dari
x
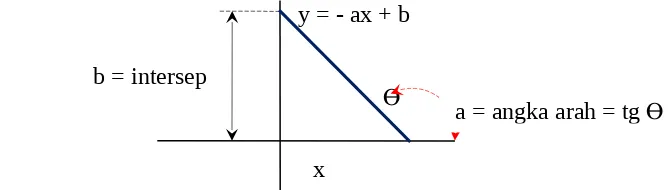
2, koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.V.3. Grafik atau kurva persamaan kuadrat
Gambar 1. Kurva dari variasi a
Gambar 2. Kurva
dari variasi b Gambar 3. Kurva dari variasi c
Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.Harga a menentukan tingkat kecekungan atau kecembungan parabola yang dibentuk oleh fungsi kuadrat, seperti ditunjukkan pada gambar 1. Nilai a > 0 akan menyebabkan parabola terbuka ke atas, sedangkan nilai a < 0 akan menyebabkan parabola terbuka ke bawah. Harga b menentukan kira-kira posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk, seperti terlihat pada gambar 2. Posisi tepatnya adalah -b/2a. Harga c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau saat x = 0, seperti terlihat pada gambar 3. .
V.4. Menghitung harga akar-akar persamaan kuadrat
V.4.1. Menghitung dengan rumus kuadrat
Rumus kuadrat dikenal pula dengan nama rumus abc karena digunakan untuk akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b dan c dari suatu persamaan kuadrat. Jika persamaan kuadrat tersebut dinyatakan seperti pada persamaan (1) , yaitu:
.
Maka rumus yang dimaksud adalah:
………(2)
Persamaan ( 2 ) hanya dapat digunakan untuk mencari akar-akar persamaan kuadrat apabila harga y pada persamaan (1) adalah nol (0) atau y = 0 . Pada kondisi ini persamaan berubah menjadi:
………(3)
Contoh:
Tentukan harga akar-akar dari persamaan: 0,75x2 – 2x -15 = 0
Jawab:
V.4.2. Menghitung akar dengan cara memfaktorkan
Berdasarkan rumus pada persaman (2) akan diperoleh akar-akar persamaan, sehingga persamaan semula yang dinyatakan dalam bentuk:
..
dapat dituliskan menjadi :
...………...(5)
Pada harga y = 0, maka persamaan (5) dapat dinyatakan sebagai:
0 = a(x - x1)(x - x2)
atau (x - x1)(x - x2) = 0 dengan x1 dan x2 adalah harga akar-akar dari persamaan hasil
pemfaktoran.
Dari persamaan (5) dapat pula dituliskan dua hubungan yang telah umum dikenal, bahwa:
………(6)
dan
. ………...(7)
Contoh:
Tentukan harga akar-akar dari persamaan: y = 0,75x2 – 2x -15
Dengan menggunakan bantuan kurva atau grafik persamaan tersebut dapat dinyatakan sebagai berikut:
Gambar 4. Ilustrasi penerapan persamaan y = 0,75x2 – 2x -15
Berdasarkan gambar 4, dapat dilhat bahwa harga akar – akar dari persamaan pada saat y = 0 adalah x1 = -3,333 dan x2 = 6. Harga akar-akar tersebut ternyata sama dengan harga
akar-akar yang dihasilkan dengan rumus a,b,c. Jika digunakan cara pemfaktoran, maka persamaan y = 0,75x2 – 2x -15 dapat dinyatakan sebagai: y = 0.75 (x + 3,333) (x –
6,000). Selanjutnya untuk mencari akar-akar persamaan dari y = 0.75 (x + 3,333) (x – 6,000), diubah terlebih dahulu menjadi:
0 = 0.75 (x + 3,333) (x – 6,000) atau
0.75 (x + 3,333) (x – 6,000) = 0 (x + 3,333) (x – 6,000) = 0 (x + 3,333) = 0 x1 = -3,333
(x – 6,000) = 0 x2 = 6,000
Pengujian hasil hitungan menggunakan persamaan (6) dan (7), yaitu:
.
Dengan x1 = -3,333 dan x2 = 6,000, maka:
x1+ x2 = -3,333 + 6,000 = 2,667= 2,67 (sama dengan hasil hitungan dengan persamaan
6)
x1. x2 = (-3,333)( 6,000) = -19,998= -20 (sama dengan hasil hitungan dengan persamaan
7). Dengan demikian didapat bahwa x1 = -3,333 dan x2 = 6,000
V.5. Diskriminan atau determinan
Dalam rumus kuadrat seperti disebutkan pada persamaan (2) tertulis suatu harga yang berada dalam naungan tanda akar. Harga yang dimaksud adalah berbentuk:
Dalam istilah matematik harga dari b2- 4ac dikenal sebagai harga diskriminan atau juga
sering disebut harga determinan dari suatu persamaan kuadrat. Notasi dari harga determinan biasanya dituliskan sebagai D. Dengan demikian harga determinan dari suatu persamaan kuadrat dapat dituliskan sebagai:
D = b2 - 4ac ……….. (8)
Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks. Dalam hal ini dikriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat tiga kasus yang mungkin muncul berkaitan dengan harga determinan, yaitu:
Jika diskriminan berharga positif (D > 0), maka akan terdapat dua akar berbeda yang kedua-duanya merupakan bilangan riil. Untuk persamaan kuadrat dengan koefisien berupa bilangan bulat, apabila diskriminan merupakan suatu kuadrat sempurna, maka akar-akarnya merupakan bilangan rasional atau sebaliknya dapat pula merupakan bilangan irrasional kuadrat.
Jika diskriminan bernilai nol (D = 0), maka diperoleh satu akar eksak dan akar yang dimaksud merupakan bilangan riil. Hal ini kadang disebut sebagai akar kembar, di mana nilainya adalah:
Jika diskriminan berharga negatif ( D < 0 ), maka tidak terdapat akar riil. Sebagai gantinya, terdapat dua buah akar kompleks (tidak-real), yang satu sama lain merupakan konjugat kompleks:
Da n
Gambar 5 menunjukkan perubahan atau pergeseran pola kurva atau grafik sebagai akibat perubahan harga dari determinan D.
Jadi akar-akar akan berbeda, jika dan hanya jika diskriminan bernilai tidak sama dengan nol, dan akar-akar akan bersifat riil, jika dan hanya jika diskriminan bernilai tidak negatif.
V.6. Akar riil dan kompleks
Persamaan kuadrat dapat memiliki sebuah akar (akar kembar) atau dua buah akar yang berbeda. Harga dua buah akar dapat bersifat riil atau kompleks tergantung dari nilai diskriminannya. Akar-akar persamaan kuadrat dapat pula dipandang sebagai titik potongnya dengan sumbu x atau garis y = 0.
Contoh:
Tentukan akar-akar dari persamaan
a. y = x2 + 4x – 6
b. y = 2x2 - 4x + 6
Jawab:
Sebagaimana disebutkan pada teori bahwa akar-akar persamaan kuadrat dapat dipandang sebagai titik potongnya dengan sumbu x atau garis y = 0. Dengan demikian akan didapat jawaban sebagai berikut:
a. y = x2 + 4x – 6
0 = x2 + 4x – 6 atau x2 + 4x – 6 = 0
Dengan menggunakan rumus a,b,c didapat akar-akar persamaan:
Uji kebenaran jawaban dengan persamaan (6):
Dari hasil hitungan telah didapat bahwa x1 =1,1623 dan x2 = -5,1623, kedua harga akar
adalah riil (nyata)
x1 + x2 = 1,1623 - 5,1623 = -4 (cocok dengan hasil uji dari persamaan 6)
b. y = 2x2 - 4x + 6
Untuk y = 0, maka persamaan dapat dituliskan menjadi: 2x2 - 4x + 6 = 0
Dengan menggunakan rumus a,b,c didapat akar-akar persamaan:
Didapat dua harga akar berbentuk bilangan kompleks dimana akar-akar tersebut merupakan konjugat satu sama lainnya.
Uji kebenaran jawaban dengan persamaan (6):
Dari hasil hitungan telah didapat bahwa x1 =1+ 1,4142 j dan x2 =1- 1,4142 j, kedua
harga akar berbentuk bilangan kompleks.
X1 + x2 = 1+ 1,4142 j + (1- 1,4142 j ) = 2 (cocok dengan hasil uji dari persamaan 6)
Latihan
Tentukan akar-akar dari persamaan
a. y = 4 x2 + 4x – 16
b. y = 2x2 – 4x + 5
c. y = 3 x2 + 2x +16
d. y = -2x2 + 4x + 5
e. y = -9 x2 – 2x -16
Uji akar yang didapat dengan persamaan:
V.7. Titik potong kurva non linier dengan garis y = d (garis linier)
Dengan cara pandang ini, rumus persamaan kuadrat dapat digunakan apabila diinginkan untuk mencari titik potong antara suatu persamaan kuadrat () dengan suatu garis mendatar (). Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.
Intepretasi yang sama pun berlaku, yaitu bila:
diskriminan positif, terdapat dua titik potong antara dan ,
diskriminan nol, terdapat hanya satu titik potong antara dan , dan
diskriminan negatif, tidak terdapat titik potong antara kedua kurva, dan .
Contoh:
Tentukan titik potong antara:
a. y = 6 dengan y = x2 + 4x – 6
b. y = 5x -8 dengan y = x2 - 4x + 12
Jawab:
a. y = 6 dengan y = x2 + 4x – 6
Lakukan subsitusi antar persamaan, sehingga didapat persamaan baru berbentuk: 6 = x2 + 4x – 6 atau x2 + 4x -12 = 0
Dengan cara memfaktorkan didapat bentuk persamaan : (x+6) (x-2) = 0
x + 6 = 0 x1 = - 6
x - 2 = 0 x2 = 2
Titik potong antara dua kurva tersebut adalah (-6, 6) dan (2,6)
b. y = 5x - 8 dengan y = x2 - 4x + 12
Lakukan subsitusi antar persamaan, sehingga didapat persamaan baru berbentuk:
5x - 8 = x2 - 4x +12 atau x2 –9 x +20 = 0
Dengan cara memfaktorkan didapat bentuk persamaan : (x - 4) (x - 5) = 0
x - 4= 0 x1 = 4
x - 5 = 0 x2 = 5
Dari x1 = 4 y1 = 5x -8 = 5(4) - 8 = 20 – 8 =12
Dari x2 = 5 y2 = 5x -8 = 5(5) - 8 = 25 – 8 =17
Titik potong antara dua kurva tersebut adalah (4,12) dan (5,17)
c. Tentukan dengan metoda kurva/grafik untuk memperkirakan titik potong antara:
y = 4x3 +8x dengan y= x2 +2x +6
Jawab:
y1 = 4x3 +8x dengan y2 = x2 +2x +6
Tabel pembantu:
x y 1 y2
-3 -36 9
-2 0 6
-1 4 5
0 0 6
1 12 9
2 64 14
3 180 21
Dari kurva nampak bahwa perkiraan x= 0,9 dan x= -1,3. Harga y dihitung dengan persamaan y = 4x3 +8x. Untuk x = 0,9 y = 10,12, untuk x = -1,3 y = -12,60
Koordinat yang didapat adalah: (0,9 , 10,12) dan ( -1,3, -12,60)
60
y= 4x3 +8x
y= x2 +2x +6
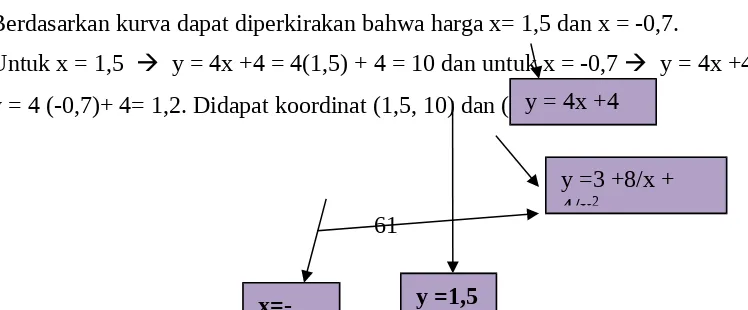
d. Tentukan dengan metoda kurva/grafik untuk memperkirakan titik potong antara:
Berdasarkan kurva dapat diperkirakan bahwa harga x= 1,5 dan x = -0,7.
Latihan
Tentukan titik potong antara kurva:
a. y = 6 -2x dengan y = x2 + 4x – 6
b. y = -5x +8 dengan y = 2x2 - 4x – 12
c. y = 3x dengan y =5x2 -8x + 9
d. y = -6 dengan y = 4x2 - 4x – 8
e. y/x = -5 dengan y = 4x2 + 4x + 6
f. y/x = -5 - 4x dengan y = 4x2 + 4x + 6
Tugas
A. Tentukan akar-akar dari persamaan:
1. y =9 x2 + 4x – 10
2. y = -2x2 + 4x - 5
3. y = -3 x2 - 2x +16
Uji akar yang didapat dengan persamaan
B. Tentukan titik potong antara kurva: 1. y = -6 -12x dengan y = 3x2 + 4x + 9
2. y = 5x + 10 dengan y = -2x2 + 4x – 12
3. y/x = -5 dengan y = -4x2 + 8x + 5
4. y/x = 5 + 6x dengan y = 9x2 + 6x – 6
5. y + 6 x = 9 dengan y = 2x2 - 4x – 12
6. y2 = x+1 dengan y = 3x + 4
8. y + x2 = 2 dengan y = 2x + 3
V.8. Titik potong dua kurva non linier
Untuk menentukan titik potong antara dua kurva non linier dapat dilakukan dengan cara subsitusi atau elemininasi.
Contoh:
1.Tentukan titik potong antara dua kurva yang mempunyai persamaan y = 2 x2 +3 x - 4
dan y = - x2 +5x +5
Jawab:
Digunakan penyelesaian dengan cara eliminasi
y = 2 x2 + 3 x - 4
y = - x2 + 5x + 5
0 = 3 x2 - 2 x - 9 atau 3 x2 - 2 x - 9 = 0
Harga akar-akar dicari dengan rumus a,b,c :
Mencari harga y1dan y2:
y1 =- x2 +5x +5= - (2,0972)2 + 5(2,0972) + 5 =11,0878
y2 =- x2 +5x +5= - (-1,4305)2 + 5(-1,4305) + 5 = - 4,1988
Jadi titk potong yang dimaksud adalah: (2,0972 , 11,0878) dan (-1,4305 , - 4,1988)
2. Tentukan titik potong antara dua kurva yang mempunyai persamaan
y = 2 x2 +3 x + 4 ...(a)