LIMIT FUNGSI ALJABAR

1 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1

LIMIT FUNGSI ALJABAR

INDIKATOR:

Menghitung nilai limit fungsi aljabar Diagram alur

Pengertian limit

Dalam kehidupan sehari-hari, seringkali Anda mendengar kata-kata hampir atau mendekati.

Misalnya, Lionel Messi hampir mencetak gol, kecepatan motor itu mendekati 120 km/jam, dan sebagainya. Kata hampir, atau medekati dalam matematika disebut limit.

Penerapan limit dalam kehidupan sehari-hari

1. Bidang Fisika: menentukan jarak focus lensa cekung kacamata pasien

2. Bidang kedokteran: menghitung kerusakan jantung yang biasa ditampilkan dalam bentuk USG pada kasus cardiac carest.

3. Bidang Kimia: menghitung kekuatan besi yang bergesekan dengan air asin dan menghitung ketahanannya dalam menghadapi pengkaratan.

4. Bidang Ekonomi: menentukan pajak yang harus dibayar oleh masyarakat. Menghitung biaya rata-rata dan bunga.

5. Dan masih banyak lagi.

Limit merupakan nilai hampiran suatu variabel pada suatu bilangan real.

2 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 Notasi: lim

𝑥→𝑎𝑓(𝑥) = 𝐿

Dibaca: limit fungsi 𝑓(𝑥) pada saat 𝑥 mendekati 𝑎 sama dengan L

Suatu limit dikatakan ada jika limit tersebut memiliki limit kiri dan limit kanan yang sama. Limit kiri adalah pendekatan nilai fungsi real dari sebelah kiri yang dinotasikan lim

𝑥→𝑎⁻𝑓(𝑥). Sedangkan limit kanan adalah pendekatan nilai fungsi real dari sebelah kanan yang dinotasikan lim

𝑥→𝑎⁺𝑓(𝑥).

Perhatikan uraian berikut ini.

Misal, diberikan suatu limt fungsi 𝑓(𝑥) = {4𝑥 , untuk 𝑥 ≤ 4

4𝑥 + 6 , untuk 𝑥 > 4

Untuk mengetahui apakah limit tersebut ada, selidiki apakah limit kiri dan kanannya sama.

 lim

𝑥→4⁻ 4𝑥 = 4(4) = 16, karena 𝑥 < 4

 lim

𝑥→4⁺ 4𝑥 + 6 = lim

𝑥→4⁺4𝑥 + lim

𝑥→4⁺ 6 = 16 + 6 = 22

Karena nilai limit kiri dan kanan berbeda, limit fungsi tersebut tidak ada.

Perhatikan gambar grafik berikut.

Selanjutnya, perhatikan bentuk fungsi

lim

𝑥→3 𝑥²−9

𝑥−3

Limit fungsi tersebut, tidak terdefinisi di 𝑥 = 3 karena daerah asal fungsi 𝑓 adalah {𝑥|𝑥 ≠ 3}.

Untuk mengetahui limit kiri dan kanannya sama, seperti pada table berikut.

3 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1

Berdasarkan tabel tersebut, dapat diketahui bahwa pada saat 𝑥 mendekati 3, nilai fungsi 𝑓(𝑥) mendekati 6. Jadi,

lim

𝑥→3 𝑥²−9

𝑥−3

=

^{(𝑥+3)(𝑥−3)}

𝑥−3

= (𝑥 + 3);

jika𝑥 ≠ 3.

Oleh karena 𝑥 + 3 mendekati 6 jika 𝑥 mendekati 3 maka ^𝑥

2−9

𝑥−3 mendekati 6 jika 𝑥 mendekati 3.

Meskipun fungsi 𝑓(𝑥) tidak terdefinisi untuk 𝑥 = 3, tetapi fungsi tersebut mendekati nilai 6 pada saat 𝑥 mendekati 3. Dengan demikian, dapat dikatakan bahwa nilai limit fungsi tersebut adalah 6.

Selanjutnya, perhatikan pula bentuk fungsi lim

𝑥→3 (𝑥 + 3)

Untuk mengetahui apakah limit tersebut ada, selidiki apakah limit kiri dan kanannya sama, seperti pada tabel berikut.

Berdasarkan table, dapat diketahui bahwa pada saat 𝑥 mendekati 3, nilai fungsi 𝑓(𝑥) mendekati 6.

Jadi, lim

𝑥→3 (𝑥 + 3) = 6.

Dapat disimpulkan bahwa lim

𝑥→3 (𝑥 + 3) = 6 dapat diperoleh tanpa menggunakan tabel. Ketika 𝑥 mendekati 3, nilai 𝑥 + 3 akan mendekati 6. Dengan demikian, dapat disimpulkan bahwa

𝑥→3

lim

𝑥²−9

𝑥−3

=

lim

𝑥→3

(

𝑥 + 3

)

= 6

4 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1

Teorema limit

Jika 𝑓(𝑥) dan 𝑔(𝑥) fungsi-fungsi yang mempunyai limit di 𝑎 dan 𝑘 (konstanta) dengan 𝑛 ∈ 𝐵⁺, maka berlaku:

1. lim

𝑥→𝑎

𝑘 = 𝑘 2. lim

𝑥→𝑎

𝑥 = 𝑎 3. lim

𝑥→𝑎

𝑘𝑓(𝑥) = 𝑘 lim

𝑥→𝑎

𝑓(𝑥) 4. lim

𝑥→𝑎

[𝑓(𝑥) + 𝑔(𝑥)] = lim

𝑥→𝑎

𝑓(𝑥) + lim

𝑥→𝑎

𝑔(𝑥) 5. lim

𝑥→𝑎

[𝑓(𝑥) − 𝑔(𝑥)] = lim

𝑥→𝑎

𝑓(𝑥) − lim

𝑥→𝑎

𝑔(𝑥) 6. lim

𝑥→𝑎

[𝑓(𝑥) ⋅ 𝑔(𝑥)] = lim

𝑥→𝑎

𝑓(𝑥) ⋅ lim

𝑥→𝑎

𝑔(𝑥) 7. lim

𝑥→𝑎 𝑓(𝑥)

𝑔(𝑥)

=

^{𝑥→𝑎lim 𝑓(𝑥)}

𝑥→𝑎lim 𝑔(𝑥)

8. lim

𝑥→𝑎

[𝑓(𝑥)]

^𝑛

= [lim

𝑥→𝑎

𝑓(𝑥)]

^𝑛

9. lim

𝑥→𝑎

√𝑓(𝑥)

^𝑛

= √lim

^𝑛 _𝑥→𝑎

𝑓(𝑥)

RUMUS:

- Bentuk lim

𝑥→𝑎𝑓(𝑥):

 Jika 𝑓(𝑎) = 𝐶, maka nilai lim

𝑥→𝑎𝑓(𝑥) = 𝐶

 Jika 𝑓(𝑎) =^𝐶

0, maka nilai lim

𝑥→𝑎𝑓(𝑥) =tidak ada

 Jika 𝑓(𝑎) = ⁰

𝐶, maka nilai lim

𝑥→𝑎𝑓(𝑥) = 0

 Jika 𝑓(𝑎) =⁰

0, maka nilai lim

𝑥→𝑎𝑓(𝑥) harus difaktorkan atau kali akar sekawan atau pakai turunan.

- Bentuk lim

𝑥→∞

𝑓(𝑥) 𝑔(𝑥):

 Jika derajat pembilang 𝑓(𝑥) lebih besar daripada derajat penyebut 𝑔(𝑥), maka nilai

𝑥→∞lim

𝑓(𝑥) 𝑔(𝑥)= ∞

 Jika derajat pembilang 𝑓(𝑥) sama dengan derajat penyebut 𝑔(𝑥), maka nilai lim

𝑥→∞

𝑓(𝑥) 𝑔(𝑥)

bilangan real.

 Jika derajat pembilang 𝑓(𝑥) lebih kecil daripada derajat penyebut 𝑔(𝑥), maka nilai

𝑥→∞lim

𝑓(𝑥) 𝑔(𝑥)= 0

5 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 - Bentuk pecahan yang masih terpisah: Samakan penyebut dan gabungkan dulu - Bentuk lim

𝑥→∞[√𝑎𝑥 + 𝑏 − √𝑝𝑥 + 𝑞]:

 Jika 𝑎 < 𝑝, maka 𝐿 = −∞

 Jika 𝑎 = 𝑝, maka 𝐿 = 0

 Jika 𝑎 > 𝑝, maka 𝐿 = ∞ - Bentuk lim

𝑥→∞[√𝑎𝑥²+ 𝑏𝑥 + 𝑐 − √𝑝𝑥²+ 𝑞𝑥 + 𝑟]:

 Jika 𝑎 < 𝑝, maka 𝐿 = −∞

 Jika 𝑎 = 𝑝, maka 𝐿 =^𝑏−𝑞

 Jika 𝑎 > 𝑝, maka 𝐿 = ∞ 2√𝑎

Contoh 1:

Tentukan nilai limit berikut ini:

a. lim

𝑥→0 𝑥³+1

𝑥+1

c. lim

𝑥→−3 𝑥+3

√𝑥+3

b. lim

𝑥→5 𝑥²−25

𝑥−5

d. lim

𝑥→1

√3𝑥−1−√𝑥+1

√2𝑥−1−√𝑥

Penyelesaian:

a.

lim

𝑥→0 𝑥³+1

𝑥+1

=

⁰³⁺¹

0+1

= 1

b.

lim

𝑥→5 𝑥²−25

𝑥−5

=

⁵²⁺²⁵

5−5

=

⁰

0

Fungsi harus difaktorkan kemudian disederhanakan karena dengan substitusi didapat bentuk tak tentu ⁰

0.

𝑥→5

lim

𝑥²−25

𝑥−5

= lim

𝑥→5

(𝑥+5)(𝑥−5)

𝑥−5

= lim

𝑥→5

(𝑥 + 5) = 5 + 5 = 10

Atau dengan menggunakan turunan

𝑥→5

lim

𝑥²−25

𝑥−5

= lim

𝑥→5 2𝑥

1

= 2(5) = 10

c.

lim

𝑥→−3 𝑥+3

√𝑥+3

=

⁰

0

Dengan pemfaktoran

𝑥→−3

lim

𝑥+3

√𝑥+3

= lim

𝑥→−3

√𝑥+3√𝑥+3

√𝑥+3

= lim

𝑥→−3

√𝑥 + 3 = 0

Dengan turunan

𝑥→−3

lim

𝑥+3

√𝑥+3

= lim

𝑥→−3 1 1

2(𝑥+3)⁻¹²

= lim

𝑥→−3

2√𝑥 + 3 = 0

6 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 d.

lim

𝑥→1

√3𝑥−1−√𝑥+1

√2𝑥−1−√𝑥

=

⁰

0

Kali dengan akar sekawannya

= lim

𝑥→1

√3𝑥−1−√𝑥+1

√2𝑥−1−√𝑥

∙

^{√3𝑥−1+√𝑥+1}

√3𝑥−1+√𝑥+1

∙

^{√2𝑥−1+√𝑥}

√2𝑥−1+√𝑥

= lim

𝑥→1

[(3𝑥−1)−(𝑥+1)](√2𝑥−1+√𝑥)

(√3𝑥−1+√𝑥+1)[(2𝑥−1)−𝑥]

= lim

𝑥→1

(2𝑥−2)(√2𝑥−1+√𝑥) (𝑥−1)(√3𝑥−1+√𝑥+1)

= lim

𝑥→1

2(𝑥−1)(√2𝑥−1+√𝑥)

(𝑥−1)(√3𝑥−1+√𝑥+1)

= lim

𝑥→1

2(√2𝑥−1+√𝑥) (√3𝑥−1+√𝑥+1)

=

2(√2(1)−1+√1)

(√3(1)−1+√1+1)

=

^2∙2

√2+√2

=

⁴

2√2

= √2

Dengan turunan

𝑥→1

lim

√3𝑥−1−√𝑥+1

√2𝑥−1−√𝑥

= lim

𝑥→1 1

2(3𝑥−1)⁻¹²∙3−¹

2(𝑥+1)⁻¹² 1

2(2𝑥−1)⁻¹²∙2−¹ 2(𝑥)⁻¹²

= lim

𝑥→1 3

2√3𝑥−1− ¹ 2√𝑥+1 1

√2𝑥−1− ¹ 2√𝑥

=

3 2√2− ¹

2√2 1−¹

2

=

⁴

2√2

= √2

Contoh 2:

Hitung nilai limit berikut ini a.

lim

𝑥→∞

6𝑥+1

2𝑥+10 c.

lim

𝑥→∞

𝑥

√𝑥²−𝑥−1

b.

lim

𝑥→∞

8𝑥+100

3𝑥²−5𝑥+10 d.

lim

𝑥→∞

𝑥³+2𝑥² 𝑥²+3

Penyelesaian:

Bagi dengan x pangkat tertinggi

a. lim

𝑥→∞

6𝑥+1

2𝑥+10

= lim

𝑥→∞

6+¹ 𝑥 2+¹⁰

𝑥

=

⁶⁺⁰

2+0

= 3 b. lim

𝑥→∞

8𝑥+100

3𝑥²−5𝑥+10

= lim

𝑥→∞

8 𝑥+¹⁰⁰

𝑥2 3−⁵

𝑥+¹⁰ 𝑥2

=

⁰⁺⁰

3−0+0

=

⁰

3

= 0 c. lim

𝑥→∞

𝑥

√𝑥²−𝑥−1

= lim

𝑥→∞

1

√1−¹ 𝑥−¹

𝑥2

=

¹

1

= 1 d. lim

𝑥→∞

𝑥³+2𝑥²

𝑥²+3

= lim

𝑥→∞

1+²_𝑥 1 𝑥+³

𝑥2

=

¹

0

= ∞

7 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 Contoh 3:

Hitunglah limit berikut.

a.

lim

𝑥→∞

(

^3𝑥

𝑥−1

−

^2𝑥

𝑥+1

) c.

lim

𝑥→∞(√4𝑥² + 2𝑥 − 6 − 2𝑥 + 1) a. lim

𝑥→∞(√𝑥²+ 2𝑥 − √𝑥² − 4𝑥) d.

Lim

𝑥→∞

𝑥−1

√4𝑥²+𝑥 +√𝑥²+𝑥−1

Penyelesaian:

a.

lim

𝑥→∞

(

^3𝑥

𝑥−1

−

^2𝑥

𝑥+1

) = lim

𝑥→∞

(

3𝑥(𝑥+1)−2𝑥(𝑥−1)

(𝑥−1)(𝑥+1)

) = lim

𝑥→∞

(

^{3𝑥2+3𝑥−2𝑥2+2𝑥}

𝑥²−1

)

= lim

𝑥→∞

𝑥²+5𝑥

𝑥²−1

= lim

𝑥→∞

1+⁵ 𝑥 1−¹ 𝑥2

= 1

b. lim

𝑥→∞(√𝑥²+ 2𝑥 − √𝑥² − 4𝑥)

= lim

𝑥→∞

(√𝑥

²

+ 2𝑥 − √𝑥

²

− 4𝑥) ∙

^{𝑥→∞lim(√𝑥}

2+2𝑥+√𝑥²−4𝑥) 𝑥→∞lim(√𝑥²+2𝑥+√𝑥²−4𝑥)

= lim

𝑥→∞

(𝑥²+2𝑥)−(𝑥²−4𝑥)

√𝑥²+2𝑥+√𝑥²−4𝑥

= lim

𝑥→∞

𝑥²+2𝑥−𝑥²+4𝑥

√𝑥²+2𝑥+√𝑥²−4𝑥

= lim

𝑥→∞

6𝑥

√𝑥²+2𝑥+√𝑥²−4𝑥

= lim

𝑥→∞

6

√1+² 𝑥+√1−⁴

𝑥

=

⁶

√1+√1

=

⁶

2

= 3

Atau gunakan rumus

𝐿 =

^𝑏−𝑞

2√𝑎 karena 𝑎 = 𝑝.

Jadi,

𝐿 =

^𝑏−𝑞

2√𝑎

=

²⁻⁽⁻⁴⁾

2√1

=

⁶

2

= 3

c. lim

𝑥→∞(√4𝑥²+ 2𝑥 − 6 − 2𝑥 + 1) = lim

𝑥→∞(√4𝑥²+ 2𝑥 − (2𝑥 − 1))

= lim

𝑥→∞(√4𝑥²+ 2𝑥 − 6 − √4𝑥²− 4𝑥 + 1) Gunakan rumus singkat

𝐿 =

^𝑏−𝑞

2√𝑎 , karena 𝑎 = 𝑝 Jadi,

𝐿 =

^𝑏−𝑞

2√𝑎

=

²⁻⁽⁻⁴⁾

2√4

=

⁶

4

= 1,5

d.

Lim

𝑥→∞

𝑥−1

√4𝑥²+𝑥 +√𝑥²+𝑥−1

=

lim

𝑥→∞

𝑥−1

2𝑥 + ….+ 𝑥 +⋯= lim

𝑥→∞

𝑥−1

3𝑥 +⋯ = ¹

3

8 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 KONTINU DAN DISKONTINU SUATU FUNGSI

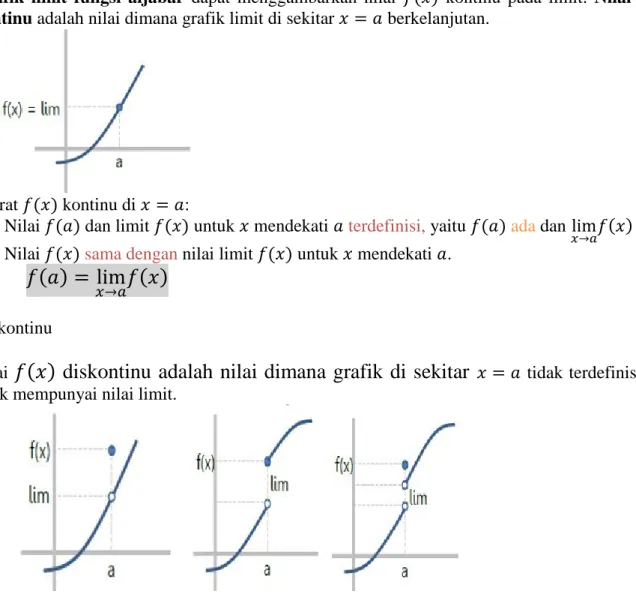
Kontinu

Grafik limit fungsi aljabar dapat menggambarkan nilai 𝑓(𝑥) kontinu pada limit. Nilai 𝒇(𝒙) kontinu adalah nilai dimana grafik limit di sekitar 𝑥 = 𝑎 berkelanjutan.

Syarat 𝑓(𝑥) kontinu di 𝑥 = 𝑎:

1. Nilai 𝑓(𝑎) dan limit 𝑓(𝑥) untuk 𝑥 mendekati 𝑎 terdefinisi, yaitu 𝑓(𝑎) ada dan lim

𝑥→𝑎𝑓(𝑥) ada 2. Nilai 𝑓(𝑥) sama dengan nilai limit 𝑓(𝑥) untuk 𝑥 mendekati 𝑎.

𝑓(𝑎) = lim

𝑥→𝑎

𝑓(𝑥)

Diskontinu

Nilai

𝑓(𝑥) diskontinu adalah nilai dimana grafik di sekitar

𝑥 = 𝑎 tidak terdefinisi dan tidak mempunyai nilai limit.

9 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1

Perhatikan gambar. Fungsi 𝑓 kontinu pada (𝑎, 𝑏) kecuali di 𝑥₁, 𝑥₂, dan 𝑥₃. Fungsi 𝑓 diskontinu di 𝑥₁ karena lim

𝑥→𝑥1

𝑓(𝑥) tidak ada, diskontinu di 𝑥₂ karena nilai lim

𝑥→𝑥2

𝑓(𝑥) tidak sama dengan nilai fungsi di 𝑥₂, dan 𝑓 diskontinu di 𝑥₃ karena nilai fungsi di 𝑥₃ tidak ada.

Contoh 1:

Perhatikan fungsi berikut ini a. 𝑓(𝑥) =^𝑥2−1

𝑥−1 tidak terdefinisi di 𝑥 = 1. Berarti syarat (1) kekontinuan fungsi tidak terpenuhi.

Jadi 𝑓 tidak kontinu di 𝑥 = 1.

b. 𝑓(𝑥) = {

𝑥 + 1 , 𝑥 > 1 10 , 𝑥 = 1 3𝑥² − 1 , 𝑥 < 1

. Fungsi 𝑓 bernilai 10 untuk 𝑥 = 1, yaitu 𝑓(1) = 10. Sedangkan

𝑥→1lim𝑓(𝑥) = 2. Jadi lim

𝑥→1𝑓(𝑥) ≠ 𝑓(1). Dengan demikian, 𝑓 diskontinu di 𝑥 = 1.

10 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 c. 𝑓(𝑥) = {

𝑥 + 1 , 𝑥 > 1 2 , 𝑥 = 1 3𝑥² − 1 , 𝑥 < 1

. Fungsi 𝑓 bernilai 2 untuk 𝑥 = 1, yaitu 𝑓(1) = 2. Sedangkan

𝑥→1lim𝑓(𝑥) = 2. Jadi lim

𝑥→1𝑓(𝑥) = 𝑓(1). Dengan demikian, 𝑓 kontinu di 𝑥 = 1.

11 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 Contoh 2:

𝑓(𝑥) = {

𝑥²+𝑥−2

√𝑥+6−2 , 𝑥 ≠ −2 3𝑎 + 6 , 𝑥 = −2

. Jika 𝑓(𝑥) kontinu di 𝑥 = −2, maka nilai 𝑎 adalah?

Penyelesaian:

Nilai 𝑓(−2) dicari menggunakan persamaan 2, sedangkan nilai limit 𝑓(𝑥) untuk 𝑥 mendekati −2 dicari menggunakan persamaan 1.

Syarat kontinu jika 𝑓(𝑎) = lim

𝑥→𝑎𝑓(𝑥), sehingga:

𝑓(−2) = 3𝑎 + 6

𝑥→−2

lim 𝑓(𝑥) = lim

𝑥→−2

𝑥²+𝑥−2

√𝑥+6−2

= lim

𝑥→−2

𝑥²+𝑥−2

√𝑥+6−2

⋅

^√𝑥+6+2

√𝑥+6+2

= lim

𝑥→−2

(𝑥+2)(𝑥−1)(√𝑥+6+2) (√𝑥+6)²−2²

= lim

𝑥→−2

(𝑥+2)(𝑥−1)(√𝑥+6+2) 𝑥+6−4

= lim

𝑥→−2

(𝑥+2)(𝑥−1)(√𝑥+6+2) 𝑥+2

= (−2 − 1)(√−2 + 6 + 2) = −12 𝑓(−2) =

lim

𝑥→−2

𝑓

⁽

𝑥

⁾

3𝑎 + 6 = −12 𝑎 = −6

Jadi, nilai 𝑎 = −6.

12 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 Contoh 3:

Pada interval berapa

𝑓(𝑥) =

^𝑥2−9

√𝑥²−4𝑥−5 diskontinu?

Penyelesaian:

Agar 𝑓(𝑥) tidak terdefinisi (bentuk ^𝑎

0 dan √𝑏𝑖𝑙. 𝑛𝑒𝑔𝑎𝑡𝑖𝑓), maka didapat:

𝑥² − 4𝑥 − 5 ≤ 0 (𝑥 + 1)(𝑥 − 5) ≤ 0 𝑥 = −1, 𝑥 = 5

Jadi, 𝑓(𝑥) tidak terdefinisi pada interval −1 ≤ 𝑥 ≤ 5.

Seperti halnya pada hitungan limit, dalam kekontinuan juga dikenal istilah kontinu satu sisi. Hal ini diberikan pada definisi berikut ini.

Definisi:

(i) Fungsi 𝑓 dikatakan kontinu dari kiri di 𝑐 jika lim

𝑥→𝑐⁻𝑓(𝑥) = 𝑓(𝑐) (ii) Fungsi 𝑓 dikatakan kontinu dari kanan di 𝑐 jika lim

𝑥→𝑐⁺𝑓(𝑥) = 𝑓(𝑐)

13 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 LATIHAN 1:

1. Jika limitnya ada, hitunglah limit fungsi berikut.

a.

lim

𝑥→4

√𝑥−2 𝑥−2

b.

lim

𝑥→1 𝑥−1

√𝑥−1

c. lim

𝑥→−1 √𝑥(𝑥 + 1) d. lim

𝑥→3 (2𝑥²− 1)√(𝑥²+ 1) e.

lim

𝑥→2

2−√𝑥+2 𝑥−2

f. lim

𝑥→−3 (𝑥 − 3)²√(𝑥 + 3)² g.

lim

𝑥→4 2−√𝑥

4−𝑥

h. lim

𝑥→1 (𝑥 − 1)√𝑥 − 4 2. Tentukan limit fungsi berikut.

a.

lim

𝑥→∞

𝑥 𝑥+1

b.

lim

𝑥→∞

3𝑥+2 4𝑥−5

c.

lim

𝑥→∞

𝑥

√𝑥²−2𝑥−1

d.

lim

𝑥→∞

𝑥²−2𝑥+1 3𝑥²−2

e.

lim

𝑥→∞

√3𝑥²−2𝑥+1 𝑥+100

f.

lim

𝑥→∞

5𝑥−3𝑥²+6 3𝑥³−8

g.

lim

𝑥→∞

2 𝑥 1−2𝑥

h.

lim

𝑥→∞

9+2𝑥 𝑥²−3

3. Hitunglah limit fungsi 𝑓(𝑥) berikut.

a.

𝑓(𝑥) =

^𝑥2+2𝑥

𝑥+2 di 𝑥 = −2 b.

𝑓(𝑥) =

^1−𝑥

𝑥²−2𝑥+1 di 𝑥 = 1 c.

𝑓(𝑥) =

^2−𝑥

𝑥²−4𝑥+4 di 𝑥 = 2 d.

𝑓(𝑥) =

^√𝑥−1

𝑥−1

di 𝑥 = 1 e.

𝑓(𝑥) =

^3−√𝑥

9−𝑥

di 𝑥 = 9 f.

𝑓(𝑥) =

^{𝑥3−9𝑥}

𝑥−3 di 𝑥 = 3 g.

𝑓(𝑥) =

^{𝑥3−9𝑥}

𝑥+3 di 𝑥 = −3 h.

𝑓(𝑥) =

^𝑥−2

√𝑥−2

di 𝑥 = 4 4. Tentukan limit fungsi berikut.

a.

lim

𝑥→∞

(4𝑥+2)²

√4𝑥⁴+9

b. lim

𝑥→∞ [√𝑥 + 1 − √𝑥 − 1]

c.

lim

𝑥→∞

𝑥√𝑥−𝑥−2

√2𝑥³+2𝑥

d. lim

𝑥→∞ [√𝑥²− 1 + √1 − 𝑥²] e. lim

𝑥→∞ [√𝑥²− 𝑥 + 5 −

√𝑥² − 2𝑥 + 3]

f. lim

𝑥→∞ [√(𝑥²+ 𝑎²) − 𝑥]

5. Tentukan limit fungsi berikut.

a.

lim

𝑥→1

𝑥³−𝑥²+𝑥−1 𝑥⁴−𝑥³+2𝑥−2

b.

lim

𝑥→2

𝑥³−2𝑥²+4𝑥−8 𝑥²+𝑥−6

c.

lim

𝑥→−1

𝑥³+2𝑥²+𝑥 𝑥⁴+𝑥³+2𝑥+2

14 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 d.

lim

𝑥→−1

𝑥³+𝑥²+3𝑥+3 𝑥⁴+𝑥³+2𝑥+2

e.

lim

𝑥→1

𝑥³−𝑥²+3𝑥−3 𝑥²+3𝑥−4

f.

lim

𝑥→3

𝑥³−3𝑥²+4𝑥−12 𝑥⁴−3𝑥³+𝑥−3

6. Tentukan limit fungsi berikut.

a.

lim

𝑥→1 1−√𝑥 1−𝑥²

b.

lim

𝑥→0

√𝑥−𝑥

√𝑥+𝑥

LATIHAN 2

1. Hitunglah nilai limit berikut ini

a. lim

𝑥→2

𝑥²+𝑥−6

𝑥²−7𝑥+10

j. lim

𝑥→3

𝑥−√2𝑥+3 𝑥²−9

b. lim

𝑥→−3

𝑥²−𝑥−12

𝑥²+𝑥−6

k. lim

𝑥→4

48−3𝑥² 5−√𝑥²+9

c. lim

𝑥→0

𝑎𝑥²+𝑏𝑥+𝑐

𝑝𝑥²+𝑞𝑥+𝑟

l. lim

𝑥→0

√4+𝑥−√4−𝑥 2𝑥

d. lim

𝑥→0

3𝑥²+5𝑥

2𝑥³+5𝑥²+10𝑥

m. lim

𝑥→0

𝑥

√1+2𝑥−√1−2𝑥

e. lim

𝑥→4

𝑥³−3𝑥²−3𝑥−4

𝑥²−4𝑥

n. lim

𝑥→3

𝑥−3

√𝑥+4−√2𝑥+1

f. lim

𝑥→4

√

^{𝑥2+6𝑥−40}

𝑥²−𝑥−12

o. lim

𝑥→−1

𝑥²−1

√3𝑥+4−√𝑥+2

g. lim

𝑥→−2 𝑥³+8

𝑥²−4

p. lim

𝑥→1

𝑥²−1

√𝑥²+3−𝑥−1

h. lim

𝑥→4 2−√𝑥

𝑥−4

q. lim

𝑥→4

𝑥(2𝑥−8)² (𝑥²−16)(√𝑥−2)

i. lim

𝑥→3

𝑥²−9

√𝑥²+7−4

2. Tentukan nilai limit berikut!

a.

lim

𝑥→∞

5𝑥³−5𝑥+10

3−𝑥−𝑥³

h.

lim

𝑥→∞ [√𝑥²+ 6𝑥 − 3 − √𝑥²− 4𝑥 + 9]

b.

lim

𝑥→∞

𝑥²−5𝑥−10

𝑥⁵−4𝑥⁴−2𝑥

i.

lim

𝑥→∞ [√𝑥(2𝑥 − 5) − √2𝑥² + 4𝑥]

15 | M A T E M A T I K A X I I P S S M A G O N Z A G A / L I M I T / 2 0 2 0 - 2 0 2 1 c.

lim

𝑥→∞

2𝑥⁴−3𝑥²+5

𝑥²+4𝑥−1

j.

lim

𝑥→∞ [√𝑥²− 5𝑥 − 𝑥 − 1]

d.

lim

𝑥→∞

𝑎𝑥²+𝑏𝑥+𝑐

𝑝𝑥²+𝑞𝑥+𝑟

k.

lim

𝑥→∞ [𝑥 − 1 − √𝑥²+ 6𝑥]

e.

lim

𝑥→∞

(2𝑥−1)³(𝑥+1)⁴

𝑥⁴(𝑥³+2)

l. lim

𝑥→∞

(2𝑥−5)⁵ (3𝑥+2)⁵

f.

lim

𝑥→∞

(4𝑥−5)²(2𝑥−1)³

4𝑥²(𝑥³−5)

m. lim

𝑥→∞

√𝑥−1+√𝑥+1

√4𝑥+3−√𝑥−2

g. lim

𝑥→∞ [√5𝑥 + 1 − √3𝑥 + 7]

n.

lim

𝑥→∞

√9𝑥−1−√𝑥+1

√4𝑥−1+√𝑥

Kunci jawaban latihan 2:

1. a. −⁵

3 b. ⁷

5 c. ^𝑐

𝑟 d. ¹

2

e. ²¹

4 f. √2 g. – 3 h. −¹

4

i. 8 j. ¹

9 k. 30 l. ¹

4

m. ¹

2 n. −2√7 o. – 2 p. – 4

q. 8

2. a. – 5 b. 0 c. ∞ d. ^𝑎

𝑝

e. 8 f. 32 g. ∞ h. 5

i. ^−9√2

4 j. −⁷

2 k. – 4 l. ³²

243

m. 2 n. ²

3