BAB II LANDASAN TEORI. pembahasan bab-bab berikutnya antara lain tentang model pergerakan harga

Pada bab ini akan dibahas beberapa teori dasar yang diperlukan pada pembahasan bab-bab berikutnya antara lain tentang model pergerakan harga saham, model keseimbangan, metode maximum likelihood estimator, opsi put

Amerika, simulasi Monte Carlo, dan metode least-square. 2.1 Model Pergerakan Harga Saham

Pada subbab ini akan dibahas tentang model pergerakan harga saham dalam bentuk persamaan diferensial stokastik. Pergerakan harga saham dikatakan memenuhi proses stokastik karena nilainya berubah terhadap waktu dengan pola yang tidak terduga. Pergerakan ini dapat digolongkan ke dalam proses stokastik variabel kontinu - waktu kontinu, hal ini disebabkan oleh fakta bahwa harga saham dapat berubah secara acak pada selang waktu tertentu, dan juga dapat berubah pada waktu kapan saja.

Pada tahun 1826 - 1827, R.Brown meneliti gerak partikel yang tidak beraturan untuk kemudian hasilnya sangat berguna untuk memodelkan pergerakan harga saham. Gerak yang tidak beraturan tersebut kemudian disebut gerak Brown (Brownian Motion). Gerak Brown atau juga dikenal dengan proses Wiener pada interval [0,T] adalah proses stokastik Z(t) yang memenuhi tiga kondisi berikut :

2. Z(t) – Z(s) berdistribusi N(0,t-s) untuk semua 0 ≤ s ≤ t. 3. Untuk 0 ≤ s < t < u < v ≤ T, Z(t) – Z(s) dan Z(v) – Z(u) saling

independen.

Selanjutnya gerak Brown tersebut akan digunakan dalam model pergerakan saham yang akan dijelaskan pada bagian selanjutnya. 2.1.1 Model Harga Saham Tanpa Pembayaran Dividen

Misalkan S adalah harga saham pada saat t dan μ merupakan ekspektasi tingkat imbal hasil saham per satuan waktu yang dinyatakan dalam desimal, maka besar imbal hasil yang diharapkan dari harga saham S

sebesar μS. Artinya untuk selang waktu yang cukup kecil δt, ekspektasi kenaikan harga saham S adalah μSδt. Jika volatilitas harga saham selalu nol, maka model pergerakan harga saham adalah

S S t

δ =μ δ (2.1)

Untuk δt→ 0 , maka persamaan di atas dapat ditulis menjadi

dS =μSdt

atau

dS dt S =μ .

Jika persamaan di atas diintegrasikan pada interval [0,T], diperoleh 0

T T

dengan S0 dan ST adalah harga saham pada waktu 0 dan T. Persamaan

diatas menunjukkan harga saham meningkat secara continuously

compounding. μS pada persamaan (2.1) disebut juga dengan proses drift

untuk S.

Pada keadaan sebenarnya, volatilitas akan muncul pada pergerakan harga saham. Dalam jangka waktu yang pendek δt, diasumsikan perubahan tingkat imbal hasil adalah sama terlepas dari seberapa besar harga

sahamnya. Akibatnya, dapat diasumsikan bahwa standar deviasi perubahan harga saham pada selang waktu δt haruslah proporsional dengan harga saham. Maka model (2.1) dengan volatilitas menjadi

dS =μSdt +σSdZ, (2.2)

atau dapat ditulis sebagai

dS dt dZ S =μ +σ

dengan μ adalah ekspektasi tingkat imbal hasil per satuan waktu, σ merepresentasikan volatilitas harga saham, dan Z adalah proses Wiener.

Secara formal dinyatakan, variabel Z mengikuti proses Wiener jika memiliki dua sifat berikut :

1. Perubahan δZ sepanjang periode yang kecil δt adalah

Z t

δ =ε δ

dimana ε adalah bilangan random yang berdistribusi normal standar.

2. Nilai δZ untuk sembarang dua interval kecil yang berbeda pada waktu δt bersifat independen.

Sehingga persamaan (2.2) untuk δt →0 dapat ditulis sebagai

dS =μSdt +σ εS dt . (2.3) Model ini disebut juga model pergerakan harga saham untuk waktu diskrit. Model ini selanjutnya akan digunakan dalam ilustrasi simulasi Monte Carlo pada subbab 2.4.

Menggunakan lemma Ito (Hull,2003), dari persamaan (2.2) juga akan diperoleh 2 ln 2 d S =⎛_⎜μ−σ ⎞_⎟dt +σdZ ⎝ ⎠ .

Dengan demikian perubahan ln(S) antara saat t = 0 dan saat mendatang t =T

, berdistribusi normal dengan mean

2 2 σ μ ⎛ ⎞ − ⎜ ⎟ ⎝ ⎠T dan variansi 2_T σ . Dengan kata lain ln ln ₀ ~ 2 , 2 T S − S N_⎢⎡_⎜⎛μ−σ _⎟⎞T σ T_⎥⎤ ⎝ ⎠ ⎣ ⎦ (2.4) dan 2 0 ln ~ ln , 2 T S N_⎢⎡ S +_⎜⎛μ −σ _⎟⎞T σ T_⎥⎤ ⎝ ⎠ ⎣ ⎦

dengan S_Tadalah harga saham pada saat mendatang t =T, dan S₀adalah harga saham pada saat t = 0. Sifat persamaan (2.4) akan digunakan pada estimasi volatilitas harga saham dan variansi short rate.

Setelah didapat model pergerakan harga saham (2.3) yang berbentuk persamaan differensial stokastik, selanjutnya akan dijelaskan tentang

pengaruh pembayaran dividen terhadap model pergerakan harga saham tersebut.

2.1.2 Pengaruh Pembayaran Dividen pada Model Pergerakan Harga Saham

Pada subbab ini akan dibahas mengenai pengaruh dividen terhadap pergerakan harga saham.

Tiap tahunnya, emiten (perusahaan penerbit saham) biasanya membagikan dividen dalam bentuk uang tunai kepada para pemegang saham perusahaan. Pada saat dimana pemegang saham akan dicantumkan sebagai penerima dividen (waktu tersebut dikenal dengan istilah recording date), para calon investor biasanya akan membeli saham perusahaan

tersebut dengan harapan mereka mendapatkan keuntungan dari pembayaran dividen. Kondisi ini mengakibatkan naiknya permintaan atas saham tersebut. Namun investor pemegang saham tidak banyak yang melepas sahamnya karena juga menginginkan dividen, sehingga suply sedikit dan harga saham akan naik. Sesaat setelah masa recording date berakhir, dikenal dengan

masa ex-dividend date, harga saham akan kembali turun sebesar dividen yang dibayarkan (R.Bali,1998).

Diasumsikan pembayaran dividen diberikan secara rutin dengan tingkat dividen tetap sebesar D. Karena saham akan turun sebesar dividen yang dibayarkan, maka model pergerakan harga saham pada persamaan (2.2) berubah menjadi 

dS =μSdt DSdt− +σSdZ Dan dapat juga ditulis sebagai

( )

dS = μ−D Sdt+σSdZ. (2.5)

Dalam kondisi dimana investor diasumsikan risk neutral, yaitu investor hanya melihat investasi sebatas ekspektasi tingkatimbal hasilnya, investor tersebutakan menerima sebesar nilai yang sama dengan tingkat suku bunga (biasanya tingkat suku bunga bebas risiko) untuk semua jenis sekuritas. Jadi ekspektasi imbal hasil semua jenis sekuritas yang diharapkan oleh investor yang risk neutral adalah sebesar tingkat suku bunga bebas risiko r. Oleh karenanya nilai μ pada persamaan (2.5) dapat digantikan dengan tingkat suku bunga bebas risiko r. Sehingga persamaan (2.5) dapat ditulis sebagai

( )

dS= r D Sdt− +σSdZ (2.6)

Persamaan (2.6) merepresentasikan proses pergerakan harga saham dengan satu faktor stokastik yaitu volatilitas harga saham. Persamaan ini akan digunakan untuk mensimulasikan lintasan harga saham pada metode

Sebelum kita dapat menggunakan persamaan (2.6), parameter yang digunakan haruslah terlebih dahulu kita ketahui. Oleh karena itu, pada subbab berikut akan dijelaskan bagaimana mengestimasi parameter yang digunakan pada persamaan (2.6).

2.1.3 Estimasi Parameter

Pada subbab ini akan dijelaskan bagaimana mengestimasi parameter yang dibutuhkan persamaan (2.6), yaitu tingkat suku bunga bebas risiko r,

tingkat hasil dividen (dividend yield) D, dan volatilitas harga saham σ. Tingkat suku bunga bebas risiko r merupakan suku bunga yang diasumsikan didapat dari investasi pada instrumen keuangan yang tidak mengandung risiko default, yaitu risiko gagal dalam membayar bunga dan pokok investasi. Di Indonesia, instrumen tersebut adalah Sertifikat Bank Indonesia (SBI), dimana pemerintah menjamin sepenuhnya pengembalian investasi pada instrumen tersebut. Oleh karena itu, tingkat suku bunga bebas risiko r di Indonesia merujuk pada suku bunga SBI. Selanjutnya akan

dijelaskan estimasi parameter D.

Estimasi nilai D didapat dengan membagi jumlah dividen yang diterima oleh pemegang saham selama satu tahun dengan harga saham saat ini. Misalkan sebuah emiten membagikan dividen sebanyak n kali yang besarnya

dv1, dv2,dv3,…, dvn pada tanggal yang berlainan dalam jangka waktu satu

1 2 ... n dv dv dv D S + + + = .

Pada kasus dimana emiten tidak membagikan dividen selama satu tahun, maka D = 0. Selanjutnya akan dijelaskan bagaimana mengestimasi nilai volatilitas harga saham σ.

Volatilitas harga saham mengukur ketidakpastian imbal hasil yang diberikan saham yang dapat diukur dengan standar deviasi dari imbal hasil yang diberikan saham selama jangka waktu tertentu (Hull,2003).

Untuk mengestimasi σsecara empiris, harga saham diamati dalam interval waktu yang tetap, misalnya setiap hari, setiap minggu atau bulan. Misalkan

n + 1 = jumlah pengamatan

Si = harga saham pada akhir interval ke-i (i = 0, 1, .. ., n)

τ = panjang interval waktu dalam setahun dan misalkan 1 1 ln i ln ln i i i i S u S S S₋ − ⎛ ⎞ = _{⎜ ⎟}= − ⎝ ⎠ untuk i = 1,2, . . ., n. Besar estimasi standar deviasi s dari uiadalah

2 1 1 ( ) 1 n i i s u u n = = − −

∑

,

dimana u adalah mean dari ui. Dari persamaan (2.4), standar deviasi dari ui

adalah σ τ , dengan kata lain s dapat mengestimasi σ τ . Kemudian volatilitas σ itu sendiri dapat diestimasi oleh σ∧ dengan

s

σ τ

∧

= .

Misalkan harga saham ditransaksikan sebanyak T hari, maka panjang interval waktu dalam setahun adalah τ= 1/T, sehingga

1 s

s T T

σ∧ = = .

Dengan estimasi parameter yang didapat, maka model pergerakan harga saham (2.6) dapat digunakan.

Selain persamaan (2.6) yang menyatakan volatilitas harga saham sebagai faktor stokastik, pada skripsi ini juga akan dilihat jika tingkat suku bunga bebas risiko sebagai faktor stokastik. Secara spesifik, diasumsikan bahwa r tidak lagi konstan, tetapi r dapat berubah setiap saat sesuai dengan teori mean reversion, dan mengikuti model keseimbangan Vasicek berikut

( )

dr =a b r dt− +νdW .

Penjelasan lebih lanjut mengenai model ini akan dijelaskan pada subbab berikut ini.

2.2 Model Keseimbangan

Pada subbab ini akan dijelaskan mengenai model keseimbangan. Model keseimbangan merupakan model yang menggambarkan perilaku atau perubahan tingkat suku bunga jangka pendek (short rate), r. Dari model ini dapat dilihat pengaruh dari proses r terhadap harga saham dan terhadap aset derivatif dari saham. Short rate r pada waktu t adalah tingkat suku bunga yang digunakan pada periode waktu yang sangat pendek pada waktu t. Atau disebut juga short rate sesaat.

Dalam suatu periode waktu yang sangat singkat antara t dan t + δt, secara rata-rata seorang investor akan mendapatkan imbal hasil sebesar

r(t)δt. Semua proses r yang akan dibahas pada bagian ini merupakan proses dalam risk neutral.

Pada model keseimbangan dengan satu faktor, proses pergerakan r

dipengaruhi oleh volatilitas r itu sendiri sebagai faktor ketidakpastian. Secara umum, model tersebut dapat dituliskan sebagai suatu persamaan differensial stokastik dengan bentuk

( ) ( )

dr =m r dt s r dW+ (2.7)

dengan drift sesaat m dan standar deviasi sesaat s diasumsikan merupakan fungsi dari r tanpa bergantung pada waku.

Sifat pergerakan yang mengikuti proses stokastik pada tingkat suku bunga jangka pendek r yang ditunjukkan oleh persamaaan (2.7) dan harga saham S pada persamaan (2.2) tidak sepenuhnya sama. Perbedaan yang

paling utama adalah tingkat suku bunga pada akhirnya terlihat akan menuju suatu level rata-rata tingkat suku bunga yang diperoleh dalam jangka waktu yang lama, dan proses ini disebut sebagai mean reversion. Sedangkan pergerakan harga saham mengikuti kinerja dari perusahaan, dimana harga saham akan cenderung terus naik jika kinerja perusahaan terus ditingkatkan. Begitu juga dengan sebaliknya, akan cenderung turun apabila kinerja

perusahaan terus menurun.

Sebuah argumentasi ekonomi yang mendukung teori mengenai mean reversion menyatakan bahwa ketika suku bunga tinggi, ekonomi cenderung melambat dan terjadi rendahnya permintaan kredit dari peminjam. Sebagai dampaknya, suku bunga akan turun. Dan ketika suku bunga rendah, akan terjadi kecenderungan naiknya permintaan kredit dari peminjam dan suku bunga akan cenderung naik.

Untuk lebih jelasnya, perhatikan ilustrasi pada gambar berikut:

Leve

Gambar 2.1 Mean Reversion

Reversion Level

Tingkat suku bunga yang tinggi memiliki trend negatif

Tingkat suku bunga yang rendah memiliki trend positif Tingkat suku bunga

Berikut ini akan dijelaskan model keseimbangan yang akan digunakan dalam skripsi ini.

2.2.1 Model Vasicek

Merujuk pada teori mean reversion yang telah dijelaskan, Vasicek pada tahun 1977 memperkenalkan model keseimbangan berdasarkan teori tersebut. Misalkan r menuju suatu level rata-rata (reversion level) tingkat suku bunga yang disebut b. Kemudian kelajuan r menuju level b adalah sebesar a. Maka suku drift pada persamaan (2.7) menjadi (a b r− ) dan model (2.7) menjadi

( ) _r

dr =a b r dt s dW− + . (2.8)

sr pada persamaan diatas kemudian diasumsikan sebagai konstanta ν yang

merupakan standar deviasi sesaat dari r, dan W adalah proses Wiener, maka persamaan (2.8) menjadi

( )

dr =a b r dt− +νdW . (2.9)

Model (2.9) disebut model Vasicek. Model tersebut akan digunakan dalam mensimulasikan short rate yang kemudian digunakan untuk membentuk lintasan harga saham. Model Vasicek merupakan contoh proses Ornstein-Uhlenbeck, atau biasa dikenal dengan proses mean reverting, yaitu proses stokastik r yang diberikan persamaan differensial stokastik berikut

( )

dr =θ μ−r dt+σdW ,

(Wikipedia, 2008). Proses Ornstein-Uhlenbeck adalah solusi unik dari persamaan berikut 0 , t t t dX cX dt dW X x σ = − + ⎧ ⎨ ₌ ⎩ (2.10)

dimana c sembarang konstanta. Solusi persamaan (2.10) dapat ditulis secara eksplisit sebagai berikut

0 t ct ct cs t s X =xe− +σe−

∫

e dW− (Yolcu, 2005).

Untuk menghitung short rate menggunakan persamaan (2.9),

diperlukan solusi rekursif dari persamaan tersebut. Subbab berikut ini akan menjelaskan penurunan persamaan tersebut.

2.2.2 Solusi Rekursif Model Vasicek

Merujuk pada model (2.9), misalkan X_t = −r_t b dengan r_t short rate pada saat t. X_tadalah solusi persamaan differensial stokastik

t t t

dX = −aX dt+νdW , yang merupakan proses Ornstein-Uhlenbeck. Misalkan pula , at t t Y =e X (2.11) maka

[

]

. at at t t t at at t t t at t dY ae X dt e dX ae X dt e aX dt dW e dW ν ν = + = + − + = Sehingga 0 0 . t as t s Y =Y +

∫

e νdW (2.12) Dari (2.11), maka 0 0 0 0. Y =e X = X (2.13)

Dari (2.11), (2.12) dan (2.13), maka

0 0 0 0 . t at as t s t at as t s e X X e dW X e X e dW ν ν − = + ⎡ ⎤ = _⎢ + _⎥ ⎣ ⎦

∫

∫

KarenaX_t = −r_t b, maka r_tdapat dihitung sebagaimana berikut

(

)

0 0 ( ) 0 0 ( ) 0 0 ( ) ( ) 1 , t at at as t s t at a t s s t at at a t s s r e r b e e dW b e r b e dW b e r b e e dW ν ν ν − − − − − − − − − = − + + = − + + = + − +

∫

∫

∫

dimana r₀adalah short rate pada saat t = 0. Sehingga untuk 0 < u < t

(

)

( ) ( ) ( ) 0 1 t a t u a t u a t s t u s r ₌e− − r ₊b ₋e− − ₊ν

∫

e− − dW _(2.14) Dari persamaan (2.14) berdasarkan persamaan (2.4), ∀ ≤u t rt berdistribusi

(

)

( ) ₁ ( ) a t u a t u u e− − r ₊b ₋e− − dan variansi 2 ₂ 2 ( ) ₁ 2 ( ) 2 t a t u a t u r u u e dW e a ν σ _≡⎛ν − − ⎞ _{= ⎡ −} − − _⎤ ⎜ ⎟ _{⎣ ⎦} ⎝

∫

⎠ .

Untuk mensimulasikan r pada waktu 0 = t0 < t1 < ... < tn, persamaan

(2.14) menjadi

(

)

1 1 ( ) ( ) 1 i i i 1 i i 2. a t t a t t t t r r e− +− r b e− +− σ ε + = + − +

dengan ε₂bilangan random yang berdistribusi N(0,1). Atau dapat ditulis pula sebagai

(

)

2 1 2 1 1 . 2 adt adt adt i i e r e r b e a ν − ε − − + − = + − + , i = 0, 1, …, n-1. (2.15)

Persamaan (2.15) ini akan digunakan untuk membentuk lintasan short rate

yang dibutuhkan untuk simulasi harga saham.

Untuk dapat menggunakan model (2.15), terlebih dahulu kita harus mengestimasi parameter pada model tersebut. Subbab berikut ini akan dijelaskan estimasi parameter model (2.15) dengan menggunakan maximum likelihood estimator (MLE).

2.3 Maximum Likelihood Estimator (MLE)

Pada subbab ini akan dibahas mengenai metode MLE dalam

mengestimasi parameter model Vasicek, yaitu , ,dan b a ν . MLE merupakan metode statistik yang sering digunakan untuk mendapatkan taksiran

parameter untuk model matematika dari sekumpulan observasi.

Data short rate yang akan diobservasi diasumsikan berdistribusi normal. Data tersebut diambil dari sembarang sampel dari populasi yang berdistribusi normal dengan parameter , ,dan b a ν yang belum diketahui. Data short rate merupakan data yang bergantung dengan data sebelumnya. MLE adalah metode yang memaksimumkan fungsi likelihood yang dapat diturunkan dari conditional probability density function (pdf bersyarat) variabel

ri+1 yang bersyarat variabel ri.

Diketahui bahwa probability density function (pdf) untuk distribusi normal adalah

(

)

2 2 2 1 ( | , ) exp 2 2 ⎛ ₋ ⎞ ⎜ ⎟ = − ⎜ ⎟ ⎝ ⎠ x f x μ σ μ σ πσ .

Sehingga untuk distribusi N(0,1) adalah

2 1 2 1 ( | 0,1) 2 x f x e π − = .

Pdf bersyarat dari variabel ri+1 yang bersyarat variabel sebelumnya ri

ditunjukkan oleh

(

)

(

(

)

)

2 1 1 ₂ 2 1 1 | ; , , exp 2 2 adt adt i i i i r r r r r e b e f r r b aσ σ πσ − − − + ⎡ _{− − −} ⎤ ⎢ ⎥ = _⎢− _⎥ ⎢ ⎥ ⎣ ⎦

Dengan σ_r adalah bentuk sederhana dari 2 2 21 2 adt r e a σ =ν − − .

Diketahui fungsi likelihood untuk sampel sebanyak n buah yang saling

independent identically distributed (i.i.d) adalah

(

)

(

)

(

(

)

)

2 1 2 1 1 2 2 1 1 1 | ; , , | , , exp 2 2 − − − = + = ⎡ _{− − −} ⎤ ⎢ ⎥ ⎛ ⎞ _{⎢ ⎥} = =_{⎜ ⎟} − ⎢ ⎥ ⎝ ⎠ ⎢ ⎥ ⎣ ⎦

∑

∏

n adt adt n i i n i i i r i r i r r r r e b e f r r b aσ f r b aσ πσ σ atau

(

)

(

)

(

(

)

)

2 2 1 2 1 1 2 2 1 1 | ; , , exp 2 2 − − − = + ⎡ _{− + − − −} ⎤ ⎢ ⎥ ⎛ ⎞ ⎢ ⎥ =_{⎜ ⎟} − ⎢ ⎥ ⎝ ⎠ ⎢ ⎥ ⎣ ⎦

∑

n adt adt n i i i i i r r r r r n r r e b e f r r b aσ πσ σ

Fungsi log-likelihood dari himpunan sampel random (r0, r1, …, rn) dapat

diturunkan dari fungsi likelihood.

(

)

(

)

(

)

L 1 1 2 1 2 1 , , ln | ; , , 1 ln(2 ) ln( ) 1 2 2 n r i i r i n adt adt r i i i r b a f r r b a n n r r e b e σ σ π σ σ − = − − − = = ⎡ ⎤ = − − − _⎣ − − − _⎦

∑

∑

Sehingga maksimum dari fungsi log-likelihood dapat diperoleh ketika turunan parsial fungsi tersebut sama dengan nol.

(

b a, , r

)

0 b σ ∂ = ∂ L

(

)

1 2 1 1 1 0 n adt adt i i i r r r e b e σ − − − = ⎡ ⎤ ⇔

∑

_⎣ − − − _⎦=

(

)

1 1 1 n adt i i i adt r r e b n e − − = − ⎡ − ⎤ ⎣ ⎦ ⇔ = −

∑

(

)

(

)(

)

(

)

(

)(

)

(

)

2 1 1 2 1 1 1 2 1 1 , , 0 . 0 1 ln r adt n adt i i i i r n i i i n i i b a a dt e r b r b e r b r b r b a dt _{r b} σ σ − − − − = − = − = ∂ = ∂ ⎡ ⎤ ⇔ − _⎣ − − − − _⎦= − − ⇔ = − −

∑

∑

∑

L

(

)

(

)

(

)

(

)

(

)

2 1 3 1 2 2 1 1 , , 0 1 0 1 r r n adt i i i r r n adt r i i i b a n r b e r b r b e r b n σ σ σ σ σ − − = − − = ∂ = ∂ ⎡ ⎤ ⇔ − _⎣ − − − _⎦ = ⎡ ⎤ ⇔ = _⎣ − − − _⎦

∑

∑

L (2.16) Masalah yang ditemukan pada perhitungan (2.16) diatas adalah, solusi yang bergantung satu sama lainnya. Akan tetapi, a dan b tidak bergantung pada σr,

jika kita mengetahui a atau b akan mudah mengetahui yang lain.

Untuk mencari b dapat dilakukan dengan mensubstitusi kondisi a

kedalam b. Sebelumnya akan diubah terlebih dahulu, notasi dari kondisi a

dan b menggunakan notasi yang sama yaitu

1 1 n x i i r r₋ = =

∑

, 1 n y i i r r = =

∑

, 2 1 1 n xx i i r r₋ = =

∑

, 2 1 n yy i i r r = =

∑

, ₁ 1 n xy i i i r r r₋ = =

∑

sehingga

(

1

)

adt y x adt r e r b n e − − − = − dan

2 2 1 ln 2 xy x y xx x r br br nb a dt r br nb − − + = − − + . Dengan mensubstitusi a ke b didapat

2 2 2 2 2 1 2 xy x y y x xx x xy x y xx x r br br nb r r r br nb b r br br nb n r br nb ⎛ − − + ⎞ − ⎜_⎜ ⎟_⎟ − + ⎝ ⎠ = ⎛ − − + ⎞ − ⎜ ⎟ ⎜ _{− +} ⎟ ⎝ ⎠ maka

(

) (

)

(

) (

)

(

)

(

)

(

)

(

) (

)

2 2 2 2 2 2 2 2 y xx x xy x y x xx x xy x y y xx x xy x x y y x xx xy y x r r br nb r br br nb r nb r br nb r br br nb r r r r b r r r b n r r r r b r r − + − − − + = − + − − − + − + − + − = − + − dan

(

)

(

2

)

xx xy x x y y xx x xy nb r −r −b r −r r =r r −r r .

Sehingga kita dapatkan solusi untuk masing-masing parameter sebagai berikut

(

)

(

2

)

y xx x xy xx xy x x y r r r r b n r r r r r − = − − − 2 2 1 ln 2 xy x y xx x r br br nb a dt r br nb − − + = − − +

(

)(

)

(

)

2

2 1 ₂ adt 2adt _{2 1} adt adt 2 ₁ adt

r _n ryy e rxy e rxx b e ry e rx nb e σ ₌ ⎡ ₋ − ₊ − _{− −} − ₋ − _{+ −} − ⎤ ⎢ ⎥ ⎣ ⎦ 2 2 2 1 r adt a e ν σ= ₋ − .

Setelah pembahasan model pergerakan harga saham dan tingkat suku bunga, selanjutnya akan dibahas mengenai opsi put Amerika yang menggunakan saham sebagai aset induk.

2.4 Opsi Put Amerika

Pada subbab kali ini akan dijelaskan mengenai opsi put Amerika. Opsi

put Amerika adalah opsi yang memberikan hak kepada holder untuk menjual sejumlah saham yang ia miliki dengan harga tertentu dimana opsi tersebut dapat dieksekusi sebelum atau pada saat jatuh tempo.

Sebelum pembahasan lebih jauh tentang opsi put Amerika, akan dijelaskan terlebih dahulu tentang payoff , posisi in the money, posisi out of the money, dan posisi at the money pada opsi put.

Payoff merupakan sejumlah uang tunai yang diterima oleh holder saat ia mengeksekusi opsi tersebut. Untuk lebih memahami tentang pengertian

payoff, perhatikan contoh berikut.

Misalkan terdapat suatu opsi put saham dengan harga eksekusi E dan harga saham S

t (0 ≤ t ≤ T), dengan T adalah waktu jatuh tempo. Jika saat t,

St < E ,maka holder akan mengeksekusi opsi tersebut karena ia dapat

menjual saham dengan harga E yang lebih mahal dari St, sehingga payoff

yang diterimanya sebesar E - St. Akan tetapi, jika St E, holder tidak harus

mengeksekusi opsi tersebut, karena ia dapat menjual saham yang dimilikinya di pasar dengan harga yang lebih mahal atau sama dengan harga eksekusi

E, sehingga payoff yang diterimanya adalah nol. Dengan demikian, dapat disimpulkan bahwa payoff yang diterima oleh seorang holder saat waktu t

adalah sebesar P(t) = max(E-St,0).

Untuk lebih jelasnya perhatikan ilustrasi berikut.

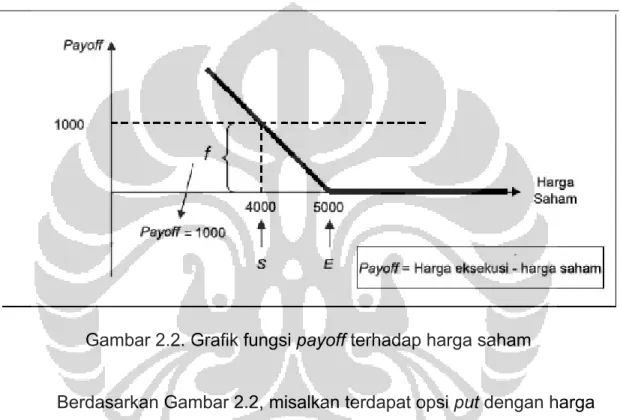
Gambar 2.2. Grafik fungsi payoff terhadap harga saham

Berdasarkan Gambar 2.2, misalkan terdapat opsi put dengan harga eksekusi E sebesar Rp 5.000,00, dan harga saham pada saat t yaitu S

t

sebesar Rp 4.000,00. Maka payoffP yang diterima holder jika ia

mengeksekusi opsi put tersebut pada saat t adalah sebesar Rp 5000,00 – Rp 4.000,00 = Rp 1.000,00.

Suatu opsi put dikatakan berada dalam posisi in the money jika saat mengeksekusi opsi, harga saham lebih rendah dari harga eksekusi yang tertera pada opsi atau St < E. Sebaliknya, jika harga saham lebih tinggi dari

money. Sedangkan ketika harga saham sama dengan harga eksekusi atau St = E, opsi put berada pada posisi at the money.

Saat waktu t, jika harga saham berada dalam posisi out of the money

maka keputusan yang paling baik adalah tidak mengeksekusi opsi saat itu. Tetapi jika harga saham berada dalam posisi in the money, holder harus menentukan apakah ia akan mengeksekusinya sekarang atau disaat

mendatang jikalau ia berfikir mendapat payoff yang lebih besar lagi. Karena adanya hak eksekusi awal dan keputusan yang harus diambil terkait waktu dimana hak tersebut akan dilaksanakan oleh holder, maka perlu bagi holder

untuk mengetahui kapan saat-saat yang optimal untuk mengeksekusi opsi yang dimilikinya.

Selanjutnya akan dijelaskan tentang simulasi Monte Carlo yang dapat digunakan untuk membuat simulasi lintasan dari aset induk opsi yaitu harga saham.

2.5 Simulasi Monte Carlo

Simulasi Monte Carlo atau Monte Carlo Simulation (MCS) dalam proses stokastik adalah metode yang secara iteratif mengevaluasi model stokastik menggunakan bilangan random sebagai input. MCS dapat dikategorikan sebagai metode pengambilan sampel (sampling), karena inputnya dibangkitkan secara random dari suatu distribusi probabilitas untuk mensimulasikan proses sampling dengan data yang aktual.

Untuk lebih jelasnya, perhatikan ilustrasi berikut. Misalkan ekspektasi tingkat imbal hasil saham sebesar 14% per tahun dan standar deviasi

(volatilitas) dari imbal hasil tersebut sebesar 20% per tahun. Misalkan juga δt

= 0,01, dengan kata lain kita membagi waktu satu tahun menjadi interval kecil dengan panjang 3,65 hari. Maka dari model pergerakan harga saham waktu diskrit kita dapatkan

0,14 0,01. 0,2 0,01

S x S S

δ = + ε

atau

δS =0,0014S+0,02εS. (2.17) harga saham (2.17) dapat disimulasikan dalam bentuk lintasan dengan

sampling berulang-ulang bilangan random ε dan mensubstitusikannya satu-persatu kedalam persamaan (2.17). Bilangan random ε merupakan data sampel yang berdistribusi N(0,1). Salah satu cara membangkitkan bilangan random tersebut adalah dengan perintah ‘rand( )’ pada Microsoft Excel atau dengan Matlab.

Banyak bilangan random ε yang diambil sesuai dengan banyaknya interval waktu selama masa pengamatan. Pada contoh diatas, maka banyaknya bilangan ε yang diambil adalah 100 buah, yaitu 365 hari dibagi dengan panjang interval 3,65.

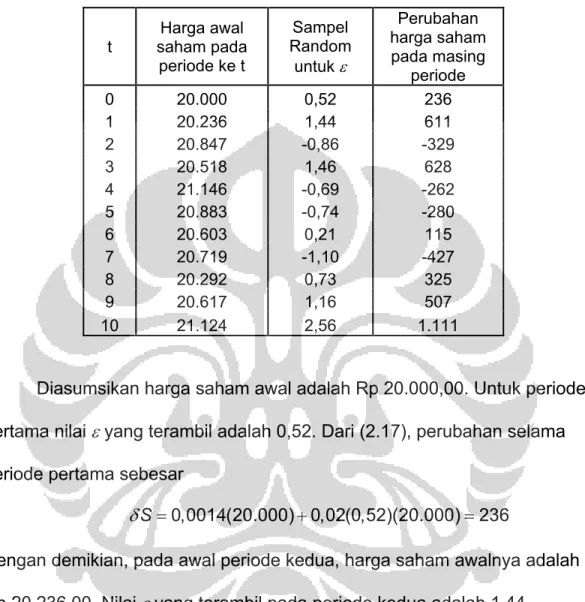
Tabel 2.1. Simulasi Monte Carlo untuk harga saham. t Harga awal saham pada periode ke t Sampel Random untuk ε Perubahan harga saham pada masing periode 0 20.000 0,52 236 1 20.236 1,44 611 2 20.847 -0,86 -329 3 20.518 1,46 628 4 21.146 -0,69 -262 5 20.883 -0,74 -280 6 20.603 0,21 115 7 20.719 -1,10 -427 8 20.292 0,73 325 9 20.617 1,16 507 10 21.124 2,56 1.111

Diasumsikan harga saham awal adalah Rp 20.000,00. Untuk periode pertama nilai εyang terambil adalah 0,52. Dari (2.17), perubahan selama periode pertama sebesar

0,0014(20.000) 0,02(0,52)(20.000) 236

S

δ = + =

Dengan demikian, pada awal periode kedua, harga saham awalnya adalah Rp 20.236,00. Nilai εyang terambil pada periode kedua adalah 1,44. Sehingga dari (2.17), perubahan selama periode kedua adalah

0,0014(20.236) 0,02(1,44)(20.236) 611

S

δ = + = .

Maka, pada awal periode ketiga harga saham awalnya adalah Rp 20.847,00, dan begitu seterusnya.

Dalam perkembangannya, metode MCS dapat diperluas

akhirnya dapat menentukan nilai opsi. Ekspektasi payoff dalam kondisi risk neutral dihitung menggunakan prosedur sampling (Hull,2003). Kemudian didiskonto pada suku bunga bebas risiko. Untuk lebih jelasnya, berikut ini akan dijelaskan prosedur untuk menentukan nilai opsi.

Misalkan suatu opsi dengan aset induk S yang menghasilkan payoff di waktu T. Dengan asumsi suku bunga konstan, kita dapat menilai opsi

tersebut dengan langkah-langkah berikut : 1. Ambil sampel lintasan S secara random 2. Hitung payoff yang didapat dari opsi

3. Ulangi langkah 1 dan 2 untuk mendapatkan banyak sampel payoff

yang didapat opsi

4. Hitung rata-rata sampel payoff untuk mendapatkan estimasi dari ekspektasi payoff

5. Diskontokan ekspektasi payoff pada suku bunga bebas risiko untuk mendapatkan estimasi nilai opsi.

Pada skripsi kali ini langkah-langkah diatas tidak dibahas secara lengkap, karena hanya langkah 1, 2 dan 3 yang akan digunakan pada metode Least-Square Monte Carlo yang akan dibahas pada bab III. Berikut ini akan dijelaskan bagaimana membentuk lintasan harga saham dan short rate.

Misalkan proses pergerakan harga saham mengikuti proses pada persamaan (2.6) berikut :

( ) .

dS= r D Sdt− +σSdZ

Untuk mensimulasi lintasan harga saham, kita bagi jangka waktu berlaku opsi menjadi N buah interval kecil dengan panjang δt kemudian aproksimasi

persamaan diatas dengan

1

( ) ( ) ( ) ( ) ( )

S t+δt −S t = r D S t t− δ +σS t ε δt (2.18) dengan ε1adalah sampel random yang berdistribusi N(0,1) dan nilai awal S

pada t = 0 yang diberikan. ε δ₁ tdapat menggantikan dZ karena sifat Z yang mengikuti proses Wiener, sehingga untuk perubahan δZ sepanjang periode yang kecil δt adalah δZ =ε δ₁ t .

Pada prakteknya, biasanya akan lebih akurat untuk mensimulasi ln S ketimbang S. Dari lemma Ito, ln S pada (2.6) mengikuti proses

2 ln 2 d S =⎛_⎜r D− −σ ⎞_⎟dt+σdZ ⎝ ⎠ maka 2 1 ln ( ) ln ( ) 2 S t+ t − S t =⎛_⎜r D− − ⎞_⎟ t+ t ⎝ ⎠ σ δ δ σε δ 2 1 ( ) ( ).exp 2 S t+ t =S t _⎢⎡_⎜⎛r D− − ⎞_⎟ t+ t⎤_⎥ ⎝ ⎠ ⎣ ⎦ σ δ δ σε δ atau 2 1 .exp 1 2 i i S₊ =S _⎢⎡_⎜⎛r D− −σ _⎟⎞dt+σε dt_⎥⎤ ⎝ ⎠ ⎣ ⎦, i = 0, 1, …, n-1. (2.19)

Persamaan ini digunakan untuk membentuk lintasan S dengan cara yang sama dengan persamaan (2.18). Perbedaannya adalah persamaan (2.18) akan akurat jika δt→0, sedangkan persamaan (2.19) menghasilkan nilai yang akurat untuk semua δt karena merupakan solusi untuk persamaan (2.6).

Dalam skripsi ini, selain untuk mensimulasi lintasan harga saham, MCS juga digunakan untuk mensimulasi lintasan tingkat suku bunga bebas risiko jangka pendek (short rate). Simulasi tersebut menggunakan persamaan (2.15) yang telah dijelaskan yaitu

(

)

2 1 2 1 1 . 2 adt adt adt i i e r e r b e a ν − ε − − + − = + − + , i = 0, 1, …, n-1.

Dimana ε2adalah sampel random yang berdistribusi N(0,1) dan nilai awal r

pada t = 0 yang diberikan.

Harga saham dan tingkat suku bunga diasumsikan memiliki goncangan yang saling berkorelasi dan dapat dinyatakan dengan

dZ(t)dW(t) = ρdt

dengan dZ adalah proses Wiener untuk persamaan harga saham dan dW

untuk short rate, maka ε1pada (2.19) dan ε2pada (2.15) memiliki koefisien

korelasi konstan yang kita sebut ρ. Sehingga 2 2 1 3 2 ( ) ( ).exp 1 2 i i S t₊ =S t _⎢⎡⎛_⎜r D− −σ _⎟⎞dt+σ dt ⎡_⎣ −ρ ε +ρε ⎤_⎦⎤_⎥ ⎝ ⎠ ⎣ ⎦ (2.20)

dengan {ε2(i),ε3(i)}, i = 1,…,n bilangan random normal standar bivariat yang

Selanjutnya akan dijelaskan tentang metode least-square yang akan digunakan dalam salah satu tahapan metode Least-Square Monte Carlo. 2.6 Metode Least-Square

Pada subbab ini akan dijelaskan mengenai metode least-square. Metode least-square adalah salah satu cara untuk menyelesaikan analisis regresi, yaitu metode yang digunakan untuk memodelkan data numerik yang didapat dari observasi dengan cara meminimalkan sum square error dari selisih antara nilai observasi dan estimasi. Data numerik tersebut pada umumnya bisa diklasifikasi menjadi sebuah variabel tak bebas dan satu atau lebih variabel bebas. Model yang paling sederhana adalah model regresi linear dengan sebuah variabel bebas x (regressor) yang memiliki relasi berupa garis lurus dengan variabel tak bebas y. Hubungan ini dimodelkan dalam bentuk berikut

0 1

i i i

y =β +βx +ω i = 1, 2, …, n (2.21) dengan β₀(intercept) dan β₁(slope) merupakan konstanta dan ω adalah komponen random error. Error pada model (2.21) diasumsikan memiliki rata-rata nol dan variansi _σ2_{. Sebagai tambahan, biasanya diasumsikan pula} bahwa antara error disetiap titik observasi tidak saling berkorelasi. Artinya nilai sebuah error tidak dipengaruhi oleh nilai sembarang error lainnya. Parameter β₀dan β₁disebut juga koefisien regresi. Interpretasi untuk

1

perubahan nilai rata-rata variabel y sebesar β₁. Sedangkan untuk β₀ memiliki interpretasi bahwa jika variabel x bernilai nol maka nilai rata-rata y

sebesar β₀.

Parameter β₀dan β₁dapat diestimasi menggunakan sampel. Misalkan kita memiliki sejumlah n buah pasang data (y1,x1), (y2,x2), … , (yn,xn). Metode

least-square akan digunakan untuk mengestimasi β₀dan β₁sedemikian sehingga jumlah kuadrat dari selisih antara nilai observasi yi dengan nilai

aproksimasi y∧_iakan mempunyai nilai yang minimum.

Dengan demikian kriteria least-square untuk persamaan (2.21) adalah sebagai berikut

(

_{0 1}

)

(

_{0 1}

)

2 1 , n _i ( _i) i S β β y β β x = =

∑

− + .

Estimator least-square β₀dan β₁yang kita sebut β∧₀dan β∧₁,haruslah memenuhi 0 1 0 , 0 S β β β ∧ ∧ ∂ ₌ ∂ dan 0 1 1 , 0 S β β β ∧ ∧ ∂ ₌ ∂ .

Sehingga akan kita dapatkan nilai estimator sebagai berikut

1 1 1 0 1 n n i i i i y x y x n n β β β ∧ ∧ ∧ = = =

∑

−

∑

= − dan

1 1 1 1 2 1 2 1 n n i i n i i i i i n i n i i i y x y x n x x n β = = ∧ = = = ⎛ ⎞⎛ ⎞ ⎜ ⎟⎜ ⎟ ⎝ ⎠⎝ ⎠ − = ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ −

∑

∑

∑

∑

∑

.

Parameter β∧₀dan β∧₁pada persamaan diatas merupakan estimator least-squares dari masing-masing parameter. Dengan demikian model regresi linear sederhana dapat dinyatakan dengan

1 0

i i

y∧ =β β∧ + ∧ x . (2.23) Selisih antara nilai pengamatan y_idan nilai estimasi y∧_i yang

berkorespondensi disebut sebagai residual. Secara matematis, residual ke-i

adalah 1 0 , i i i i i e =y −y∧ =y −_⎜⎛β β∧ + ∧ x ⎞_⎟ ⎝ ⎠ i = 1, 2, …, n.

Residual menjadi bagian penting di dalam hal kita akan menyelidiki ketepatan model regresi yang didapat dan dalam mendeteksi penyimpangan dari

asumsi dasar.

Selain model dengan satu variabel bebas, terdapat pula kondisi dimana terdapat banyak variabel bebas yang mempengaruhi satu variabel tak bebas, yaitu model regresi dengan lebih dari satu variabel regressor . Model ini disebut juga model regresi berganda. Model tersebut secara umum dinyatakan sebagai berikut

0 1 , k i j ij i j y β β x ω = = +

∑

+ i = 1, 2, …, n. . (2.24) Selain bentuk-bentuk diatas, terdapat model regresi lain yang akan digunakan pada skrpsi ini yaitu regresi polinomial. Sebagai contoh , regresi polinomial order dua dengan satu variabel

2

0 1 2

y =β +β x+β x +ω (2.25) dan regresi polinomial order dua dengan dua variabel

2 2

0 1 1 2 2 11 1 22 2 12 1 2

y =β +β x +β x +β x +β x +β x x +ω. (2.26) Polinomial digunakan manakala terjadi kondisi dimana variabel y membentuk kurva yang tidak linear.

Model regresi untuk sampel yang berhubungan dengan persamaan (2.26) dapat ditulis sebagai berikut

2 2

0 1 1 2 2 11 1 22 2 12 1 2

i i i i i i i i

y =β +βx +β x +β x +β x +β x x +ω (2.27) Dalam skripsi ini, fungsi ekspektasi bersyarat yang digunakan pada langkah ke dua pada metode Least-Square Monte Carlo (LSM) yang akan dibahas pada bab III adalah menggunakan persamaan (2.27), dengan variabel harga saham dan tingkat suku bunga sebagai variabel regressor dan variabel tak bebasnya adalah nilai diskonto payoff mendatang. Dalam notasi matriks, model (2.27) dapat ditulis sebagai

y X= β ω+ dimana

y = 1 2 : : n y y y ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ , X = 2 2 11 12 11 12 11 12 2 2 21 22 21 22 21 22 2 2 31 32 31 32 31 32 2 2 1 2 1 2 1 2 1 1 1 : : : : : : 1 _{n n n n n n} x x x x x x x x x x x x x x x x x x x x x x x x ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ β = 0 1 2 11 22 12 β β β β β β ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ , ε = 1 2 : : n ω ω ω ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ .

Fungsi least-square dari model (2.27) adalah

(

)

(

)

2 2 2 0 1 2 11 22 12 0 1 1 2 2 11 1 22 2 12 1 2 1 ( , , , , , ) n _{i i i i i i i} i S β β β β β β y β βx β x β x β x β x x = =

∑

− + + + + + (2.28) Persamaan (2.28) dapat pula ditulis sebagai berikut

( ) S β = 2 1 n i i ω =

∑

=ω ω' =(y X− β)'(y X− β). sehingga ( ) ' ' ' ' ' ' = ' 2 ' ' ' ' S y y X y y X X X y y X y X X β β β β β β β β = − − + − +

Fungsi S diatas harus diminimumkan dengan pemilihan β β β β β β₀, , ,_{1 2 11}, ₂₂, ₁₂ yang sesuai. Estimator least-square dari β β β β β β₀, , ,_{1 2 11}, ₂₂, ₁₂ harus memenuhi

0 1 2 11 22 12 0 _{, , , , ,} 0 S β β β β β β β ∧ ∧ ∧ ∧ ∧ ∧ ∂ = ∂ dan

0, ,1 2, 11, 22, 12 0, 1, 2, 11, 22,dan 12. j S j β β β β β β β ∧ ∧ ∧ ∧ ∧ ∧ ∂ _{= =} ∂

Maka estimator least-square harus memenuhi

2 ' 2 ' 0 S X y X X β β β ∧ ∧ ∂ _{= − + =} ∂

yang dapat disederhanakan menjadi

' '

X Xβ∧ = X y (2.29)

Persamaan (2.29) merupakan persamaan normal least-square. Untuk menyelesaikannya, kalikan dua ruas dengan invers dariX X' . Maka , estimator least-square dari β adalah

1 ( ' )X X X y'

β∧ ₌ − _{. (2.30)}

Dari perhitungan diatas, akan diperoleh taksiran parameter dari (2.27), sehingga model estimasi yang didapat adalah

2 2

0 1 1 2 2 11 1 22 2 12 1 2

i i i i i i i

y∧ =β∧ +β∧ x +β∧ x +β∧ x +β∧ x +β∧ x x . (2.31) Persamaan (2.31) merupakan aproksimasi fungsi ekspektasi bersyarat

payoff opsi dimasa mendatang dan akan digunakan pada langkah kedua metode LSM yang dibahas pada bab III.