Hamburan Partikel Ber-Spin 0 dan
1
2
Dalam
Basis Momentum-Helicity
Skripsi diajukan sebagai salah satu syarat memperoleh gelar Sarjana Sains
oleh:
Irga Abdulrahman
0301020336
Departemen Fisika
Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Indonesia
Depok
2006
Hamburan Partikel Ber-Spin 0 dan
1
2
Dalam
Basis Momentum-Helicity
oleh:
Irga Abdulrahman
0301020336
Departemen Fisika
Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Indonesia
Depok
2006
Halaman Persetujuan
Judul Skripsi : Hamburan Partikel Ber-Spin 0 dan 1
2 Dalam Basis Momentum-Helicity
Nama : Irga Abdulrahman
NPM : 0301020336
Skripsi ini telah diperiksa dan disetujui
Depok, 22 Mei 2006 Mengesahkan Pembimbing
Dr. I. Fachruddin
Penguji I Penguji II
Dr. Anto Sulaksono Dr. Agus Salam
Tanggal Lulus Ujian Sarjana : 22 Mei 2006
Penguji I : Dr. Anto Sulaksono
Kata Pengantar
Alhammdulillah, penuh rasa syukur, penulis agungkan nama-Mu yang Maha Suci. Tugas ini adalah representasi dari sebagian pengetahuan yang penulis dap-atkan selama berguru pada, ”orang-orang luar biasa”, Dosen-dosen Fisika UI.
Ucapan terima kasih penulis ucapkan pada :
Dr Imam Fachruddin, sebagai pembimbing, yang telah sangat-sangat penulis repotkan dengan berbagai kemalasan dan ketidaktahuan penulis. tanpa bimbin-gannya (yang sangat komperhensif) penulis merasa tidak akan mampu menyele-saikan tugas ini. Dr Anto Sulaksono dan Dr Agus Salam sebagai penguji. Dosen-dosen Fisika Nuklir dan Partikel : Dr. Terry Mart, Dr. LT Handoko, dan lainnya. Drs Djonaedi Soleh sebagi Pembibing Akademis penulis, Dr.rer.nat Rosari Saleh, serta seluruh dosen fisika UI.
Dr. Djoko Sasmita (Isiteks) semoga Imogiri kembali tetap sama.
Papa, mumku, dan keluarga, yang mau mengerti bahwa salah satu anggotanya sementara ’hilang’, tenggelam dalam tumpukan kertas-kertas. Tante Merry, atas dukungan finansial.
Teman-teman di Lab Teori : Handika, Adriana Arum, Zu(zu)hrianda, Freddy, Anton, Ardy, Nita, Nowo, dan lainnya. Seluruh teman-teman Fisika UI 2001 (Aulia, Yudho, Zicko, Justo, Mba Dita, Ivo)
Mbak Ratna, yang mau mengerti ketidakdisiplinan penulis dalam urusan ad-ministrasi.
”Pemandu sorak” yang tidak pernah berhenti berteriak(mengomel) memberi semangat : Anindya(FEUI), R Artistik(Usakti), Rheny, Annisa(Unpad).
Dengan selesainya tugas ini tidak berarti topik ini selesai, pembahasan lebih lanjut serta berbagai aplikasi, masih sangat terbuka untuk dikerjakan.
Abstrak
Hamburan 2 partikel berspin 0 dan 1
2 dijabarkan dengan teknik perhitungan
yang menggunakan basis momentum-helicity. Dengan cara yang disebut teknik tiga dimensi (3D) ini, elemen matriks T dihitung sebagai solusi dari persamaan Lippmann-Schwinger, demikian pula penampang lintang differensial dan polari-sasi. Sebagai input digunakan sebuah model potensial spin-orbit sederhana. Efek kinematika relativistik juga dipelajari.
Kata kunci: hamburan, persamaan Lippmann-Schwinger, teknik 3D, kinematika relativistik, potensial spin-orbit.
vi+67 hlm.; lamp.
Daftar Acuan: 10 (1957-2003)
Abstract
Scattering of 2 particles of spin 0 and 1
2 is evaluated by means of a technique,
which uses momentum-helicity basis. Using this so called three dimensional (3D) technique, the T-matrix elements are calculated as solution of the Lippmann-Schwinger equation, as well as differential cross section and polarization. As input a simple spin-orbit potential model is used. Relativistic kinematics effects are also investigated.
Keywords: scattering, Lippmann-Schwinger equation, 3D technique,relativistic kinematics, spin-orbit potential.
vi+67 pp.; appendices. References: 10 (1957-2003)
Daftar Isi
Halaman Persetujuan i Kata Pengantar ii Abstrak iii Daftar Isi iv Daftar Gambar vi 1 Pendahuluan 1 1.1 Latar Belakang . . . 1 1.2 Perumusan Masalah . . . 2 1.3 Metode Penelitian . . . 2 1.4 Tujuan . . . 22 Hamburan Dua Partikel 3 2.1 Kinematika Hamburan Dua Partikel . . . 3
2.2 Persamaan Lippmann-Schwinger . . . 5
2.3 Observable . . . 10
2.4 Persamaan Lippman-Schwinger Dalam Basis Gelombang Parsial . 12 3 Formulasi Tiga Dimensi 15 3.1 Basis Momentum-Helicity . . . . 16
3.2 Struktur Umum Potensial . . . 18
3.3 Persamaan Lippmann-Schwinger . . . 22
3.5 Hubungan Dengan Elemen Matriks-T Dalam Basis Gelombang Parsial . . . 28 3.6 Kinematika Relativistik . . . 30
4 Aplikasi 40
4.1 Potensial . . . 40 4.2 Hasil Dan Diskusi . . . 41
5 Kesimpulan Dan Saran 53
A Basis Gelombang Parsial 55
B Matriks Rotasi 58 C Transformasi Potensial 60 D Penyelesaian Numerik 63 D.1 Integrasi . . . 63 D.2 Eliminisasi Singularitas . . . 64 D.3 Persamaan Lippmann-Schwinger . . . 65 Daftar Acuan 67
Daftar Gambar
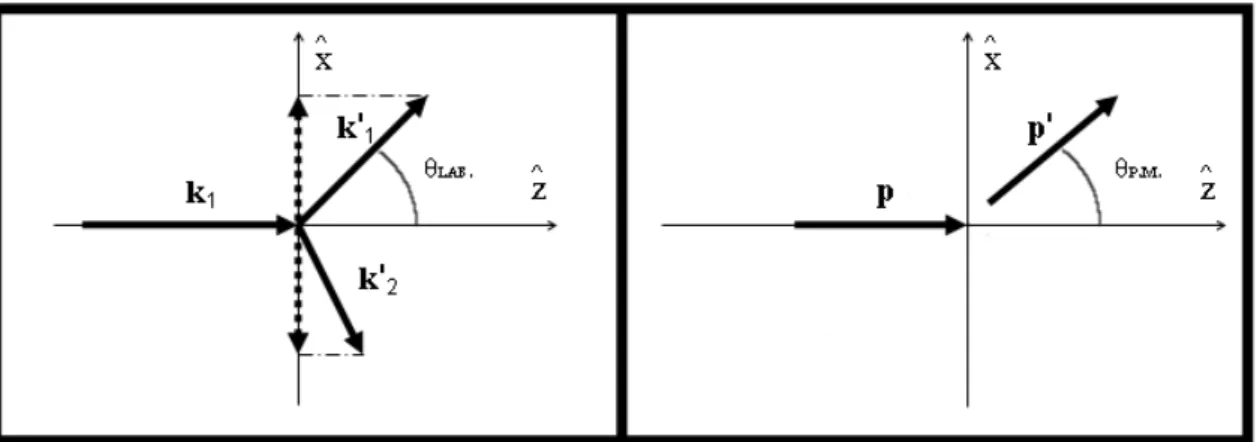
2.1 Hamburan dalam kerangka laboratorium dan kerangka P.M. . . . 4
2.2 Diagram hamburan dua partikel . . . 7
2.3 Titik pengamatan . . . 8
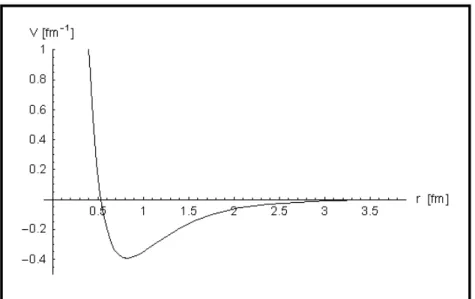
4.1 Potensial Malfliet-Tjon . . . 41
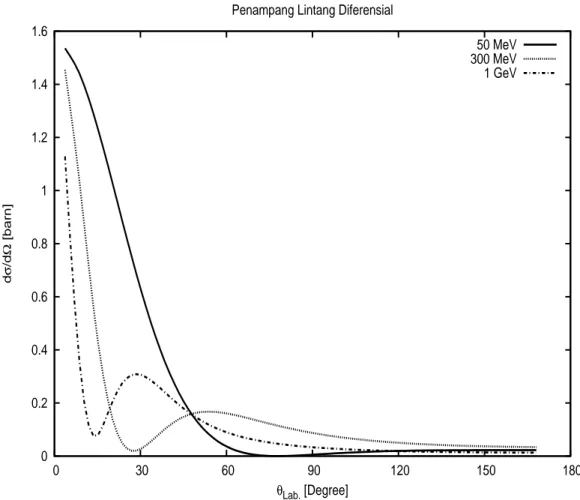
4.2 Penampang Lintang Differensial Pada Beberapa Nilai Energi . . . 42
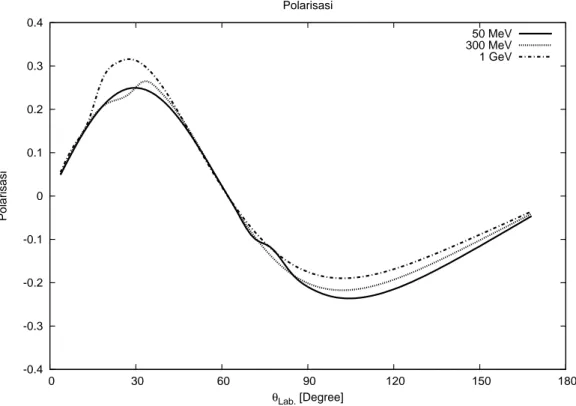
4.3 Polarisasi Pada Beberapa Nilai Energi . . . 43
4.4 Penampang lintang differensial pada energi Lab. 30 MeV . . . 45
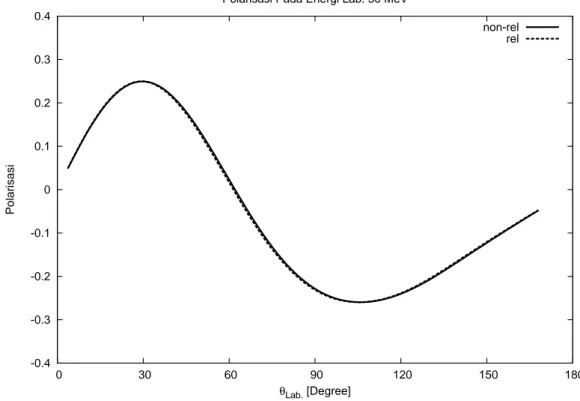
4.5 Polarisasi pada energi Lab. 30 MeV . . . 45
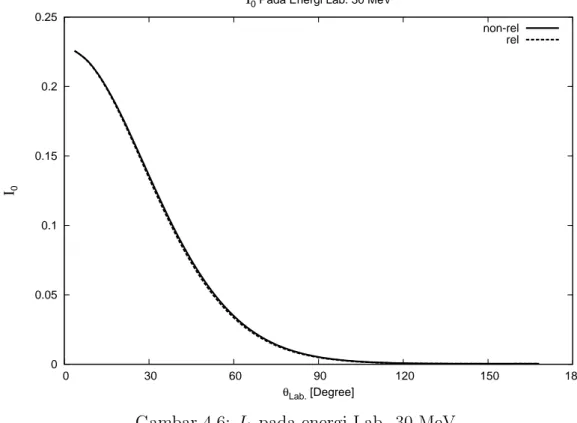
4.6 I0 pada energi Lab. 30 MeV . . . 46
4.7 Faktor Ruang Fase pada energi Lab. 30 MeV . . . 46
4.8 Penampang lintang differensial pada energi Lab. 100 MeV . . . . 47
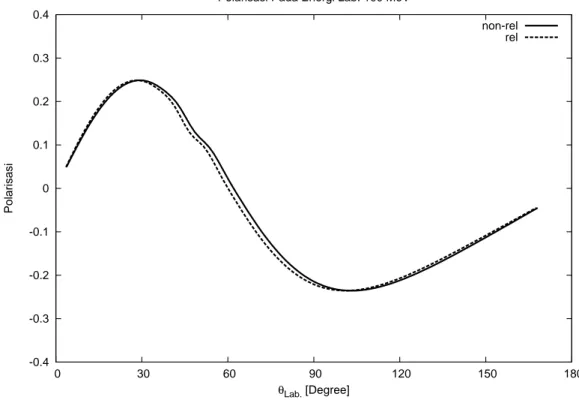
4.9 Polarisasi pada energi Lab. 100 MeV . . . 47
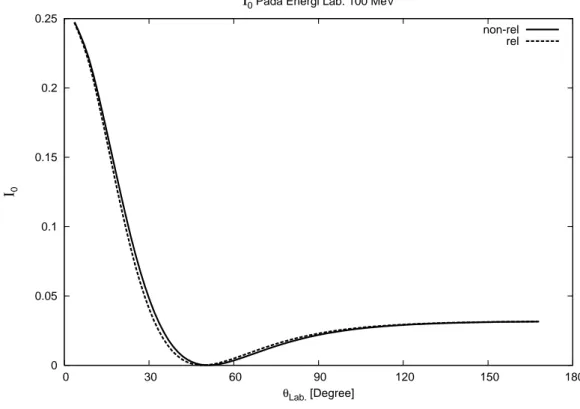
4.10 I0 pada energi Lab. 100 MeV . . . 48
4.11 Faktor Ruang Fase pada energi Lab. 100 MeV . . . 48
4.12 Penampang lintang differensial pada energi Lab. 300 MeV . . . . 49
4.13 Polarisasi pada energi Lab. 300 MeV . . . 49
4.14 I0 pada energi Lab. 300 MeV . . . 50
4.15 Faktor Ruang Fase pada energi Lab. 300 MeV . . . 50
4.16 Penampang lintang differensial pada energi Lab. 1 GeV . . . 51
4.17 Polarisasi pada energi Lab. 1 GeV . . . 51
4.18 I0 pada energi Lab. 1 GeV . . . 52
Bab 1
Pendahuluan
1.1
Latar Belakang
Sebagian besar dari yang kita ketahui tentang berbagai gaya dan interaksi antar partikel diperoleh melalui eksperimen hamburan. Secara garis besar eksperimen hamburan dilakukan dengan membombardir target, yang dapat berupa atom, inti atom atau partikel, dengan partikel lain. Sifat-sifat dan kondisi awal dari partikel proyektil dan target diketahui. Setelah tumbukan, proyektil akan dihamburkan oleh target ke suatu arah.
Dalam bidang few-body nuclear physics perhitungan biasa dilakukan dalam basis eigenstate momentum angular total. Ini bisa dimengerti mengingat gaya nuklir bersifat short range, sehingga untuk energi rendah sebuah proses hambu-ran bisa dijelaskan dengan memperhitungkan hanya beberapa momentum angular total terendah. Namun, pada energi yang lebih tinggi diperlukan jumlah momen-tum angular yang lebih banyak, sehingga perumusan dan perhitungan numerik menjadi berat. Karena itu, diperlukan suatu teknik perhitungan yang lain, yang tidak berbasis pada eigenstate momentum angular. Dalam ruang momentum pi-lihannya yaitu memakai state vektor momentum sebagai basis. Teknik seperti ini dikenal dengan nama teknik 3D (3 Dimensi). Untuk sistem 2 partikel identik tanpa spin, penggunaan teknik ini dapat ditemukan pada [1], sedangkan untuk sistem nukleon-nukleon pada, contohnya, [2] dan [3].
1.2
Perumusan Masalah
Dalam penelitian ini akan dikembangkan teknik perhitungan berbasis state vek-tor momentum dan helicity, selanjutnya disebut basis state momentum-helicity, untuk sistem dua partikel berspin 0 dan 1
2. Mengingat perhitungan dengan teknik
3D lebih bermanfaat untuk energi tinggi, maka efek relativitas juga perlu diper-timbangkan, karena itu kinematika relativistik juga akan digunakan, mengikuti formulasi dalam Ref. [4].
1.3
Metode Penelitian
Mula-mula dikerjakan formulasi persamaan Lippmann-Schwinger dalam basis momentum-helicity. Kemudian untuk dapat menyelesaikan persamaan Lippmann-Schwinger tersebut, dilakukan perhitungan numerik menggunakan metode-metode numerik yaitu dekomposisi LU dan kuadratur Gauss-Legendre.
1.4
Tujuan
Menghasilkan suatu formulasi hamburan 2 partikel, yang satu bespin 0 dan yang lain berspin 1
2, yang bermanfaat terlebih lagi untuk energi tinggi, dengan memilih
Bab 2
Hamburan Dua Partikel
Hamburan adalah fenomena yang sudah lama dikenal, khususnya dalam fisika nuklir, sehingga penjelasan tentang fenomena ini telah banyak menjadi topik dalam berbagai buku teks fisika kuantum dan fisika nuklir. Penjelasan tentang hamburan dalam bab ini hanya bersifat singkat sebagai dasar untuk formulasi pada bab-bab selanjutnya.
2.1
Kinematika Hamburan Dua Partikel
Dalam eksperimen hamburan besaran-besaran seperti energi, momentum dan sudut hambur diamati dalam kerangka pengamat, atau biasa disebut kerangka laboratorium. Dalam formulasi teoritis akan sangat membantu bila kerangka yang digunakan adalah kerangka pusat massa kedua partikel (kerangka P.M.).
Sebut ki sebagai momentum awal partikel ke-i dalam kerangka laboratorium
dan k0
i adalah momentum akhir. Selanjutnya tanda ” ’ ” melambangkan keadaan
akhir. Besarnya momentum relatif dalam Kerangka P.M. p dihitung sebagai momentum Jacobi:
p = m2k1− m1k2
m1+ m2
, (2.1)
dengan mi massa partikel-i. Pada keadaan awal, salah satu partikel dalam
keadaan diam (target), k2 = 0, maka:
p = µ
m1
k1 , (2.2)
dengan µ adalah massa tereduksi:
µ = m1 m2
m1+ m2
Gambar 2.1: Hamburan dalam kerangka laboratorium dan kerangka P.M. Energi total dalam kerangka laboratorium dan kerangkan P.M.:
ELab. = E1 = E10 + E20 (2.4) ELab. = k2 1 2m1 = k 02 1 2m1 + k 02 2 2m2 (2.5) EP.M. = p2 2µ = p02 2µ . (2.6)
Besarnya energi awal dan energi akhir sama, karena hamburan bersifat elastik. Perbandingan antara ELab. dan EP.M.:
EP.M. = p2 2µ = µ 2m2 1 k2 1 = µ m1 ELab. . (2.7)
Selain itu perlu dicari hubungan antara sudut hambur dalam kedua kerang-ka. Sudut hambur adalah besarnya sudut antara vektor momentum awal dan akhir dari proyektil. Dengan menentukan momentum awal searah sumbu-z serta hamburan pada bidang ˆx − ˆz, seperti pada gambar 2.1, vektor momentum akhir
dalam kerangka P.M. yaitu: p0 = p0
xx + pˆ 0zˆz
= p sin θP.M. x + p cos θˆ P.M. ˆz , (2.8)
dan dapat juga dinyatakan sebagai:
p0 = m2k01− m1k02
m1+ m2
Pada kerangka laboratorium vektor momentum awal hanya memiliki komponen pada z, sehingga vektor momentum akhir total juga hanya pada sumbu-z, komponen sumbu-x dari vektor momentum akhir akan saling menghilangkan (lihat gambar 2.1), sehingga:
k2 x0 = −k01 x (2.10)
Maka dengan memasukan persamaan (2.8) kedalam persamaan (2.9) dan dengan kondisi (2.10), bisa didapatkan hubungan antara sudut hambur dalam kedua kerangka: θP.M. = θLab.+ arcsin µ m1 m2 sin θLab. ¶ (2.11) Menggunakan persamaan (2.2), (2.7) dan (2.11) di atas, bisa dilakukan transfor-masi dari kerangka laboratorium ke kerangka P.M., dan juga sebaliknya.
2.2
Persamaan Lippmann-Schwinger
Interaksi antara proyektil dan target direpresentasikan dengan potensial di dalam Hamiltonian. Maka Hamiltonian ditulis sebagai gabungan antara hamiltonian partikel bebas dan komponen potensial,
H = H0+ V (2.12)
Dimana H0 adalah Hamiltonian partikel bebas,
H0|φi = E |φi , (2.13)
dengan |φi merupakan keadaan bebas (free state). Untuk keadaan hamburan berlaku:
(H0+ V ) |ψi = E |ψi (2.14)
dengan |ψi merupakan keadaan hamburan. Digunakan ansazt bahwa keadaan hamburan:
|ψi = |φi + |χi , (2.15)
dimana saat V = 0, maka |ψi = |φi, tanpa adanya interaksi maka hamburan tidak terjadi. Solusi keadaan hamburan didapatkan dengan mengerjakan persamaan
Schr¨odinger (2.14) dengan menggunakan ansazt (2.15):
E |χi = H0|χi + V |φi + V |χi
|χi = 1 E − H0 V |ψi , (2.16) sehingga: |ψi = |φi + 1 E − H0 V |ψi
= |φi + G0(E)V |ψi , (2.17)
dengan G0(E) merupakan Free Propagator:
G0(E) = 1
E − H0
. (2.18)
Solusi pada persamaan (2.17) memiliki titik singular, yaitu pada E = H0,
se-hingga untuk menghindari singularitas ini nilai E dibuat sedikit kompleks, yaitu
E → E ± i², dengan ² ≈ 0 [5]. maka persamaan (2.17) menjadi: |ψi = |φi + lim
²→0
1
E ± i² − H0
V |ψi
= |φi + G±0(E)V |ψi , (2.19)
dengan: G±0(E) = lim ²→0 1 E ± i² − H0 (2.20) Persamaan (2.19) disebut sebagai persamaan Lippmann-Schwinger untuk fungsi gelombang.
Untuk menunjukan transisi dari keadaan awal ke keadaan akhir pada proses hamburan, maka didefinisikan operator transisi, yaitu matriks-T:
T |φi ≡ V |ψi . (2.21)
Dengan memasukkan |ψi pada persamaan (2.19) ke persamaan (2.21) diperoleh:
T |φi = V |φi + V G±0(E)T |φi (2.22)
Maka didapatkan persamaan Lippmann-Schwinger untuk matriks-T:
T = V + V G±
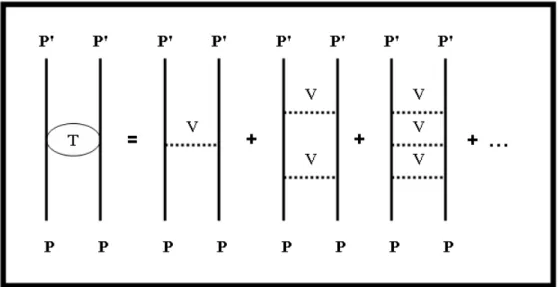
Gambar 2.2: Diagram hamburan dua partikel
Menurut persamaan (2.23) matriks-T merupakan deret tak hingga dari V ,
T = V + V G±
0V + V G±0V G±0V + V G0±V G±0V G±0V + · · · (2.24)
yang menunjukan bahwa hamburan yang terjadi tidak hanya hamburan tunggal, namun juga hamburan berganda (multiple scattering). Lihat gambar (2.2) untuk ilustrasi.
Keadaan hamburan |ψi pada persamaan (2.19) bisa dievaluasi pada pilihan basis tertentu, contohnya basis ruang konfigurasi:
hr|ψi = hr|pi +r¯¯G± 0(E)V ¯ ¯ ψ® = hr|pi + Z dr0 r¯¯G± 0(E) ¯ ¯ r0® | {z } Green0s F unction hr0|V | ψi . (2.25)
Suku pertama persamaan di atas merupakan fungsi gelombang bebas berupa fungsi gelombang bidang:
hr|pi = 1
(2π)3/2e
ip·r . (2.26)
Representasi free propagator dalam ruang konfigurasi dikenal sebagai Fungsi Green partikel bebas [5]: r¯¯G± 0(E) ¯ ¯ r0®= −2µ 4π e±ip0|r−r0| |r − r0| (2.27)
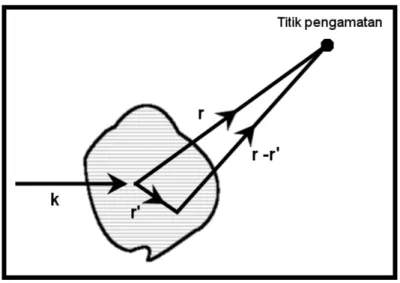
Gambar 2.3: Titik pengamatan
dari target, atau dalam skala partikel jarak titik pengamatan menuju tak hingga,
r → ∞, maka bisa dituliskan |r − r0| ' r − ˆr · r0, (lihat gambar 2.3). Maka
persamaan (2.27) menjadi: r¯¯G±0(E)¯¯ r0®= −2µ 4π e±ipr r e ∓ip0· r0 . (2.28)
Masukan persamaan (2.26) dan (2.28) ke persamaan (2.25) maka diperoleh:
ψ(r) = 1 (2π)3/2 " eip· r− µ√2π e ±ipr r Z dr0 e∓ip0· r0hr0|T | φi # (2.29) Fungsi gelombang di atas memiliki dua suku. Suku pertama ialah fungsi gelom-bang datang, yang merupakan fungsi gelomgelom-bang bidang. Sedangkan suku kedua merupakan fungsi gelombang radial, yang harus menunjukan fungsi gelombang terhambur. Karena fungsi gelombang terhambur haruslah mengarah keluar
propagator yang digunakan dalam formulasi selanjutnya adalah G+ 0(E). ψ(r) = 1 (2π)3/2 " eip· r− µ√2π eipr r Z dr0 e−ip0· r0 hr0|T | φi # = 1 (2π)3/2 " eip· r− 4µπ2 eipr r Z dr0 1 (2π)3/2e −ip0· r0 hr0|T | φi # = 1 (2π)3/2 " eip· r− 4µπ2 e ipr r Z dr0 hp0|r0i hr0|T | φi # = 1 (2π)3/2 " eip· r− 4µπ2 e ipr r hp 0|T | pi # , (2.30)
|φi merupakan keadaan bebas sistem dengan momentum p. Karena itu, pada
baris terakhir persamaan (2.30) |φi diganti |pi.
Pada persamaan (2.30) terdapat suku hp0|T | pi yang merupakan elemen
matriks-T dalam basis vektor momentum, ini merupakan matriks yang akan kami hitung. Bila didefinisikan amplitudo hamburan f (p0, p) sebagai berikut:
f (p0, p) ≡ −4µπ2 hp0|T | pi , (2.31)
maka fungsi gelombang (2.30) menjadi:
ψ(r) = 1 (2π)3/2 · eip·r+eipr r f (p 0, p) ¸ (2.32) Formulasi di atas dikerjakan tanpa memasukan spin. Spin turut dimasukan dalam perhitungan dengan menambahkan keadaan spin, baik pada keadaan bebas
maupun pada keadaan hamburan. Untuk sistem 2 partikel berspin 0 dan 1
2,
diperoleh spin total s = 1
2. Maka pada keadaan bebas dan keadaan hamburan
ditambahkan keadaan spin |ni sebagai berikut:
keadaan bebas: |φni ≡ |φi |ni (2.33)
keadaan hamburan: |ψni ≡ |ψi |ni , (2.34)
dengan |ni merupakan kombinasi linier dari ¯¯1 2λ
®
, dengan λ = ±1
2 merupakan
proyeksi spin pada sumbu kuantisasi (bilangan kuantum magnetik spin):
|ni = 1 2 X λ=−12 an λ ¯ ¯1 2λ ® (2.35)
Setelah ditambah komponen spin, maka persamaan (2.19) menjadi:
|ψni = |φni + G+0(E)V |ψni . (2.36)
Bila keadaan hamburan dengan spin pada persamaan (2.36) direpresentasikan ke ruang spasial:
hr|ψni = hr|φni +X
λ0
Z
dr0r¯¯G+0(E)¯¯ r0λ0®hr0λ0|T | φni , (2.37)
karena propagator tidak bergantung pada keadaan spin, maka:
ψ(r) |ni = eip·r (2π)3/2|ni + X λ0 ¯ ¯1 2, λ 0® Z dr0r¯¯G+ 0(E) ¯ ¯ r0®hr0λ0|T | pni = e ip·r (2π)3/2|ni − µ √ 2π e ipr r X λ0 ¯ ¯1 2, λ0 ® hp0λ0|T | pni = 1 (2π)3/2 · eip·r|ni + e ipr r X λ0 ¯ ¯1 2, λ 0®f λ0(p0, p) ¸ , (2.38) dengan: fλ0(p0, p) ≡ −4µπ2 hp0λ0|T | pni . (2.39)
Bergantung pada potensial, dalam proses hamburan proyeksi spin pada sumbu kuantisasi dapat berubah, sementara besar spin itu sendiri tetap, 1
2.
2.3
Observable
Matriks-T berhubungan dengan matriks hamburan M sebagai berikut:
Mλ0λ(p0, p) ≡ −4µπ2 hp0λ0|T | pλi , (2.40)
sehingga amplitudo hamburan berhubungan dengan matriks hamburan M seba-gai: fλ0(p0, p) = 1 2 X λ=−12 an λ Mλ0λ(p0, p) . (2.41)
Observable proses hamburan diperoleh dari amplitudo hamburan. Karena
ham-buran bersifat elastik, maka p0 = p, sehingga:
Obervable dihitung menggunakan observable spin umum (gunakan cara dalam
Ref.[6] namun untuk sistem partikel berspin 0 dan 1
2) yaitu: I hσµif = 1 2 X α hσαiiT r © MσαM†σµ ª . (2.43) dengan: σ0 = µ 1 0 0 1 ¶ σ1 = µ 0 1 1 0 ¶ σ2 = µ 0 −i i 0 ¶ σ3 = µ 1 0 0 −1 ¶ (2.44) Apabila spin proyektil tidak terpolarisasi, dan keadaan spin partikel terham-bur tidak diukur, maka diperoleh:
I0 =
1 2T r
©
MM†ª , (2.45)
yang disebut sebagai penampang lintang diferensial yang dirata-ratakan terhadap spin (spin averaged differential cross section). Sedangkan untuk mengetahui apakah proses hamburan menyebabkan proyektil yang semula tidak terpolarisasi menjadi terpolarisasi, maka spin partikel terhambur diukur. Menurut persamaan (2.43) didapatkan: I hσµif = 1 2T r © MM†σµ ª (µ = 1, 2, 3) , (2.46)
dan polarisasi partikel terhambur didefinisikan sebagai: Pµ = 1 2I0 T r©MM†σ µ ª . (2.47)
Bila arah proyektil mula-mula ditentukan pada arah sumbu-z dan bidang ham-buran pada bidang ˆx-ˆz, maka sesuai sifat invarian proses hamburan terhadap
paritas, polarisasi hanya ada pada arah normal hamburan [6], yaitu: ˆ
n ≡ k
0× k
|k0× k| = ˆy . (2.48)
Sehingga polarisasi pada arah normal (ˆy) ialah: Py = 1 2I0 T r©MM†σ y ª (σy = σ2) . (2.49)
2.4
Persamaan Lippman-Schwinger Dalam
Ba-sis Gelombang Parsial
Dalam fisika nuklir, khususnya bidang few body problem, representasi yang biasa digunakan untuk menyelesaikan persamaan Lippmann - Schwinger yaitu repre-sentasi gelombang parsial, dengan basis state ¯¯p(l1
2); jm
®
. Pada basis ini nilai momentum angular total J:
J = L + S , (2.50)
dan nilai m adalah proyeksi J pada sumbu-z. Lebih lanjut mengenai basis ini dapat dilihat pada Lampiran A.
Elemen matriks-T dan potensial pada basis gelombang parsial: p0(l0 12); j0m0|T | p(l1 2); jm ® (2.51) p0(l0 1 2); j0m0|V | p(l12); jm ® (2.52) Karena konservasi momentum angular total J, maka baik matriks pontensial maupun matriks-T, bersifat diagonal untuk j dan m:
p0(l0 1 2); j0m0|V | p(l12); jm ® = δjj0 δmm0Vljm0l (p0, p) (2.53) p0(l0 1 2); j 0m0|T | p(l1 2); jm ® = δjj0 δmm0Tjm l0l (p0, p) , (2.54) dengan: Vljm0l (p0, p) ≡ p0(l0 1 2); jm |V | p(l12); jm ® (2.55) Tljm0l (p0, p) ≡ p0(l0 1 2); jm |T | p(l12); jm ® . (2.56)
Dengan begitu persamaan Lippmann-Schwinger untuk matriks-T, persamaan (2.23), pada basis gelombang parsial menjadi:
Tljm0l (p0, p) = Vljm0l (p0, p) + p0(l0 1 2); j0m0 ¯ ¯V G+ 0(E)T ¯ ¯ p(l1 2); jm ® = Vljm0l (p0, p) + X j00l00m00 X j000l000m000 Z ∞ 0 dp00dp000p002p0002p0(l0 1 2); j0m0|V | p00(l00 12); j00m00 ® ×p00(l00 12); j00m00¯¯G+0(E)¯¯ p000(l000 12); j000m000® p000(l000 12); j000m000|T | p(l1 2); jm ® (2.57)
dengan kondisi pada persamaan (2.53) dan (2.54) maka: Tljm0l (p0, p) = Vljm0l (p0, p) + X l00l000 Z ∞ 0 dp00dp000p002p0002 Vlj0l000m0(p0, p00) ×p00(l00 1 2); j0m0 ¯ ¯G+ 0(Ep) ¯ ¯ p000(l000 1 2); jm ® Tljm000l(p000, p) . (2.58)
Selanjutnya perlu dicari elemen matriks dari propagator dalam basis gelombang parsial¯¯p(l1
2); jm
®
. Karena propagator tidak berpengaruh pada spin, maka cukup dikerjakan: p00(l00 1 2); j0m0 ¯ ¯G+ 0(Ep) ¯ ¯ p000(l000 1 2); jm ® = Z dp00dp000 p00(l00 1 2); j0m0|p00 ® hp00|G(E p)| p000i p000|p000(l000 1 2); jm ® = 2µ lim ²→0 Z dp00dp000 p00(l00 1 2); j0m0|p00 ® ¿ p000 ¯ ¯ ¯ ¯p2+ i² − ˆ1 Op2 ¯ ¯ ¯ ¯ p00 À p000|p000(l000 1 2); jm ® = 2µδ(p00− p000) p00p000 δj0jδm0mδl000l00 lim²→0 1 p2+ i² − p002 (2.59)
Dengan memasukan elemen matriks propagator dari persamaan (2.59), persamaan (2.58) menjadi: Tljm0l (p0, p) = Vljm0l (p0, p) + 2µ lim ²→0 X l00 Z ∞ 0 dp00p002 Vljm0l00(p0, p00) p2+ i² − p002T jm l00l(p00, p) (2.60)
Persamaan di atas merupakan persamaan Lippmann-Schwinger untuk matriks-T pada basis gelombang parsial.
Hubungan antara elemen matriks Mλ0λ(p0, p) dan Tjm
l0l (p0, p), didapatkan melalui persamaan (2.40): Mλ0λ(p0, p) = −4µπ2 X j0m0l0 X jml C(l0 1 2j0; m0− λ0, λ0)C(l12j; m − λ, λ) p0(l0 12); j0m0|T | p(l1 2); jm ® Yl0,m0−λ0(ˆp0)Yl,m−λ∗ (ˆp) = −4µπ2 X jmll0 C(l0 1 2j; m − λ0, λ0)C(l12j; m − λ, λ) Tljm0l (p0, p) Yl0,m−λ0(ˆp0)Yl,m−λ∗ (ˆp) . (2.61)
Untuk memudahkan pengerjaan maka ditentukan ˆp = ˆz, sehingga:
Y∗
l,m−λ(ˆp) = Yl,m−λ(ˆp) =
r 2l + 1
dengan m = λ. Sehingga persamaan (2.61) menjadi: Mλ0λ(p0, pˆz) = −4µπ2 X jll0 r 2l + 1 4π C(l 0 1 2j; λ − λ0, λ0)C(l12j; 0, λ) Tljλ0l(p0, p) Yl0λ−λ0(ˆp0) . (2.63)
Bab 3
Formulasi Tiga Dimensi
Dalam penggunaan metode gelombang parsial, matriks T diselesaikan untuk se-tiap nilai angular momentum j, dan perhitungan dilakukan hingga suatu nilai
jmax, dimana perhitungan konvergen. Untuk energi rendah hal ini tidak menjadi
masalah berarti, karena banyaknya nilai j yang diperhitungkan sedikit. Namun pada energi tinggi metode gelombang parsial tidak lagi efisien, karena banyaknya perhitungan yang harus dilakukan. Selain itu terdapatnya fungsi Legendre ter-asosiasi pada formulasi amplitudo hamburan, persamaan (2.63), menyebabkan penurunan tingkat akurasi perhitungan, karena osilasi yang besar dari fungsi
Legendre terasosiasi pada orde tinggi.
Dalam bab ini akan diformulasikan suatu teknik penyelesaian persamaan Lipp-mann - Schwinger dengan menggunakan state vektor momentum |pi , sebagai ba-sis untuk menyelesaikan persamaan Lippmann-Scwhinger. Teknik ini untuk se-lanjutnya disebut teknik tiga dimensi (3D). Karena perhitungan dilakukan tanpa menggunakan dekomposisi gelombang parsial, maka masalah diatas dapat dihin-dari. Dimulai dengan mendefinisikan basis state yang akan digunakan, yaitu basis
state momentum-helicity, serta membahas sifat-sifat basis tersebut. Basis state
momentum-helicity dibentuk dari state vektor momentum dan state helicity yang merepresentasikan keadaan spin. State helicity digunakan untuk mempermudah pengerjaan [7], karena state ini merupakan eigenstate dari operator helicity σ · ˆp, yang terdapat pada potensial yang diturunkan dalam ruang momentum.
3.1
Basis Momentum-Helicity
Basis state momentum-helicity dibentuk dari state vektor momentum dan state helicity. Helicity adalah proyeksi spin pada vektor momentum. Eigenstate he-licity didapatkan dengan memutar eigenstate spin, yang dikuantisasi pada arah
sumbu-z, ke arah momentum ¯ ¯ˆp1 2λ ® = R(ˆp)¯¯ˆz1 2λ ® , (3.1)
Dengan operator rotasi R adalah:
R(ˆp) = e−iSzφe−iSyθ . (3.2)
Completness relation dan Orthogonalitas state helicity ini:
X λ ¯ ¯ˆp1 2λ ® ˆ p1 2λ ¯ ¯ = 1 (3.3) ˆ p1 2λ 0|ˆp1 2λ ® =zˆ1 2λ 0¯¯R−1(ˆp)R(ˆp)¯¯ ˆz1 2λ ® =zˆ 1 2λ0|ˆz 12λ ® = δλ0λ . (3.4)
Dengan menggabungkan state helicity pada persamaan (3.1) di atas dengan state vektor momentum maka bisa didefinisikan basis momentum-helicity :
¯ ¯p; ˆp1 2λ ® ≡ |pi¯¯ˆp1 2λ ® (3.5) Tapi basis diatas tidak memiliki paritas yang jelas. Kini perlu didefinisikan basis yang memiliki paritas yang jelas:
¯ ¯p; ˆp1 2λ ® π = 1 √ 2(1 + ηπP) ¯ ¯p; ˆp1 2λ ® . (3.6)
dengan eigenvalue paritas ηπ = ±1. Bila operator paritas dioperasikan ke basis
tersebut diperoleh: P¯¯p; ˆp1 2λ ® π = 1 √ 2(P + ηπ) ¯ ¯p; ˆp1 2λ ® = √1 2 ηπ(ηπP + 1) ¯ ¯p; ˆp1 2λ ® = ηπ ¯ ¯p; ˆp1 2λ ® π . (3.7)
Persamaan (3.7) membuktikan bahwa basis momentum-helicity pada persamaan (3.6) memiliki paritas yang jelas. Orthogonalitas dari basis ini:
π0 p0; ˆp0 1 2λ0|p; ˆp12λ ® π = 1 2 p0; ˆp0 1 2λ 0|(1 + η π0P)(1 + ηπP)| p; ˆp1 2λ ® = 1 2 p0; ˆp0 12λ0¯¯ (1 + ηπ0P) n ¯ ¯p; ˆp1 2λ ® + ηπ ¯ ¯−p; ˆp1 2λ ® o = 1 2 p0; ˆp0 1 2λ 0¯¯ ½¯ ¯p; ˆp1 2λ ® + ηπ ¯ ¯−p; ˆp1 2λ ® + ηπ0 ¯ ¯−p; ˆp1 2λ ® + ηπηπ0 ¯ ¯p; ˆp1 2λ ®¾ = 1 2 h (1 + ηπηπ0) hp0|pi ˆ p0 1 2λ0|ˆp12λ ® + (ηπ0 + ηπ) hp0| − pi ˆ p0 1 2λ0|ˆp12λ ® i (3.8) Untuk dapat menyelesaikan persamaan (3.8) diperlukan hubungan antara¯¯−ˆp1
2λ
® dan ¯¯ˆp1
2λ
®
. Dengan menggunakan sifat fungsi-D Wigner[8] berikut:
Djm0m(ˆr) = i Djm0−m(−ˆr) , (3.9)
dengan i = √−1. Lebih lanjut tetang fungsi-D Wigner dapat dilihat pada
lam-piran B. Maka bisa didapatkan hubungan: ¯ ¯−ˆp1 2λ ® = R(−ˆp)¯¯ˆz1 2λ ® =X λ0 D 1 2 λ0λ(−ˆp) ¯ ¯ˆz1 2λ 0® = i X λ0 D 1 2 λ0,−λ(ˆp) ¯ ¯ˆz1 2λ 0® = i ¯¯ˆp1 2, −λ ® (3.10) Sehingga hubungan Orthogonalitas (3.8) dapat diselesaikan:
π0 p0; ˆp0 12λ0|p; ˆp1 2λ ® π = 1 2 h (1 + ηπηπ0) hp0|pi ˆ p0 1 2λ0|ˆp12λ ® − i(ηπ0 + ηπ) hp0| − pi ˆ p0 1 2λ0| − ˆp12 − λ ® i = 1 2 h (1 + ηπηπ0)δ(p0− p)δλ0λ − i(ηπ0 + ηπ)δ(p0+ p)δλ0,−λ i = δηπ0ηπ · δ(p0− p)δ λ0λ− i ηπ δ(p0+ p)δλ0,−λ ¸ . (3.11)
Sedangkan untuk Completness relation, digunakan: X πλ Z dp ¯¯p; ˆp1 2λ ® πρπ p; ˆp1 2λ ¯ ¯ = 1 , (3.12)
dengan ρ adalah faktor normalisasi, yang nilainya dicari melalui: π0 p0; ˆp0 1 2λ0|p; ˆp12λ ® π = X π00λ00 Z dp00 π0 p0; ˆp0 1 2λ 0|p00; ˆp00 1 2λ 00® π00ρπ00 p00; ˆp00 1 2λ 00|p; ˆp1 2λ ® π = ρ X π00λ00 Z dp00 π0 p0; ˆp0 12λ0|p00; ˆp00 12λ00®π00 × δηπ00ηπ h δ(p − p00)δ λλ00− i ηπ0 δ(p + p00)δλ,−λ00 i = ρ h π0 p0; ˆp0 12λ0|p; ˆp1 2λ ® π− i ηπ π0 p0; ˆp0 12λ0| − p; −ˆp1 2 − λ ® π i = ρ h π0 p0; ˆp0 1 2λ0|p; ˆp12λ ® π− i ηπ π0 p0; ˆp0 1 2λ0|P| p; −ˆp12 − λ ® π i = ρ h π0 p0; ˆp0 1 2λ0|p; ˆp12λ ® π− i ηπ π0 p0; ˆp0 1 2λ0|i ηπ| p; ˆp12λ ® π i = 2ρ π0 p0; ˆp0 12λ0|p; ˆp1 2λ ® π . (3.13)
Sehingga didapatkan faktor normalisasi ρ = 1 2, X πλ Z dp ¯¯p; ˆp1 2λ ® π 1 2 π p; ˆp1 2λ ¯ ¯ = 1 (3.14)
3.2
Struktur Umum Potensial
Kami asumsikan V invarian terhadap operasi paritas PV P−1 = V . Elemen
matriks potensial pada basis momentum-helicity, yaitu:
Vπ λ0λ(p0, p) ≡π p0; ˆp0 1 2λ0|V | p; ˆp12λ ® π = √1 2 p0; ˆp0 1 2λ0|(1 + ηπP)V | p; ˆp12λ ® π = √1 2 p0; ˆp0 1 2λ0|V (1 + ηπP)| p; ˆp12λ ® π =√2p0; ˆp0 1 2λ0|V | p; ˆp12λ ® π , (3.15)
Dengan persamaan (3.15) di atas, bisa ditentukan hubungan antara Vπ
dan Vπ λ0λ(p0, −p) sebagai berikut: Vπ λ0−λ(p0, p) = √ 2p0; ˆp0 1 2λ0|V | p; ˆp12 − λ ® π =p0; ˆp0 1 2λ 0|V | p; ˆp1 2 − λ ® + ηπ p0; ˆp0 1 2λ 0|V | − p; ˆp1 2 − λ ® = −i p0; ˆp0 1 2λ0|V P| − p; −ˆp12λ ® − i ηπ p0; ˆp0 1 2λ0|V | − p; −ˆp12λ ® = −i ηπ · p0; ˆp0 1 2λ 0|V η πP| − p; −ˆp12λ ® +p0; ˆp0 1 2λ 0|V | − p; −ˆp1 2λ ®¸ = −i ηπ √ 2p0; ˆp0 1 2λ 0|V | − p; −ˆp1 2λ ® π = −i ηπ Vλπ0λ(p0, −p) . (3.16) Hubungan Vπ
−λ0λ(p0, p) dengan Vλπ0λ(−p0, p) diperoleh sebagai berikut:
V−λπ 0λ(p0, p) = √ 2p0; ˆp0 12 − λ0|V | p; ˆp1 2λ ® π =√2 i p0; −ˆp0 1 2λ0 ¯ ¯PV P−1¯¯ p; ˆp1 2λ ® π =√2 i ηπ −p0; −ˆp0 12λ0|V | p; ˆp1 2λ ® π = i ηπ Vλπ0λ(−p0, p) . (3.17)
Dengan cara yang sama bisa didapatkan:
Vπ
−λ0−λ(p0, p) = Vλπ0λ(−p0, −p) (3.18)
Persamaan (3.16), (3.17) dan (3.18) menunjukan sifat simetri dari matriks poten-sial dalam basis momentum-helicity. Sifat simetri ini juga berlaku untuk sem-barang operator yang invarian terhadap operasi paritas, seperti matriks T .
Bentuk potensial yang dipilih di sini adalah salah satu bentuk yang sederhana, yaitu:
V (p0, p) = V
c(p0, p) + Vs(p0, p) s · (p × p0) , (3.19)
yang dalam ruang spasial dapat dituliskan:
V (r) = Vc(r) + Vs(r) l · s , (3.20)
dengan l = r × p. Potensial tersebut jelas invarian terhadap rotasi. Bentuk potensial seperti di atas juga invarian terhadap operasi pembalikan waktu (time
reversal). Operasi pembalikan waktu akan mengakibatkan: p → −p0, p0 → −p
dan s → −s , sehingga:
Potensial (3.19) juga invarian terhadap operasi paritas. Operasi paritas akan mengakibatkan: p → −p, p0 → −p0 dan s → s, sehingga:
s · (−p × −p0) = s · (p × p0) . (3.22)
Untuk memudahkan pengerjaan, potensial (3.19) di atas perlu diubah kedalam bentuk potensial yang terdiri dari operator helicity σ · ˆp, dimana σ merupakan matriks Pauli. Sebelumnya perlu dikerjakan hubungan antara s · (p × p0) dan
(σ · ˆp0)(σ · ˆp), yaitu: s · (p × p0) = 1 2σ · (p × p 0) = −i 2 n p0· p − (σ · p0)(σ · p) o = −i 2 p 0pnα0− (σ · ˆp0)(σ · ˆp)o , (3.23)
dimana α0 = ˆp0 · ˆp. Lebih lengkap mengenai transformasi ini bisa dilihat
pa-da lampiran C. Dengan hubungan (3.23) di atas maka potensial (3.19) pa-dapat dituliskan sebagai: V (p0, p) = Vc(p0, p) + Vs(p0, p) · −i 2 p 0pnα0 − (σ · ˆp0)(σ · ˆp)o¸ = fcs(p0, p) + fs(p0, p)(σ · ˆp0)(σ · ˆp) , (3.24) dengan fcs(p0, p) ≡ Vc(p0, p) − i 2 p 0p α0V s(p0, p) , (3.25) dan, fs(p0, p) ≡ i 2 p 0p V s(p0, p) . (3.26)
Untuk mencari matriks potensial pada basis momentum-helicity, dikerjakan potensial (3.24) menggunakan basis pada persamaan (3.5) sebagai permulaan, sehingga didapatkan: Vλ0λ(p0, p) ≡ p0; ˆp0 12λ0|V | p; ˆp1 2λ ® =pˆ0 1 2λ0|V (p0, p)| ˆp12λ ® = fcs(p0, p, α0) ˆ p0 1 2λ 0|ˆp1 2λ ® + fs(p0, p, α0) ˆ p0 1 2λ 0|(σ · ˆp0)(σ · ˆp)| ˆp1 2λ ® = · fcs(p0, p, α0) + 4fs(p0, p, α0) λ0λ ¸ ˆ p0 1 2λ0|ˆp12λ ® , (3.27)
bila didefinisikan:
F (p0, p, α0, λ0, λ) ≡ fcs(p0, p, α0) + 4λ0λ fs(p0, p, α0) (3.28)
Persamaan (3.27) dapat ditulis:
Vλ0λ(p0, p) = F (p0, p, α0, λ0, λ) ˆ p0 1 2λ 0|ˆp1 2λ ® . (3.29)
Selanjutnya potensial (3.24) dievaluasi menggunakan basis momentum-helicity pa-da persamaan (3.6), sehingga dipa-dapatkan:
Vπ λ0λ(p0, p) = √ 2p0; ˆp0 1 2λ0|V | p; ˆp12λ ® π =p0; ˆp0 12λ0|V | p; ˆp1 2λ ® − iηπ p0; ˆp0 12λ0|V | − p; −ˆp1 2 − λ ® = Vλ0λ(p0, p) − i ηπ Vλ0,−λ(p0, −p) = F (p0, p, α0, λ0, λ) hˆp0λ0|ˆpλi − iη πF (p0, p, −α0, λ0, −λ) hˆp0λ0| − ˆp − λi = h F (p0, p, α0, λ0, λ) + ηπF (p0, p, −α0, λ0, −λ) i hˆp0λ0|ˆpλi . (3.30) Dapat dilihat bahwa matriks potensial ini bergantung terhadap sudut melalui α0
dan hˆp0λ0|ˆpλi, seperti ditunjukkan sebagai berikut:
α0 = p0· p = cos θ0cos θ + sin θ0sin θ cos(φ0− φ) , (3.31)
sedangkan untuk hˆp0λ0|ˆpλi digunakan fungsi-D Wigner, sehingga didapatkan:
hˆp0λ0|ˆpλi =X m ei m(φ0−φ) d 1 2 mλ0(θ0) d 1 2 mλ(θ) , (3.32)
karena fungsi-D Wigner dapat dituliskan sebagai:
Djm0m(θ, φ) = e−im 0φ
djm0m(θ) . (3.33)
Untuk nilai j = 1
2 maka matriks-d ialah [8] :
d12(θ) = cosθ 2 − sin θ 2 sinθ 2 cos θ 2 (3.34)
Oleh karena itu, matriks potensial bergantung pada sudut azhimut φ dan φ0
melalui cos(φ0− φ) dan ei m(φ0−φ)
. Maka, untuk memperlihatkan kebergantungan matriks potensial terhadap sudut azimuth, dapat ditulis sebagai:
Vλπ0λ(p0, p) = Vλπ0λ
©
3.3
Persamaan Lippmann-Schwinger
Pada sub-bab sebelumnya telah didapatkan elemen matriks potensial pada basis momentum-helicity, sifat simetrinya dan bagaimana matriks potensial tersebut bergantung pada sudut. Dengan hasil tersebut, pada sub-bab ini kami akan menghitung elemen matriks-T pada basis momentum-helicity. Elemen matriks-T pada basis momentum-helicity didefinisikan sebagai:
Tλπ0λ(p0, p) ≡ π p0; ˆp0 12λ0|T | p; ˆp1 2λ ® π . (3.36)
Karena persamaan Lippmann-Schwinger untuk matriks-T dapat dilihat se-bagai ekspansi matriks-T dalam potensial V, seperti yang ditunjukan pada per-samaan (2.24), maka sifat matriks potensial juga akan dimiliki oleh matriks-T, seperti sifat simetrisitas matriks potensial pada persamaan (3.16), (3.17) dan (3.18) : Tλπ0−λ(p0, p) = −i ηπTλπ0λ(p0, −p) (3.37) Tπ −λ0λ(p0, p) = iηπTλπ0λ(−p0, p) (3.38) Tπ −λ0−λ(p0, p) = Tλπ0λ(−p0, −p) , (3.39)
Begitu pula untuk kebergantungan matriks-T terhadap sudut, karena
propaga-tor tidak bergantung sudut, sama seperti yang dimiliki matriks potensial pada
persamaan (3.35). Sehingga kebergantungan matriks-T terhadap sudut azimuth ialah: Tπ λ0λ(p0, p) = Tλπ0λ © eim(φ0−φ) , cos(φ0 − φ)ª . (3.40)
Menggunakan persamaan Lippmann-Schwinger untuk matriks-T persamaan (2.23) dan completeness relation pada persamaan (3.14), didapatkan persamaan Lippmann-Schwinger untuk matriks-T pada basis momentum-helicity, sebagai berikut: Tπ λ0,λ(p0, p) = Vλπ0,λ(p0, p) +π p0; ˆp0 1 2λ0 ¯ ¯V G+ 0(p)T ¯ ¯ p; ˆp1 2λ ® π = Vπ λ0,λ(p0, p) + 1 2 X λ00 Z dp00 Vπ λ0,λ00(p0, p00)G0+(p00)Tλπ00,λ(p00, p) (3.41)
Pada persamaan (3.41) di atas nilai λ00 = ±1
2 . Menggunakan sifat simetri matriks
(3.38), bagian integral dari persamaan (3.41) untuk nilai λ00 = −1 2, dapat diker-jakan sebagai: Z dp00 Vπ λ0,−1 2 (p0, p00)G+ 0(p00)T−π1 2 ,λ (p00, p) = Z dp00 Vπ λ0,1 2 (p0, −p00)G+ 0(p00)T1π 2 ,λ (−p00, p) = Z dp00 Vπ λ0,1 2 (p0, p00)G+0(p00)T1π 2 ,λ (p00, p) (3.42) Persamaan terakhir didapat karena integral di atas dievaluasi pada seluruh nilai p00. Dengan hasil dari persamaan (3.42), maka persamaan (3.41) dapat
diseder-hanakan menjadi: Tλπ0,λ(p0, p) = Vλπ0,λ(p0, p) + Z dp00 Vπ λ0,1 2 (p0, p00)G+0(p00)T1π 2 ,λ (p00, p) . (3.43)
Persamaan ini adalah persamaan Lippmann-Scwhinger untuk matriks-T pada basis momentum-helicity.
Pada kondisi awal kami tentukan ˆp = ˆz. Maka:
α0 = cos θ0 , (3.44) dan hˆp0λ0|ˆzλi =X m eim(φ0) d 1 2 mλ0(θ0) d 1 2 mλ(0) = eiλφ0 d 1 2 λλ0(θ0) , (3.45)
sehingga bagian sudut azimuth dari matriks potensial, yang telah didapatkan pada persamaan (3.35), dapat ditulis sebagai:
Vπ
λ0λ(p0, pˆz) = eiλφ 0
Vπ
λ0λ(p0, p, α0) . (3.46)
Sedangkan untuk matriks-T, kebergantungannya pada sudut azimuth, yang telah dinyatakan pada persamaan (3.40), menjadi:
Tπ
λ0λ(p0, pˆz) = eiλφ 0
Tπ
λ0λ(p0, p, α0) (3.47)
Maka persamaan (3.43) menjadi:
Tπ λ0,λ(p0, pˆz) = Vλπ0,λ(p0, pˆz) + Z dp00 Vπ λ0,1 2 (p0, p00) G+ 0(p00) T1π 2 ,λ (p00, pˆz) . (3.48)
Dengan menggunakan persamaan (3.46), (3.47) dan dengan mendefinisikan:
α00 = p00· p = cos θ00 (3.49)
β = p00· p0 = cos θ0cos θ00+ sin θ0sin θ00cos(φ00− φ0)
= α0α00+√1 − α02√1 − α002cos(φ00− φ0) , (3.50) persamaan (3.48) menjadi: Tπ λ0,λ(p0, pˆz) = eiλφ 0 Vπ λ0,λ(p0, p, α0) + Z ∞ 0 dp00p002 Z 1 −1 dα00 Z 2π 0 dφ00 × Vπ λ0,1 2 n p0, p00, eim(φ0−φ00) , β o G+ 0(p00) eiλφ 00 Tπ 1 2 ,λ (p00, p, α00) = eiλφ0 · Vπ λ0,λ(p0, p, α0) + Z ∞ 0 dp00p002 Z 1 −1 dα00 Z 2π 0 dφ00 × Vπ λ0,1 2 n p0, p00, eim(φ0−φ00) , β o G+ 0(p00) eiλ(φ 00−φ0) Tπ 1 2 ,λ (p00, p, α00) ¸ = eiλφ0 Tπ λ0λ(p0, p, α0) (3.51) dengan Tπ
λ0λ(p0, p, α0) memenuhi persamaan berikut:
Tπ λ0,λ(p0, pˆz) = Vλπ0,λ(p0, p, α0) + Z ∞ 0 dp00p002 Z 1 −1 dα00 Z 2π 0 dφ00 × Vπ λ0,1 2 n p0, p00, eim(φ0−φ00) , β o G+ 0(p00) eiλ(φ 00−φ0) Tπ 1 2 ,λ (p00, p, α00) (3.52) Pada persamaan (3.51) di atas bagian yang bergantung pada sudut azimuth
φ00 dapat dipisahkan dengan mendefinisikan:
Vπ λ01 2 (p0, p00, α0, α00) ≡ Z 2π 0 dφ00 eiλ(φ00−φ0)Vπ λ01 2 (p0, p00) . (3.53) Dan untuk suku Vπ
λ0,λ(p0, p, α0) digunakan: Vπ λ0λ(p0, p, α0, 1) = Z 2π 0 dφ00 e−iλφ0 Vπ λ0λ(p0, pˆz) = (2π)Vλπ0,λ(p0, p, α0) . (3.54)
Sehingga persamaan untuk Tπ
λ0λ(p0, p, α0) pada persamaan (3.51) ialah:
Tλπ0λ(p0, p, α0) = 1 2πV π λ0λ(p0, p, α0, 1) + Z ∞ 0 dp00p002 Z 1 −1 dα00 Vπ λ01 2 (p0, p00, α0, α00)G+ 0(p00)T1π 2 ,λ (p00, p, α00) (3.55)
Persamaan (3.55) merupakan bentuk akhir dari persamaan Lippmann-Schwinger untuk matriks-T pada basis momentum-helicity yang akan dipecahkan. Untuk setiap keadaan paritas ηπ diperlukan 2 persamaan, masing-masing untuk
men-cari Tπ 1 212 (p0, p, α0) dan Tπ 1 2 ,−12
(p0, p, α0). Sehingga untuk semua keadaan paritas
diperlukan 4 persamaan. Namun akan kami tunjukan di bawah, bahwa dengan memanfaatkan sifat simetri dari matriks-Tπ
λ0λ(p0, p, α0) diperlukan hanya 2
per-samaan saja.
Dengan menggunakan sifat simetri pada persamaan (3.38) pada persamaan (3.47) bisa didapatkan: Tπ −λ0λ(p0, p, α0) = e−iλφ 0 Tπ −λ0λ(p0, pˆz) = iηπ e−iλφ 0 Tπ λ0λ(−p0, pˆz) = iηπ e−iλφ 0 eiλ(φ0+π)Tλπ0λ(p0, p, −α0) = (−)λiη π Tλπ0λ(p0, p, −α0) (3.56)
sedangkan dengan menggunakan sifat simetri pada persamaan (3.37) didapatkan hubungan berikut: Tλπ0,−λ(p0, p, α0) = eiλφ 0 Tλπ0,−λ(p0, pˆz) = −iηπ eiλφ 0 Tπ λ0λ(p0, −pˆz) , (3.57)
untuk menyelesaikan persamaan (3.57) di atas, maka digunakan sifat seperti yang ditunjukan dalam persamaan (3.30) untuk matriks V, dimana bagian dari matriks V (matriks-T) yang bergantung terhadap momentum dan spin dapat dipisahkan.
Tλπ0λ(p0, p) ∼ fπ(p0, p) hˆp0λ0|ˆpλi , (3.58)
dengan fπ(p0, p) merupakan bagian yang bergantung terhadap momentum.
Deng-an sifat ini maka:
Tπ
λ0λ(p0, −pˆz) ∼ fπ(p0, −pˆz) hˆp0λ0| − ˆzλi , (3.59)
dan dengan sifat parity invariance dari matriks-T, didapatkan:
untuk bagian yang bergantung pada spin digunakan: hˆp0λ0| − ˆzλi =X m eim(φ0−π) d 1 2 mλ0(θ0)d 1 2 mλ(π) =X m eim(φ0−π)d 1 2 mλ0(θ0)(−)− 1 2 −λδ−m,λ = e−iλ(φ0−π) d 1 2 −λ,λ0(θ0)(−)− 1 2 −λ = e−iλ(φ0+π)e2iλπd 1 2 λ,λ0(π − θ0)(−)− 1 2 −λ(−)12 +λ0 = (−)(−)λ0−λ e−iλ(φ0+π) d 1 2 λ,λ0(π − θ0) = (−)(−)λ0e−iλφ0d 1 2 λ,λ0(π − θ0) , (3.61)
dan dengan memasukan kembali ke persamaan (3.60):
Tλπ0λ(p0, −pˆz) ∼ (−)(−)λ 0 e−iλφ0fπ(−p0, pˆz)d 1 2 λ,λ0(π − θ0) (3.62)
menggunakan persamaan (3.47), maka:
Tπ λ0λ(p0, −pˆz) = (−)(−)λ 0 e−iλφ0 Tπ λ0λ(p0, p0, −α) . (3.63) Dengan memasukan Tπ
λ0λ(p0, −pˆz) dari persamaan (3.63) kedalam persamaan
(3.57) bisa didapatkan hubungan:
Tλπ0,−λ(p0, p, α0) = (−)λ 0
iηπ Tλπ0λ(p0, p0, −α) . (3.64)
Dengan menggunakan persamaan (3.56) dan persamaan (3.64), bisa didapatkan hubungan:
Tπ
−λ0,−λ(p0, p, α0) = −Tλπ0,λ(p0, p, α0) . (3.65)
3.4
Elemen Matriks M
Dalam menghitung matriks M pada persamaan (2.40), digunakan sumbu-z seba-gai sumbu kuantisasi spin. Maka diperlukan hubungan antara elemen matriks-T dalam basis momentum-helicity dan elemen matriks-T dalam basis berikut:
|pνi ≡ |pi¯¯1
2 ν
®
dengan ¯¯1 2 ν
®
yaitu keadaan spin dengan sumbu kuantisasi pada arah ˆz. Elemen matriks-T dalam basis ini yaitu:
Tν0ν(p0, p) ≡ hp0ν0|T | pνi . (3.67)
Kemudian, untuk dapat menghubungkannya dengan elemen matriks-T dalam basis momentum-helicity, perlu dikerjakan overlap berikut:
ˆ p1 2λ|ˆz12ν ® =zˆ1 2λ ¯ ¯R−1(ˆp)¯¯ ˆz1 2ν ® = D 1 2 ∗ νλ (ˆp) = eiνφd12 νλ(θ) (3.68)
Menggunakan hasil dari persamaan (3.68) di atas, serta dengan completness
re-lation (3.14), didapatkan: Tν0ν(p0, p) = 1 4 X πλ0λ Z dp00dp000 p0ν0|p00; ˆp00 1 2λ0 ® π T π λ0λ(p00, p000)π p000; ˆp000 1 2λ|pν ® = 1 8 X πλ0λ Z dp00dp000 n p0ν0|p00; ˆp00 1 2λ 0®+ η π p0ν0| − p00; ˆp00 1 2λ 0® o Tπ λ0λ(p00, p000) ×n p000; ˆp000 1 2λ|pν ® + ηπ −p000; ˆp000 1 2λ|pν ® o = 1 8 X πλ0λ Z dp00dp000 · δ(p0− p00) + ηπδ(p0+ p00) ¸ D 1 2 ν0λ0(ˆp00) Tλπ0λ(p00, p000) × · δ(p − p000) + η πδ(p + p000) ¸ D 1 2 ∗ νλ (ˆp000) = 1 8 X πλ0λ · D 1 2 ν0λ0(ˆp0) Tλπ0λ(p0, p) D 1 2 ∗ νλ (ˆp) + ηπD 1 2 ν0λ0(−ˆp0) Tλπ0λ(−p0, p) D 1 2 ∗ νλ (ˆp) + ηπD 1 2 ν0λ0(ˆp0)Tλπ0λ(p0, −p) D 1 2 ∗ νλ (−ˆp) + D 1 2 ν0λ0(−ˆp0) Tλπ0λ(−p0, −p)D 1 2 ∗ νλ (−ˆp) ¸ = 1 8 X πλ0λ D 1 2 ν0λ0(ˆp0) D 1 2 ∗ νλ (ˆp) h Tπ λ0λ(p0, p) + i ηπ T−λπ 0λ(−p0, p) − i ηπ Tλπ0−λ(p0, −p) + T−λπ 0−λ(−p0, −p) i . (3.69)
Dengan sifat simetri matriks-T, yaitu persamaan (3.37), (3.38) dan (3.39), per-samaan (3.69) menjadi: Tν0ν(p0, p) = 1 2 X πλ0λ D 1 2 ν0λ0(ˆp0) D 1 2 ∗ νλ (ˆp) Tλπ0λ(p0, p) (3.70)
Selanjutnya, dengan kondisi ˆp = ˆz, persamaan (3.70) menjadi: Tν0ν(p0, pˆz) = 1 2 e −iν0φ0 X πλ0λ d 1 2 ν0λ0(θ0) δλν eiλφ 0 Tπ λ0λ(p0, p, α0) = 1 2 e −i(ν0−ν)φ0X πλ0 d 1 2 ν0λ0(θ0) Tλπ0ν(p0, p, α0) (3.71)
Dengan memasukan persamaan (3.71) ke persamaan (2.40), didapatkan ele-men matriks M sebagai berikut:
Mν0ν(p0, pˆz) = −2µπ2 e−i(ν 0−ν)φ0X πλ0 d 1 2 ν0λ0(θ0) Tλπ0ν(p0, p, α0) (3.72)
3.5
Hubungan Dengan Elemen Matriks-T Dalam
Basis Gelombang Parsial
Pada sub-bab ini kami tunjukan hubungan antara elemen matriks-T dalam basis
momentum-helicity Tπ
λ0λ(p0, p) dan elemen matriks-T dalam basis gelombang
parsial Tljm0l (p0, p). Dengan menggunakan completness relation basis gelombang
parsial, dapat dilihat pada lampiran A, didapatkan hubungan berikut:
Tλπ0λ(p0, p) = X j0l0m0 X jlm Z ∞ 0 p0002dp000 Z ∞ 0 p002dp00 πp0; ˆp0λ0|p000(l0 12); j0m0® p0000(l0 1 2); j0m0|T | p00(l12); jm ® p00(l1 2); jm|p; ˆpλ ® π . (3.73)
Untuk mengerjakan persamaan (3.73), perlu diformulasikan overlap antara basis momentum-helicity dengan basis gelombang parsial:
p(l1 2); jm|p 0; ˆp0λ0® =X µ C(l1 2j; m − µ, µ) hplm − µ|p 0i1 2µ|ˆp 0,1 2λ 0® =X µ C(l1 2j; m − µ, µ) δ(p0− p) p0p Y ∗ lm−µ(ˆp0) D 1 2 µλ0(ˆp0) (3.74)
Dengan overlap pada persamaan (3.74), serta konservasi nilai j dan m, yang diperlihatkan pada persamaan (2.54), maka didapatkan:
Tλπ0λ(p0, p) = 1 2 X jmll0 Z ∞ 0 p0002dp000 Z ∞ 0 p002dp00 Tljm0l (p000, p00) δ(p000− p0) p000p0 δ(p00− p) p00p ×X µ0 C(l0 1 2j; m − µ0, µ0)D 1 2 ∗ µ0λ0(ˆp0) · Yl0,m−µ0(ˆp0) + ηπYl0,m−µ0(−ˆp0) ¸ ×X µ C(l1 2j; m − µ, µ)D 1 2 µλ(ˆp) · Yl,m−µ∗ (ˆp) + ηπYl,m−µ∗ (−ˆp) ¸ (3.75) karena Ylm(−ˆr) = (−)l Ylm(ˆr), maka persamaan (3.75) menjadi:
Tπ λ0λ(p0, p) = 1 2 X jmll0 Tljm0l (p0, p) ³ 1 + ηπ(−)l 0´³ 1 + ηπ(−)l ´ ×X µ0 C(l0 1 2j; m − µ0, µ0)D 1 2 ∗ µ0,λ0(ˆp0) Yl0m−µ0(ˆp0) ×X µ C(l1 2j; m − µ, µ)D 1 2 µ,λ(ˆp) Ylm−µ∗ (ˆp) . (3.76)
Pada persamaan di atas terdapat syarat, yaitu:
ηπ(−)l = 1 dan ηπ(−)l
0
= 1 , (3.77)
maka untuk keadaan paritas ganjil hanya nilai l dan l’ ganjil yang berkontribusi, dan sebaliknya untuk paritas genap, hanya nilai l dan l’ genap yang berkontribusi. faktor ³ 1+ηπ(−)l 0´ dan ³ 1+ηπ(−)l ´
bersama-sama memberikan nilai 4, sehinga persamaan (3.76) menjadi: Tλπ0λ(p0, p) = 2 X jmll0 Tljm0l (p0, p) X µ0 C(l0 12j; m − µ0, µ0)D 1 2 ∗ µ0,λ0(ˆp0) Yl0m−µ0(ˆp0) ×X µ C(l1 2j; m − µ, µ)D 1 2 µ,λ(ˆp) Ylm−µ∗ (ˆp) . (3.78)
Dengan memasukan kondisi ˆp = ˆz, didapatkan:
Tπ λ0λ(p0, pˆz) = 2 X jll0 Tljλ0l(p0, p) r 2l + 1 4π C(l 1 2j; 0, λ) ×X µ0 C(l0 12j; λ − µ0, µ0)D 1 2 ∗ µ0,λ0(ˆp0) Yl0,λ−µ0(ˆp0) . (3.79)
Sebagai pengujian terhadap hubungan (3.79), yang berarti juga pengujian untuk formulasi elemen matriks-T dalam basis momentum-helicity, persamaan (3.79) dimasukan ke persamaan (3.70), sehingga menghasilkan:
Tν0ν(p0, pˆz) = X jll0 r 2l + 1 4π X λ0λ Tljλ0l(p0, p) C(l12j; 0, λ) ×X µ0 C(l0 12j; λ − µ0, µ0)D 1 2 ∗ µ0,λ0(ˆp0) Yl0,λ−µ0(ˆp0)D 1 2 ν0λ0(ˆp0) δνλ, (3.80)
dengan menggunakan sifat matriks-D Wigner sebagai berikut: X m Dmj ∗0m(ˆr)Djm00m(ˆr) = δm00m0 , (3.81) persamaan (3.80) menjadi: Tν0ν(p0, pˆz) = X jll0 Tljν0l(p0, p) r 2l + 1 4π C(l 1 2j; 0, ν)C(l 0 1 2j; ν − ν 0, ν0)Y l0,ν−ν0(ˆp0). (3.82) Persamaan (3.82) dimasukan ke persamaan (2.40), maka dihasilkan
Mν0ν(p0, pˆz) = −4µπ2 X jll0 Tljν0l(p0, p) r 2l + 1 4π C(l 1 2j; 0, ν) × C(l0 12j; ν − ν0, ν0) Yl0,ν−ν0(ˆp0) . (3.83)
Persamaan (3.83) identik dengan persamaan (2.63). Hal ini menunjukan bahwa elemen matriks-T yang kami hitung, dengan teknik 3D, menghasilkan besaran yang dapat diamati yang sama dengan yang dihasilkan pada teknik gelombang parsial.
3.6
Kinematika Relativistik
Teknik 3D diformulasi karena kebutuhan akan suatu teknik perhitungan alternatif untuk hamburan pada energi tinggi. Karena pada energi tinggi efek relativitas berpengaruh cukup signifikan, maka perlu diperhitungkan. Di sini hanya akan dilihat efek kinematika relativistik. Untuk memasukan efek kinematika relativis-tik, digunakan hubungan relativistik energi dan momentum:
serta transformasi Lorentz dari kerangka laboratorium ke kerangka pusat massa (P.M.).
Dalam perhitungan yang menggunakan kinematika non-relativistik, elemen matriks-T dihitung untuk hamburan pada energi ELab. dalam kerangka
labora-torium. Kami dapatkan hubungan antara ELab., EP.M., dan besar momentum
relatif p sebagai berikut:
ELab. =
m1
µ EP.M. =
m1 p2
2µ2 , (3.85)
lebih jelas dapat dilihat sub-bab 2.1. Karena sebelumnya digunakan hubungan non-relativistik energi dan momentum, ELab merupakan energi kinetik proyektil
EkLab. dalam kerangka laboratorium, dan EP.M. merupakan energi kinetik sistem
EkP.M. dalam kerangka P.M. Sehingga hubungan (3.85) dapat ditulis sebagai:
EkLab. =
m1
µ EkP.M.=
m1 p2
2µ2 , (3.86)
Setelah memasukan efek kinematika relativistik hubungan antara EkLab., EkP.M.
dan p harus dicari lagi.
Transformasi Lorentz dari kerangka laboratorium ke kerangka P.M. dikerjakan sebagaimana pada [4]. Dimulai dengan mendefinisikan momentum four vectors (momentum-4) pada kerangka awal, yaitu kerangka laboratorium, untuk partikel ke-i, sebagai berikut:
kµi ≡ (Ei, ki) , (3.87)
dengan ki ialah vektor momentum dalam ruang spasial, dan Ei ialah energi total
partikel ke-i dalam kerangka laboratorium. Maka dengan transformasi Lorentz
L(v), dimana v adalah kecepatan relatif kerangka baru terhadap kerangka lama,
didefinisikan:
pµi ≡ L(v) kµi , (3.88)
pµ ialah momentum-4 pada kerangka baru, yaitu kerangka P.M.. pµ didapat
melalui:
p1 = p = k1+ (γ − 1)(k1· ˆv)ˆv − γE1v , (3.89)
dan:
Ei P.M. = γ(Ei− ki· v) , (3.91)
dimana
γ ≡ √ 1
1 − v2 . (3.92)
Maka, transformasi sistem dari kerangka laboratorium ke kerangka P.M., di-lakukan menggunakan persamaan (3.88)-(3.92).
Energi partikel-1 (proyektil) pada keadaan awal, sesuai persamaan (3.84), ialah:
E1 = (m21+ k21)1/2 . (3.93)
Karena pada keadaan awal target diam (k2 = 0), maka energinya:
E2 = m2 . (3.94)
Sehingga momentum-4 pada keadaan awal:
kµ1 = (E1, k1) (3.95)
kµ2 = (m2, 0) , (3.96)
maka momentum-4 total pada keadaan awal: kµ = kµ
1 + kµ2
= (ELab., k1) , (3.97)
dimana ELab. ialah energi total dalam kerangka laboratorium, ELab. = E1 + m2.
Kecepatan relatif kerangka P.M. terhadap kerangka laboratorium yaitu:
v = k
k0
= k1
ELab.
. (3.98)
Faktor γ didapat dengan memasukan kecepatan v pada persamaan (3.98) kedalam persamaan (3.92), maka didapatkan:
γ = pk0 kµk µ = ELab. M0 , (3.99)
dengan massa invarian sistem M0 didefinisikan sebagai: M0 ≡ p kµk µ = q m2 1+ m22+ 2E1m2 (3.100)
Maka momentum relatif p dalam kerangka P.M. menurut transformasi Lorentz, yaitu: p = k1+ (γ − 1)(k1· ˆv)ˆv − γE1v = γ(k1− E1v) = ELab. M0 Ã k1− k1 ELab. E1 ! = m2 M0 k1 , (3.101)
dan energi dalam kerangka P.M. :
E1 P.M. = γ(E1− v · k1) = ELab. M0 Ã E1− k1 ELab. k1 ! = m 2 1+ m2E1 M0 (3.102) E2 P.M. = γ m2 = m 2 2+ m2E1 M0 , (3.103)
sehingga momentum-4 dalam kerangka P.M. untuk tiap partikel:
pµ1 = (E1 P.M., p) (3.104)
pµ2 = (E2 P.M., −p) , (3.105)
jadi momemtum-4 total dalam kerangka P.M., yang merupakan energi total dalam kerangka P.M., yaitu:
pµ= pµ
1 + pµ2
= E1 P.M.+ E2 P.M. ≡ EP.M. . (3.106)
Karena M0 invarian terhadap transformasi Lorentz:
pµp
maka:
EP.M.= M0 . (3.108)
Kini kami cari relasi antara EkLab., EkP.M. dan p. Kami mulai dengan:
E1 = EkLab.+ m1 , (3.109)
maka, hubungan antara EkLab. dan EkP.M. yaitu:
EkP.M. = EP.M.− (m1+ m2) = q m2 1+ m22+ 2E1m2 − (m1+ m2) = q m2 1+ m22+ 2(EkLab.+ m1)m2 − (m1+ m2) . (3.110)
Untuk menentukan p (besar momentum p) digunakan persamaan (3.101), dengan
k1 didapatkan melalui persamaan (3.93) :
k1 = q E2 1 − m21 =pEkLab.(EkLab.+ 2m1) , (3.111) sehingga didapatkan: p = m2 p EkLab.(EkLab.+ 2m1) p m2 1+ m22+ 2(EkLab.+ m1)m2 (3.112) Untuk menentukan hubungan antara sudut hambur dalam kedua kerang-ka, maka asumsikan bahwa partikel-1 bergerak pada arah sumbu-z. sehingga momentum-4 partikel-1, dalam kerangka laboratorium, ialah:
kµ1 = (E1, 0, 0, k1) , (3.113)
sedangkan dalam kerangka P.M., momentum-4 partikel-1 ialah:
pµ1 = (E1 P.M., 0, 0, p1) . (3.114)
Apabila sudut hambur dalam kerangka P.M. θP.M, maka momentum-4, dalam
kerangka P.M., setelah hamburan p0
1: