BAB III TEORI MEDAN KUANTUM UNTUK FORWARD RATES DENGAN VOLATILITAS STOKASTIK Lagrangian Forward Rates dengan Volatilitas Deterministik

BAB III

TEORI MEDAN KUANTUM UNTUK FORWARD RATES DENGAN VOLATILITAS STOKASTIK

3.1. Lagrangian Forward Rates dengan Volatilitas Deterministik

Pertama akan dibahas secara singkat tentang pentingnya teori medan

forward rates dengan volatilitas deterministik. Sebagai bentuk konkretnya,

misalkan forward rates di mulai dari waktu T sampai pada masa mendatang di _i

f

t T= . Karena semua forward rates f t x selalu untuk masa mendatang, maka

( )

, dalam hal ini x t> , oleh karena itu medan kuantum f t x didefinisikan sebagai

( )

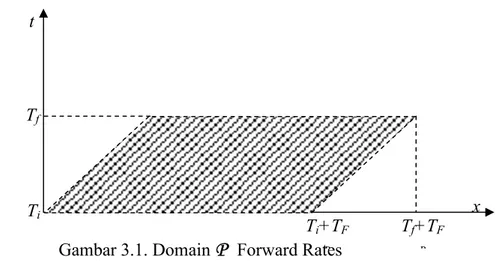
, medan dengan domain berbentuk jajaran genjang yang dibatasi oleh garis-garis sejajar x t= dan x T= _FR+tdalam arah sumbu maturitas ; serta garis t T= _idan

f

t T= dalam arah sumbu waktu sebagaimana digambarkan dalam gambar 3.1. dibawah ini:

Gambar 3.1. Domain

_P

Forward Rates

Setiap titik dalam domain

_P

merepresentasikan suatu variabel integrasi

( )

,

f t x yang independen.

Interpretasi teori medan pada evolusi forward rates sebagaimana dinyatakan dalam domain

_P

yaitu suatu string kuantum (non-relativistik) yang berpindah dengan satuan kecepatan dalam arah x.

Ti+TF R Tf+TF R t Tf Ti x

Dari model HJM, forward rates memiliki kecepatan drift

( )

t x, dan volatilitas

( )

t x , dan kedua kuantitas ini akan tampak dalam persamaan ,

Lagrangian untuk forward rates. Guna mendefiniskan Lagrangian, pertama kita

membutuhkan suku kinetik, yang dilambangkan dengan Lkinetik, guna

mendefinisikan standar waktu evolusi forward rates.

Guna mendefinisikan Lagrangian maka perlu diperkenalkan suku lain sebagai gangguan yang merubah bentuk forward rates dalam arah sumbu x. Analogi dengan hal ini dalam string biasa adalah suku potensial dalam

Lagrangian yang membuat bentuk runcing dalam string, karena bentuk string

sendiri sebenarnya mengandung suku potensial.

Untuk memodelkan sifat-sifat yang mirip dengan string pada forward

rates, tidak dapat menggunakan suku turunan

( )

f_x 2

(

( _{dalam Lagrangiannya, karena}

hal ini hanya berlaku pada kondisi tanpa kehadiran arbitrase saja. Kondisi tanpa arbistrase diperlukan ini agar Lagrangian mengandung suku turunan dengan orde yang lebih tinggi, khususnya suku dengan bentuk

( )

_x2f_t 2

( (

( _{; yang mirip dengan}

sistem string yang memiliki rigiditas berhingga. Istilah seperti ini dalam Lagrangian forward rates dinamakan

L

rigiditas dengan parameter baruµ, diberikan

oleh_µ12, yang menunjukkan kuantitas fluktuasi dari forward rates terhadap waktu

dalam arah sumbu x. Jika diberlakukan limit µ -0, akan diperoleh hasil yang sama dengan model HJM, yang juga akan mirip dengan string dengan rigiditas tak hingga.

Aksi dari forward rates diberikan oleh persamaan :

[ ]

+

[ ]

=

_.

f

_.

FR i T t T T t S f dt dx

L

f (1)

[ ]

/

_.

f P

L

(2)

[ ]

f = kinetik

[ ]

f + rigiditas

[ ]

f

L

L

L

(3)

( ) ( )

( )

( ) ( )

( )

2 2 2 , , , , 1 1 2 , µ , $ 0 ( ( $ 0 ! ! ! ! ₍ ! ₍ ! ! ₍ ! = # 1 + #₍ 1 ! ! ! ! ! ! ! ! " 2 " 2 f t x f t x t x t x t t t x x t x

( )

, 3 f t x +3 (4)

Adanya suku kedua dalam persamaan aksi yang diberikan persamaan (3) tidak dicantumkan dalam [14] ketika kondisinya tanpa arbitrase, dan studi empiris yang dilakukan [11] menguatkan bukti bahwa suku ini merupakan suku evolusi forward

rates. Singkatnya, menurut [11] forward rates berlaku seperti string kuantum,

dengan ruang dan waktu bergantung kepada kecepatan drift

( )

t x, , massa efektifnya diberikan oleh _{( )t,}1_{x , dan rigiditas string sebanding dengan}

2

1

µ .

Karena teori medan didefinisikan dalam dalam domain , maka perlu untuk menspesifikasi syarat batas untuk seluruh empat batas jajaran genjang tersebut.

a. Kondisi Terikat Dirichlet (awal dan akhir)

Syarat batas awal dan akhir untuk kondisi Dirichlet dalam arah sumbu t diberikan oleh :

( )

( )

:

(

,

)

,

( )

,

i f i f FR i f

T T < x < T T +T f T x f T x (5)

yang meliputi kurva forward rates dari awal sampai akhir. b. Kondisi Bebas Neumann

Dalam menspesifikasi syarat batas dalam arah sumbu x, perlu menganalisis aksi yang diberikan oleh persamaan (1) guna menentukan bahwa dalam kondisi itu aksi tidak mengandung suku permukaan. Analisis ini kemudian menghasilkan kondisi Neumann dengan versi sebagai berikut :

( ) ( )

( )

, 0 , , , ( = ( ( ( < < x t x t t x t f x T t T_{i f} (6) dan FR T t x t x = atau = + (7)

Forward rates dalam teori medan kuantum didefinisikan oleh Integral

Lintasan Feynmann dengan mengintegrasikan terhadap semua konfigurasi yang mungkin, dan hasil untuk f t x

( )

, adalah:

[ ] S f Z =

.

D f e (8)

( )

( ), , t x D f +3df t x 3 =

4

.

.

P (9)

Perhatikan bahwa eS[ ]f Z _{adalah probabilitas untuk konfigurasi medan yang}

berbeda yang terjadi ketika dibentuk integral fungsional f t x .

( )

, 3.2 Lagrangian Forward Rates dengan Volatilitas Stokastik

Untuk menyatakan fungsi volatlitas ( xt, )stokastik, dalam formalisme teori medan kuantum perlu untuk menaikkan ( xt, )dari fungsi yang deterministik ke dalam fungsi yang random. Ada dua cara yang dapat digunakan guna menaikkan volatilitas menjadi kuantitas yang stokastik, yaitu:

a. Meninjau volatilitas sebagai suatu fungsi dari forward rates f ,

( )

t x

b. Meninjau volatlitas sebagai suatu medan kuantum yang independen dalam tesis ini akan dikaji kemungkinan keduanya.

3.2.1. Volatilitas sebagai Fungsi Forward Rates

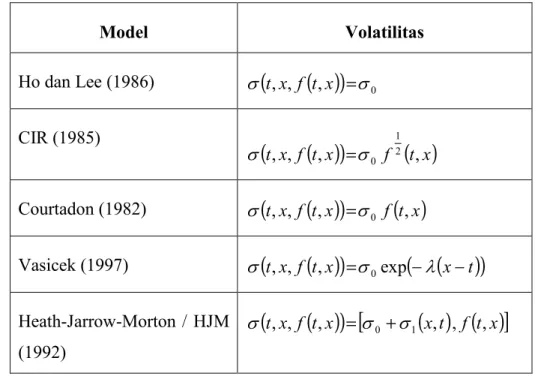
Dalam [13] telah diindikasikan bahwa volatilitas sebenarnya merupakan fungsi dari forward rates. Model standar menggunakan pendekatan ini dengan persamaan volatilitas secara ringkas diberikan oleh :

( ) ( )

t_,x _, f t_,x

( ) ( )

t_,x fv t_,x

0

= (10)

dengan

( )

t,x

0 adalah fungsi deterministik (11)

karena volatilitas ( xt, )> 0, maka f ,

( )

t x juga >0, berlawanan dengan persamaan (4), diperoleh:

( )

_{t x = f e} ( ) _{> 3}

_{( )}

_{t x +3}

f _, t,x _{0 ; ,}

0 ) ) (12)

dengan f ,

( )

t x > 0 karena forward rates di pasar finansial selalu positif dan hal ini akan dipakai dalam perhitungan selanjutnya. Dengan limit µ -0 dalam persamaan (10) akan menghasilkan cakupan volatilitas model HJM.

Adapun pandangan-pandangan empiris volatilitas sebelumnya menurut [13] diberikan dalam tabel 3.1. berikut:

Model Volatilitas Ho dan Lee (1986)

(

t,x,f

( )

t,x

)

= ₀ CIR (1985)

( )

(

t,x, f t,x

)

f 2

( )

t,x 1 0 = Courtadon (1982)

(

t,x,f

( )

t,x

)

= ₀ f

( )

t,x Vasicek (1997)

(

t,x,f

( )

t,x

)

= ₀exp

(

5

(

x t

)

)

Heath-Jarrow-Morton / HJM (1992)

( )

(

t,x,f t,x

)

=

[

₀ + ₁

( ) ( )

x,t ,f t,x

]

Tabel 3.1. Berbagai Rumusan Volatilitas

Tesis ini akan membahas bentuk umum Lagrangian dalam persamaan (3) untuk kasus forward rates yang selalu positip. Interpretasi Lagrangian dalam

persamaan (3) akan valid jika semua forward rates mendekati nilai tertentu f .₀

Oleh karena itu menghasilkan persamaan:

( )

( )

( )

t x t e f t x t f tx ( ( = ( ( , , , 0 ) (13)

( )

_{( )}

2 0 , ₎ ) O t x t f + ( ( 6 (14)

oleh karena itu dibuat mapping sebagai berikut:

( )

( )

t x t f t x t f ( ( -( ( , , 0 ) (15) Persamaan (3) kemudian digeneralisir menjadi :

[ ]

)

_L

_kinetik

[ ]

)

_L

_rigiditas

[ ]

)

L

= +

( ) ( )

( )

( )

( ) ( )

( )

( ) ! ! 2 !! 1 0 ! ! " !! # $ ( ( ( ( + ! ! 2 !! 1 0 ! ! " !! # $ ( ( = 2 , 0 0 2 2 , 0 0 , , , 1 , , , 2 1 x t v x t v _{t x e} x t t x t f x e x t x t t x t f ) ) ) µ ) (16) nantinya dalam penurunan Hamiltonian- sistem akan memerlukan perhitungan dengan solusi trivial dalam integrasinya

Fungsi Partisi didefinisikan secara teori oleh Integral Lintasan Feynmann sebagai berikut: [ ]

.

= _{D) f} v_eS) Z (17)

( )

( )

( )

4 .

.

/ +33 P x t v v _{d t x f t x} f D , , , ) ) (18)

dengan syarat batas yang diberikan untuk f ,

( )

t x dalam persamaan (5) dan (6) tetap berlaku untuk mempertahankan volatilitas stokastik dalam Lagrangian di persamaan (16).

3.2.2. Volatilitas sebagai Suatu Medan Kuantum yang Independen

Sekarang akan dibahas asumsi yang kedua, yaitu jika volatilitas ₀

( )

t,x

ditinjau sebagai suatu medan kuantum yang independen. Karena hanya dapat menentukan efek dari volatilitas pada forward rates, maka seluruh efek-efek dari volatilitas stokastik akan dimanifestasikan hanya melalui perilaku forward rates saja.

Guna penyederhanaan, ditinjau forward rates sebagai suatu medan kuantum sebagaimana dalam persamaan (4), dengan:

( )

t x 3 f

( )

t x +3

f , : , (19)

karena fungsi volalititas ₀

( )

t,x selalu positif, yaitu ₀

( )

t,x >0 maka diperkenalkan sebuah medan kuantum lain h

( )

t, dengan hubungan sebagai x

berikut :

( )

_{t,x = e} h( )t,x _{, 3 h}

_{( )}

_{t,x +3}

0

0 (20)

tanda – (negatif) diambil bertujuan untuk meyakinkan secara notasi saja.

Sekarang sistem terdiri atas dua medan kuantum yang saling berinteraksi, dinamakan dengan f

( )

t,x dan h

( )

t,x serta mengikuti aturan-aturan sebagai berikut :

• Parameter 7 adalah kuantitas yang menentukan bahwa medan h

( )

t,x tidak deterministik. Suatu Limit 7 -0akan membekukan semua fluktuasi medan

( )

t x

• Parameter 8 berfungsi mengendalikan fluktuasi h ,

( )

t x dalam arah sumbu x, yang hal ini sama dengan parameter µ yang mengendalikan fluktuasi dari

forward rates f

( )

t,x dalam arah sumbu x juga.

• Parameter 9 dengan: 1 9 +1 adalah kuantitas korelasi medan kuantum

forward rates f

( )

t,x dengan medan kuantum volatilitas h

( )

t, . x

• Suku drift dari volatilitas dinamakan&

( )

t,x , dimana analog dengan suku drift

( )

t,x untuk forward rates.

Lagrangian untuk sistem yang berinteraksi di sini tidak unik, artinya ada

sejumlah pilihan yang dapat memenuhi kondisi di atas. Suatu Lagrangian yang mungkin untuk sistem yang berinteraksi dituliskan dengan analogi Lagrangian untuk kasus volatilitas stokastik pada sekuritas tunggal di [9], yaitu :

(

)

( ( ( ( ( ( ( ( ( ( ( ( ( ( = 2 2 2 2 2 2 2 2 1 2 1 2 1 1 2 1 7 & 8 µ 7 & 7 & 9 9 t h x t f x t h t h t f L (21)

dengan persamaan aksi :

[ ]

=

_.

P

L

h f

S , (22)

disini perlu untuk menspesifikasi syarat batas bagi sistem yang berinteraksi. Kondisi awal dan akhir dari forward rates f ,

( )

t x yang diberikan oleh persamaan (5) tetap dipertahankan untuk kasus sistem yang berinteraksi, dan untuk medan volatilitas syarat batasnya mirip, sebagai berikut :

a. Syarat Batas Terikat Dirichlet (awal dan akhir) Nilai awal dispesifikasi dari data sebagai berikut:

( )

T x T

( )

T x

( )

T x

yang berlaku khusus kurva volatlitas awal dan akhir.

Syarat batas dalam arah sumbu x untuk forward rates f ,

( )

t x sebagaimana dalam persamaan (6) tetap dipertahankan pada kasus sistem yang berinteraksi, dan untuk medan volatilitas syaratnya sebagai berikut :

b. Syarat Batas Bebas Neumann

( ) ( )

, , 0 ; = ( ( ( ( < < t x t x t h x T x T_{i f} & (24) FR T t x atau t x= = + ; (25)

untuk keperluan kuantisasi medan volatilitas

( )

t, , syarat batas forward rates x

( )

t x

f , yang diberikan oleh persamaan (6) sebenarnya tidak biasa. Guna memecahkan kondisi tanpa arbitrase, ditemukan bahwasanya merupakan fungsional berbentuk kuadratik dari medan volatilitas

( )

t, . Oleh karena itu x

syarat batas dalam persamaan (6) sesungguhnya adalah bentuk interaksi antara medan f ,

( )

t x dan medan h , .

( )

t x

Dalam hal ini perlu mendefinisikan perhitungan integrasi untuk medan h , .

( )

t x

Hamiltonian untuk sistem yang berinteraksi adalah sebagai berikut :

( )

( )

( )

4 .

.

= +33 P x t x t d x t df D f D , 1 1 _{, , (26)}

( ) ( )

( ) ( )

4 .

+3 3 P x t x t h e x t dh x t df , , , , (27)

Fungsi partisi teori medan kuantum untuk forward rates dengan volatilitas stokastik didefinisikan oleh Integral Lintasan Feynmann sebagai berikut :

.

= _{D f D} 1

Z (28)

Nilai pasar yang diamati oleh suatu instrumen keuangan, disebut

O

[ ]

f ,h , menyatakan nilai rata-rata instrumen keuangan yang melingkupi semua nilai-nilai yang mungkin dari medan kuantum f ,

( )

t x dan h ,

( )

t x -dinotasikan dengan

[ ]

f h

O , -, dengan rapat probabilitas diberikan oleh aksi (yang telah dinormalisasi) dengan simbol :

[ ]

_{> =}

_.

[ ]

[ ] < _{D f D f h e}S f h Z h f_, 1 1

_O

_, ,

O

(29)

Jika ditinjau limitnya volatilitas akan terseduksi menjadi fungsi yang deterministik, dimana untuk limit ini nilai 7,9dan 8 -0. Suku kinetik medan

( )

t x

h , dalam aksi di persamaan (22) memiliki limit :

4

4

.

- ( ( -! ! 2 !! 1 0 ! ! " !! # $ ( ( P P P tx x t t h t h , , 2 0 2 1 exp lim , & 7 & 7 (30)

yang mengimplikasikan bahwa:

( )

_{> = <} ( )_> < _{t x e} ht,x 0 , (31)

( )

{

'& ,'

}

(

7,8,9

)

exp 0 0 +

O

=

.

t t dt t x (32)

3.3. Hamiltonian dan Ruang Keadaan

Integral Lintasan Feynmann yang diberikan di persamaan (17) dan (18) berfungsi untuk menghitung nilai ekspektasi dari medan kuantum. Guna mempelajari evolusi waktu dari kuantitas-kuantitas laju bunga, maka perlu untuk menurunkan Hamiltonian sistem dari persamaan Lagrangiannya. Cara yang ditempuh dalam tesis ini akan berlawanan dengan cara [9], dimana dalam [9]

Lagrangian untuk harga saham dengan volatilitas stokastik justru diturunkan dari

Hamiltonian sistemnya.

Ruang keadaan dari teori medan adalah ruang keadaan vektor linier, yang dinotasikan dengan

V

, terdiri atas sejumlah fungsional medan konfigurasi pada waktu terikat t [9]. Dua ruang keadaan dari

V

–dinotasikan dengan

V

rangkap- terdiri

merupakan ruang vektor linier. Tinjau sebuah elemen

_V

dinotasikan oleh g dan

sebuah elemen

V

rangkap dinotasikan oleh p ; maka p g adalah suatu bilangan

kompleks. Dalam hal ini ditinjau

_V

dan

_V

rangkap sebagai ruang keadaan suatu

sistem.

H

, operator Hamiltonian –yang dalam kuantum analog dengan energi- adalah sebuah elemen tensor produk ruang

V

:

V

_rangkap. Matriks elemen

H

adalah bilangan kompleks yang diberikan oleh p g .

Dalam kasus ini, akan dipelajari lebih lanjut mengenai ruang keadaan dan Hamiltonian forward rates. Untuk mudahnya notasi ditinjau medan kuantum

forward rates f ,

( )

t x memenuhi medan kuantum f ,

( )

t x dan h , . Karena

( )

t x Lagrangian di persamaan (21) merupakan turunan pertama terhadap waktu saja,

maka akan ada sebuah generator infinitesimal yang disebut dengan hamiltonian

H

. Merumuskan hamiltonian untuk forward rates adalah hal yang sulit karena domain

P

memiliki struktur non-trivial, dan medan kuantum forward rates akan memiliki ruang keadaan yang berbeda-beda untuk tiap waktu sesaat t.

Untuk mengatasinya, perlu mendiskritisasi baik t dan x dalam suatu kisi yang berhingga, dengan ruang kisi meliputi arah t dan x dinotasikan dengan (untuk sebuah string yang bergerak dengan kecepatan ; , maturitas kisi akan berjarak ; ). Dalam kisi ini, waktu minimum suatu kontrak berjangka dinotasikan dengan waktu ; dan untuk aplikasinya =1 hari. Domain yang baru

P

~

adalah sebagai berikut:

Gambar 3.2. Domain diskrit

P

~

t

Tf

Definisi diskrit dari domain

P

~

diberikan oleh :

( )

t,x -

( )

n,l dengan n,l integer (33)

(

Ti,Tf,TFR

)

-

(

Ni,Nf,NFR

)

(34)

( )

(

)

{

n l Ni n Nf n l n+NFR

}

= , : ~ kisi P (35)

( )

t x fnl f , - _, (36)

( )

( )

₆ ( ( 6 ( ( n+ l n l fn l+ fn l t x t f f f t x t f 1, , , , 1 , ; , (37) fungsi partisinya sekarang berupa integral lipat berhingga yang dinamakan:

[ ] ( )

4 .

= P l n f S l n e df Z ~ , , ) (38)

( )

'

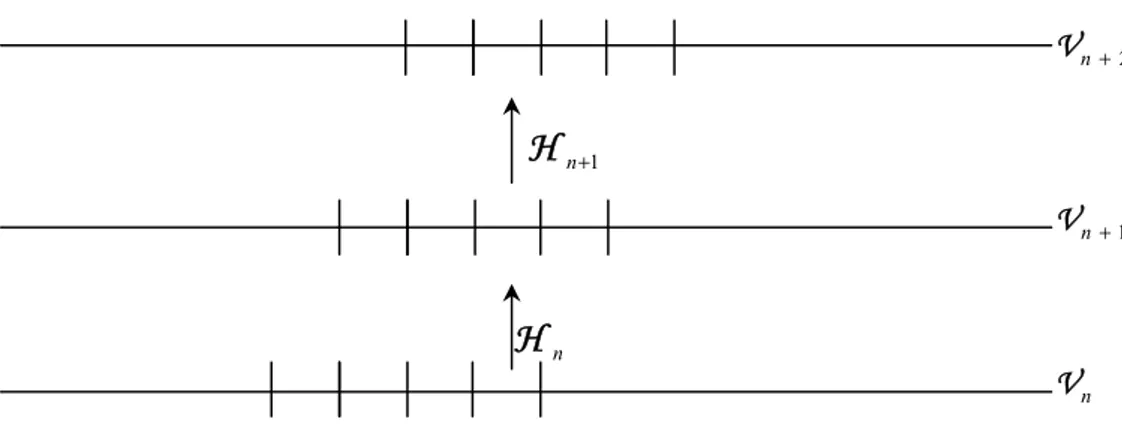
= n n S S (39)

Sekarang tinjau dua irisan kisi yang berdekatan yang diberi label n dan

1 +

n sebagaimana ditunjukkan dalam gambar 3.3 dibawah ini. S

( )

n adalah aksi yang berkaitan dengan forward rates pada dua irisan waktu ini.

Gambar 3.3.Potongan dua kisi untuk t=n< dan t =

(

n+1

)

<

Dapat dilihat dalam Gambar 3.3, untuk 2 irisan kisi waktu ini ada dua tempat kisi di sudut yang tidak sebanding, kisi pada lokasi kisi

( )

n,n pada waktu

n dan

(

n+1,n+1+N_FR

)

pada waktu n+1 tidak umum. Kita akan mengisolasi variabel yang tidak sebanding ini sebagai berikut:

Variabel-variabel pada waktu n berlaku:

{

fn,n Fn

}

Fn/

{

fn+1,l n l n+NFR

}

~ ; ~

, (40)

Variabel-variabel yang berada pada waktu

(

n+1

)

berlaku :

{

Fn,fn+1,n+1+NFR

}

; Fn/

{

fn+1,l n+1 l n+1+NFR

}

(41)

Perhatikan bahwasanya meskipun variabel F mengacu kepada waktu _n

(

n+1

)

, tetapi tetap diarahkan labelnya dengan waktu sebelumnya untuk pembuktian lebih lanjut. Dari gambar 3.3, sejumlah variabel F_n dan F~_n

melingkupi lokasi kisi yang sama dalam arah x yaitu pada n+1 l n+N_FR, dan oleh karena itu memiliki jumlah forward rates yang sama yang dinamakan

1 FR

N . Hamiltonian akan dapat diekspresikan dalam ungkapan variabel-variabel ini.

Dari turunan diskrit waktu yang didefinisikan di pers (37), aksi diskrit

( )

n

S mengandung suku-suku yang berpasangan karena adanya titik-titik bersama dalam kisi untuk 2 irisan kisi waktu yang nama-nama variabelnya dimiliki oleh sejumlahF~_n;F . Untuk itu aksinya adalah: _n

( )

[

]

{ }

'

+ = l l n l n n f f n S

L

_, , _1, (42)

( )

[

]

{ }

'

= l n n n F F n S

L

~ ; (43)

sebagaimana ditunjukkan dalam gambar 3.4, aksi untuk seluruh domain

_P

~

yang ditunjukkan oleh gambar 3.2 dapat dibangun dengan mengulang konstruksi di gambar 3.3 dan menjumlahkan seluruh aksi S

( )

n terhadap semua waktu

f

i n N

Hamiltonian dari forward rates adalah sebuah operator yang bekerja pada ruang keadaan forward rates; oleh karena itu perlu untuk menentukan koordinat-koordinat dari ruang keadaannya.

Tinjau lagi 2 irisan waktu yang berurutan n dan n+1 dari Gambar 3.4. Sekarang interpretasikan 2 forward rates sesaat pada 2 irisan waktu yang berurutan,

{

f_n,n,F~_n

}

dan

{

F_n, f_n+1,n+1+NFR

}

yang diberikan di persamaan (40) - yang tampak dalam persamaan aksi di (42)- sebagai koordinat ruang keadaan

V

dan

_V

dual

Untuk tiap waktu sesaat n, ada sejumlah ruang keadaan V dan_n Vrangkap,n.

Koordinat-kordinat ruang keadaan V dan _n Vn+1 diberikan oleh tensor produk dari

ruang keadaan untuk setiap titik maturitas l, yang dinamakan:

n n n l n N n l n n f f F f FR ~ ~ , , / : = + (44)

yaitu koordinat keadaan untuk Vrangkap,n

FR FR n l n nn N N n l n n f F f f _{+ ++} + + + + = : 1, / , 1 1 1 1 (45)

yaitu koordinat keadaan untuk V_n+1

Vektor keadaan F_n milik yang ruang keadaan V_n+1, tapi kembali diinterpretasikan bahwa F_n sebagai ruang keadaan

F

_n pada waktu sebelum n,

maka dari interpretasi ini dapat dipelajari sistem secara sesaat menggunakan formalisme Hamiltonian. Ruang keadaan V_n terdiri dari semua unsur kemungkinan fungsi N forward rates _R

{

f_n,n,F~_n

}

. Ruang keadaan V ini berbeda _n

untuk tiap n yang berbeda, karena sejumlah forward rates berisi sejumlah variabel

Meskipun ruang keadaan V dan _n Vn+1 tidak identik, ada suatu irisan dua

ruang ini yang disebut V_n =V_n+₁ yang melingkupi interval yang sama dalam arah

maturitas, dan terkopel oleh aksi S

( )

n . Irisan ini menghasilkan sebuah ruang keadaan

_F

_n dimana didalamnya berlangsung Hamiltonian evolusi forward rates. Dalam simbol-simbolnya, kita memiliki :

FR N n n n f + ++ +1 =

F

: 1, 1 n V (46) n rangkap n n n rangkap, f .

F

, V = : (47) 1 , : _n - _n > _{n rangkap n} : _n+ n

F

F

H V V

H

(48)

Hamiltonian

H

_n adalah elemen produk tensor ruang yang dilingkupi oleh operator F_n F~_n , penamaan operator ruang diberikan oleh

F

_n:

F

_rangkap,n. Ruang vektor V dan Hamiltonian _n

H

n bekerja pada ruang seperti ditunjukkan dalam Gambar 3.5 berikut

Gambar 3.5. : Propagasi Hamiltonian

H

_ndalam Ruang Forward rates V_n

Perhatikan bahwa kedua keadaan F_n dan F~_n memiliki ruang keadaan yang sama

F

_n, dan dengan menggunakan aturan putar untuk mengindikasikan dua keadaan ini berbeda; sebagai contoh dua keadan f dan f mengidikasikan

n

H

1 + n

H

n V 1 + n V 2 + n V

Setelah dikaji semua kemungkinan nilai forward rates dan fˆ, maka sekarang perlu untuk mengkaji basis lengkap dari ruang keadaan V , terutama _n

operator untuk V , dilambangkan _n

I

n yang merefleksikan bahwa basis ruang keadaan adalah lengkap. Persamaannya menurut [9] diberikan oleh:

4.

+ = FR N n l n n n l n n df , f f

I

(49) n n n n n n n n n dF f F f F df _, . ~ _, ; ~ _, ;~

.

/ (50)

Hamiltonian sistem

H

didefinisikan oleh Formulasi Feynmann (sampai di normalisasi) dari persamaan (42), yaitu:

[ ] { } FR n l n nl n l N n n n n n n f f ne ' = f F e F f + ++ + + 1 , 1 , , , ~ , 1 , _H L 9 (51)

dimana secara umum 9_nadalah suatu suku medan independen. Dengan menggunakan sifat aksi diskrit yang diberikan di persamaan (43), kita peroleh:

[ ] { } FR n l n n n N n n n n n n F F ne ' = f , F e F f +1, +1+ ~ , , ~ , H L 9 (52) n n e F F Hn = ~ (53)

Berangkat dari persamaan (50) ke persamaan (53) ternyata hubungan irisan kisi waktu n dan n+1 masing-masing tidak mengandung variabel f_n,ndan

FR N n

f ₊₁₊ . Hal ini menjadikan Hamiltonian tidak bergantung pada variabel-varibel ini. Interpretasi persamaan (53) adalah bahwa Hamiltonaian mempropagasi keadaan awal F~_n dalam waktu menjadi keadaan akhir F . Perhatikan _n

hubungan ini: n n N n n n n n n F e F f F e F f n FR n H H + + + = ~ , ~ , _{1, 1} , (54)

menunjukkan bahwa ada suatu asimetri dalam arah waktu, dengan Hamiltonian masih tidak bergantung pada forward rates paling awal f_n,n di keadaan mula-mula dan forward rates terakhir

FR N n

f ₊₁₊ di keadaan akhir. Inilah asimetri dalam propagasi forward rates yang menghasilkan domain jajaran genjang

_P

~

di gambar 3.2, dan merefleksikan bahwa forward rates f ,

( )

t x hanya eksis untuk x>t.

Guna penyederhanaan notasi, mulai sekarang digunakan notasi kontinu kembali, khususnya ruang keadaan dilabelkan dengan V , vektor keadaan oleh _t

t

f . Elemen dari ruang keadaan forward rates V mencakup semua instrumen _t

keuangan yang diperdagangkan di pasar pada waktu t. Dalam notasi kontinu dari persamaan (45) diperoleh:

( )

t x f f FR T t x t t

:

, + = (55)

( )

t x f F FR T t x t t

:

, + = (56)

dalam notasi kontinu, perbedaan antara vektor keadaan f_t dan F_t hanya di persamaan (56), yaitu saat titik x=t tidak termasuk dalam tensor produk untuk yang kontinu.

Fungsi pastisi Z yang diberikan di persamaan (38) dapat direkonstruksi dari Hamiltonian dengan menerapkan secara rekursif prosedur yang dibahas untuk dua irisan kisi waktu yang berurutan. Maka untuk notasi kontinu kita peroleh:

[ ]

.

= _{D f e}S f Z (57) akhir T T t mula mula dt f f f i 210 " #$ =

T

exp

_.

H

(58)

dimana simbol

_T

dalam persamaan diatas berkedudukan sebagai operator waktu (non-commut) dalam argument, dengan waktu paling mula-mula diletakkan di kiri.

3.3.1. Vektor Keadaan Obligasi

Vektor keadaan yang paling penting dalam keuangan adalah kupon obligasi biasa dan obligasi tanpa bunga (zero coupon bonds). Tinjau sebuah obligasi tanpa bunga bebas resiko yang jatuh tempo (maturitas) pada waktu T dengan pembayaran sebesar $1. Harga obligasi pada waktu t<Tt diberikan oleh :

( )

t T e ( ) P

[

f t T

]

P f txdx

T

t ; ,

, = . , / (59)

vektor keadaan P ,

( )

t T adalah sebuah elemen ruang keadaan V . vektor keadaan _t

saham dapat dituliskan sebagai berikut:

( )

t T f P

( )

t T P , / _t , (60) ( )x dx f T t e . = (61)

vektor keadaan yang lain adalah kupon obligasi biasa

_B

dengan pembayaran sejumlah c pada saat _l T , dan pembayaran akhir L pada waktu T. Vektor keadaan _l

obligasi biasa adalah superposisi linier dengan zero coupon bond dan diberikan oleh persamaan:

( )

=

_'

( )

+

( )

l l l Pt T L P t T c t , ,

B

(62)

3.4. Hamiltonian untuk Forward Rates dengan Volatilitas Stokastik

Sebelumnya telah diperoleh persamaan umum untuk Hamiltonian dan ungkapan suku aksi S sebagaimana dalam persamaan (53), dan perlu untuk menerapkan formula ini dalam kasus khusus Largangian forward rates guna memperoleh persamaan Hamiltoniannya secara eksplisit. Dari persamaan (53) diperoleh persamaan sebagai berikut:

( )_n { }_l n[Hn Hn Fn Fn] S ne e ~ , ; ~ , ' = L 9 (63)

n n n n H e F H F~ ; ~ Hn ; = (64)

dimana dalam persamaan diatas secara eksplisit sudah memuat volatilitas medan kuantum h , .

( )

t x

Untuk penyederhaan notasi, tinjau sumbu arah x maturitas adalah kontinu, dan tinjau hanya waktu yang diskrit. Dalam notasi kontinu keberadaan variabel waktu t dan t+ dihitung dan di analisis variabel yang tampak pada batas interval

[

t x t+TFR

]

. Aksi S

( )

n untuk t=n sebagai berikut:

( )

n

( )

t x

S =

.

L

_n , (65)

.

.

/ t=TFR

t dx (66)

3.4.1.Hamiltonian untuk Forward Rates dengan Volatilitas Stokastik

Sebelumnya telah diperoleh Hamiltonian untuk kasus sederhana dari volatilitas sebagai suatu fungsi forward rates. Mengingat kembali Lagrangian sistem yang diberikan oleh :

[ ]

)

_L

_kinetik

[ ]

)

_L

_rigiditas

[ ]

)

L

= +

( ) ( )

( )

( )

( ) ( )

( )

( ) ! ! 2 !! 1 0 ! ! " !! # $ ( ( ( ( + ! ! 2 !! 1 0 ! ! " !! # $ ( ( = 2 , 0 0 2 2 , 0 0 , , , 1 , , , 2 1 x t v x t v _{t x e} x t t x t f x e x t x t t x t f ) ) ) µ ) (67) Pada diskritisasi Lagrangian yang diperoleh menggunakan syarat batas persamaan (6), bahwa:

( )

n =

_.

=

_.

A ( A S 2 1 1 1

L

(68)

(

) )

)

;) 1 0 1 0 0 + = f e f A _{t t} (69)

Sekarang kembali menuliskan persamaan (68) menggunakan Integrasi Gaussian akan diperoleh : (konstanta yang tidak berhubungan diabaikan)

( )

_4.

( )

_.

( ) (

) ( )

_.

( ) ( )

2 1 0 " # $ ₊ = x n S _{dp x p x D x x t p x i p x A x} e , ;' ' 2 exp (70) dengan

(

, ;'

) (

'

)

1 1 ₂ 2 2 _(x D x x t = x x ( _, µ

merupakan syarat batas kondisi Neumann.

Sebuah turunan eksplisit didefinisikan dari propagator D

(

x,x;'t

)

menghasilkan :

(

)

₍

₎

[

(

T x x

)

(

T

(

x x t

)

)

]

T t x x D _{FR FR} FR 2 ' cosh ' cosh sinh 2 ;' , = µ µ + µ µ + µ µ (71) Tinjau definisikan suku yang didefinisikan sebagai berikut:

(

)

4

= x n f ; n ,x 9 (72)

dengan menskala kembali p

( )

x sebagai berikut : p e f p 1 ₀ ;) 0 - (73)

maka akan diperoleh:

( )

_{( )}

{

_{( )}

(

)

_{( )}

( ) (

)

( )

2 1 0 =

.

4.

.

+ ' ;' , 2 exp 0 0 2 0 1 0 x p e t x x D x p e f x f x p i x dp e x t t n S n ) ; ;) ) ) 9 (74)

( ) + = t t n S ne ) e ) 9 H) ₍₇₅₎ ( )

_.

. ( ) =_e H_nt _Dpei p)t+ )t ₍₇₆₎

Dan dengan menghilangkan t dalam )_t, Hamiltonian forward rates menjadi:

( )

=

_.

( ) (

)

_{( ) ( ) ( )}

_.

,) , ,) ,) , ) ; ) ; ) 0 2 0 0 2 0 1 ' ' ;' , 2 1 f x x x e t x x D x e f t

H

(77) Hamiltonian adalah non-hermitian dengan nilai eigen kompleks. Meskipun hal ini merupakan masalah dalam fisika, hal ini tidak terjadi di finansial karena Hamiltonian bukanlah besaran kuantitas (seperti energi) yang memiliki nilai eigen yang observabel, dan oleh karena itu tidak harus memiliki nilai eigen yang real. 3.4.2 Hamiltonian untuk Forward Rates dan Volatilitas Medan Kuantum

Sekarang tinjau kasus ketika fluktuasi forward rates dan volatilitas yang direpresentasikan sebagai medan kuantum yang terpisah, sebelumnya menguji

Lagrangian yang diberikan dalam persamaan (21), yaitu:

(

)

( ( ( ( ( ( ( ( ( ( ( ( ( ( = 2 2 2 2 2 2 2 2 1 2 1 2 1 1 2 1 7 & 8 µ 7 & 7 & 9 9 t h x t f x t h t h t f

L

(78)

kemudian ingat kembali

( ) ( )

+3

3 f t,x ,h t,x (79)

( )

[

]

( ) (

, ;'

)

( )

' 2 1 1 1 1 1 _x B A t x x x B A n S =

.

7 7

M

(80) dimana:

(

)

(

'

)

1 1 1 1 1 1 1 1 ;' , 2 2 2 2 2 2 2 2 2 2 x x x x t x x ( ( ( ( = , 8 9 9 9 9 9 µ 9

M

(81) dan / f_t+ f_t A ~ (82) & /h_t+ h_t B ~ (83)

Perhatikan bahwa dalam memperoleh persamaan (80) untuk S

( )

n telah menggunakan syarat batas kondisi medan yang diberikan dalam persamaan (6) dan (24).

Sekarang kembali menuliskan persamaan (80) menggunakan Integrasi Gaussian dan memperoleh (abaikan konstanta yang tidak relevan):

( )₌

_4.

( ) ( )

_.

[

]

₊

_.

[

]

B A q p i q p q p x dq x dp e x n S 1 1 1 2 exp 7

M

(84) mengingat dari persamaan (37) bahwa Integral Lintasan Feynman memiliki perhitungan non-trivial dalam menghitung 1

( )

t,x _{dan dalam memperoleh}

Hamiltonian perhitungan ini akan dilibatkan. Definisikan suku perhitungan dengan:

( )

4

/ x n 1 x 9 (85)

p

p - (86)

q

q - 7 (87)

kemudian diperoleh dari persamaan (84) :

( )

[

]

[

]

+ + × =

.

.

.

& 7 7 9 h h f f q p i q p q p DpDq eS n n ~ ~ 2 exp

_M

1 (88)

menunjukan bahwa perhitungan di atas dapat dibatalkan. Kemudian sebelumnya diperoleh: ( ) _{f h e f h} eS n n n ; ~ ; ~ _H = 9 (89) ( ) ( )

.

. . =e n DpDqei p f f +i q h h ~ ~ H ₍₉₀₎

dan yang menghasilkan Hamiltonian untuk forward rates serta volatilitas sebagai suatu medan kuantum independen diberikan oleh persamaan berikut :

( )

_.

_.

2 1 0 " # $ + = h f h i f i h i f i t _{~ ~} ~ ~ ~ ~ 2 1 1 , , & , , , , 7 , , , , 7 , ,

M

H

(91)

dari persamaan (81) diperoleh:

(

)

(

)

(

)

(

)

(

)

(

)

(

)

+

(

)

(

)

+ = + + + + + + + + D r D r D D D D D D D r D r D D c t x x 2 2 2 2 1 1 1 ;' , 8 9 9 9 8 9

M

dimana :

(

2 2

)

2 2 2 2 2 2 49 µ 8 µ 8 8 µ + = c (92)

(

)

+ ±

(

)

+ = ± 2 2 2 2 2 2 2 2 2 4 1 2 1 _{µ 8 8 µ 9 µ 8} 9 r (93)

(

) (

)

2 2 r D x x t, '; x x' x ± ± , ( + =

( dengan kondisi batas Neumann

(94) Untuk memecahkan keadaan tanpa kehadiran arbitrase, dibutuhkan :

(

x x t

)

(

x x t

)

G ; ,' 1 ; ,' 11 /

M

(95)

(

)

[

(

+

)

+

(

)

(

+ +

)

]

+ = 2 D D 2 r D r D 2 2 2 2 2 2 1 49 µ 8 8 9 µ 8 µ ₍₉₆₎

3.5. Perumusan Hamiltonian untuk Keadaan Tanpa Kehadiran Arbitrase

Prinsip keadaan tanpa kehadiran arbistrase adalah pusat dari teori finansial, dan integral lintasan yang membahas formulasi prinsip ini diberikan dalam [10]. Untuk kasus volatilitas deterministik, Lagrangian forward rates yang diberikan oleh persamaan (3) adalah kuadratis, dan kemudian kondisi tanpa kehadiran arbitrase dapat dipecahkan dengan tepat dengan melakukan Integrasi Lintasan Gaussian [10]. Sedangkan untuk kasus volatilitas yang stokastik,

Lagrangiannya adalah non-linier dan kemudian kondisi tanpa kehadiran arbitrase

tidak dapat dipecahkan secara eksplisit menggunakan integral lintasan; untuk alasan inilah kemudian akan kembali dirumuskan kondisi tanpa kehadiran arbitrase menggunakan Hamiltonian. Perumusan Hamiltonian untuk teori non-linier dari forward rates dengan volatilitas stokastik memenuhi solusi yang eksak untuk keadaan tanpa arbitrase.

Pertama, akan menurunkan perumusan Hamiltonian untuk kasus sekuritas tunggal S, karena untuk produk turunan untuk forward rates akan lebih kompleks

Tinjau suatu opsi dalam sebuah sekuritas _{S e=} x_{yang akan jatuh tempo} pada waktu T dan memiliki fungsi payoff diberikan oleh g x K dimana K adalah

(

,

)

strike price. Sebagaimana telah didiskusikan dalam [10], evolusi bebas resiko

suatu sekuritas diberikan oleh Hamiltonian

_H

_s, dengan nilai opsi pada waktu t T< diberikan oleh:

( )

( )

_.

3 ( )

_{( )}

3 = ' ' ' ,x e dx x e x g x t f rT t T tHs (97)

dimana r adalah suatu konstanta laju bunga bebas resiko sesaat)

Kondisi martingale untuk evolusi bebas resiko dari suatu sekuritas merupakan potongan evolusi dari harga mendatang sekuritas itu pada waktu mendatang tertentu, sebut saja t_*,. Nilai ini adalah sama, pada saat rata-rata, dengan harga sekuritas ketika waktu mula-mula t. Persamaan kondisi martingale menyatakan bahwa:

( )

( )

xt E[ ],*

[

e (* ) S

(

x

( )

t*

)

]

S t tr t t = (98)

dimana notasi E_{[ ]t,t*}

[ ]

Y merupakan rata-rata dari nilai Y untuk semua variabel stokastik dalam interval waktu

[ ]

t,t_* . Dari persamaan (97) dapat diperoleh :

( )

x e (* ) dx_' x e (* ) x_' S

_{( )}

x_' S rt t

.

3 t t s 3 = H ₍₉₉₎ ( )( ) _{x x S} e x dx S x 3 ' t* t s+r ' ' 3

.

= > H ₍₁₀₀₎

dengan menggunakan kelengkapan persamaan untuk sekuritas tunggal yang diberikan oleh :

.

33

= dx x x

I

(101)

(_* )(ˆ ) ₀

=

=_e + _S

S t t Hs r (102)

Karena t adalah waktu arbitrase, maka diperoleh: _*

(

_H

_s +r

)

S =0 (103)

3.5. 2. Perumusan Forward Rates Tanpa Kehadiran Arbistrase

Prinsip tanpa kehadiran arbitrase menyatakan bahwa harga dari obligasi

( )

t T

P _*, pada waktu di masa mendatang T >t* >t adalah sama dengan harga

obligasi itu pada waktu t, di potong oleh laju bunga bebas resiko r

( ) ( )

t = f t,t . Dengan kata lain :

( )

t T = E[ ] e . ( ) P

( )

t T P t t rt dt t t , , _{, *} * * (104) dimanaE_{[ ]tt}

[ ]

Y *

, menunjukkan nilai rata-rata Y yang meliputi seluruh variabel

stokastik dalam interval waktu

[ ]

t,t_* . Dalam kaitannya dengan Integral Lintasan Feynmann, Persamaan (104) menghasilkan (dihitung untuk 9 ):

( )

_{t T =}

_.

_Df

[ ]

_{f e} . ( ) _e [ ]_P

_{( )}

_{t T} P rt dt S f t t , , _* * 9 (105)

Terdapat dua domain yang dilibatkan dalam integral lintasan di persamaan (105), disebut dengan domain dari treasury bond yang juga berada di dalam domain

forward rates. Domain ini ditunjukkan oleh gambar 3.6 berikut:

Gambar 3.6. Domain tanpa Arbitrase untuk Treasury Bonds

t Tf Ti x T Ti+TF t* t

Meskipun dituliskan dalam bentuk integral, kondisi persamaan (105) sebenarnya merupakan suatu diferensial karena mengandung bentuk t kemudian _*

diambil t_*=t+ . Alasan perlu untuk meninjau perubahan yang infinitesimal saja untuk forward rates adalah karena ruang keadaan V memiliki sifat bergantung _t

terhadap waktu. Untuk evolusi waktu infinetesimal, fungsi dalam persamaan (105) gagal untuk mengintegrasikan terhadap variabel waktu akhir ~f_t+ pada waktu kisi

+ t , sehingga:

( )

₌

_.

( ) . [ ]

[

₊

]

+ + e e P f t T f D T t P f tt f f t t ; , ~ ~ , ₉ , L ,~ ₍₁₀₆₎

kemudian dituliskan kembali persamaan diatas dalam bahasa vektor keadaan, yang dinamakan dengan:

( )

₌

_.

( )

₍

₊

₎

+ + + f e e f f P t T f D T t P f f tt _{t t} t t t , ~ ~ ~ , , H ₍₁₀₇₎

Telah dimiliki dari kelengkapan yang diberikan persamaan (49) bahwa :

+ + + + =

.

t t t t Df f f ~ ~ ~

I

(108)

kemudian dari persamaan (107) bahwa :

( )

_{t T f e} ( )_e ( ) _P

₍

_{t T}

₎

P f f tt t t t , = , H + , (109)

( )

_{t T e} ( )_e ( )_P

₍

_{t T}

₎

P _{, =} f t,t t _{+ ,} > H ₍₁₁₀₎

dapat dibuktikan dengan menggunakan representasi zero coupon bond secara eksplisit dari persamaan (61) bahwa :

( ) _P

_{( )}

_{t T P}

₍

_{t T}

₎

e+ f t,t _{, = + , (111)}

kemudian kita punya:

(

_{t T}

)

_e ( ) _P

₍

_{t T}

₎

( ) (

+ ,

)

=0

>H t P t T (113)

Perumusan diferensial untuk tak ada arbitrase, yang dinamakan zero coupon bond –yang juga berlaku untuk tiap zero coupon bond- dianihilasi oleh Hamiltonian Hˆ, yaitu :

( ) ( )

t Pt,T =0

H

untuk semua t, T (114)

Perhatikan similaritas persamaan diatas dengan kasus untuk sekuritas tunggal dalam persamaan (103). Adanya kasus pemotongan terlihat sangat berbeda untuk kedua kasus. Spot rate r merupakan suatu konstanta dalam kasus sekuritas tunggal , sementara dalam kasus forward rates pemotongan oleh spot rate merupakan suatu faktor yang dibutuhkan untuk mentransformasikan waktu mendatang dari obligasi P

(

t+ ,T

)

ke waktu sebelumnya, yang dinamakan P ,

( )

t T

3.6. Kondisi Tak Ada Arbitrase untuk Volatilitas Stokastik

Dengan menggunakan Hamiltonian untuk forward rates dengan volatilitas stokastik yang diberikan dalam persamaan (77) dan (91), dapat diaplikasikan pada keadaan tanpa arbitrase yang diperoleh di persamaan (114), yaitu:

( ) ( )

t P t,T =0

H

(115)

atau secara lebih eksplisit lagi adalah :

( ) ( )

,

( )

( ) 0 , = . = T t x t f dx t t P t T t e f

_H

_H

(116)

3.6.1 Kondisi Tak Ada Arbitrase Untuk Volatilitas Sebagai Suatu Fungsi Forward rates

( )

₌ T

_.

( ) t x t e dx f T t P , 0 exp , ) (117)

yang kemudian menghasilkan :

( ) ( )

( )

_{( )}

" # $ > < < = T x T x t T t P e f T t P x t x t 0 , , , , , 0 ) ,) , (118)

Sementara dari persamaan (116) dan (77) dapat diperoleh:

( )

_{( ) (}

₎

( )

_{( )}

( ) ( ) ( )

, , , 0 ' , ;' , , ' 2 1 , ' 0 , 0 = +

.

.

T t P x t f x t dx x t f e t x x D x t f e dx dx T t T t x t x t ;) ) ;

( )

₌ ( )

_.

₍

₎

( )

_{( )}

> T t x t x t _{dx D x x t e f t x} e f x t, ' , ;' , ' , ' 0 , 0 ;) ;) ₍₁₁₉₎

merupakan persamaan untuk kondisi tanpa arbistrase

Perhatikan bahwa kondisi tanpa arbitrase yang diberikan di atas tidak terkandung dalam solusi model HJM untuk kecepatann drift yang semuanya berbentuk kuadratis dalam medan-medan volatilitas [13]. Kehadiran forward rates

( )

t x

f , secara langsung dalam kecepatan drift muncul secara alamiah dalam formulasi teori medan kuantum, dan hal ini menunjukkan bahwa suku kinetik dalam Lagrangian untuk kasus f

[

3,+3

]

- yang disebut

2 ( ( t f - digantikan oleh 2 ( ( t ) untuk f

[

0,+3

]

.

Secara fakta, dapat dibuktikan suatu hasil yang lebih umum dari aksi S

[ ]

)

untuk kasus dimana volatilitas stokastik merupakan fungsi dari forward rates. Dituliskan Lagrangian secara umum sebagai :

[ ]

_.

( )

+

_.

( )

( ( + = W t x t x t U umum , , ) )

L

L

(120)

U, W : arbitrase lokal yang merupakan fungsi dari f ,

( )

t x (121) kemudian dari keadaan tanpa arbitrase menghasilkan :

( )

t,x =W

( )

t,x =0

U (122)

suku tensi string dalam Lagrangian akan memiliki bentuk:

( )

, 2 ( ( A x f x t W (123)

dimana hal ini tidak diijinkan dalam keadaan tanpa arbitrase.

3.6.2. Keadaan Tanpa Arbitrase Untuk Volatilitas Sebagai Medan Kuantum Yang Independen

Dari Hamiltonian yang diberikan dalam persamaan (91) dapat dilihat bahwa, sebagaimana dalam kasus di bawah,

h ,

,

bernilai nol dalam persamaan (116) karena dalam zero coupon bond tidak bergantung secara eksplisit pada medan volatilitas. Dengan menggunakan fakta bahwa :

( )

( )

( )

( ) !" ! # $ > < < . = . T x T x t e e x t f T t T t x t f dx m x t f dx m m , 0 , 1 , , , , , (124)

kemudian dari menggabungkan persaman (116), (91) dan (124) diperoleh:

( ) (

, , ;'

) ( )

, '

( ) ( )

, , 0 ' 2 1 _{+ =}

.

.

dxdx t x G x x t t x dx t x Pt T T t T t

( ) ( )

=

_.

(

) ( )

> x t x t t x x G dx x t x t, , ' , ;' , ' (125)

Karena tidak ada instrumen dalam pasar finansial sekarang ini yang dapat menyajikan perdagangan dalam volatlitas dari forward rates secara langsung, maka sulit untuk mengaplikasikan kondisi martingale dari medan volatilitas, khususnya kecepatan drift dari medan volatilitas, yang disebut dengan&

( )

t,x , menjadi fungsi medan lain dan parameter-parameter teori lainnya. Dari alasan inilah kemudian & harus ditentukan secara empiris dari pasar. Untuk memperoleh limit volatilitas deterministik, maka perlu untuk mengambil limit 7,9, dan

0

-8 . Dari sini akan diperoleh:

0 , ,9 8 -7 (126) µ -+ r (127) 0 -r (128)

(

x x t

)

D

(

x x t

)

G , ;' - , ;' (129)

dengan propagator D

(

x,x;'t

)

diberikan oleh persamaan (71).

Dengan menerapkan beberapa identitas, propagator D

(

x,x;'t

)

yang diberikan dalam persamaan (71) diatas benar-benar sama dengan hasil yang diperoleh dalam [10] dengan menggunakan teknik integral. Kemudian dari keadaan tanpa arbitrase diperoleh untuk kasus volatilitas deterministik menggunakan Hamiltonian sama dengan yang diperoleh dengan hasil sebelumnya yang menggunakan integral lintasan. Sedangkan dengan memasukkan

( )

t,x

yang diberikan dalam persamaan (125) ke dalam Lagrangian menghasilkan hasil akhir dalam tesis ini. Sebagai notasi, didefinisikan fungsi non-lokal dalam medan volatilitas berikut :

( )

=

_.

x

(

) ( )

t x t t x x G dx x t v , ' , ;' , ' (130)

( )

_{( )} 2 2 1 2 1 2 1 2 2 1 2 1 1 2 1 2 2 2 , ( ( ( ( ( ( ( ( = ( ( ( ( ( ( 7 & 7 & 7 & 9 µ 9 t h K t h t h x v t f x v t f x t

L

(131)

Lagrangian yang diberikan oleh persamaan diatas merupakan deskripsi yang utuh

secara teori dari forward rates dengan volatilitas stokastik. Semua paraameter dalam teori, yang dinamakan dengan fungsi &

( )

t,x dan parameter µ, K,9 dan 7 perlu untuk ditentukan dari data pasar. Selama adanya medan v , , dapat

( )

t x

diperoleh bahwasanya Lagrangian non-lokal, dengan fungsi G

(

x,x;'t

)

mengandung semua informasi yang dibutuhkan dengan asumsi tidak ada arbitrase. Jadi, ada 2 generalisasi yang dapat dilakukan dengan Lagrangian: dalam persamaan (131), yang menunjukkan bahwa forward rates dapat dibuat positip, yaitu f >0, dan yang kedua adalah bahwa propagator G

(

x,x;'t

)

dapat memuat efek-efek lain yang lebih kompleks yang datang dari depedensi maturitas terhadap parameter rigiditas µ.