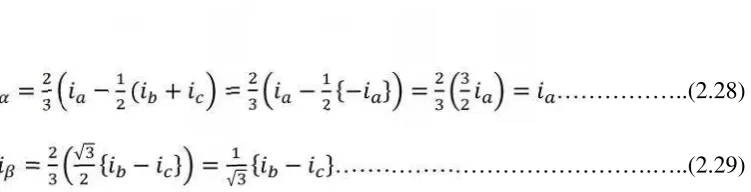77
Transfromasi Clarke dan Park
Transformasi Clark
Transformasi Clark digunakan untuk mentransformasikan
arus stator dari system tiga fasa (a,b,c) ke sistem dua fasa orthogonal
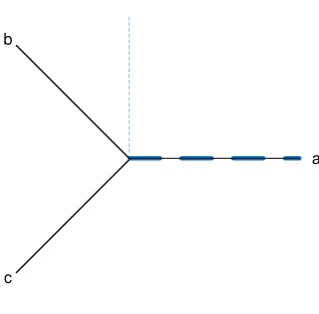
(α ,β ). Ruang vektor dapat dipresentasikan dalam dua sumbu tegak
lurus (α ,β ), dengan asumsi bahwa sumbu a dan sumbu α mempunyai
arah vector yang sama seperti terlihat pada Gambar 2.15.Maka secara
matematis transformasi Clarke dapat dirumuskan sbb:
Rumus untuk arus pada motor induksi 3 fasa dalam bentuk dua phasa
atau α dan β .
= ( cos 0 cos 60 cos 60) = …….(2.17)
= ( cos 90 + cos 30 cos 30) = …….(2.18)
Lalu kita menambahkan arus nol
= ( + + )………(2.19)
Sehingga dalam bentuk matriks menjadi
78 =
1
0 = ……….(2.20)
Invers dari adalah
=
0
………..(2.21)
Lalu kita mengalikan invers matriks dengan matriks dasarnya
=
Sehingga dengan mengalikan persamaan (2.20) dengan (2.21) kita mendapatkan
nilai =
Dalam sistem yang setimbang jumlah dari arus 3 fasa adalah 0
+ + = 0………...(2.26)
+ = ……….(2.27)
Dengan menstubtitusikan persamaan (2.26) dan (2.27) kita mendapatkan
79
= ( + = { } = = ………..(2.28)
= { } = { }……….…..(2.29)
Maka untuk persamaan rumus tegangan dan
= ……….. ………(2.30)
Gambar 4.43 Transformasi Park dalam bidang vektor
Transformasi park digunakan untuk mentrasnformasikan bentuk
orthogonal (α ,β ) kedalam bentuk bidang putar atau sistem dua fasa
(d,q). Besar sudut antara d dan q adalah 90°. Hal tersebut dapat kita
lihat pada gambar 2.16. Transformasi park dapat dirumuskan sebagai
berikut :
Untuk rumus arus transformasi park
i = i cos + i sin ………….………..(2.32)
i = i sin + i cos ……….(2.33)
80 Jika posisi vector α dan d sama maka = 0maka persamaan (2.32)
dan (2.33) menjadi
i = i ………..………(2.34)
i = ………..….(2.35)
Nilai tegangan d dan q adalah
= ………(2.36)
= ………..………(2.37)