BAB IV HASIL PENELITIAN. Hasil penelitian ini berdasarkan data yang diperoleh dari kegiatan penelitian

BAB IV 

HASIL PENELITIAN 

Hasil  penelitian  ini  berdasarkan  data  yang  diperoleh  dari  kegiatan  penelitian  yang telah dilaksanakan oleh peneliti di MTs Salafiyah II Randublatung Blora pada  kelas  VIII­A  tahun  ajaran  2010­2011.  Data  hasil  penelitian  tersebut  kemudian  dianalisis dengan  menggunakan  metode analisis data pada bab III untuk selanjutnya  dideskripsikan. Data yang disajikan dalam penelitian ini adalah sebagai berikut: 

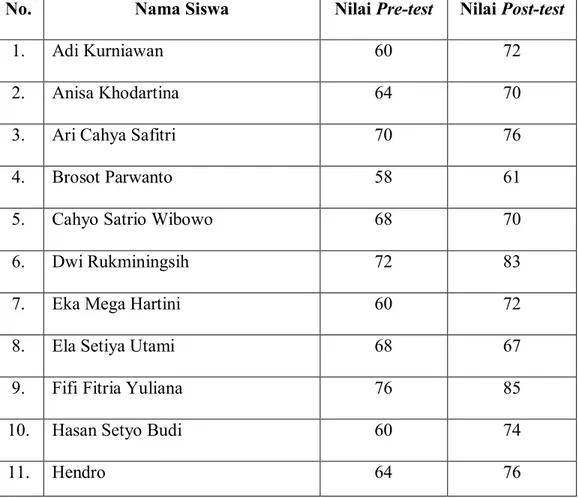
Table 4.1: Daftar Nama Siswa Beserta Nilai Pre­Test dan Post­Test 

No.  Nama Siswa  Nilai Pre­test  Nilai Post­test 

1.  Adi Kurniawan  60  72  2.  Anisa Khodartina  64  70  3.  Ari Cahya Safitri  70  76  4.  Brosot Parwanto  58  61  5.  Cahyo Satrio Wibowo  68  70  6.  Dwi Rukminingsih  72  83  7.  Eka Mega Hartini  60  72  8.  Ela Setiya Utami  68  67  9.  Fifi Fitria Yuliana  76  85  10.  Hasan Setyo Budi  60  74  11.  Hendro  64  76  45

12.  Imam Rifa’i  62  72  13.  Kalfin Ananto  52  65  14.  Malikhatun Mukhayaroh  62  72  15.  Mu’arofah  62  67  16.  Mundorin  64  80  17.  Nanang Ahmad Baidhowi  62  72  18.  Prihadi Sutego  58  70  19.  Siti Dwi Septiyani  60  70  20.  Siti Khoirurrohmah  64  80  21.  Siti Kriswahyuningsih  64  70  22.  Sumarno  56  59  23.  Wahyu Hastuti  68  65  24.  Wahyu Putra  62  72  25.  Yeni Indrawati  54  65  26.  Zaenal Arifin  64  76  27.  Sumuati  68  70  28.  Ina Lestari  72  80

Analisis Data dan Pengujian Hipotesis  1.  Uji Normalitas 

a 

.  Merumuskan hipotesis  0  H  = Data berdistribusi normal.  1  H  = Data tidak berdistribusi normal. 

b 

.  Menentukan derajat kesalahan atau α  α= 5% atau α = 0,05 

c

.  Statistik uji 

Uji  statistik    yang  digunakan  untuk  menguji  kenormalan  data  dalam  penelitian  ini  adalah  uji  statistik  Chi­Kuadrat  dengan  rumus  sebagai  berikut:

(

)

÷ ÷ ÷ ÷ ø ö ç ç ç ç è æ - =

å

=  h  k  i  h  hitung  f  f  f  1  2  0  2 c Keterangan:  hitung  2 c  : Nilai Chi­Kuadrat yang dihitung

0 

f  : Frekuensi yang di observasi 

h 

f  : Frekuensi yang diharapkan 

Untuk  uji  normalitas  menggunakan  Chi­Kuadrat,  data  harus  berjenis  data interval. Untuk itu, data berupa pre­test dan post­test yang semula  data  tunggal  terlebih  dahulu  diubah  menjadi  data  jenis  interval,  sehingga bentuknya menjadi: · Banyak kelas interval  1 · Derajat kebebasan · Rentang · Panjang kelas interval  5  6  30  )  ( =  = = K  R  P  Table 4.2: Nilai Pre­Test 

kelas  f  x _i  fx _i  x _i - x 

(

x _i - x 

) 

2  f 

(

x _i - x 

) 

2 

76 ­ 80  1  77.5  77.5  9.1  82.81  82.81 

71 ­ 75  1  73.5  73.5  5.1  26.01  26.01 

66­70  5  69.5  347.5  1.1  1.21  6.05 

61 ­ 65  11  65.5  720.5  ­2.9  8.41  92.51 

56 ­ 60  7  61.5  430.5  ­6.9  47.61  333.27  51 ­ 55  3  57.5  172.5  ­10.9  118.81  356.43  jumlah  28  405  1822  ­5.4  284.86  897.08

( ) 

f  fx  x  k  i  i

å

= =  1  28  1822 =  x  1  .  65 =  x  Simpangan  )  1  (  )  (  2 - - =

å 

n  x  x  f  S  27  08  .  897 =  S  8  .  5 =  S  Tabel 4.3: Nilai Post­Test 

kelas  f  x _i  fx _i  x _i - x 

(

x _i - x 

) 

2  f 

(

x _i - x 

) 

2 

81 – 85  2  83  166  11.8  139.24  278.5 

71­ 75  7  73  511  1.8  3.24  22.7  66 – 70  8  68  544  ­3.2  10.24  81.9  61­ 65  4  63  252  ­8.2  67.24  269.0  56 – 60  1  58  58  ­13.2  174.24  174.2  Jumlah  28  423  1999  ­4.2  440.44  1103.7

( ) 

f  fx  x  k  i  i

å

= =  1  28  1999 =  x  2  .  71 =  x  Simpangan  )  1  (  )  (  2 - - =

å 

n  x  x  f  S  27  7  .  1103 =  S  4  ,  6 =  S  Langkah­langkah uji normalitas dengan rumus Chi­Kuadrat:

1)  Menentukan  batas­batas  kelas  interval  untuk  menghitung  luas  daerah kurva normal. 

2)  Menghitung  luas  daerah  tiap  kelas  interval  berdasarkan  table  daerah kurva normal. 

3)  Menghitung frekuensi teoritis (frekuensi harapan, fh). 

4)  Hasil  perhitungan  perhitungan  tersebut  kemudian  disajikan  dalam  bentuk table sebagai berikut 2 .  Tabel 4.4: Pengujian Normalitas Data Pre­test dengan Rumus Chi­Kuadrat  Kelas  f  f _h  f - ₀ f _h 

₍

f - ₀  f _h 

₎ 

2 

(

) 

h  h  f  f  f ₀ -  2  76 – 80  1  0.7560  0.24  0.06  0.079  71 – 75  2  3.7884  ­1.79  3.20  0.844  66 – 70  5  9.5564  ­4.56  20.76  2.172  61 – 65  11  9.5564  1.44  2.08  0.218  56 – 60  7  3.7884  3.21  10.31  2.723  51 – 55  2  0.7560  1.24  1.55  2.047  Jumlah  28  28.2016  ­0.20  37.96  8.083 

083  .  8  2 =  hitung c

(

6 - 1 

) 

= 5  =  db 

d 

.  Kesimpulan  Dalam perhitungan di temukan chi kuadrat hitung  : 8.083  Nilai  tabel  2 c  untuk db = 5 dan α = 5% adalah 11.070 

Berdasarkan perhitungan diatas, dapat diketahui  bahwa  nilai  hitung  2 c  lebih kecil  dari pada harga  tabel  2

c  Maka H0 diterima dan H1 ditolak  artinya dapat disimpulkan bahwa data berdistribusi normal.  Tabel 4.5: Pengujian Normalitas Data Post­Test dengan Rumus Chi­Kuadrat  Kelas  f  f _h  f - 0 f _h 

(

) 

2  0  f h  f -

(

) 

h  h  f  f  f 0 -  2  81 – 85  2  0.76  1.24  1.55  2.05  76­ 80  6  3.79  2.21  4.89  1.29  71­ 75  7  9.56  ­2.56  6.54  0.68  66 – 70  8  9.56  ­1.56  2.42  0.25  61­ 65  4  3.79  0.21  0.04  0.01  55 – 60  1  0.76  0.24  0.06  0.08

Jumlah  28  28.20  ­0.20  15.50  4.37  37  .  4  2 =  hitung c

(

6 - 1 

) 

= 5  =  db 

e 

.  Kesimpulan  Dalam perhitungan di temukan chi kuadrat hitung  : 4,37  Nilai  tabel  2 c  untuk db = 5 dan α = 5% adalah 11.070 

Berdasarkan perhitungan diatas, dapat diketahui  bahwa  nilai  hitung  2 c  lebih kecil  dari pada harga  tabel  2

c  Maka H0 diterima dan H1 ditolak  artinya dapat disimpulkan bahwa data berdistribusi normal. 

2.  Uji Homogenitas  Langkah – langkah: 

0  H  = data bersifat homogen.  1  H  = data tidak bersifat homogen.  2.  Menentukan derajat kesalahan atau α  α = 5% atau α = 0.05  3.  Statistik uji  Rumus yang digunakan adalah: =  hitung  F  (Sanapiyah Faisal, 1984) 3  4.  Kesimpulan  Daerah penolakan H  : 0  hitung  tabel  F  F <

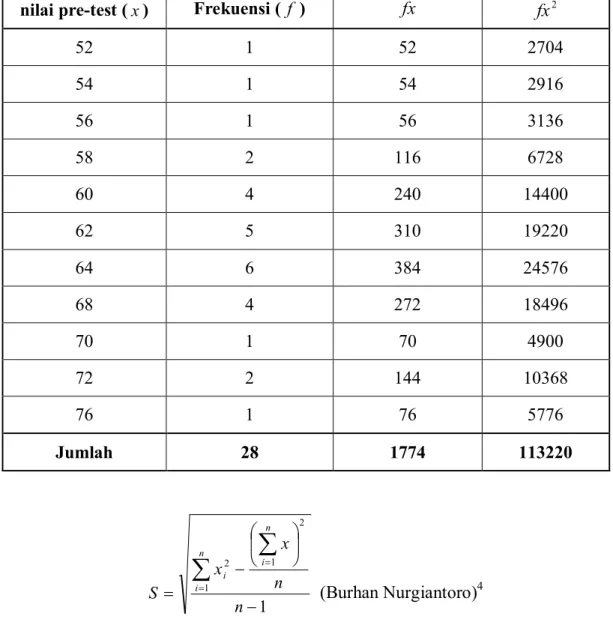
Tabel 4.6: Pengujian Homogenitas Data Pre­Test  nilai pre­test (x)  Frekuensi (  f  )  fx  2  fx  52  1  52  2704  54  1  54  2916  56  1  56  3136  58  2  116  6728  60  4  240  14400  62  5  310  19220  64  6  384  24576  68  4  272  18496  70  1  70  4900  72  2  144  10368  76  1  76  5776  Jumlah  28  1774  113220  1  1  2  1  2 - ÷ ø ö ç è æ - =

å

å

= =  n  n  x  x  S  n  i  n  i  i  (Burhan Nurgiantoro) 4 

27  28  1774  113220  2 - =  S  =  5.4262  Tabel 4.7: Pengujian Homogenitas Data Post­Test 

nilai post­test (y)  frekuensi (  f  )  fy  2 

fy  59  1  59  3481  61  1  61  3904  65  3  195  12675  67  2  134  8978  70  6  420  29400  72  6  432  31104  74  1  74  5476  76  3  228  17328  80  3  240  19200  83  1  83  6889  85  1  85  7225  Jumlah  28  2011  145660  1  1  2  1  2 - ÷ ø ö ç è æ - =

å

å

= =  n  n  x  x  S  n  i  n  i  i

27  28  2011  145660  2 - =  S  = 6.7415  54  .  1  4436  .  29  4478  .  45  4262  .  5  7415  .  6  2  2 = = =  hitung  F  dk pembilang = 28­1 = 27, dk penyebut = 28­1 = 27 

harga  f _tabel  untuk 5% dk pembilang 50, dk penyebut 28 adalah 1.78 

berdasar  perhitungan  diatas,  nilai  F _hitung  = 1 . 54  lebih  kecil  dari  harga  78  .  1 =  tabel  F 

Karena nilai F _hitung  lebih kecil dari pada F _tabel  maka H0 diterima. Artinya  kedua data tersebut bersifat homogen. 

3.  Uji Hipotesis Data Berpasangan  a.  Merumuskan hipotesis 

0 

H  =  hasil  belajar  siswa  setelah  diterapkan  pembelajaran 

matematika  dengan  menggunakan  teknik  probing  sama  dengan  hasil  belajar  siswa  sebelum  diterapkan

pembelajaran  matematika  dengan  menggunakan  teknik 

probing. 

1 

H =  hasil  belajar  siswa  setelah  diterapkan  pembelajaran  matematika  dengan  menggunakan  teknik  probing  tidak  sama  dengan  hasil  belajar  siswa  sebelum  diterapkan  pembelajaran  matematika  dengan  menggunakan  teknik 

probing.  atau  2  1  0 :m = m H  2  1  1 :m ¹ m H  b.  Menentukan derajat kesalahan atau α  α = 5% atau α = 0.05  c.  Statistik uji 

Uji  statistik  yang  digunakan  untuk  menguji  apakah  ada  peningkatan  dari  pre­test  ke  post­test  dalam  penelitian  ini  adalah  uji statistic datan berpasangan rumus yang digunakan adalah:

n  s  d  t  d  hitung =  (Djarwanto, 2001)  5  Dengan:  n  d  d  n i  i

å

= =  1

(

) 

1  1  2 - - =

å

=  n  d  d  S  n i  i  d  Keterangan:  d = Selisih antara nilai pre­test dan post­test.  d  = Rata­rata dari d  d  S  = Standart deviasi  n = Jumlah sampel.  Tabel 4.8: Daftar Nilai untuk Uji Statistik Data Berpasangan  No. urut  Nialai Pre­  Test  Nilai Post­  Test  d i 

(

) 

2  d  d _i - 5 

_{Djarwanto OpCit  h} 

_{,  .  .,  . 145}

1  60  72  12  12.001374  2  64  70  6  6.4297745  3  70  76  6  6.4297745  4  58  61  3  30.643974  5  68  70  2  42.715374  6  72  83  11  6.0727745  7  60  72  12  12.001374  8  68  67  ­1  90.929574  9  76  85  9  0.2155745  10  60  74  14  29.858574  11  64  76  12  12.001374  12  62  72  10  2.1441745  13  52  65  13  19.929974  14  62  72  10  2.1441745  15  62  67  5  12.501174  16  64  80  16  55.715774  17  62  72  10  2.1441745  18  56  70  14  29.858574  19  60  70  10  2.1441745  20  64  80  16  55.715774  21  64  70  6  6.4297745  22  56  59  3  30.643974  23  68  65  ­3  133.07237  24  62  72  10  2.1441745

25  54  65  11  6.0727745  26  64  76  12  12.001374  27  68  70  2  42.715374  28  72  80  8  0.2869745  Jumlah  1772  2011  239  664.96429  5357  .  8  28  239 = =  d  9627  .  4  1  28  96429  .  664 = - =  d  S  n  S  d  t  d  hitung =  28  9627  .  4  5357  .  8 =  9379  .  0  5357  .  8 =  =9.1009  Db = 28­1 = 27  27  ;  025  .  0  ,  2  05  .  0  t  t  db =  = 2.052

Berdasarkan  perhitungan  diatas,  nilai  t  yang  dihitung  1009  .  9 =  hitung 

t  lebih  besar  dari  harga  t  pada  table  distribusi  052  .  2 =  tabel  t  . 

d.  Dengan  melihat  rumusan  hipotesis  bahwa  hasil  belajar  siswa  setelah diterapkan pembelajaran matematika dengan menggunakan  teknik  probing  tidak  sama  dengan  hasil  belajar  siswa  sebelum  diterapkan pembelajaran  matematika dengan  menggunakan teknik 

probing, atau H ₁ :m ¹ ₁  m ₂ . Artinya H  di tolak. ₀ 

Dengan  demikian  dapat  disimpulkan  bahwa  setelah  diterapkan  pembelajaran  matematika  dengan  menggunakan  teknik  probing  mempunyai dampak positif terhadap hasil belajar siswa.