1
ditularkan melalui batuk atau bersin. Dalam tulisan ini, model endemi flu babi dengan probabilitas penularan pada populasi pasien dengan gejala (symptomatic) dan pasien tanpa gejala (asymptomatic) yang berbeda dikonstruksi sebagai suatu sistem dinamik. Selain itu, diselidiki pula pengaruh karantina terhadap tingkat penyebaran flu babi. Kestabilan titik kesetimbangan model dianalisis menggunakan kriteria Routh-Hurwitz. Hasil analisis tersebut kemudian dikaji untuk mengetahui pengaruh karantina. Pada bagian akhir dilakukan simulasi numerik untuk mengilustrasikan hasil analisis yang telah diperoleh.
Kata Kunci : model endemi flu babi, karantina, titik kesetimbangan, kriteria Routh-Hurwitz, kestabilan lokal.
1. PENDAHULUAN
Flu babi pertama kali terdeteksi di sebuah pertanian di Meksiko pada tahun 2009. Di Indonesia, flu babi sudah terdeteksi hampir 25 propinsi dengan jumlah korban terinfeksi mencapai 1.127 orang. Mudahnya penyebaran flu babi dikarenakan kurangnya informasi kepada warga mengenai penyakit flu babi yang pada saat itu masih merupakan penyakit baru (Aditama, 2010).
Flu babi adalah infeksi yang disebabkan oleh salah satu atau beberapa jenis Swine Influenza Virus (SIV) yang pada awalnya terjangkit pada babi. Flu babi adalah penyakit yang cukup berbahaya karena virus ini tergolong virus baru (Pongsumpun dan Tang, 2011).
Sejak tahun 2010 telah dikaji model-model matematika mengenai endemi flu babi. Pada tahun 2010, Pongsumpun memodelkan endemi tersebut dengan membagi populasi menjadi dua subpopulasi, yaitu populasi dengan risiko (risk) dan tanpa risiko (non-risk) terinfeksi (Pongsumpun, 2010). Pada tahun 2011, Pongsumpun dan Tang, memodelkan endemi flu babi dengan memperhitungkan aspek populasi terinfeksi symptomatic dan asymptomatic tanpa memperlihatkan pengaruh karantina (Pongsumpun dan Tang, 2011).
Berbeda dari kajian yang dilakukan sebelumnya, pada tulisan ini dilakukan analisis terhadap model endemi flu babi dengan memperhitungkan aspek populasi terinfeksi symptomatic dan asymptomatic, serta pengaruh karantina terhadap populasi terinfeksi. Dengan menggunakan analisis sistem dinamik, ditentukan titik kesetimbangan dan perilaku kestabilan di setiap titik kesetimbangan. Selanjutnya, dilakukan simulasi numerik untuk mengetahui perilaku solusi model.
2. FORMULASI MODEL
Model yang dibahas dalam tulisan ini adalah model endemi SEIQR di mana populasi terinfeksi terbagi menjadi dua, yaitu symptomatic dan asymptomatic infectives. Dengan demikian populasi terbagi menjadi enam subpopulasi, yaitu susceptible (s), exposed (e), symptomatic infectives ( ), asymptomatic infectives ( ), quarantine (q), dan recovered (r). Jika dalam model endemi tidak dilakukan karantina maka tidak terdapat kompartemen , sehingga diperoleh model endemi tanpa karantina dengan lima persamaan. Dengan dimikian diperoleh dua model endemi flu babi yang diberikan pada Tabel 1.
Pada sistem (1) dan (2), menyatakan laju kematian populasi manusia, adalah laju transmisi flu babi, adalah probabilitas transmisi flu babi ke manusia yang membuat manusia menjadi individu terinfeksi dengan gejala, adalah probabilitas transmisi flu babi ke manusia yang membuat manusia menjadi individu terinfeksi tanpa gejala,
dimana atau Incubation Period adalah masa
inkubasi flu babi di dalam tubuh manusia, adalah laju pertambahan populasi yang dikarantina, dan adalah laju kesembuhan pasien.
2 variabel . Pada sistem (1), perilaku dapat diketahui dari perilaku . Sedangkan pada sistem (2), perilaku dapat diketahui dari perilaku dan .
Tabel 1 Model endemi flu babi dengan karantina dan tanpa karantina
Model Endemi Flu Babi dengan Karantina Model Endemi Flu Babi tanpa Karantina
Berdasarkan kriteria Routh-Hurwitz, titik stabil jika kondisi-kondisi berikut dipenuhi.
i.
ii.
iii. ( ) .
3
3.2. Model Endemi Flu Babi tanpa Karantina
Terdapat dua titik kesetimbangan, yaitu dan dengan
,
, ,
dan
adalah angka reproduksi dasar. Titik eksis jika .
Kestabilan diselidiki dengan mensubstitusikan ke matriks Jacobi sistem (2), sehingga didapatkan persamaan karakteristik dengan nilai eigen
, ,
√
Nilai dan selalu bernilai negatif, sebab seluruh parameter bernilai positif. Jika , maka dan bernilai negatif dan bernilai positif jika namun tidak stabil, sehingga titik stabil asimtotik jika
Kestabilan diperiksa dengan memisalkan , , , pada matriks Jacobi sistem (2), sehingga diperoleh persamaan karakteristik dengan
.
Berdasarkan kriteria Routh-Hurwitz, titik stabil jika kondisi-kondisi berikut dipenuhi.
i.
ii.
iii.
Kondisi (i) terpenuhi, jika . Seperti halnya pada titik , karena sulitnya menyatakan kondisi (ii) dan (iii), maka kondisi (ii) dan (iii) diperlihatkan sebagai syarat kestabilan untuk titik kesetimbangan dalam simulasi numerik.
4. SIMULASI NUMERIK DAN INTERPRETASI MODEL
Simulasi numerik dengan bantuan software Matlab menggunakan nilai parameter . Simulasi model dengan karantina
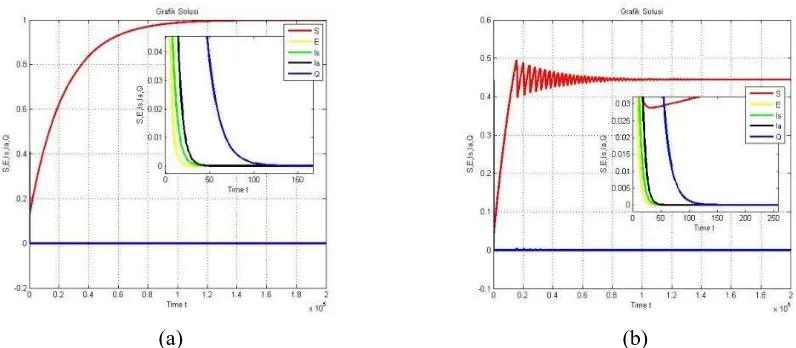
dilakukan untuk kasus dan . Untuk kasus , diambil sehingga . Hasil simulasi dengan nilai awal pada Gambar 1(a) memperlihatkan bahwa stabil. Untuk kasus , diambil sehingga . Dapat diperiksa bahwa kondisi (i), (ii), dan (iii) pada sub bab 3.1 terpenuhi.
Grafik solusi dengan nilai awal pada gambar 1(b) menuju titik , jadi titik stabil jika .
(a) (b)
4 Simulasi model tanpa karantina dilakukan untuk kasus dan . Untuk kasus , diambil sehingga . Hasil simulasi dengan nilai awal pada Gambar 2(a) memperlihatkan bahwa stabil. Untuk kasus , diambil sehingga . Dapat diperiksa bahwa kondisi (i), (ii), dan (iii) pada sub bab 3.2 terpenuhi. Grafik solusi dengan nilai awal pada gambar 2(b) menuju titik , jadi titik stabil jika
.
(a) (b)
Gambar 2. (a) Grafik Solusi untuk , (b) Grafik Solusi untuk
Untuk memperlihatkan pengaruh karantina, dilakukan simulasi numerik dengan memperhatikan perilaku dari populasi recovered terhadap waktu t. Perilaku tersebut diperlihatkan pada gambar berikut.
Gambar 3. Perilaku kelas recovered
Berdasarkan Gambar 3, terlihat proporsi populasi recovered dengan karantina lebih kecil dari pada populasi tanpa karantina, dikarenakan pengaruh dari karantina yang memperkecil laju penyebaran penyakit pada populasi tersebut. Dengan demikian dapat disimpulkan, dengan adanya karantina dapat memperkecil laju penyebaran penyakit pada suatu populasi yang terinfeksi.
DAFTAR PUSTAKA
Aditama, T.Y., (2010), Situasi Terkini Influenza Baru A H1N1 di Indonesia, http://www.penyakit menular.info/userfiles/Situasi%20terkini%20H1N1%20di%20Indonesia.pdf. Tanggal akses : 8 Januari 2013.
Pongsumpun, P., (2010), Swine Flu Transmission Model in Risk and Non-Risk Human Population, World Academy of Science, Engineering and Technology, 68, hal. 1166-1171.