MELALUI PEMBELAJARAN BERBASIS MASALAH
DITINJAU DARI KEMAMPUAN AWAL
MATEMATIKA SISWA MAN NGAWI
Ulfa Masamah
STAIN Kudus Jawa Tengah Indonesia [email protected]
Abstract
This study aims to examine the retention of students' reflective mathematical thinking abilities, as a result of the use of problem-based learning. This research is a quasi-experimental research with non equivalent control group design (The Non Equivalent Control Group Design). This research was conducted at MAN Ngawi. The results conclude that there is a significant difference in retention of reflective mathematical thinking among students who have problem-based learning and students who have received conventional learning. Furthermore, the retention of mathematical reflective thinking skills of students who acquired problem-based learning was significantly better than that of students who received conventional learning. This is because in the implementation of problem-based learning is supported by teaching materials that take into account the aspects of mathematical reflective thinking ability, the accuracy of teacher interventions in providing scaffolding, and implementation of problem-based learning itself that requires the active involvement of students to interact, reflect, construct and create knowledge and experience of the students themselves into new problems or situations.
Keywords: Reflective Thinking, Retention, Problem-Based, Conventional Learning
Abstrak
merupakan penelitian eksperimen semu dengan desain kelompok kontrol non ekuivalen (The Non Equivalent Control Group Design). Penelitian ini dilakukan di MAN Ngawi. Hasil penelitian menyimpulkan bahwa, terdapat perbedaan retensi kemampuan berpikir reflektif matematis yang signifikan antara siswa yang memperoleh pembelajaran berbasis masalah dan siswa yang memperoleh pembelajaran konvensional. Lebih lanjut, bahwasanya retensi kemampuan berpikir reflektif matematis siswa yang memperoleh pembelajaran berbasis masalah lebih baik secara signifikan dibanding dengan siswa yang memperoleh pembelajaran konvensional.Hal ini dikarenakan dalam pelaksanaan pembelajaran berbasis masalah didukung dengan bahan ajar yang mamperhatikan aspek kemampuan berpikir reflektif matematis, adanya ketepatan intervensi guru dalam memberikan scaffolding, serta pelaksanaan pembelajaran berbasis masalah itu sendiri yang menuntut adanya keterlibatan aktif siswa untuk berinteraksi, refleksi, konstruksi, dan mengkreasikan pengetahuan dan pengalaman siswa sendiri ke dalam permasalahan ataupun situasi baru.
Kata kunci: Berpikir Reflektif, Retensi, Pembelajaran Berbasis-Masalah, Konvensional
A. Pendahuluan
Adanya pergeseran paradigma matematika nyatanya berpengaruh terhadap cara penyampaian pembelajaran matematika kepada siswa. Paradigma lama dimana pembelajaran terpusat pada guru (teachercentered approach) bergeser pada pembelajaran terpusat pada siswa (student centered approach).Pendekatan teacher centered merupakan suatu pembelajaran berpusat pada guru dengan penekanan pada peliputan dan penyebaran materi, sementara siswa kurang aktif, sudah tidak memadai tuntutan era pengetahuan saat ini (Ching & Gallow dalam Amir, 2010: 3); (Tan, 2004: 2). Implikasinya pada pembelajaran matematika adalah turut bergesernya paradigma
matematika dari “Strict body of knowledge” menuju matematika sebagai aktivitas kehidupan (Ibrahim dan Suparni, 2008: 24-26).
bahwa siswa adalah obyek yang pasif, karena yang diutamakan
adalah “knowledge of mathematics”. Sehingga menyebabkan matematika dipandang sebagai hal yang statis dan pertumbuhan teori matematika sangat lamban, yang berdampak pada guru senantiasa menjadi pusat pembelajaran, karena harus mendemonstrasikan matematika yang sudah siap saji dan siswa diharapkan mampu menirukan perilaku guru terhadap matematika yang diberikannya (teacher centered approach).
Matematika sebagai aktivitas kehidupan manusia,
Freudenthal mengistilahkannya sebagai “Mathematics as human sense making and problem solving activity.” Pandangan ini telah menggeser pemahaman bahwa matematika sebagai kumpulan konsep dan keterampilan ke suatu cara sedemikian rupa, seperti yang diungkapkan Cobb (Suherman, 2001: 71), belajar matematika bukanlah proses pengepakan pengetahuan secara berhati-hati, melainkan hal mengorganisir aktivitas dimana kegiatan ini diinterpretasikan secara luas termasuk aktivitas dan berpikir konseptual atau dikenal dengan student centered approach.
Kilpatrick et.al.(2001) menyatakan bahwa pembelajaran matematika seharusnya tidak lagi berfokus pada pencapaian keahlian rutin tetapi lebih membantu pada pengembangan keahlian yang bersifat adaptip. Hal ini dikarenakan, belajar matematika merupakan proses siswa mengkonstruksi pengetahuan yang dilakukan secara aktif dan kontinu (Cobb, 1992). Karena pada dasarnya pilar utama dalam belajar matematika adalah pemecahan masalah (Sabandar, 2009). Pemecahan masalah menuntut adanya pelibatan kemampuan berpikir tingkat tinggi (High-Order Thinking Skills/HOTS).
dari apa yang sudah dilakukan dan apa yang masih dapat dilakukan untuk meningkatkan kualitas pekerjaannya (Suherman, 2001: 95).
Marpaung (Yahya, 2010) menemukan bahwa selama ini dalam pembelajaran matematika, siswa hampir tidak pernah dituntut untuk mencoba cara dan strategi lain dalam episode pemecahan masalah. Suatu episode pemecahan masalah tidak semua siswa dapat dengan cepat menemukan solusi, dan jika solusi tersebut ditemukan, siswa cenderung merasa puas dan mengakhiri proses belajarnya. Salah satu sekolah yang mengalami hal tersebut adalah MAN Ngawi. Berdasar pada hasil studi pendahuluan diketahui bahwasanya terkait dengan aspek berpikir reflektif matematis, rata-rata nilai siswa dalam skala 0-16 untuk aspek reacting adalah 8,9 dengan standar deviasi sebesar 4,99. Sedangkan untuk aspek comparing rata-rata nilai siswa adalah 8,67 dengan standar deviasinya adalah 4,02, dan aspek comparing nilai rata-ratanya adalah 5,6 dengan standar deviasinya adalah 1,83. Nilai rata-rata pada setiap aspek menunjukkan bahwa nilai-nilai tersebut terletak pada interval sedang (bawah).
Menurut pandangan pragmatism (Azhar dalam Yahya 2010), pengembangan kemampuan berpikir reflektif menuntut guru untuk menciptakan suatu situasi yang membuat siswa merasakan adanya masalah dan menimbulkan minat memecahkan masalah tersebut, serta dapat menciptakan kerjasama dalam belajar. Karena situasi dan suasana belajar di kelas dipandang sebagai suatu lingkungan yang penuh dengan tantangan ataupun sumber yang dapat dirujuk siswa, sehingga guru perlu tindakan tepat untuk membuat proses pembelajaran matematika ataupun proses menyelesaikan suatu soal matematika di kelas menjadi suatu tempat serta kesempatan dimana siswa dapat meningkatkan keterampilan berpikirnya (Sabandar, 2009).
bentuk pemecahan masalah yang beberapa ide dirantai bersama-sama dengan menghubungkan setiap gagasan dengan pendahulunya dalam rangka untuk menyelesaikan masalah.
Mendasar pada permasalahan-permasalahan yang ada, maka diperlukan inovasi baru untuk mengembangkan kemampuan berpikir reflektif dalam pembelajaran matematika (Dewey dalam Rodgers, 2002: 845. Pendapat Dewey ini diperkuat olehVon Glasersfeld (Dewanti, 2009: 57) bahwa, dalam kelompok belajar siswa harus mengungkapkan bagaimana siswa melihat persoalan dan apa yang akan dibuatnya dengan persoalan itu. Hal ini berarti bahwa, salah satu jalan mengembangkan kemampuan berpikir reflektif adalah dengan adanya interaksi dengan siswa lain untuk mengembangkan pengetahuan (Mezirow dalam Rogers, 2000: 133) .Salah satu alternatif yang diduga mampu menyelesaikan masalah tersebut adalah dengan meningkatkan kualitas pembelajaran melalui pembelajaran berbasismasalah.
Pembelajaran berbasis masalah berfokus pada optimalisasi peran guru sebagai perancang dan organisator pembelajaran sehingga siswa mendapat kesempatan untuk memahami dan memaknai matematika melalui aktivitas belajar.Herman (2007: 49) menambahkan bahwa karakteristik pembelajaran berbasis masalah adalah 1) memposisikan siswa sebagai self-directed problem solver melalui kegiatan kolaboratif; 2) mendorong siswa untuk mampu menemukan masalah dan mengelaborasinya dengan mengajukan dugaan-dugaan dan merencanakan penyelesaian; 3) memfasilitasi siswa untuk mengeksplorasi berbagai alternatif penyelesaian dan implikasinya, serta mengumpulkan dan mendistribusikan informasi; 4) melatih siswa untuk terampil menyajikan temuan, dan 5) membiasakan siswa untuk merefleksi tentang efektivitas cara berpikir mereka dalam menyelesaikan masalah.
guru, bantuan ini disesuaikan dengan kemampuan atau pengetahuan sebelumnya. Pengetahuan yang pernah dipelajari atau diperoleh digunakan untuk mendapatkan pengetahuan yang baru. Hal ini sesuai dengan pernyataan Reigeluth (Uno, 2010: 160), yang menyatakan bahwa kemampuan awal dapat dipakai untuk memudahkan perolehan, pengorganisasian, dan pengungkapan kembali pengetahuan baru. Jika informasi-informasi atau pengetahuan yang lama seringkali harus diajarkan kembali, dalam hal ini berarti proses belajar seseorang tidak efisien. Hal ini menunjukkan bahwa informasi atau pengetahuan yang telah kita punyai masih digunakan untuk membantu proses perekonstruksian pengetahuan baru.
Kualitas pengetahuan baru yang diperoleh siswa dipengaruhi oleh kualitas seseorang dalam menyimpan informasidan berinteraksi dalam kelompok diskusi (Ibrahim dan Nur, 2000: 18). Kemampuan seseorang untuk mempertahankan seberapa banyak hal yang telah dialami atau dipelajari tersebut dikenal dengan istilah retensi.Retensi siswa juga tidak bisa dilepaskan dari pengaruh kemampuan awal matematika siswa. Karena, kemampuan awal yang dimiliki siswa merupakan titik tolak bagi proses belajar mengajar selanjutnya (Musfiroh, 2009: 2). Dengan modal kemampuan awal matematika yang dimiliki oleh siswa, tentu akan mempermudah memahami pengetahuan baru untuk membangun pengertian baru (advancedorganizer) (Ibrahim& Nur, 2000: 18).
way anova). Pengujian dilakukan dengan bantuan software SPSS 16.0 dan Microsoft excel 2007.
B. Pembahasan Hasil Penelitian
Tujuan penelitian ini adalah untuk mengungkap perbedaan retensi kemampuan berpikir reflektif matematis siswa berdasar pada faktor pembelajaran dan kemampuan awal matematika siswa. Lebih jauh, penelitian ini juga mengungkap interaksi antara pembelajaran dan kemampuan awal matematika siswa terhadap retensi kemampuan berpikir reflektif matematis siswa. Analisis data yang dimaksud meliputi analisis peningkatan kemampuan berpikir reflektif matematis berdasarkan pembelajaran dan kemampuan awal matematika siswa. Analisis yang dilakukan didasarkan pada nilai N-Gainpostes dan tes retemsi.
Data retensi kemampuan berpikir reflektif matematis diperoleh berdasarkan hasil postes dan tes retensi kemampuan berpikir reflektif matematis. Tes retensi ini dilaksanakan dua minggu setelah penelitian atau diadakan dua minggu setelah postes. Dalam selang waktu dua minggu tersebut, subjek penelitian (siswa) tidak diberikan pembelajaran yang berkaitan langsung dengan materi tes kemampuan berpikir reflektif matematis juga tidak diberikan tes dan diberikan tes kembali pada dua minggu kemudian.Skor retensi diperoleh dari hasil postes kemampuan berpikir reflektif matematis dan tes retensi kemampuan berpikir reflektif matematis. Adapun perhitungan skor retensi dengan menggunakan rumus N-Gain dengan menganggap postes sebagai pretes dan tes retensi adalah postes.
memberikan pengaruh secara signifikan terhadap retensi kemampuan berpikir reflektif matematis siswa.
Berdasar hasil perhitungan statistic diperoleh F = 10,033 dan P = 0,000 untuk faktor interaksi. Hal ini berarti bahwa terdapat interaksi antara pembelajaran dan kemampuan awal matematika siswa yang memberikan pengaruh signifikan terhadap N-Gain yang merupakan gambaran tingkat retensi kemampuan berpikir reflektif matematis siswa. Interaction Plot antara faktor pembelajaran dan kemampuan awal matematika terhadap retensi kemampuan berpikir reflektif matematis diperlihatkan oleh Gambar C.1.
Gambar C.1.
Interaction Plot antara Pembelajaran dan Kemampuan Awal Matematika Terhadap Retensi Kemampuan Berpikir
Reflektif Matematis Siswa
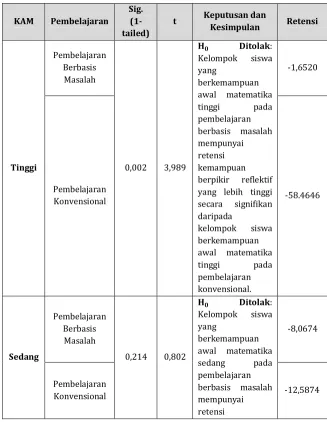
reflektif matematis siswa, pada kelompok kemampuan awal matematika tinggi, sedang, dan rendah.Berdasar hasil pengujian diperoleh rangkuman yang disajikan pada Tabel C.1..berikut ini.
Tabel C.1.
Rangkuman Hasil Uji t Satu Pihak Retensi
Kemampuan Berpikir Reflektif Matematis antar Pembelajaran pada Kemampuan Awal Matematika Tinggi, Sedang, dan Rendah
kemampuan kemampuan awal matematika siswa. Pengujian yang pertama untuk kemampuan awal matematika siswa yang memperoleh pembelajaran berbasis masalah. Pengujian ini bertujuan untuk mengetahui kelompok kemampuan awal matematika mana yang lebih baik di antara kelompok tinggi, sedang, dan rendah dalam retensi kemampuan berpikir reflektif matematis siswa.
Pada pengujian Anova satu jalur diperoleh nilai F = 3,800, P (Sig. ) = 0,034. Dari hasil pengujian tersebut, nilai probabilitas Sig.
=0,034 < 0,05, maka H0ditolak atau minimal terdapat satu kelompok
kelompok kemampuan awal matematika tinggi, sedang, dan rendah. Kemudian, untuk mengetahui pasangan kelompok yang saling berbeda secara signifikan dan pasangan kelompok yang tidak berbeda secara signifikan dilakukan uji Tukey.Setelah dilakukan uji t satu pihak retensi kemampuan berpikir reflektif matematis setiap pasangan kelompok kemampuan awal matematika siswa pada pembelajaran berbasis masalah, diperoleh hasil yang disajikan pada Tabel C.2.berikut.
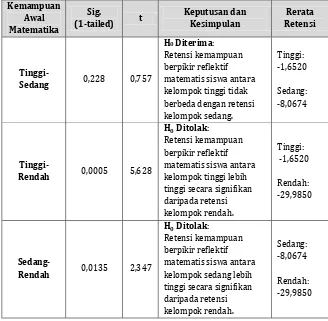
Tabel C.2.
Rangkuman Hasil Uji t Satu Pihak: Retensi Kemampuan Berpikir Reflektif Matematis antar Kelompok Kemampuan Awal
Tabel C.2. memberikan informasi bahwa kelompok siswa berkemampuan awal matematika tinggi dan sedang lebih tinggi secara signifikan dari kelompok siswa kemampuan awal matematika rendah dalam retensi kemampuan berpikir reflektif matematis siswa. Selanjutnya dapat dikatakan bahwakelompok siswa berkemampuan awal matematika tinggi dan sedang lebih baik secara signifikan dari kelompok siswa kemampuan awal matematika rendah dalam retensi kemampuan berpikir reflektif matematis siswa.Retensi kemampuan berpikir reflektif matematis antara kemampuan awal matematika tinggi dan sedang tidak ditemukan bukti untuk menyimpulkan bahwa retensi kemampuan berpikir reflektif matematis siswa dari kelompok kemampuan awal matematika tinggi lebih baik secara signifikan dibanding siswa dari kelompok sedang. Dengan kata lain, retensi kemampuan berpikir reflektif matematis antara siswa dari kelompok kemampuan awal matematika tinggi dan siswa dari kelompok kemampuan awal matematika sedang tidak berbeda secara signifikan.
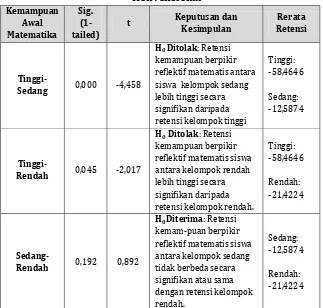
Tabel C.3.
Rangkuman Hasil Uji t Satu Pihak
Retensi Kemampuan Berpikir Reflektif Matematis antar Kelompok Kemampuan Awal Matematika Pada Pembelajaran
Konvensional
tidak ditemukan bukti untuk menyimpulkan bahwa retensi kemampuan berpikir reflektif matematis siswa dari kelompok kemampuan awal matematika sedang lebih baik secara signifikan dibanding siswa dari kelompok rendah. Dengan kata lain, retensi kemampuan berpikir reflektif matematis antara siswa dari kelompok kemampuan awal matematika sedangdan siswa dari kelompok kemampuan awal matematika rendah tidak berbeda secara signifikan.
Pembahasan Hasil Penelitian
Hasil penelitian tersebut berkaitan dengan temuan-temuan berdasarkan implementasi pembelajaran berbasis masalah dan pembelajaran konvensional. Sementara itu, pembahasan hasil penelitian dilakukan berdasarkan hal-hal yang dicermati dalam studi yaitu, pembelajaran, kemampuan awal matematika siswa, dan kemampuan berpikir reflektif matematis siswa.Penelitian ini telah menghasilkan beberapa temuan berdasarkan implementasi pembelajaran berbasis masalah dibandingkan dengan pembelajaran konvensional. Pembelajaran Konvensional adalah pembelajaran yang biasa dilakukan oleh guru SMA/MAN dalam mengajarkan matematika selama ini. Pada pembelajaran konvensional, guru adalah model terbaik yang dapat diteladani oleh siswa karena semua aspek yang menyangkut keberhasilan belajar siswa dimulai dan berpusat pada guru. Pada proses belajar mengajarnya lebih menekankan pada ceramah guru yang monoton, terlalu bersumber pada buku, hafalan dan kecepatan berhitung sehingga siswa kurang membuka wawasan pengetahuan, dapat menjadikan siswa pasif dan menyebabkan verbalisme, yaitu siswa tidak paham dan tidak mengerti dengan apa yang dipelajarinya dan akan sulit untuk mengembangkan kemampuan siswa dalam hal kemampuan sosialisasi, hubungan interpersonal, serta kemampuan berpikir (Sanjaya, 2008: 191).
menjelaskan materi pelajaran, memberikan contoh-contoh soal dan penyelesaiannya, serta memberikan ideatau gagasan secara langsung kepada siswa (Ibrahim, 2011). Sedangkan siswa cenderung menerima materi pelajaran kemudian menghafal materi tersebut dan mengerjakan soal-soal latihan yang sifatnya rutin. Sehingga pembelajaran tidak ada kegiatan yang dimana siswa kurang ada kesempatan untuk menggali, menemukan dan mengkreasikan pengetahuan matematis itu sendiri.
Pembelajaran konvensional merupakan one-way communication, maka kesempatan untuk mengontrol pemahaman siswa tentang materi pembelajaran akan sangat terbatas pula. Selain itu, pengetahuan yang dimiliki siswa akan terbatas pada yang diberikan guru, tidak ada transformasi pengetahuan, bahkan stock knowledge siswa juga akan statis, dan tidak berkembang, atau dalam hal ini, kebermaknaan belajar siswa relatif rendah.Menurut Cobb (Suherman, 2001: 71), belajar matematika bukanlah proses pengepakan pengetahuan secara berhati-hati, melainkan hal mengorganisir aktivitas dimana kegiatan ini diinterpretasikan secara luas termasuk aktivitas dan berpikir konseptual. Lebih lanjut Cobb (1992) menyatakan bahwa, belajar matematika merupakan proses dimana siswa secara aktif mengkonstruksi pengetahuan mereka. Hal ini berarti bahwa, dalam pembelajaran matematika seharusnya siswa difasilitasi untuk mengembangkan dan mengkreasikan pengetahuan matematis yang telah mereka punya sebagai modal untuk menyelesaikan permasalahan matematika yang baru.
Dalam pemecahan masalah membutuhkan kemampuan berpikir reflektif. Berpikir reflektif dipandang sebagai proses, yang universal kognitif aktif dan berkelanjutanyang dapatditerapkan di berbagai pengaturan dan konteks. Dukungan secara teoritis tentang berpikir reflektif juga diberikan oleh Boyd & Fales (1983) yang mendefinisikan berpikir reflektif sebagai,
The process of creating and clarifying the meaning of experience (past or present) in terms of self (self in relation to self and self in relation to the world) and reflective thinking is a part of the critical thinking process referring specifically to the processes of analyzing, evaluating, and making judgments about what has happened.
Berpikir reflektif merupakan suatu proses menciptakan dan memperjelas makna pengalaman dalam diri yang berkaitan dengan diri sendiri dan lingkungan. Oleh karena itu, berpikir reflektif merupakan pedoman untuk mempertimbangkan dan menentukan langkah selanjutnya dengan berdasarkan kepada pengalaman yang telah dimiliki sebelumnya.
Keterampilandalam pengambilan keputusan dapat ditingkatkan melalui belajar dari kesuksesan, kegagalan dan pengalaman mental yang telah terjadi dan mengapa hal itu bisa terjadi, untuk menghadapi masa depan. Oleh karena itu, untuk mengembangkan kemampuan berpikir reflektif dalam pembelajaran matematika, siswa harus dilibatkan dalam suatu episode pemecahan masalah matematika (Sabandar, 2009).Melalui penyelidikan, bekerja sama, dan berdiskusi dengan orang lain, maka proses pemecahan masalah tersebut akan menuntun siswa menuju ke tingkat berpikir reflektif.
secara kontinu sedemikian sehingga menjadi bagian integral dari penerapan kurikulum dalam suatu instansi pendidikan, maka tidak menutup kemungkinan kompetensi-kompetensi tersebut dapat ditingkatkan secara optimal (Arends, 2008: 44; Amir, 2010: 21).
Ada dua hal utama dalam pelaksanaan kegiatan pembelajaran di dalam kelas eksperimen, yaitu penggunaan bahan ajar dan proses pelaksanaan pembelajaran berbasis masalah sesuai dengan kerangka pedagogis yang direncanakan dan tertuang dalam rencana pelaksanaan pembelajaran (RPP). Sesuai dengan karakteristik pembelajaran berbasis masalah, bahan ajar disajikan dalam bentuk masalah matematis, disiapkan untuk memicu dan memacu terjadinya interaksi multiarah antarkomunitas kemampuan awal matematika siswa sehingga tercipta iklim pembelajaran yang kondusif dan bermakna.
penelitian yang dilakukan oleh Maulidah (2008), bahwasanya berdasar pada hasil uji statistik, dapat diketahui bahwa terdapat perbedaan yang signifikan antara rerata retensi yang diperoleh kelompok eksperimen (memperoleh pembelajaran model siklus belajar) dengan kelompok kontrol (yang memperoleh pembelajaran konvensional). Rerata kelompok eksperimen (99,86%) lebih tinggi daripada kelompok kontrol (91,30%) dalam interval tiga minggu setelah pembelajaran.
Berbagai alasan dapat dikemukakan untuk memperkuat hasil analisis yang berkaitan dengan retensi kemampuan berpikir reflektif matematis. Dalam pembelajaran berbasis masalah banyak aktivitas yang melibatkan siswa untuk mengkonstruksi pengetahuan matematis, dengan semakin banyak mereka menggunakan apa yang sudah mereka ketahui untuk membantu mereka memahami dan menafsirkan pengetahuan baru maka semakin efektif mereka menyimpan dan mengingat pengetahuan tersebut. Sehingga dengan proses tersebut pembelajaran menjadi lebih bermakna. Hal ini diperkuat oleh Ormrod (2008), pembelajaran yang bermakna adalah pembelajaran yang memperkuat retensi hasil belajar siswa.
Akan tetapi, berdasarkanhasil anova dua jalur retensi, ternyata diperoleh retensi kemampuan berpikir reflektif matematis kelompok sedang kelas eksperimen tidak berbeda secara signifikan dengan rerata retensi kelompok sedang kelas kontrol. Selain itu, retensi kemampuan berpikir reflektif matematis siswa berkemampuan rendah kelas eksperimen lebih rendah secara signifikan dibanding dengan retensi kelompok rendah kelas kontrol. Temuan ini kemungkinan disebabkan sebagian siswa cenderung mencampuradukan antara beberapa konsep matematika, dalam hal ini berarti siswa belum mampu ataupun kurang mampu menyeleksi pengetahuan mana yang relevan yang harus digunakan dan ditransformasikan untuk menyelesaikan dan membangun pengetahuan baru.
mengubah budaya siswa yang cenderung bersikap pasif menerima penjelasan guru menjadi lebih aktif dalam membangun pengetahuannya sendiri. Kebiasaan yang dilakukan secara terus menerus seakan semakin kuat dan menetap pada diri individu sehingga sulit diubah. Salah satu jenis kebiasaan yang dipandang sangat mempengaruhi kebiasaan individu adalah kebiasaan berpikir (habit of mind).
Berdasarkan hasil perolehan siswa di atas, menunjukkan bahwa untuk meningkatkan kemampuan berpikir reflektif matematis serta retensinya, bukan sesuatu yang mudah dilaksanakan baik bagi guru maupun siswa. Hal ini semakin memperjelas bahwa untuk meningkatkan kemampuan berpikir reflektif matematis bukan suatu pekerjaan yang mudah. Akan tetapai tidak dapat dipungkiri bahwa siswa yang memperoleh pembelajaran berbasis masalah mempunyai peningkatan dan retensi yang lebih baik secara signifikan dibanding siswa yang memperoleh pembelajaran konvensional.Hal ini dikarenakan dalam pelaksanaan pembelajaran berbasis masalah didukung dengan bahan ajar yang mamperhatikan aspek kemampuan berpikir reflektif matematis, adanya ketepatan intervensi guru dalam memberikan scaffolding, serta pelaksanaan pembelajaran berbasis masalah itu sendiri yang menuntut adanya keterlibatan aktif siswa untuk berinteraksi, refleksi, konstruksi, dan mengkreasikan pengetahuan dan pengalaman mereka sendiri ke dalam permasalahan ataupun situasi baru. Tentu saja karena matematika bukanlah sekumpulan teori atau hanya sekedar pengepakan pengetahuan saja. Akan tetapi matematika adalah sebuah aktivitas kehidupan manusia (human activities)
C. Simpulan
Daftar Pustaka
Amir, M.T. 2010. Inovasi Pendidikan Melalui Problem Based-Learning (Bagaimana Pendidik Memberdayakan Pemelajar di Era Pengetahuan). Jakarta:Kencana Prenada Media Group
Arends, R. I. 2008. Learning To Teach. Yogyakarta: Pustaka Pelajar Boyd & Fales. 1983. Reflective Learning: Key to Learning from
Experience. Journal of Humanistic Psychology. [Online]. Tersedia. http://intl.feedfury.com/content/1691329-metode-ilmiah-john-dewey.html. Diakses [18 Maret 2011] Budiyono. 2003.Metodologi Penelitian Pendidikan. Surakarta: Sebelas
Maret University Press.
Dewanti, S. S. 2008.Psikologi Belajar Matematika. Yogyakarta: Bidang Akademik UIN Sunan Kalijaga.
Herman, T. 2007. Pembelajaran Berbasis Masalah untuk Meningkatkan Kemampuan Berpikir Matematis Tingkat Tinggi Siswa Sekolah Menengah Pertama, No. 1 Vol. 1 Januari. Educationist.
Ibrahim. 2011. Peningkatan Kemampuan Komunikasi, Penalaran, dan Pemecahan Masalah Matematis serta Kecerdasan Emosional Melalui Pembelajaran BerbasisMasalah Pada Siswa Sekolah Menengah Atas. Disertasi UPI. Bandung: Tidak Diterbitkan. Ibrahim dan Suparni. 2008. Strategi Pembelajaran Matematika.
Yogyakarta: Bidang Akademik UIN Sunan Kalijaga
Kilpatrick, J., Swafford, J., & Findell, B. 2001. Adding it up. Helping Children Learn Mathema- tics. Washington, D. C.: National Academy Press.
Mahmudi, A. 2010. Pengaruh Pembelajaran dengan Strategi MHM Berbasis Masalah Terhadap Kemampuan Berpikir Kreatif, Kemampuan Pemecahan Masalah, dan Disposisi Matematis serta Persepsi Terhadap Kreativitas. Disertasi UPI Bandung: Tidak Diterbitkan
Maulidah, L. 2008. Pengaruh Penggunaan Model Siklus Belajar Terhadap Retensi Siswa pada Konsep Ekosistem. Skripsi UPI Bandung: Tidak Diterbitkan
Rogers, R. R. 2000. Reflective Thinking in Professional Practice: a Model, CPD Journal Volume (3). Chicago USA: Associate Professor (Professional Studies) DePaul University
Sabandar, J. 2009. Berpikir Reflektif dalam Pembelajaran Matematika [online]. Tersedia http://math.sps.upi.edu/wp-content/uploads/2009/11/Berpikir-Reflektif.pdf. Diakses [10 Maret 2011]
Sabandar, J. 2009. Berpikir Reflektif. [Online]. Tersedia
http://math.sps.upi.edu/wp-content/uploads/2009/11/Berpikir-Reflektif.pdf. Diakses [10 Maret 2011]
Sanjaya, W. 2008. Strategi Pembelajaran Berorientasi Standar Proses Pendidikan. Jakarta: Kencana Prenada Media Grup
Suherman, E. 2001. Strategi Pembelajaran Matematika Kontemporer. Bandung: JICA UPI
Tan, O. S. 2004. Cognition, Metacognition, and Problem-Based Learning, in Enhancing Thinking through Problem-based Learning Approaches. Singapore: Thomson Learning.