Modul 5 OPTIMALISASI MELALUI LINEAR PROGRAMMING

(1)

Modul 5 ESDH 2019

Modul 5

O

PTIMALISASI MELALUI LINEAR

PROGRAMMING

Kompetensi yang ditawarkan:

Setelah membaca Modul ini, diharapkan mahasiswa dapat memahami dan memiliki kompetensi dasar tentang aplikasi linear programming dalam kehutanan serta memeiliki sikap dan perilaku yang efisien dan efektif dalam kehidupan keseharian.

Rencana perkuliahan untuk pertemuan 10 dan 11:

Rencana Perkuliahan 2 x 120 menit Aktivitas Pertemuan 7 Langkah 1 10 menit

Aktivitas: menjelaskan kompetensi yang akan dicapai dan menyepakati perubahan yang diperlukan sesua hasil refleksi pembelajaran.

1. Menjelaskan hasil dan rekomendasi refleksi pembelajaran yang telah dilaksanakan; 2. Mereview materi modul 1dan hubungannya dengan modul 2.

Langkah 2 90 menit

Aktivitas: memahami hutan sebagai modal untuk berinvestasi.

1. Mahasiswa dibagi kedalam dua kelompok diskusi, yaitu kelompok Konsep LP dan Kelompok Metode Grafis;

2. Masing-masing kelompok membaca dengan cepat modul, terutama bagian yang menjadi tanggung jawab mereka;

3. Dosen menfasilitasi diskusi. Langkah 3

20 menit

Aktivitas: membuat rangkuman hasil diskusi. Pertemuan 9

Langkah 1 100 menit

Aktivitas: menjelaskan Metode Siplex.

Kedua kelompok mempelajari materi yang sama tentang Metode Simplex lalu berdiskusi. Langkah 2

10 menit

Aktivitas: membuat rangkuman.

Semua kelompok secara bersama-sama membuat rankuman. Langkah 3

10 menit

Aktivitas: refleksi pembelajaran.

Mahasiswa secara bersama sama mengisi kusioner refleksi yang tersedia kemudian merumuskan rekomendasi perbaikan proses pembelajaran berikutnya.

A. Konsep dan Pengertian

Modul ini akan menjelaskan berbagai contoh sederhana tentang bagaimana persoalan-persoalan optimalisasi melalui formulasi model matematika yang disebut Program Linear atau

Linear Programming. Linear Programming merupakan teknik optimasi yang sangat umum

yang dapat diaplikasikan dalam banyak hal/permasalahan, yang beberapa di antaranya tidak ada hubungannya dengan kehutanan atau bahkan dengan ilmu menejemen.

(2)

Pemrograman Garis Luru adalah nama lain dari Linear Programming sehingga kita sering mendapatkan kedua istiah tersebut pada berbagai sumber yang berbeda namun untuk memudahkan sering disingkat LP yang berasal dari istilah aslinya, yaitu Linear Programming. Linear Programming (LP) adalah suatu metode pemrograman dimana variabelnya disusun dengan persamaan linear. LP merupakan alat kuantitatif untuk melakukan pemrograman yang memiliki kelebihan dan kelemahan sehingga dalam penggunaannya perlu dikenali agar supaya kita mampu mengidentifikasi kapan seharusnya kita menggunakan LP dan kapan tidak. Untuk itu dipergunakan pemahaman ilmu pengetahuan pendukungnya, seperti metode penelitian sosial-ekonomi, ekonomi produksi, dan lain sebagainya.

Metode Linear Programming banyak dipakai oleh berbagai kalangan baik peneliti maupun mahasiswa sejak beberapa tahun terakhir ini, bahkan oleh pengembang dan juga konsultan. Mereka menggunakan cara ini tentu saja didasarkan pada kelebihan-kelebihan yang dimiliki oleh LP. Begitu pula aplikasinya dalam bidang kehutanan serta bidang lainnya seperti pertanian, pengairan, transportasi, kesehatan, menejemen produksi, program transmigrasi, perencanaan pembangunan dan sebagainya, maka cara LP sudah banyak digunakan. Kecenderungan berbagai kalangan menggunakan LP karena metode ini memiliki paling tidak tiga kelebihan yaitu: (1) mudah dilaksanakan, apalagi kalau menggunakan alat bantu komputer; (2) dapat menggunakan banyak variabel, sehingga berbagai kemungkinan untuk memperoleh pemanfaatan sumber daya yang optimum dapat dicapai; dan (3) Fungsi tujuan

(objective function) dapat difleksibelkan sesuai dengan tujuan penelitian atau berdasarkan

data yang tersedia. Misalnya bila ingin meminimumkan biaya atau memaksimumkan keuntungan dengan data yang terbatas.

Kelemahan menggunakan LP adalah bila alat bantu komputer tidak tersedia, maka metode LP dengan menggunakan banyak variabel akan menyulitkan dalam melakukan proses analisis dan bahkan tidak mungkin dikerjakan dengan cara manual saja. Penggunaan variabel yang sedikit jumlahnya, yaitu sekitar enam variabel, maka LP dapat digunakan secara manual dengan bantuan cara perhitungan Simplex, yaitu suatu cara penyelesaian dengan melakukan iterasi berbagai variabel untuk memenuhi cara yang dikenal dengan istilah Simplex. Metode Simplex adalah sebuah prosedur aljabar yang dapat menyelesaikan persoalan-persoalan dengan ribuan variable dan konstrain atau kendala.

LP itu sendiri sebenarnya merupakan metode perhitungan untuk perencanaan terbaik sehubungan dengan kemungkinan-kemungkinan tindakan yang dapat dilakukan. Penentuan rencana terbaik tersebut dari tersedianya banyak alternatif dalam perencanaan untuk mencapai tujuan spesifik pada suatu keadaan sumber daya yang terbatas. Kondisi seperti ini banyak

(3)

dijumpai dalam kehutanan dan perkebunan serta pertanian dalam arti luas. Wanatani yang dikelola oleh individu atau rumah tangga atau pada tinggkat masyarakat desa dapat saja selalu berhadapan dengan keterbatasan sumber daya yang tersedia. Kondisi tersebut antara lain berbentuk: lahan yang keseluruhannya atau sebagiannya memiliki tipe yang berbeda, penggunaan tenaga kerja keluarga yang berbeda setiap bulan atau setiap tahun, keterbatasan dana yang tersedia untuk kegiatan usaha, bangunan-bangunan khusus yang penggunaannya untuk kepentingan yang berbeda-beda, traktor atau kapasitas mesin dan sumber daya fisik lainnya yang berbeda-beda, dan sebagainya.

Sebagai contoh misalnya, seorang keluarga kehutanan (petani hutan) selalu mempunyai alternatif dan cara yang berbeda-beda untuk merumuskan perencanaan, misalnya perbedaan dalam memanfaatkan sumber daya yang terbatas sebagai retriksi dalam mencapai keuntungan atau profit. Hal ini banyak dijumpai pada keluarga kehutanan yang mengusahakan lahan dan sumber daya lain yang terbatas untuk mengembangkan usahanya, misalnya menanam pohon, rumput, sayur-mayur; atau keluarga kehutanan yang terbatas dalam melayani pemberian pakan, pupuk, menyediakan tenaga kerja dan modal untuk menumbuhkan tanaman dan menggemukkan ternaknya. Khusus keluarga kehutanan yang mengusahakan satu cabang usaha tani, maka ia mempunyai berbagai alternatif untuk memakai sumber daya terbatas tersebut guna mencapai tujuan dalam memaksimumkan keuntungannya. Misalnya, andaikan keluarga kehutanan tersebut memproduksi jagung di kebun hutan dalam musim tanam yang biasanya dilakukan dengan sistem multiple cropping dengan tanaman lainnya; maka akan ditemukan sebidang tanah atau lahan dengan lebih dari satu tanaman. Cara seperti ini merupakan alternatif persaingan pemakaian lahan dalam waktu yang bersamaan dan keluarga kehutanan dihadapkan pada pilihan single cropping atau multiple cropping. Demikian juga varietas jagung yang berlainan akan mampu bersaing pada suatu usahatani dalam jangka waktu yang sama, misalnya dengan teknik pemupukan yang berlainan atau waktu panen yang berbeda merupakan alternatif bersaing dari keunggulan varietas tersebut.

Umumnya seorang keluarga kehutanan bertujuan memaksimumkan keuntungan (profit) atau memaksimumkan total penerimaan usahatani dalam jangka waktu yang tepat dan singkat. Keuntungan maksimum bisa juga untuk periode dimana rencana tunggal dibuat, atau untuk beberapa tahun yang merupakan penggabungan dari rencana-rencana terpisah. Tujuan penggabungan dari rencana-rencana terpisah ini adalah dapat dipakai sebagai salah satu cara untuk memperoleh penerimaan maksimum selama beberapa tahun atau menggunakan investasi yang minimum untuk mencapai penerimaan atau keuntungan yang maksimum yang disebabkan oleh tingkat pendapatan keluarga pada jumlah tertentu atau keuntungan

(4)

maksimum dengan pemakaian kendala yang terbatas dapat dihitung melalui teknik Linear Programming. Setiap usaha tani kehutanan, terdapat rencana untuk meminimalkan biaya kegiatan dan untuk itu mungkin terdapat kendala yang menggambarkan tingkat minimum dari biaya yang dikeluarkan untuk melakukan kegiatan usaha tersebut. Dengan demikian, maka LP dapat digunakan melalui dua cara, yaitu:

1. Meminimumkan biaya dalam rangka tetap mendapatkan total penerimaan atau total keuntungan sebesar mungkin. Selanjutnya cara seperti ini dikenal dengan istilah program ”minimisasi”.

2. Memaksimumkan total penerimaan atau total keuntungan pada kendala sumber daya yang terbatas. Selanjutnya disebut dengan istilah program “memaksimumkan”.

Kedua cara tersebut hasilnya relatif sama. Penggunaan salah satu dari cara tersebut dilakukan karena tersedianya data yang berbeda. Hal ini dapat terjadi karena data yang digunakan di LP ini dapat berupa data yang dikumpulkan sendiri (data primer), sehingga peneliti yang bersangkutan dapat menggunakan program LP sesuai dengan kehendaknya; dan data sekunder.

Dengan penjelasan di atas, maka bila seseorang akan menggunakan teknik LP untuk perencanaan usaha tani hutannya atau pengusaha HPH/HPHTI maka diperlukan pemahaman tentang:

1. Bagaimana keuntungan dapat dimaksimalkan dengan cara meningkatkan total penerimaan pada kondisi biaya usahatani yang relatif konstan. Jadi, bila:

Π = TP - TB dimana: Π = total keuntungan

TP = total penerimaan, dan TB = total biaya;

Maka Π akan naik bila TP naik dan kondisi TB relatif konstan. Karena TP dibentuk dari hasil perkalian antara produksi pertanian dan harga jual, maka tindakan yang dilakukan untuk meningkatkan keuntungan adalah dengan cara antara lain melalui pelaksanaan silvikultur moderen, yaitu dengan melakukan kegiatan pemeliharaan yang baik.

2. Bagaimana keuntungan dapat dimaksimumkan dengan cara menekan biaya produksi. Artinya keuntungan akan meningkat kalau total penerimaan relatif

(5)

konstan dan total biaya dapat ditekan. Caranya adalah dengan melaksanakan tindakan efisiensi penggunaan sarana produksi dan tenaga kerja. Bila penggunaan sarana produksi dan tenaga kerja dapat dilakukan secara efisien berarti besarnya TB dapat ditekan pada kondisi TP yang relatif konstan, maka keuntungan akan meningkat.

Dalam bidang sosial ekonomi dikenal tiga karakteristik pemilihan dan penentuan beberapa variable yang akan dipakai pada cara LP, yaitu: (1) berkaitan dengan tujuan yang ingin dicapai; (2) adanya sumber daya yang terbatas; (3) adanya persaingan untuk menggunakan sumber daya dalam pencapaian tujuan tersebut.

Apabila ketiga karakteristik tersebut dapat dikuantitatifkan dalam penggunaan persamaan matematis, maka perhitungan rencana optimasi dapat dilakukan dengan teknik LP secara mudah. Cara LP ini merupakan salah satu dari beberapa cara yang ada dan yang dikenal sebagai bagian program matematik. Berbagai program matematik yang lain adalah goal

programming, recursive programming, dynamic programming, quadratic programming, dan

sebagainya.

B. Problem dalam Linear Programming

Problem dalam Linear Programming adalah memperhatikan penggunaan atau alokasi yang efisien dari sumber daya-sumber daya yang terbatas untuk mencapai tujuan yang dinginkan. Problem ini dicirikan oleh sejumlah solusi untuk memenuhi kondisi-kondisi dasar dari setiap problem. Pemilihan suatu solusi yang diutamakan meliputi pemecahan terbaik untuk suatu problem yang terikat pada beberapa tujuan atau untuk semua tujuan, yang dinyatakan secara tidak langsung di dalam statement dari problem tersebut. Suatu solusi yang memuaskan semua kondisi problem dari tujuan yang telah ditetapkan dinamakan solusi optimum. Misalnya, dari suatu perusahaan yang akan mendeterminasi bentuk kombinasi dari sumber daya yang dimiliki untuk kemungkinan menghasilkan produk dalam suatu cara di mana tidak hanya memenuhi rencana produk tetapi juga memaksimumkan profit. Problem ini mempunyai kondisi dasar atas ketersediaan sumber daya yang terbatas dan persyaratan rencana produksi, serta sebagai tujuan yang diinginkan oleh perusahaan untuk memaksimumkan keuntungan.

Pernyataan di atas dapat dituliskan secara sederhana dengan bantuan persamaan matematis sebagai berikut (memaksimumkan atau meminimumkan):

Fungsi tujuan: Z = c1 x1 + c2x2 + ... + cn xn

(6)

Modul 5 ESDH 2019 Fungsi kendala a11 x11 + a21 x21 + …….. + an1 xn1 ≥ b1 a12 x12 + a22 x22 + ……… + an2 xn2 ≥ b2 . . . . . . . . . . . . a1mx1m+ a2mx2m + ………+ anm xnm ≥ bm Asumsi: x1 , x2 , ………, xn ≥ 0

Berdasarkan rumusan pernyataan tersebut di atas, maka dapat disimpulkan tiga hal sebagai berikut:

1. Bahwa dalam LP harus ada fungsi tujuan yang dinyatakan dengan persamaan garis lurus fungsi Z atau f(Z) yaitu sesuatu yang dimaksimumkan atau diminimumkan; c adalah cost coefisien dan X adalah aktivitas.

2. Dalam LP harus ada kendala yang dinyatakan dengan persamaan garis lurus; dimana a = koefisien input output, dan b = jumlah sumber daya yang tersedia.

3. Bahwa semua nilai X adalah positif atau sama dengan nol. Atau dengan kata lain, tidak boleh ada nilai X yang negatif. Dengan demikian, maka besarnya nilai koefisien input-output tidak boleh negatif.

Sebagian besar penjelasan di dalam buku ini hanya menghususkan pada sebagian problem-problem programming yang disebut problem LP. Problem LP dapat dirumuskan dengan bantuan model matematika; atau dengan kata lain, diskripsi problem LP dapat ditetapkan dengan menggunakan hubungan yang disebut straight line atau linear. Secara matematis hubungan ini dapat ditunjukkan dalam bentuk:

a1 x1 + a2 x2 + …….. + aj xj + ……… + an xn≤ bj

dimana aj dan bj merupakan koefisien yang diketahui;

a = koefisien input-output dan b = jumlah sumber daya yang tersedia; dan xj merupakan

variable yang idak diketahui.

(7)

Pernyataan matematis lengkap dari problem LP meliputi suatu set persamaan linear yang simultan, dimana persamaan ini mewakili kondisi problem yang telah ditetapkan dan sekaligus dapat menggambarkan tujuan problem tersebut.

Untuk memecahkan suatu problem LP, pertama-tama yang perlu diperhatikan ialah solusi dari kumpulan set persamaan linear. Ada bermacam-macam kriteria yang dapat diterapkan pada suatu set persamaan linear untuk mengungkapkan suatu solusi. Misalnya saja suatu set terdiri dari dua persamaan dari dua variable;

2x1 + 3x2 = 8 …………..(Persamaan 1)

x1 + 1,5x2 = 4 …………..(Persamaan 2)

Solusi dari dua persamaan tersebut adalah sebagai berikut: Persamaan 1 dapat dituliskan sebagai berikut:

2x1 = 8 – 3x2 atau

x1 = 4 – 1,5x2

Kalau x1 ini dimasukkan kedalam Persamaan 2, maka:

(4 – 1,5x2 ) + 2 x2 = 5

0,5 x2 = 1

x2 = 2

Kalau x2 tersebut dimasukkan ke Persamaan 1, maka:

2x1 + 3(2) = 8

X1 = 1

Penyelesaian Persamaan 1 dan Persamaan 2 mempunyai solusi yang unik, yaitu x1 = 1 dan

x2 = 2. Sebaliknya pada persamaan tunggal, misalnya

x1 + 2x2 = 8 ;

(8)

maka solusi persamaan tersebut adalah mempunyai jumlah solusi yang infinite, yaitu:

x1 = 8 – 2x2 ; atau

x2 = 4 – 0,5x1

Untuk setiap nilai x2 (atau x1 ) merupakan nilai yang cocok dari x1 (atau x2 ). Jika lebih

lanjut kita membatasi pada variable yang non negatif, dimana x1 ≥ 0 dan x2 ≥ 0, dan kita

membatasi range dari variable x1 dan x2 , maka hal tersebut dapat dituliskan sebagai berikut:

x1 = 8 – 2x2 ≥ 0 sehingga 0 ≤ x2 < 4 ……..(Persamaan 3)

x2 = 4 – 1/2x1≥ 0 seingga 0 ≤ x1 < 8 …...(Persamaan 4)

Tampak dalam penyelesaian solusi di atas bahwa sejumlah solusi yang infinite pada Persamaan 3 dan 4, tetapi penambahan restriksi dengan cara membuat range maka kendala dari Persamaan 3 dan 4 mengakibatkan kurangnya kebebasan untuk memilih berapa besarnya x1 dan x2 . Seperti yang telah ditunjukkan sebelumnya, terlihat bahwa kondisi non negatif

dari variabel x merupakan syarat penting dari problem LP. Sistem seperti persamaan yang tidak dapat dideterminasi (undertermined). Pada umumnya undertermined system dari persamaan dua linear salah satunya tidak mempunyai solusi; sehingga dapat dikatakan bahwa solusinya adalah infinite.

Satu cara penting untuk mendeterminasi solusi dalam persamaan yang undertermined

system adalah dengan mereduksi sistem kedalam suatu set yang hanya mengandung beberapa

variabel dalam persamaan yakni suatu set yang dideterminasi. Ini dapat diselesaikan dengan melepaskan variabel tertentu dalam keadaan yang sama dengan nol.

Contoh undertermined system dari tiga variabel yang tidak diketahui pada dua persamaan:

2x1 + 3x2 + x3 = 8 ... (Persamaan 5)

x1 + 2x2 + 2x3 = 5

(9)

Persamaan di atas mempunyai tiga solusi, yaitu:

Bila x1 = 0 , maka 3x2 + x3 = 8 atau

x3 = 8 – 3x2 ; dan 2x2 + 2x3 = 5 ; dan

x3 = 2,5 - x2

Dengan mempersamakan nilai x3 , maka:

8 – 3x2 = 2,5 - x2

2x2 = 5,5

x2 = 11/4

Dengan demikian x3 = 8 – 3(11/4)

= -1/4

Begitu pula bila x2 = 0 dan x3 = 0; maka hasil hitungannya adalah sebagai berikut:

x1 = 0 ; x2 = 11/4 ; x3 = -1/4 ...(Persamaan 6)

x1 = 11/3 ; x2 = 0 ; dan x3 = 2/3

x1 = 1 ; x2 = 2 ; x3 = 0

Secara matematis, LP mempersoalkan solusi-solusi yang non negatif untuk sistem-sistem yang undertermined dari persamaan-persamaan linear. Kalau saja diteliti lebih lanjut, maka solusi-solusi yang dapat dipakai untuk mendeterminasi subset-subset dari persamaan-persamaan di atas adalah dengan cara mengandalkan salah satu dari nilai variabel x = 0; dan hasilnya diperoleh bilangan yang tidak negatif. Sebagai contoh, jika Persamaan 5 mewakili kondisi-kondisi dari suatu problem LP, maka ditemukan dua solusi non-negatif sebagai berikut:

x1 = 1 ; x2 = 2 ; x3 =0

dan

x1 = 11/3 ; x2 = 0 ; x3 = 2/3

dimana solusi-solusi yang sisa, tidak memenuhi syarat non negatif, sehingga dikeluarkan dari model.

(10)

Sebagaimana umumnya, problem LP mempunyai beberapa tujuan sebagai penuntun untuk seleksi solusi yang digunakan. Problem LP mempunyai suatu fungsi linear dari variable-variabel tertentu untuk menolong memilihkan solusi terhadap problem yang telah ditetapkan. Kombinasi variable-variabel dalam bentuk linear tersebut dinamakan objective function (fungsi tujuan) yang harus dimaksimumkan atau diminimumkan.

Dengan ditambahnya kondisi untuk memaksimumkan atau meminimumkan objective

function, maka dapat dipilih solusi tunggal yang memenuhi semua kondisi suatu problem.

Mungkin akan ada solusi berganda yang lebih dari satu solusi non negatif di dalam persamaan yang memberikan nilai optimum yang sama pada objective function. Pada umumnya kombinasi constraint (pembatas/kendala) yang linear dari problem LP dalam mengoptimasikan objective function secara linear, dapat melalui undertermined system dari persamaan-persamaan linear.

Berikut akan diberikan pernyataan atau statement matematis secara umum dari problem LP.

o Minimumkan atau maksimumkan objective function

c1 x1 + c2 x2 + ... + cj xj + ... + cn xn ...(P ersamaan 7)

o Fungsi kendala (pembatas)

a11 x11 + a12 x12 + ... + aij xij + ……+ a1n x1n ≥ b1 a21 x21 + a22 x22 + …….+ a2jx2 j+ ……+ a2n x2n ≥ b2 . . . . . . . . . . ai1 xi1 + ai2 xi2 + …...+ aij x ij + ...+ ain xin ≥ bi . . . . . . . . . . a m1 x m1 + a m2 x m2 + ….+ a mj x mj + …..+ a mn x mn ≥ b m o Dengan syarat: x 1 ≥ 0 x 2 ≥ 0 . . 115 | P a g e

(11)

Modul 5 ESDH 2019 . . . . x j ≥ 0 . . . . x n ≥ 0;

dimana c j ke j = 1 , 2 , ………., n (cost coefficients);

b i ke I = 1 , 2 , ………, m (sumber daya yang tersedia)

dan semua a ij adalah constant (koefisien input-output), dan m < n.

Setiap problem LP mempunyai cirri-ciri:

1. Solusi optimum tidak akan terjadi, bila didapatkan hubungan dengan nilai-nilai negatif dari variable x dan

2. Suatu solusi non negatif menghasilkan nilai finite pada objective function; Berdasarkan pada problematika seperti diuraikan di atas, maka dapat disimpulkan bahwa penyelesaian liniar programming (LP) diperlukan asumsi-asumsi tertentu yang harus dipenuhi. Asumsi tersebut adalah konsekuensi dari limitasi (keterbatasan) LP dibandingkan dengan model programming yang lain.

Asumsi yang harus dipenuhi oleh LP adalah:

a. Kalau vektor x = (x 1 , x 2 , ... , x n ) bernilai positif dan faktor pembatas Ax = b

juga bernilai positif, maka pemecahan problem LP (feasible solution) dapat diperoleh. Jadi bila:

1) Problem meminimumkan, maka minimumkan:

Dengan faktor pembatas:

∑

= n 1 j aij xij ≥ bi (i = 1 , 2 , ... , m) (j = 1 , 2 , ..., n) dan x1 ... i …..j ≥ 0 ;

maka feasible solution dapat diperoleh.

∑

= = n 1 j j j j cx Z 116 | P a g e

(12)

2) Problem memaksimumkan, maka

Maksimumkan

∑

= = n 1 j j j j cx Z

dengan faktor pembatas :

∑

= n 1 j aij xij ≤ bi (1 = 1 , 2 , ... , m) ( j = 1 , 2 , ..., n) dan xj...i...j ≥ 0

b. Program LP dapat diselesaikan dengan baik kalau koefisien aij tidak bernilai negatif;

atau dengan kata lain semua koefisien adalah positif.

c. Semua faktor pembatas merupakan fungsi linear atau F(X) = linear function atau aij

xij = b1 adalah fungsi linear.

d. Dengan demikian, maka fungsi tujuannya juga merupakan fungsi linear. Jadi: cj xj =

F(X) = fungsi linear.

C. Sistem Model Grafis dan Matematis

Dalam pengelolaan hutan, menejer menggunakan model sebagai alat bantu dalam pengambilan keputusan. Model merupakan representasi abstrak dari dunia nyata yang sangat berguna dalam proses berfikir, meramal, dan pengambilan keputusan. Model dapat bersifat sangat tidak formal, sangat bersifat intuisi yang didukung oleh pengalaman dan informasi yang disusun secara bersama-sama sehingga memperlihatkan satu kesatuan yang sistimatis. Namun demikian dalam konteks proses berfikir tentang suatu persoalan pengelolaan hutan, merenungkan dan mempertimbangkan berbagai alternatif, dan kemudian mencapai tujuan, seseorang seharusnya menggunakan model yang merupakan sesuatu yang sangat abstrak mempresentasikan bagaimana sebenarnya atau kenyataannya persoalan yang tengah dihadapi. Kebanyakan keputusan dibuat dengan cara model informal seperti ini. Hasil yang dicapai dapat sangat baik, terutama bila menejernya adalah seorang yang cerdas, berpengalaman, dan proses ini bersifat unik bagi setiap individu dan biasanya sulit untuk dipelajari.

(13)

Sebenarnya dalam pengelolaan hutan penggunaan model yang bersifat lebih konkrit telah lama dikenal, bahkan model ini ada yang secara fisik sangat serupa dengan apa yang direpresentasikannya. Sebagai contoh, ahli hidrologi hutan dapat menggunakan model pasir dan air untuk sebuah daerah aliran sungai dimana perbedaannya dengan daerah aliran sungai yang diwakilinya hanya terletak kepada skala. Dengan kata lain model dan pasir tersebut merupakan miniatur dari suatu daerah aliran sungai tertentu. Aliran air dapat dibuat dengan berbagai kecepatan yang berbeda untuk mensimulasikan variasi curah hujan dan banjir. Tentunya laju erosi juga dapat diukur dan berbagai sistem irigasi dan bendungan dapat diuji dengan menggunakan model atau miniatur daerah aliran sungai tersebut.

Peta suatu kawasan hutan merupakan contoh model yang lebih abstrak. Sangat sedikit hubungan yang menjelaskan secara fisik antara peta dengan kawasan hutan yang diwakilinya. Namun demikian peta merupakan sesuatu yang penting bagi aktivitas dalam pengelolaan hutan. Sedikit keputusan yang dapat diambil tanpa menggunakan peta.

Linear Programming menggunakan model matematik yang lebih abstrak dari peta. Pada model matematik tidak ada analogi visual yang terlihat antara dunia nyata dengan model. Dunia nyata direpresentasikan berupa simbol-simbol dan variable-variabel serta dengan menggunakan metode aljabar, dapat dijelaskan hubungan-hubungan antara simbol-simbol dan variabel-variabel tersebut.

Model matematik bukan merupakan sesuatu yang baru dalam disiplin ilmu kehutanan. Hubungan biometrik antara volume tegakan per hektar dengan jenis-jenis pepohonannya, umur, dan kondisi tempat tumbuh sudah lama diekspresikan dalam bentuk tabel dan fungsi matematika. Ekonom kehutanan mengembangkan rumus untuk menghitung nilai lahan hutan dalam bentuk produksi yang diharapkan, nilai pasar output yang dapat dihasilkan, ongkos manajemen, dan bunga uang dimana kesemuanya itu merupakan model investasi yang merupakan hal yang sangat mendasar dalam pengambilan keputusan dalam kehutanan.

Persoalan-persoalan yang muncul dalam pengelolaan hutan melibatkan berbagai variable. Diantaranya ada yang bersifat biologis seperti variable tentang potensi pertumbuhan tegakan dari kombinasi kondisi tanah dengan spesies pohon; dan diantaranya yang lain bersifat ekonomi seperti harga kayu dan ongkos tenaga kerja; serta yang lainnya lagi dapat bersifat sosial seperti hukum-hukum lingkungan yang dapat mengatur dan menentukan jenis perlakuan-perlakuan yang memungkinkan pada pengelolaan hutan. Yang penting untuk difahami bahwa sering variable-variabel tersebut saling berhubungan sehingga perubahan nilai salah satu variable akan mempengaruhi variable lainnya.

(14)

Semua variable-variabel tersebut serta hubungan-hubungannya membentuk sebuah sistem. Oleh karena sistem kehutanan merupakan sistem yang kompleks, maka meramalkan konsekuensi-konsekuensi yang dapat muncul dari suatu keputusan yang sudah dibuat merupakan pekerjaan yang tidak mudah. Sebagai contoh, untuk menjawab tingginya permintaan kayu, menejer kehutanan suatu perusahaan Hak Pengusahaan Hutan dapat berfikir bahwa perlu meningkatkan volume kayu yang akan ditebang. Tetapi peraturan perundang-undangan (mungkin) mengatakan bahwa aliran produksi kayu tidak boleh menurun. Sehingga yang perlu difikirkan adalah apakah keputusan untuk meningkatkan volume kayu yang akan ditebang pada tahun berjalan tetap diputuskan dengan resiko akan terjadi penurunan jatah tebang pada masa yang akan datang? Persoalan ini banyak diacukan dalam pengelolaan hutan sistem HPH di Indonesia sehingga tidak sedikit perusahaan HPH yang tidak dapat beroperasi hingga akhir masa konsesi yang diberikan oleh pemerintah kepadanya.

Dalam situasi seperti di atas, model dapat membantu menejer dalam memprediksi konsekuensi-konsikuensi keputusan mereka. Dengan suatu pemahaman bahwa sebuah model merupakan suatu instrumen yang dapat membawa dunia nyata ke dalam laboratorium atau ke dalam ruang kerja kantor. Menejer dapat melakukan percobaan-percobaan yang sulit bahkan tidak mungkin dilakukan pada dunia nyata. Sebagai contoh, seorang menejer dapat mencoba berbagai macam bentuk penebangan melalui suatu model hutan dan mengamati konsekuensi-konsekuensi yang ditimbulkan oleh setiap bentuk penebangan tersebut yang tidak mungkin dilakukan pada hutan yang sebenarnya.

Penggunaan model sistem dan metode penyelesaian masalah seperti itu dikembangkan pertama kali dalam Perang Dunia II untuk membantu operasi militer. Perkembangan disiplin ilmu ini lebih dikenal sebagai “riset operasi“ dan setelah Perang Dunia II, metode riset operasi mulai diaplikasikan dengan sangat berhasil dibidang, industri, pertanian, dan pemerintahan.

The Operation Society of America dan the Institute of Management Science dibentuk waktu

itu, dan universitas universitas mengembangkan jurusan akademis atau departemen yang secara khusus mempelajari dan mengembangkan metode riset operasi. Aplikasi riset operasi di bidang pengelolaan hutan pertama kali pada awal tahun 1960-an. Bahkan dewasa ini the

Society of American Foresters memiliki kelompok kerja di bidang riset operasi, yang juga

diikuti oleh berbagai Institut Ilmu Menejemen untuk membentuk kelompok kerja serupa dalam aplikasinya terhadap bidang kehutanan.

Model yang paling baik adalah model yang paling sederhana, memberikan pertanyaan-pertanyaan yang harus dijawab. Terdapat tiga element suatu pengembangan model, yaitu: pendefinisian masalah, membangun model, dan implementasi model. Kendatipun dalam

(15)

penjelasan nantinya kita akan banyak membicarakan bagaimana membangun model, tetapi dua elemen lainnya merupakan elemen-elemen penting dalam keberhasilan pengembangan model. Terdapat hubungan yang sangat erat antara tahapan mendefinisikan persoalan, membangun model, dan implementasi model. Bagaimana jenis model yang dapat dibangun dipengaruhi oleh beberapa hal yang berhubungan dengan bagaimana persoalan didefinisikan, dan seterusnya juga berhubungan dengan bagaimana model tersebut diimplementasikan.

D. Penyelesaian Model Linear dengan Cara Grafis

Bentuk grafis model linear berbeda berdasarkan apakah model tersebut dirancang untuk model memaksimumkan atau meminimumkan. Secara sepintas kedua penyelesaian model linear yang “memaksimumkan” berbentuk cekung menghadap ke atas dan model linear yang “meminimumkan” berbentuk cembung menghadap ke atas. Suatu penyelesaian program LP apakah itu program memaksimumkan atau meminimumkan, tergantung dari kerangka teoritis dari problem-statement yang telah ditetapkan. Bila problemanya adalah efisiensi penggunaan biaya, maka problem LP-nya adalah problem meminimumkan biaya tersebut. Demikian pula sebaliknya bila problemanya adalah bagaimana memaksimumkan total penerimaan penjualan kayu, maka problema LP tersebut adalah problem memaksimumkan.

1. Model Linear Memaksimumkan

Seperti telah dijelaskan pada bagian awal, fungsi tujuan atau objective function yang dimaksimumkan dapat berupa:

a. Keuntungan kotor (gross-margin) b. Keuntungan bersih (net-margin)

c. Total penerimaan kotor (gross-total-revenue) atau d. Total penerimaan bersih (net-total revenue)

Dalam kaitannya dengan penyelesaian secara grafis, maka bentuk standar dari LP dituliskan dalam tiga persyaratan, yaitu:

a. ada fungsi tujuan b. ada fungsi kendala, dan c. ada asumsi bahwa xij≥ 0

Perlu diasumsikan pula bahwa fungsi tujuan dan fungsi kendala harus dituliskan dalam bentuk persamaan linear.

Dengan demikian, aplikasi LP dalam program “memaksimumkan“ dapat dituliskan sebagai berikut:

(16)

Modul 5 ESDH 2019 a. Fungsi tujuan: Maksimumkan Z= 3x1 + 2x2 b. Faktor kendala 2x1 + x2≤ 60 …………..(1) x1 + x2 ≤ 35 ...(2) c. Dengan syarat x1 , x2 ≥ 0

Tahapan penyelesaian yang harus dikerjakan adalah sebagai berikut:

1). Periksa kembali bentuk rumus matematis yang telah ditetapkan. Telitilah apakah penulisan rumus matematis sesuai dengan problem statement yang ada;

2). Periksa kembali tanda-tanda koefisien yang ada (apakah itu berupa cost coeficients atau input-output coefficients), apakah nilainya sudah positif;

3). Periksa kembali tanda di faktor pembatas; misalnya program memaksimumkan adalah ≤ dan program meminimumkan adalah ≥ .

4). Selanjutnya, gambarlah bentuk dua dimensi, x1 dan x2. Tetapkan sumbu tegak x1 dan

sumbu datar x2 , atau sebaliknya.

5). Tariklah garis fungsi tujuan dan faktor pembatas. Ingat, agar dapat digambar dengan mudah, maka persamaan pada faktor pembatas berlaku azas equality, artinya bentuk ≥ dan ≤ diganti dengan bentuk persamaan (=). Misalnya:

x1 + x2 ≤ 35 ; dapat diganti dengan

x1 + x2 = 35

Berdasarkan uraian di atas, maka penyelesaian dengan cara grafik dapat diselesaikan sebagai berikut:

1). Pada Persamaan (1), pada faktor pembatas dapat dihitung: bila x1 = 0 , maka x2 = 60; dan

bila x2 = 0 , maka x1 = 30

2). Pada persamaan (2), pada faktor pembatas, juga dapat dihitung: bila x1 = 0 , maka x2 = 35 ; dan

bila x2 = 0 , maka x1 = 35

(17)

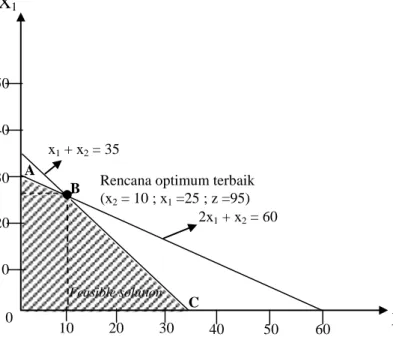
Gambar VI-1. Penyelesaian model LP cara grafis.

3). Konsekuensi dari 1) dan 2) dapat digambarkan seperti yang terlihat pada Gambar VI-1. Pada Gambar tersebut terlihat bahwa daerah yang memungkinkan untuk rencana optimum (tanda atsir) disebut feasible region. Sedangkan titik optimum berada di titik A, B dan C.

Masalahnya sekarang adalah bagaimana mencari nilai titik optimum di A , B dan C. Caranya dapat dijelaskan sebagai berikut:

1). Titik A berada di daerah feasible solution dan terletak di garis 2x1 + x2 = 60; dimana

pada saat x2 = 0, maka x1 = 30. Jadi rencana optimum di titik A adalah x1 = 30 dan

x2 = 0 ; dan pada kondisi seperti itu, maka: Z = 3 (30) + 2 (0) = 90. Jadi rencana

optimum di titik A adalah bila x1 = 30 , x2 = 0 dan Z = 90.

2). Titik B berada di daerah feasible region dan terletak di garis x1 + x2 = 35 dan 2x1 +

x2 = 60. Untuk mencari nilai x1 dan x2 , maka: x1 + x2 = 35; atau:

x1 = 35 – x2 2 x2 + x2 = 60; atau 2(35 – x2 ) x1 + x2 = 60 70 - 2 x2 + x2 = 60 x2 = 10 10 20 30 40 50 60 10 20 30 40 50 0 _X₂ X1 A B C 2x1 + x2 = 60 x1 + x2 = 35

Rencana optimum terbaik (x2 = 10 ; x1 =25 ; z =95)

Feasible solution

(18)

Kalau x2 = 10, maka x1 + 10 = 35

x1 = 25

Pada kondisi seperti itu, maka besarnya nilai Z adalah sama dengan 3(25) + 2(10) = 95. Jadi, rencana optimum di titik B adalah bila x1 = 25 ; x2 = 10 dan Z = 95.

3). Titik C berada di daerah feasible region dan berada di garis x1 + x2 = 35; dimana

pada x1 = 0, maka x2 = 35. Pada kondisi seperti itu, maka besarnya nilai z = 3(0) +

2(35) = 70. Jadi, rencana optimum di titik C adalah bila: x1 = 0 ; x2 = 35 dan Z = 70.

Berdasarkan perhitungan di atas, maka dapat dibandingkan nilai-nilai kombinasi x berapa yang mampu menghasilkan Z maksimum. Kesimpulan dari perhitungan di atas bahwa pada titik A, x1 = 30 dan x2 = 0, serta Z = 90. Pada titik B, x1 = 25 dan x2 = 10, serta Z = 95.

Sedangkan pada titik C, x1 = 0 dan x2 = 35, serta Z = 70. Dengan demikian dari perbandingan

nilai Z pada masing-masing titik maka dapat disimpulkan bawa titik B adalah titik paling optimum karena titik tersebut memberikan nilai Z yang paling tinggi.

2). Model Linear Meminimumkan

Sebagaimana yang telah dijelaskan sebelumnya, bahwa dalam program LP, yang dimaksud dengan “meminimumkan“ adalah meminimumkan total biaya. Artinya, bagaimana biaya yang digunakan dalam proses produksi dapat ditekan seminimum mungkin untuk mendapatkan produksi yang optimum.

Bila contoh yang dipakai dalam program LP “maksimisasi“ seperti yang dijelaskan, maka secara matematis, penyelesaian dengan cara meminimumkan ini dapat ditulis sebagai berikut:

a. Fungsi tujuan:

Minimumkan Z = 3x1 + 2x2

b. Faktor kendala : 2 x1 + x2 ≥ 60 ...(1)

x1 + x2 ≥ 35 ...(2)

c. Dengan syarat : x1 dan x2 ≥ 0

Tahapan penyelesaian program meminimumkan tidak berbeda dengan cara penyelesaian program memaksimumkan. Hanya saja terdapat perbedaan sedikit, yaitu terletak pada tanda ≥ atau ≤. Tanda ≥ pada faktor pembatas artinya penyelesaian secara minimisasi; sedangkan tanda ≤ artinya penyelesaian secara maksimisasi.

Mengikuti penyelesaian program LP seperti yang dijelaskan pada program maksimisasi, maka penyelesaian dengan minimisasi dapat diselesaikan dengan cara sebagai berikut:

(19)

1). Pada persamaan (1), maka

bila x1 = 0, maka x2 = 60 ; pada kondisi seperti ini, maka Z = 2 (0) + 1 (60) = 60 ,

dengan catatan berlaku kaidah equality yang artinya bahwa tanda ≥ identik dengan tanda = (lihat titik C).

2). Pada persamaan (2), maka bila x2 = 0, maka x1 = 35 ; dan pada kondisi seperti ini,

maka Z = 3 (0) + 2 (35) = 70 (lihat titik A).

3). Pada persamaan (1) dan (2) akan terjadi titik potong yang harus dicari berapa nilainya. Secara matematis, hal ini dapat diselesaikan sebagai berikut:

2 x1 + x2 = 60 ; atau

x2 = -2 x1 + 60

x1 + (-2 x1 + 60) = 35

x1 = 25 , dan

x2 = 10

Pada kondisi seperti ini maka besar nilai Z adalah sebagai berikut: Z = 3 (x1) + 2(x2)

= 3(25) + 2(10) = 95 (lihat titik B).

Perhitungan di atas menjelaskan bahwa pada titik A, nilai x1 = 35 dan x2 = 0 serta Z = 70.

Pada titik B diperoleh nilai x1 = 25 dan x2 = 10, serta Z = 95. Sedangkan pada titik C

diperoleh nilai x1 = 0 dan x2 = 60 serta nilai Z = 60. Dengan demikian titik yang paling

efisien adalah titik B dimana keuntungan yang diperoleh pada titik ini adalah tertinggi.

E. Contoh Aplikasi Metode Grafis dalam Kehutanan

Untuk menjelaskan penerapan metode grafis dalam kehutanan, bagian ini akan memberikan dua buah contoh. Contoh yang pertama akan membahas persoalan hipotesis seorang keluarga kehutanan yang memiliki hutan seluas 90 hektar. Contoh kedua mengenai aplikasi metode grafis dalam menejemen industri pulp.

1. Contoh Pertama:

a. Mendefinisikan Persoalan

Seorang petani kaya (keluarga kehutanan) yang juga seorang pengusaha menengah tertarik dengan program pemerintah tentang Hutan Rakyat (HR). Oleh karena itu ia ingin mencoba

(20)

mengelola lahan seluas 90 hektar dengan kondisi hutan yang baik dan produktif yang ia beli sepuluh tahun lalu. Ia juga membeli sebuah villa kecil beserta lahan (hutan) tersebut.

Sang petani kaya bukan saja ingin mengusahakan lahan hutan yang telah dibelinya sehingga dapat memberikan keuntungan finansial, tetapi ia juga ingin melakukan aktivitas rekreasi, misalnya berjalan-jalan di antara rimbunan pepohonan untuk menyegarkan fikiran dan inspirasinya. Tetapi pemikiran-pemikiran yang ia buat tidaklah membuatnya cukup puas untuk mencari solusi bagaimana seharusnya ia mengelola lahan miliknya. Yang jelas ia tidak ingin menghabiskan lebih dari setengah waktunya untuk mengelola hutan tersebut sebab ia juga memiliki aktivitas lainnya. Untunglah sang petani kaya tersebut pernah membaca buku tentang Linear Programming, yaitu buku tentang metode mengalokasikan sumber daya yang terbatas untuk mengoptimalkan tujuan-tujuan tertentu.

b. Data

Agar petani kaya dapat mengembangkan modelnya, ia terlebih dahulu merangkai semua informasi yang ia miliki dan butuhkan yang kurang lebih dapat dituliskan sebagai berikut:

Dari 90 hektar lahan hutan yang dimilikinya, terdapat seluas 40 hektar lahan yang dimilikinya ditumbuhi oleh tanaman pinus dan sisanya seluas 50 hektar merupakan hutan campuran, akasia dan jenis-jenis pohon lokal yang bernilai ekonomi. Berdasarkan catatan yang ia miliki, sejak ia membeli lahan sepuluh tahun lalu, ia telah menghabiskan waktu sebanyak 800 hari untuk mengelola hutan pinusnya dan 1500 hari untuk mengelola hutan campurannya.

Total pendapatan bersih yang ia peroleh selama itu adalah Rp 3,6 milyar dari hutan pinus dan Rp 6 milyar dari hutan campuran.

c. Menformulasikan Masalah

Untuk menformulasikan model yang akan dibangun, sang petani kaya harus menentukan variabel-variabel sebagai simbol dari keputusan-keputusan yang ia ambil. Memilih variabel merupakan tahapan yang sangat penting dalam membangun sebuah model. Namun demikian boleh dikatakan bahwa tidak ada metode tertentu tentang memilih variabel-variabel yang akan digunakan. Memilih model merupakan bagian dari seni membangun model yang hanya dapat dipelajari melalui praktek. Namun demikian sebuah tips yang berharga sehubungan dengan penentuan variable adalah sebaiknya petani kaya tersebut memperhatikan tujuan yang ingin

(21)

dicapainya. Sebab pemahaman terhadap tujuan yang ingin dicapai akan memberikan beberapa isyarat penting tentang variable-variabel yang akan ditentukan.

Dari penjelasan di atas dapat difahami bahwa tujuan sang petani adalah memaksimumkan perolehan (revenue). Untuk memudahkan dalam perhitungan, maka perolehan yang akan dihitung tersebut bersifat tertentu, yaitu memiliki satuan waktu yang jelas, misalnya per tahun. Maka dengan demikian selanjutnya tujuan tadi dapat dituliskan secara formal sebagai berikut:

Maksimumkan Z = rupiah perolehan bersih per tahun

Perolehan yang disimbolkan sebagai Z diperoleh dari hasil mengelola hutan pinus atau hutan campuran atau keduanya. Dengan demikian selanjutnya variable-variabel dapat dituliskan sebagai berikut:

x1 = luas hutan pinus yang dikelola (hektar)

x2 = luas hutan campuran yang dikelola (hektar).

Kemudian selanjutnya kita dapat menghitung nilai x1 dan x2 yang menjadikan Z bernilai

terbesar (maksimum).

Fungsi Tujuan:

Fungsi tujuan mengekspresikan hubungan antara Z, perolehan yang dahasilkan dari pengelolaan hutan, dengan variabel-variabel x1 dan x2 . Untuk menuliskan fungsi ini, kita

harus mengestimasi perolehan tahunan yang dihasilkan dari pengelolaan masing-masing tipe hutan. Dari hasil estimasi diketahui bahwa selama sepuluh tahun telah diperoleh Rp 3,6 milyar dari 40 hektar hutan pinus dan Rp 6 milyar dari 50 hektar hutan campuran. Sehingga dapat dihitung perolehan per hektar per tahun adalah Rp 9 juta per hektar per tahun dari hutan pinus dan Rp 12 juta per hektar per taun dari hutan campuran. Dengan menggunakan hasil perhitungan ini, maka selanjutnya dapat dihitung perolehan yang diharapkan oleh sang petani pada tahun-tahun yang akan datang. Untuk itu selanjutnya kita tuliskan fungsi tujuan sebagai berikut:

Max Z = 9 x1 + 12 x2

(Rp/thn) (Rp/ha/thn) (Rp/ha/thn)

Permodelan yang baik selalu mengecek homogenitas dari semua ekspresi aljabar dengan memperhatikan unit ukuran setiap variable. Pada contoh di atas, Z diekspresikan dalam satuan

(22)

rupiah per tahun. Dengan demikian komponen-komponen persamaan yang berada di sebelah kanan dari tanda sama dengan harus menghasilkan satuan rupiah per tahun.

Fungsi Kendala:

Kendala pada kasus petani di atas adalah masalah luas lahan hutan yang dikelola yang dapat ditulis sebagai berikut:

x1 ≤ 40 hektar hutan pinus, artinya petani hanya bisa mengelola hutan pinus tidak

lebih dari 40 hektar.

X2 ≤ 50 hektar hutan campuran, artinya petani hanya bisa mengelola hutan

campurannya tidak lebih dari 50 hektar.

Kendala ketiga yang dapat kita rumuskan berdasarkan informasi yang telah dikumpulkan sebelumnya adalah masalah alokasi waktu. Petani mengalokasikan waktunya untuk mengelola lahan hutan miliknya tidak lebih dari separuh waktu yang ia miliki. Jadi dalam setahun ia hanya bisa mengalokasikan waktunya maksimum 180 hari per tahun untuk mengelola hutan miliknya. Agar supaya kendala ini dapat ditulis dalam bentuk variable-variabel, terlebih dahulu kita catat bahwa selama sepuluh tahun, petani telah menggunakan waktunya sebanyak 800 hari untuk mengelola hutan pinus, atau rata-rata 2 hari per hektar per tahun. Demikian juga halnya dengan pengelolaan hutan campuran, dimana selama sepuluh tahun petani tersebut telah menghabiskan waktunya sebanyak 1500 hari untuk 50 hektar. Sehingga diperoleh bahwa rata-rata petani menggunakan waktunya selama 3 hari per hektar per tahun. Dengan demikian dalam konteks variable-variabel, total waktu yang digunakan oleh petani kaya tadi untuk mengelola hutan miliknya adalah:

2 x1 + 3 x2

(hari/ha/thn) (hari/ha/thn)

Dan pengekspresian kendala yang terbatas kepada ketersediaan waktu, yaitu 180 hari per tahun, maka dapat ditulis:

2 x1 + 3 x2 ≤ 180

(hr/thn) (hr/thn)

(23)

Perlu dijelaskan di sini bahwa waktu yang dibutuhkan untuk mengelola hutan campuran lebih banyak dibandingkan dengan waktu yang dibutuhkan untuk mengelola hutan pinus yang seragam karena hutan campuran terdiri atas berbagai jenis pohon sehingga beberapa pekerjaan, misalnya memberi tanda penjualan kayu, membutuhkan waktu yang lebih banyak. Demikian juga dari aspek silvikultur, hutan campuran yang terdiri berbagai jenis pohon-pohon akan memerlukan juga berbagai jenis teknik silvikultur sehingga pertumbuhan tegakan heterogen tersebut dapat maksimum. Namun demikian hutan campuran dapat menghasilkan perolehan yang lebih besar per hektar sebagaimana yang ditunjukkan oleh fungsi tujuan.

Kendala terakhir yang harus menyelesaikan formulasi persoalan menyatakan bahwa tidak ada variable bernilai negatif, sehingga:

x1 ≥ 0 dan x2≥ 0 Model yang Dihasilkan:

Sebagai ringkasan, dengan menggabungkan fungsi tujuan dan kendala, kita peroleh formulasi yang lengkap dari permasalahan yang dihadapi oleh sang petani, yaitu:

Max Z = 9 x1 + 12 x2

Dengan subjek kepada: x1 ≤ 40

x2 ≤ 50

2 x1 + 3 x2 ≤ 180

x1 , x2≥ 0

Wilayah yang Feasible:

Model yang dihasilkan di atas menunjukkan bahwa x1 adalah luas hutan pinus yang petani

seharusnya kelola dan x2 merupakan luas hutan campuran yang seharusnya dikelola. Tujuan

yang dirumuskan adalah menemukan nilai kedua variable tadi yang dapat memberikan nilai Z yang maksimum sebagai indikasi perolehan sang petani dalam mengelola lahan hutannya.

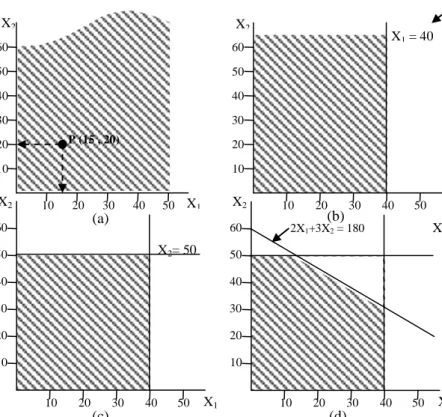
Oleh karena variable terdiri atas dua buah maka memungkinkan mempresentasikannya dalam bentuk grafik seperti pada Gambar VI-2. Gambar tersebut terdiri atas empat grafik,

(24)

yaitu Grafik a, Grafik b, Grafik c, dan Grafik d. Luas hutan pinus yang dikelola direpresentasikan oleh axis horisontal, dan luas hutan campuran yang dikelola direpresentasikan oleh axis vertikal. Setiap titik pada diagram tersebut merupakan representasi dari sebuah pilihan menejemen. Sebagai contoh, titik P pada Gambar VI-2a menjelaskan suatu keputusan untuk mengelola hutan pinus seluas 15 hektar dan mengelola hutan campuran seluas 20 hektar.

Gambar VI-2. Cara grafis menetukan wilayah feasibel.

Oleh karena x1 dan x2 tidak dapat bernilai negatif maka hanya wilayah yang diarsir pada

Gambar VI-2a memungkinkan sebagai wilayah yang dapat memberikan solusi yang feasibel. Bila kita memperhatikan kendala x1 ≤ 40 maka ini berarti bahwa sebuah titik feasible (x1 ,

x2 ) tidak dapat terletak di sebelah kanan garis vertikal x1 = 40. Kondisi ini diperlihatkan pada

Gambar VI-2b. Kemudian kita mempertimbangkan kendala berikutnya yaitu x2 ≤ 50 yang

membatasi semua titik titik di atas garis horisontal x2 = 50. Sehingga sekarang wilayah

feasibel adalah wilayah semua titik yang berada di dalam persegi empat yang diarsir (Gambar VI-2c). (a) x1 = 40 (b) (c) (d) 10 20 30 40 50 60 10 20 30 40 50 P (15 , 20) X2 X1 X1 X2= 50 10 20 30 40 50 60 10 20 30 40 50 X2 X1 X2 10 20 30 40 50 60 10 20 30 40 50 X1 = 40 50 10 20 30 40 50 60 10 20 30 40 X2 X1 2X1+3X2 = 180 129 | P a g e

(25)

Kendala terakhir adalah alokasi waktu yang digambarkan lewat persamaan 2x1 + 3 x2 ≤

180. Sehingga hanya titik-titik yang terletak pada satu sisi dari garis 2x1 + 3 x2 = 180 yang

bisa memenuhi persyaratan tersebut. Untuk meletakkan garsi lurus 2x1 + 3 x2 = 180 ke grafik

yang telah dibuat maka kita bisa memasukkan nilai x1 untuk memperoleh nilai x2 atau

sebaliknya. Sehingga diperoleh grafik seperti pada Gambar VI-2d. Dengan demikian pada akhirnya diperoleh wilayah yang feasibel yaitu wilayah poligon yang diarsir pada Gambar VI-2d.

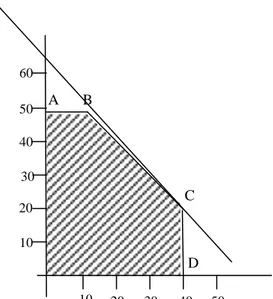
Solusi Optimum:

Solusi optimum dapat didekati dengan membaca koordinat C pada gambar VI-3 dimana x1 =

40 dan x2 = 33. Solusi yang lebih meyakinkan dapat diperoleh dengan mengerjakan

persamaan dua garis yang mendefinisikan titik C, yaitu:

x1 = 40 dan 2 x1 + 3 x2 = 180

Gambar VI-3. Menentukan solusi optimum secara grafis.

Dengan demikian nilai optimal x1 , yang kita tulis sebagai x* adalah 40 hektar. Dan bila

kita masukkan nilai x* ke persamaan kedua maka dapat ditulis sebagai berikut:

hektar 33,33 3 80 180 x*₂ = − = Z*= 759,96= 9X1 + 12X2 D A B C 10 20 30 40 50 10 20 30 40 50 60 130 | P a g e

(26)

Sehingga nilai optimum dari fungsi tujuan (yaitu memaksimumkan perolehan) yang sang petani dapat lakukan adalah:

Z* = 9x1 + 12x2 = 759,96 milyar per tahun

2. Contoh Kedua

a. Formulasi Persoalan

Pada contoh kedua ini diceritakan sebuah industri pulp yang terletak di pinggiran sebuah ibukota provinsi. Industri pulp ini menghasilkan pulp mekanis dan pulp kimia. Sayangnya industri ini juga mengakibatkan polusi terhadap sungai yang mengalir membelah kota dan bermuara di laut. Dan hal ini menimbulkan kekacauan dan bahkan bentrok dengan masyarakat kota sehingga pada akhirnya pihak industri merubah sistem pengelolaannya.

Pemilik melakukan kalkulasi terhadap usaha pengurangan polusi. Namun pemiliknya menghasilkan suatu kesimpulan bahwa dibutuhkan biaya yang sangat besar untuk memperkecil persoalan polusi. Akhirnya ia memutuskan untuk menjual industri pulp tersebut. Dan yang menarik adalah bahwa yang membeli industri tersebut adalah para karyawan dan pengusaha lokal yang membentuk sistem koperasi.

Pola menejemen baru digunakan oleh koperasi dimana tujuan pengelolaan industri pulp adalah ingin mempertahankan paling tidak 300 orang tenaga kerja diperusahaan untuk menghasilkan paling tidak Rp 400 juta perolehan kotor setiap harinya. Dengan estimasi perolehan seperti itu maka perusahaan diperkirakan akan dapat membayar semua ongkos operasional dan menghasilkan keuntungan yang dapat menyebabkan perusahaan menjadi lebih kompetitif dalam jangka panjang. Dan juga dengan kondisi seperti itu, segala sesuatunya dilakukan untuk meminimalkan polusi.

Seorang rimbawan ahli yang telah mempersiapkan sebuah solusi yang cemerlang tentang persoalan yang dihadapi perusahaan pulp tersebut diminta untuk memberikan berbagai masukan tentang strategi operasional bagi perusahaan sehingga tujuan-tujuan yang ditetapkan dapat tercapai. Sang rimbawan merasa bahwa hal itu dapat dicapai dengan melakukan analisis Linear Programming. Oleh sebab itu ia mencoba menyusun data dan informasi yang dibutuhkan.

Data:

(27)

Baik pulp mekanik dan pulp kimia membutuhkan tenaga kerja dimana satu orang tenaga kerja yang bekerja satu hari (HOK) akan menghasilkan satu ton produksi. Satu ton pulp kimia dijual seharga Rp 2 juta dan pulp mekanis terjual seharga Rp 1 juta per ton.

Polusi diukur dengan menggunakan satuan BOD (biological oxygen demand). Satu ton pulp mekanis menghasilkan 1 unit BOD, dan satu ton pulp kimia menghasilkan 1,5 unit BOD.

Kapasitas maksimum industri untuk membuat pulp mekanis sebesar 300 ton per hari dan untuk pulp kimia sebesar 200 ton per hari. Dua mesin tersebut berjalan sendiri-sendiri, artinya mesin penghasil pulp mekanis tidak dapat digunakan untuk menghasilkan pulp kimia, dan demikian pula sebaliknya.

Fungsi Tujuan:

Fungsi tujuan adalah ingin meminimumkan jumlah polusi Z yang diukur dalam satuan BOD per unit waktu, katakanlah per hari (BOD/hari). Analisis menghasilkan variable-variabel x1 =

jumlah pulp mekanis yang dihasilkan dalam satun ton per hari, dan x2 = jumlah pulp kimia

yang dihasilkan dalam satuan ton per hari. Dengan demikian fungsi tujuan dapat diekspresikan sebagai berikut:

min Z = 1x1 + 1,5x 2

(BOD/hr) (BOD/t)(t/hr) (BOD/t)(t/hr)

Kendala kedua mengatakan bahwa paling tidak sebanyak Rp 40 juta perolehan yang dihasilkan setiap hari, sehingga:

1.000.000 x1 + 2.000.000 x2 ≥ 400 juta

(Rp/t)(t/hr) (Rp/t)(t/hr) (Rp/hr)

Dua kendala lainnya berhubungan dengan data yang mengatakan bahwa kapasitas produksi industri tidak dapat melebihi ketentuan seperti berikut:

Untuk pulp mekanis x1 ≤ 300 (t/hr)

Untuk pulp kimia x2≤ 200 (t/hr)

(28)

Kendala terakhir adalah ketentuan bahwa baik pulp mekanis dan pulp kimia yang diproduksi harus bernilai nol atau positif atau secara matematis dapat ditulis x1 , x2≥ 0. Model yang Dihasilkan:

Dari hasil formulasi tadi dapat dirangkum model yang dihasilkan sebagai berikut:

Min Z = x1 + 1,5 x2 (polusi, unit BOD/hari)

Subjek terhadap: x1 + x2≥ 300 1.000.000 x1 + 2.000.000 x2≥ 400 juta x1 ≤ 300 x2 ≤ 200 x1 , x2 ≥ 0 Wilayah yang Feasibel:

Solusi secara grafis dapat dijelaskan sebagai berikut: hanya ada dua variabel dalam permasalahan yang akan dibahas yang keduanya diukur melalui aksis pada Gambar VI-4. Terlebih dahulu kita harus menentukan nilai yang memungkinkan bagi x1 dan x2 (wilayah

yang feasibel) dan selanjutnya menentukan atau menemukan titik-titik dalam wilayah tersebut yang akan meminimalkan fungsi tujuan (solusi optimum).

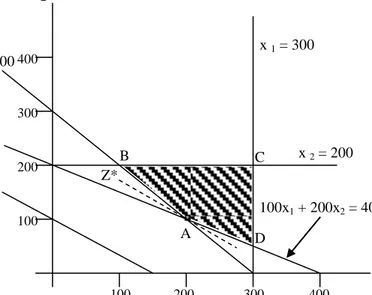
Gambar VI-4. Solusi metode grafis permasalahan industri pulp.

x 2 = 200 x1 x2 100 200 300 400 100 200 300 400 x 1 = 300 A B C D Z* x1 + x2 = 300 100x1 + 200x2 = 40 ribu Z = 150 133 | P a g e

(29)

Kendala tenaga kerja (x1 + x2 ≥ 300) membatasi solusi dari setengah bidang di sebelah

kanan atas garis batas (x1 + x2 = 300) yang melewati titik-titik (x1 = 0 , x2 = 300) dan (x2 =

0 , x1 = 300). Hal ini dapat diuji atau dibuktikan denga mengamati bahwa setiap titik yang

berada di sebelah kiri garis tersebut akan memperlihatkan bahwa kendala tenaga kerja tidak sesuai.

Wilayah yang feasible lebih lanjut dibatasi oleh kendala perolehan (100x1 + 200x2 ≥ 40

ribu per hari). Garis batas dari kendala ini melewati titik-titik (x1 = 0 , x2 = 200) dan (x2 =

0 , x1 = 400). Wilayah feasibel terletak di sebelah kanan dari garis batas.

Akhirnya, solusi yang mungkin dan harus memuaskan kendala kapasitas (x1≤ ton per hari

pulp mekanis, dan x2 ≤ 200 ton per hari pulp kima). Jadi wilayah feasibel terletak dibawah

garis x2 = 200 dan di sebelah kiri x1 = 300.

Dengan ringkas dapat dirangkum bahwa wilayah feasibel adalah luasan poligon ABCD pada Gambar VI-4. Gambar tersebut memperlihatkan bahwa setiap solusi dari permasalahan membutuhkan produksi paling tidak beberapa dari salah satu jenis pulp, atau kedua jenis pulp tersebut. Atau lebih jelas dapat dikatakan di sini bahwa semua tujuan dapat dicapai secara simultan hanya jika paling tidak 100 ton per hari produksi pulp mekanis (titik B) dan paling tidak 50 ton per hari produksi pulp kimia (titik D).

Solusi Optimum:

Untuk mencari solusi optimum boleh dilakukan dengan memperhatikan koordinat A yang dapat dibaca secara langsung pada grafik:

x1 + x2 = 300 dan 100x1 + 200x2 = 40.000

Kita dapat mengeliminsai x1 dengan cara mengalikan persamaan pertama dengan 100 dan

selanjutnya persamaan kedua dikurangi dengan hasil perkalian 100 persamaan pertama, maka diperoleh: kimia pulp hari per ton 100 100 10.000 x*₂ = =

Kemudian disubtitusikan hasil tersebut ke persamaan pertama, maka diperoleh:

(30)

Modul 5 ESDH 2019 mekanis pulp hari per ton 200 x*₁ =

Nilai fungsi tujuan yang berhubungan dengan strategi operasi optimum ini adalah:

x* = x1* + 1,5 x2* = 350 unit BOD per hari.

Inilah jumlah minimum polusi yang industri pulp dapat hasilkan sehingga tujuan lainnya dapat terpuaskan.

F. Metode Simplex

Metode Grafik yang telah dibahas pada Bab terdahulu hanya mampu menyelesaikan model-model yang memiliki dua atau tiga variable. Metode Simplex adalah teknik mencari penyelesaian program LP yang optimum dengan menggunakan prosedur aljabar. Teknik ini dapat dikerjakan dengan cara yang lebih gampang jika variable yang dipakai dalam LP jumlahnya tidak banyak. Bila jumlah variable yang dipakai banyak, maka cara atau metode simplex sulit dipraktekkan secara manual. Bila memang benar bahwa variable yang dipakai jumlahnya banyak, maka disarankan untuk menggunakan program paket komputer. Bila prosedur aljabar ini diprogramkan ke dalam komputer, maka ia dapat menyelesaiakn ribuan variable dan kendala.

Agar dapat menyelesaikan metode simplex dengan mudah maka pekerjaan yang perlu diperhatikan terlebih dahulu adalah membuat “tabel dasar” atau “basic-table”. Tahapan pekerjaan ini merupakan pekerjaan yang paling penting dalam metode simplex sebab bila pada tahapan ini ternyata ada kekeliruan, maka penyelesaian yang dilakukan selanjutnya juga akan keliru. Biasanya bila pada tahap penyusunan tabel dasar ini ada kekeliruan; misalnya tanda koefisien fungsi tujuan atau koefisien input-output, maka feasible solution tidak akan dihasilkan.

1) Beberapa Pengertian

1. Penetapan atau penyusunan tabel dasar, yaitu tabel awal yang berisikan informasi tentang besaran parameter dalam problem LP. Misalnya besaran koefisien fungsi tujuan (cij) , besaran koefisien input-output (aij) pada faktor pembatas dan besaran

sumber daya yang tersedia (bij)

2. Penetapan problem LP yang maksimum atau minimum. Bila salah satu problem ini telah ditetapkan, maka konsekuensinya ialah terhadap tanda ≤ atau ≥. Seperti

(31)

dijelaskan sebelumnya tanda ≤ mengisyaratkan problem maksimisasi dan sebaliknya tanda ≥ mengisyaratkan problema minimisasi.

3. Penetapan non-negative coefficients, artinya koefisien fungsi tujuan (cij) dan

koefisien input-output (aij) tidak boleh negatif. Sebab bila ada nilai negatif, maka

tidak akan terjadi penyelesaian optimum, melainkan yang diperoleh adalah penyelesaian yang tidak terbatas.

4. Semua bentuk persamaan yang ikut dalam model merupakan garis lurus.

5. Koefisien fungsi tujuan (cij) maupun koefisien input-output (aij) bersifat divisible

artinya dapat dibagi menjadi bilangan (besaran) kecil. Maksudnya untuk memudahkan perhitungan. Karena kalau menggunakan bilangan atau besaran yang nilainya besar, maka akan menyulitkan perhitungan secara manual.

Contoh:

10x1 + 40x2 ≤ 60

Persamaan tersebut dapat disederhanakan menjadi:

5x1 + 20x2 ≤ 30 ; atau

x1 + 4x2 ≤ 6

6. Penetapan equality, artinya semua tanda ≤ atau ≥ digantikan dengan tanda sama dengan (=). Hal ini akan dijelaskan lebih lanjut.

7. Penetapan pivot-element; artinya bilangan yang dipakai sebagai dasar melakukan iterasi.

8. Perhitungan iterasi yaitu mengubah nilai atau bilangan disesuaikan maksud analisis. 9. Penetapan feasible solution berarti hasil akhir penyelesaian problem LP yang

memungkinkan (feasible) untuk ditarik suatu kesimpulan.

10. Penetapan hal-hal yang dikategorikan sebagai non feasible solution yaitu hasil akhir penyelesaian LP yang tidak feasible. Bila kasus seperti ini terjadi, maka pekerjaan harus diulang mulai dari awal lagi. Cek apakah koefisien yang dipakai sudah benar, tandanya apa sudah positif atau cara melakukan iterasi sudah benar atau belum.

2) Variabel Slack dan Variabel Surplus

(32)

Langkah pertama dalam menggunakan Metode Simplex adalah mentransformasikan semua pertidaksamaan dalam model LP menjadi persamaan. Hal ini dilakukan dengan tujuan bahwa menyelesaikan sebuah persamaan lebih mudah secara matematis dibandingkan menyelesaiakan sebuah pertidaksamaan. Untuk melakukan hal ini, maka caranya adalah dengan menambahkan slack variable pada program LP memaksimumkan dan menambahkan

surplus variable pada program LP meminimumkan.

Sebagai contoh, di sini akan digunakan kasus petani kaya yang penyelesaian persoalannya telah diulas pada pembahasan Metode Grafis.

Maks Z = 9x1 + 12x2 rupiah per tahun

Subjek terhadap:

x1 ≤ 40 hektar hutan pinus

x2≤ 50 hektar hutan campuran

2 x1 + 3 x2 ≤ 180 hari kerja

x1 , x2 ≥ 0

Kendala pertama dapat diubah menjadi suatu persamaan dengan memasukkan satu variabel tambahan yang kita sebut slack variabel, S1 , sehingga kendala pertama dapat

dituliskan sebagai berikut:

x1 + S1 = 40 dimana S1 ≥ 0

Perlu diketahui di sini bahwa S1 merupakan representasi luasan hutan pinus yang tidak

dikelola. Selanjutnya kita harus melakukan hal yang sama untuk kendala-kendala lainnya. Sehingga yang harus dilakukan adalah sebagai berikut:

max Z = 9x1 + 12x2 Subjek terhadap: x1 + S1 = 40 x2 + S2 = 50 2x1 + 3x2 + S3 = 180 x1 , x2 , S1 , S2 , S3 ≥ 0 137 | P a g e

(33)

dimana S2 dan S3 adalah slack variable yang mempresentasikan hutan campuran dan waktu

petani yang tidak digunakan dalam pengelolaan hutan miliknya.

Penyelesaian peroblem LP “meminimumkan” memerlukan bantuan surplus variable agar penyelesaian problem LP dengan cara Simplex dapat diselesaikan. Misalnya:

Semula: x1 + x2 -S1 = 4

2x1 + 2x2 -S3 = 7

Diubah menjadi:

x1 + x2 -S1 + S3 = 4

2x1 + 2x2 -S3 + S4 = 7

Dalam terminologi LP, maka cara ini disebut dengan istilah “proses tahap ganda dua” atau

two-phase process. Cara penyelesaiannya hampir sama dengan penyelesaian “slack variable”,

hanya saja sebelumnya diperlukan pekerjaan memilih variabel buatan terlebih dahulu.

3) Solusi Dasar yang Memungkinkan

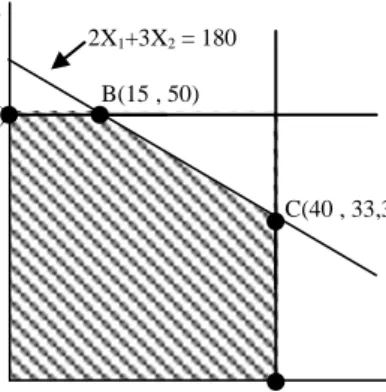
Coba kita kembali kepada representasi geometri solusi yang mungkin untuk LP ini. Untuk lebih jelasnya dapat dilihat pada Gambar VII-1 dimana wilayah feasibel adalah luas area poligon OABCD. Persamaan-persamaan setiap garis batas dapat dilihat pada gambar tersebut.

Gambar VII-1. Titik ekstrim dan solusi feasibel dasar.

O _{D(40 , 0)} A(0 , 50) C(40 , 33,3) 2X1+3X2 = 180 X2 X1 B(15 , 50) 138 | P a g e

(34)

Solusi dasar yang memungkinkan dari LP ini berhubungan dengan sudut-sudut poligon OABCD. Kita menyebut sudut-sudut tersebut sebagai titik-titik ekstrim dari wilayah feasibel. Sebagai contoh, titik ekstrim sudut O berhubungan dengan solusi feasibel dasar:

( X1 , X2 , S1 , S2 , S3 ) = ( 0 , 0 , 40 , 50 , 180)

Karena pada titik O diketahui X1 = X2 = 0 maka dari kendala diperoleh S1 = 40 , S2 = 50 ,

dan S3 = 180. Hal yang sama dapat dilakukan pada titik A sehingga diperoleh:

( X1 , X2 , S1 , S2 , S3 ) = ( 0 , 50 , 40 , 0 , 30)

Perlu dicatat bahwa pada masing-masing solusi yang mungkin terdapat jumlah yang sama antara variabel positif dengan kendala positif. Variabel positif disebut juga variabel dasar, sedangkan variabel yang bernilai nol disebut variabel non dasar.

4) Teorema Linear Programming

Teorema dasar LP mengatakan bahwa bila terdapat sebuah solusi optimum maka paling tidak satu solusi feasibel dasar merupakan solusi optimum. Teori ini memiliki implikasi bahwa pada sebuah LP, mungkin terdapat satu, banyak, atau tidak ada solusi optimum. Teorema ini bersifat dasar sebab hal ini berarti bahwa menyelesaikan sebuah LP, seseorang harus hanya mempertimbangkan sejumlah tertentu solusi.

Oleh karena solusi optimum sebuah LP adalah sebuah solusi feasibel dasar, maka terdapat dalam jumlah yang sama antara variabel positif dengan kendala bebas. Bila sebuah masalah mempunyai 10 kendala bebas dan 10.000 variabel, maka hanya 10 variabel yang merupakan solusi optimum yang memiliki nilai positif; sisanya bernilai nol. Bahkan terdapat variabel positif yang lebih sedikit bila semua kendala tidak bebas. Asumsikan bahwa terdapat 10 kendala dalam sebuah program dimana hanya terdapat 8 variabel positif dalam solusi optimum, maka dua kendala dalam model harus tidak digunakan.

5) Algoritma Solusi

Teorima LP yang telah diberikan di atas menggunakan prosedur solusi yang mungkin (algoritma). Algoritma ini akan menghitung semua solusi feasibel dasar dan menemukan salah satu diantaranya yang dapat memaksimumkan atau meminimumkan fungsi tujuan. Tapi cara ini menjadi tidak praktis untuk permasalahan besar sebab jumlah solusi feasibel dasar

(35)

yang sangat besar sehingga sulit dalam pengolahannya, kendatipun dengan menggunakan komputer.

Dengan pertimbangan itulah maka Metode Simplex menggunakan algoritma

steepest-ascent. Algoritma ini dilakukan dengan cara berpindah dari satu titik puncak ke titik puncak

berikutnya dari suatu wilayah feasibel. Perpindahan dilakukan dengan arah yang paling dapat memperbaiki fungsi tujuan.

Untuk memudahkan penjelasan di atas, kita dapat membayangkan wilayah feasibel sebagai sebuah gunung. Puncak gunung berhubungan dengan solusi optimum. Seorang pendaki gunung tersesat dalam hutan berkabut dan hampir tidak dapat melihat kakinya sendiri. Untuk mencapai puncak, pendaki gunung tersebut melanjutkan perjalanannya dengan sangat hati-hati, tetapi pasti. Menapakkan kaki selangkah demi selangkah, ia melangkahkan kaki ke sekeliling mencari tempat yang lebih tinggi. Jika salah satu kakinya mendapatkan tempat yang lebih tinggi di sekelilingnya, barulah ia melangkahkan kakinya. Dan ketika salah satu kakinya tidak lagi menemukan tempat yang lebih tinggi barulah ia menyimpulkan bahwa ia telah berada di puncak gunung.

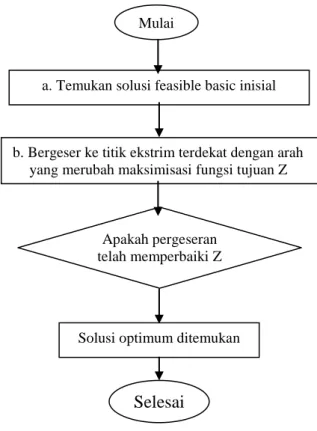
Flowchart pada Gambar VII-2 merupakan ringkasan langkah-langkah dalam algoritma metode simplex:

Gambar VII-2. Flow chart untuk Metode simplex.

Mulai

a. Temukan solusi feasible basic inisial

b. Bergeser ke titik ekstrim terdekat dengan arah yang merubah maksimisasi fungsi tujuan Z

Apakah pergeseran telah memperbaiki Z

Selesai

Solusi optimum ditemukan

(36)

Contoh:

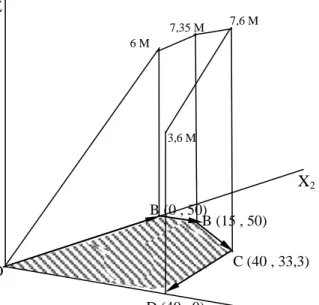
Untuk mengilustrasikan prinsip-prinsip Metode Simplex, kita akan menggunakan metode ini untuk menyelesaikan persoalan yang dihadapi petani kaya dengan mengikuti langkah-langkah yang digambarkan pada Gambar VII-3.

Gambar VII-3. Iterasi algoritma Metode simplex.

Langkah a: Temukan solusi feasibel dasar. Dalam konteks ini adalah titik O pada Gambar

VII-3, yaitu:

Variabel non-dasar : X1 = 0 , X2 = 0

Variabel dasar : S1 = 40 , S2 = 50 , S3 = 180

Fungsi tujuan: Z0 = 0

Pada solusi inisial ini, ketiga slack variabel bersifat dasar.

Langkah b1: Oleh karena koefisien X1 pada fungsi tujuan bernilai Rp 9 juta per hektar,

sedangkan koefisien X2 sebesar Rp 12 juta, fungsi tujuan akan meningkat lebih besar melalui

perpindahan dari titik O ke arah OX2 yaitu menuju titik ekstrim A. Sehingga diperoleh solusi

feasibel dasar baru sebagai berikut:

X1 X2 Z O D (40 , 0) C (40 , 33,3) B (15 , 50) B (0 , 50) 6 M 7,35 M 7,6 M 3,6 M 141 | P a g e

(37)

Variabel bukan dasar : S2 = 0 , X1 = 0

Variabel dasar : X2 = 50 , S1 = 40 , S3 = 30

Fungsi tujuan: ZA = Rp 6 milyar per tahun

Dalam pergeseran dari titik ekstrim O ke A, variabel X2 yang tadinya bersifat bukan dasar

telah menjadi variabel dasar, dan variabel S2 yang tadinya bersifat dasar menjadi variabel non

dasar. Hal ini bersifat umum bahwa equivalen aljabar dari suatu titik ekstrim terdekat adalah suatu solusi feasibel dasar dengan satu variabel dasar tunggal yang berbeda. Pendakian yang lebih menanjak pada Gambar VII-3 terpilih sebagai variabel dasar yang baru yaitu titik ekstrim yang memiliki nilai fungsi tujuan yang terbaik.

Langkah b2: Dari titik ekstrim A sekarang kita akan bergeser ke arah OX1 karena hanya

melalui cara itu fungsi tujuan dapat ditingkatkan. Titik ekstrim terdekat adalah B, yang berhubungan dengan solusi feasibel dasar berikut:

Variabel bukan dasar: S2 = 0 , S3 = 0

Variabel dasar : X1 = 15 , X2 = 50 , S1 = 25

Fungsi tujuan: ZB = Rp 7,35 milyar per tahun

Langkah b3: Oleh karena iterasi terakhir telah meningkatkan nilai Z, kita coba cara lain

lagi dengan melakukan pergeseran atau pergerakan ke titik ekstrim C yang berhubungan dengan solusi feasibel dasar:

Variabel bukan dasar : S1 = 0 , S3 = 0

Variabel dasar : X1 = 40 , X2 = 33,3 , S1 = 16,7

Fungsi tujuan : ZC : Rp 7,6 milyar per tahun

Langkah b4: Iterasi terakhir juga meningkatkan fungsi tujuan sehingga kita harus

mencoba lagi dengan melakukan pergeseran ke titik ekstrim D. Sehingga diperoleh:

Variabel bukan dasar : S1 = 0 , X2 = 0

Variabel dasar : X1 = 40 , S3 = 100 , S2 = 50

Fungsi tujuan : ZD : Rp 3,6 milyar per tahun

(38)

Kita lihat bahwa iterasi ini telah menurunkan nilai fungsi tujuan. Sehingga dengan demikian dapat disimpulkan bahwa solusi optimum adalah solusi feasibel dasar yang dimiliki oleh titik C.

Soal Latihan:

1. Jelaskan pengertian linear programming.

2. Sebutkan alasan kecenderungan berbagai kalangan menggunakan linear programming. 3. Jelaskan dua cara atau karakteristik teknik linear programming dalam mengoptimalkan

usaha.

4. Jelaskan beberapa istilah berikut: (1) fungsi tujuan; (2) kendala atau pembatas; (3) asumsi.

Rangkuman:

1. Petunjuk:

Berikut tersedia kata-kata kunci yang diambila dari modul/bahan kuliah.

Kata kunci:

1. Liner Programming 4. Solusi

2. Kendala 5. Metode Grafis

3. Variabel 6. Metode Simplex

2. Merujuk kepada kata kunci tersebut, tuliskan rangkuman anda ke dalam kotak rangkuman berikut: ... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 143 | P a g e

(39)

Refleksi Pembelajaran

No Deskripsi/Pertanyaan Jawaban

SS CS RR B SB

1. Capaian pembelajaran yang ditawarkan

2. Antusiasme mahasiswa mengikuti kuliah di dalam kelas

3. Core content yang diberikan 4. Proses perkuliahan

5. Metode evaluasi perkuliahan

6. Tingkat kehadiran mahasiswa dalam perkuliahan

Keterangan: SS: sangat sempurna CS: cukup sempurna RR: ragu-ragu B : buruk SB: sangat buruk Rekomendasi perbaikan: ... .... ... ... ... ... ... ... ... ... Vidio: http://sagehenforest.blogspot.com/2016/06/saving-west.html 144 | P a g e