PAM 252 Metode Numerik
Bab 3 Sistem Persamaan Linier
Mahdhivan Syafwan
Jurusan Matematika FMIPA Universitas Andalas
Bentuk-bentuk khusus matriks persegi
Matriks simetrik
Matriks diagonal
Matriks identitas
Matriks segitiga atas
Matriks segitiga bawah
Matriks tridiagonal
Matriks Hessenberg
Bentuk umum
Bentuk umum dari SPL:
a
11
x
1
+
a
12
x
2
+
· · ·
+
a
1
n
x
n
=
b
1
a
21
x
1
+
a
22
x
2
+
· · ·
+
a
2
n
x
n
=
b
2
..
.
..
.
..
.
..
.
a
n
1
x
1
+
a
n
2
x
2
+
· · ·
+
a
nn
x
n
=
b
n
Dalam bentuk matriks, SPL di atas dapat ditulis dengan
A
x
=
b
,
dimana
A
=
a
11
a
12
· · ·
a
1
n
a
21
a
22
· · ·
a
2
n
..
.
..
.
..
.
a
n
1
a
n
2
· · ·
a
nn
,
x
=
x
1
x
2
..
.
x
n
,
b
=
b
1
b
2
..
.
b
n
.
Tentang solusi SPL
Ada tiga kemungkinan mengenai solusi SPL:
(a)
Tidak ada solusi
(b)
Tak-hingga solusi
(c)
Solusi tunggal
Tafsiran geometris:
Matriks koefisien, matriks lengkap SPL, dan OBE
Pada persamaan sebelumnya,
A
disebut
matriks koefisien
.
Matriks yang dibentuk oleh matriks
A
dengan penambahan
vektor kolom
b
disebut
matriks lengkap
dari SPL, yaitu
a
11
a
12
· · ·
a
1n
b
1
a
21
a
22
· · ·
a
2n
b
2
..
.
..
.
..
.
..
.
an1
an2
· · ·
ann
bn
.
Operasi baris elementer (OBE):
Menukarkan dua buah baris
Mengalikan suatu baris dengan suatu konstanta tak-nol
Menambahkan
k
kali baris ke-
i
pada baris ke-
j
SPL segitiga atas
Bentuk umum dari SPL segitiga atas:
a
11
x
1
+
a
12
x
2
+
· · ·
+
a
1
n
x
1
=
b
1
a
22
x
2
+
· · ·
+
a
2
n
x
2
=
b
2
. ..
..
.
..
.
a
nn
x
n
=
b
n
Matriks lengkap dari SPL segitiga atas:
a
11
a
12
· · ·
a
1
n
b
1
a
22
· · ·
a
2
n
b
2
. .. ...
..
.
a
nn
b
n
.
Sifat:
SPL segitiga atas mempunyai solusi tunggal jika dan hanya
jika setiap elemen diagonal dari matriks koefisiennya tidak nol, yaitu
a
kk
6
= 0,
k
= 1,
2, ...,
n
.
Substitusi mundur
Solusi dari SPL segitiga atas dapat dihitung sebagai berikut:
x
n
=
b
n
/
a
nn
x
n
−
1
= (
b
n
−
1
−
a
n
−
1
x
n
)/
a
n
−
1
,
n
−
1
x
n
−
2
= (
b
n
−
2
−
(
a
n
−
2
,
n
−
1
x
n
−
1
+
a
n
−
2
,
n
x
n
))/
a
n
−
2
,
n
−
2
..
.
x
k
=
b
k
−
n
X
i
=
k
+1
a
ki
x
i
!
/
a
kk
..
.
x
1
=
b
1
−
n
X
i
=2
a
1
i
x
i
!
/
a
11
Algoritma substitusi mundur
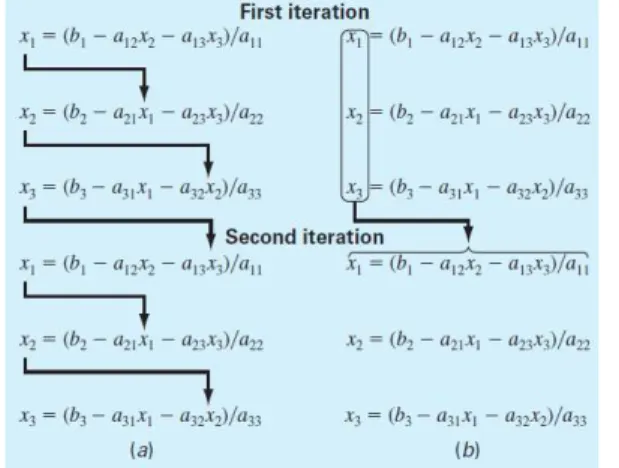
Apa saja yang harus diperhatikan?
Dalam setiap iterasi, sebelum nilai
x
k
dihitung, dilakukan
pemeriksaan terlebih dahulu terhadap elemen diagonal
a
kk
(proses
dihentikan jika ...)
Misalkan ˜
A
adalah matriks lengkap. Maka vektor
b
berada pada
kolom ke ... dari matriks ˜
A
.
Metode eliminasi Gauss - contoh
Dengan menggunakan metode eliminasi Gauss, selesaikan SPL
berikut ini:
−
x
1
+
x
2
+ 2
x
3
= 1
,
3
x
1
−
x
2
+
x
3
= 1
,
−
x
1
+ 3
x
2
+ 4
x
3
= 1
.
Dua tahap besar pada metode eliminasi Gauss
1
Tahap eliminasi (maju),
yaitu mengubah SPL semula
menjadi SPL segitiga atas
melalui serangkaian OBE
(operasi ini tidak mengubah
solusi dari SPL semula).
2
Tahap substitusi mundur,
yaitu menyelesaikan SPL
segitiga atas yang terbentuk.
Metode eliminasi Gauss - tahap eliminasi
Langkah pertama:
membuat agar elemen-elemen kolom pertama mulai baris ke-2,
3, ...,
n
(yaitu
a
11,
a
21, ...,
a
n
1) menjadi nol.
a
11
a
12
· · ·
a
1
n
a
1
,
n
+1
a
21
a
22
· · ·
a
2
n
a
2
,
n
+1
..
.
..
.
..
.
..
.
a
n
1
a
n
2
· · ·
a
nn
a
n
,
n
+1
∼
a
11
a
12
· · ·
a
1
n
a
1
,
n
+1
0
a
22
· · ·
a
2
n
a
2
,
n
+1
..
.
..
.
..
.
..
.
0
a
n
2
· · ·
a
nn
a
n
,
n
+1
Catatan:
Notasi
∼
menyatakan bahwa proses yang dilakukan adalah melalui
serangkaian OBE.
Elemen-elemen pada kedua matriks lengkap di atas menggunakan
notasi yang sama, yaitu
a
ij
. Hal ini tidak berarti bahwa nilainya juga
sama. Pemakaian notasi yang sama ini ditujukan untuk keperluan
pada pemograman komputer.
Metode eliminasi Gauss - tahap eliminasi
Langkah pertama
- ilustrasi
a11 a12 · · · a1n a1,n+1 a21 a22 · · · a2n a2,n+1 a31 a32 · · · a3n a3,n+1 . . . . . . . . . . . . an1 an2 · · · ann an,n+1 (b)2←(b)2−a21 a11(b)1 a11 a12 · · · a1n a1,n+1 0 a22 · · · a2n a2,n+1 a31 a32 · · · a3n a3,n+1 . . . . . . . . . . . . an1 an2 · · · ann an,n+1 a11 a12 · · · a1n a1,n+1 a21 a22 · · · a2n a2,n+1 a31 a32 · · · a3n a3,n+1 . . . . . . . . . . . . an1 an2 · · · ann an,n+1 (b)3←(b)3−a31 a11(b)1 a11 a12 · · · a1n a1,n+1 0 a22 · · · a2n a2,n+1 0 a32 · · · a3n a3,n+1 . . . . . . . . . . . . an1 an2 · · · ann an,n+1 . . . a11 a12 · · · a1n a1,n+1 a21 a22 · · · a2n a2,n+1 a31 a32 · · · a3n a3,n+1 . . . . . . . . . . . . an1 an2 · · · ann an,n+1 (b)n←(b)n−an1 a11(b)1 a11 a12 · · · a1n a1,n+1 0 a22 · · · a2n a2,n+1 0 a32 · · · a3n a3,n+1 . . . . . . . . . . . . 0 an2 · · · ann an,n+1
Metode eliminasi Gauss - tahap eliminasi
Langkah pertama
- algoritma
(
b
)2
←
(
b
)2
−
a21
a
11(
b
)1
(
b
)3
←
(
b
)3
−
a31
a
11(
b
)1
..
.
(
b
)
n
←
(
b
)
n
−
a
a11
n1(
b
)1
Metode eliminasi Gauss - tahap eliminasi
Langkah kedua: mengeliminasi kolom kedua dari matriks lengkap SPL.
a11 a12 a13 · · · a1n a1,n+1 0 a22 a23 · · · a2n a2,n+1 0 a32 a33 · · · a3n a3,n+1 . . . . . . . . . . . . 0 an2 an3 · · · ann an,n+1 (b)3←(b)3−a32 a22(b)2 (b)4←(b)4−a42 a22(b)2 . . . (b)n←(b)n−an2 a22(b)2 a11 a12 a13 · · · a1n a1,n+1 0 a22 a23 · · · a2n a2,n+1 0 0 a33 · · · a3n a3,n+1 . . . . . . . . . . . . 0 0 an3 · · · ann an,n+1
Langkah ke-3
,
4
, ...,
n
−
1: mengeliminasi kolom ke-3,
4, ...,
n
−
1 dari
matriks lengkap SPL.
Hasil akhir dari tahap eliminasi adalah suatu SPL segitiga atas. Solusi
SPL dapat diperoleh dengan menjalankan algoritma substitusi mundur.
Metode eliminasi Gauss - algoritma tahap eliminasi
→
Kelemahan metode eliminasi Gauss & perbaikannya
Kelemahan metode eliminasi Gauss:
Proses eliminasi tidak dapat dilakukan jika elemen penumpu (pivot)
bernilai nol.
Jika nilai mutlak dari elemen pivot sangat kecil, maka pada realisasi
komputer akan menimbulkan perambatan galat pembulatan yang
besar.
Kelemahan metode eliminasi Gauss & perbaikannya
Kelemahan metode eliminasi Gauss:
Proses eliminasi tidak dapat dilakukan jika elemen penumpu (pivot)
bernilai nol.
Jika nilai mutlak dari elemen pivot sangat kecil, maka pada realisasi
komputer akan menimbulkan perambatan galat pembulatan yang
besar.
Cara memperbaikinya?
Perlu dipilih elemen penumpu yang nilai mutlaknya besar.
Hal ini direalisasikan dengan melakukan pertukaran baris dan/atau
kolom pada matriks lengkap.
Pertukaran baris tidak mengubah solusi SPL.
Pertukaran kolom bagaimana?
Kelemahan metode eliminasi Gauss & perbaikannya
Kelemahan metode eliminasi Gauss:
Proses eliminasi tidak dapat dilakukan jika elemen penumpu (pivot)
bernilai nol.
Jika nilai mutlak dari elemen pivot sangat kecil, maka pada realisasi
komputer akan menimbulkan perambatan galat pembulatan yang
besar.
Cara memperbaikinya?
Perlu dipilih elemen penumpu yang nilai mutlaknya besar.
Hal ini direalisasikan dengan melakukan pertukaran baris dan/atau
kolom pada matriks lengkap.
Pertukaran baris tidak mengubah solusi SPL.
Pertukaran kolom bagaimana?
Teknik pemilihan elemen penumpu ini dinamakan
teknik penumpuan
(pivoting).
Beberapa macam teknik penumpuan
Penumpuan total
Elemen penumpu diambil dari max
k
≤
i
,
j
≤
n
|
a
ij
|
Memerlukan pertukaran baris dan/atau kolom
Penumpuan parsial
Elemen penumpu diambil dari max
k
≤
i
≤
n
|
a
ik
|
Hanya memerlukan pertukaran baris saja
Penumpuan parsial terskala
Elemen penumpu diambil dari max
k
≤
i
≤
n
|
a
ik
/
a
kk
|
Hanya memerlukan pertukaran baris saja
Elemen penumpu yang dipilih kemudian ditempatkan pada posisi
(
k
,
k
) dari matriks lengkap SPL.
Eliminasi Gauss dengan penumpuan parsial - contoh
Eliminasi Gauss dengan penumpuan parsial - algoritma?
Beberapa SPL dengan matriks koefisien sama
Pandang dua SPL berikut:
x
1+
2x
2+
x
3+
4x
4=
13
2x
1+
4x
3+
3x
4=
28
4x
1+
2x
2+
2x
3+
x
4=
20
−
3x
1+
x
2+
3x
3+
2x
4=
0
x
1+
2x
2+
x
3+
4x
4=
8
2x
1+
4x
3+
3x
4=
9
4x
1+
2x
2+
2x
3+
x
4=
9
−
3x
1+
x
2+
3x
3+
2x
4=
3
Matriks lengkap dari dua SPL tersebut dapat ditulis:
1
2
1
4
13
8
2
0
4
3
28
9
4
2
2
1
20
9
−
3
1
3
2
6
3
.
Solusi dari masing-masing SPL dapat ditentukan dengan metode eliminasi Gauss.
Perhitungan determinan - dasar teori
Teorema (determinan matriks segitiga atas)
Jika
A
matriks segitiga atas berukuran
n
×
n
, maka det(
A
) =
n
Y
i=1