PENDEKATAN QUADRATIC PROGRAMMING DALAM FAKTORISASI MATRIKS
NON NEGATIF
TESIS
Oleh
HERI YUSUF SIMBOLON 167021009/MT
PROGRAM STUDI MAGISTER MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2018
PENDEKATAN QUADRATIC PROGRAMMING DALAM FAKTORISASI MATRIKS
NON NEGATIF
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
HERI YUSUF SIMBOLON 167021009/MT
Telah diuji pada
Tanggal : 16 April 2018
PANITIA PENGUJI TESIS
PERNYATAAN ORISINALITAS
PENDEKATAN QUADRATIC PROGRAMMING DALAM FAKTORISASI MATRIKS NON NEGATIF
TESIS
Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing dituliskan sum- bernya
Medan, Penulis,
Heri Yusuf Simbolon
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS
Sebagai sivitas akademika Universitas Sumatera Utara, Saya yang bertanda tangan di bawah ini:
Nama : Heri Yusuf Simbolon
NIM : 167021009
Program Studi : Matematika Jenis Karya Ilmiah: Tesis
Demi pengembangan ilmu pengetahuan, menyetujui untuk memberikan kepada Universitas Sumatera Utara Hak Bebas Royalti Non-Eksklusif (Non-Exclusive Royalty Free Right) atas tesis saya yang berjudul:
Pendekatan Quadratic Programming dalam Faktorisasi Matriks Non Negatif.
Beserta perangkat yang ada. Dengan Hak Bebas Royalti NonEksklusif ini, Universitas Sumatera Utara berhak menyimpan, mengalih media, memformat mengelola dalam bentuk data-base, merawat dan mem- publikasikan Tesis saya tanpa meminta izin dari saya selama mencan- tumkan nama saya sebagai pemegang dan atau sebagai penulis dan sebagai pemilik hak cipta.
Demikian pernyataan ini dibuat dengan sebenarnya.
Medan, Penulis,
Heri Yusuf Simbolon
PENDEKATAN QUADRATIC PROGRAMMING DALAM FAKTORISASI MATRIKS NON NEGATIF
ABSTRAK
Faktorisasi Matriks Non-negatif adalah suatu algoritma optimasi iterasi, yaitu menguraikan satu matriks menjadi beberapa matriks yang komponennya tidak negatif. Faktorisasi Matriks Non-negatif (FMN) berfungsi untuk memperoleh gambaran dari data non-negatif.
Terdapat permasalahan dalam Faktorisasi Matriks Non-negatif yaitu optimasi pada pada batas kendala, dimana dalam solusi optimasi pa- da batas kendala perlu dilakukan iterasi yang panjang dan tentunya sangat sulit dan memerlukkan waktu yang lama. Quadratic Prog- raming merupakan pendekatan penyelesaian permasalahan optimisasi linier dimana kendalanya berupa fungsi linier dan fungsi tujuannya merupakan kuadrat dari variable keputusan ataupun perkalian dari dua variable keputusan. Metode ini dianggap mampu menjadi metode yang efektif untuk mengatasi optimasi batas kendala dalam Faktorisasi Matriks Non-negatif.
Kata kunci : Matriks nonnegatif, Faktorisasi matriks, Quadratic programming.
QUADRATIC PROGRAMMING APROACH IN THE NON-NEGATIVE MATRIX FACTORIZATION
ABSTRACT
Non-negative Matrix Factorization is an iteration optimization algorithm, to decipher one matrix into several non-negative com- ponent matrices. Non-negative Matrix Factorization (FMN) serves to obtain a picture of non-negative data. There is a problem in the Non-negative Matrix Factorization that is optimization at the constraint boundary, where in the optimization solution on the con- straint boundary it is necessary to do long iteration and of course very difficult and conquers a long time. Quadratic Programing is an approach to solving linear optimization problems where the con- straint is linear function and its purpose function is the square of the decision variable or multiplication of the two decision variables.
This method is considered to be an effective method to overcome the optimization in the Non-negative Matrix Factorization.
Keyword : Non-negative Matrix, Matrix Factorization, Quadratic Programming.
.
KATA PENGANTAR
Setinggi puji dan sedalam syukur penulis serahkan kehadirat Allah SWT yang telah memberikan berkat dan rahmad-Nya sehingga penulis dapat menyelesaikan tesis yang berjudul PENDEKATAN QUADRA- TIC PROGRAMMING DALAM FAKTORISASI MATRIKS NON NEGATIF. Tesis ini merupakan salah satu syarat untuk menyelesaikan studi pada Program Studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara.
Pada kesempatan ini, penulis ingin menyampaikan terima kasih kepa- da:
Ayahanda (Alm). Hasanuddin Simbolon dan Ibunda Masnaini Hasi- buan, sosok orang tua yang mencurahkan seluruh kasih sayang dan dukungan kepada penulis. Orang tua yang penulis kagumi dan cintai, yang telah memberikan tauladan, membimbing, mengajarkan kesabaran, kerendahan hati dan selalu bersyukur dalam menghadapi kehidupan ini, serta senantiasa memanjatkan do’a yang tulus dan ikhlas bagi ke- berhasilan anak-anaknya.
Prof. Dr. Runtung, S.H., M.Hum selaku Rektor Universitas Sumatera Utara yang telah memberikan kesempatan penulis untuk menempuh pendidikan di Universitas Sumatera Utara.
Dr. Kerista Sebayang, M.S selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara.
Prof. Dr. Saib Suwilo, M.Sc selaku Ketua Program Studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Uni- versitas Sumatera Utara.
Dr. Sawaluddin, M.IT selaku Sekretaris Program Studi Magister Ma- tematika FMIPA USU dan selaku Pembimbing penulis yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis
sehingga tesis ini dapat diselesaikan dengan baik.
Prof. Dr. Marwan Ramli, M.Si selaku pembimbing penulis yang telah banyak memberikan bimbingan dan arahan serta motivasi kepa- da penulis sehingga tesis ini dapat diselesaikan dengan baik
Prof. Dr. Tulus, M.Si selaku Pembanding penulis yang telah banyak memberikan bimbingan dan araha serta motivasi kepada penulis se- hingga tesis ini dapat diselesaikan dengan baik.
Dr. Open Darnius, M.Sc selaku pembanding penulis yang telah banyak memberi arahan, bimbingan dalam bentuk kritik dan saran, dan juga motivasi kepada penulis dalam pengerjaan tesis ini.
Seluruh Staf Pengajar di Program Studi Magister Matematika FMIPA USU yang telah banyak memberikan ilmu pengetahuan kepada penulis selama masa perkuliahan.
Kak Misiani, S.Si selaku Staf Administrasi Program Studi Magister Matematika FMIPA USU yang telah banyak memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.
Seluruh rekan-rekan Mahasiswa angkatan 2016 Ganjil Program Studi Magister Matematika FMIPA Universitas Sumatera Utara. Semoga Tuhan Yang Maha Kuasa senantiasa memberi rahmat dan hidayahNya kepada kita semua. Amin.
Tak lupa penulis mengucapkan terima kasih sebesar-besarnya dan penghor- matan yang setinggi-tingginya kepada kedua mertua, Ayahanda Prof.
Dr. Ir. H. Abdul Rauf, MP dan Ibunda Dra. Hj. Erlinawati yang telah memberikan motivasi, materi, serta doa kepada penulis.
Terkhusus kepada istri tercinta Zuhrina Aidha, S.Kep., M.Kes., yang selalu ada untuk penulis dengan memberikan motivasi dan mencu- rahkan kasih sayang serta dukungan do’a, moril maupun materil kepa- da penulis
Semua pihak yang telah membantu, baik langsung maupun tidak
langsung yang tidak dapat penulis sebutkan namanya satu per satu, hanya Allah SWT yang mampu memberikan balasan terbaik. Mudah- mudahan tesis ini dapat memberikan sumbangan yang berharga bagi perkembangan dunia ilmu dan bermanfaat bagi orang banyak. Semoga Allah SWT senantiasa memberi rahmat dan hidayah-NYA kepada kita semua. Aamiin.
Penulis menyadari bahwa tesis ini masih jauh dari sempurna, un- tuk itu penulis mengharapkan kritik saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya. Terimakasih.
Medan, 16 April 2018 Penulis,
Heri Yusuf Simbolon
RIWAYAT HIDUP
Heri Yusuf Simbolon, dilahirkan di Rantauprapat pada tanggal 25 Juni 1986 dari Pasangan Alm. Bapak Hasanuddin Simbolon dan Ibu Masnaini Hasibuan sebagai anak keenam dari enam bersaudara.
Penulis menammatkan pendidikan sekolah dasar di SD 112162 Ranataupra- pat pada tahun 1999, selanjutnya Penulis meneruskan pendidikan dit- ingkat Sekolah Menengah Pertama di SMP Negeri 1 Rantauprapat dan tammat pada tahun 2002 dan melanjutkan ke tingkat Sekolah Menen- gah Atas di SMA Negeri 02 Rantau Utara dan tammat pada tahun 2005. Pada tahun 2014 Penulis lulus sarjana dari Fakultas Keguru- an dan Ilmu Pendidikan Universitas Islam Sumatera Utara, Medan.
Dan pada September 2016, melanjutkan studi Magister Matematika (S-2) di Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara, Medan.
Demikian riwayat hidup ini penulis perbuat dengan sebenar-benarnya.
DAFTAR ISI
Halaman
ABSTRAK i
ABSTRACT ii
KATA PENGANTAR iii
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR GAMBAR ix
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 3
1.3 Tujuan Penelitian 3
1.4 Manfaat Penelitian 3
BAB 2 TINJAUAN PUSTAKA 4
2.1 Matriks Non-negatif 4
2.2 Faktorisasi Matriks 6
2.3 Kondisi Karush-Kuhn-Tucker 6
2.4 Quadratic Programing 8
2.5 Successive Quadratic Programming 8
BAB 3 HASIL DAN PEMBAHASAN 9
3.4 Pemrograman Kuadrat Berurutan (Successive Quad-
ratic Programming) 16
BAB 4 KESIMPULAN DAN SARAN 24
4.1 Kesimpulan 24
4.2 Saran 24
DAFTAR PUSTAKA 25
DAFTAR GAMBAR
Nomor Judul Halaman
3.1 Kurva harga permintaan 10
3.2 Kurva harga permintaan 10
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Matriks Non-negatif adalah matriks yang seluruh elemannya tidak be- nilai negatif. Faktorisasi matriks adalah proses pemecahan atau pen- guraian suatu matriks menjadi beberapa matriks. Secara umum fak- torisasi matriks dibagi menjadi dua kelompok yaitu metode langsung dan aproksimasi.
Faktorisasi Matriks Non-negatif adalah suatu algoritma optimasi iterasi. yaitu menguraikan satu matriks menjadi beberapa matriks yang komponennya tidak negatif. Faktorisasi Matriks Non-negatif (FMN) berfungsi untuk memperoleh gambaran dari data non-negatif.
Dengan adanya data n × m data matriks V integer dengan Vij > 0 dan bilangan bulat positif r < min(n, m) faktorisasi matrik non-negatif memperoleh 2 (dua) matriks non negatif W ∈ Rn×r dan H ∈ Rr×m seperti :
V ≈ W H (1.1)
Jika setiap kolom V refresentatif pada suatu objek; faktorisasi matriks non-negatif memperkirakannya dengan kombinasi linier dari r basis kolom W . Pendekatan konvensional untuk mendapatkan W dan H dengan memperkecil perbedaan antara V dan W H:
min f (W, H) = 1 2
Xn i=1
Xm j=1
(Vij(W H)ij)2 kendala:
Wia ≥ 0, Wbj ≥ 0, ∀i, a, b, j
Ketidaksamaan seperti variable atas dan bawah adalah mengacu kepada batas kendala. Kerena itu, persamaan (1.1) adalah suatu ma-
2
Xn i=1
Xm j=1
(Vij − (W H)ij)2 =k V − W H k2F
dimana k ◦ k adalah norm Frobenius.
Pada penelitian sebelumnya beberapa metode digunakan dalam penyelesaian faktorisasi matriks non-negatif. Metode yang dilakukan antara lain Algoritma Multiplivicative (Lee dan Seung, 2001). Metode ini mudah dilakukan dan sering memberikan hasil yang baik. Setiap iterasi metode ini, elemen W dan H dikalikan dengan faktor-faktor tertentu.
Kemudian ada pula metode yang sudah digunakan yaitu metode Projected Gradient terhadap optimisasi batas kendala dengan beber- apa modifikasi yang bermanfaat menghasilkan efisiensi dalam pelak- sanaannya. Metode ini menjadi menarik karena maetode ini konvergen lebih cepat dari metode multiplicative. Dari kedua metode terdahu- lu tersebut tentunya mempunyai kelebihan dan kekurangan terutama dalam hal problema non linier.
Banyak metode untuk faktorisasi matriks non-negatif. Beber- apa diskusi dalam membahas batas kendala tidak dilakukan dengan tepat. (Paatero, 1999). Dibutuhkan sifat-sifat tertentu dalam ma- salah faktorisasi matriks non-negatif serta perlu dilakukan pemerik- saan solusi pada setiap iterasi. Ini berarti beberapa metode terdahulu membutuhkan banyak waktu dan juga dianggap sulit. Oleh sebab itu penulis mencoba melakukan penelitian terhadap faktorisasi matriks non-negatif dengan pendekatan quadratik programing diharapkan da-
3
Dalam hal ini karena masalah yang dihadapi adalah masalah batas kendala, maka peneliti berasumsi bahwa ada kaitan Quadratic Prog- raming untuk menyelesaikan permasalahan batas kendala tersebut de- ngan mengunakan metode Kuhn Tucker.
1.2 Perumusan Masalah
Berdasarkan latar belakang diatas dapat dirumuskan masalah antara lain:
1. Optimisasi batas kendala pada faktorisasi matriks non-negatif;
2. Menggunakan pendekatan Quadratic Programming dalam penye- lesaian optimasi faktorisasi matriks non-negatif.
1.3 Tujuan Penelitian
Tujuan penelitian ini adalah untuk mendeskripsikan ide dasar dari faktorisasi matriks non negatif, menunjukkan bagaimana pendekatan quadratic programing dapat mengoptimisasi faktorisasi matriks non- negatif.
1.4 Manfaat Penelitian
Manfaat dari penelitian ini adalah untuk menambah wawasan penge- tahuan dalam penelitian dibidang matematika, khususnya hal-hal yang berkaitan faktorisasi matriks non-negatif.
BAB 2
TINJAUAN PUSTAKA
2.1 Matriks Non-negatif
Matriks non-negatif adalah suatu matriks real atau integer A = [aij] dimana untuk setiap elemen pada A merupakan bilangan non-negatif (sama dengan nol atau lebih besar dari nol). Adapun karakteristik yang melekat dari bentuk matriks tak negatif ini jika ukurannya n × n, adalah jumlah diagonal matriks nya tak negatif dan terdapat nilai eigen yang positif sedemikian hingga absolut nilai eigen yang lain tidak lebih besar dari nilai eigen tersebut, dan disebut nilai eigen maksimal. Namun untuk matriks tak negatif n × m dapat dilihat pada nilai singular terbesarnya. Berikut ini untuk menentukan nilai skalar V − W H akan digunakan bentuk nilai singularnya sebagai salah satu bentuk normnya. Norm ini berguna sebagai fungsi tujuan agar pro- ses pencarian berulang-ulang atau iterasinya menjadi konvergen ke faktor-faktor yang dapat mendekati keorisinalitas matriks V . Misal- kan A adalah matriks berukuran n × m maka yang dimaksud dengan norm matriks adalah sebuah skalar yang menyatakan ukuran dari ma- triks yang bergantung pada entri-entrinya. Notasinya adalah k A k, sedemikian sehingga memenuhi sifat:
1. k A k≥ 0 dan akan sama dengan nol jika A = 0.
2. k cA k=k c kk A k untuk semua c skalar.
5
k A k2= (X
ij
a2ij)12
6
2.2 Faktorisasi Matriks
Faktorisasi matriks adalah proses pemecahan atau penguraian suatu matriks menjadi beberapa matriks. Pada Matriks Non-negatif matriks V berukuran m × n dengan vij ≥ 0, akan diuraikan menjadi dua matriks non-negatif W ∈ Rn×r dan H ∈ Rr×m dengan r < min(n, m) sedemikian sehingga:
V ≈ W H (2.1)
Sebagai penjelasan Faktorisasi Matriks dengan menggunakan Fak- torisasi Matriks Non negatif.
Diberikan suatu matriks Vm×n, non negatif matriks faktorization akan menguraikan matriks V menjadi:
Vm×n ≈ Wm×rHr×n
dimana W dan H adalah matriks orthogonal, P
adalah matriks diag- onal dengan nilai-nilai pada diagonal lebih besar atau sama dengan nol.
2.3 Kondisi Karush-Kuhn-Tucker
Pada tahun 1951 Kuhn Tucker mengemukakan suatu teknik optimisasi yang dapat digunakan untuk pencarian titik optimum dari suatu fungsi yang berkendala. Metode Karush Kuhn Tucker ini dapat digunakan untuk mencari solusi yang optimum dari suatu fungsi tanpa meman- dang sifat dari fungsi tersebut apakah linier atau non linier.
Terdapat beberapa syarat Karush Kuhn Tucker untuk masalah
7
Misalkan f (x) dan gi(x) merupakan suatu masalah yang berpola me- maksimumkan. Jika x = (x1, x2, . . . , xn) merupakan suatu solusi op- timal untuk f (x) dan gi(x), maka x = (x1, x2, . . . , xn) harus memenuhi (3.21) dan terdapat pengali λi, λ2, . . . , λm serta variabel slack s1, s2, . . . , sn
sehingga memenuhi:
1. ∂x∂f
j −Pm
i=1λi∂gi
∂xj + sj untuk j = 1, 2, . . . , n 2. λi[bi− gi(x)] = 0 untuk i = 1, 2, . . . , m 3. (∂x∂f
j
−Pm
i=1λ1∂gi
∂xj)xj untuk j = 1, 2, . . . , n 4. λi ≥ 0 untuk i = 1, 2, . . . , m 5. sj ≥ 0 untuk j = 1, 2, . . . , n
Teorema 2.2 (Syarat KKT masalah minimasi (Winston, 2003))
Misalkan f (x) dan gi(x) merupakan suatu masalah berpola memini- mumkan. Jika x = (x1, x2, . . . , xn) merupakan suatu solusi optimal untuk f (x) dan gi(x), maka x = (x1, x2, . . . , xn) harus memenuhi (3.21) dan terdapat pengali λi, λ2, . . . , λm serta variabel surplus s1, s2, . . . , sn
sehingga memenuhi:
1. ∂x∂f
j +Pm
i=1λi
∂gi
∂xj + sj untuk j = 1, 2, . . . , n 2. λ1[bi− gi(x)] = 0 untuk i = 1, 2, . . . , m 3. (∂x∂f
j +Pm
i=1λi∂gi
∂xj)xj untuk j = 1, 2, . . . , n 4. λi ≥ 0 untuk i = 1, 2, . . . , m 5. ej ≥ 0 untuk j = 1, 2, . . . , n
Pada syarat kedua dari Teorema 2.1 dan Teorema 2.2 berakibat gi(x) − bi≤ 0. Hal ini dapat dilihat pada saat λi = 0, sehingga bi− gi(x) 6=
0. Berdasarkan bentuk umum fungsi kendala, maka bi− gi(x) > 0 yaitu
8
2.4 Quadratic Programing
Quadratic programing merupakan pendekatan penyelesaian permasala- han optimisasi linier dimana kendalanya berupa fungsi linier dan fungsi tujuannya merupakan kuadrat dari variable keputusan ataupun perkalian dari dua variable keputusan (Hiller dan Lieberman, 2001).
min f (x) = CTX +1
2XTQX + d kendala:
AX ≤ B, X ≥ 0
Ketika fungsi objektif f (x) adalah cembung sempurna (konkaf ) untuk semua daerah layak diperoleh titik yang merupakan minimum lokal dan juga global. Maka dalam kondisi seperti ini menjamin bahwa Q adalah definit positif.
2.5 Successive Quadratic Programming
Metode pemrograman kuadratik berurutan (SQP) adalah kelas metode yang sangat kuat dan populeruntuk memecahkan masalah pemrogra- man nonlinier, terutama yang memiliki batasan nonlinier yang ku- at (Han, 1976). Selama dekade terakhir, SQP telah terbukti tampil cukup andal dan efisien pada masalah optimasi proses kimia berukuran kecil dan menengah (katakanlah, naik sampai 1000 variabel yang tidak diketahui) bila dibandingkan dengan metode pemrograman nonlinier lainnya (NLP). (Berna, 1980), Hal ini umumnya diyakini (Sargent, et al., 1992; Lucia et al., 1992) bahwa pemrograman nonlinier skala besar masalah (yaitu, dengan beberapa ribu tidak diketahui) berada dalam
BAB 3
HASIL DAN PEMBAHASAN
Optimisasi pada faktorisasi matriks non-negatif pada umumnya berben- tuk nonlinier yang dipaksaksan untuk bersifat non-negatif, memper- timbangkan bentuk umum permasalahan non-linier yang kemudian ki- ta transformasikan ke dalam bentuk qadratic programming.
3.1 Program Non-Linier
Pada penerapan pemrograman linear, asumsi penting yang harus dipenuhi adalah bahwa semua fungsi berupa linear. Sering kali dalam per- masalahan nyata sehari-hari asumsi penting ini tidak dapat terpenuhi.
Hal inilah yang kemudian menimbulkan konsep baru yaitu masalah pemrograman non-linear. Menurut Hiller dan Lieberman (2001) ben- tuk umum dari pemrograman non-linear adalah menemukan nilai x = (x1, x2, . . . , xn) sehingga:
min / max
f (x), dimana f (x) berupa fungsi-fungsi non-linear (3.1) dengan kendala gi(x) untuk setiap i = 1, 2, . . . , m (3.2)
dan x ≥ 0 (3.3)
Fungsi kendala gi(x) dapat berupa fungsi non-linear ataupun fungsi linear. Selain itu, f (x) dan fungsi gi(x) adalah fungsi-fungsi dengan n variabel.
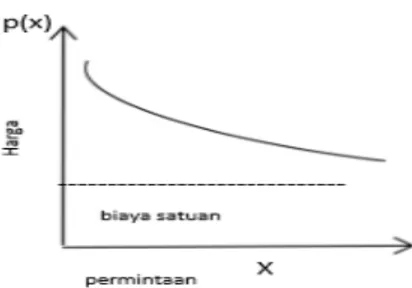
Salah satu contoh penggunaan pemrograman non-linear adalah tentang masalah produk campuran dan elastisitas harga. Suatu pe- rusahaan besar memiliki kemungkinan menghadapi elastisitas harga dimana banyaknya barang yang dijual berbanding terbalik dengan harganya. Gambar 3.1. berikut menjelaskan kurva harga permintaan
10
Gambar 3.1 Kurva harga permintaan
Nilai dari p(x) adalah harga yang ditetapkan agar terjual x satuan barang. Jika biaya satuan produksi barang selalu konstan (c), maka keuntungan perusahaan akan dinyatakan dalam bentuk fungsi non- linear P (x) = p(x) − cx seperti yang dijelaskan dalam Gambar 3.1.
Gambar 3.2 Kurva harga permintaan
Apabila terdapat n jenis produk yang dihasilkan dengan fungsi keuntungan serupa, dimana Pj(xj) menyatakan fungsi keuntungan dari penjualan xj satuan dari produk j(j = 1, 2, . . . , n), maka fungsi tujuan secara keseluruhan adalah f (x) = Pjnj = 1(xj) yaitu penjumlahan dari beberapa fungsi keuntungan yang nonlinear. (Hillier dan Lieberman, 2001).
3.2 Kondisi Kuhn-Tucker
11
berkendala persamaan yang dikerjakan dengan mencari titik titik sta- sionernya, yaitu titik yang berpotensi menjadi titik optimal.
Terdapat beberapa syarat Karush Kuhn Tucker untuk masalah optimasi berkendala. Syarat tersebut dirumuskan oleh Karush dan Kuhn Tucker. Teorema 2.1 dan 2.2 merupakan syarat KKT untuk masalah maksimasi dan minimasi.
Teorema 3.1 (Syarat KKT masalah maksimasi (Winston, 2003)) Misalkan f (x) dan gi(x) merupakan suatu masalah berpola memak- simumkan. Jika x = (x1, x2, . . . , xn) merupakan suatu solusi optimal untuk f (x) dan gi(x), maka x = (x1, x2, . . . , xn) harus memenuhi (3.21) dan terdapat pengali λi, λ2, . . . , λm serta variabel slack s1, s2, . . . , sn se- hingga memenuhi:
1. ∂x∂f
j −Pm
i=1λi∂gi
∂xj + sj untuk j = 1, 2, . . . , n 2. λi[bi− gi(x)] = 0 untuk i = 1, 2, . . . , m 3. (∂x∂f
j
−Pm
i=1λ1∂gi
∂xj)xj untuk j = 1, 2, . . . , n 4. λi ≥ 0 untuk i = 1, 2, . . . , m 5. sj ≥ 0 untuk j = 1, 2, . . . , n
Teorema 3.2 (Syarat KKT masalah minimasi (Winston, 2003))
Misalkan f (x) dan gi(x) merupakan suatu masalah berpola memini- mumkan. Jika x = (x1, x2, . . . , xn) merupakan suatu solusi optimal untuk f (x) dan gi(x), maka x = (x1, x2, . . . , xn) harus memenuhi (3.21) dan terdapat pengali λ1, λ2, . . . , λm serta variabel surplus s1, s2, . . . , sn
sehingga memenuhi:
1. ∂x∂f
j +Pm
i=1λi∂gi
∂xj + sj untuk j = 1, 2, . . . , n
12
3. (∂x∂f
j +Pm
i=1λi
∂gi
∂xj)xj untuk j = 1, 2, . . . , n 4. λi ≥ 0 untuk i = 1, 2, . . . , m 5. ej ≥ 0 untuk j = 1, 2, . . . , n
Pada syarat kedua dari Teorema 2.1 dan Teorema 2.2 berakibat gi(x) − bi ≤ 0. Hal ini dapat dilihat pada saat λi = 0, sehingga bigi(x) 6=
0. Berdasarkan bentuk umum fungsi kendala, maka bigi(x) > 0 yaitu gi(x) ≤ bi.
3.3 Quadratic Programming
Quadratic programming merupakan pendekatan penyelesaian permasala- han optimasi nonlinear dimana kendalanya berupa fungsi linear dan fungsi tujuannya merupakan kuadrat dari variabel keputusan ataupun perkalian dari dua variabel keputusan (Hillier dan Lieberman, 2001).
Model nonlinear yang akan diselesaikan dengan menggunakan quadra- tic programming memiliki bentuk umum yaitu (Peressini, et al., 1988).
min f (x) = CTX +1
2XTQX + d kendala:
AX ≤ B, X ≥ 0
Konsep matriks CT, X, A, dan B masih sama seperti yang telah dijelaskan Adapun d merupakan suatu konstanta, sedangkan Q meru- pakan matriks simetris yang tersusun dari nilai qij, dimana qij meru- pakan hasil dari turunan parsial kedua terhadap xi dan xj dari fungsi tujuan. Matriks Q merupakan matriks simetris, sehingga nilai q = q .
13
tidak, yaitu : Meminimumkan f (x1, x2) = 15x1+ 30x2+ 4x1x2− 2x12− 4x22, dengan kendala x1+ 2x2 ≤ 30 dan x1, x2 > 0.
Pada masalah ini, bentuk model non-linear yang diselesaikan de- ngan quadratic programming dapat dicari yaitu dengan menentukan CT, X, A, Q dan b Matriks CT merupakan matriks baris koefisien-koefisien dari x sehingga CT = [1530].
Matriks X adalah matriks kolom untuk variabel-variabel kepu- tusan, sehingga
h x1
x2
i
, sedangkan Q =
h −4 4 4 −8
i
. Matriks A seba- gai matriks koefisien koefisien fungsi kendala, karena Contoh hanya memiliki satu kendala maka matriks A menjadi matriks satu baris yaitu A = [ 1 2 ], sehingga dapat ditentukan B = [30].
Setelah teridentifikasi, bentuk permasalahan dapat disusun ulang, yaitu :
f (x1, x2) = 15x1 + 30x2+ 4x1x2− 2x21− 4x22
= [ 15 30 ] h x1
x2
i 1 2
h x1
x2
i h −4 4 4 −8
i h x1
x2
i + 0.
atau,
min f (x) = CTX +1
2XTQX + d kendala:
x1+ 2x2 ≤ 30.
atau
AX ≤ B
Berdasarkan identifikasi yang telah dilakukan, maka bentuk pa- da Contoh 3.3 dapat diselesaikan dengan menggunakan pendekatan quadratic programming.
3.3.1 Penyelesaian quadratic programming
Permasalahan pada quadratic programming dapat diselesaiakan de-
14
pada Teorema 2.1 dan Teorema 2.2. Selain itu, dalam quadratic pro- gramming juga terdapat kondisi complementary slackness khusus. Se- cara umum, kondisi complementary slackness pada quadratic program- ming dapat dinyatakan dalam Sifat 3.1 berikut :
Sifat 3.1 Complementary slackness pada quadratic programming (Win- ston, 2003)
(1) ej dan sj pada kondisi Kuhn-Tucker dan xj tidak dapat kedua- duanya bernilai positif.
(2) Variabel surplus (excess) ataupun slack untuk kendala ke−i dan λi tidak dapat kedua-duanya bernilai positif.
Bukti Sifat 3.1.
1. Diperhatikan syarat (1) dan (3) pada teorema 2.1 yaitu : syarat (1) yaitu, ∂x∂f
j −Pm
i=1λi∂gi
∂xj + sj = 0, sehingga :
∂f
∂xj −Pm i=1λi
∂gi
∂xj = −sj disubsitusikan ke syarat (3)
∂f
∂xj −Pm i=1λi∂gi
∂xj)xj = 0 sjxj = 0
jika sj = 0, maka xj 6= 0, yaitu, xj > 0
xj = 0, maka xj 6= 0, yaitu, sj > 0 or sj < 0. berdasarkan syarat (4) maka sj > 0.
Hal ini berlaku juga untuk Teorema 2.2, sehingga terbukti bahwa ej dan sj pada kondisi Kuhn-Tucker dan xj tidak dapat kedua-
15
Jika λi = 0 maka s01 6= 0, yaitu s01 > 0. Jika s01 = 0 maka λi 6= 0, yaitu λi > 0 atau λi < 0. Berdasarkan Syarat (5) maka λi > 0.
Pada fungsi kendala gi(x) ≥ bi dapat diubah menjadi gi(x) + e0i= bi. Melalui cara yang sama maka didapat pula λie0i = 0, sehingga terbukti bahwa variabel surplus (excess) ataupun slack untuk kendala ke−i dan λi tidak dapat kedua-duanya bernilai positif.
Persamaan persamaan yang didapat dari langkah a merupakan langkah pelinearan masalah pemrograman non-linear dengan menggu- nakan syarat Kuhn Tucker, selanjutnya masalah tersebut dapat dise- lesaikan dengan substitusi atau cara cara yang lain. Contoh berikut merupakan contoh masalah model nonlinear dengan quadratic pro- gramming
Contoh Diketahui model non-linear kuadratik yang meminimumkan z = −x1− x2+ (1
2)x21+ x22 (3.4) kendala:
x1 + x2 ≤ 3 (3.5)
−2x1− 3x2 ≤ 6 (3.6)
x1, x2 ≥ 0
Penyelesaian :
Diperhatikan bahwa (2.26) dan (2.27) dapat diselesaikan dengan quadratic programming dengan langkah sebagai berikut:
Membentuk syarat Kuhn-Tucker dari model nonlinear.
Berdasarkan Teorema 2.4, maka pada Contoh 2.4 dapat ditentukan syarat Kuhn Tuckernya yaitu:
1. 1 + x1− x2+ λ1− 2λ2− e1 = 0
16
2. λ1[3 − (x1+ x2)] = 0 λ2[−6 − (−2x1− 3x2)] = 0 3. 1 + x1− x2+ λ1− 2λ2 = 0
1 + 2x2− x1+ λ1 − 3λ1x2 = 0 4. λ1, λ2 ≥ 0
5. e1, e2 ≥ 0
Sebagai akibat dari (2.31) maka x1+ x2− 3 ≤ 0
(2x1− 3x2) − (−6) ≤ 0
Bentuk 2 dapat dijadikan bentuk kanonik sehingga menjadi :
x1+ x2+ s01 = 3 2x1+ 3x2− e01 = 6
3.4 Pemrograman Kuadrat Berurutan (Successive Quadratic Pro- gramming)
Metode pemrograman kuadratik berurutan (SQP) adalah kelas metode yang sangat kuat dan populer untuk memecahkan masalah pemrogra- man nonlinier, terutama yang memiliki batasan nonlinier yang kuat (Han, 1976).
17
tidak segera diterima sebagai titik selanjutnya untuk melanjutkan pen- carian, namun pencarian variabel tunggal dilakukan antara titiktitik lama dan baru agar memiliki titik yang lebih baik dan layak.
Dalam pemrograman kuadrat, model ekonomi adalah fungsi kuadrat, dan kendalanya adalah semua persamaan linier. Untuk mengatasi masalah ini fungsi Lagrangian terbentuk, dan kondisi Kuhn-Tucker diterapkan pada fungsi Lagrangian untuk mendapatkan satu set per- samaan linier. Himpunan persamaan linier ini kemudian dapat dipe- cahkan dengan Metode Simpleks untuk optimum. Ternyata variabel buatan diperlukan untuk bagian dari kendala dan variabel kendur da- pat digunakan untuk kendala lain agar memiliki basis yang pada awal- nya layak dilakukan. Selain itu, menemukan solusi layak dasar awal mungkin satu-satunya solusi yang layak, jadi usaha komputasi linier minimal. Pada titik ini, penting untuk memahami solusi dari masalah pemrograman kuadratik, dan prosedur ini akan dijelaskan selanjutnya dan diilustrasikan dengan sebuah contoh. Kemudian algoritma pem- rograman kuadratik berturutan akan dijelaskan dan diilustrasikan de- ngan sebuah contoh. Juga, modifikasi prosedur akan dibahas yang me- ngurangi usaha komputasi dalam menghitung secara numerik matriks Hessian yang harus diperoleh dari masalah pemrograman nonlinier.
Secara teoritis, dengan menggunakan fungsi kuadratik untuk mendekati model ekonomi nonlinier dari proses dapat dianggap lebih unggul dari fungsi linier untuk mewakili model ekonomi. Ini adalah bagian dari motivasi untuk menggunakan pemrograman kuadratik yang dapat di- tunjukkan oleh persamaan berikut:
max Xn
j=1
cjXj− 1 2
Xn j=1
Xn k=1
qjkXjXk (3.7)
kendala:
Xn j=1
aijXi ≤ bi untuk i = 1, 2, . . . , m X ≥ 0, untuk i = 1, 2, . . . , n
18
dimana qjk = qkj adalah derivatif parsial kedua berkenaan dengan xj
dan xk model ekonomi nonlinier. Prosedur pemrograman kuadratik dimulai dengan menambahkan variabel kendur xn+ike persamaan kendala linier. Tidak perlu menggunakan x2n+i karena masalahnya akan dipe- cahkan dengan pemrograman linier, dan semua variabel harus positif atau nol. Fungsi Lagrangian terbentuk sebagai berikut:
L(X, λ) = Xn
j=1
cjXj −1 2
Xn j=1
Xn k=1
qjkXjXk − Xm
i=1
λi( Xn
j=1
aijXj + xn+1− bi)
Pengali Lagrange positif diperlukan, jadi tanda negatif digunakan pada persamaan dengan persamaan kendala.
Menetapkan turunan parsial pertama dari fungsi Lagrangian berke- naan dengan xj dan i sama dengan nol memberikan himpunan aljabar linier (n + m) linier berikut ini:
cj− Xn
k=1
qjkXk − Xm
i=1
aijλ1 ≤ 0 untuk j = 1, 2, . . . , n (3.8)
Xn m
aijXj+ xn+1− bi = 0 untuk j = 1, 2, . . . , m (3.9)
Bentuk ketidaksetaraan kondisi Kuhn-Tucker, digunakan untuk memperhitungkan xj > 0. Juga, kondisi kelonggaran komplementer harus dipuaskan, yaitu produk variabel kendur Xn+1 dan multiplier Lagrange i adalah nol.
λiXn+1 = 0 untuk i = 1, 2, · · · , m (3.10)
Jika Xn+1 = 0, maka kendalanya aktif, persamaan; dan λ1 6= 0.
19
Xn+i dapat berfungsi sebagai variabel untuk basis yang awalnya layak untuk persamaan (3.9). Namun, variabel buatan diharuskan memili- ki dasar yang layak untuk persamaan (3.8). Menambahkan variabel buatan zj dengan koefisien cj ke persamaan (3.8) adalah cara mudah untuk memulai dengan zj = 1
Juga, fungsi objektifnya adalah meminimalkan jumlah variabel buatan untuk memastikan bahwa mereka tidak berada dalam solusi optimal akhir Sebagai hasil dari modifikasi ini, persamaan (3.8) dan (3.9) menjadi:
min : Xn
j=1
zj (3.11)
kendala:
Xn i=1
qjkXk + Xm
i=1
aijλi− sj+ cjzj = ci untuk j = 1, 2, · · · , n
Xn j=1
aijXj + Xn1 = b1 untuk j = 1, 2, · · · , m
Ini sekarang merupakan masalah pemrograman linier yang dapat dipecahkan untuk nilai optimal x dan λ, solusi dari masalah pemrogra- man kuadratik. Selain itu, solusinya harus memenuhi x ≥ 0, λ ≥ 0 dan λiXn+i = 0. Oleh karena itu, Algoritma Simplex harus dimodifikasi un- tuk menghindari kedua λi dan Xn+i menjadi variabel dasar, yaitu nol, untuk memenuhi kondisi kelonggaran yang bebas (26). Ini mungkin memerlukan pemilihan variabel kedua yang terbaik untuk masuk ke dasar dalam melanjutkan Algoritma Simplex jika salah satu λi atau Xn+i berada dalam basis dan yang lainnya adalah untuk masuk.
Franklin (23) telah memberikan keunikan dan eksistensi teorema yang membuktikan prosedur di atas adalah solusi untuk masalah pem- rograman kuadratik dan merupakan rujukan yang direkomendasikan untuk rincian tersebut. Pada titik ini metode diilustrasikan dengan sebuah contoh.
20
Contoh. Menggunakan pemrograman kuadrat menentukan maksimum fungsi berikut yang tunduk pada batasan yang diberikan.
max 5x1+ x2 −1
2(2x21− 2x1x2− 2x2x1+ 2x22) kendala:
x1+ x2 ≤ 2
Masalah pemrograman kuadrat dibangun menggunakan persamaan (3.11) dengan c1 = 5, c2 = 1, q11= 2, q12= −2, q21= −2, q22= 2, a11= 1, a12= 1 dan b1= 2.
Masalah pemrograman linier dari persamaan (3.11) adalah:
min z1+ z2
kendala:
2x12x2+ λ1− s1+ 5z1 = 5
2x1 + 2x2+ λ1− s2+ z2 = 1 x1+ x2+ x3 = 2
21
Eliminasi z1 dan z2 dari fungsi objektif memberikan rangkaian persamaan berikut untuk penerapan Metode Simpleks:
13
5x1 − 13
5x2 − 11
5λ1+ 1
5s1+ s2 = c − 2 c = 2 2x1 − 2x2+ λ1− s1+ 5z1 = 5 z1 = 1 2x1+ 2x2+ λ1− s2+ z2 = 1 z2 = 1
x1+ x2+ x=2 x3 = 2
x2 masuk basis, x1 meninggalkan dasar:
0x1 −2
5λ1− 1
5s2+15s2+43z2 = c − 115 c = 115 2λ1 − s1− s2+ 5z1+ z2 = 6 z2 = 65
−x1+ x2+ 12λ1− 1
2s2 +12z2 = 12 x2 = 112
2x1 + x3− 1
2λ1+ 12s2− 1
2z2 = 12 x3 = 112
λ1 akan masuk basis, dan persamaan kendala kedua akan digunakan untuk manipulasi aljabar untuk memastikan sisi kanan positif dari persamaan kendala sesuai dengan Algoritma Simplex. Namun, ini akan memiliki keduanya λ1 dan x3 dalam basis (nol nol); dan kondisi kelonggaran pelengkap, λ1x3 = 0, tidak akan terpenuhi. Akibatnya, variabel lain harus dipilih untuk masuk basis. Ini biasanya satu dengan koefisien kecil berikutnya dan untuk masalah ini adalah x1. Pilih x1
untuk masuk basis, dan x3 meninggalkan dasarnya λ1 masuk basis, z1 meninggalkan dasar:
z1+ z2 = c − 0 c = 0
λ1− 1
3s1− 1
3s2+ 53s2+ 53z2+ 13z2 = 315 λ1 = 3 2λ1 − s1− s2+ 5z1+ z2 = 6 z2 = 65 x2+ x3+ 121s1+121 s2− 5
12z1− 1
6z2 = 12 x2 = 12
2x1 + x3− 1
12s1+121 s2+125z1− 1
6z2 = 32 x1 = 132
Minimum telah tercapai Semua koefisien variabel dalam fungsi objektif
22
bersifat positif. Karena itu, solusi optimal untuk masalah pemrogra- man kuadrat ini adalah:
x1 = 3
2, x2 = 1
2, λ1 = 3, x3 = 0
Pengali Lagrange positif konsisten dengan kondisi Kuhn-Tucker un- tuk persamaan maksimum, karena tanda negatif digunakan pada per- samaan (3.7).
Pemrograman kuadrat berurutan secara iteratif memecahkan ma- salah pemrograman nonlinier dengan menggunakan pendekatan kuadratik dengan model ekonomi dan pendekatan linier dengan persamaan kendala.
Seiring rangkaian masalah pemrograman kuadrat dipecahkan, solusi menengah ini menghasilkan urutan titik yang harus tetap berada di wilayah yang layak atau cukup dekat dengan kawasan ini untuk berte- mu secara optimal. Logika yang digunakan dengan metode ini adalah mencari sepanjang garis antara titik baru dan sebelumnya untuk mem- pertahankan solusi yang layak atau mendekati solusi yang layak. Selain itu, usaha komputasi dalam mengevaluasi matriks Hessian signifikan, dan perkiraan kuasi-Newton telah digunakan untuk mengurangi upaya ini. Contoh berikut menggambarkan pemrograman kuadrat berurutan untuk masalah sederhana. Pembahasan berikut ini menjelaskan mod- ifikasi pada prosedur komputasi untuk meningkatkan efisiensi metode.
Contoh Selesaikan masalah berikut dengan pemrograman kuadrat beru- rutan dimulai pada titik 0(0, 0).
min : (x1− 1)2+ (x2− 2)2
23
bentuk berikut.
(0.208x1k− 0.75x1) + x2 ≤ 0.85 + 0.104x21k
Menempatkan masalah dalam bentuk persamaan (3.7), memberi:
max : (0.208x1k− 0.75x1) + x2 ≤ 0.85 + 0.104x21k x1 + x2 ≤ 4
Masalah pemrograman kuadrat dibuat menjadi
dengan c1 = 2, c2 = 4, q1 = 2, q12 = q21 = 0, q22 = 2, a11 = (0, 208x1k − 0, 75), a12= 1, a21= 1, a22= 1, b1 = 0.85 + 0.104x1k, dan b2 = 4:
min : z1+ z2
kendala:
2x1 + (0.208x1k0.75)λ1+ λ2s1+ 2z1 = 2 2x1 + λ1+ λ2− s2− 4z2 = 4
(0.208x1k0.75)x1 + x2+ x3 = 0.85 + 0.10x1k2
x1+ x2+ x3 = 4
Memecahkan masalah pemrograman linier di atas dengan Metode Sim- plex dengan x0 = (0, 0) dan memastikan kondisi kelonggaran komple- menter terpenuhi memberikan hasil sebagai berikut untuk x∗0.
x1 = 1.192, x2 = 1.740 λ1 = 0.512
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Faktorisasi Matriks Non Negatif berbentuk non-linier dan karena berben- tuk non-linier maka permasalahan optimasinya dapat diselesaikan de- ngan pendekatan Quadratic Programming.
4.2 Saran
Perlu dikaji beberapa metode untuk menyelesaikan faktorisasi matriks non-negatif yang lebih efisien , sehingga dapat digunakan terutama dalam program linier dan program non linier.
DAFTAR PUSTAKA
Bertekas, D. (1999). Non Linear Programing. Athena Scientific, MA.
Dostal, Z., (2009). Optimal Quadratic Programming Algorithms.
Springer. Vol 23.
Kuhn, H.W. dan Tucker, A.W.(1951). Nonlinear Programming.
Proc.second berkeley symp. on Math.Statist.and Prob.
Lee, D. D. H. S. Seung, (2001). Algorithms for Non-Negative Matrix Factorization. Adv, Neural Inf. Process. Syst. Vol. 13: pp 556–
562.
Lucia, A dan XU.J (1994). Methods Of Successsive Quadratic Pro- gramming. Computers & Chemical Engineering Vol 18.
Sargent, R., Ding W. M., dan Morales P.J.L (1992). A new SQP Al- gorithm for Large-Scale nonlinier Programming. AIChE Annual Meeting, paper 137b
Sharma, K.C., dan Singh, J (2013). Solution Methods For Linier Fac- torized Quadratic Optimization and Quadratic Fractional Opti- mization problem. IOSR Journal of Mathematics. Vol 8.
Yang, Z dan Oja, E.(2012). Quadratic Nonnegatif Matriks Factoriza- tion. Pattern Recognition. Vol.45 pp 1500-1510
Zdunek, R., dan Chichoki, A (2006). Nonnegative Matrix Factorization With Quadratic Programing. Neurocomputing Vol. 71 pp 2309- 2320