0
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018TRIGONOMETRI
Untuk SMA dan Sederajat
Husein Tampomas
1
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018BAB 1
PENGANTAR KE FUNGSI TRIGONOMETRI
PENGERTIAN
Dalam bahasa Yunani, trigonometri terdiri dari dua kata, yaitu trigono yang artinya
segitiga dan metro yang artinya ukuran.
Trigonometri adalah ilmu yang mempelajari hubungan antara sisi dan sudut dari segitiga.
1.
PENAMAAN SISI DAN SUDUT PADA SEGITIGA
Dalam geometri dasar, segitiga ABC dinotasikan ABC mempunyai unsur-unsur yang meliputi sisi dan sudut. Penamaan sisinya adalah sisi BCa (di depan A), sisiACb (di depan B) , dan sisiABc (di depan C). Tetapi kadang-kadang sisi-sisi suatu segitiga dapat dinotasikan dengan huruf kecil lainnya seperti
x, y, z, h, dan sebagainya.
Sudut ABC dinotasikan ABC biasa juga menggunakan nama titik sudutnya B. Tetapi kadang-kadang hanya menggunakan huruf kapital dari titik sudutnya, misalnya A, B, P, W, X, dan sebagainya atau huruf kecil, misalnya p, t, x, y, z, dan sebagainya. Penamaan sudut tersebut juga kerapkali menggunakan huruf kapital atau kecil dari alphabet Yunani, misalnya BAC A A ,
ABC B B
, dan ACB C C .
Tabel 1 Alphabet Yunani
Huruf Nama Huruf Nama Huruf Nama
Gambar 1 b
a c
A
2
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 20182.
PENGUKURAN SUDUT
Ukuran sudut yang dipergunakan di sini adalah derajat dan radian.
a. Ukuran Sudut dalam Derajat
Definisi:
putaran 360
1 1
O adalah pusat lingkaran
r adalah jari-jari lingkaran
OA = OB = r 1
= 1° = putaran 360
AOB
Sehingga,1putaran360
Ukuran sudut yang lebih kecil (halus) adalah menit dan detik. 1 60'
(menit)
1'60"
(detik)
" 600 . 3 1Contoh 1:
Nyatakan dalam ukuran derajat, menit, dan detik dari 65,37.
Solusi:
65,38 63 0,38 63 0,38 60 ' 63 22,8'63 22 ' 0,8'
63 22 ' 0,8 60" 63 22' 48" Jadi, 63,38 63 22 ' 48" .
Contoh 2:
Nyatakan dalam ukuran derajat dari 126 48'54" .
Solusi:
1 1
126 48'54" 126 48 54
60 3600
126 0,8 0, 015 126,815
Contoh 3:
Diberikan 56,18. Nyatakan dalam derajat, menit, dan detik dari 4dan 7
8. Solusi:
4 4 56,18 224, 72 224 0, 72 224 0, 72 60 ' 224 43, 2 '
224 43' 0, 2 ' 224 43' 0, 2 60" 22443' 12" Jadi, 4224 43'12"
7 7
56,18 49,1575
8 8 49 0,1575 49 0,1575 60 ' 49 9, 45'
49 9 ' 0, 45 60" 49 9' 27"
r r 1
A
B O
3
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018b. Ukuran Sudut dalam Radian
Definisi:
Satu radian ditulis 1 rad, adalah besar sudut yang dihasilkan oleh perputaran sebesar jari-jari lingkaran.
O adalah pusat lingkaran
r adalah jari-jari lingkaran Busur AB = OA = OB = r
c. Konversi Ukuran Putaran, Derajat, dan Radian
Konversi dari ukuran radian ke derajat:
π 180 rad
1
Konversi dari ukuran derajat ke radian:
rad 180
π 1
Konversi ukuran derajat ke putaran:
1
1 putaran 360
Konversi ukuran putaran ke derajat:
4
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018 Konversi ukuran radian ke putaran:
1
1rad putaran 2
Konversi ukuran putaran ke radian:
1putaran2 rad dengan 3,14159...
Catatan:
Perhatikan bahwa dan22 7
rasional. Kedua bilangan dan22 7
sama senilai pada nilai 3,14.
Contoh 5:
Tentukan dalam ukuran derajat dari a. 1 putaran
2 putaran 360 990
4 4
b. 5putaran 5 360 100
18 18 d. nputaran n 360 Contoh 6:
Tentukan dalam ukuran putaran dari
a. 60 b. 150 c. 270 d. n
5
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018 Tentukan setiap sudut berikut ini dalam putaran.a. 3 rad b. 3 rad
Tentukan setiap sudut berikut ini dalam derajat. a. 2 rad b. 3 rad
Tentukan setiap sudut berikut ini dalam
(radian).
a. 45 b. 210 c. 300 d. n
Jika jika 3,14
, tentukan setiap sudut berikut ini dalam radian.
a.
145b.
72 54'c.
38 36'45"Solusi:
a.
145 145 145 3,14 2,53rad180 180
SOAL-SOAL LATIHAN 1
Selesaikanlah setiap soal berikut ini.
6
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018a. 0, 49 b. 8,51 c. 54, 28 d. 108,355
2. Nyatakan dalam ukuran derajat dari
a. 9 30' b. 728 36" c. 25 36'54" d. 48 12'45"
5. Tentukan dalam ukuran derajat dari a. 1putaran
6. Tentukan dalam ukuran putaran dari
a. 75 b. 120 c. 240 d. 315 7. Tentukan setiap sudut berikut ini dalam radian.
a. 5 putaran
8. Tentukan setiap sudut berikut ini dalam putaran. a. 2 rad 9. Tentukan setiap sudut berikut ini dalam derajat.
a. 0,54 rad b. 3,84 rad c. 11 rad
18 d. 35
4 rad
36 10. Tentukan setiap sudut berikut ini dalam
(radian).
a. 50 b. 135 c. 255 d. 330
3.
PENERAPAN PADA LINGKARAN
Pada lingkaran yang berpusat di O berjari-jari r dan diameternyad2r, dengan
3. Sudut pusat dalam derajat: Panjang busur AB: 2
Sudut dalam radian:
7
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018 4. Sudut dalam derajat:Luas juring AOB: 2
Sudut dalam radian:
Luas juring AOB:
5. Hubungan Panjang Busur, Sudut Pusat, dan Luas Juring (sector)
Dalam suatu lingkaran, panjang busur sebanding dengan sudut pusatnya dan juga sebanding dengan luas juringnya.
Panjangbusur Besar Luas juring Panjangbusur Besar Luas juring
AB AOB AOB
Suatu lingkaran berjari-jari 12 cm. Hitunglah a. diameter lingkaran.
b. keliling lingkaran. c. luas lingkaran.
d. panjang busur lingkaran dihadapan sudut pusat 60. e. luas juring lingkaran dihadapan sudut pusat
3
2 3,14 12 12,56cm 360
e. Luas juring lingkaran dihadapan sudut pusat
8
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018Perhatikan gambar 5. Titik O adalah pusat lingkaran,
AD adalah diameter,
LuasjuringCOD COD LuasjuringAOB AOB
Jadi, jari-jari lingkaran adalah 15 cm. Luas Juring
LuasLingkaran 2 Luas JuringAOB AOB
9
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018Kita dapat juga mengerjakannya sebagai berikut.
Panjang busur Panjangbusur 9, 42 9, 42 20, 93cm
9 Tentukan jari-jari lingkaran agar luas juring tersebut maksimum. Berapakah besar sudut pusat AOB?
Solusi:
Misalnya r adalah jari-jari, adalah sudut pusat dalam radian, sehingga
Dari persamaan (1) dan (2) diperoleh
SOAL-SOAL LATIHAN 2
Selesaikanlah setiap soal berikut ini.
1. Suatu lingkaran berjari-jari 15 cm. Hitunglah a. diameter lingkaran.
b. keliling lingkaran. c. luas lingkaran.
d. panjang busur lingkaran dihadapan sudut pusat 150. e. luas juring lingkaran dihadapan sudut pusat 5
10
|
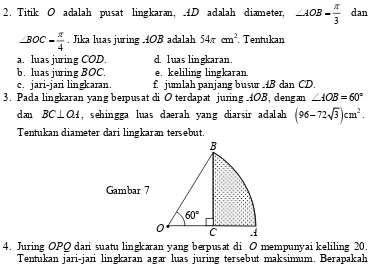
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018 2. Titik O adalah pusat lingkaran, AD adalah diameter,3
AOB
dan
4
BOC
. Jika luas juring AOB adalah 54 cm2. Tentukan a. luas juring COD. d. luas lingkaran.
b. luas juring BOC. e. keliling lingkaran.
c. jari-jari lingkaran. f. jumlah panjang busur AB dan CD.
3. Pada lingkaran yang berpusat di O terdapat juring AOB, dengan AOB 60 dan BCOA, sehingga luas daerah yang diarsir adalah
96 72 3 cm
2. Tentukan diameter dari lingkaran tersebut.4. Juring OPQ dari suatu lingkaran yang berpusat di O mempunyai keliling 20. Tentukan jari-jari lingkaran agar luas juring tersebut maksimum. Berapakah besar sudut pusat POQ?
4.
JENIS-JENIS SUDUT
Sekilas kita mengingat kembali pada pelajaran geometri dasar tentang definisi sudut lancip, sudut siku-siku, sudut tumpul, dan sudut lurus.
Definisi:
a. Sudut lancip adalah sudut yang besarnya antara 0°dan90. (Gambar 8 (a)) b. Sudut siku-siku adalah sudut yang besarnya 90. (Gambar 8 (b))
c. Sudut tumpul adalah sudut yang besarnya antara 90°dan180. (Gambar 8 (c))
d.
udut lurus adalah sudut yang besarnya 180. (Gambar 8 (d))Contoh 15:
Diberikan tiga buah sudut x, y, dan z. Jika x y z 180dan x y z: : 1: 5 : 6. Tentukan jenis-jenis sudut tersebut.
Solusi:
Misalnya xk y, 5 , dank z6k, sehingga
180
x y z
Gambar 8
(a)Sudut lancip (b) Sudut siku-siku (c) Sudut tumpul (d) Sudut lurus Gambar 7
C A
B
O
60
11
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018SOAL-SOAL LATIHAN 3
Selesaikanlah setiap soal berikut ini.
1. Jika a, b, dan c adalah tiga buah sudut, dengan 2a b c 180dan
: : 5 : 9 :1
a b c . Tentukan jenis-jenis sudut tersebut.
2. Jika x, y, dan z adalah tiga buah sudut, dengan 3
x z . Tentukan jenis-jenis sudut tersebut.
3. Jika p, q, dan r adalah tiga buah sudut, dengan 5
p r . Tentukan jenis-jenis sudut tersebut.
5.
JENIS-JENIS PASANGAN SUDUT
Jenis-jenis pasangan sudut meliputi sudut komplemen (sudut yang berpenyiku), sudut suplemen (sudut yang berpelurus), dan sudut kojugat.
Definisi: b. Sudut suplemen (sudut yang berpelurus) adalah dua sudut antara 0 dan 90yang
jumlahnya 180. Dengan perkataan lain, andaikan 0 , 180 maka sudut dan
saling bersuplemen jika 180.Kita mengatakan bahwa sudut adalah pelurus sudut dan sebaliknya sudut adalah pelurus sudut . c. Sudut konjugat adalah dua sudut antara 0 dan 360 yang jumlahnya 360.
Dengan perkataan lain, andaikan 0 , 360 maka sudut dan saling berkonjugat jika 360.
Gambar 9 (a)Sudut Komplemen
90
(b) Sudut Suplemen 180
(c) Sudut Konjugat
360
12
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018Contoh 16:
Diketahui sudut-sudut x 20 dan 3x 10 . Jika sudut-sudut dansaling berkomplemen, tentukan nilai x.
Solusi:
Jika sudut-sudut dan saling berkomplemen, maka haruslah
90
20 3 10 90
x x
4x 80 20
x
Contoh 17:
Diketahui sudut-sudut 70 x dan 6x 40 . Jika sudut-sudut dan saling berpelurus, tentukan nilai x.
Solusi:
Jika sudut-sudut dan saling berpelurus, maka haruslah
180
70 x 6x 40 180 5x 150
30
x
SOAL-SOAL LATIHAN 4
Selesaikanlah setiap soal berikut ini.
1. Diketahui sudut-sudut 2x 40 dan 3x 20 . Jika sudut-sudut dan saling berpelurus, tentukan nilai x, , dan.
2. Diketahui sudut-sudut
4
x
dan 5 15
x
. Jika sudut-sudut dan saling berkomplemen, tentukan nilai x, , dan.
3. Dua buah sudut saling berkomplemen. Selisih dua kali sudut dan sudut kedua adalah pertama 90. Tentukan kedua sudut tersebut.
6.
JENIS-JENIS SEGITIGA
Pada pelajaran geometri dasar telah didefinisikan bahwa: “Jumlah sudut-sudut pada suatu segitiga adalah 180.” Di samping itu telah dikemukakan pula tentang jenis-jenis segitiga yang ditinjau dari sudut-sudutnya, jenis-jenis segitiga ditinjau dari panjang sisi-sisinya, serta jenis-jenis segitiga ditinjau dari besar sudut dan panjang sisinya.
1.
Jenis-jenis Segitiga Ditinjau dari Sudut-sudutnya
13
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018a. Segitiga Lancip (Acute Triangle)
Segitiga lancip adalah segitiga yang besar setiap sudutnya lancip atau besar setiap sudutnya berkisar antara 0 dan 90(acute angle).
Pada gambar 10: ABCadalah segitiga lancip,0 A, B, C 90
b.
Segitiga Siku-siku (Right Triangle)
Segitiga siku-siku adalah segitiga yang salah satu sudutnya siku-siku atau besar sudutnya 90(right angle)
Pada gambar 11: ABCadalah segitiga siku-siku, C 90 (Csiku-siku)
c.
Segitiga Tumpul (Obtuse Triangle)
Segitiga tumpul adalah segitiga yang salah satu sudutnya merupakan sudut tumpul atau besar sudutnya berkisar antara 90 dan180 (obtuse angle). Pada gambar 12: ABCadalah segitiga tumpul,0 A, B 90 dan
90 C 180 (Btumpul).
2.
Jenis-jenis Segitiga Ditinjau dari Panjang Sisi-sisinya
Ada 3 jenis segitiga ditinjau dari panjang sisi-sisinya, yaitu segitiga sembarang (scalene), segitiga sama kaki (isosceles), segitiga sama sisi (equilateral).
a. Segitiga Sembarang (Scalene)
Segitiga sembarang adalah segitiga yang besar ketiga sudutnya berbeda dan juga ketiga panjang sisinya berbeda.
Gambar 10
A
B C
A
B C
Gambar 11
Gambar 12
A
14
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018Pada gambar 13: ABCadalah segitiga sembarang, A B Cdan
BCACAB.
b. Segitiga Sama Sisi (Equilateral)
Segitiga sama sisi adalah segitiga yang ketiga sisinya sama panjang. Pada gambar 14: ABCadalah segitiga sama sisi, A B Cdan
BCACAB.
Karena ABCadalah segitiga sama sisi, maka A B C 180 : 3 60
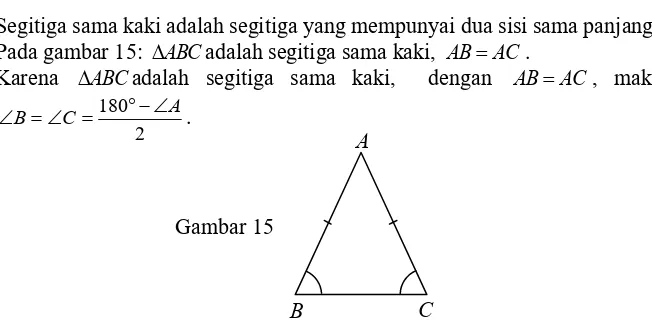
c. Segitiga Sama Kaki (Isosceles)
Segitiga sama kaki adalah segitiga yang mempunyai dua sisi sama panjang. Pada gambar 15: ABCadalah segitiga sama kaki, ABAC.
Karena ABCadalah segitiga sama kaki, dengan ABAC, maka 180
2
A
B C
.
3. Jenis-jenis Segitiga Ditinjau dari besar sudut dan Panjang Sisinya
Ada 7 macam jenis-jenis segitiga ditinjau dari besar sudut dan panjang sisinya.
a. Segitiga Sembarang
Ada 3 jenis segitiga sembarang, yaitu segitiga lancip sembarang, segitiga siku-siku sembarang, dan segitiga tumpul sembarang.
Gambar 13
A
B C
Gambar 14
A
B C
Gambar 15
A
15
|
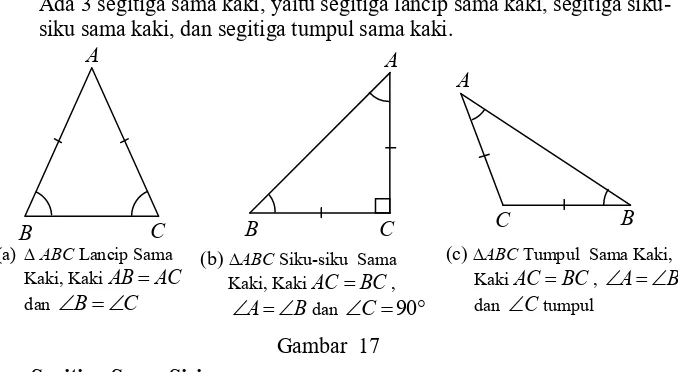
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018b. Segitiga Sama Kaki
Ada 3 segitiga sama kaki, yaitu segitiga lancip sama kaki, segitiga siku-siku sama kaki, dan segitiga tumpul sama kaki.
c. Segitiga Sama Sisi
Segitiga sama sisi adalah segitiga yang ketiga sisinya sama panjang. Segitiga sama sisi dapat dilihat gambar Gambar 14.
3.
Jenis-jenis Segitiga Istimewa
Segitiga istimewa atau khusus adalah segitiga yang mempunyai sifat-sifat istimewa atau khusus, yang berkaitan dengan panjang sisi-sisinya maupun besar sudut-sudutnya. Adapun yang tergolong ke dalam jenis-jenis segitiga istimewa tersebut adalah segitiga sama sisi (Gambar 14), segitiga sama kaki (Gambar 15), dan segitiga siku-siku (Gambar 16 (b)).
Contoh 18:
Diketahui ABC dengan sudut-sudut A, B, dan C berbanding sebagai 2 : 7 : 9 . Tentukan sudut-sudut segitiga dan jenis segitiga tersebut.
Solusi:
Misalnya sudut-sudut A2 ,k B7 , dank C9k.
Dalam ABC berlaku bahwa jumlah sudut-sudutnya adalah 180. Gambar 16
(a)ABCLancip Sembarang
A
B C
(b)ABCSiku-siku Sembarang
(c) ABC Tumpul Sembarang A
C B
A
B C
(a) ABC Lancip Sama Kaki, KakiABAC
dan B C A
B C
Gambar 17
(c) ABC Tumpul Sama Kaki, KakiACBC, A B
dan Ctumpul
A
C B
(b) ABC Siku-siku Sama Kaki, KakiACBC,
A B
dan C 90
A
16
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018 180A B C
2k7k9k180
18k180
10
x
20 , 70 , dan 90
A B C
Jadi, jenis ABC adalah segitiga siku-siku.
Contoh 19:
Diketahui ABC dengan sudut-sudutnya adalah A x 20 , B 7x 10 , dan 110 5
C x
. Tentukan jenis segitiga tersebut.
Solusi:
180
A B C
20 7 10 110 5 180
x x x
3x 60 20
x
20 20 20 40
A x
7 10 140 10 130
B x
110 100 10
C
Jadi, jenis ABC adalah segitiga tumpul.
SOAL-SOAL LATIHAN 5
Selesaikanlah setiap soal berikut ini.
1. Diketahui ABC dengan sudut-sudutnya berbanding sebagai 1: 2 : 6 . Tentukan besar sudut-sudut segitiga dan jenis segi tiga tersebut.
2. Tentukan besar sudut-sudut dan jenis PQR yang sudut-sudutnya adalah 50
P x
, Q 5x 30 , dan R 1202x.
3. Tentukan jenis segitiga yang sudut-sudutnya berbanding sebagai 1: 2 : 3 .
7.
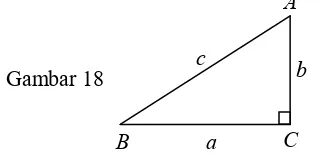
TEOREMA PYTHAGORAS
Pada segitiga siku-siku, sisi yang terletak di depan sudut siku-siku disebut adalah hipotenusa (hypotenuse) atau sisi miring dan sisi-sisi yang lainnya disebut kaki-kaki atau sisi-sisi siku. Hipotenusa selalu lebih panjang dari sisi siku-sikunya. Pada gambar 14 ditunjukkan ABC dengan sudut siku-siku C, sehingga hipotenusanya adalah segmen garis AB yang panjangnya c, dan sisi-sisi
dan
AC BCadalah kaki-kakinya atau sisi siku-sikunya yang panjangnya masing-masing a dan b.
Gambar 18
A
B a C
c
17
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018Hubungan sisi-sisi pada segitiga siku-siku dapat ditentukan menggunakan Teorema Pythagoras yang dirumuskan sebagai berikut.
“Kuadrat panjang hipotenusa dari segitiga siku-siku sama dengan jumlah
kuadrat panjang sisi siku-sikunya”
Kita dapat menuliskan teorema Pythagoras dari gambar 14:
18
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018 Menurut Pythagoras dalam BCD:2 2 2
CD BC BD
2 132 2 169 2
CD x x …. (1) Menurut Pythagoras dalam ACD.
2 2 2
Dari persamaan (1) dan (2) diperoleh
2 2
19
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018GCF GAE GCF GAE GFC GEA
segi empat BEDF adalah belah ketupat Menurut Pythagoras dalam ABD:
2 2 2 2 2
Menurut Pythagoras dalam ABE:
2 2 2
Menurut Pythagoras dalam DEG: 2
8.
TRIPEL PYTHAGORAS
Perhatikan pasangan bilangan
3, 4, 5
. Bilangan ini memenuhi hubungan2 2 2
20
|
Husein Tampomas, Trigonometri, Unntuk SMA dan Sederajat, 2018dengan sisi-sisi tegak a dan b dan hipotenusa (sisi miring) c dengan a, b, dan c
tidak harus merupakan bilangan bulat, tetapi sembarang bilangan real positif. Untuk mendapatkan Triple Pythagoras digunakan rumus sebagai berikut ini.
Pada tabel 1 disajikan beberapa tripel Pythagoras. Tabel 1:
Contoh 23:
Tentukan nilai x dan y dari setiap pasangan tiga bilangan
88,105,x
dan
44,125,y
yang merupakan Tripel Pythagoras.Solusi:
2 2 2
a b c , dengan a, b, dan c adalah Tripel Pythagoras Dasar, sehingga a genap,
b ganjil, dan c ganjil atau a ganjil, b genap, dan c ganjil.
88,105,x
berarti a88,b105,cxataua88,bx c, 1052 2 2 2
88 105 18769 137
x
x 137
44,125,y
berarti a44,b125,cyataua44,by c, 125 y24421252 17561(bukan bilangan kuadrat sempurna)2 2 2
125 44 y
y21252442 136891172
y 117
SOAL-SOAL LATIHAN 6
Selesaikanlah setiap soal berikut ini.
1. Diberikan ABCsiku-siku di C. Lengkapilah table 2 berikut ini. Tabel 2:
No. m n am2n2 b2mn cm2n2
1. 2 1 3 4 5
2 3 2 5 12 13
3 4 1 15 8 17
4 4 3 7 24 25
5 5 2 21 20 29
6 5 4 7 40 41
Panjang Sisi Nomor Soal
(1) (2) (3) (4) (5) (6)
a 12 …. 24 25 …. 43
b 35 84 …. 312 840 ….
c …. 85 145 …. 841 925
Untuk m dan n anggota bilangan bulat positif, m dan n tidakmempunyai faktor sekutu selain 1, FPB = 1 dan mn, berlaku am2n2,
2
b mn, dan
2 2