BAB III
METODE PENELITIAN
A. Desain Penelitian
Berdasarkan latar belakang dan rumusan masalah yang telah dipaparkan
pada bab sebelumnya, maka penelitian ini merupakan penelitian quasi eksperimen atau eksperimen semu yang terdiri dari dua kelompok penelitian yaitu kelompok
eksperimen (kelas perlakuan) merupakan kelompok siswa yang pembelajarannya
menggunakan strategi problem solving menurut Wankat dan Oreovicz dan kelompok kontrol (kelas pembanding) adalah kelompok siswa yang
pembelajarannya tidak menggunakan strategi problem solving menurut Wankat dan Oreovicz (ekspositori).
Alasan mengunakan metode kuasi eksperimen adalah karena pengambilan
sampel tidak dilakukan secara acak. Penelitian ini bertujuan untuk melihat
hubungan sebab akibat dan perlakukan yang dilakukan terhadap variabel bebas
dilihat hasilnya pada variabel terikat.
Desain dari penelitian ini adalah kuasi eksperimen dengan menggunakan
Nonequivalent Control Group Design dengan tiga variabel yaitu Pangaruh Strategi Problem Solving menurut Wankat dan Oreovicz (X) sebagai variabel bebas (independent variable) dan Kemampuan Pemahaman Konsep Matematis (Y1) dan Self Regulated Learning Siswa (Y2) sebagai variabel terikat (dependent variable). Penelitian ini didesain dalam dua kelompok yaitu kelompok eksperimen (pretest dan posttes) dan kelompok kontrol / control group pretest dan posttest design (Arikunto, 2010, hlm.124). Desain penelitian ini, kelompok eksperimen dan kelompok kontrol tidak dipilih secara random. (Sugiyono, 2013, hlm. 118)
Kelompok Pretest Treatment Posttest
Eksperimen O X O
Keterangan
O : Pre-tes dan post-tes kemampuan pemahaman konsep matematis dan self regulated learning siswa
X : perlakuan terhadap kelompok eksperimen
Kelompok eksperimen adalah kelompok siswa yang mengikuti
pembelajaran Matematika dengan menggunakan strategi problem solving menurut Wankat dan Oreovicz sedangkan kelompok kontrol adalah kelompok siswa yang
mengikuti pembelajaran secara ekspositori melalui ceramah, diskusi dan
penugasan secara individual. Terhadap kedua kelompok tersebut diberikan pre-test dan post-test dengan menggunakan perangkat alat tes, pedoman observasi dan lembar angket likert yang dimodifikasi. Mekanisme penelitian ini dapat
digambarkan sebagai berikut:
B. Subjek Penelitian
1. Populasi
Populasi merupakan wilayah generalisasi yang terdiri atas objek/subjek yang
mempunyai kualitas dan karakteristik tertentu yang ditetapkan oleh peneliti
untuk dipelajari dan kemudian ditarik kesimpulannya (Sugiyono, 2009, hlm.
56).
Populasi dalam penelitian ini adalah seluruh Sekolah Dasar Negeri yang
berada di Kecamatan Blanakan, Kabupaten Subang dengan karakteristik yang
sama.
Pemahaman Konsep Matematika
(Y1) Strategi Problem Solving
Menurut Wankat Dan Oreovicz (X)
Self Regulated Learning
2. Sampel
Adapun teknik pengambilan sampel pada penelitian ini dilakukan dengan
purposive sampling yaitu teknik pengambilan sampel berdasarkan petimbangan tertentu. Yang artinya sampel diambil berdasarkan kesepakatan antara pihak
sekolah dengan peneliti. Hal tersebut dilakukan agar tidak banyak menggangu
aktivitas di sekolah tersebut. Oleh kerena itu, sampel dalam penelitian ini adalah
dua kelas pada sekolah yang berbeda dimana satu kelas sebagai kelas dengan
menggunakan strategi problem solving menurut Wankat dan Oreovicz dan kelas yang satunya lagi adalah kelas dengan pendekatan ekspositori.
Dalam penelitian ini, sampel yang diambil adalah para siswa dari dua
sekolah yang mempunyai karakteristik yang sama, dengan status Sekolah Negeri
yang terakreditasi B. Adapun faktor-faktor pendukung yang ada seperti, jumlah
siswa yang akan dijadikan kelas eksperimen dan kelas kontrol mempunyai siswa
dengan jumlah yang tidak jauh berbeda dan latar belakang keluarga yang
berbeda-beda pula. Demikina pula basic pendidikan guru pada kedua sekolah hampir sama
yaitu telah menempuh Strata 1. Letak kedua SDN yang berada pada satu
kecamatan yaitu Kecamatan Blanakan Kabupaten Subang.
C. Variabel Penelitian
Variabel penelitian ini melibatkan dua jenis variabel yaitu variabel bebas, dan
variabel terikat.
1. Variabel bebas
Variabel bebas adalah variabel yang mempengaruhi, disebut juga variabel
stimulus, predictor, antecedent, atau independent variable (Sugiono, 2009, hlm. 39). Pada penelitian ini pembelajaran matematika dengan menggunakan strategi
problem solving menurut Wankat dan Oreovicz merupakan variabel bebas.
2. Variabel terikat
Variabel terikat adalah variabel yang dipengaruhi atau yang menjadi akibat,
D. Instrumen Penelitian
Karakteristik yang akan diukur dalam penelitian ini adalah pemahaman
konsep matematis dan self-regulated learning siswa. Alat test yang digunakan dalam penelitian ini terdiri dari dua jenis yaitu tes dan non tes yang diberikan
kepada kelompok siswa yang diberi perlakuan (eksperimen) dan kelompok siswa
sebagai pembanding (kontrol). Instrumen penelitian tersebut meliputi soal tes
hasil belajar untuk mengukur pemahaman siswa terhadap konsep matematis,
lembar angket untuk mengumpulkan data yang berhubungan dengan self-regulated learning siswa terhadap pembelajaran, dan catatan harian untuk mendukung hasil observasi. Secara garis besarnya dapat diuraikan Instrumen yang
digunakan dalam penelitian meliputi :
1. Instrumen Tes Pemahaman Konsep Matematika
Tes pemahaman konsep matematika diberikan untuk pre-tes dan post-tes. Pre-tes diberikan dengan tujuan untuk mengetahui kemampuan pemahaman konsep matematis siswa pada awal penelitian. Post-tes diberikan dengan tujuan untuk mengetahui pengaruh terhadap kemampuan pemahaman konsep matematis
siswa setelah menggunakan strategi problem solving menurut Wankat dan Oreovicz dan pembelajaran ekspositori. Soal tes matematika yang digunakan
berbentuk tes uraian sebanyak 10 soal. Pemilihan tes uraian ini bertujuan untuk
melihat proses pengerjaan yang dilakukan siswa agar dapat diketahui bagaimana
kemampuan pemahaman masalah matematika siswa.
Selain itu, tes bentuk uraian memilki beberapa kelebihan seperti yang
dikemukakan oleh Suherman (2003, hlm.77) yaitu diantarnya: (1) pembuatan soal
bentuk uraian relatif lebih mudah dan dapat dibuat dalam kurun waktu yang tidak
terlalu lama; (2) karena dalam menjawab soal bentuk uraian siswa dituntut untuk
menjawabnya secara rinci, maka proses berpikir, ketelitian, sistematika
penyusunan dapat dievaluasi. Terjadinya bias hasil evaluasi dapat dihindari karena
tidak ada sistem tebakan atau untung-untungan. Hasil evaluasi dapat
mencerminkan kemampuan siswa sebenarnya; (3) proses pengerjaan tes akan
siswa agar berpikir secara sistematik, menyampaikan pendapat dan argumentasi,
mengaitkan fakta-fakta yang relevan.
Dalam penyusunan soal tes tersebut, diawali dengan penyusunan kisi-kisi
soal yang dilanjutkan dengan menyusun soal beserta kunci jawaban dan aturan
pemberian skor masing-masing butir soal.
Untuk mengevaluasi kemampuan pemahaman konsep matematis siswa, peneliti
menggunakan kriteria penilaian dengan berpedoman pada rubik sederhana yang
dikembangkan oleh “New standards project” dikemukakan oleh Van De Walle
(2008, hlm. 85) dan kemudian dimodifikasi. Kriteria penskoran rubik jawaban tes
Tabel 3.1
Pedoman Penskoran Jawaban Tes Kemampuan Pemahaman Konsep Matematika
Respon Siswa Skor
Siswa belum mengerti (siswa menunjukkan kesalahpahaman besar tehadap
konsep dan prosedur yang salah atau kegagalan dalam menyelesaikan soal)
Tidak ada jawaban 0
Tidak memuaskan: pencapaian sedikit (tugas dikerjakan dan prosedur
penyelesaian dibuat. Ada bagian pencapaian tapi hanya sedikit atau tidak ada
keberhasilan.
Ada jawaban tapi jawaban salah 1
Kecil: pencapaian sebagian (sebagian tugas diselesaikan, tapi kurang
memahami, masukan langsung atau pengerjaan lebih jauh dibutuhkan)
Jawaban benar tetapi penggunaan konsep kurang lengkap dan jawaban mengandung pergitungan yang salah
2
Pandai ; pencapaian pokok (sedikit kesalahan dan pemahaman cukup
Jawaban benar tetapi penggunaan konsep hampir lengkap, menggunakan algoritma secara lengkap, perhitungan secara umum benar namun mengandung sedikit kesalahan
3
Bagus: pencapaian penuh (strategi penyelesaian masalah sudah benar, memiliki pemahaman konsep yang tinggi, prosedur pengerjaan sudah secara
sistematis)
Jawaban benar, penggunaan konsep secara lengkap, hampir semua petunjuk soal diikuti, penggunaan
algoritma secara lengkap dan benar, melakukan peritungan secara sistematis.
4
Dapat kita ketahui bahwa penilaian merupakan proses pengumpulan
informasi selengkap-lengkapnya tentang peserta didik untuk tujuan pembuatan
keputusan pembelajaran (Ibrahim dan Nur dalam Zalinar, 2012, hlm. 51)
mengemukakan ada empat prinsip-prinsip yang dijadikan landasan untuk
melakukan penilaian yaitu: (1) penilaian harus ditujukkan untuk meningkatkan
kualitas pembelajaran; (2) metode penilaian harus dirancang sehingga
bukan mengungkapkan apa yang tidak diketahui; (3) penilaian bersifat opersional,
untuk mencapai pembelajaran matematika; dan (4) kualitas alat penilaian tidak
ditentukan oleh mudahnya pemberian skor, dan alat penilaian seyogyanya bersifat
praktis untuk dilakukan.
Demikain pula pernyataan yang dikemukakan oleh Suydam (dalam Zalinar,
2012, hlm. 52) mengenai penulisan evaluasi matematis haruslah memperhatikan
beberapa hal berikut ini: (1) memilih teknik pengukuran yang paling efektif untuk
tujuan yang lebih spesifik; (2) menggunakan kalimat yang sederhana dan jelas,
dengan bahasa yang mudah diapahami oleh peserta didik; (3) merangsang setiap
item tes sedemikian hingga dapat sebagai bukti bahwa tujuan telah tercapai; (4)
memulai dengan soal tes yang mudah; (5) buatlah petunjuk dengan jelas, ringkas;
(6) analisislah jawaban siswa pada tiap-tiap soal, untuk digunakan sebagai
diagnostik. Masingilia dan Wisnowska (dalam Zaliniar, 2012, hlm. 52)
menyatakan bahwa rubrik skoring (scoring rubrics) merupakan suatu alat yang dapat digunakan untu menilai tugas-tugas menulis matematis. Demikain halnya
peneliti merujuk pada pernyataan tersebut dimana penilaian dalam penelitian ini
menggunakan rubrik skoring.
Soal tes sebelum digunakan sebagai instrumen pengumpulan data terlebih
dahulu dilakukan uji coba. Uji coba dilakukan dengan tujuan untuk memperoleh
perangkat instrumen pengumpul data yang handal, sehingga data yang didapat
akan lebih akurat. Hal yang serupa diungkapkan oleh Suherman dan Kusumah
(1990, hlm. 134) bahwa untuk memperoleh hasil evaluasi yang baik diperlukan
alat evaluasi yang baik pula dan evaluasi yang baik adalah yang dapat memberi
gambaran yang benar tentang kemajuan terhadap peserta didik.
Ada satu tahapan sebelum soal-soal diuji cobakan, yaitu peneliti meminta
pertimbangan pada rekan yang dianggap berkompeten dibidangnya, dosen
pembimbing dan para ahli untuk menguji validitas yang terdiri dari validitas muka
dan validitas isi terhadap soal-soal tersebut, barulah soal tersebut diujikan secara
empirik dengan cara soal tes kemampuan pemahaman konsep matematis siswa
diujicobakan kepada siswa kelas VI Sekolah Dasar. Jumlah siswa yang mengikuti
uji coba itu dianalisis validitas, reliabilitas, daya pembeda, dan tingkat kesukaran
soal.
a. Analisis Validitas Tes
1) Validitas logis
Uji validitas yang termasuk dalam validitas logis yang digunakan pada
penelitian ini adalah validitas isi dan validitas muka (face validity). Validitas muka dilakukan dengan melihat tampilan dari soal itu yaitu keabsahan susunan
kalimat atau kata-kata dalam soal sehingga jelas pengertiannya tidak salah
tafsir atau kejelasan bahasa/redaksional dan gambar/representasi dari setiap
butir tes yang diberikan. Suatu instrumen dikatakan memiliki validitas muka
yang baik apabila instrumen tersebut mudah dipahami maksudnya, sehingga
siswa tidak mengalami kesulitan ketika menjawab soal tersebut (Suherman,
2003, hlm. 106)
Validatas isi suatu evaluasi artinya ketepatan alat tersebut ditinjau dari segi
materi yang dievaluasikan. Validitas isi dilakukan dengan melihat kesesuaian
materi tes dengan kisi-kisi tes, materi ajar yang telah diajarkan dan apakah soal
pada instrumen penelitian sesuai atau tidak dengan indikator kemampuan yang
diukur dan tingkat kesukaran untuk siswa.
2) Validitas empiris
Uji validitas yang termasuk dalam validitas empiris yang digunakan pada
penelitian ini adalah validitas butir soal. Untuk menguji validitas setiap butir
soal, maka skor-skor yang ada pada butir soal yang dimaksud dikorelasikan
dengan skor total. Rumus yang digunakan adalah rumus korelasi Product Moment Pearson (Arikunto, 2009, hlm. 72), rumusnya dinyatakan sebagai berikut:
∑ ∑ ∑ √ ∑ ∑ ∑ ∑
= koefisien korelasi antara variabel X dan variabel Y, dua veriabel yang
dikorelasikan.
N = banyak pasangan nilai
X = nilai rata-rata soal-soal tes pertama perorangan
Y = nilai rata-rata soal soal-soal tes kedua perorangan
Klasifikasi untuk menginterpretasikan besarnya koefisien korelasi
(Suherman, 2003, hlm. 113) adalah sebagai berikut:
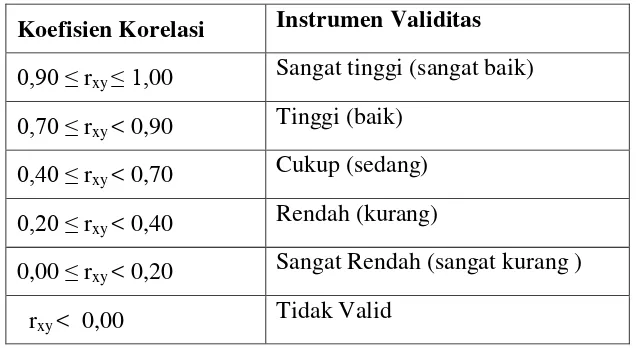
Tabel 3.2
Klasifikasi Koefisien Korelasi Validitas Instrumen
Koefisien Korelasi Instrumen Validitas
0,90 ≤ rxy ≤ 1,00 Sangat tinggi (sangat baik)
0,70 ≤ rxy < 0,90 Tinggi (baik)
0,40 ≤ rxy < 0,70 Cukup (sedang)
0,20 ≤ rxy < 0,40 Rendah (kurang)
0,00 ≤ rxy < 0,20 Sangat Rendah (sangat kurang )
rxy < 0,00 Tidak Valid
Penjelasan dari tabel di atas adalah, jika butir soal dengan koefisien korelasi
lebih dari atau sama dengan 0,90 dan kurang dari atau sama dengan 1,00 maka
interpretasi untuk soal tersebut sangat tinggi. Jika koefisien korelasi lebih dari
atau sama dengan 0,70 dan kurang dari 0,90 maka interpretasi untuk soal tersebut
tinggi, jika koefisien korelasi lebih dari atau sama dengan 0,40 dan kurang dari
0,70 maka interpretasi untuk soal tersebut cukup, jika koefisien korelasi lebih dari
atau sama dengan 0,20 dan kurang dari 0,40 maka interpretasi untuk soal tersebut
rendah, jika koefisien korelasi lebih dari atau sama dengan 0,00 dan kurang dari
0,20 maka interpretasi untuk soal tersebut sangat rendah, jika koefisien korelasi
kurang dari 0,00 maka interpretasi untuk soal tersebut tidak valid.
Pada taraf signifikansi 5% dengan n = 40 diperoleh rtabel sebesar 0,312. Selanjutnya rxy dibandingkan dengan rtabel. Tiap item tes dikatakan valid apabila
Hasil perhitungan dengan menggunakan Exel dan interpretasi validasi butir
soal untuk tes kemampuan pemahaman konsep matematis dalam penelitian ini
seperti yang terdapat pada lampiran C1 secara singkat dapat dilihat pada Tabel
3.3.
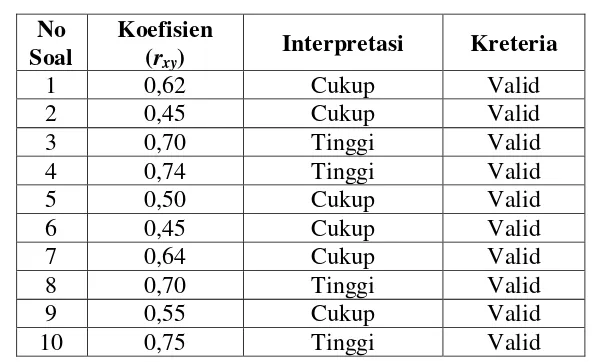
Tabel 3.3
Data Hasil Uji Coba Validitas Butir Soal Tes Kemampuan Pemahaman Konsep Matematis
Tabel di atas menunjukkan data hasil uji coba validitas butir soal untuk tes
kemampuan pemahaman konsep matematis dengan rincian soal nomor satu
koefisien korelasi sebesar 0,62 masuk dalam kategori cukup maka dinyatakan
valid, rincian soal nomor dua koefisien korelasi sebesar 0,45 masuk dalam
kategori cukup maka dinyatakan valid, rincian soal nomor tiga koefisien korelasi
sebesar 0,70 masuk dalam kategori tinggi maka dinyatakan valid, rincian soal
nomor empat koefisien korelasi sebesar 0,74 masuk dalam kategori tinggi maka
dinyatakan valid, rincian soal nomor lima koefisien korelasi sebesar 0,50 masuk
dalam kategori cukup maka dinyatakan valid, rincian soal nomor enam koefisien
korelasi sebesar 0,45 masuk dalam kategori maka cukup dinyatakan valid, rincian
soal nomor tujuh koefisien korelasi sebesar 0,64 masuk dalam kategori cukup
maka dinyatakan valid, rincian soal nomor delapan koefisien korelasi sebesar
0,70 masuk dalam kategori tinggi maka dinyatakan valid, rincian soal nomor
sembilan koefisien korelasi sebesar 0,55 masuk dalam kategori cukup maka
dinyatakan valid, rincian soal nomor sepuluh koefisien korelasi sebesar 0,75
Melihat hasil penyajian data di atas maka dapat dinyatakan terdapat empat
soal masuk dalam kategori tinggi, dan enam soal masuk dalam kategori cukup.
Maka dari itu 10 soal itu dinyatakan valid.
b. Analisis Reliabilitas Tes
Reliabilitas tes adalah tingkat keajegan (konsistensi) suatu tes, yaitu sejauh
mana suatu tes dapat dipercaya untuk menghasilkan skor yang ajeg/konsisten.
Untuk mencari reliabilitas butir soal tes berbentuk uraian menggunakan rumus
Alpha (Suherman, 2003, hlm. 154), yaitu:
= ∑
Keterangan
= koefisien reliabilitas n = banyaknya butir soal
∑ = jumlah varians skor setiap item = varians skor total
Jumlah varians skor setiap item dan varians total, dapat dihitung dengan
menggunakan rumus:
= ∑ (∑ )
Keterangan:
= varians tiap skor soal ∑ = jumlah tiap skor soal
∑ = jumlah kuadrat tiap skor soal = jumlah siswa
Untuk menginterpretasikan koefisien reliabilitas digunakan tolak ukur Guilford
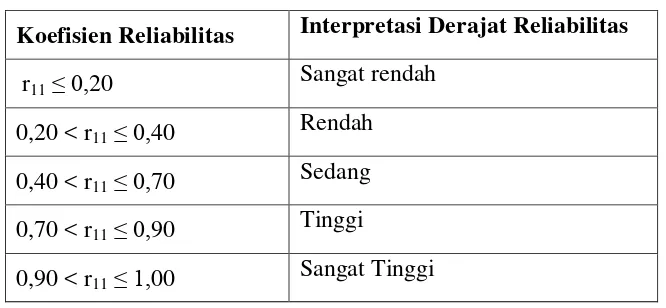
Tabel 3.4
Klasifikasi Interpretasi Koefisien Reliabilitas
Koefisien Reliabilitas Interpretasi Derajat Reliabilitas
r11≤ 0,20 Sangat rendah
0,20 < r11 ≤ 0,40 Rendah
0,40 < r11≤ 0,70 Sedang
0,70 < r11 ≤ 0,90 Tinggi
0,90 < r11≤ 1,00 Sangat Tinggi
Tabel di atas menunjukkan interprestasi koefisien reliabilitas, jika koefisien
reliabilitas kurang dari atau sama dengan 0,20 maka soal tersebut dinyatakan
sangat rendah, jika koefisien reliabilitas lebih dari 0,20 dan kurang dari atau sama
dengan 0,40 maka interpretasi untuk soal tersebut dinyatakan rendah, jika
koefisien reliabilitas lebih dari 0,40 dan kurang dari atau sama dengan 0,70 maka
interpretasi untuk soal tersebut dinyatakan sedang, jika koefisien reliabilitas lebih
dari 0,70 dan kurang dari atau sama dengan 0,90 maka interpretasi untuk soal
tersebut dinyatakan tinggi, dan jika koefisien reliabilitas lebih dari 0,90 dan
kurang dari atau sama dengan 1,00 maka interpretasi untuk soal tersebut
dinyatakan sangat tinggi.
Untuk mengetahui instrumen yang digunakan reliabel atau tidak, maka
dilakukan pengujian reliabilitas dengan menggunakan rumus alpha cronchbach dengan bantuan exel realstat, seperti yang terdapat pada lampiran C1, secara ringkasnya disajikan pada tabel 3.5 berikut ini:
Tabel 3.5 Data Reliabilitas
Tes Kemampuan Pemahaman Konsep Matematis
rhitung Kriteria Kategori
Berdasarkan analisis reliabilitas uji soal kemampuan pemahaman konsep
matematis siswa pada tabel di atas, diperoleh reliabilitas sebesar 0,8. Bila
diinterprestasikan dalam kriteria di atas, maka tes r tersebut memiliki reliabilitas
tinggi. Dengan kata lain soal memiliki kekonsistenan yang sedang atau akan
memberikan hasil yang relatif sama bila diberikan kepada subjek yang sama
meskipun pada waktu yang berbeda, serta tempat dan kondisi yang berbeda pula.
c. Analisis Daya Pembeda
Dalam bukunya Arikunto (2009, hlm. 214) menyatakan bahwa daya
pembeda soal adalah kemampuan suatu soal untuk membedakan antara siswa
yang pandai (berkemampuan tinggi) dengan siswa yang kurang (berkemampuan
rendah). Sebuah soal dikatakan memiliki daya pembeda yang baik bilamana
memang siswa yang pandai dapat menyelesaikan soal dengan baik, dan siswa
yang kurang pandai tidak dapat mengerjakan soal tersebut dengan baik. Daya
pembeda dihitung dengan membagi testee ke dalam dua kelompok, yang pertama kelompok atas (the higher group), yaitu kelompok testee yang tergolong pandai dan kelompok bawah (the lower group), yaitu kelompok yang tergolong rendah. Untuk menentukan daya pembeda digunakan rumus (Suherman, 2003, hlm. 160) ,
yaitu:
Keterangan
DP =daya pembeda
= jumlah benar untuk kelompok atas = jumlah benar untuk kelompok bawah = jumlah siswa kelompok atas
Hasil perhitungan daya pembeda kemudian diinterpretasikan dengan klasifikasi
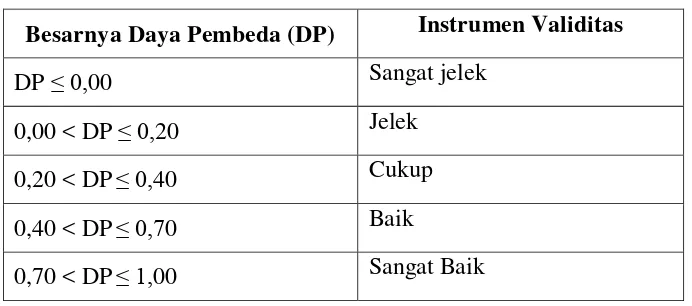
Tabel 3.6
Klasifikasi Koefisien Daya Pembeda
Besarnya Daya Pembeda (DP) Instrumen Validitas
DP ≤ 0,00 Sangat jelek
0,00 < DP ≤ 0,20 Jelek
0,20 < DP≤ 0,40 Cukup
0,40 < DP ≤ 0,70 Baik
0,70 < DP≤ 1,00 Sangat Baik
Tabel di atas menunjukkan klasifikasi daya pembeda butir soal, jika daya
pembeda butir soal berada pada nilai 0,00 maka daya pembeda butir soal tersebut
dinyatakan sangat jelek, jika daya pembedanya lebih dari 0,00 dan kurang dari
atau sama dengan 0,20 maka daya pembeda butir soal tersebut dinyatakan jelek,
jika daya pembedanya lebih dari 0,20 dan kurang dari atau sama dengan 0,40
maka daya pembeda soal tersebut dinyatakan cukup, jika daya pembedanya lebih
dari 0,40 dan kurang dari atau sama dengan 0,70 maka daya pembeda soal
tersebut dinyatakan baik, jika daya pembedanya lebih dari 0,70 dan kurang dari
atau sama dengan 1,00 maka daya pembeda soal dapat dinyatakan sangat baik.
Jika DP sama dengan 1,00 akan diperoleh kesamaan 1,00 =
sehingga = =
Kondisi ini hanya dapat dipenuhi jika = 0 sehingga = . Hal ini
berarti semua siswa kelas atas (pandai) dapat menjawab benar dan semua siswa
kelas bawah (kurang pandai) menjawab dengan salah. Demikain dengan soal yang
mempunyai daya pembeda = 1,00 dapat membedakan kemampuan siswa pandai
dan kurang pandai dengan sempurna, sehingga kategori daya pembeda soal
tersebut sangat baik.
Adapun hasil analisisi daya pembeda instrumen tes kemampuan pemahaman
konsep matematis siswa dapat dilihat pada lampiran C2, secara ringkasnya
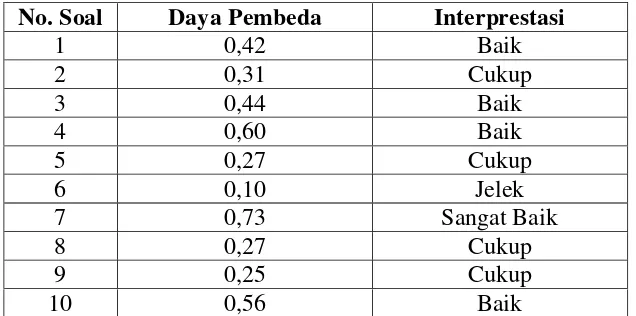
Tabel 3.7 Data Daya Pembeda
Tes Kemampuan Pemahaman Konsep Matematis Siswa
No. Soal Daya Pembeda Interprestasi
1 0,42 Baik
Tabel di atas menunjukkan bahwa daya pembeda dengan klasifiaksi jelek
sebanyak satu yaitu soal nomor enam dengan daya pembeda 0,01. Untuk
mengatasi hal yang demikian ini peneliti mengkonsultasikan soal nomor enam
tersebut kepada guru kelas, sehingga didapatkan solusi dengan melakukan
perbaikan konteks/keterbacaan pada soal tersebut agar lebih dimengerti oleh
siswa. Dari sepuluh soal terdapat daya pembeda dengan klasifikasi cukup
sebanyak empat butir soal dengan masing-masing besarnya daya pembeda sebagai
berikut soal nomor dua besarnya daya pembeda yaitu 0,31, soal nomor lima dan
nomor delapan memilki daya pembeda yang sama yaitu 0,27, soal nomor
sembilan dengan daya pembeda sebesar 0,25.
Dari tabel di atas dapat kita lihat ada empat kategori baik daya pembeda soal
yang masing–masing yaitu soal nomor satu dengan besar daya pembeda 0,42, soal
nomor tiga dengan daya pembeda sebesar 0,44, soal nomor empat dengan daya
pembeda sebesar 0,60. Hanya terdapat satu daya pembeda dengan kategori sangat
baik, yaitu terdapat pada soal nomor tujuh dengan daya pembeda sebesar 0,73.
d. Analisis Tingkat Kesukaran Soal
Indeks kesukaran adalah suatu bilangan yang menyatakan derajat kesukaran
suatu butir soal. Suatu butir soal dapat dikatakan memiliki indeks kesukaran yang
Tingkat kesukaran pada masing-masing butir soal dihitung dengan
menggunakan rumus (Suherman 2003, hlm. 170):
Keterangan
IK = indeks kesukaran
= jumlah benar untuk kelompok atas = jumlah benar untuk kelompok bawah = jumlah siswa kelompok atas
= jumlah skor yang diperoleh seluruh siswa pada butir soal yang diolah
Hasil perhitungan tingkat kesukaran diinterpretasikan dengan menggunakan
kriteria tingkat kesukaran butir soal (Suherman 2003, hlm. 170) sebagai berikut:
Tabel 3.8
Klasifikasi Tingkat Kesukaran
Indeks Kesukaran
IK = 0,00 Terlalu sukar
0,00 < IK ≤ 0,30 Sukar
0,30 < IK≤ 0,70 Sedang
0,70 < IK < 1,00 Mudah
IK= 1,00 Terlalu mudah
Tabel di atas menunjukkan klasifikasi tingkat kesukaran, jika tingkat
kesukaran suatu butir soal sebesar 0,00 maka soal tersebut dinyatakan teralu
sukar, jika tingkat kesukaran berada pada nilai lebih dari 0,00 dan kurang dari
atau sama dengan 0,30 maka soal tersebut dinyatakan sukar, bila tingkat
kesukaran butir soal ada pada nilai lebih dari 0,30 dan kurang dari atau sama
dengan 0,70 maka soal tersebut dinyatakan sedang, jika tingkat kesukaran butir
soal tersebut dinyatakan mudah, jika tingkat kesukaran suatu butir soal sama
dengan 1,00 maka soal tersebut dinyatakan teralu mudah.
Hasil perhitungan indeks kesukaran instrumen tes kemampuan pemahaman
konsep matematis dalam penelitian dapat dilihat pada lampiran C3, dan secara
ringkas disajikan pada tabel di bawah ini:
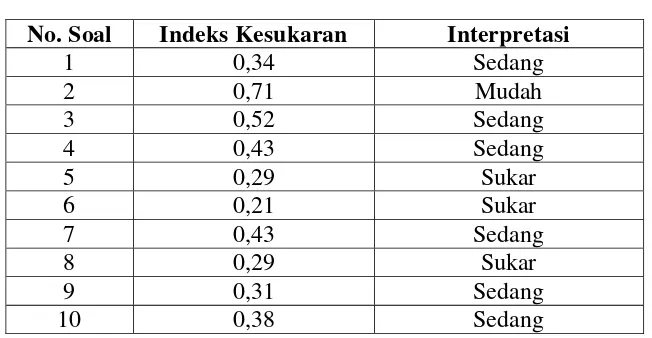
Tabel 3.9
Data Tingkat Kesukaran
Tes Kemampuan Pemahaman Konsep Matematis
No. Soal Indeks Kesukaran Interpretasi
1 0,34 Sedang
2 0,71 Mudah
3 0,52 Sedang
4 0,43 Sedang
5 0,29 Sukar
6 0,21 Sukar
7 0,43 Sedang
8 0,29 Sukar
9 0,31 Sedang
10 0,38 Sedang
Berdasarkan data dari tabel di atas, terdapat satu butir soal yang termasuk
kategori mudah yaitu soal nomor dua dengan indeks kesukaran 0,71, dan terdapat
enam butir soal yang berkategori sedang dengan indeks kesukaran masing-masing
yaitu: soal nomor satu dengan indeks kesukaran 0,34, soal nomor tiga dengan
indeks kesukaran 0,52, soal nomor empat dan tujuh memiliki indeks kesukaran
yang sama 0,43, soal nomor sembilan dengan indeks kesukaran 0,31, serta soal
nomor sepuluh dengan indeks kesukaran 0,38, sedangkan soal yang termasuk
kategori sukar ada tiga butir yaitu: soal nomor lima dan delapan yang mempunyai
indeks kesukaran yang sama 0,29, serta soal nomor enam dengan indeks
kesukaran 0,21.
Setelah melakukan perhitungan uji coba maka dapat dianalisis semua soal
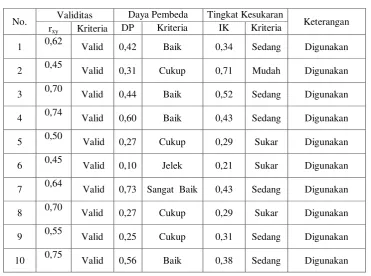
Tabel 3.10
Rangkuman Interpretasi Hasil Uji Coba Butir Soal
No. Validitas Daya Pembeda Tingkat Kesukaran Keterangan rxy Kriteria DP Kriteria IK Kriteria
1 0,62 Valid 0,42 Baik 0,34 Sedang Digunakan
2 0,45 Valid 0,31 Cukup 0,71 Mudah Digunakan
3 0,70 Valid 0,44 Baik 0,52 Sedang Digunakan
4 0,74 Valid 0,60 Baik 0,43 Sedang Digunakan
5 0,50 Valid 0,27 Cukup 0,29 Sukar Digunakan
6 0,45 Valid 0,10 Jelek 0,21 Sukar Digunakan
7 0,64 Valid 0,73 Sangat Baik 0,43 Sedang Digunakan
8 0,70 Valid 0,27 Cukup 0,29 Sukar Digunakan
9 0,55 Valid 0,25 Cukup 0,31 Sedang Digunakan
10 0,75 Valid 0,56 Baik 0,38 Sedang Digunakan
2. Instrumen Non Tes
a. Klasifikasi Self-Regulated Learning
Instrumen self-regulated learning siswa diukur dengan menggunakan lembaran angket self-regulated learning. Angket self-regulated learning siswa mencerminkan kemandirian belajar yang dimiliki siswa menurut aspek ciri-ciri
self-regulated learning siswa. Hal ini dilakukan untuk mengetahui kekonsistenan tanggapan siswa terhadap angket self-regulated learning. Tanggapan yang diberikan kepada siswa terhadap angket ini menggunakan skala Likert yang
dimodifikasi.
Mengenai skala Likert manurut Widoyoko (2012, hlm. 115) bahwa prinsip
pokok skala Likert adalah menentukan lokasi kedudukan seseorang dalam suatu
kontinum sikap terhadap objek sikap, mulai sangat negatif sampai dengan sangat
positif. Penentuan lokasi dilakukan dengan mengkuantifikasi pernyataan
seseorang terhadap butir pernyataan yang disediakan.
Untuk skala Likert digunakan skala dengan 4 angka. Skala 1 (satu) berarti
bentuk suatu pernyataan dan diikuti oleh pilihan respon yang menunjukkan
tingkatan. Contoh pilihan respons:
SS = Sangat Sering
S = Sering
J = Jarang
TP = Tidak Pernah
Untuk menilai validitas semua pernyataan motivasi belajar, dilakukan
judgement oleh tiga orang pakar dengan kualitas doktor. Untuk memperoleh item soal angket yang layak pakai, seluruh aspek dikembangkan menjadi indikator
yang kemudian dari indikator tersebut dikembangkan menjadi item-item
pernyataan sebanyak 32 item. Menurut para penimbang item-item yang kurang
layak, baik secara konstruk maupun kebahasaannya, dilakukan revisi sesuai
dengan saran-saran para penimbang tersebut.
b. Analisis Validitas Tes Self-Regulated Learning Siswa
1) Validitas empiris
Untuk mengetahui apakah uji coba tes self-regulated learning siswa itu valid atau tidak, maka dilakukanlah uji validitas tes, dengan tujuan apakah tes tersebut
dapat digunakan untuk instrumen penelitian. Untuk lebih jelasnya dapat dilihat
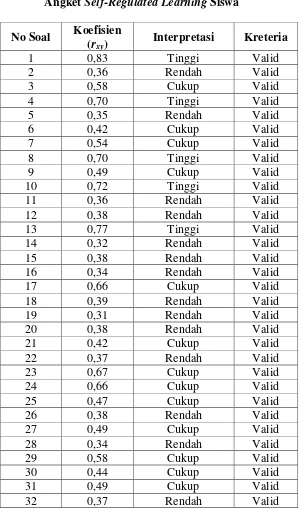
Tabel 3.11
Data Hasil Uji Coba Validitas Angket Self-Regulated Learning Siswa
No Soal Koefisien
terdapat lima soal masuk dalam kategori tinggi, dan 13 soal masuk dalam kategori
cukup, dan 14 soal masuk dalam kategori rendah. Maka dari itu 32 soal itu
b. Analisis Reliabilitas Tes
Reliabilitas tes adalah tingkat keajegan (konsistensi) suatu tes, yaitu sejauh
mana suatu tes dapat dipercaya untuk menghasilkan skor yang ajeg/konsisten.
Hasil perhitungan reliabilitas soal uji coba self-regulated learning siswa dapat dilihat pada lampiran C4, berikut disajikan secara singkat pada tabel 3.12.
Tabel 3.12 Data Reliabilitas
Angket Self-Regulated Learning Siswa
rhitung Kriteria Kategori
0,89 Reliabel Tinggi
Berdasarkan analisis reliabilitas uji tes self-regulated learning siswa pada tabel di atas, diperoleh reliabilitas sebesar 0,89. Bila diinterprestasikan dalam
kriteria di atas, maka tes tersebut memiliki reliabilitas tinggi. Dengan kata lain
soal memiliki kekonsistenan yang sedang atau akan memberikan hasil yang relatif
sama bila diberikan kepada subjek yang sama meskipun pada waktu yang
berbeda, serta tempat dan kondisi yang berbeda pula.
E. Observasi
Dalam melakukan pengamatan secara langsung aktivitas guru dan siswa pada
saat proses pembelajaran matematika yang dilakukan oleh guru, peneliti
melakukan observasi. Sentosa (2013, hlm. 19) menyatakan “observasi atau
pengamatan langsung adalah kegiatan pengumpulan data dengan melakukan
penelitian langsung terhadap kondisi lingkungan objek penelitian yang
mendukung penelitian, sehingga didapat gambaran secara jelas tentang kondisi
objek penelitian tersebut.” Observasi pada penelitian ini dilakukan pada setiap tindakan aktivitas belajar siswa dan guru pada kelas eksperimen. Lembar
observasi ini hanya digunakan pada kelas eksperimen karena indikator-indikator
pengamatan dikembangkan dibuat hanya untuk memonitor pelaksanaan
berkenaan dengan perilaku manusia, proses kerja, serta gejala-gejala yang terjadi
terhadap objek yang diobservasi (Sugiyono, 2009, hlm. 117).
F. Prosedur Penelitian
Secara garis besar penelitian ini dilakukan melalui empat tahapan yang
digambarkan dalam bentuk diagram berikut ini:
Tahap 1: Persiapan
1. Pengajuan judul dan pembuatan proposal 2. Seminar proposal dan perbaikan hasil proposal 3. Membuat instrumen dan merancang bahan ajar 4. Validasi instrumen dan merevisinya
5. Mengurus perizinan melakukan penelitian 6. Uji coba instrumen
7. Analisis hasil uji coba
Tahap 2: Pelaksanaan
1. Pre-tes kemampuan awal pemahaman konsep matematis siswa, dan 2. Angket self-regulated learning siswa pada kelas kontrol dan
eksperimen
Kelas kontrol Kelas Esperimen
Pembelajaran menggunakan 1. Pembelajaran menggunakan Ekspositori strategi problem solving
menurut Wankat dan Oreovicz
2. Pengisian lembar observasi
Tahap 3: Analisis Data
Data kuantitatif : pre-tes dan post-tes Data kualitatif : lembar observasi,
angket self-regulated learning
Tahap 4: Penarikan kesimpulan dan saran
menarik kesimpulan dari data kuantitarif mendeskripsikan data kualitatif
penyusunan lapor
Bagan 3.1
Rancangan Alur Kegiatan Penelitian
1. Tahap Persiapan
Langkah-langkah yang dilakukan dalam tahap ini adalah:
a. Mengajukan judul penelitian, menyusun proposal penelitian;
b. kemudian diseminarkan dan setelah mendapat masukan dari tim penelaah
seminar proposal maka proposal akan diperbaiki;
c. Membuat instrumen penelitian dan merancang Rencana Pelaksanaan
Pembelajaran (RPP) atau bahan ajar;
d. Memvalidasi instrumen, menganalisis, dan merevisinya sebelum penelitian;
e. Mengajukan permohonan izin penelitian kepada pihak-pihak terkait;
f. Melaksanakan uji coba lapangan, mengumpulkan data hasil uji coba dan
menganalisis data tersebut.
2. Tahap Pelaksanaan
Langkah-langkah yang dilakukan dalam penelitian ini adalah:
a. Menentukan sampel penelitian, memberikan soal pretes baik di kelas eksperimen maupun kelas kontrol untuk menetahui kemampuan awal
b. Memberikan perlakuan berupa pembelajaran matematika dengan
menggunakan strategi problem solving menurut Wankat dan Oreovicz di kelas eksperimendan pembelajaran ekspositori di kelas kontrol
c. Di kelas dengan menggunakan strategi problem solving menurut Wankat dan Oreoviczdilakukan observasi pada guru dan siswa di setiap pertemuan untuk
mengamati situasi yang terjadi dalam kelas ketika pembelajaran itu
berlangsung;
d. Memberikan post-tes baik di kelas eksperimen maupun di kelas kontrol untuk mengetahui kemampuan pemahaman konsep matematis siswa, dan
memberikan angket self-regulated learning siswa untuk mengetahui peningkatan kemandirian belajar siswa setelah mendapat perlakuan.
3. Tahap Akhir
Langkah-langkah yang dilakukan dalam tahapan ini adalah:
a. Mengumpulkan hasil data kuantitatif dan kualitatif;
b. Melakukan analisis data kuantitatif terhadap data pre-tes dan post-tes; c. Melakukan analisis data kualitatif terhadap data lembar observasi.
4. Tahap Penarikan Kesimpulan, Implikasi dan Rekomendasi
Langkah-langkah yang dilakukan dalam tahap ini yaitu:
i. Menarik kesimpulan dari data kuantitatif yang diperoleh, yaitu mengenai
kemampuan pamahaman konsep matematis dan self-regelated learning siswa;
ii. Menarik kesimpulan dari data kualitatif yang diperoleh, yaitu mengenai
proses pembelajaran dengan strategi problem solving menurut Wankat dan Oreovicz.
iii. Penyusunan laporan
G. Teknik pengumpulan Data
Data dalam penelitian ini dikumpulkan melalui tes, skala sikap, dan lembar
observasi. Data yang berkaitan dengan kemampuan pemahaman konsep
yang berkaitan self-regulated learning siswa dikumpulkan melalui skala sikap, lembar observasi.
Dalam pengumpulan data ini terlebih dahulu menentukan sumber data,
kemudian jenis data, teknik pengumpulan data, dan instrumen yang digunakan.
Teknik pengumpulan data secara lengkap dapat dilihat pada Tabel 3.13 berikut
diberikan sebelum dan setelah diberikan perlakuan
Jenis data yang dianalisis dalam penelitian ini adalah data kuantitatif berupa
hasil tes kemampuan pemahaman konsep matematis siswa. Analisis data hasil tes
dimaksudkan untuk mengetahui besarnya pengaruh pembelajaran dengan
menggunakan strategi problem solving menurut Wankat dan Oreovicz terhadap kemampuan pemahaman konsep matematis siswa dan self-regulated learning siswa.
Pengolahan dan analisis data hasil tes kemampuan pemahaman konsep
matematis siswa dilakukan dengan bantuan software SPSS versi 20. Adapun langkah-langkahnya uji statistik yang dilakukan oleh peneliti adalah uji
Berikut ini akan diuraikan langkah demi langkah dalam perhitungan secara
statistiknya:
1. Analisis Data Kuantitatif
a. Uji Normalitas
Uji normalitas dilakukan untuk menentukan apakah data yang didapat
berdistribusi normal atau tidak. dikarenakan jumlah data sebanyak 32 orang, maka
untuk melakukan uji normalitas digunakan uji Saphiro Wilk dengan taraf signifikansi 5%. Uji normalitas ini dilakukan terhadap pre-tes dan N-Gain dari dua kelompok (kelas eksperimen dan kelas kontrol).
Jika hasil pengujian menunjukkan bahwa sebaran data berdistribusi normal
maka dalam menguji kesamaan dua rerata digunakan uji t. Apabila hasil pengujian
menunjukkan bahwa sebaran data tidak berdistribusi nomal maka untuk menguji
kesamaan dua rerata digunakan perhitungan dengan statistik nonparametrik, yaitu
uji Man-Whitney. Uji normalitas menggunakan bantuan SPSS 20 pada taraf signifikansi 5%.
Hipotesis yang diuji adalah:
H0 : data sampel berasal dari populasi yang berdistribusi normal
H1 : data sampel berasal dari populasi yang tidak berdistribusi normal
Kriteria pengujian yang digunakan adalah: jika Sig. lebih besar dari α = 0,05 maka H0 diterima, dan H1 ditolak (Pramesti, 2014, hlm. 28)
b. Uji Homogenitas
Pengujian homogenitas variansi antara dua kelas dilakukan dengan tujuan
untuk mengetahui apakah variansi kedua kelas sama atau berbeda. Uji
homogenitas dilakukan apabila pada uji normalitas diperoleh kesimpulan bahwa
data berdistribusi normal. Uji homogenitas varians digunakan untuk menguji
kesamaan variansi dari skor pretes, postes, dan gain pada kedua kelompok (kelas
eksperimen dan kelas kontrol) untuk setiap aspek kemampuan matematis. Uji
homogenitas yang digunakan adalah uji Levene dengan bantuan SPSS 20 pada
taraf signifikansi 5%.
Hipotesis yang akan diuji dapat juga dinyatakan sebagai berikut (Sudjana, 2005,
H0 : Variansi skor tes kemampuan pemahaman konsep matematika
kelompok homogen.
H1 : Variansi skor tes kemampuan pemahaman konsep matematika
kelompok tidak homogen.
Keterangan:
Variansi skor tes kelas dengan menggunakan strategi problem solving menurut Wankat dan Oreovicz
Variansi skor tes kelas ekspositori
Kriteria pengujian yang digunakan adalah jika Sig. lebih besar dari α = 0,05 maka H0 diterima, dan H1 ditolak (Pramesti, 2014, hlm. 33)
c. Uji Perbedaan Dua Rerata
Untuk mengetahui ada atau tidak adanya perbedaan kemampuan
pemahaman konsep matematis dan self-regulated learning siswa yang mendapatkan pembelajaran dengan menggunakan strategi problem solving menurut Wankat dan Oreovicz dibandingkan dengan siswa yang mendapatkan
pembelajaran secara ekspositori maka dilakukan pengujian perbedaan dua rerata
dengan α = 0,05.
Jika hasil dari pengujian normalitas dan homogenitas didapatkan bahwa data
itu berdistribusi normal dan homogen terhadap data pre-tes dan pot-tes, pada kedua kelas maka langkah selanjutnya dilakukanlah uji perbedaan dua rerata yang
digunakan adalah uji t independent sample test.
Adapun hipotesis untuk kemampuan pemahaman konsep matematis adalah:
H0 : µ1 = µ2 Tidak terdapat perbedaan rerata kemampuan pemahaman
konsep matematika siswa yang mendapatkan pembelajaran
dengan menggunakan strategi problem solving menurut Wankat dan Oreovicz dibandingkan dengan siswa yang mendapatkan
pembelajaran matematika dengan metode ekspositori.
H1 : µ1 ≠ µ2 Terdapat perbedaan rerata kemampuan pemahaman konsep
matematika siswa yang mendapatkan pembelajaran matematika
dan Oreovicz dibandingkan dengan siswa yang mendapatkan
pembelajaran matematika dengan metode ekspositori.
Hipotesis self regulated learning siswa adalah:
H0 : µ1 = µ2 Tidak terdapat perbedaan rata-rata self regulated learning siswa yang mendapatkan pembelajaran matematika dengan
menggunakan strategi problem solving menurut Wankat dan Oreovicz dibandingkan dengan siswa yang mendapatkan
pembelajaran matematika dengan metode ekspositori.
H1 : µ1≠ µ2 Terdapat perbedaan rata-rata self regulated learning siswa yang mendapatkan pembelajaran matematika dengan menggunakan
strategi problem solving menurut Wankat dan Oreovicz dibandingkan dengan siswa yang mendapatkan pembelajaran
matematika dengan metode ekspositori.
Keterangan
µ1 = rerata skor postes kelas dengan menggunakan strategi problem solving menurut Wankat dan Oreovicz
µ2 = rerata skor postes kelas dengan pembelajaran secara ekspositori.
Jika data hasil tes kedua kelas berdistribusi normal dan homogen, maka uji
perbedaan dua rerata untuk data pretes dan postes menggunakan uji t-independen.
Jika data hasil tes kedua kelas berdistribusi normal dan variansi keduanya tidak
homogen, maka digunakan uji t’ independen. Jika data hasil tes kedua kelas tidak
berdistribusi normal dan variansi keduanya tidak homogen, maka uji statistik yang
digunakan adalah pengujian bebas asumsi atau uji nonparametrik, yaitu uji Mann-Whitney U (uji-U).
Berikut uji statistik yang digunakan untuk uji t independen dengan rumus
(Sudjana, 2005, hlm. 239):
x x √
Keterangan:
S = Simpangan baku gabungan dari kedua kelompok.
S1 = Simpangan baku kelas yang menggunakan strategi problem solving
menurut Wankat dan Oreovicz
S2 = Simpangan baku kelas yang menggunakan pembelajaran secara ekspositori.
X 1= Rerata skor post-tes pada strategi problem solving menurut Wankat dan
Oreovicz
X = Rerata skor post-tes yang menggunakan pembelajaran secara ekspositori n1 = Banyak siswa kelas yang menggunakan strategi problem solving menurut
Wankat dan Oreovicz.
n2 = Banyak siswa kelas yang menggunakan pembelajaran secara ekspositori
Dalam menghitung uji perbedaan dua rerata ini peneliti menggunakan sofware SPSS 20. Sehingga pengujian hipotesisnya berdasarkan p value (significance atau sig) dengan kriteria sebagi berikut:
Jika sig (1 tailed) = sig (2 taliled) < dengan = 0,05 maka H0 ditolak
Jika sig (1 tailed) = sig (2 taliled) ≥ dengan = 0,05 maka H0 diterima
d. Data N-Gain
Untuk mengetahui peningkatan kamampuan pemahaman konsep matematis
dan sel-regulated learning siswa, baik kelas eksperimen maupun kelas kontrol dilakukan perhitungan skor N-Gain dengan rumus dalam Hake (1999, hlm. 1), yaitu:
Hasil perhitungan kemudian diinterpretasikan dengan menggunakan N-Gain ternormalisasi berikut:
Tabel 3.14
Kriteria Indeks Gain Ternormalisasi
Indeks Gain Kriteria
≥ 0,70 Tinggi
0,30 ≤ < 0,700 Sedang
< 0,30 Rendah
Berdasarkan pemaparan di atas selanjutnya peneliti menggambarkan alur
analisis untuk data kuantitatif pada penelitian ini disajikan secara singkat pada
bagan di bawah ini:
Data
Tidak
Uji Normalitas Uji Non Parametrik
(Mann Whitney)
Ya Tidak
Uji Homogenitas Uji Perbedaan Dua Rerata
(Uji )
Ya
Uji Perbedaan Dua Rerata
(Uji t)
Bagan 3.2
Alur Analisis Data Kuantitatif
2. Analisis Data Kualitatif
Kelas eksperimen, dengan melakukan analisis kualitatif terhadap data hasil
observasi.
Data hasil observasi Data kualitatif diperoleh dengan menggunakan lembar
observasi. Dengan lembar observasi ini peneliti dapat mengamati semua kegiatan
atau aktivitas baik siswa maupun guru pada saat kegiatan pembelajaran
berlangsung di kelas eksperimen. Tujuan dari pengamatan ini tidak lain ingin
memperoleh gambaran mengenai proses pelaksanaan pembelajaran dengan
strategi problem solving menurut Wankat dan Oreovicz di kelas tersebut kemudian dianalisis secara deskriptif untuk mengetahui aktivitas guru dan siswa