1
Penerapan Metode Barvinok Rational Functions
Pada Optimasi Integer Programming
Riska Kurniawati1, Rully Soelaiman, S.Kom, M.Kom2
1Jurusan Teknik Informatika, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia 2Jurusan Teknik Informatika, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia
Permasalahan optimasi sering kali menjadi permasalahan yang sangat penting dalam menentukan suatu keputusan yang akan diambil, contohnya saja pada proses pembuatan produksi produk pada suatu bidang industri. Kebanyakan hasil yang didapatkan dari proses optimasi ini berupa bilangan pecahan yang tidak memungkinkan untuk digunakan dalam proses pengambilan keputusan. Oleh karena itu perlu diterapkan metode integer programming untuk menghasilkan solusi optimal dalam bilangan bulat sehingga dapat digunakan dalam proses pengambilan keputusan.
Tugas Akhir ini menganalisa suatu metode baru yang dapat digunakan untuk menyelesaikan kasus integer programming yaitu dengan menggunakan metode Barvinok Rational Functions.
Metode barvinok rational function ini mampu memberikan kemudahan dalam menyelesaikan kasus integer programming serta mempunyai waktu komputasi yang lebih cepat dan lebih efisien dalam penggunaan memori.
Kata Kunci : Integer Programming, Barvinok Rational Function I. PENDAHULUAN
ermasalahan optimasi merupakan bagian yang tidak asing lagi dalam kehidupan manusia sehari-hari. Sering kali dalam usaha untuk memenuhi kebutuhannya, manusia membutuhkan proses optimasi dalam pekerjaannya. Bentuk optimasi tersebut dapat berupa meminimumkan biaya yang dikeluarkan atau juga dapat berupa memaksimumkan pendapatan yang ingin diperoleh.
Akan tetapi kadang kala terdapat permasalahan jika hasil yang didapatkan dari proses optimasi tersebut berupa bilangan pecahan, padahal hasil yang diinginkan tidak memungkinkan jika menggunakan bilangan pecahan. Oleh karena itu digunakan proses optimasi dengan menggunakan metode integer programming untuk menyelesaikan masalah tersebut.
Saat ini, metode yang digunakan untuk proses optimasi pada kasus integer programming sangat banyak sekali, tetapi pada pembahasan kali ini hanya difokuskan pada penggunaan metode Barvinok Rational Functions. Metode Barvinok Rational Functions ini memberikan solusi untuk menyelesaikan kasus integer programming dengan lebih cepat dan lebih efisien dalam penggunaan memori.
II. DASAR TEORI
A. Pemrograman Integer
Tipe data integral terbagi menjadi dua buah kategori, baik itu bertanda (signed) ataupun tidak bertanda (unsigned). Bilangan bulat bertanda mampu merepresentasikan nilai bilangan bulat negatif, sementara bilangan bulat tak bertanda hanya mampu merepresentasikan bilangan bulat positif [12].
Pemrograman Integer atau juga disebut pemrograman bulat sering kali dibutuhkan ketika keputusan harus dilakukan dalam bentuk bilangan bulat (bukan pecahan yang sering terjadi bila menggunakan metode simplex). Model matematis dari pemrograman bulat sebenarnya sama dengan model linier programming, dengan tambahan batasan bahwa variabelnya harus bilangan bulat [11].
B. Teori Fungsi Polynomial
Monomial merupakan suatu fungsi yang terdiri dari
term tunggal, misalnya cxn , dimana c merupakan
konstanta, x merupakan variabel, dan n bernilai nol atau positif integer. Sedangakan polynomial bisa juga diartikan sebagai suatu fungsi yang mengandung operasi baik penjumlahan ataupun perkalian dari sejumlah
monomial term yang terbatas (finite) [14].
Fungsi polynomial
f
(x
)
merupakan fungsi yang didefinisikan dengan mengevaluasi bentuk polynomial tersebut.Bentuk fungsi polynomial pada umumnya :
0 0 1 2 2 1 1 ... ) (x a x a x a x ax ax f n n n n + + + + + = − − (1) C. Lattice Point
Lattice Points merupakan suatu kumpulan (set)
titik-titik integer yang berada dalam suatu region yang terbatas (bounded polyhedron), baik yang berada tepat di batas
region maupun yang berada didalam region [2].
D. Polyhedra
Polyhedra merupakan representasi geometris dari
sistem persamaan baik linier maupun tidak linier.
Polyhedra dapat berupa suatu bidang . Perpotongan
(intersection) dari beberapa polyhedra akan membentuk suatu polyhedron [2].
Bounded Polyhedron biasanya disebut juga sebagai Polytope. Polyhedron yang bounded akan convergen
terhadap semua nilai.
Sistem polyhedra dibentuk oleh sekumpulan cone dimana cone tersebut merupakan kombinasi linier dari x (titik) didalam polyhedra P yang mempunyai koordinat integer, dengan v (vertex) dari P.
E. Generating function
Generating function merupakan suatu proses untuk
mendapatkan suatu bentuk persamaan yang tidak dipengaruhi oleh faktor rekursifnya. Disini generating
function digunakan untuk proses pemecahan cone
(decompose cone).
Bentuk umum dari generating function :
∑
∈=
d z m mx
x
P
f
(
,
)
(2) F. Rational functionJika terdapat dua buah fungsi polynomial, dan dilakukan operasi baik penjumlahan, pengurangan, maupun perkalian terhadap keduanya, maka hasil operasi dari kedua fungsi polynomial tersebut akan menghasilkan bentuk polynomial pula.
Akan tetapi, jika terdapat dua buah fungsi
polynomial, dan dilakukan operasi pembagian atau dicari
rasio dari kedua fungsi polynomial tersebut, maka hasil dari operasi tersebut bukan merupakan bentuk
polynomial, tetapi akan menghasilkan suatu fungsi yang
rasional.
Untuk lebih mudahnya, Rational function merupakan suatu fungsi yang dituliskan berdasarkan ratio dari 2 fungsi polynomial, contoh
)
(
)
(
)
(
x
Q
x
P
x
f
=
, dimana P dan Q merupakan fungsi polynomial.Rational Function merupakan salah satu bentuk
expansi dari generating function, dimana semua variabel dalam persamaan tersebut berupa bilangan integer. Jika inputan yang digunakan dalam persamaan Rational
Function tersebut berupa Lattice Point, maka persamaan
tersebut disebut rational polyhedron Bentuk umum dari Rational function :
( )
(
) (
)
∑
=−
−
=
n i ui uid ix
x
x
p
x
P
f
11
1...
1
)
,
(
(3)G. Metode Barvinok Rational function.
Metode Barvinok rational functions pertama kali diperkenalkan oleh A.I Barvinok pada tahun 1993. Metode Barvinok rational functions ini merupakan suatu metode baru yang ditawarkan untuk memperbaiki dan menyempurnakan penyelesaian kasus integer
programming.
Tujuan dari metode Barvinok rational functions ini adalah untuk menemukan solusi optimal dari :
Maximize c.x subject to : Ax ≤ b
x ≥ 0 x
∈
Zddengan input data berupa mxd integral matrix A, dimana
m merupakan panjang vektor dari b dan d merupakan
panjang vector dari c. Input data ini mendeskripsikan
non-empty full-dimensional convex polytope
{
∈ℜ : ≤ , ≥0}
= x Ax b x
P d . bentuk umum dari Barvinok
Rational Function adalah sebagai berikut :
∑
Π
∈ = − = I i dj v u i ij i z z E z P f ) 1 ( ) ; ( 1 (4) Persamaan (4) merupakan bentuk dari rationalfunction dimana, dalam bentuk fungsi rational tersebut
selalu ada komponen pembilang dan penyebut, yaitu : - Denominator (penyebut) dari fungsi diatas berupa
hasil kali binomial dari
1
−
z
vij, dimana vij
merupakan generator dari cone Pi (ray dari cone Pi).
Dan bentuk dari penyebut ini berupa polynomial
)
1
(
−
z
vijΠ
.- Numerator (pembilang) dari fungsi diatas berupa single monomial
z
uiH. Algoritma Binary search
Algoritma Binary search ini merupakan algoritma
straightforward dimana hanya menggunakan metode Binary search. Algoritma ini menghitung jumlah Lattice Point P yang memenuhi syarat c . x ≥ M, dimana rentang
nilai maksimum dari c . x dapat dipersempit. Ketika dilakukan proses pengulangan maka akan didapatkan hasil integer M terbesar adalah tidak nol. Algoritma
Binary Search ini memberikan kemungkinan
penghitungan baru dalam integer programming dengan dimensi yang tetap.
Algoritma :
Input : A
∈
Zm×d, b∈
Zm, c∈
ZdOutput : Nilai Optimal dari M = maximize[c . x : Ax ≤ b,
x ≥ 0, x
∈
Zd]1. Selesaikan masalah Integer Programming dengan menggunakan metode linier programming relaxation dimana M = [max { c . x : Ax ≤ b, x ≥ 0}] dan m = [min{ c . x : Ax ≤ b, x ≥ 0}] . Dengan demikian, [M,m] merupakan initial range untuk algoritma
binary search ini
2. Algoritma: While M > m do new := ⎥⎥ ⎤ ⎢⎢ ⎡ + 2 m M
Using Barvinok algorithm compute qnew = | P ∩ {x: c.x ≥ new}∩ Zd|
If qnew > 0 then set m = new Else M = new -1
Return M
I. Monomial Substitution
Dari metode barvinok rational function f(P,z) suatu
polytope P, jumlah dari Lattice Point di dalam P menjadi
terbatas ketika vektor (z1...zd) mendekati nilai (1,....,1).
Untuk mengatasi hal tersebut, substitusi vektor tidak dapat dilakukan dengan mudah. Oleh karenanya dilakukan general monomial substitution dengan mensubstitusikan suatu bentuk monomial (misal : y1a1,
y2a2...., ynan) kedalam variabel zi, dengan y1a1
∈
Zd.Jika diberikan suatu cost vector c
∈
Zd yangditerapkan untuk mensubstitusikan zk = tck , maka bentuk
rational functionnya dalam t adalah
∑
Π
∈ = − = I i kj cv u c i ij i t t E t P f ) 1 ( ) , ( . 1 . (5) III. METODOLOGISecara keseluruhan terdapat 4 proses utama yang harus dilakukan dalam menyelesaikan kasus integer programming untuk mendapatkan solusi optimal yang diinginkan, yaitu :
1. Proses Inisialisasi yaitu proses untuk mendapatkan bentuk persamaan Barvinok Rational Function dari suatu kasus permasalahan integer programming. Pada
3 proses inisialisasi ini terdapat 2 tahapan yang dilalui yaitu:
a. Tahap pengecekan inputan b. Tahap baca problem data
2. Proses Decompose Cone dengan metode Barvinok
Rational Function untuk mendapatkan unimodular
cone.
3. Proses Compute Lattice Point dengan menggunakan metode monomial substitution untuk mendapatkan
Lattice Point yang paling optimal.
4. Proses Optimasi yaitu mencari nilai dan solusi optimal dari permasalahan IP menggunakan algoritma
binary search dan algoritma digging dalam software
Latte v1.2.
Untuk lebih jelasnya diagram alir keseluruhan sistem dapat dilihat pada Gambar 3.2
Gambar III.1 Diagram Alir Keseluruhan Sistem
A. Proses Inisialisasi
Proses inisialisasi ini merupakan suatu proses untuk menginisialisasi permasalahan integer programming yang akan diselesaikan menggunakan metode Barvinok
Rational Function. Proses inisialisasi ini terdiri dari dua
proses yaitu proses cek inputan dan proses baca problem data.
1. Tahap Pengecekan Inputan
Pada tahap ini dilakukan pengecekan terhadap inputan yang akan diselesaikan menggunakan metode Barvinok
Rational Function yaitu salah satu proses yang dilakukan
dalam tahapan ini yaitu proses pengecekan inputan apakah inputan tersebut kosong atau tidak. Disini maksud dari kosong adalah apakah inputan tersebut mengandung
Lattice Point ataukah tidak. Jika inputan yang
dimasukkan tidak mengandung Lattice Point, maka inputan tersebut dianggap kosong dan tidak dapat diselesaikan. Tahapan ini menghasilkan keluaran berupa persamaan integer programming yang telah dilakukan pengecekan inputan.
2. Tahap Baca Problem Data
Pada tahap ini dilakukan proses pembacaan problem data. Inputan yang sudah dicek pada tahap cek inputan kemudian dibaca problem data yang terkandung didalamnya. Kemudian di inisialisasi apakah problem pada inputan tersebut berupa permasalahan integer ataukah bukan. Jika hasil inisialisasi terhadap problem data tersebut bukan merupakan permasalahan integer maka inputan tersebut dianggap kosong dan tidak dapat dikerjakan.
B. Proses Pemecahan Cone
Proses pemecahan cone dapat dikatakan sebagai bagian yang paling penting dalam metode Barvinok
rational functions ini. Proses Decompose cone
merupakan proses pemecahan suatu cone kedalam beberapa unimodular cone. Salah satu cara yang digunakan untuk memecah suatu cone (decompose cone) kedalam beberapa bentuk unimodular cone dengan tepat adalah dengan menerapkan fungsi generating function. C. Proses Menghitung Lattice Point
Setelah didapatkan unimodular cone dari proses
decompose cone diatas, maka untuk menentukan Lattice Point yang paling optimal adalah dengan melakukan
proses monomial substitution. D. Proses Optimasi
Pada proses optimasi ini, akan dicari solusi dan nilai optimal dari permasalahan yang ada dengan menganalisa jalannya algoritma binary search.
E. Penerapan Metode Barvinok rational functions dalam suatu kasus IP
1. Proses Inisialisasi
Jika proses inisialisasi ini diterapkan dalam suatu kasus permasalahan integer maka bentuk inisialisasi berupa menterjemahkan permasalahan IP yang ada. Contoh: Maximize z = 100x + 90 y Subject to : x + y ≤ 100 x ≤ 50 x , y ≥ 0 x , y
∈
Ζ
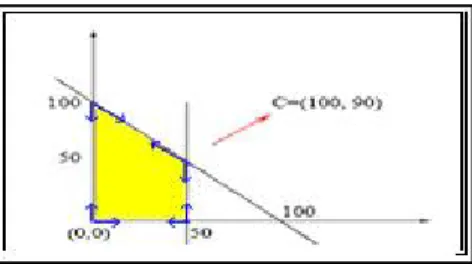
dDari permasalahan IP yang ada, kemudian dicari vertice yang memenuhi constrain dengan melakukan proses substitusi, sehingga jika persamaan tersebut diterapkan pada persamaan garis 2 dimensi, maka batasan dari persamaan tersebut adalah:
1. Pada batasan x + y ≤ 100 jika x = 0 maka x + y ≤ 100 y ≤ 100 jika y = 0 maka x + y ≤ 100 x ≤ 100 2. Pada batasan x ≤ 50
Gambar III.2 Bentuk persamaan garis dari max Z = 100x + 90y
2. Proses Pemecahan Cone
Dari persamaan garis diatas, maka terbentuk suatu bidang P (dalam gambar berwarna kuning) yang nantinya pada bidang tersebut akan dilakukan proses decompose cone.
a. Proses cari vertice dan edge
Setelah bidang P terbentuk, maka dari bidang tersebut dapat dicari komponen vertice dan edge nya. - ui (vertice)= Koordinat dari zd (dalam gambar
berupa (x,y)), sehingga dihasilkan ::
u1 = (0,0) u2 = (50,0)
u3 = (0,100) u4 = (50,50)
- vij (edge) = Generators Cone Pi berupa arah dari
vektor z (dalam gambar berupa (xij,yij)) • Jika i mempunyai arah vektor ke kanan maka
bernilai = 1
• Jika i mempunyai arah vektor ke kekiri maka bernilai = -1
• Jika j mempunyai arah vektor ke atas maka bernilai = 1
• Jika j mempunyai arah vektor ke bawah maka bernilai = -1 Sehingga dihasilkan : v11 = (1,0) v31 = (0,-1) v12 = (0,1) v32 = (1,-1) v21 = (-1,0) v41 = (0,-1) v22 = (0,1) v42 = (-1,1)
b. Proses Generating Function
Setelah didapatkan komponen ui dan vij maka proses
decompose cone dengan menerapkan metode Barvinok Rational function pada persamaan (4) dapat
dilakukan. Sehingga dihasilkan :
∑
Π
∈ = − = I i dj v u i ij i z z E z P f ) 1 ( ) ; ( 1+
−
−
+
−
−
=
−)
1
)(
1
(
)
1
)(
1
(
1 2 0 1 0 2 1 1 0 2 50 1 1 2 0 1 0 2 1 1 0 2 0 1z
z
z
z
z
z
z
z
z
z
z
z
) 1 )( 1 ( ) 1 )( 1 ( 1 2 1 1 1 2 0 1 50 2 50 1 1 2 1 1 1 2 0 1 100 2 0 1 z z z z z z z z z z z z − − − − − + − − − = + − − + − − − ) 1 )( 1 ( ) 1 )( 1 ( 1 2 1 1 50 1 2 1 z z z z z + ) 1 )( 1 ( ) 1 )( 1 ( 12 1 1 2 50 2 50 1 1 2 1 1 2 100 2 z z z z z z z z z − − − − − + − − −Setelah dilakukan proses decompose cone berdasarkan Gambar III.2 diatas , maka didapatkan 4 buah unimodular
cones dan bentuk rational functionnya adalah:
+
−
−
+
−
−
=
−)
1
)(
1
(
)
1
)(
1
(
1
)
;
(
2 1 1 50 1 2 1z
z
z
z
z
z
P
f
) 1 )( 1 ( ) 1 )( 1 ( 12 1 1 2 50 2 50 1 1 2 1 1 2 100 2 z z z z z z z z z − − − − − + − − −3. Proses Hitung Lattice Point
a. Jika unimodular cone sudah didapatkan, maka
dilakukan proses monomial substitution dengan mensubstitusikan zk = tck , dimana c merupakan suatu
cost vector c
∈
Zb. Terapkan substitusi zk = tck pada persamaan (4),
sehingga menghasilkan persamaan (5), dari multivariate monomial menjadi univariate monomial. c. Dengan mengasumsikan bahwa c dipilih secara
random dari suatu dimensi Zd, maka jika ditetapkan
cost vector c = (100,90) maka z1 = t100 dan z2 = t90.
d. Lakukan proses perhitungan persamaan (5) dengan cost vector yang sudah ditentukan, sehingga menghasilkan
∑
Π
∈ = − = I i kj cv u c i ij i t t E t P f ) 1 ( ) , ( . 1 . + − − + − − = − ) 1 )( 1 ( ) 1 )( 1 ( 1 2 1 1 50 . 100 2 1 z z t z z ) 1 )( 1 ( ) 1 )( 1 ( 21 11 2 50 . 90 50 . 100 1 2 1 1 2 100 . 90 z z z t t z z z t − − − − − + − − −Setelah didapatkan lattice point yang paling optimal dari masing-masing unimodular cone maka untuk mendapatkan nilai optimal dari persamaan integer diperlukan penerapan algoritma binary search
4. Proses Optimasi
Berdasarkan proses perhitungan diatas, maka dapat diketahui bahwa nilai dari :
- Maximize z = 100x1 + 90x2
Subject to :
x1+ x2 ≤ 100
x1≤ 50
x1 , x2 ≥ 0 dan integer
adalah 9500 dengan x1 = 50 dan x2=50 - Minimize z = 100x1 + 90x2
Subject to :
x1+ x2 ≤ 100
x1≤ 50
x1 , x2 ≥ 0 dan integer
adalah 0 dengan x1 = 0 dan x2=0
Oleh karena nilai optimum yang dihasilkan merupakan bilangan integer, maka proses linear programming relaxation menghasilkan M = 9500 dengan x1 = 50, dan x2 = 50, serta m = 0 dengan x1 =0 dan x2 =0:
Identifikasi setiap unimodular cone yang dihasilkan dari proses cari lattice point, dan dilakukan pengecekan apakah unimodular cone tersebut berada dalam range [M,m] dan integer, sehingga dihasilkan :
5 P1 (0,0) Æ Maximize z = 100x1 + 90x2 = 0 P2 (50,0) Æ Maximize z = 100x1 + 90x2 = 5000 P3 (0,100) Æ Maximize z = 100x1 + 90x2 = 9000 P4 (50,50) Æ Maximize z = 100x1 + 90x2 = 9500
Dari hasil diatas dapat diketahui bahwa terdapat 4 buah unimodular cone yang memiliki batasan yang integer. Proses Dari hasil iterasi didapatkan :
- Unimodular cone P1
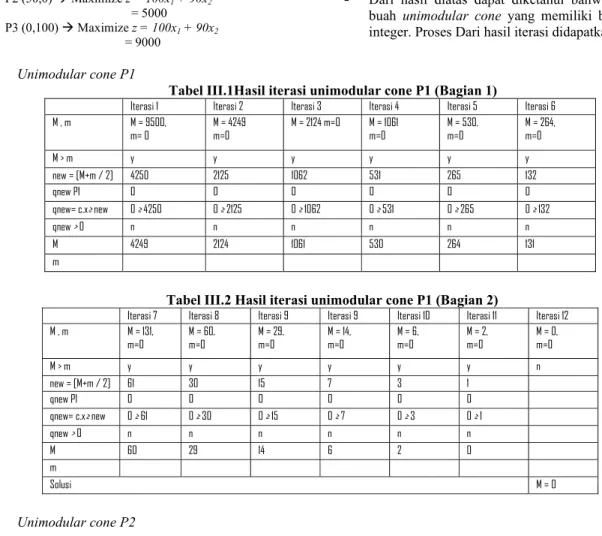
Tabel III.1Hasil iterasi unimodular cone P1 (Bagian 1)
Iterasi 1 Iterasi 2 Iterasi 3 Iterasi 4 Iterasi 5 Iterasi 6 M , m M = 9500, m= 0 M = 4249 m=0 M = 2124 m=0 M = 1061 m=0 M = 530, m=0 M = 264, m=0 M > m y y y y y y new = [M+m / 2] 4250 2125 1062 531 265 132 qnew P1 0 0 0 0 0 0 qnew= c.x≥ new 0 ≥ 4250 0 ≥ 2125 0 ≥ 1062 0 ≥ 531 0 ≥ 265 0 ≥ 132 qnew > 0 n n n n n n M 4249 2124 1061 530 264 131 m
Tabel III.2 Hasil iterasi unimodular cone P1 (Bagian 2)
Iterasi 7 Iterasi 8 Iterasi 9 Iterasi 9 Iterasi 10 Iterasi 11 Iterasi 12 M , m M = 131, m=0 M = 60, m=0 M = 29, m=0 M = 14, m=0 M = 6, m=0 M = 2, m=0 M = 0, m=0 M > m y y y y y y n new = [M+m / 2] 61 30 15 7 3 1 qnew P1 0 0 0 0 0 0 qnew= c.x≥ new 0 ≥ 61 0 ≥ 30 0 ≥ 15 0 ≥ 7 0 ≥ 3 0 ≥ 1 qnew > 0 n n n n n n M 60 29 14 6 2 0 m Solusi M = 0 - Unimodular cone P2
Tabel III.3 Hasil iterasi unimodular cone P2 (Bagian 1)
Iterasi 1 Iterasi 2 Iterasi 3 Iterasi 4 Iterasi 5 Iterasi 6 Iterasi 7 M , m M = 9500, m= 0 M = 9500 m=4250 M = 6874 m=4250 M = 5561 m=4250 M = 5561, m=4901 M = 5230, m=4901 M= 5065 m=4901 M > m y y y y y y y new = [M+m / 2] 4250 6875 5562 4901 5231 5066 4983 qnew P2 5000 5000 5000 5000 5000 5000 5000 qnew= c.x≥ new 5000 ≥ 4250 5000≥ 6875 5000≥ 5562 5000≥ 4901 5000≥ 5231 5000≥ 5066 5000≥ 4983 qnew > 0 y n n y n n y M 6874 5561 5230 5065 m 4250 4901 4983
Tabel III.4 Hasil iterasi unimodular cone P2 (Bagian 2)
Iterasi 8 Iterasi 9 Iterasi 9 Iterasi 10 Iterasi 11 Iterasi 11 Iterasi 12 M , m M=5065 m=4983 M = 5023, m=4983 M = 5002, m= 4983 M = 5002, m=4993 M=5002, m=4998 M=5002, m=5000 M = 5000, m= 5000 M > m y y y y y y n new = [M+m / 2] 5024 5003 4993 4998 5000 5001 qnew P2 5000 5000 5000 5000 5000 5000 qnew= c.x≥ new 5000≥ 5024 5000≥ 5003 5000≥ 4993 5000≥ 4998 5000≥ 5000 5000≥ 5001 qnew > 0 n n y y y n M 5023 5002 5000 m 4993 4998 5000 Solusi M = 5000
- Unimodular cone P3
Tabel III.5 Hasil iterasi unimodular cone P3 (Bagian 1)
Iterasi 1 Iterasi 2 Iterasi 3 Iterasi 4 Iterasi 5 Iterasi 6 Iterasi 7 M , m M = 9500, m= 0 M = 9500 m=4250 M = 9500 m=6875 M = 9500 m=8188 M = 9500, m=8844 M = 9171, m=8844 M= 9007 m=8844 M > m y y y y y y y new = [M+m / 2] 4250 6875 8188 8844 9172 9008 8926 qnew P3 9000 9000 9000 9000 9000 9000 9000 qnew= c.x≥ new 9000≥ 4250 9000≥ 6875 9000≥ 8188 9000≥ 8844 9000≥ 9172 9000≥ 9008 9000≥ 8926 qnew > 0 y y y y n n y M 9171 9007 m 4250 6875 8188 8844 8926
Tabel III.6 Hasil iterasi unimodular cone P3 (Bagian 2)
Iterasi 8 Iterasi 9 Iterasi 9 Iterasi 10 Iterasi 11 Iterasi 12 Iterasi 13 Iterasi 13 M , m M=9007 m=8926 M= 9007 m= 8967 M = 9007, m= 8987 M = 9007, m=8997 M=9001, m=8997 M=9001, m=8999 M= 9001, m= 9000 M = 9000, m= 9000 M > m y y y y y y y n new = [M+m / 2] 8967 8987 8997 9002 8999 9000 9001 qnew P3 9000 9000 9000 9000 9000 9000 9000 qnew= c.x≥ new 9000≥ 8967 9000≥ 8987 9000≥ 8997 9000≥ 9002 9000≥ 8999 9000≥ 9000 9000≥ 9001 qnew > 0 y y y n y y n M 9001 9000 m 8967 8987 8997 8999 9000 Solusi M = 9000 - Unimodular cone P4
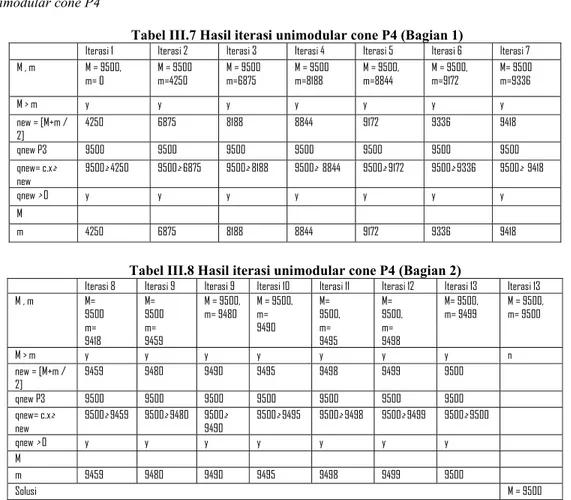
Tabel III.7 Hasil iterasi unimodular cone P4 (Bagian 1)
Iterasi 1 Iterasi 2 Iterasi 3 Iterasi 4 Iterasi 5 Iterasi 6 Iterasi 7 M , m M = 9500, m= 0 M = 9500 m=4250 M = 9500 m=6875 M = 9500 m=8188 M = 9500, m=8844 M = 9500, m=9172 M= 9500 m=9336 M > m y y y y y y y new = [M+m / 2] 4250 6875 8188 8844 9172 9336 9418 qnew P3 9500 9500 9500 9500 9500 9500 9500 qnew= c.x≥ new 9500≥ 4250 9500≥ 6875 9500≥ 8188 9500≥ 8844 9500≥ 9172 9500≥ 9336 9500≥ 9418 qnew > 0 y y y y y y y M m 4250 6875 8188 8844 9172 9336 9418
Tabel III.8 Hasil iterasi unimodular cone P4 (Bagian 2)
Iterasi 8 Iterasi 9 Iterasi 9 Iterasi 10 Iterasi 11 Iterasi 12 Iterasi 13 Iterasi 13 M , m M= 9500 m= 9418 M= 9500 m= 9459 M = 9500, m= 9480 M = 9500, m= 9490 M= 9500, m= 9495 M= 9500, m= 9498 M= 9500, m= 9499 M = 9500, m= 9500 M > m y y y y y y y n new = [M+m / 2] 9459 9480 9490 9495 9498 9499 9500 qnew P3 9500 9500 9500 9500 9500 9500 9500 qnew= c.x≥ new 9500≥ 9459 9500≥ 9480 9500≥ 9490 9500≥ 9495 9500≥ 9498 9500≥ 9499 9500≥ 9500 qnew > 0 y y y y y y y M m 9459 9480 9490 9495 9498 9499 9500 Solusi M = 9500
7 Bandingkan nilai M dari tiap unimodular cone, nilai M yang terbesar adalah nilai optimal dari persamaan integer. Dari hasil iterasi diatas,
nilai M pada polytope P4 merupakan nilai M terbesar sehingga dapat disimpulkan bahwa nilai optimal untuk: Maximize z = 100x1 + 90x2
Subject to :
x1+ x2 ≤ 100
x1≤ 50
x1 , x2 ≥ 0 dan integer
adalah 9500 dengan x1 = 50 dan x2 = 50
IV. HASIL UJI COBA DAN EVALUASI
Uji coba dilakukan pada Intel (R)Pentium (R) Dual CPU T2390 1,86 GHz . Pada bagian ini akan ditampilkan data uji coba dengan beberapa ukuran persoalan dengan jumlah constrain dan variabel yang berbeda. Data uji coba ini adalah matrik data yang berisi variable serta
constrains dari persamaan integer. Data variabel tiap
persamaan dituliskan dalam bentuk file dengan ekstensi .cost sedangkan data constrains dituliskan dalam bentuk file input.
Data yang digunakan sebagai uji coba sistem ini diambil dari [4] dan [9]. Berikut data dan hasil uji coba dapat dilihat pada Tabel IV.1, Tabel IV.2, dan Tabel IV.3
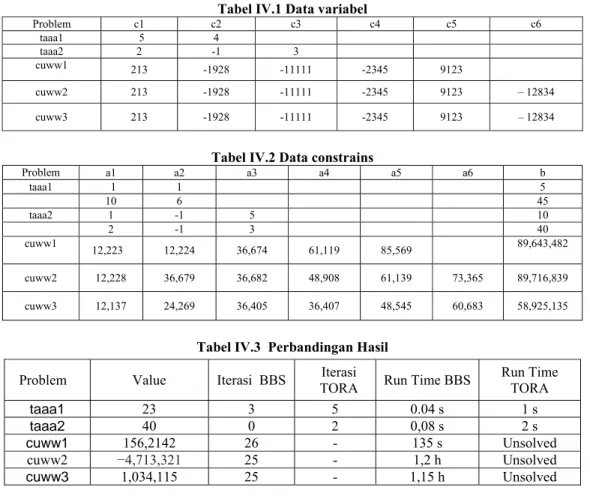
Tabel IV.1 Data variabel
Problem c1 c2 c3 c4 c5 c6 taaa1 5 4 taaa2 2 -1 3 cuww1 213 -1928 -11111 -2345 9123 cuww2 213 -1928 -11111 -2345 9123 – 12834 cuww3 213 -1928 -11111 -2345 9123 – 12834
Tabel IV.2 Data constrains
Problem a1 a2 a3 a4 a5 a6 b taaa1 1 1 5 10 6 45 taaa2 1 -1 5 10 2 -1 3 40 cuww1 12,223 12,224 36,674 61,119 85,569 89,643,482 cuww2 12,228 36,679 36,682 48,908 61,139 73,365 89,716,839 cuww3 12,137 24,269 36,405 36,407 48,545 60,683 58,925,135
Tabel IV.3 Perbandingan Hasil
A. Skenario Uji Coba Kebenaran Hasil
Dari hasil uji coba, dapat dianalisa bahwa data uji coba dengan menggunakan 2 variabel dapat diselesaikan menggunakan program Latte v1.2 maupun menggunakan program TORA dan dapat menghasilkan nilai optimal. Hal ini dapat dilihat pada record satu dengan problem = taaa1 dengan nilai optimal 23.
Dari hasil uji coba, dapat dianalisa bahwa data uji coba dengan menggunakan 3 variabel dapat diselesaikan menggunakan program Latte v1.2 maupun menggunakan program TORA dan dapat menghasilkan nilai optimal. Hal ini dapat dilihat pada record dua dengan problem = taaa2 dengan nilai optimal 40.
B. Skenario Uji Coba Kinerja
Dari hasil uji coba, dapat dianalisa bahwa jumlah iterasi yang dibutuhkan program latte v1.2 lebih sedikit
dibandingkan dengan program TORA, hal ini dapat dilihat pada record satu dengan problem = taaa1 dengan jumlah iterasi untuk BBS = 3 sedangkan untuk TORA =5. Begitu pula pada record dua dengan problem = taaa2 dengan jumlah iterasi untuk BBS = 0 sedangkan untuk TORA =2.
Dari hasil uji coba, dapat dianalisa bahwa program Latte v1.2 yang menerapkan algoritma binary seach mempunyai waktu eksekusi program yang lebih cepat dibandingkan dengan waktu eksekusi program TORA. Hal ini dapat dilihat pada record satu dengan problem = taaa1 dengan nilai optimal 23 yang memiliki waktu eksekusi program untuk Latte v1.2 = 0,04 s sedangkan waktu eksekusi program untuk TORA = 1 s. Hal ini dapat dilihat pula pada record dua dengan problem = taaa2 dengan nilai optimal 40 yang memiliki waktu eksekusi program untuk Latte v1.2 = 0,08 s sedangkan waktu eksekusi program untuk TORA = 2 s
Problem Value Iterasi BBS TORA Iterasi Run Time BBS Run Time TORA
taaa1 23 3 5 0.04 s 1 s
taaa2 40 0 2 0,08 s 2 s
cuww1 156,2142 26 - 135 s Unsolved cuww2 −4,713,321 25 - 1,2 h Unsolved cuww3 1,034,115 25 - 1,15 h Unsolved
Dari hasil uji coba dengan menggunakan 5 variabel, dapat dianalisa bahwa penyelesaian persamaan integer programming menggunakan program TORA dengan metode Branch and Bound tidak dapat menghasilkan solusi yang diharapkan, karena semua data uji coba tidak dapat terselesaikan (unsolved). Hal ini dapat dilihat pada record tiga dengan problem = cuww1 didapatkan output
unsolved pada saat menggunakan program TORA.
Sedangkan pada record empat dengan problem = cuww2 didapatkan output unsolved pada saat menggunakan program TORA. Begitu pula dengan record lima dengan problem = cuww3 didapatkan output unsolved pada saat menggunakan program TORA. Sedangkan hasil uji coba dengan menggunakan program Latte v1.2 semua record dapat terselesaikan dan menghasilkan nilai optimal.
Untuk algoritma binary search, waktu yang tertera pada output program tidak sesuai dengan kondisi. Hal ini terbukti dengan saat eksekusi program waktu yang tertera pada output program record 4 dengan problem = cuww1 adalah 0,15 detik kenyataannya waktu yang dibutuhkan pada saat eksekusi program 135 detik. Sedangkan pada record 5 dengan problem = cuww3, saat eksekusi program waktu yang tertera pada output program adalah 0,09 detik, kenyatannya waktu yang dibutuhkan pada saat eksekusi program 1,15 jam.
Lingkungan implementasi mempengaruhi waktu eksekusi dari program Latte v1.2. Berdasarkan paper acuan, uji coba program Latte diimplementasikan pada 1Ghz Pentium PC Red Hat Linux menghasilkan waktu eksekusi untuk record empat dengan problem = cuww 1 sebesar 414 sec. Sedangkan pada uji coba tugas akhir ini, program Latte v1.2 diimplementasikan pada 1,86 Ghz Intel (R)Pentium (R) Dual CPU T2390 pada record empat dengan problem = cuww1 waktu eksekusinya sebesar 135 sec. Begitu pula pada record enam dengan problem = cuww3 , pada paper acuan waktu eksekusi program 1,7 jam sedangkan pada tugas akhir ini waktu eksekusi program 1,15 jam.
V. Kesimpulan
Dari hasil pengamatan selama perancangan, implementasi, dan proses uji coba, penulis mengambil kesimpulan sebagai berikut :
1. Berdasarkan hasil uji coba yang telah dilakukan, maka dapat disimpulkan bahwa Program Latte v1.2 yang menerapkan metode barvinok rational function mampu memberikan kemudahan dalam menyelesaikan kasus integer programming serta mempunyai waktu komputasi yang lebih cepat dan lebih efisien dalam penggunaan memori .
2. Algoritma binary search yang diterapkan dalam metode barvinok rational function, merupakan algoritma yang efektif dalam menyelesaikan kasus integer programming dibandingkan dengan metode
branch and bound yang digunakan dalam TORA.
3. Penerapan metode barvinok rational function ini mampu menghasilkan one feasible integer solution untuk masing – masing data uji coba sehingga memudahkan pengguna dalam pengambilan keputusan.
4. Program Latte v1.2 mampu menghasilkan nilai optimal yang sama dari suatu permasalahan integer
programming dengan solver IP lainnya yang sudah umum.
VI. DAFTAR PUSTAKA
[1] A.I. Barvinok, J. Pommersheim, An algorithmic theoryof lattice points in polyhedra, in: New Perspectives in Algebraic Combinatorics (Berkeley, CA, 1996–1997), Mathematical Science and Research Institute Publications, vol. 38, Cambridge University Press, Cambridge, 1999, pp. 91–147 [2] A.I Barvinok, Lattice Points, Polyhedra, and
Complexity, IAS/Park City Mathematics Series Volume , 2004
[3] A.I. Barvinok, Polynomial time algorithm for counting integral points in polyhedra when the dimension is fixed, Math. Oper. Res. 19 (1994) 769– 779.
[4]
.
J.A De Loera, D.Haws, R. Hemmecke, P. Huggins, R. Yoshida, A computational study of integer programming algorithms based on Barvinok rational functions, Discrete Optimization 2 (2005) 135 – 144[5] J.A. De Loera, R. Hemmecke, J. Tauzer, R.Yoshida, Effective lattice point counting in rational convex polytopes, J. Symbolic Comput. 38 (2004) 1273– 1302.
[6] J.A. De Loera, D. Haws, R. Hemmecke, P. Huggins, J. Tauzer, R.Yoshida, A User’s Guide for LattE v1.1, 2003, Software package LattE is available at
http://www.math.ucdavis.edu/~latte/
[7] M. F. Muthohar, Penerapan Algoritma Branch and
bound pada Masalah Integer Knapsack , ITB,
2008
[8] R. Maharesi, Perbandingan Antara Pendekatan
Branch and Bound dan Pemrograman Linier: Dengan Sebuah Contoh Kasus Optimasi,
Universitas Gunadarma, 2002.
[9] Taha, Hamdi A. 1982. Operation Research : An Introduction, Eight Edition, Macmillan Publishing Co.Inc. .New York
[10] ……..2007, Barvinok, <URL : http://freshmeat.net/ projects/ barvinok/>
[11] ...2007, Bilangan Bulat <URL : http://id.wikipedia.org/wiki/Bilangan_bulat>
[12] ...2007, Integer <URL : http://id.wikipedia.org/wiki/Integer_(ilmu_kompute r) >
[13] ...2009, Laurent Polynomial <URL : http://en.wikipedia.org/wiki/Laurent_series>
[14] ...2009, Polynomial <URL : http://en.wikipedia.org/ wiki/Polynomial>