Metoda Numerik hal. 16
Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta
Bab
D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)
2.
PERSAMAAN NON-LINIER
Di dalam matematika aplikasi pencarian akar persamaan f(x)=0 sering dijumpai. Biasanya jawaban analitis dari persamaan diatas tidak ada, sehingga harus dicari jawaban numeriknya yang biasa dilaksanakan dengan metode iterasi.
2.1.
Metode Bagi Paruh (Bisection)
Jika terdapat suatu f(x) yang menerus ∈ [a,b] dan f(a)f(b) < 0, maka menurut Teorema 1.1 paling tidak f(x) mempunyai satu akar f(x) mempunyai satu akar
∈ [a,b].
♦ Algoritma
Bisect(f, a, b, akar, ε) 1. Hitung c := (a+b)/2
2. Jika b – c≤ε , maka akar:= c, dan ‘ exit’
3. Jika {tanda f(b)•tanda f(c)} i 0, maka a := c , jika tidak b := c
4. Kembali ke langkah nomor 1.
♦ Definisi
Suatu deret hasil suatu iterasi {xn|nj0} dikatakan menuju ke titik dengan
derajat p j1 , jika
0
1 ≤ − ≥
−xn+ cα xn p n
α
untuk beberapa nilai c>0. Jika p=1, deretnya disebut menuju ke titik secara linier. Pada kasus ini diperlukan nilai c<1; c disebut laju linier dari xn menuju .
Ada beberapa metode yang membutuhkan definisi yang agak berbeda dengan diatas yaitu 0 0 1 ≤ − ≥ −xn+ cnα x n α
Persamaan Non-Linier Buku kuliah
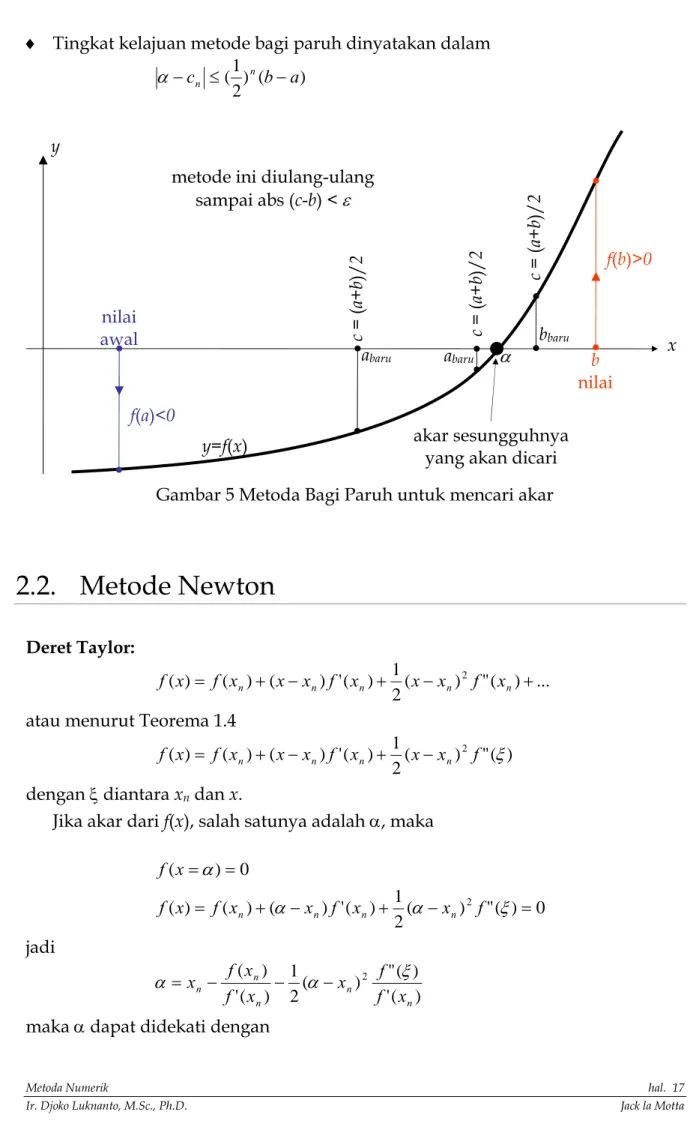
♦ Tingkat kelajuan metode bagi paruh dinyatakan dalam
) ( ) 2 1 ( b a cn ≤ n − − α
Gambar 5 Metoda Bagi Paruh untuk mencari akar
2.2.
Metode Newton
Deret Taylor: ... ) ( " ) ( 2 1 ) ( ' ) ( ) ( ) (x = f xn + x−xn f xn + x−xn 2 f xn + fatau menurut Teorema 1.4
) ( " ) ( 2 1 ) ( ' ) ( ) ( ) ( 2 ξ f x x x f x x x f x f = n + − n n + − n
dengan ξ diantara xn dan x.
Jika akar dari f(x), salah satunya adalah α, maka
0 ) ( " ) ( 2 1 ) ( ' ) ( ) ( ) ( 0 ) ( 2 = − + − + = = = ξ α α α f x x f x x f x f x f n n n n jadi ) ( ' ) ( " ) ( 2 1 ) ( ' ) ( 2 n n n n n x f f x x f x f x α ξ α = − − −
maka α dapat didekati dengan
y
x
y=f(x)
α
akar sesungguhnya yang akan dicari nilai awal b nilai c = ( a + b )/ 2 f(a)<0 f(b)>0 abaru abaru bbaru
metode ini diulang-ulang sampai abs (c-b) < ε c = ( a + b )/ 2 c = ( a + b )/ 2
Persamaan Non-Linier Buku kuliah
Metoda Numerik hal. 18
Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta
D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)
0 ) ( ' ) ( 1 = − ≥ + n x f x f x x n n n n dengan ‘errornya’ 0 ) ( ) ( ' 2 ) ( " 2 1 =− − ≥ − + x n x f f x n n n α ξ α
Untuk nilai n ∞, ξ α dan xn α, jadi
2 2 1 ) ( konstanta ) ( ) ( ' 2 ) ( " n n n x x f f x − × = − − = − + α α α α α
Sehingga metode Newton dikatakan mempunyai derajat kelajuan = 2
Gambar 6 Metoda Newton untuk mencari akar
♦ Algoritma
Newton (f, df, x0, ε, akar, itmax, ierr)
1. Keterangan : df adalah f’(x), itmax adalah iterasi maximum, ierr adalah ‘error flag’
2. noiter:=1
3. penyebut:=df(x0)
4. jika penyebut = 0 maka ierr:=2, dan ‘exit’ 5. x1:= x0 - f(x0)/penyebut
6. jika |x1 – x0|iε, maka ierr:= 0, akar:= x1, dan ‘exit’ 7. jika noiter = itmax maka ierr:= 1, dan ’exit’
8. noiter:= noiter +1, x0:=x1, dan ulangi langkah 3.
y x y=f(x) x0 x1 grs singgung α
Persamaan Non-Linier Buku kuliah
2.3.
Metode Sekan
Dengan menggunakan sifat segitiga sebangun diperoleh
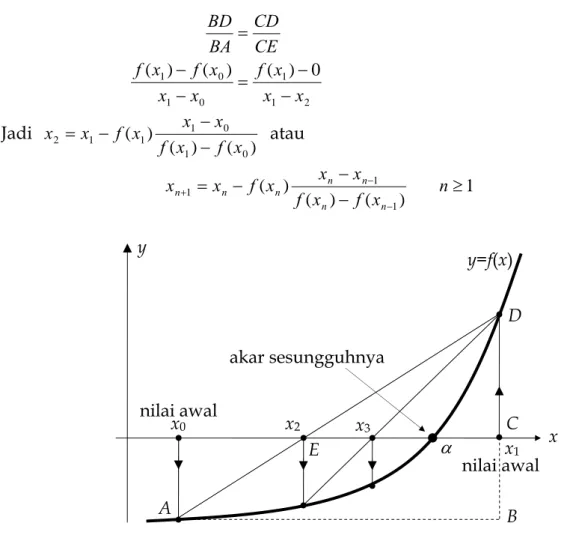
2 1 1 0 1 0 1) ( ) ( ) 0 ( x x x f x x x f x f CE CD BA BD − − = − − = Jadi ) ( ) ( ) ( 0 1 0 1 1 1 2 x f x f x x x f x x − − − = atau 1 ) ( ) ( ) ( 1 1 1 − ≥ − − = − − + n x f x f x x x f x x n n n n n n n
Gambar 7 Metoda Sekan untuk mencari akar
Metode sekan dapat dijabarkan dari metode Newton dimana
1 1) ( ) ( ) ( ' − − − − = n n n n n x x x f x f x f Derajat Konvergensi:
•
untuk metode Newton p = 2•
untuk metode sekan p = ½(1+√5) = 1,618•
untuk metode ‘bisection’ p = 1y x y=f(x) x0 x1 α akar sesungguhnya nilai awal nilai awal x2 x3 B D E C A
Persamaan Non-Linier Buku kuliah
Metoda Numerik hal. 20
Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta
D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)
2.4.
Akar dari Persamaan Polinomial
p(x) = a0 + x(a1 + x(a2+…+x(an-1 + anx)…) (A)
atau
p(x) = a0 + a1x + a2x2+…+ anxn (B)
Pada Pers.(A) terdapat n perkalian & pertambahan, sedangkan dalam
Pers.(B) terdapat: (2n–1) perkalian & pertambahan. Oleh karena itu dalam pemrograman komputer lebih disukai bentuk dalam Pers.(A), karena lebih efisien. Pers. (A) jika ditulis dalam FORTRAN menjadi
p = a(n)
do 10 i = n,1,-1 10 p = p*x + a(i–1)
Untuk menghitung akar dari persamaan p(x) = 0 akan digunakan Metoda Newton. Untuk keperluan itu polinomial p(x) akan dimodifikasi sebagai berikut Disyaratkan: bn = an
bk = ak + zbk+1 , k = n–1, n–2,… , 0
Dari syarat ini p(x) dapat ditulis sebagai
p(x) = b0 + (x– z)q(x) dengan q(x) = b1 + b2x +…+ bnx n-1
sehingga p’(x) = (x– z)q’(x) + q(x) p’(z) = q(z)
♦ Algoritma:
Polynew (a, n, x, ε, itmax, akar, b, ier)
1. Keterangan: a adalah vektor coef. dengan dimensi n, itmax adalah iterasi maksimum, b adalah vektor coef. dari polinomial yang baru, ier adalah indikator adanya error.
2. noiter: = 1
3. x: = x0 , bn:= c := an
4. Untuk k = n-1, …, 1, bk := ak+ zbk+1, c := bk + zc
5. b0:= a0 + zb1
6. Jika c = 0, ier := 2, dan ‘exit 7. x1:= x0 – b0/c
8. Jika ⏐x1 – x0⏐≤ε , ier :=0 ,akar:= x1, dan ‘exit’ 9. Jika noiter:= itmax, ier:= 1, dan ‘exit’
Persamaan Non-Linier Buku kuliah
Metoda Numerik hal. 22
Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta
Bab
D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)
3.
TEORI INTERPOLASI
Jika kita mempunyai satu set data:
(x0, y0) , (x1, y1), …, (xn, yn)
maka dalam bab ini akan di jelaskan bagaimana harus mencarti polinomial yang melalui, data di atas.
Jika polinomial ini ditulis sebagai:
p(x) = a0 + a1x +… + anxn
maka jika data diatas disubstitusikan akan didapat (n+1) persamaan dengan (n+1) variabel tidak diketahuinya yaitu:
n n n n n n n y x a x a a y x a x a a = + + + = + + + L M M L 1 0 0 0 0 1 0
Persamaan diatas jika diselesaikan akan menghasilkan a0, …, an sehingga
polinomial p(x) dapat dicari .
3.1.
Metoda Beda Terbagi Newton
Notasi yang digunakan:
[
]
[
] [
]
0 1 1 1 ... ... -x x ,x , x f ,x , x f , ... ,x ,x x f n n n n o − = Contoh Order 0: ƒ[x0] =ƒ[xn] Order 1:[
]
[ ] [ ]
0 1 0 1 1 0, x x x f x f x x f − − = Order 2:[
]
[
] [
]
0 2 1 0 2 1 2 1 0 , , , , x x x x f x x f x x x f − − = Order 3:[
]
[
] [
]
0 2 1 0 3 2 1 3 2 1 0 , , , , , , x x x x f x x x f x x x x f − − =Teori Interpolasi Buku kuliah
Rumus beda terbagi Newton:
pn(x) = ƒ[x0]+ (x3-x0)ƒ[x0,x1]+(x3-x0)(x-x1)ƒ[x0,x1]+… +(x–x0)…(x–xn-1)ƒ[x0,x1,…,xn]
Contoh: Kita buat tabel beda terbagi berdasarkan polinomial
ƒ(x) = x3 – 2x2 + 7x – 5 i xi f[xi] f[xi, xi+1] f2[ ] f3[ ] 0 0.0 -5.0 6 2 1 1 1.0 1.0 12 6 2 3.0 25.0 30 3 4.0 55.0 Keterangan:
( )
6 0 1 5 1 = − − − = A 12 1 3 1 25 = − − = B 30 3 4 25 55 = − − = C 2 0 3− = − = B A D 6 1 4 12 30 = − − = E 1 0 4− = − = E D F Contoh hitungan pn(x=0.5) = ?•
p1(x) = -5 + (x-0)6 = 6x – 5 ∴p1 (0.5) = -2•
p2(x) = -5 + (x-0)6 + (x-0)(x–1)2 = 2x2 + 4x – 5 ∴p2 (0.5) = -2,5•
p3(x) = -5 + (x-0)6 + (x-0)(x–1)2 +(x-0)(x-1)(x-3)1 = x3 – 2x2 + 7x – 5 ∴ p2 (0.5) = -15/8 = - 1.875♦ Algoritma metoda beda terbagi Newton
Divdif (d, x , n)
1. Keterangan: d dan x adalah vektor f(xi) dan xi = 0,1,…,n. Pada saat ‘exit’ di
akan terisi oleh nilai f[x0,…,xi]
2. Kerjakan s/d langkah 4 untuk i = 1, 2 ,… ,n
3. Kerjakan sampai dengan langkah 4 untuk j = n, n-1, i
4. dj := (dj -dj-1) /(x-xj-1)
Teori Interpolasi Buku kuliah
Metoda Numerik hal. 24
Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta
D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)
Interp(d, x, t, p)
1. Keterangan: Pada awalnya d dan x adalah vektor dari ƒ[x0,…,xi] dan xi, i = 0,
1 , …, n. Pada saat ‘exit’ p akan berisi pn(t).
2. p := dn
3. Kerjakan s/d langkah 4 untuk i = n-1 , n--2, …, 0 4. p := di + (t– xi)p
5. ‘ exit’
3.2.
Interpolasi dengan tabel beda hingga
3.2.1.
Beda Maju
Notasi: Δƒ(xi) = ƒ(xi+1) - ƒ(xi) dengan xi = x0 + ih, i = 0, 1, 2, 3, …
Untuk r≥ 0,
Δr+1ƒ(z) = Δrƒ(z+h) - Δrƒ(z)
Δrƒ(z) disebut ‘ beda maju order r ,‘ Δ disebut ‘operator beda maju ‘
Contoh: Δ0ƒ(x) = ƒ(x)
Δƒ(x) = Δ0ƒ(z+h) - Δ0ƒ(z) = ƒ(x+h) - ƒ(x)
Δ2ƒ(x) = Δƒ(x+h) - Δƒ(x)
Contoh hitungan : Kita gunakan polinomial x3 – 2x2 + 7x – 5 dengan h = 1,0
i xi f(xi) Δ2ƒ Δ3ƒ Δ4ƒ 0 0.0 -5.0 6 2 6 0 1 1.0 1.0 8 8 6 2 2.0 9.0 16 14 3 3.0 25.0 30 4 4.0 55.0
Korelasi antara ‘beda maju’ dengan ‘ beda terbagi’
[
]
[ ] [ ]
h x f h x f h x f x x x f x f x x f , ( 0 ) ( 0) ( 0) 0 1 0 1 1 0 Δ = − + = − − =Teori Interpolasi Buku kuliah
[
]
20 2 0 2 0 1 0 1 1 2 1 2 2 1 0 2 ) ( ) ( ) ( ) ( ) ( , , h x f x x x x x f x f x x x f x f x x x f = Δ − − − − − − = Secara umum:[
]
n n n h n x f x x x f ! ) ( ,..., , 0 1 0 Δ =Akan dijabarkan rumus interpolasi ‘beda maju’ dari rumus interpolasi ‘beda terbagi’ Newton. Didefinisikan
h x x− 0
=
α yang menunjukkan letak titik x
terhadap x0. Jadi misalnya α = 1.6, maka x terletak pada jarak 6/10 dari x1 ke arah
x2.
Diinginkan rumus untuk:
(x – x0) (x – x1) … (x – xk) dinyatakan dalam α x – xj = x0 + αh – (x0 + jh) = (α-j)h Jadi (x – x0) (x – x1) … (x – xk) = α(α -1)… (α -k)hk+1 sehingga n n n n h n f h n h f h h f h f x p ! ) 1 )...( 1 ( ... ! 2 ) 1 ( ) ( 0 2 0 2 2 0 0 Δ + − − + + Δ − + Δ + = α α α α α α
Jika didefinisikan koefisien binomial sbb:
! ) 1 )...( 1 ( k k k + − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛α α α α , k>0 dan 1 0⎟⎟⎠= ⎞ ⎜⎜ ⎝ ⎛α maka didapat rumus interpolasi ‘beda maju’ sbb:
h x x x f j x p j n j n 0 0 0 dengan ) ( ) ( ⎟⎟Δ = − ⎠ ⎞ ⎜⎜ ⎝ ⎛ =
∑
= α α Contoh hitungan: p(x=1.5) = ? 5 . 1 0 . 1 0 . 1 5 . 1 0 = − = − = h x x α 1) p1(x) = ƒ(x0) + αΔƒ(x0) = -5 + 1.5 (6) = 4 2) p2(x) = ƒ(x0) + αΔƒ(x0) + α(α-1)∆2f(x0)/2! = -5 + 1.5 (6) + 1.5 (0.5)2/2! = 4.75Teori Interpolasi Buku kuliah
Metoda Numerik hal. 26
Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta
D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)
3.2.2.
Beda Mundur
Notasi: ∇ƒ(z) = ƒ(z) - ƒ(z-h) ∇r+1ƒ(z) = ∇rƒ(z) - ∇rƒ(z-h) rj1 Rumus interpolasinya 1 0 1 , dengan ) ( 1 ) ( 0 0 0 = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛− − − = ∇ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − =∑
= α α α h x x x f j j x p j n j n i xi f(xi) ∇2ƒ ∇3ƒ ∇4ƒ -4 0.0 -5.0 6 2 6 0 -3 1.0 1.0 8 8 6 -2 2.0 9.0 16 14 -1 3.0 25.0 30 0 4.0 55.0 Contoh hitungan: p(x=3.5) = ? 5 . 0 0 . 1 0 . 4 5 . 3 0 − = − + = = h x x α 1) p1(x) = ƒ(x0) + (-α)∇ƒ(x0) = 55 + (-0.5) 30 = 40 2) p2(x) = p1(x) + (-α)(-α+1)∇2f(x0)/2! = 40 + (-0.5)(0.5)14/2! = 38.25 3) p3(x) = p2(x) + (-α)(-α+1) (-α+2)∇3f(x0)/3! = 38.25 + (-0.5)(0.5)(1.5)6/3! = 37.8753.3.
Lagrange
Polinomial Lagrange dibentuk dengan fomulasi berikut:
( )
( ) ( )
i n i i n x L x f x p∑
= = 0( )
∑
≠ = = − − = n i j j i j j i i n x x x x x L 0 ,..., 1 , 0 Contoh:( )
( )
( )
1 1 0 0 0 1 0 1 f x x x x x x f x x x x x pi − − + − − =( ) (
(
)(
)(
)
) ( )
(
(
)(
)(
)
) ( )
(
(
)
)(
(
)
)
( )
2 2 1 2 0 2 1 0 1 2 1 0 1 2 0 0 2 0 1 0 2 1 2 f x x x x x x x x x x f x x x x x x x x x f x x x x x x x x x p − − − − + − − − − + − − − − =Teori Interpolasi Buku kuliah
Contoh: hitung p2
( )
x yang melalui titik-titik(
0,15) ( ) (
;1,1; 3,25)
( ) (
(
)(
)(
)
)
(
(
)(
)(
)
)
3 3 4 3 0 1 0 3 1 2 2 0 1 0 2 1 0 + − = − − − − = − − − − = x x x x x x x x x x x x x L( ) (
(
)(
)(
)
)
(
(
)(
)(
)
)
2 3 3 1 0 1 3 0 2 2 1 0 1 2 0 1 − − = − − − − = − − − − = x x x x x x x x x x x x x L( ) (
(
)(
)(
)
)
(
(
)(
)(
)
)
6 1 3 0 3 1 0 2 1 2 0 2 1 01 2 x x x x x x x x x x x x x L = − − − − − = − − − − = Jadi p2( )
x =L0( ) ( )
x × −5 +L1( ) ( )
x × 1 +L2( ) ( )
x × 25 =2x2 +4x−53.4.
Beberapa fakta penting dari’beda terbagi’
1.
[
]
( )( )
! ,..., , 1 0 m f x x x f m m ξ = untuk ξ∈X{
x0,x1,...,xn}
dimana X{
x0,...,xm}
artinya interval terkecil dimana x0,x1,...,xm tercakup!Contoh:
[ ]
( )( )
( )
0 0 0 ! 0 f x f x f = ξ =[
,]
( ) ( )
'( )
ξ 0 1 0 1 1 0 f x x x f x f x x f = − − = ξ∈[
x0,x1]
[
]
'( )
ξ 2 1 , , 1 2 0 x x f x f = ξ∈X{
x0,x1,x2}
2. Jika f( )
x adalah polynomial derajad m, maka[
]
⎪ ⎩ ⎪ ⎨ ⎧ − > − = − < − − = 1 0 1 1 1 derajad polinomial , ,..., 0 m n m n a m n n m x x x f n m dengan( )
1 0 1 1x ... a x a a x a x f = m m + m− m− + + +3. Kesalahan dalam interpolasi
( )
( ) (
)(
(
) (
)
)
( )( )
x n n n f n x x x x x x x p x f 0 1 1 ξ ! 1 ... + + − − − = − dengan ξx∈Η{
x0,....,xn,x}
4. f[
x x x] [
f x x x x x]
dx d n n, , ,..., , , ,..., 0 0 =Metoda Numerik hal. 28
Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta
Bab
D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)
4.
INTEGRASI NUMERIS
4.1.
Rumus trapesium dan Simpson
Pada bab ini akan dibicarakan cara menghitung integral secara numeris dari
∫
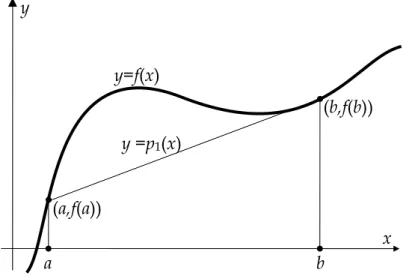
= b a f(x)dx I(f) dimana [a,b] berhinggaGambar 8 Konsep integrasi trapesium
Rumus trapesium pada dasarnya adalah mendekati f(x) dengan garis lurus yang melalui (a,f(a)) dan (b,f(b))
[
( ) ( )]
2 ) ( 1 f a f b a b f I = − − y x y=f(x) b y =p1(x) a (b,f(b)) (a,f(a))Integrasi Numeris Buku kuliah Error:
[
abx]
f b x a x b f a b a x a f b a b x x f x p x f , , ) )( ( ) ( ) ( ) ( ) ( ) ( 1 − − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − + − − − = −ingat definisi ‘beda terbagi f[a,b,x]. Jadi ‘error’:
[
abx]
dx f b x a x b f a f a b dx x f f E b a b a∫
∫
− − = + − − = , , ) )( ( )] ( ) ( )[ ( 2 1 ) ( ) ( 1dengan harga tengah integral, didapat:
[
]
) ( " 12 ) ( ] , [ ) ( 6 1 ) ( " 2 1 ) )( ( , , ) ( 3 3 1 η η η ξ ξ f a b b a a b f b a dx b x a x b a f f E b a − − = ∈ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ≤ ≤ − − =∫
Jika interval [a,b] dibagi menjadi n pias sehingga untuk nj1, h = (b-a)/n dan
xj = a + jh, j = 0,1,…,n, didapat:
[
]
∑
∑ ∫
∫
= − = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − = = = − n j j j j n j x x b a f h x f x f h f(x)dx f(x)dx I(f) j j 1 3 1 1 ) ( " 12 ) ( ) ( 2 1 η dengan xj-1injixj.Sehingga integralnya dapat didekati dengan
1 2 1 ... 2 1 ) (f =h⎢⎣⎡ f0 + f1 + + f =1 + f ⎤⎥⎦ n≥ In n n
Kesalahan In(f) terhadap I(f) adalah
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = − = − =
∑
∑
= = n j j n j j n n f n n h f h f E f I f E 1 3 1 3 ) ( " 1 12 ) ( " 12 ) ( ) ( ) ( η ηIntegrasi Numeris Buku kuliah
Metoda Numerik hal. 30
Ir. Djoko Luknanto, M.Sc., Ph.D. Jack la Motta
D:\My Documents\Publikasi\Metoda Numerik\Metoda Numerik.doc (2028 Kb)
) ( " ) ( " 1 ) ( " 1 x f Max f n x f Min b x a n j j b x a≤ ≤ ≤
∑
= η ≤ ≤ ≤ karena f”(x) menerus pada aixib, makaη η η η ( " 12 ) ( ) ( " 12 ) ( ] , [ ) ( " 12 ) ( 2 3 2 3 f n a b f a b h b a f n h f En − − = − − = ∈ − =
Estimasi kesalahan asimtotis E~n(f)
∫
∑
∑
− = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = = ∞ → = ∞ → ∞ → b a n j j n n j j n n n dx x f h f Limit h f Limit h f E Limit ) ( " 12 1 ) ( " 12 1 ) ( " 12 1 ) ( 1 1 2 η η maka{
'( ) '( )}
12 ) ( ~ 2 a f b f h f En ≡− − Definisi:Jika En(f) adalah kesalahan eksak, sedangkan ( )
~
f
En adalah estimasi darinya, maka
) ( ~
f
En disebut estimasi kesalahan asimtotis dari En(f) jika:
1 ) ( ) ( ~ = ∞ → E f f E Limit n n n atau ( ) 0 ) ( ~ ) ( = − ∞ → E f f E f E Limit n n n n
4.1.1.
Rumus trapesium terkoreksi
Dengan menggunakanE~n(f), rumus trapesium dapat ditingkatkan menjadi: