OPTIMASI FUNGSI TANPA KENDALA DENGAN
ALGORITMA GENETIKA
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Sains
Program Studi Matematika
Disusun Oleh:
Yolenta Asri Astuti Prany
NIM : 023114002
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
ABSTRAK
Secara umum, permasalahan optimasi dalam kehidupan sehari – hari lebih
sering menggunakan pemrograman linear, karena lebih mudah untuk diselesaikan
dari pada dengan menggunakan pemrograman tak linear. Karena pemrograman
tak linear selalu menimbulkan kesulitan dalam penanganan analitik dan numerik
(teknik konvensional), bahkan untuk fungsi dua variabel pun terkadang sulit untuk
diselesaikan. Algoritma Genetika merupakan salah satu teknik yang dapat dipilih
untuk menyelesaikan permasalahan pemrograman tak linear tersebut, karena
Algoritma Genetika merupakan teknik pencarian stokastik dengan sistem
pencarian berdasarkan mekanisme genetika dalam biologi.
Pada skripsi ini, generasi baru (anak) terbentuk dari rekombinasi dan mutasi
dengan menggunakan metode pemotongan satu titik. Pemilihan anak pada proses
rekombinasi atau mutasi dilakukan secara acak. Dari percobaan, solusi optimal
akan lebih mendekati dengan nilai konvensionalnya pada probabilitas rekombinasi
0.5 dengan probabilitas mutasi 0.08. Namun, probabilitas tersebut tidak mutlak,
karena Algoritma Genetika menggunakan teknik pencarian secara acak.
ABSTRACT
Generally, the optimization problems in daily life is more regular using the
linear programming, because it is easier to solved than nonlinear programming.
Because nonlinear programming are difficultly in analytic handling and numeric
(conventional technique), even for two variables function it is difficult to be
solved, sometimes. Genetic Algorithm are one of technique that could be chosen
to solved it, because Genetic Algorithm are stochastic search techniques based on
the mechanism of genetic on biology.
On this mini thesis, a new generation (offspring) formed of crossover or
mutation with one cut point method. Selection of new generation by crossover and
mutation conducted at random. According to the experiments, it is visible to get
the optimal solution close to a value by conventional with crossover probabilities
0.5 and mutation probabilities 0.08. But, that is not absolute, because the
searching technique of Genetic Algorithm are randomly.
KATA PENGANTAR
Puji syukur kepada Bapa di Surga dan Bunda Maria yang memberikan
kasih-Nya dan melimpahkan karunia-Nya sehingga penulisan skripsi ini dapat
diselesaikan. Skripsi ini disusun dalam rangka menyelesaikan pendidikan tingkat
Sarjana Strata Satu Jurusan Matematika, Fakultas Matematika dan Ilmu
Pengetahuan Alam, Universitas Sanata Dharma Yogyakarta.
Penulis dalam menyusun skripsi ini dari awal sampai akhir mendapatkan
dukungan dan bantuan dari berbagai pihak. Oleh karena itu, pada kesempatan ini
penulis menyampaikan ucapan terima kasih yang sebesar-besarnya kepada:
1.
Bapak Ig. Aris Dwiatmoko, M.Si selaku Dekan Fakultas Matematika dan
Ilmu Pengetahuan Alam Universitas Sanata Dharma Yogyakarta.
2.
Bapak Drs. HJ Haris Sriwindono, M.Kom selaku Dosen Pembimbing I
dan Bapak Y.G Hartono, S.Si selaku Dosen Pembimbing II yang dengan
sabar telah banyak membimbing dan memberikan petunjuk dalam
penyusunan skripsi ini.
3.
Bapak dan Ibu dosen yang telah memberikan ilmu dan pengetahuan
selama masa perkuliahan.
4.
Staff fakultas MIPA terima kasih atas dorongan dan pelayanan yang telah
diberikan.
5.
Bapak dan Mama yang telah memberikan kasih, dorongan semangat, serta
doa yang melimpah selama kehidupanku di dunia ini.
6.
Abang dan adikku (Yacobus dan Ade (Nenek Lampir)) terima kasih untuk
“kata-kata” yang membuatku semakin termotivasi .
7.
Keluarga besarku yang tersebar di berbagai kota. Terima kasih atas doa
dan bantuan yang telah kalian berikan.
8.
T Agusta Dwi Handaru yang telah menambah warna dalam kehidupanku.
Terima kasih atas kesabaran dan cinta mu.
9.
Sahabat-sahabatku nan jauh di sana: Yulia, Maria, dan Uthe terima kasih
buat persahabatan, perhatian dan dukungannya.
10.
Teman-teman angkatan 2002: Ngq, Debby, Lia, Ika, Sari, Aan, Tato, Bani,
Lili, Taim, Ijup, Markus, Felix, Vida (Ipid), Retno, Priska, Galih, Aning,
Desy, Rita, Wuri, Deon, Cheea, Nunung, Dani , Palma, dan Asih. Esp.
Debby, Lia, dan Ijup yang selalu menemaniku ketika masa-masa
ngantukku dengan chating bersama.
11.
Teman-teman kostku (Wisma Lestari) esp. Lia, Kawat (thanks atas
printernya), M`Nchis, dan M`Mitha yang menjadi setan serta malaikat
ketika skripsi ini dibuat. Thanks untuk hari-hari ceria yang telah kita
lewati bersama.
12.
Teman seperjuanganku dalam menyusun skripsi (Ipid Manyiiit), terima
kasih atas bantuan dan perhatiannya.
13.
Teman-teman kost (tumpangan) ku, Ipid (namamu paling banyak
terucap…), Endra, Primtul, M`Lina, Ine, Maria, Lili. Terima kasih atas
tumpangannya, tanpa kalian entah bagaimana nasibku.
14.
Teman-teman KKN ku, yang berlomba-lomba untuk menyelesaikan
skripsi. Serta warga Caben. Terima kasih untuk dorongan dan semangat
yang telah kalian berikan.
15.
Teman-teman P3W Terima kasih untuk dorongan dan semangat yang telah
kalian berikan.
16.
Teman-Teman Pondok Baca Kota Baru, tempatku menghilangkan
kepenatan belajar. Teruslah berusaha mengembangkan Pondok Baca, upah
kalian besar di Surga.
17.
Semua pihak yang telah turut membantu hingga skripsi ini selesai yang
tidak dapat disebutkan satu persatu.
Penulis menyadari masih ada kekurangan, kekeliruan, dan masih jauh dari
sempurna. Oleh karena itu, penulis mengharapkan saran dan kritik yang bersifat
membangun demi kemajuan yang akan datang.
Semoga penulisan skripsi ini dapat memberikan manfaat bagi pembaca.
Yogyakarta, Juli 2007
Penulis
xi
DAFTAR ISI
HALAMAN JUDUL... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN... iii
HALAMAN PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
ABSTRAK ... vi
ABSTRACT... vii
KATA PENGANTAR ... viii
DAFTAR ISI... xi
DAFTAR TABEL... xiv
DAFTAR GAMBAR……… xxi
BAB I PENDAHULUAN... 1
A. Latar Belakang. ... 1
B. Perumusan Masalah ... 4
C. Pembatasan Masalah ... 4
D. Tujuan Penulisan... 4
E. Metode Penulisan ... 5
F. Manfaat Penulisan... 5
xii
BAB II OPTIMASI FUNGSI TANPA KENDALA... 7
A. Optimasi Fungsi Satu Variabel Tanpa Kendala Dengan Kalkulus ... 7
B. Optimasi Fungsi Beberapa Variabel Tanpa Kendala Dengan Kalkulus... 21
BAB III ALGORITMA GENETIKA... 50
A. Latar Belakang Biologi ... 50
B. Struktur Umum Algoritma Genetika... 51
C. Komponen-komponen Utama Algoritma Genetika. ... 56
1. Teknik Penyandian... 56
2. Prosedur Inisialisasi ... 57
3. Fungsi Evaluasi (fitness function) ... 58
4. Seleksi ... 59
4.1. Seleksi Roda Rolet ... 59
4.2. Seleksi Rangking... 60
4.3. Seleksi Turnamen... 61
5. Operator Genetika ... 62
5.1. Rekombinasi (crossover) ... 62
5.2. Mutasi... 63
xiii
BAB IV ALGORITMA GENETIKA UNTUK OPTIMASI
FUNGSI TANPA KENDALA... 66
BAB V PENUTUP... 112
A. Kesimpulan ... 112
B. Saran... 113
DAFTAR PUSTAKA ... 114
xiv
DAFTAR TABEL
Tabel 3.2.1 Tabel Istilah dalam Algoritma Genetika ... 53 Tabel 3.3.1.1 Pemetaan nilai biner ke nilai real ... 57 Tabel 3.4.2.1 Contoh populasi dengan 5 kromosom yang diberi fitness
baru... 61 Tabel 4.1 Tabel nilai maksimum fungsi f
(
x1,x2)
=x12+2x1x2+x22dengan probabilitas rekombinasi 0.2 dan probabilitas mutasi 0.01 hingga 0.1 ... 70 Tabel 4.2 Tabel nilai maksimum fungsi f
(
x1,x2)
=x12+2x1x2+x22dengan probabilitas rekombinasi 0.25 dan probabilitas mutasi 0.01 hingga 0.1 ... 71 Tabel 4.3 Tabel nilai maksimum fungsi
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + +
dengan probabilitas rekombinasi 0.3 dan probabilitas mutasi 0.01 hingga 0.1 ... 72 Tabel 4.4 Tabel nilai maksimum fungsi f
(
x1,x2)
=x12+2x1x2+x22dengan probabilitas rekombinasi 0.35 dan probabilitas mutasi 0.01 hingga 0.1 ... 73 Tabel 4.5 Tabel nilai maksimum fungsi f
(
x1,x2)
=x12+2x1x2+x22xv
Tabel 4.6 Tabel nilai maksimum fungsi f
(
x1,x2)
=x12+2x1x2+x22dengan probabilitas rekombinasi 0.45 dan probabilitas mutasi 0.01 hingga 0.1 ... 75 Tabel 4.7 Tabel nilai maksimum fungsi
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + +
dengan probabilitas rekombinasi 0.5 dan probabilitas mutasi 0.01 hingga 0.1 ... 76 Tabel 4.8 Tabel nilai maksimum fungsi f
(
x1,x2)
=x12+2x1x2+x22dengan probabilitas rekombinasi 0.2-0.5 dan probabilitas mutasi 0.08 ... 77
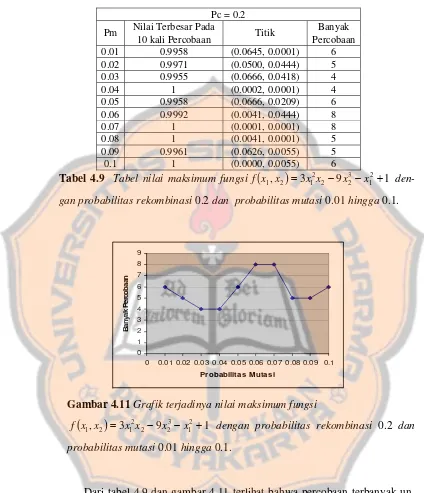
Tabel 4.9 Tabel nilai maksimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.2 dan probabilitas mutasi 0.01 hingga 0.1. 83
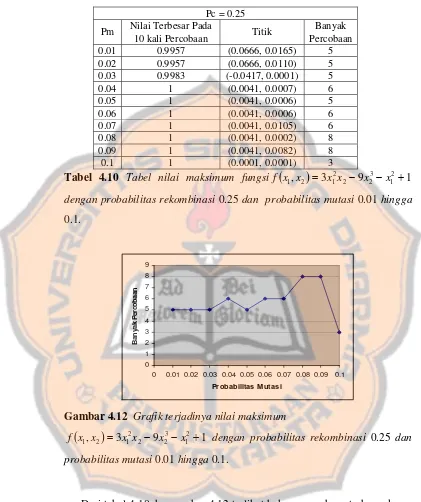
Tabel 4.10 Tabel nilai maksimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.25 dan probabilitas mutasi 0.01 hingga 0.1 84
Tabel 4.11 Tabel nilai maksimum fungsi
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan probabilitas
rekombinasi 0.3 dan probabilitas mutasi 0.01 hingga 0.1. 85
Tabel 4.12 Tabel nilai maksimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
xvi
Tabel 4.13 Tabel nilai maksimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.4 dan probabilitas mutasi 0.01 hingga 0.1. 87
Tabel 4.14 Tabel nilai maksimum fungsi
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan probabilitas
rekombinasi 0.45 dan probabilitas mutasi 0.01 hingga 0.1 88
Tabel 4.15 Tabel nilai maksimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.5 dan probabilitas mutasi 0.01 hingga 0.1. 89
Tabel 4.16 Tabel nilai minimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.2 dan probabilitas mutasi 0.01 hingga 0.1. 90
Tabel 4.17 Tabel nilai minimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.25 dan probabilitas mutasi 0.01 hingga 0.1 91
Tabel 4.18 Tabel nilai minimum fungsi
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan probabilitas
rekombinasi 0.3 dan probabilitas mutasi 0.01 hingga 0.1. 92
Tabel 4.19 Tabel nilai minimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
xvii
Tabel 4.20 Tabel nilai minimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.4 dan probabilitas mutasi 0.01 hingga 0.1. 94
Tabel 4.21 Tabel nilai minimum fungsi
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan probabilitas
rekombinasi 0.45 dan probabilitas mutasi 0.01 hingga 0.1 95
Tabel 4.22 Tabel nilai minimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.5 dan probabilitas mutasi 0.01 hingga 0.1. 96
Tabel 4.23 Tabel nilai maksimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.2-0.5 dan probabilitas mutasi 0.08 ... 97
Tabel 4.24 Tabel nilai minimum fungsi
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.2-0.5 dan probabilitas mutasi 0.08 ... 98
Tabel 4.25 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas rekombinasi 0.2 dan probabilitas mutasi 0.01 hingga 0.1... 101
Tabel 4.26 Tabel nilai maksimum fungsif
( )
x =x1e−(x12+x22) denganxviii
Tabel 4.27 Tabel nilai maksimum fungsif
( )
x =x1e−(x12+x22) denganprobabilitas rekombinasi 0.3 dan probabilitas mutasi 0.01 hingga 0.1... 102
Tabel 4.28 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas rekombinasi 0.35 dan probabilitas mutasi 0.01 hingga 0.1... 103
Tabel 4.29 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas rekombinasi 0.4 dan probabilitas mutasi 0.01 hingga 0.1... 103
Tabel 4.30 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas rekombinasi 0.45 dan probabilitas mutasi 0.01 hingga 0.1... 104
Tabel 4.31 Tabel nilai maksimum fungsi f
( )
x =x1e−(x12+x22)denganprobabilitas rekombinasi 0.5 dan probabilitas mutasi 0.01 hingga 0.1... 104
Tabel 4.32 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas mutasi 0.01 dan probabilitas rekombinasi 0.2 hingga 0.5... 105
Tabel 4.33 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
xix
Tabel 4.34 Tabel nilai maksimum fungsi f
( )
x =x1e−(x12+x22)denganprobabilitas mutasi 0.03 dan probabilitas rekombinasi 0.2 hingga 0.5... 106
Tabel 4.35 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas mutasi 0.04 dan probabilitas rekombinasi 0.2 hingga 0.5... 106
Tabel 4.36 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas mutasi 0.05 dan probabilitas rekombinasi 0.2 hingga 0.5... 107
Tabel 4.37 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas mutasi 0.06 dan probabilitas rekombinasi 0.2 hingga 0.5... 107
Tabel 4.38 Tabel nilai maksimum fungsi f
( )
x =x1e−(x12+x22)denganprobabilitas mutasi 0.07 dan probabilitas rekombinasi 0.2 hingga 0.5... 108
Tabel 4.39 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas mutasi 0.08 dan probabilitas rekombinasi 0.2 hingga 0.5... 108
Tabel 4.40 Tabel nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
xx
Tabel 4.41 Tabel nilai maksimum fungsi f
( )
x =x1e−(x12+x22)denganxxi
DAFTAR GAMBAR
Gambar 2.1.1 Grafik f(x)= x3−x2−x+2... 8
Gambar 2.1.2 x* titik batas dari I atau f(x′ *)=0 ... 9
Gambar 2.1.3 Grafik fungsi f(x)=7x2−3x+5... 11
Gambar 2.1.4 Grafik fungsi pada selang tertutup [a, b]. ... 12
Gambar 2.1.5 Fungsi kontinu pada selang tertutup [a, b]... 14
Gambar 2.1.6 Grafik fungsi f(x)=x2−4x+5... 20
Gambar 2.2.1 Grafik fungsi ( , )= 2 + 2 − − +1 y x y x y x f ... 33
Gambar 2.2.2 Grafik fungsi ( , ) 3 3 1 12 2 20 2 3 1 2 1 x =x +x − x − x + x f ... 47
Gambar 3.2.1. Ilustrasi Algoritma Genetika ... 54
Gambar 3.3.1.1 Representasi string bit ... 56
Gambar 3.3.1.2 Representasi panjang kromosom ... 57
Gambar 3.4.1.1 Contoh penggunaan metode seleksi roda roulette... 59
Gambar 3.5.1.1 Rekombinasi satu titik... 62
Gambar 4.1 Grafik fungsi f
(
x1,x2)
= x12 +2x1x2+x22 ... 67xxii
Gambar 4.3 Grafik terjadinya nilai maksimum
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + + dengan probabilitas
rekombinasi 0.25 dan probabilitas mutasi 0.01 hingga 0.1…... 71
Gambar 4.4 Grafik terjadinya nilai maksimum
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + + dengan probabilitas
rekombinasi 0.3 dan probabilitas mutasi 0.01 hingga 0.1.. 72
Gambar 4.5 Grafik terjadinya nilai maksimum
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + + dengan probabilitas
rekombinasi 0.35 dan probabilitas mutasi 0.01 hingga 0.1. 73
Gambar 4.6 Grafik terjadinya nilai maksimum
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + + dengan probabilitas
rekombinasi 0.4 dan probabilitas mutasi 0.01 hingga 0.1.. 74
Gambar 4.7 Grafik terjadinya nilai maksimum
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + + dengan probabilitas
rekombinasi 0.45 dan probabilitas mutasi 0.01 hingga 0.1. 75
Gambar 4.8 Grafik terjadinya nilai maksimum
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + + dengan probabilitas
rekombinasi 0.5 dan probabilitas mutasi 0.01 hingga 0.1... 76 Gambar 4.9 Grafik terjadinya nilai maksimum
(
)
22 2 1 2 1 2
1,x x 2xx x
x
f = + + dengan probabilitas
xxiii
Gambar 4.10 Grafik fungsi f
(
x1,x2)
=3x12x2 −9x23−x12+1... 78Gambar 4.11 Grafik terjadinya nilai maksimum
fungsi
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan
probabilitas rekombinasi 0.2 dan probabilitas mutasi 0.01 hingga 0.1... 83 Gambar 4.12 Grafik terjadinya nilai maksimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.25 dan probabilitas mutasi 0.01 hingga 0.1. 84
Gambar 4.13 Grafik terjadinya nilai maksimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.3 dan probabilitas mutasi 0.01 hingga 0.1.. 85
Gambar 4.14 Grafik terjadinya nilai maksimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.35 dan probabilitas mutasi 0.01 hingga 0.1 86
Gambar 4.15 Grafik terjadinya nilai maksimum
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan probabilitas
rekombinasi 0.4 dan probabilitas mutasi 0.01 hingga 0.1.. 87
Gambar 4.16 Grafik terjadinya nilai maksimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
xxiv
Gambar 4.17 Grafik terjadinya nilai maksimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.5 dan probabilitas mutasi 0.01 hingga 0.1.. 89
Gambar 4.18 Grafik terjadinya nilai minimum
fungsi
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan
probabilitas rekombinasi 0.2 dan probabilitas mutasi 0.01 hingga 0.1... 90
Gambar 4.19 Grafik terjadinya nilai minimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.25 dan probabilitas mutasi 0.01 hingga 0.1 91
Gambar 4.20 Grafik terjadinya nilai minimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.3 dan probabilitas mutasi 0.01 hingga 0.1.. 92
Gambar 4.21 Grafik terjadinya nilai minimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.35 dan probabilitas mutasi 0.01 hingga 0.1 93
Gambar 4.22 Grafik terjadinya nilai minimum
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan probabilitas
rekombinasi 0.4 dan probabilitas mutasi 0.01 hingga 0.1.. 94
Gambar 4.23 Grafik terjadinya nilai minimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
xxv
Gambar 4.24 Grafik terjadinya nilai minimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.5 dan probabilitas mutasi 0.01 hingga 0.1.. 96
Gambar 4.25 Grafik terjadinya nilai maksimum
(
,)
3 9 2 11 3 2 2 2 1 2
1 x = x x − x −x +
x
f dengan probabilitas
rekombinasi 0.2-0.5 dan probabilitas mutasi 0.08 ... 97
Gambar 4.26 Grafik terjadinya nilai minimum
(
x1,x2)
=3x12x2−9x23−x12+1f dengan probabilitas
rekombinasi 0.2-0.5 dan probabilitas mutasi 0.08 ... 98
Gambar 4.27 grafik fungsi
(
1 2)
1 ( 22) 2 1 ,x x e x x xf = − + ... 99
Gambar 4.28 Grafik nilai maksimum fungsi f
( )
x =x1e−(x12+x22) denganprobabilitas rekombinasi 0.2 dan probabilitas mutasi 0.01 hingga 0.1... 103
Gambar 4.29 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas rekombinasi 0.25 dan probabilitas mutasi 0.01 hingga 0.1... 103
Gambar 4.30 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
xxvi
Gambar 4.31 Grafik nilai maksimum fungsi f
( )
x =x1e−(x12+x22) denganprobabilitas rekombinasi 0.35 dan probabilitas mutasi 0.01 hingga 0.1... 104
Gambar 4.32 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas rekombinasi 0.4 dan probabilitas mutasi 0.01 hingga 0.1... 105
Gambar 4.33 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas rekombinasi 0.45 dan probabilitas mutasi 0.01 hingga 0.1... 105
Gambar 4.34 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − +
dengan probabilitas rekombinasi 0.5 dan probabilitas mutasi 0.01 hingga 0.1 ... 106
Gambar 4.35 Grafik nilai maksimum fungsi f
( )
x =x1e−(x12+x22) denganprobabilitas mutasi 0.01 dan probabilitas rekombinasi 0.2 hingga 0.5... 106
Gambar 4.36 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − +
dengan probabilitas mutasi 0.02 dan probabilitas rekombinasi 0.2 hingga 0.5 ... 107
Gambar 4.37 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − +
xxvii
Gambar 4.38 Grafik nilai maksimum fungsi f
( )
x =x1e−(x12+x22)dengan probabilitas mutasi 0.04 dan probabilitas rekombinasi 0.2 hingga 0.5 ... 108
Gambar 4.39 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − +
dengan probabilitas mutasi 0.05 dan probabilitas rekombinasi 0.2 hingga 0.5 ... 108
Gambar 4.40 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − + dengan
probabilitas mutasi 0.06 dan probabilitas rekombinasi 0.2 hingga 0.5... 109
Gambar 4.41 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − +
dengan probabilitas mutasi 0.07 dan probabilitas rekombinasi 0.2 hingga 0.5 ... 109
Gambar 4.42 Grafik nilai maksimum fungsi f
( )
x =x1e−(x12+x22)dengan probabilitas mutasi 0.08 dan probabilitas rekombinasi 0.2 hingga 0.5 ... 110
Gambar 4.43 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − +
dengan probabilitas mutasi 0.09 dan probabilitas rekombinasi 0.2 hingga 0.5 ... 110
Gambar 4.44 Grafik nilai maksimum fungsi
( )
1 ( 22) 2 1 x xe x
f x = − +
BAB I
PENDAHULUAN
A.
Latar Belakang
Teori optimasi secara klasik dibangun dengan menggunakan
kalkulus diferensial untuk menentukan nilai minimum atau maksimum
(optimum) dari fungsi dengan kendala atau tanpa kendala. Untuk fungsi
tanpa kendala,
f
(
x)
harus memenuhi setiap
x
yang memenuhi
pembatas-pembatas:
x≥0dimana
f
(
x
)
adalah fungsi yang bernilai real
dari
R
n. Jika
ada beberapa atau semua fungsi dari
f
(
x
) adalah tidak linear
maka masalah
tersebut dikatakan pemrograman tak linear.
Secara matematis, suatu titik dikatakan pembuat maksimum apabila
terdapat suatu titik
x
*=
(
x
1*,
x
*2,
x
*3,...,
x
n*)
yang memenuhi
,
atau pembuat minimum apabila
.
)
(
)
(
x
*f
x
f
≥
)
(
)
(
x
*f
x
f
≤
Secara umum, optimasi pemrograman tak linear selalu menimbulkan
kesulitan dalam penangan analitis dan numerik, dan lebih sulit dari
pemrograman linear. Walaupun dalam kasus dimana semua kendala adalah
linear dan hanya fungsi tujuannya yang tak linear, tetap saja sulit untuk
diselesaikan. Oleh sebab itu diperlukan teknik lain yang dapat
menyelesaikan masalah optimasi dalam pemrograman tak linear.
Algoritma Genetika tergolong dalam algoritma yang bersifat heuristik,
sehingga dapat memberikan banyak kemungkinan penyelesaian dan
memberikan pertimbangan untuk mengambil suatu keputusan.
Sejak tahun 1960, mulai berkembang perhatian dalam menirukan
kehidupan makhluk hidup untuk menyelesaikan masalah optimasi yang
sulit. Saat ini, terdapat tiga topik utama dalam penelitian yang menirukan
kehidupan makhluk hidup, yaitu Algoritma Genetika, Pemrograman
Evolusi, dan Strategi Evolusi. Diantara ketiga topik tersebut, yang paling
sering digunakan adalah Algoritma Genetika.
Algoritma Genetika banyak dipakai pada aplikasi bisnis, teknik,
maupun bidang keilmuan lainnya. Algoritma Genetika dapat dipakai untuk
mendapatkan solusi yang tepat untuk masalah optimasi yang kompleks dan
sulit diselesaikan.
Menurut Goldberg (1989) Algoritma Genetika adalah teknik
pencarian stokastik berdasarkan mekanisme seleksi alam dan sifat
genetika. Pada dasarnya, Algoritma Genetika merupakan implementasi
dari teori evolusi dan teori genetika yang dikemukakan oleh Darwin dalam
konsep biologi. Seperti proses evolusi di alam, Algoritma Genetika
umumnya terdiri dari tiga operator, yaitu operator reproduksi, operator
persilangan (
crossover
), dan operator mutasi. Suatu individu mempunyai
sifat tertentu ditentukan dengan susunan gen dalam kromosom individu
tersebut. Dalam Algoritma Genetika, teori genetika tersebut digunakan
untuk merepresentasikan setiap solusi dari masalah yang ada. Karena tiap
kromosom merupakan solusi dari masalah yang akan diselesaikan,
kromosom yang terbaik merupakan pendekatan dari solusi optimal dari
Darwin, dalam menyelesaikan suatu masalah, Algoritma Genetika
memulai pekerjaannya dengan sekumpulan solusi yang disebut populasi.
Setiap individu pada populasi disebut kromosom yang menggambarkan
suatu solusi dari masalah yang akan diselesaikan. Kromosom-kromosom
terus berkembang terus menerus yang disebut generasi. Pada setiap
generasi, kromosom dievaluasi dengan menggunakan alat ukur yang
disebut
fitness
(tingkat kesesuaian). Nilai
fitness
dari suatu kromosom
akan menunjukkan kualitas kromosom dalam populasi tersebut.
Kromosom yang terpilih membentuk kromosom baru, yaitu anak atau
keturunan (
offspring
) yang terbentuk dari gabungan dua kromosom
generasi sekarang yang bertindak sebagai induk (
parent
) dengan
menggunakan operator penyilangan (
crossover
) atau dengan mengubah
suatu kromosom dengan menggunakan operator mutasi. Generasi baru
dibentuk dengan cara menyeleksi nilai
fitness
dari kromosom induk dan
nilai
fitness
dari kromosom anak serta menghilangkan kromosom lainnya
sehingga ukuran populasi konstan. Setelah melalui beberapa generasi,
algoritma ini akan konvergen ke arah kromosom yang terbaik dengan
harapan kromosom tersebut merupakan solusi optimal dari masalah yang
diselesaikan.
Sistem pencarian untuk mendapatkan nilai yang paling optimum
pada Algoritma Genetika diharapkan dapat memberikan penyelesaian yang
terbaik, dan semakin memudahkan menyelesaikan masalah Optimasi
B.
Perumusan Masalah
Masalah yang akan dibahas pada skripsi ini adalah :
1.
Bagaimana cara Algoritma Genetika dalam mencari nilai optimum dari
masalah optimasi fungsi tanpa kendala?
2.
Bagaimana mendapatkan nilai optimum fungsi tanpa kendala dengan
menggunakan Algoritma Genetika?
C.
Pembatasan Masalah
Pembatasan mengenai optimasi fungsi tanpa kendala pada skripsi ini
hanya untuk program tak linear dengan dua variabel.
Penulis akan
menggunakan software aplikasi MATLAB untuk menyelesaikan masalah
optimasi tanpa kendala tersebut.
D.
Tujuan Penulisan
Skripsi ini bertujuan untuk memenuhi salah satu persyaratan untuk
memperoleh gelar Sarjana Sains dalam bidang matematika. Selain itu
skripsi ini bertujuan untuk:
1.
Lebih memahami penerapan Algoritma Genetika dalam
menyelesaikan masalah optimasi fungsi tanpa kendala.
2.
Mendapatkan nilai yang paling optimum dari masalah optimasi
E.
Metode Penulisan
Penulisan skripsi ini menggunakan metode studi pustaka, yaitu
de-ngan menggunakan buku-buku, jurnal-jurnal, dan makalah-makalah yang
telah dipublikasikan, sehingga tidak ditemukan hal baru.
F.
Manfaat Penulisan
Manfaat yang diharapkan dari penulisan skripsi ini adalah semakin
memperdalam pemahaman akan Algoritma Genetika dalam
menyelesaikan masalah optimasi, terutama dalam menyelesaikan masalah
optimasi fungsi tanpa kendala, dan dapat mencari nilai optimum dengan
menggunakan Algoritma Genetika.
G.
Sistematika Penulisan
BAB I PENDAHULUAN
Pada Bab I dipaparkan mengenai latar belakang skripsi ini,
perumusan masalah, pembatasan masalah, tujuan penulisan, metode
penulisan, dan manfaat penulisan.
BAB II OPTIMASI FUNGSI TANPA KENDALA
Bab II dengan judul Optimasi Fungsi Tanpa Kendala terdiri atas dua
subbab. Dalam bab ini dibahas mengenai optimasi fungsi satu variabel
tanpa kendala dengan kalkulus dan optimasi fungsi beberapa variabel
BAB III ALGORITMA GENETIKA
Bab III dengan judul Algoritma Genetika terdiri atas empat subbab.
Dalam bab ini dibahas mengenai latar belakang biologi, struktur umum
Algoritma Genetika, dan komponen–komponen utama Algoritma
Genetika.
BAB
IV
OPTIMASI FUNGSI TANPA KENDALA DENGAN
ALGORITMA GENETIKA
Bab IV dengan judul Algoritma Genetika Untuk Optimasi Fungsi
tanpa kendala Tanpa Kendala merupakan inti permasalahan yang diangkat
dalam skripsi ini. Dalam bab ini akan diperlihatkan contoh – contoh
permasalahan optimasi tanpa kendala disertai dengan penyelesainnya
menggunakan teknik konvensional (kalkulus) dan dengan menggunakan
Algoritma Genetika.
BAB V PENUTUP
Bab V merupakan bab terakhir dalam skripsi ini. Bab ini berisi
kesimpulan dari skripsi ini dan saran yang diharapkan berguna untuk
perkembangan penelitian mengenai optimasi dengan Algoritma Genetika
7
BAB II
OPTIMISASI FUNGSI TANPA KENDALA
A. Optimisasi Fungsi Satu Variabel Tanpa Kendala Dengan Kalkulus Definisi 2.1.1
Misalkan f(x) adalah fungsi bernilai real yang didefinisikan pada selang I.
(Selang I dapat terbatas atau tidak terbatas, tertutup atau terbuka, atau
setengah terbuka). Suatu titik x* di I adalah :
a. Pembuat minimum mutlak (global) untuk f(x) pada I jika f(x*)≤ f(x)
untuk setiap x di I;
b. Pembuat minimum mutlak tegas untuk f(x) pada I jika ( *) ( )
x f x
f < untuk
setiap x di I dan x≠x*;
c. Pembuat minimum relatif (lokal) untuk f(x) jika ada bilangan positif δ
sedemikian hingga f(x*)≤ f(x) untuk setiap x di I dimana
δ
δ < < +
− *
*
x x
x ;
d. Pembuat minimum relatif tegas untuk f(x) jika ada bilangan positif δ
sedemikian hingga ( *) ( )
x f x
f < untuk setiap x di I dimana
δ
δ < < +
− *
* x x
x dan x≠ x*;
e. Pembuat maksimum mutlak untuk f(x) pada I jika f(x*)≥ f(x) untuk
setiap x di I;
f. Pembuat maksimum mutlak tegas untuk f(x) pada I jika f(x*)> f(x)
g. Pembuat maksimum relatif untuk f(x) jika ada bilangan positif δ
sedemikian hingga f(x*)≥ f(x) untuk setiap x di I dimana
δ
δ < < +
− *
*
x x
x ;
h. Pembuat maksimum relatif tegas untuk f(x) jika ada bilangan positif δ
sedemikian hingga f(x*)> f(x) untuk setiap x di I dimana
δ
δ < < +
− *
*
x x
x dan x≠ x*;
i. Titik kritis dari f(x) jika f′(x*) ada dan sama dengan nol.
Contoh 2.1.1
Gambar 2.1.1Grafik f(x)= x3 −x2−x+2
Pada gambar grafik di atas terlihat bahwa setiap x di [-3, 4]. Titik x* = -2
I y=f(x)
Titik batas dan maksimum
(f′(x*)≠0) pembuat
mini-mum f′(x*)=0
maksimum mutlak. Titik x* =
3 1
− adalah pembuat maksimum relatif tegas,
dan titik x* = 1 adalah pembuat minimum relatif tegas.▲
Teorema 2.1.1
Misalkan f(x) adalah fungsi yang terdiferensialkan pada selang I. Jika x*
adalah pembuat minimum relatif atau pembuat maksimum relatif pada f(x),
maka salah satu dari yang berikut berlaku:
i. x* adalah titik batas/akhir dari I
ii. f′(x*)=0.
x* x*
Gambar 2.1.2 x* titik batas dari I atau f(x′ *)=0
Bukti :
Misalkan x* adalah pembuat minimum relatif dari f(x) dan x* bukan titik dalam
dari I. Berdasarkan hipotesa f′(x∗) ada. Akan dibuktikan f′(x∗)= 0.
* *
* ( ) ( )
lim ) (
*
x x
x f x f x
f
x
x −
− =
′
Karena f(x*)≤f(x) untuk x mendekati x*, f(x) - f(x*) adalah tak negatif untuk
setiap x mendekati x*. Oleh karena itu, karena x – x* > 0 untuk x*< x, dan
x – x* < 0 untuk x*> x, dapat terlihat
0 ) ( ) (
* *
≥ −
− x x
x f x f
untuk x*< x,
dan
0 ) ( ) (
* *
≤ −
− x x
x f x f
untuk x*> x,
selama x mendekati x*. Berdasarkan persamaan (1) dan persamaan di atas
diperoleh 0f′(x*)≥ dan f′(x*)≤0. Hal ini membuktikan bahwa
0 )
( * =
′ x
f . Untuk x* pembuat maksimum relatif, bukti analog.■
Definisi 2.1.2
Bila x* suatu titik dalam daerah asal f dan bila f′(x*)=0 atau f′(x*) tidak
ada, maka x* dikatakan titik kritis dari f.
Contoh 2.1.2
Misalkan 5f(x)=7x2−3x+ .
Maka f′(x)=14x−3. Ditentukan
0 )
( =
′ x f
0 3
14x− =
14 3 =
x .
Gambar 2.1.3 grafik fungsi f(x)=7x2 −3x+5
Maka f′(x)=14x−3. Ditentukan
0 )
( =
′ x
f
0 3
14x− =
14 3 =
x .
Titik kritis dari f(x) adalah 143 .▲
Teorema 2.1.2 (Teorema Nilai Ekstrim)
Jika fungsi f kontinu pada selang tertutup [a, b], maka f mencapai nilai
mini-mum mutlak dan maksimini-mum mutlak pada selang [a, b].
f(c)
f(a)
a c d b
•
•
Teorema nilai ekstrim dapat tercapai apabila terjadi pada:
i. Selang tertutup; dan
ii. Fungsi bersifat kontinu pada selang tersebut.
Jika kondisi (i) dan (ii) tidak terpenuhi, maka titik ekstrim belum tentu ada.
Jika domain suatu fungsi adalah selang tertutup, untuk menentukan ekstrim
mutlak, fungsi tersebut harus diuji tidak hanya pada titik kritis tapi juga pada
titik batas selang. Teorema titik kritis menjamin bahwa ekstrim mutlak terjadi
di dalam selang.
Gambar 2.1.4 Grafik fungsi pada selang tertutup [a, b].
Gambar 2.1.4 dapat dilihat bahwa titik batas selang terjadi pada x = a dan b,
sedangkan titik kritis terjadi pada x = c dan d. Nilai maksimum mutlak terjadi
pada titik kritis c, dan nilai minimum mutlak terjadi pada titik batas selang a.
Maka baik nilai maksimum mutlak atau minimum mutlak terletak dalam
Teorema 2.1.3 (Teorema Rolle)
Misalkan f adalah fungsi yang memenuhi syarat:
1. f kontinu pada selang tertutup [a, b].
2. f mempunyai turunan pada selang terbuka (a, b).
3. f(a) = f(b) = 0.
Maka ada suatu c∈(a, b) sehingga f′(c)= 0.
Bukti :
Jika f(x) = 0 untuk semua x pada selang [a, b], maka f′(x) = 0 untuk semua x
pada (a, b), sehingga setiap bilangan di antara a dan b dapat diambil sebagai c.
Jika f(x) tidak nol untuk suatu x pada selang terbuka (a, b) dan karena f
kon-tinu pada selang tertutup [a, b], maka menurut teorema 2.1.2, f mempunyai
nilai maksimum mutlak dan minimum mutlak pada [a, b]. Dari (3) diketahui
f(a) = 0 dan f(b) = 0. Selanjutnya f(x) tidak nol untuk suatu x pada (a, b). Maka
f akan mempunyai nilai maksimum mutlak yang positif untuk suatu c1 pada
(a, b) atau mempunyai nilai minimum mutlak yang negatif di suatu c2 pada
(a, b), atau dua-duanya terjadi. Jadi untuk c = c1 atau c = c2 atau
kedua-duanya, terdapat ekstrim mutlak di titik dalam selang [a, b]. Oleh karena itu
ekstrim mutlak f(c) juga ekstrim relatif. Karena f′(c) ada berdasarkan
A
B
a x b x
y
•
•
y=g(x)
f(x)
Teorema 2.1.4 (Teorema Nilai Rata-Rata)
Misalkan f adalah fungsi yang memenuhi syarat:
1. f kontinu pada selang tertutup [a, b].
2. f mempunyai turunan pada selang terbuka (a, b).
Maka ada suatu c∈(a, b) sehingga
a b a f b f c f − − = ′( ) ( ) ( ). Bukti :
Gambar 2.1.5 fungsi kontinu pada selang tertutup [a,b].
Misalkan fungsi f(x) untuk x∈[a,b] seperti ditunjukkan pada gambar 2.1.5
Fungsi g(x) adalah persamaan garis yang melalui titik A dan B. Dibentuk
fungsi s(x) yaitu s(x)= f(x)−g(x) untuk setiap x∈[a,b]. Karena garis ini
mempunyai kemiringan a b a f b f − − ( ) ) (
dan melalui (a, f(a)), maka bentuk titik
kemiringan untuk persamaannya adalah
) ( ) ( ) ( ) ( )
( x a
a b a f b f a f x g − − − =
− atau
) ( ) ( ) ( ) ( )
( x a
) ( ) ( )
(x f x g x
s = −
⇔ ( ) ( ) ( ) ( ) ( )(x a)
a b a f b f a f x f x s − − − − − =
Perhatikan bahwa s(b) = s(a) = 0 dan bahwa untuk x dalam (a, b)
a b a f b f x f x s − − − ′ = ′( ) ( ) ( ) ( ).
Menurut teorema 2.1.2 fungsi s harus mencapai nilai maksimum atau nilai
minimum pada [a, b]. Jika kedua nilai tersebut adalah 0, maka s(x) secara
identik adalah 0 pada [a, b], akibatnya s′(x)=0 untuk semua x dalam (a, b).
Jika salah satu nilai maksimum atau minimum tidak sama dengan 0, maka
nilai tersebut tercapai pada suatu titik dalam c. Karena s(a) = s(b) = 0. Dan s
mempunyai turunan di setiap titik dari (a, b), sehingga menurut teorema 2.1.3
0 )
( =
′ c
s .
Karena diketahui terdapat suatu bilangan c dalam (a, b) yang memenuhi
0 )
( =
′ c
s , maka
Teorema 2.1.5
Misalkan )f(x), f′(x), f′′(x ada pada selang tertutup [a, b].
Jika x*, x adalah dua titik yang berbeda pada [a, b], maka terdapat titik z tepat
berada di antara x* dan x sehingga
2 * * * * ) ( 2 ) ( ) )( ( ) ( )
(x f x f x x x f z x x
f = + ′ − + ′′ − .
Bukti :
Misalkan suatu fungsi
2 * * * *) ( )( ) ( ) ( )
(x f x f x x x R x x
f = + ′ − + − …(2)
Pandang F(x),
2 * * * * ) ( ) )( ( ) ( ) ( )
(x f x f x f x x x R x x
F = − − ′ − − − …(3)
Maka dari (2) diperoleh F(x) = 0. Karena F(x) = 0, maka F(a) = F(b) = 0.
) ( ), ( ),
(x f x f x
f ′ ′′ kontinu pada selang tertutup [a, b], maka penjumlahan dan
pengurangan fungsi – fungsi (F(x)) tersebut juga kontinu pada selang tertutup
[a, b], dan
) ( 2 ) ( ) ( )
(x f x f x* R x x*
F′ = ′ − ′ − − …(4)
terlihat bahwa F(x) mempunyai turunan. Karena ketiga syarat dari teorema
Rolle dipenuhi, maka menurut teorema Rolle, terdapat bilangan z1 antara x dan
*
x (x< z1< x*) sedemikian sehingga
0 )
( 1 =
′ z
F …(5a)
Dari (4) diperoleh
0 )
( =
′ x
(5a) dan (5b) menunjukkan bahwa F′(x) memenuhi teorema Rolle dalam (x,
z1). Jadi terdapat bilangan z antara x dan z1 sedemikian sehingga F′′(z)=0,
dan dari (4) diperoleh F′′(x)= f′(x)−2R. Karena F′′(z)=0, maka
) (
2 1 f z
R= ′′ .
Substitusi R dalam (2), maka
2 * 2
1 * *
*
) )( ( )
)( ( ) ( )
(x f x f x x x f z x x
f = + ′ − + ′′ − .■
Definisi 2.1.1 merupakan cara untuk mengetahui apakah suatu titik x* di I
adalah minimum atau maksimum mutlak atau relatif di I. Namun pada definisi
2.1.1 tidak diketahui apakah memang benar titik x* tersebut adalah pembuat
minimum / maksimum mutlak tegas atau pembuat minimum / maksimum
relatif tegas. Oleh sebab itu diperlukan cara lain yang lebih baik, yaitu teorema
2.1.6, yang dapat menentukan apakah pembuat maksimum / minimum (baik
mutlak ataupun relatif) tersebut tegas atau tidak.
Teorema 2.1.6
Misalkan )f(x), f′(x),f ′′(x kontinu pada selang I dan x*∈I adalah titik kritis
dari f(x).
a. Jika f′′(x)≥0 untuk setiap x∈I, maka x* adalah pembuat minimum
mutlak dari f(x) di I.
b. Jika 0f ′′(x)> untuk setiap x∈I sedemikian hingga *
x
x≠ , maka x*
adalah Pembuat minimum mutlak tegas dari f(x) di I.
d. Jika 0f′′(x)≤ untuk setiap x∈I, maka x* adalah pembuat maksimum
mut-lak dari f(x) di I.
e. Jika f′′(x)<0 untuk setiap x∈I sedemikian hingga *
x
x≠ , maka x*
adalah Pembuat maksimum mutlak tegas dari f(x) di I.
f. Jika 0f′′(x*)< , maka x* adalah pembuat maksimum relatif tegas dari f(x).
Bukti :
Bukti (a): Jika x∈I dan x≠x*, maka berdasarkan teorema 2.1.5 dan hipotesa
)
(x*
f′ =0 menghasilkan
2 *
* ( )
2 ) ( ) ( )
(x f x f z x x
f − = ′′ − , …(6)
dimana z adalah titik yang berada tepat di antara x* dan x. Karena itu, jika
0 )
( ≥
′′ x
f untuk setiap x∈I, maka f(x)≥ f(x*) untuk setiap x∈I karena
0 2
) x
-(x * 2 ≥
untuk setiap x∈I.
Bukti (b): Jika x∈I dan x≠x*, maka berdasarkan teorema 2.1.5 dan hipotesa
)
(x*
f′ =0 menghasilkan
2 * *
) ( 2
) ( ) ( )
(x f x f z x x
f − = ′′ − , …(7)
dimana z adalah titik yang berada tepat di antara x* dan x. Karena itu, jika
0 ) ( >
′′ x
f untuk setiap x∈I, maka f(x)> f(x*) untuk setiap x∈I karena
0 2
) x
-(x * 2
Bukti (c): Jika f ′′(x*)>0, kekontinuitas dari f ′′(x) mengimplikasikan bahwa
ada δ > 0 sehingga f′′(x) > 0 untuk setiap x∈I sedemikian hingga x* -δ < x
< x* + δ . Namun persamaan (7) menunjukkan bahwa f(x) > f(x*) untuk setiap
x∈I sedemikian hingga x≠ x*, x*−
δ
< x< x*+δ
, dimana x* adalah satu -satunya pembuat minimum relatif dari f(x).
Bukti (d): Jika x∈I dan x≠x*, maka berdasarkan teorema 2.1.5 dan hipotesa
)
(x*
f′ =0 menghasilkan
2 * *
) ( 2
) ( ) ( )
(x f x f z x x
f − = ′′ − , …(8)
dimana z adalah titik yang berada tepat di antara x* dan x. Karena itu, jika
0 )
( ≤
′′ x
f untuk setiap x∈I, maka f(x)≤ f(x*) untuk setiap x∈I karena
0 ) ( )
(x − f x* ≤
f untuk setiap x∈I.
Bukti (e): Jika x∈I dan x≠x*, maka berdasarkan teorema 2.1.5 dan hipotesa
)
( *
x
f′ =0 menghasilkan
2 * *
) ( 2
) ( ) ( )
(x f x f z x x
f − = ′′ − , …(9)
dimana z adalah titik yang berada tepat di antara x* dan x. Karena itu, jika
0 )
( <
′′ x
f untuk setiap x∈I, maka ( ) ( *)
x f x
f < untuk setiap x∈I karena
0 ) ( )
(x − f x* ≤
Bukti (f): Jika f ′′(x*)<0, kekontinuitasan dari f ′′(x) mengimplikasikan
bahwa ada δ > 0 sehingga f′′(x) < 0 untuk setiap x∈I sedemikian hingga x*
-δ < x < x* + δ . Namun persamaan (9) menunjukkan bahwa f(x) < f(x*) untuk
setiap x∈I sedemikian hingga x≠ x*, x*−
δ
< x<x*+δ
, dimana x* adalahsatu - satunya pembuat maksimum relatif dari f(x). ■
Contoh 2.1.3
Tentukan ekstrim mutlak dari fungsi f(x)=x2 −4x+5 pada selang [1,4].
Gambar 2.1.6 grafik fungsi f(x)= x2−4x+5.
i. Mencari titik kritis
0 )
( =
′ x
f
0 4
2x− =
2
= x
ii. Mengevaluasi f(x) pada titik akhir dan titik kritis
2 5 1 4 1 ) 1
( = 2− × + =
f
1 5 2 4 2 ) 2
( = 2 − × + =
5 5 4 4 4 ) 4
( = 2− × + =
f
Dari langkah 9, dapat disimpulkan bahwa nilai maksimum mutlak terjadi pada
titik (4, 5), dan nilai minimum mutlak terjadi pada titik (2,1).▲
B. Optimisasi Fungsi Beberapa Variabel Tanpa Kendala Dengan Kalkulus
Perluasan dari fungsi satu variabel adalah fungsi lebih dari satu variabel
den-gan mengkombinasikan beberapa teori kalkulus denden-gan aljabar linear. Oleh
sebab itu, untuk permulaan akan dibahas beberapa terminologi dan notasi.
Vektor pada Rn adalah pasangan terurut n-tupel x = (x1, x2, …, xn) dari
bilan-gan real xi yang disebut dengan komponen dari x. Vektor x = (x1, x2, …, xn)
disebut vektor baris, dan vektor
⎟⎟ ⎟ ⎟ ⎟
⎠ ⎞
⎜⎜ ⎜ ⎜ ⎜
⎝ ⎛
=
n x x x
M
2 1
x disebut vektor kolom.
Maka dapat dilihat bahwa fungsi f(x1, x2, …, xn) dari n variabel sebagai fungsi
f(x) dari vektor tunggal variabel x = (x1, x2, …, xn).
Definisi 2.2.1
Didefinisikan penjumlahan dari dua vektor x = (x1, x2, …, xn) dan y = (y1, y2,
…, yn) pada Rn dengan
x + y = (x1 + y1, x2 + y2, …, xn+ yn),
dan perkalian dari x dan bilangan real λ dengan
Definisi 2.2.2
Jika x = (x1, x2, …, xn) dan y = (y1, y2, …, yn) adalah vektor-vektor di Rn,
maka perkalian titik atau perkalian dalam x•y didefinisikan sebagai
∑
== + + + =
• n
k k k n
ny x y
x y
x y x
1 2
2 1
1 ...
y
x .
Akibat 2.2.1
Perkalian titik adalah linear pada kedua variabel; yaitu,
), ( ) ( )
(
α
x+β
y •z=α
x•z +β
y•z) ( ) ( )
( y z x y x z
x•
α
+β
=α
• +β
• ,untuk semua vektor x, y, z pada Rn dan bilangan real
α
,β
.Bukti :
(
, , ,)
( , , , ))
(αx+βy •z= αx1+βy1 αx2 +βy2 K αxn+βyn • z1 z2 K zn
(
)
(
)
(
)
(
αx1+βy1 .z1+ αx2 +βy2 .z2+ + αxn+βyn .zn)
= K
(
αx1.z1+βy1.z1+αx2.z2+βy2.z2 + +αxn.zn+βyn.zn)
= K
(
) (
)
(
αx1.z1+αx2.z2+ +αxn.zn + βy1.z1+βy2.z2+ +βyn.zn)
= K K
(
) (
)
(
x1.z1+x2.z2+ +xn.zn + y1.z1+y2.z2 + +yn.zn)
= α K β K
) ( )
(x•z + y•z
=α β
(
n n)
n y z y z y z
x x
x α β α β α β
β
α + = • + + +
•( y z) ( 1, 2,K, ) 1 1, 2 2,K,
x
(
)
(
)
(
)
(
x αy +βz +x αy +βz + +xn αyn+βzn)
(
x1.αy1+x1.βz1+x2.αy2++x2.βz2 + +xn.αyn+xn.βzn)
= K
(
x1.αy1+x2.αy2 + +xn.αyn+x1.βz1+x2.βz2+ +xn.βzn)
= K K
(
) (
)
(
α x1.y1+x2.y2+ +xn.yn +β x1.x1+x2.βx2+ +xn.βxn)
= K K
=α(x•y)+β(x•z).■
Definisi 2.2.3
Dua vektor x dan y adalah ortogonal jika x•y = 0.
Definisi 2.2.4
Norm atau panjang x pada vektor x = (x1, x2, …, xn) adalah fungsi real pada
Rn dengan syarat:
1. x ≥0 untuk setiap vektor di Rn.
2. x = 0 jika dan hanya jika x adalah vektor nol 0.
3. αx = α x untuk setiap vektor di Rn dan semua bilangan real α.
4. x+y ≤ x + y untuk semua vektor x, y di Rn (ketidaksamaan segitiga).
Contoh 2.2.1
x pada vektor x = (x1, x2, …, xn) adalah
2 / 1 2
/ 1 2 2
2 2
1 ... ) ( )
( x x
x
y Definisi 2.2.5
Untuk vektor tak nol x dan y di R2 atau R3, perkalian titik x•y secara umum
didefinisikan
θ
cos
y x y
x• = …(1)
dimana
θ
∈[0,π
] adalah sudut antara x dan y.θ
Untuk vektor x dan y di Rn dengan n > 3, formula (1) untuk perkalian titik
tetap dapat digunakan jika cos didefinisikan. Untuk θ x, y ∈ Rn didefinisikan
y x
y x
cosθ = •
Teorema 2.2.1
Pertidaksamaan Cauchy – Schwarz untuk setiap vektor x dan y,
y x y x• ≤
Bukti :
Apabila x dan y adalah vektor nol, maka 0≤0, dimana hal tersebut adalah
benar untuk setiap x dan y. Jika x atau y (salah satunya) vektor tak nol, maka
dari persamaan (1) didapatkan
y x y
x y
karena cosθ ≤1 untuk setiap nilai pada θ.■
Pada pertidaksamaan Cauchy – Schwarz, −1≤cosθ ≤1 dan cosθ =1 jika
hanya jika terdapat satu vektor yang merupakan kelipatan vektor lainnya.
Definisi 2.2.6
Jika x dan y adalah vektor di Rn, panjang atau jarak d(x,y) di antara x dan y
didefinisikan sebagai:
2 1
1
2
) ( )
,
( ⎟
⎠ ⎞ ⎜
⎝
⎛ −
= −
=
∑
=
n
i
i
i y
x
d x y x y
Definisi 2.2.7
Bola )B(x,r yang berpusat pada x dengan radius r adalah himpunan semua
vektor y di Rn, dimana jarak dari x kurang dari r, maka
{
R r}
B(x,r)= y∈ n y−x < .
Definisi 2.2.8
Titik x pada sub himpunan D di Rn adalah titik dalam dari D jika terdapat r >
0, dimana bola B(x,r) dalam D. Bagian dalam Do pada D adalah himpunan
dari semua titik dalam dari D. Himpunan G di Rn terbuka jika Go =G, artinya,
tertutup jika F mencangkup setiap titik x sehingga terdapat barisan {x(k)} di F
dengan lim ( ) − =0
∞
→ x x
k
k .
Definisi 2.2.9
Himpunan D di Rn adalah terbatas jika terdapat suatu konstanta M > 0
se-hingga x <M untuk setiap x∈D, artinya, D adalah terbatas jika dan hanya
jika D termasuk dalam bola besar B(0, M) dengan pusat 0.
Contoh 2.2.1
Pada R2, himpunan F dengan komponennya adalah titik – titik tak
nega-tif, yaitu F =
{
x=(x1,x2)∈R2x1≥0,x2 ≥0}
, adalah tertutup tapi tidakterba-tas. Titik x = (x1, x2) pada F adalah titik dalam dari F jika dan hanya jika x1 >
0, x2 >0 karena bola B(x, r) termasuk di dalam F walaupun r adalah bilangan
positif terkecil dari x1, x2.▲
Definisi 2.2.10
Misalkan f(x) adalah fungsi yang bernilai real didefinisikan pada sub
him-punan D di Rn. Titik x*di D adalah:
a Pembuat mi