Catatan Kuliah (3 sks) GM 114 Kalkulus 2

(1)

GM 114 Kalkulus 2

(Revisi Terakhir: Januari 2010)

Oleh:

Didit Budi Nugroho, S.Si, M.Si.

Program Studi Matematika Fakultas Sains dan Matematika Universitas Kristen Satya Wacana

(2)

1 Teknik-teknik Integrasi 1

1.1 Antiderivatif . . . 1

1.2 Integrasi dengan Substitusi Sederhana . . . 5

1.3 Integrasi Parsial . . . 11

1.4 Integral Fungsi Hiperbolik . . . 17

1.5 Integral Trigonometri . . . 19

1.6 Substitusi Trigonometri . . . 26

1.7 Integral Fungsi Rasional . . . 33

1.8 Integral Fungsi Irasional . . . 38

1.9 Substitusitan 1₂x . . . 41

2 Integral Tentu 43 2.1 Integral Riemann . . . 43

2.2 Teorema Fundamental dari Kalkulus Integral . . . 47

3 Integral Tak Wajar 49 3.1 Pengantar . . . 49

3.2 Integral atas Interval Tak Terbatas . . . 50

3.3 Tak Kontinu di Suatu Titik . . . 51

3.4 Uji Perbandingan . . . 52

4 Aplikasi Integral 55 4.1 Luas Bidang Datar . . . 55

4.1.1 Persamaan Kartesius . . . 55

4.1.2 Persamaan Parameter . . . 59

4.1.3 Persamaan Kutub . . . 60

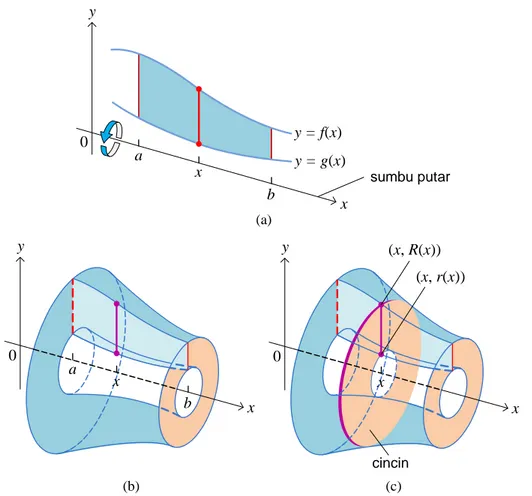
4.2 Volume Benda Putar . . . 68

4.2.1 Metode Cakram . . . 69

4.2.2 Metode Cincin . . . 72

4.2.3 Metode Kulit Silindris . . . 75

4.3 Panjang Kurva . . . 83

4.3.1 Persamaan Kartesius . . . 83

4.3.2 Persamaan Parameter . . . 86

4.3.3 Persamaan Kutub . . . 88

(3)

Kata Pengantar

(4)

Teknik-teknik Integrasi

Dalam bab ini dibahas berbagai teknik integrasi. Integral-integral yang dibicarakan adalah integral tak tentu. Topik-topik yang dicakup dalam bab ini yaitu pengertian antiderivatif beserta aturan-aturannya, integrasi dengan substitusi sederhana, integrasi dengan parsial, integral yang melibatkan fungsi hiperbolik, integral yang melibatkan fungsi trigonometri, integrasi dengan substitusi trigonometri, integrasi yang melibatkan fungsi rasional, integrasi yang melibatkan akar, dan integral dengan substitusitan 1₂x .

1.1 Antiderivatif

Pertama kali didiskusikan proses kebalikan dari diferensiasi. Dengan kata lain, dibe-rikan suatu fungsi f(x) dan diinginkan untuk mencari suatu fungsi F(x) sedemikian sehingga dF(x)

dx = F

0₍_x_{) =} _f₍_x₎_{. Setiap fungsi} _F₍_x₎ _{yang demikian tersebut}

dina-makan suatu antiderivatif, atau integral tak tentu (inde…nite integral), dari fungsi

f(x), dan dituliskan

F(x) =

Z

f(x)dx:

Di sini f(x) dinamakan integran (yang diintegralkan) dan x dinamakan integrator. Dinamakan integral tak tentu sebab tidak merujuk pada nilai numerik tertentu, atau tidak menunjuk suatu interval tertentu untuk daerah integrasi. Langkah untuk mencari antiderivatif darif(x) dinamakanantidiferensiasiatau integrasi.

Pengamatan pertama yaitu bahwa antiderivatif, jika ada, tidaklah tunggal. Diandaikan bahwa fungsi F(x) adalah suatu antiderivatif dari fungsi f(x), berartiF0(x) =f(x). DiambilG(x) =F(x) +k, dimanakadalah sembarang bilangan riil. Ini mudah dilihat bahwa G0(x) =F0(x) =f(x), yang berarti bahwaG(x) juga merupakan antiderivatif darif(x). Secara umum dapat dituliskan

Z

f(x)dx=F(x) +k

dengank selanjutnya dinamakankonstanta integrasi. Sebagai contoh, diberikanf(x) = 2x, maka

F(x) =x2; G(x) =x2 10; H(x) =x2+k

(5)

merupakan antiderivatif darif karena

F0(x) =G0(x) =H0(x) = 2x:

Pengamatan kedua yaitu bahwa untuk sembarang fungsi f(x), selisih dari sembarang dua antiderivatif berbeda dari f(x) pasti merupakan suatu konstanta. Dengan kata lain, jika F(x) dan G(x) adalah antiderivatif-antiderivatif dari f(x), maka F(x)

G(x) adalah suatu konstanta. Suatu konsekuensi dari pengamatan kedua yaitu hasil sederhana berikut ini yang berkaitan dengan derivatif dari suatu konstanta.

ANTIDERIVATIF DARI NOL. Dipunyai

Z

0 dx=k:

Dengan kata lain, antiderivatif dari fungsi nol secara tepat adalah semua fungsi konstan.

Tentu saja, beberapa antiderivatif secara sederhana dapat diperoleh dari beberapa aturan mengenai derivatif. Berikut ini didaftar hasil-hasil tersebut. Hasil pertama yaitu berkaitan dengan aturan kelipatan konstan untuk diferensiasi.

ATURAN PERKALIAN KONSTAN. Jika suatu fungsi f(x) mempunyai anti-derivatif, maka untuk sembarang bilangan riil c, dipunyai

Z

cf(x) dx=c

Z

f(x) dx:

ANTIDERIVATIF DARI PANGKAT.

(a) Jikanadalah suatu bilangan riil sedemikian sehingga n₆= 1, maka

Z xn dx= 1 n+ 1x n+1₊_k: (b) Dipunyai Z x 1 _dx_{= ln}_j_x_j₊_k:

ATURAN PENJUMLAHAN. Jikaf(x)dang(x)mempunyai antiderivatif, maka

Z (f(x) +g(x))dx= Z f(x) dx+ Z g(x) dx:

(6)

ANTIDERIVATIF UNTUK FUNGSI TRIGONOMETRI. Rumus-rumus an-tiderivatif berikut ini adalah valid:

(a) Z cos (x) dx= sin (x) +k (b) Z sin (x) dx= cos (x) +k (c) Z csc2(x) dx= cot (x) +k (d) Z sec2₍_x₎ _dx_{= tan (}_x_{) +}_k (e) Z cot (x) csc (x) dx= csc (x) +k (f) Z

tan (x) sec (x) dx= sec (x) +k

(g)

Z

csc (x) dx= ln_jcot (x) + csc (x)_j+k

(h)

Z

sec (x) dx= ln_jtan (x) + sec (x)_j+k

ANTIDERIVATIF UNTUK FUNGSI EKSPONENSIAL UMUM. Diandaikan

a >0 dan a₆= 1, maka

Z

axdx= a x ln (a) +k:

Secara khusus, dengan pengambilan a=eakan dipunyai

Z

ex dx=ex+k:

Contoh 1.1 Menggunakan aturan penjumlahan, aturan perkalian konstan, dan anti-derivatif dari pangkat, diperoleh

Z x3+ 3x+ 1 dx = Z x3dx+ Z 3x dx+ Z x0dx = 1 4x 4₊ 3 2x 2₊_x₊_k:

Contoh 1.2 Menggunakan aturan penjumlahan, antiderivatif dari pangkat dan fungsi trigonometri, diperoleh Z x3+ sin (x) dx= Z x3dx+ Z sin (x) dx= 1 4x 4 _{cos (}_x_{) +}_k:

(7)

Contoh 1.3 Diperoleh Z (sin (x) + sec (x)) dx = Z sin (x) dx+ Z sec (x) dx

= cos (x) + ln_jtan (x) + sec (x)_j+k:

Contoh 1.4 Diperoleh Z (ex+ 3 cos (x)) dx= Z ex dx+ Z 3 cos (x) dx=ex+ 3 sin (x) +k: Contoh 1.5 Diperoleh Z 1 sin (x) 1 + sin (x) dx = Z (1 sin (x)) (1 sin (x)) (1 + sin (x)) (1 sin (x)) dx = Z ₁ _{2 sin (}_x_{) + sin}2₍_x₎ 1 sin2(x) dx = Z ₁ _{2 sin (}_x_{) + sin}2₍_x₎ cos2₍_x₎ dx = Z

sec2(x) 2 tan (x) sec (x) + tan2(x) dx

=

Z

sec2(x) 2 tan (x) sec (x) + sec2(x) 1 dx

=

Z

2 sec2(x) 2 tan (x) sec (x) 1 dx

= 2 tan (x) 2 sec (x) x+k:

SOAL-SOAL UNTUK

SUBBAB

1.1

Hitung setiap integral tak tentu berikut ini:

(1) Z x3dx (2) Z x52dx (3) Z (5x+ 3) dx (4) Z 1 + 2x+ 3x2 dx (5) Z 2x2 3x+ 1 dx (6) Z 12x7 3x5+ 2x2+ 1 dx (7) Z 5 +x 2 ₄_x 3 _dx ₍₈₎ Z 3x4_{+ 19}_x 3 _dx (9) Z x12 +x 1 2 dx (10) Z 2x13 3x 2 3 dx (11) Z (x 3)2dx (12) Z (2x 3)2dx

(8)

(13) Z x2₊_a 2_dx ₍₁₄₎ Z 1 +x 1 2_dx (15) Z x+ 1 x 2 dx (16) Z x 1 x 2 dx (17) Z (x 2) (x+ 3) dx (18) Z x 2x3+ 1 2dx (19) Z x+ 1 x dx (20) Z 2x2 3x+ 6 x2 dx (21) Z _x3₊_x2 _x ₁ x 1 dx (22) Z _x3 _a3 x a dx (23) Z _x3 ₈ x2_{+ 2}_x_{+ 4} dx (24) Z _p 3dx (25) Z p x dx (26) Z p 2px dx (27) Z xpx dx (28) Z x13 + 8p3x 3x dx (29) Z (3 +px) (4 2px) dx (30) Z ₃_x_{+ 1} 3px dx (31) Z _{4 + 3}p x+xpx x2 dx (32) Z p x 5 + 4 4 p x dx (33) Z ₄ 4 p_x r 3x 27 ! dx (34) Z 8ex dx (35) Z 16 (ex+ 1) dx (36) Z _x2_ex₊_x x2 dx (37) Z 5x+ 3 e x dx (38) Z (x+ 1)3+ex dx (39) Z 5 cos (x) dx (40) Z (1 2 cos (x)) dx (41) Z (5 cos (x) + 4x) dx (42) Z (sin (x) + cos (x)) dx (43) Z 10 sec2(x) dx (44) Z sec2(x) + 1 dx (45) Z (px+ sec (x) tan (x)) dx

1.2 Integrasi dengan Substitusi Sederhana

Sekarang didiskusikan bagaimana kita dapat menggunakan aturan rantai dalam di-ferensiasi untuk membantu menyelesaikan masalah dalam integrasi. Teknik ini biasanya

(9)

dinamakan integrasi dengan substitusi. Perlu ditekankan bahwa teknik tersebut tidak selalu dapat digunakan. Pertama, kita tidak mengetahui antiderivatif dari fungsi. Ke-dua, tidak ada jalan sederhana dimana kita dapat menggambarkannya untuk menolong kita mencari suatu substitusi yang sesuai dalam kasus dimana teknik dapat digunakan. Di sisi lain, ketika teknik dapat digunakan, mungkin terdapat lebih dari satu substitusi yang sesuai.

INTEGRASI DENGAN SUBSTITUSI VERSI 1. Jika kita membuat sub-stitusix=g(u), maka dx=g0(u) du, dan

Z

f(x) dx=

Z

f(g(u)) g0(u) du:

Contoh 1.6 Diperhatikan integral tak tentu

Z

xpx+ 1 dx:

Jika kita membuat substitusix=u2 ₁_{, maka} _dx_{= 2}_{u du}_{, dan}

Z xpx+ 1 dx = Z 2 u2 1 u2du= Z 2u4du Z 2u2du = 2 5u 5 2 3u 3₊_k₌ 2 5(x+ 1) 5 2 2 3(x+ 1) 3 2 +k: Di sisi lain, jika kita membuat substitusi x=v 1, makadx=dv, dan

Z xpx+ 1 dx = Z (v 1)v12dv = Z v32dv Z v12du = 2 5v 5 2 2 3v 3 2 +k= 2 5(x+ 1) 5 2 2 3(x+ 1) 3 2 ₊_k:

Kita bisa menegaskan bahwa integral tak tentu tersebut adalah benar dengan memeriksa bahwa d dx 2 5(x+ 1) 5 2 2 3(x+ 1) 3 2 +k =xpx+ 1:

INTEGRASI DENGAN SUBSTITUSI VERSI 2. Diandaikan bahwa suatu fungsi f(x) dapat dituliskan dalam bentuk f(x) =g(h(x))h0₍_x₎_{. Jika kita membuat}

substitusi u=h(x), makadu=h0(x)dx, dan

Z f(x) dx= Z g(h(x))h0(x) = Z g(u) du:

Dicatat bahwa dalam Versi 1, variabelx pada awalnya ditulis sebagai fungsi dari vari-abel baru u, sedangkan dalam Versi 2, variabel baru u dituliskan sebagai fungsi dari

x. Bedanya, untuk substitusi x = g(u) dalam Versi 1 harus mempunyai invers agar variabel ubisa dikembalikan ke variabel asli x di akhir proses.

(10)

Z

x x2+ 3 4dx:

Pertama kali dicatat bahwa derivatif dari fungsi x2+ 3 sama dengan 2x, sehingga ini tepat untuk membuat substitusi u=x2+ 3. Selanjutnya du= 2x dx, dan

Z x x2+ 3 4dx= 1 2 Z 2x x2+ 3 4dx= 1 2 Z u4du= 1 10u 5₊_k₌ 1 10 x 2_{+ 3} 5₊_k:

Z

1

xln (x)dx:

Pertama kali dicatat bahwa derivatif dari fungsi ln (x) sama dengan 1

x, sehingga ini

tepat untuk membuat substitusi u= ln (x). Selanjutnya du= 1

xdx, dan Z 1 xln (x)dx= Z 1 udu= lnjuj+k= lnjln (x)j+k:

Z

x2ex3dx:

Pertama kali dicatat bahwa derivatif dari fungsix3 sama dengan3x2, sehingga ini tepat untuk membuat substitusiu=x3. Selanjutnya du= 3x2dx, dan

Z x2ex3dx= 1 3 Z 3x2ex3dx= 1 3 Z eudu= 1 3e u₊_k₌ 1 3e x3 ₊_k:

Z

tan3(x) sec2(x) dx:

Pertama kali dicatat bahwa derivatif dari fungsitan (x) sama dengansec2(x), sehingga ini tepat untuk membuat substitusi u= tan (x). Selanjutnya du= sec2(x) dx, dan

Z tan3(x) sec2(x) dx= Z u3du= 1 4u 4₊_k₌ 1 4tan 4₍_x_{) +}_k:

Kadang-kadang, kemungkinan dari substitusi tidak bisa terlihat secara jelas dengan cepat, dan banyak terjadi trial dan error. Kenyataan bahwa suatu substitusi tidak terlihat muncul bukan berarti bahwa metode tersebut gagal. Ini bisa terjadi dalam kasus ketika kita menggunakan suatu subtitusi yang tidak sesuai. Atau barangkali kita pertama kali melupakan modi…kasi dari masalah. Hal ini diilustrasikan dalam contoh berikut ini.

(11)

Z

tan (x) dx:

Di sini tidak terlihat sembarang substitusi yang akan digunakan. Tetapi, jika dituliskan

Z

tan (x) dx=

Z _{sin (}_x₎

cos (x)dx;

maka kita mengamati bahwa derivatif dari fungsi cos (x) sama dengan sin (x), se-hingga ini tepat untuk membuat substitusi u= cos (x). Selanjutnya du= sin (x) dx, dan Z tan (x) dx= Z _{sin (}_x₎ cos (x) dx= Z ₁ udu= lnjuj+k= lnjcos (x)j+k:

Lebih lanjut, berikut ini diperoleh rumus-rumus antiderivatif dari fungsi eksponensial dan trigonometri yang lebih umum dari pada fungsi dalam subbab sebelumnya, dengan cara membuat substitusiu=px+q dandu=p dx.

(a) Z (px+q)ndx= 1 p(n+ 1)(px+q) n+1₊_k (b) Z (px+q) 1dx= 1 plnjpx+qj+k (c) Z apx+qdx= 1 pln (a)a px+q₊_k;_jika _{a >}₀_{; a} 6 = 1. (d) Z epx+qdx= 1 pe px+q₊_k_. (e) Z cos (px+q) dx= 1 psin (px+q) +k. (f) Z sin (px+q) dx= 1 pcos (px+q) +k. (g) Z csc2₍_px₊_q₎ _dx₌ 1 pcot (px+q) +k. (h) Z sec2(px+q) dx= 1 ptan (px+q) +k. (i) Z cot (px+q) csc (px+q) dx= 1 pcsc (px+q) +k. (j) Z tan (px+q) sec (px+q) dx= 1 psec (px+q) +k. (k) Z cot (px+q) dx= 1 plnjsin (px+q)j+k.

(12)

(l) Z tan (px+q) dx= 1 plnjcos (px+q)j+k. (m) Z csc (px+q) dx= 1 plnjcsc (px+q) + cot (px+q)j+k. (n) Z sec (px+q) dx= 1 plnjsec (px+q) + tan (px+q)j+k.

SOAL-SOAL UNTUK

SUBBAB

1.2

Dalam soal (1) (60), hitung setiap integral tak tentu dengan menggunakan substitusi yang diberikan. (1) Z sin (3x) dx, u= 3x (2) Z cos (5x) dx, u= 5x (3) Z xsin x2 dx, u=x2 (4) Z xcos 1 +x2 dx, u= 1 +x2 (5) Z x2tan x3+ 1 dx, u=x3+ 1 (6) Z sec2(3x+ 1) dx, u= 3x+ 1 (7) Z csc2(2x 1) dx, u= 2x 1 (8) Z xsin x2 dx, u=x2 (9) Z x2_cos _x3_{+ 1} _dx_, _u₌_x3_{+ 1} ₍₁₀₎ Z sec (3x+ 5) dx, u= 3x+ 5 (11) Z csc (5x 7) dx, u= 5x 7 (12) Z sin3(x) dx, u= cos (x) (13) Z cos3(x) dx, u= sin (x) (14) Z tan3(x) dx, u= tan (x) (15) Z cot3(x) dx, u= cot (x) (16) Z sec4(x) dx, u= tan (x) (17) Z csc3₍_x₎ _dx_, _u_{= cot (}_x₎ ₍₁₈₎ Z

sin3(x) cos (x) dx, u= sin (x)

(19)

Z

tan5(x) sec2(x) dx, u= tan (x) (20)

Z

cot3(x) csc2(x) dx, u= cot (x)

(21)

Z

sec3(x) tan (x) dx, u= sec (x) (22)

Z csc3(x) cot (x) dx, u= csc (x) (23) Z _arcsin4₍_x₎ p 1 x2 dx, u= arcsin (x) (24) Z _arctan3₍_x₎ 1 +x2 dx, u= arctan (x) (25) Z x2 2x3+ 1 3dx, u= 2x3+ 1 (26) Z ₂ 3x 4dx, u= 3x 4

(13)

(27) Z ₄ 5x+ 2dx, u= 5x+ 2 (28) Z _x 3x2_{+ 1}dx, u= 3x 2_{+ 1} (29) Z _x (x2 ₁₎32 dx, u=x2 1 (30) Z _x_{+ 1} x2_{+ 2}_x_{+ 2}dx, u=x 2_{+ 2}_x_{+ 2} (31) Z _x2 x3_{+ 4}dx, u=x 3_{+ 4} ₍₃₂₎ Z ₂_x ₅ x2 ₅_x_{+ 3}dx, u=x 2 ₅_x_{+ 3} (33) Z x+ 6 (x+ 2)2dx, u=x+ 2 (34) Z x (1 +x2₎4dx, u= 1 +x 2 (35) Z ₁ p x(1 +px)dx, u= 1 + p_x ₍₃₆₎ Z x+ 3 x 1dx, u=x 1 (37) Z _x3 (x4_{+ 16)}2dx, u=x 4_{+ 16} ₍₃₈₎ Z x3px2_{+ 1}_dx_, _u₌_x2_{+ 1} (39) Z cos (x) 1 + sin (x)dx, u= 1 + sin (x) (40) Z csc2(x) 1 + cot (x)dx, u= 1 + cot (x) (41) Z _{sin (}p_x₎ p x dx, u=

p_x ₍₄₂₎ Z _{sin (}_x₎p_{cos (}_x₎ _dx_, _u_{= cos (}_x₎

(43) Z _{sin (ln (}_x₎₎ x dx, u= ln (x) (44) Z _{sin (2}_x₎ 4 cos (2x)dx, u= 4 cos (2x) (45) Z _{cos (}_x₎ sin4(x)dx, u= sin (x) (46) Z _sec2₍₂_x₎ 1 + tan (2x)dx, u= 1 + tan (2x) (47) Z

10sin(x)cos (x) dx, u= sin (x) (48)

Z epx p xdx, u= p x (49) Z xpx+ 2dx, u=x+ 2 (50) Z x 3x2+4_dx_, _u₌_x2_{+ 4} (51) Z _{(1 + ln (}_x₎₎10 x dx, u= ln (x) (52) Z ex(4 ex)32 dx, u= 4 ex (53) Z ₁ p 9 x2dx, x= 3 cos (u) (54) Z ₁ xpx2 ₄dx, x= 2 sec (u) (55) Z 1 4 +x2dx, x= 2 tan (u) (56) Z 1 x2_{(1 +}_x 1₎dx, u= 1 +x 1 (57) Z x 3_dx_, _u_{= 1 +}_x 1 ₍₅₈₎ Z x 3p_{3 + 5}_x 2_dx_, _u_{= 3 + 5}_x 2 (59) Z ₄_x ₁ p 4x+ 1dx, u= 4x+ 1 (60) Z _ex_{+ cos (}_x₎ ex_{+ sin (}_x₎dx, u=e x_{+ sin (}_x₎

Dalam soal (61) (80), hitung setiap integral tak tentu menggunakan substitusi yang sesuai. (61) Z _ex ex ₁dx (62) Z _e x 1 +e xdx

(14)

(63) Z ex_{sec (}_ex_{) tan (}_ex₎ _dx ₍₆₄₎ Z _{sin (ln (}_x₎₎ x dx (65) Z esin(x)cos (x) dx (66) Z _eln(x) x dx (67) Z _{ln (}_x₎ x dx (68) Z _{(1 + 2 ln (}_x₎₎4 x dx (69) Z 1 x(1 + 2 ln (x))dx (70) Z (ln (x))32 x dx (71) Z _x2_ln3 _{1 +}_x3 1 +x3 dx (72) Z tan (x) ln (cos (x)) dx (73) Z 4esin(3x)cos (3x) dx (74) Z 3etan(2x)sec2(2x) dx (75) Z _x_{cos ln 1 +}_x2 1 +x2 dx (76) Z tan3(2x) sec2(2x) dx (77) Z 2earcsin(x) p 1 x2 dx (78) Z 4arctan(x) 1 +x2 dx (79) Z ₅arcsec(x) xpx2 ₁dx (80) Z p_{1 +}p x p x dx

1.3 Integrasi Parsial

Aturan hasil kali dari diferensiasi menghasilkan suatu teknik integrasi yang dikenal sebagai integrasi parsial. Dimulai dengan aturan hasil kali:

d dx(u(x)v(x)) = du(x) dx v(x) +u(x) dv(x) dx

atau dapat dituliskan dalam bentuk diferensial menjadi

d[u(x)v(x)] = v(x)du(x)

dx +u(x) dv(x)

dx dx:

Selanjutnya kedua ruas diintegralkan untuk memperoleh

Z d[u(x)v(x)] = Z v(x)du(x) dx dx+ Z u(x)dv(x) dx dx u(x)v(x) = Z v(x)u0(x) dx+ Z u(x)v0(x) dx:

Bentuk baku dari rumus integrasi parsial tersebut dituliskan sebagai

Z

u(x)v0(x) dx=u(x)v(x)

Z

v(x)u0(x) dx

atau disingkat menjadi

Z

u dv=uv

Z

(15)

Dalam hal ini penyelesai dituntut untuk mampu memilihudandv yang tepat sehingga rumus (1.1) bisa diaplikasikan.

Z

xcos (x) dx:

Untuk menghitung integral di atas, diambilu=x dandv = cos (x) dxdengan du=dx

danv=

Z

cos (x) dx= sin (x)+k. Kita menghilangkan konstantak, karena kita hanya memerlukanv(x). Selanjutnya, berdasarkan rumus integrasi parsial(1:1) diperoleh

Z

xcos (x) dx=xsin (x)

Z

sin (x) dx=xsin (x) + cos (x) +c:

Z

x2sin (x) dx:

Untuk menghitung integral di atas, diambil u = x2 dan dv = sin (x) dx dengan du = 2x dx dan v=R sin (x) dx= cos (x). Jadi,

Z x2sin (x) dx = x2cos (x) Z cos (x) 2x dx = x2cos (x) + 2 Z xcos (x) dx

= x2cos (x) + 2 (xsin (x) + cos (x)) +k:

Z

ln (x) dx:

Diambilu= ln (x) dan dv=dxdengan du= 1

xdx danv =x. Jadi, Z ln (x) dx=xln (x) Z x 1 xdx=xln (x) x+k:

Z

x2exdx:

Pertama kali diambil u = x2 dan dv = exdx dengan du = 2x, v =

Z exdx = ex. Diperoleh _Z x2exdx=x2ex Z 2xexdx=x2ex 2 Z xexdx:

(16)

Untuk menghitung integral terakhir, diambil u=x dandv =exdx dengandu=dxdan v=ex. Diperoleh _Z xexdx=xex Z exdx=xex ex+k: Jadi, _Z x2exdx=x2ex 2 (xex ex+k) =ex x2 2x+ 2 +c:

Z

excos (x) dx:

Untuk menghitung integral di atas, diambil u =ex dan dv = cos (x) dx dengan du =

exdx dan v=R cos (x) dx= sin (x). Diperoleh

Z

excosxdx=exsin (x)

Z

exsin (x) dx:

Untuk menghitung integral terakhir, diambil substitusi u = ex dan dv = sin (x) dx

dengan du=ex_dx _dan _v₌ _cos_x_{. Diperoleh}

Z exsin (x) dx= excos (x) Z cos (x) exdx= excos (x) + Z excos (x) dx:

Oleh karena itu, sekarang dipunyai

Z

excos (x) dx=exsin (x) excos (x) +

Z

excos (x) dx

dan selanjutnya kita menggunakan aljabar untuk menyelesaikan integral seperti berikut:

Z

excos (x) dx+

Z

excos (x) dx = exsin (x) +excos (x)

2

Z

excosxdx = exsin (x) +excos (x)

Z

excosxdx = 1 2e

x_{(sin (}_x_{) + cos (}_x_{)) +}_k:

Contoh 1.17 Dicari rumus reduksi untuk integral-integral berikut:

Z xnexdx; Z xnln (x) dx; Z lnn(x) dx; Z xnsin (x) dx; Z xncos (x) dx; Z eax+bsin (px+q) dx; Z eax+bcos (px+q) dx dimanan₂_N.

(17)

(a) Diambilu=xn dan dv =exdx dengan du=nxn 1dxdan v=ex, maka Z xnexdx=xnex Z ex nxn 1 dx: Jadi, Z xnexdx=xnex n Z exxn 1dx:

(b) Diambil u= ln (x) dan dv =xndxdengan du= 1

xdx dan v= 1 n+1x n+1_{, maka} Z xnln (x) dx = ln (x) x n+1 n+ 1 Z _xn+1 n+ 1 1 xdx= xn+1ln (x) n+ 1 1 n+ 1 Z xndx = x n+1_{ln (}_x₎ n+ 1 xn+1 (n+ 1)2 +k: Jadi, Z xnln (x) dx= x n+1 (n+ 1)2 [(n+ 1) ln (x) 1] +k:

(c) Diambil u= lnn(x) dandv =dx dengan du=nlnn 1(x) 1

x dxdan v=x, maka Z lnn(x) dx=xlnn(x) Z x nlnn 1(x) 1 x dx: Jadi, Z lnn(x) dx=xlnn(x) n Z lnn 1(x) dx:

(d) Diambil u = xn dan dv = sin (x) dx dengan du = nxn 1dx dan v = cos (x), maka Z xnsin (x) dx = xncos (x) Z ( cos (x))nxn 1dx = xncos (x) +n Z xn 1cos (x) dx: (1.2)

Untuk menghitung integral terakhir, diambilu=xn 1_dan_dv _{= cos (}_x₎ _dx_dengan du= (n 1)xn 2dx danv= sin (x), maka

Z xn 1cos (x) dx = xn 1sin (x) Z sin (x) (n 1)xn 2dx = xn 1sin (x) (n 1) Z xn 2sin (x) dx: (1.3)

Dengan substitusi (1:3)ke (1:2), diperoleh rumus reduksi

Z

xnsin (x) dx= xncos (x) +nxn 1sin (x) n(n 1)

Z

(18)

(e) Dengan menggunakan (1:3)dan (1:2)diperoleh Z xn 1cos (x) dx = xn 1sin (x) (n 1) Z xn 2sin (x) dx = xn 1sin (x) (n 1) xn 2cos (x) + (n 2) Z xn 3cos (x) dx = xn 1sin (x) + (n 1)xn 2cos (x) (n 1) (n 2) Z xn 3cos (x) dx:

Jika kita menggantin dengan n+ 1 pada persamaan terakhir, maka

Z

xncos (x) dx=xnsin (x) +nxn 1cos (x) n(n 1)

Z

xn 2cos (x) dx:

(f ) Diambil u = sin (px+q) dan dv = eax+b_dx _dengan _du ₌ _p_{cos (}_px₊_q₎ _dx _dan

v= 1 ae ax+b_{, maka} Z eax+bsin (px+q) dx= 1 ae ax+b_{sin (}_px₊_q₎ p a Z eax+bcos (px+q) dx:

Dalam integral terakhir, diambilu= cos (px+q) dandv =eax+bdxdengan du=

psin (px+q) dan v= 1 ae ax+b_{, maka} Z eax+bcos (px+q) dx= 1 ae ax+b_{cos (}_px₊_q_{) +} p a Z eax+bsin (px+q) dx: (1.4)

Karena itu diperoleh

Z eax+bsin (px+q) dx = 1 ae ax+b_{sin (}_px₊_q₎ p a 1 ae ax+b_{cos (}_px₊_q₎ +p a Z eax+bsin (px+q) dx = e ax+b a2 [asin (px+r) pcos (px+q)] p2 a2 Z eax+bsin (px+q) dx:

Dibawa suku terakhir di ruas kanan ke ruas kiri untuk mendapatkan 1 +p 2 a2 Z eax+bsin (px+q) dx= e ax+b a2 [asin (px+q) pcos (px+q)]: Jadi, Z eax+bsin (px+q) dx= e ax+b a2₊_p2 [asin (px+q) pcos (px+q)] +k: (1.5)

(19)

(g) Jika (1:5) disubstitusikan ke (1:4) tanpa konstanta k, diperoleh Z eax+bcos (px+q) dx = 1 ae ax+b_{cos (}_px₊_q₎ +p a eax+b a2₊_p2 [asin (px+q) pcos (px+q)] +k = eax+b 1 acos (px+q) + 1 a2₊_p2 psin (px+q) p2 a cos (px+q) +k: Jadi, Z eax+b_{cos (}_px₊_q₎ _dx₌ eax+b a2₊_p2 [psin (px+q) +acos (px+q)] +k:

SOAL-SOAL UNTUK

SUBBAB

1.3

Untuk soal (1) (6), buktikan setiap rumus dari integral fungsi-fungsi trigonometri invers. Integral diselesaikan pertama kali menggunakan rumus integrasi parsial dengan mengambilu sama dengan fungsi integran.

(1) Z arcsin (x) dx=xarcsin (x) p1 x2₊_k (2) Z arccos (x) dx=xarccos (x) p1 x2₊_k (3) Z arctan (x) dx=xarctan (x) 1 2ln 1 +x 2 ₊_k (4) Z arccot (x) dx=xarccot (x) +1 2ln 1 +x 2 ₊_k (5) Z arcsec (x) dx=xarcsec (x) ln x+px2 _{1 +}_k (6) Z arccsc (x) dx=xarccsc (x) + ln x+px2 _{1 +}_k

Hitung integral-integral berikut ini dan anda bisa menggunakan rumus-rumus reduksi yang sudah diperoleh sebelumnya.

(7) Z xe x dx (8) Z xe 2x dx (9) Z x3ln (x) dx (10) Z xln2(x) dx (11) Z ln3(x) dx (12) Z e2x_{sin (3}_x₎ _dx (13) Z e3xcos (2x) dx (14) Z x2sin (2x) dx (15) Z sin (ln (x)) dx (16) Z xln (x+ 1) dx (17) Z xln3(x) dx (18) Z x2ln (x) dx

(20)

(19) Z x2_ln3₍_x₎ _dx ₍₂₀₎ Z sin2(x) dx (21) Z x3_{sin (}_x₎ _dx (22) Z x3cos (x) dx (23) Z x3cos 2x2 1 dx (24) Z xarccot (x) dx (25) Z xsin2(x) dx (26) Z x3arcsec (x) dx (27) Z xarcsec (x) dx (28) Z x3sin x2 dx (29) Z xsin (x) cos (x) dx (30) Z xarctan (x) dx

1.4 Integral Fungsi Hiperbolik

Rumus-rumus integrasi berikut ini adalah valid:

(a) Z sinh (x) dx= cosh (x) +k (b) Z cosh (x) dx= sinh (x) +k (c) Z tanh (x) dx= ln (cosh (x)) +k (d) Z coth (x) dx= ln_jsinh (x)_j+k (e) Z sech (x) dx= 2 arctan (ex) +k (f) Z csch (x) dx= ln tanh x 2 +k

Setiap rumus di atas dapat secara mudah dibuktikan dengan diferensiasi ruas kanan untuk mendapatkan integran di ruas kiri dan juga mengingat bahwa

sinh (x) = e

x _e x

2 dan cosh (x) =

ex+e x

2 :

Contoh 1.18 Untuk n₂_Ndicari rumus reduksi untuk integral-integral berikut:

Z

sinhn(x) dx dan

Z

coshn(x) dx:

(a) Digunakan rumus integrasi parsial dengan mengambil

u= sinhn 1(x) dan dv = sinh (x) dx;

sehingga diperoleh Z sinhn(x) dx = Z sinhn 1(x) sinh (x) dx = sinhn 1(x) cosh (x) Z

cosh (x) (n 1) sinhn 2(x) cosh (x) dx

= sinhn 1(x) cosh (x) (n 1) Z sinhn 2(x) cosh2(x) dx = sinhn 1(x) cosh (x) (n 1) Z sinhn 2(x) 1 + sinh2(x) dx:

(21)

Karena itu,

Z

sinhn(x) dx = sinhn 1(x) cosh (x)

(n 1)

Z

sinhn 2(x) dx (n 1)

Z

sinhn(x) dx:

Dibawa suku terakhir di ruas kanan ke ruas kiri untuk memperoleh

n

Z

sinhn(x) dx= sinhn 1(x) cosh (x) (n 1)

Z sinhn 2(x) dx: Jadi, Z sinhn(x) dx= 1 nsinh n 1₍_x_{) cosh (}_x₎ (n 1) n Z sinhn 2(x) dx:

(b) Dengan cara yang sama seperti di atas, diambil

u= coshn 1(x) dan dv = cosh (x) dx;

maka Z coshn(x) dx = Z coshn 1(x) cosh (x) dx = coshn 1(x) sinh (x) Z

sinh (x) (n 1) coshn 2(x) sinh (x) dx

= coshn 1(x) sinh (x) (n 1) Z coshn 2(x) sinh2(x) dx = coshn 1(x) sinh (x) (n 1) Z coshn 2(x) cosh2(x) 1 dx = coshn 1(x) sinh (x) (n 1) Z coshn(x) dx + (n 1) Z coshn 2(x) dx:

Dibawa suku kedua di ruas kanan ke ruas kiri untuk memperoleh

n

Z

coshn(x) dx= coshn 1(x) sinh (x) + (n 1)

Z coshn 2(x) dx: Jadi, Z coshn(x) dx= 1 ncosh n 1₍_x_{) sinh (}_x_{) +}(n 1) n Z coshn 2(x) dx:

(22)

SOAL-SOAL UNTUK

SUBBAB

1.4

Untuk soal (1) (2), buktikan setiap rumus reduksi, dimana n ₂ _N, dengan cara menyelesaikan masalah integral menggunakan rumus integrasi parsial.

(1)

Z

xnsinh (x) dx=xncosh (x) nxn 1sinh (x) +n(n 1)

Z

xn 2sinh (x) dx

(2)

Z

xncosh (x) dx=xnsinh (x) nxn 1cosh (x) +n(n 1)

Z

xn 2cosh (x) dx

Hitung setiap integral berikut ini dan anda bisa menggunakan rumus-rumus reduksi yang sudah diperoleh sebelumnya.

(3) Z sinh (3x) dx (4) Z xsinh (x) dx (5) Z xcosh (x) dx (6) Z sech (ax+b) dx (7) Z csch (ax+b) dx (8) Z tanh (ax+b) dx (9) Z coth (ax+b) dx (10) Z sinh (x) cosh (x) dx (11) Z sinh2(x) dx (12) Z cosh2(x) dx (13) Z xcosh2(x) dx (14) Z sinh3(x) dx (15) Z x2sinh (x) dx (16) Z x2cosh (x) dx (17) Z x3sinh (x) dx (18) Z x3cosh (x) dx (19) Z e xsinh (x) dx (20) Z e 2xcosh (2x) dx

1.5 Integral Trigonometri

Seringkali terdapat kemungkinan untuk mentransformasikan suatu integral ke salah satu dari bentuk:

Z sinn(x) dx; Z cscn(x) dx; Z cosn(x) dx; Z secn(x) dx; Z tann(x) dx; Z cotn(x) dx:

Integral-integral tersebut dapat dihitung dengan rumus reduksi yang diperoleh meng-gunakan rumus integrasi parsial seperti dalam contoh-contoh berikut ini.

(23)

Contoh 1.19 Diperhatikan integral tak tentu:

Z

sinn(x) dx:

Diambil

u = sinn 1(x); dv= sin (x) dx;

du = (n 1) sinn 2(x) cos (x) dx; v = cos (x);

maka Z sinn(x) dx = Z sinn 1(x) sin (x) dx = sinn 1(x) ( cos (x)) Z

( cos (x)) (n 1) sinn 2(x) cos (x) dx

= sinn 1(x) cos (x) + (n 1) Z sinn 2(x) 1 sin2(x) dx = sinn 1(x) cos (x) + (n 1) Z sinn 2(x) dx (n 1) Z sinn(x) dx:

Sekarang kita menggunakan aljabar untuk menyelesaikan integral:

Z

sinn(x) dx+ (n 1)

Z

sinn(x) dx = sinn 1(x) cos (x)

+ (n 1)

Z

sinn 2(x) dx

n

Z

sinn(x) dx = sinn 1(x) cos (x)

+ (n 1)

Z

sinn 2(x) dx

sehingga diperoleh rumus reduksi

Z sinn(x) dx= 1 nsin n 1₍_x_{) cos (}_x_{) +}(n 1) n Z sinn 2(x) dx: _(1.6) Untuk n= 2, diperoleh Z sin2(x) dx = 1 2sin (x) cos (x) + 1 2 Z 1 dx= 1 2sin (x) cos (x) + 1 2x+k = 1 2(x sin (x) cos (x)): Untuk n= 3, diperoleh Z sin3(x) dx = 1 3sin 2₍_x_{) cos (}_x_{) +}2 3 Z sin (x) dx = 1 3sin 2₍_x_{) cos (}_x₎ 2 3cos (x) +k:

(24)

Untuk n= 4, diperoleh Z sin4(x) dx = 1 4sin 3₍_x_{) cos (}_x_{) +}3 4 Z sin2(x) dx = 1 4sin 3₍_x_{) cos (}_x_{) +}3 8(x sin (x) cos (x)) +k:

Contoh 1.20 Sekarang diandaikan n= m di persamaan(1:6), maka (n 1) n Z sinn 2(x) dx = 1 nsin n 1₍_x_{) cos (}_x_{) +} Z sinn(x) dx Z sinn 2(x) dx = 1 n 1sin n 1₍_x_{) cos (}_x_{) +} n n 1 Z sinn(x) dx; n₆= 1 Z sin m 2(x) dx = 1 m 1sin m 1₍_x_{) cos (}_x₎ + m m 1 Z sin m(x) dx; m₆= 1 Z cscm+2(x) dx = 1 m+ 1csc m₍_x_{) cot (}_x_{) +} m m+ 1 Z cscm(x) dx; m₆= 1:

Ini memberikan rumus reduksi

Z cscp(x) dx= 1 p 1csc p 2₍_x_{) cot (}_x_{) +}p 2 p 1 Z cscp 2(x) dx; p₆= 1:

Contoh 1.21 Digunakan metode yang serupa dengan Contoh 1.19 untuk menghitung

integral tak tentu _Z

cosn(x) dx:

Diingat bahwa cos (x) = sin

2 x dancos 2 x = sin (x). Karena itu

Z cosn(x) dx = Z sinn 2 x dx; h dimisalkan u= 2 x; du= dx i = Z sinn(u) ( du) = Z sinn(u) du = 1 nsin n 1₍_u_{) cos (}_u_{) +}n 1 n Z sinn 2(u) du = 1 nsin n 1 2 x cos 2 x n 1 n Z sinn 2 2 x ( dx) yang memberikan rumus reduksi

Z cosn(x) dx= 1 ncos n 1₍_x_{) sin (}_x_{) +}n 1 n Z cosn 2(x) dx: _(1.7)

(25)

Contoh 1.22 Sekarang diandaikan n= m di persamaan(1:7), maka Z cos m(x) dx = 1 mcos m 1₍_x_{) sin (}_x_{) +} m 1 m Z cos m 2(x) dx Z secm(x) dx = 1 msec m₍_x_{) tan (}_x_{) +}m+ 1 m Z secm+2(x) dx:

Pada penyelesaian untuk integral terakhir, diperoleh

Z secm+2(x) dx= 1 m+ 1sec m₍_x_{) tan (}_x_{) +} m m+ 1 Z secm(x) dx; m₆= 1

dan pada akhirnya dihasilkan rumus reduksi

Z secp(x) dx= 1 p 1sec p 2₍_x_{) tan (}_x_{) +}p 2 p 1 Z secp 2(x) dx; p₆= 1:

Z

tann(x) dx:

Dicatat bahwa tan2(x) = sec2(x) 1, sehingga dapat dituliskan kembali

Z tann(x) dx = Z tann 2(x) tan2(x) dx= Z tann 2(x) sec2(x) 1 dx = Z tann 2(x) sec2(x) dx Z tann 2(x) dx:

Untuk integral pertama di ruas kanan, diambilu= tan (x) sebagai suatu substitusi.

Z tann(x) dx= Z un 2du Z tann 2(x) dx= u n 1 n 1 Z tann 2(x) dx; n₆= 1:

Oleh karena itu diperoleh rumus reduksi

Z tann(x) dx= tan n 1₍_x₎ n 1 Z tann 2(x) dx; n₆= 1: _(1.8)

Contoh 1.24 Digunakan rumus reduksi tan

2 x = cot (x) di (1:8) untuk mem-peroleh Z cotn(x) dx = Z tann 2 x dx; h dimisalkan u= 2 x; du= dx i = Z tann(u) ( du) = Z tann(u) du = tan n 1₍_u₎ n 1 Z tann 2(u) du ; n₆= 1 = cot n 1₍_x₎ n 1 + Z cotn 2(x) ( dx); n₆= 1::

(26)

Oleh karena itu diperoleh rumus reduksi Z cotn(x) dx= cot n 1₍_x₎ n 1 Z cotn 2(x) dx; n₆= 1:

Selanjutnya, menggunakan identitas sin2(x) + cos2(x) = 1 kita dapat menghitung

integral berbentuk _Z

sinm(x) cosn(x) dx (1.9)

dimana m dan n adalah bilangan-bilangan bulat positif. Aturannya adalah seperti berikut:

(a) Jikam adalah ganjil, maka diambil substitusi u= cos (x). (b) Jikan adalah ganjil, maka diambil substitusiu= sin (x).

(c) Jikam dannadalah genap, maka (1.9) dapat ditransformasikan ke integral jumlahan dari pangkat-pangkat genap untukcos (x) atausin (x).

Dicatat bahwa aturan (a) dan (b) di atas akan mentransformasikan integral ke suatu polinomial dalamu. Sementara itu, dalam aturan (c) perlu digunakan rumus reduksi untuk menyelesaikan integral yang dijumpai.

Z

sin4(x) cos3(x) dx:

Pertama kali dinyatakan

Z

sin4(x) cos3(x) dx =

Z

sin4(x) cos2(x) cos (x) dx

=

Z

sin4(x) 1 sin2(x) cos (x) dx:

Diambil substitusiu= sin (x), du= cos (x) dx, maka

Z sin4(x) cos3(x) dx = Z u4 1 u2 du= 1 5u 5 1 7u 7₊_k = 1 5sin 5₍_x₎ 1 7sin 7₍_x_{) +}_k:

Metode di atas juga bekerja untuk suatu pangkat ganjil darisin (x)dikalikan sembarang pangkat dari cos (x), dan juga sebaliknya.

Z p

(27)

Z p

cos (x) sin3(x) dx = Z pcos (x) sin2(x) sin (x) dx

= Z pcos (x) 1 cos2(x) sin (x) dx:

Diambil substitusiu= cos (x), du= sin (x) dx, maka

Z p cos (x) sin3(x) dx = Z p u 1 u2 ( 1) du= Z u12 +u 5 2 du = 2 3u 3 2 +2 7u 7 2 +k = 2 3cos 3 2 (x) +2 7cos 7 2 (x) +k: Contoh 1.27 Z sin4(x) cos4(x) dx = Z sin4(x) 1 sin2(x) 2dx = Z

sin4(x) 2 sin6(x) + sin8(x) dx:

Sekarang rumus reduksi untuksin (x)dapat digunakan dan ditinggalkan sebagai latihan.

Kita juga dapat menghitung integral-integral berbentuk

Z

tanm(x) secn(x) dx dan

Z

cotm(x) cscn(x) dx:

Aturannya adalah seperti berikut:

(a) Ketika m adalah genap, maka digunakan identitas tan2(x) = sec2(x) 1

untuk integral pertama ataucot2(x) = csc2(x) 1 untuk integral kedua. (b) Jikam adalah ganjil, maka digunakan substitusi u= sec (x) untuk integral

pertama atauu= csc (x) untuk integral kedua.

Dicatat bahwa dalam aturan (a) perlu digunakan rumus reduksisecn₍_x₎ _atau_cscn₍_x₎ untuk menyelesaikan integral yang dijumpai setelah dilakukan substitusi. Sementara itu aturan (b) akan mentransformasikan integral ke suatu polinomial dalamu.

Contoh 1.28 Z tan4(x) sec (x) dx = Z sec2(x) 1 2sec (x) dx = Z

sec5(x) 2 sec3(x) + sec (x) dx:

Sekarang rumus reduksi untuk secn(x) dapat digunakan dan ditinggalkan sebagai lati-han.

(28)

Z

cot3(x) csc3(x) dx:

Z cot3(x) csc3(x) dx = Z cot2(x) csc2(x) (cot (x) csc (x)) dx = Z csc2(x) 1 csc2(x) (cot (x) csc (x)) dx:

Diambil substitusiu= csc (x),du= cot (x) csc (x) dx, maka

Z cot3(x) csc3(x) dx = Z u2 1 u2 du= 1 5u 5 1 3u 3₊_k = 1 5csc 5₍_x_{) +} 1 3csc 3₍_x_{) +}_k:

Berikutnya, dengan menggunakan identitas-identitas trigonometri:

sin (x) cos (y) = 1 2[sin (x y) + sin (x+y)]; sin (x) sin (y) = 1 2[cos (x y) cos (x+y)]; cos (x) cos (y) = 1 2[cos (x y) + cos (x+y)];

kita mendapatkan rumus-rumus integrasi seperti berikut ini:

(1) Z sin (ax) cos (bx) dx= 1 2 cos ((b a)x) b a cos ((b+a)x) b+a +k; a 2 6 =b2 (2) Z sin (ax) sin (bx) dx= 1 2 sin ((b a)x) b a sin ((b+a)x) b+a +k; a 2 6 =b2 (3) Z cos (ax) cos (bx) dx= 1 2 sin ((b a)x) b a + sin ((b+a)x) b+a +k; a 2₆₌_b2

untuk bilangan-bilangan riiladan b:

SOAL-SOAL UNTUK

SUBBAB

1.5

Untuk soal (1) (9), hitung setiap integral yang diberikan dan anda bisa menggunakan rumus-rumus reduksi yang sudah diperoleh sebelumnya.

(1) Z _cos2₍p_x₎ p x dx (2) Z cot2₍_x₎ _dx ₍₃₎ Z sec3₍_x₎ _dx (4) Z cos4(x) dx (5) Z tan5(x) dx (6) Z sec5(x) dx (7) Z csc3(x) dx (8) Z ₁ sin4(x) dx (9) Z sec4(3x 1) dx

(29)

Hitung setiap integral berikut ini. (10) Z sin5(x) cos4(x) dx (11) Z sin3(x) cos5(x) dx (12) Z sin4(x) cos4(x) dx (13) Z sin2(x) cos4(x) dx (14) Z tan5(x) sec4(x) dx (15) Z cot5(x) csc4(x) dx (16) Z tan4(x) sec5(x) dx (17) Z cot4(x) csc5(x) dx (18) Z tan4₍_x_{) sec}4₍_x₎ _dx ₍₁₉₎ Z cot4₍_x_{) csc}4₍_x₎ _dx (20) Z tan3(x) sec3(x) dx (21) Z cot5(x) csc5(x) dx (22) Z sin (x) cos (7x) dx (23) Z sin (2x) cos (3x) dx (24) Z sin (4x) cos (4x) dx (25) Z sin (3x) cos (3x) dx (26) Z sin (2x) sin (3x) dx (27) Z sin (4x) sin (6x) dx (28) Z sin (3x) sin (5x) dx (29) Z cos (3x) cos (5x) dx (30) Z cos (2x) cos (4x) dx

1.6 Substitusi Trigonometri

Integral-integral yang memuat salah satu dari

a2 x2; a2+x2; atau x2 a2 (1.10) seringkali dapat diintegralkan dengan suatu substitusi trigonometri. Idenya adalah mengambil x, a, dan akar kuadrat sebagai sisi-sisi dari suatu segitiga siku-siku dan menggunakan salah satu sudut lancipnya sebagai suatu variabel baru . Terdapat tiga jenis substitusi trigonometri yang diberikan dalam subbab ini.

BENTUK-BENTUK a2 x2. Diandaikan bahwa x = asin ( ) dengan a > 0. Kondisi ini dapat dinyatakan pada suatu segitiga siku-siku seperti berikut:

a θ x 2 2 x a −

(30)

Selanjutnya diperoleh: dx = acos ( ) d ; a2 x2 =a2cos2( ); p a2 _x2 ₌ _a_{cos ( )}_; _{= arcsin} x a ; sin ( ) = x a; cos ( ) = p a2 _x2 a ; tan ( ) = x p a2 _x2; csc ( ) = a x; sec ( ) = a p a2 _x2; cot ( ) = p a2 _x2 x .

Dengan penggunaan substitusi di atas diperoleh rumus-rumus integrasi berikut:

(1) Z _x a2 _x2 dx= 1 2ln a 2 _x2 ₊_k (2) Z ₁ a2 _x2 dx= 1 2aln a x a+x +k (3) Z _x p a2 _x2 dx= p a2 _x2₊_k (4) Z 1 p a2 _x2 dx= arcsin x a +k (5) Z 1 xpa2 _x2 dx= 1 aln a pa2 _x2 x +k (6) Z _p a2 _x2 _dx₌ a 2 2 arcsin x a + 1 2x p a2 _x2₊_k

Z

x3 p

9 x2 dx:

Diambil substitusix= 3 sin ( ), dx= 3 cos ( ) d , maka

Z _x3 p 9 x2 dx = 27 Z _sin3_{( )} p 1 sin2( )cos ( ) d = 27 Z sin3( ) d = 27 1 3sin 2_{( ) cos ( )} 2 3cos ( ) +k = 27 p 9 x2 3 1 3 x2 9 2 3 +k = 9p9 x2 1 27x 2 2 3 +k:

(31)

BENTUK-BENTUK a2 +x2. Diandaikan bahwa x = atan ( ) dengan a > 0. Kondisi ini dapat dinyatakan pada suatu segitiga siku-siku seperti berikut:

x θ a 2 2 x a − Selanjutnya diperoleh: dx = asec2( ) d ; a2+x2 =a2sec2( ); p a2₊_x2 ₌ _a_{sec ( )}_; _{= arctan} x a ; sin ( ) = _p x a2₊_x2; cos ( ) = a p a2₊_x2; tan ( ) = x a; csc ( ) = p a2₊_x2 x ; sec ( ) = p a2₊_x2 a ; cot ( ) = a x.

Dengan penggunaan substitusi di atas diperoleh rumus-rumus integrasi berikut:

(1) Z _x a2₊_x2 dx= 1 2ln a 2₊_x2 ₊_k (2) Z ₁ a2₊_x2 dx= 1 aarctan x a +k (3) Z x p a2₊_x2 dx= p a2₊_x2₊_k (4) Z ₁ p a2₊_x2 dx= ln x+ p a2₊_x2 ₊_k (5) Z ₁ xpa2₊_x2 dx= 1 aln p a2₊_x2 _a x +k (6) Z _p a2₊_x2 _dx₌ a 2 2 ln x+ p a2₊_x2 ₊1 2x p a2₊_x2₊_k

Z ₁

(x2_{+ 2)}2 dx:

Diambil substitusiu=p2 tan ( ), dx=p2 sec2_{( )} _d _{, maka}

Z ₁ (x2_{+ 2)}2 dx = Z p 2 sec2( ) (2 tan2( ) + 2)2 d = p 2 4 Z ₁ sec2_{( )} d = p 2 4 Z cos2( ) d :

(32)

Selanjutnya bisa digunakan rumus reduksi daricosn( ) untuk mendapatkan Z 1 (x2_{+ 2)}2 dx = p 2 4 1 2cos ( ) sin ( ) +k = p 2 4 1 2 p 2 p x2_{+ 2} x p x2_{+ 2} arctan x p 2 ! +k = x 4 (x2_{+ 2)} p 2 4 arctan x p 2 +k:

BENTUK-BENTUK x2 a2. Diandaikan bahwa x = asec ( ) dengan a > 0. Kondisi ini dapat dinyatakan pada suatu segitiga siku-siku seperti berikut:

x θ a 2 2 _a x − Selanjutnya diperoleh

dx = asec ( ) tan ( ) d ; x2 a2 =a2tan2( );

p x2 _a2 ₌ _a_{tan ( )}_; _{= arcsec} x a ; sin ( ) = p x2 _a2 x ; cos ( ) = a x; tan ( ) = p x2 _a2 a ; csc ( ) = _p x x2 _a2; sec ( ) = x a; cot ( ) = a p x2 _a2. Dengan penggunaan substitusi di atas diperoleh rumus-rumus integrasi berikut:

(1) Z x x2 _a2 dx= 1 2ln x 2 _a2 ₊_k (2) Z ₁ x2 _a2 dx= 1 2aln x a x+a +k (3) Z _x p x2 _a2 dx= p x2 _a2₊_k (4) Z 1 p x2 _a2 dx= ln x+ p x2 _a2 ₊_k (5) Z ₁ xpx2 _a2 dx= 1 aarcsec x a +k (6) Z _p x2 _a2 _dx₌ a 2 2 ln x+ p x2 _a2 ₊ 1 2x p x2 _a2₊_k

(33)

Contoh 1.32 Diperhatikan integral tak tentu Z p x2 ₄_x x 2 dx: Dipunyai x2 4x= x2 4x+ 4 4 = (x 2)2 4 =u2 4 dimana kita menggunakan substitusi u=x 2. Karena itu

Z p x2 ₄_x x 2 dx= Z p u2 ₄ u du:

Untuk menghitung integral di ruas kanan, digunakan substitusi trigonometriu= 2 sec ( ),

du= 2 sec ( ) tan ( ) d , maka

Z p u2 ₄

u du =

Z p_{4 sec}2_{( )} ₄

2 sec ( ) 2 sec ( ) tan ( ) d = 2

Z tan2( ) d = 2 (tan ( ) ) +k= 2 p u2 ₄ 2 arcsec u 2 ! +k:

Oleh karena itu, dengan substitusiu=x 2 diperoleh

Z p x2 ₄_x x 2 dx= p x2 ₄_x _{2 arcsec} x 2 2 +k:

Dua contoh berikut ini menunjukkan bagaimana metode pelengkapan kuadrat ( com-pleting the square) digunakan untuk membawa suatu pernyataan kuadratik ke salah satu dari pernyataan di (1.10).

Z

1

p

c+bx ax2 dx, dengan syarata >0 dan D=b

2 ₄_{ac <}₀_.

Pertama kali dilakukan metode pelengkapan kuadrat:

c+bx ax2 = a c a+ b ax x 2 = a c a+ b 2a 2 b 2a 2 + 2 b 2ax x 2 ! = a " c a+ b 2a 2 x b 2a 2# = a h q+p2 (x p)2 i dimanap= b 2a danq = c

a. Karena itu, sekarang dipunyai integral tak tentu

Z ₁ p c+bx ax2 dx= 1 p_a Z ₁ q (q+p2₎ ₍_x _p₎2 dx, dengan syarat p2 < q.

(34)

Untuk menyelesaikan integral terakhir, kita membuat substitusi y = x p, dy = dx, maka _Z 1 q (q+p2₎ ₍_x _p₎2 dx= Z 1 p (q+p2₎ _y2 dy.

Selanjutnya dibuat substitusi y=p(q+p2_{) sin (}_u₎_, _dy₌p₍_q₊_p2_{) cos (}_u₎ _du_{, maka}

Z ₁ p (q+p2₎ _y2 dy = Z p₍_q₊_p2_{) cos (}_u₎ p (q+p2₎ ₍_q₊_p2_{) sin}2₍_u₎du = Z _{cos (}_u₎ p 1 sin2(u)du=u+k = arcsin _p y (q+p2₎ ! +k:

Oleh karena itu,

Z 1 p c+bx ax2 dx= 1 p aarcsin 2a p b2_{+ 4}_ac x b 2a +k:

Z

1

ax2₊_bx₊_c dx, dengan syarat D=b

2 ₄_{ac <}₀_.

Dilakukan metode pelengkapan kuadrat:

ax2+bx+c = a x2+ b ax+ c a = a x2+ 2 b 2ax+ b 2a 2 b 2a 2 + c a ! = a " x+ b 2a 2 + c a b 2a 2!# = ah(x+p)2+ q p2 i dimanap= b 2a danq = c

a. Karena itu, sekarang dipunyai integral tak tentu

Z ₁ ax2₊_bx₊_c dx= 1 a Z ₁ (x+p)2+ (q p2₎ dx, dengan syarat p 2 _{< q}_.

Untuk menyelesaikan integral terakhir, kita membuat substitusi y = x+p, dy = dx,

maka _Z

1

(x+p)2+ (q p2₎ dx=

Z ₁

(35)

Selanjutnya dibuat substitusi y=p(q p2_{) tan (}_u₎_, _dy₌p₍_q _p2_{) sec}2₍_u₎ _du_{, maka} Z ₁ y2_{+ (}_q _p2₎dy = Z p₍_q _p2_{) sec}2₍_u₎ (q p2_{) tan}2₍_u_{) + (}_q _p2₎du = _p 1 (q p2₎ Z _sec2₍_u₎ tan2₍_u_{) + 1}du= 1 p (q p2₎u+k = _p 1 (q p2₎arctan y p (q p2₎ ! +k:

Oleh karena itu,

Z ₁ ax2₊_bx₊_c dx= 2 p 4ac b2arctan 2a p 4ac b2 x+ b 2a +k:

S

OAL-SOAL UNTUK

S

UBBAB

1.6

Hitung integral-integral berikut ini.

(1) Z x p 4 x2 dx (2) Z 1 p 4 x2 dx (3) Z x 4 x2 dx (4) Z ₁ 4 x2 dx (5) Z _x 9 +x2 dx (6) Z ₁ 9 +x2 dx (7) Z _x p 9 +x2 dx (8) Z ₁ p 9 +x2 dx (9) Z _x x2 ₁₆ dx (10) Z ₁ x2 ₁₆ dx (11) Z _x p x2 ₁₆ dx (12) Z ₁ p x2 ₁₆ dx (13) Z 1 xpx2 ₄ dx (14) Z 1 xp9 x2 dx (15) Z dx xpx2_{+ 16} (16) Z _p 9 x2 _dx ₍₁₇₎ Z _p 4 9x2 _dx ₍₁₈₎ Z _x2 p 1 x2 dx (19) Z _x2 p 4 +x2 dx (20) Z _x2 p x2 ₁₆ dx (21) Z ₁ (9 +x2₎2 dx (22) Z 1 (9 x2₎2 dx (23) Z 1 (x2 ₁₆₎2 dx (24) Z 1 (4 +x2₎32 dx (25) Z p 4 +x2 x dx (26) Z p x2 ₄ x dx (27) Z ₁ x2p_x2_{+ 4} dx (28) Z ₁ x2p₄ _x2 dx (29) Z ₁ x2p_x2 ₄ dx (30) Z ₁ x2 ₂_x_{+ 5} dx (31) Z ₁ x2 ₄_x_{+ 12} dx (32) Z ₁ p 4x x2 dx (33) Z _dx p x2 ₄_x_{+ 12}

(36)

(34) Z ₁ 4x x2 dx (35) Z _dx p x2 ₂_x_{+ 5} (36) Z _x x2 ₄_x ₁₂ dx (37) Z _{x dx} p x2 ₂_x_{+ 5} (38) Z _{x dx} x2_{+ 4}_x_{+ 13} (39) Z _p 5 4x x2 _dx (40) Z ₂_x_{+ 7} x2_{+ 4}_x_{+ 13}dx (41) Z _x_{+ 3} p x2_{+ 2}_x_{+ 5}dx (42) Z ₁ p 4x2 ₁ dx (43) Z x+ 4 p 9x2_{+ 16} dx (44) Z x+ 2 p 16 9x2 dx (45) Z 1 p 6x 4x2dx (46) Z ₁ p 4x x2 dx (47) Z ₁ p 9x 4x2 dx (48) Z _dx p 8x 25x2 (49) Z _x p 4x x2 dx (50) Z _dx p x2 ₂_x_{+ 8} (51) Z _dx p 3 + 4x 4x2 (52) Z x dx p 6 +x 2x2 (53) Z x x2₊_x_{+ 1}dx (54) Z 1 x2_{+ 3}_x_{+ 5}dx (55) Z _dx 3x2 ₁₂_x_{+ 16} (56) Z _dx 12x2_{+ 56}_x_{+ 72} (57) Z ₈_dx 9x2 ₁₂_x_{+ 20} (58) Z ₍_x_{+ 1)} 1 p x2_{+ 2}_x ₈dx (59) Z ₍₃_x_{+ 1)} 1 p 3x2_{+ 2}_x ₅dx (60) Z _e2x _dx p 5 e2x₊_e4x

1.7 Integral Fungsi Rasional

Pada subbab ini didiskusikan masalah integrasi fungsi rasional berbentuk

R(x) = P(x)

Q(x);

dimanaP(x) danQ(x)adalah polinomial yang tidak mempunyai faktor persekutuan. Idenya adalah menuliskan kembali fungsi rasional sebagai suatu jumlahan dari pecahan lebih sederhana yang dinamakan pecahan parsial. Ini dapat dilakukan dengan cara seperti berikut:

(1) Jika derajat dari P(x) lebih besar atau sama dengan derajat dari Q(x), maka digunakan pembagian panjang dari polinomial untuk mendapat suatu hasil bagi

p(x) dan suatu sisa r(x), sehingga fungsi rasional dituliskan kembali sebagai

R(x) = P(x)

Q(x) =p(x) +

r(x)

Q(x)

dimana derajat darir(x)lebih kecil dari pada derajat dari Q(x).

(2) Faktorisasi penyebut: Q(x) = q1(x)q2(x): : : qk(x), dimana setiap faktor qi(x) mempunyai bentuk linierax+b, atau kuadratikirreducible(tidak bisa difaktorkan lagi)ax2+bx+c, atau suatu pangkat berbentuk(ax+b)natau ax2+bx+c n.

(3) r(x)

Q(x) dinyatakan sebagai jumlahan dari pecahan-pecahan parsial. Jika (ax+b) n

(37)

suku-suku berikut: A1 ax+b+ A2 (ax+b)2 +:::+ An (ax+b)n;

dimanaA1,A2, ...,Anadalah konstanta-konstanta tertentu. Jika muncul bentuk

ax2+bx+c m, jumlahan dari pecahan parsial akan memuat

B1x+C1 ax2₊_bx₊_c + B2x+C2 (ax2₊_bx₊_c₎2 +:::+ Bmx+Cm (ax2₊_bx₊_c₎m;

dimanaB1,B2, ..., Bm dan C1,C2, ..., Cm adalah konstanta-konstanta tertentu.

Pecahan parsial bertipe A

(ax+b)n secara mudah diintegralkan menggunakan Aturan

Pangkat _Z un dx= 1 n+ 1u n+1₊_{k; n} 6 = 1; dan Z 1 udu= lnjuj+k:

Pecahan parsial bertipe Bx+C

(ax2₊_bx₊_c₎m dapat diintegralkan seperti berikut.

Pertama kali penyebut dibagi olehamsehingga pecahan mempunyai bentuk lebih seder-hana:

Bx+C am₍_x2₊_b

1x+c1)m :

Jika dilakukan pelengkapan kuadrat dengan membuat substitusi u = x+ 1₂b1, kita memperoleh x2+b1x+c1 =u2+ c1 1 4b 2 1 =u2+k2;

dimanak=c1 1₄b21. Sekarang integral mengambil bentuk lebih sederhana:

1 am Z _Bu₊_C (u2₊_k2₎m du= 1 am Z _Bu (u2₊_k2₎m du+ 1 am Z _C (u2₊_k2₎m du:

Integral pertama di ruas kanan dapat dihitung dengan mengambil w=u2₊_k2_,_dw ₌

2u du. Integral kedua dapat dihitung dengan substitusi trigonometri u = ktan ( ), yang akhirnya diselesaikan menggunakan rumus reduksi untukcos (x).

Untuk mencari pecahan parsial, kita harus menyelesaikan untuk konstanta-konstanta tak diketahui Ai, Bi, dan Ci. Dalam tiga contoh pertama berikut ini ditunjukkan bagaimana hal tersebut dilakukan.

Contoh 1.35 Diperhatikan fungsi rasional 5x+ 17

x2 ₃_x ₁₀:

Pertama kali kita memfaktorkan penyebut:

(38)

Karena terdapat dua faktor linear, maka haruslah dibentuk jumlahan dari dua pecahan parsial: 5x+ 17 x2 ₃_x ₁₀ = A x+ 2+ B x 5:

Cara kita mencari A dan B adalah dengan menggunakan (x+ 2) (x 5)sebagai suatu penyebut persekutuan sehingga pembilang dari kedua ruas persamaan adalah sama.

5x+ 17

x2 ₃_x ₁₀ =

A(x 5) +B(x+ 2) (x+ 2) (x 5) 5x+ 17 = A(x 5) +B(x+ 2):

Penyelesaian untuk A dan B dapat dicari dengan memsubstistusikan sembarang dua nilaix (untuk kemudahan biasanya diambil akar-akar dari penyebut):

x= 2 =₎ 5 ( 2) + 17 =A ( 7) + 0 =₎ A= 1;

x= 5 =₎ 5 5 + 17 = 0 +B 7 =₎ B = 6:

Oleh karena itu,

5x+ 17 x2 ₃_x ₁₀ = 1 x+ 2+ 6 x 5:

Contoh 1.36 Diperhatikan fungsi rasional 2x3+x+ 1

x4_{+ 2}_x3₊_x2:

Faktorisasi dari penyebut yaitu

x4+ 2x3+x2=x2 x2+ 2x+ 1 =x2(x+ 1)2:

Karena terdapat empat faktor linear (tidak harus berbeda), maka dibentuk jumlahan dari empat pecahan parsial:

2x3+x+ 1 x4_{+ 2}_x3₊_x2 = A x + B x2 + C x+ 1+ D (x+ 1)2: Disamakan penyebut dari kedua ruas untuk memperoleh:

2x3+x+ 1

x4_{+ 2}_x3₊_x2 =

Ax(x+ 1)2+B(x+ 1)2+Cx2(x+ 1) +Dx2 x2₍_x_{+ 1)}2

2x3+x+ 1 = Ax(x+ 1)2+B(x+ 1)2+Cx2(x+ 1) +Dx2:

Penyelesaian untukA,B,C, danD dapat dicari dengan memsubstistusikan sembarang empat nilaix:

x= 0 =₎ 0 + 0 + 1 = 0 +B+ 0 + 0 =₎ B = 1;

x= 1 =₎ 2 + ( 1) + 1 = 0 + 0 + 0 +D =₎ D= 2;

x= 1 =₎ 2 + 1 + 1 = 4A+ 4 + 2C+ ( 2) =₎ 2A+C = 1;

x= 2 =₎ 16 + 2 + 1 = 18A+ 9 + 12C+ ( 8) =₎ 3A+ 2C= 3:

Penyelesaian untuk dua persamaan terakhir yaituA= 1 danC= 3. Oleh karena itu, 2x3+x+ 1 x4_{+ 2}_x3₊_x2 = 1 x + 1 x2 + 3 x+ 1+ 2 (x+ 1)2:

(39)

Contoh 1.37 Diperhatikan fungsi rasional

x4_{+ 4}_x3_{+ 11}_x2_{+ 12}_x_{+ 8}

(x+ 1) (x2_{+ 2}_x_{+ 3)}2 :

Karena terdapat tiga faktor, maka dibentuk jumlahan dari tiga pecahan parsial:

x4+ 4x3+ 11x2+ 12x+ 8 (x+ 1) (x2_{+ 2}_x_{+ 3)}2 = A x+ 1+ Bx+C x2_{+ 2}_x_{+ 3}+ Dx+E (x2_{+ 2}_x_{+ 3)}2:

Disamakan penyebut dari kedua ruas untuk memperoleh:

x4+ 4x3+ 11x2+ 12x+ 8 =

A x2+ 2x+ 3 2+ (Bx+C) (x+ 1) x2+ 2x+ 3 + (Dx+E) (x+ 1):

Penyelesaian untuk A, B, C, D dan E dapat dicari dengan memsubstistusikan sem-barang lima nilaix:

x= 1 =₎ 1 4 + 11 12 + 8 = 4A =₎ A= 1; x= 0 =₎ 0 + 0 + 0 + 0 + 8 = 9A+ 3C+E =₎ 3C+E = 1; x= 1 =₎ 1 + 4 + 11 + 12 + 8 = 36A+ 12 (B+C) + 2 (D+E) =₎ 6 (B+C) +D+E = 0; x= 2 =₎ 16 + 32 + 44 + 24 + 8 = 121A+ 33 (2B+C) + 3 (2D+E) =₎ 11 (2B+C) + 2D+E= 1; x= 2 =₎ 16 32 + 44 24 + 8 = 9A 3 ( 2B+C) ( 2D+E) =₎ 3 ( 2B+C) ( 2D+E) = 3:

Penyelesaian untuk empat persamaan terakhir yaituB =C = 0, D= 1, dan E = 1. Oleh karena itu,

x4+ 4x3+ 11x2+ 12x+ 8 (x+ 1) (x2_{+ 2}_x_{+ 3)}2 = 1 x+ 1+ x 1 (x2_{+ 2}_x_{+ 3)}2:

Sekarang kita siap untuk menghitung integral dari fungsi pecah rasional.

Z

x3+ 4x2 1

x+ 2 dx:

Karena derajat dari pembilang lebih besar dari pada penyebut, maka langkah pertama adalah membagi pembilang dengan penyebut menggunakan pembagian panjang. Hasil-nya adalah

x3+ 4x2 1

x+ 2 =x

2_{+ 2}_x _{4 +} 7 x+ 2:

Sekarang dengan mudah kita dapat mengintegralkan setiap suku dalam jumlahan.

Z x3+ 4x2 1 x+ 2 dx = Z x2+ 2x 4 + 7 x+ 2 dx = 1 3x 3₊_x2 ₄_x_{+ 7 ln} jx+ 2_j+k:

(40)

Z ₅_x_{+ 17}

x2 ₃_x ₁₀ dx:

Karena pembilang mempunyai derajat yang lebih kecil dibandingkan dengan penyebut, maka tidak perlu dilakukan pembagian panjang. Dari hasil di Contoh 1.35 dipunyai

5x+ 17 x2 ₃_x ₁₀ = 1 x+ 2+ 6 x 5; maka Z 5x+ 17 x2 ₃_x ₁₀ dx = Z 1 x+ 2 dx+ Z 6 x 5 dx = ln_jx+ 2_j+ 6 ln_jx 5_j+k:

Contoh 1.40 Dengan menggunakan hasil di Contoh 1.36,

Z ₂_x3₊_x_{+ 1} x4_{+ 2}_x3₊_x2 dx = Z ₁ x dx+ Z ₁ x2 dx+ Z ₃ x+ 1 dx+ Z ₂ (x+ 1)2 dx = ln_jx_j 1 x + 3 ln (x+ 1) + 2 x+ 1+k.

Contoh 1.41 Dengan menggunakan hasil di Contoh 1.37,

Z _x4_{+ 4}_x3_{+ 11}_x2_{+ 12}_x_{+ 8} (x+ 1) (x2_{+ 2}_x_{+ 3)}2 dx = Z ₁ x+ 1 dx+ Z _x ₁ (x2_{+ 2}_x_{+ 3)}2 dx = ln_jx+ 1_j+ Z _x ₁ (x2_{+ 2}_x_{+ 3)}2 dx:

Dengan membuat substitusiu=x+1₂ 2 =x+ 1, dipunyaix2_{+ 2}_x_{+ 3 =}_u2_{+ 2}_{. Karena}

itu Z _x ₁ (x2_{+ 2}_x_{+ 3)}2 dx= Z _u ₂ (u2_{+ 2)}2 du= Z _u (u2_{+ 2)}2 du+ Z ₂ (u2_{+ 2)}2 du:

Integral pertama di ruas kanan dihitung dengan mengambil w=u2+ 2, dw = 2u du, maka Z _u (u2_{+ 2)}2 du= 1 2 Z ₂_u (u2_{+ 2)}2 du= 1 2 Z ₁ w2 dw = 1 2w = 1 2 (u2_{+ 2)}:

Integral kedua dihitung dengan substitusi trigonometri u = p2 tan ( ), dan dengan menggunakan hasil di Contoh 1.31 diperoleh bahwa

Z ₂ (u2_{+ 2)}2 du= 2 " u 4 (u2_{+ 2)} p 2 4 arctan u p 2 # :

Terakhir, dengan substitusi baliku=x+ 1didapatkan

Z _x4_{+ 4}_x3_{+ 11}_x2_{+ 12}_x_{+ 8} (x+ 1) (x2_{+ 2}_x_{+ 3)}2 dx = lnjx+ 1j 1 2 (x2_{+ 2}_x_{+ 3)} 2 " x+ 1 4 (x2_{+ 2}_x_{+ 3)} p 2 4 arctan x+ 1 p 2 # +k:

(41)

SOAL-SOAL UNTUK

SUBBAB

1.7

(1) Z 1 (x 1) (x 2) (x+ 4) dx (2) Z 1 (x 4) (10 +x) dx (3) Z ₁ (x a) (x b) dx (4) Z ₁ (x a) (b x) dx (5) Z ₁ (x2_{+ 1) (}_x2_{+ 4)} dx (6) Z ₁ (x 1) (x2_{+ 1)} dx (7) Z 2x x2 ₅_x_{+ 6} dx (8) Z x (x+ 3) (x+ 4) dx (9) Z _x_{+ 1} (x+ 2) (x2_{+ 4)} dx (10) Z _x_{+ 2} (x+ 3) (x2_{+ 1)} dx (11) Z ₂ (x2_{+ 4) (}_x2_{+ 9)} dx (12) Z ₁ (x2 _{4) (}_x2 ₉₎ dx (13) Z _x2 (x2_{+ 4) (}_x2_{+ 9)} dx (14) Z _x (x2 _{4) (}_x2 ₉₎ dx (15) Z x 4 (x2_{+ 4) (}_x_{+ 1)} dx (16) Z 1 x2 ₅_x_{+ 4} dx (17) Z ₁ x4 ₁₆ dx (18) Z _x x4 ₈₁ dx (19) Z _x3₊_x2_{+ 2} x2 ₁ dx (20) Z _x3 _x2 ₇_x_{+ 8} x2 ₄_x_{+ 4} dx (21) Z _x6 ₂ x4₊_x2 dx (22) Z _x2₊_x ₃ x3 ₂_x2 _x_{+ 2} dx (23) Z x5+ 2x4+ 4x3+x+ 1 x2₊_x_{+ 1} dx (24) Z x2+ 3x 1 x4₊_x3₊_x2₊_x dx (25) Z ₂_x3 ₁₁_x2_{+ 17}_x ₁₆ x4 ₄_x3_{+ 5}_x2 ₄_x_{+ 4} dx (26) Z _{9 + 6}_x_{+ 2}_x2₊_x3 4 +x2 dx

1.8 Integral Fungsi Irasional

Terdapat dua bentuk irasional yang akan didiskusikan dalam subbab ini. Dengan sub-stitusi yang sesuai, masalah integrasi dibawa menjadi integrasi fungsi rasional.

Jika integran memuat satu atau lebih pangkat-pangkat pecahan berbentuk xsr, maka masalah integrasinya bisa diselesaikan dengan membuat substitusi x = un _dimana _n adalah kelipatan persekutuan terkecil (disingkat KPK) dari penyebut-penyebut dalam pangkat pecahan. Dengan substitusi tersebut, masalah integral dibawa menjadi inte-grasi fungsi rasional.

(42)

Z p3_x 1 +px dx:

Karena KPK dari3 dan 2 adalah 6, maka dibuat substitusi x=u6, dx= 6u5du, dan

Z p3_x 1 +px dx = Z p3 u6 1 +pu66u 5_du₌ Z u2 1 +u36u 5_du = 6 Z u7 1 +u3du:

Sekarang dipunyai masalah integrasi fungsi rasional dan untuk penyelesaiannya diting-galkan sebagai latihan.

Z p

x+p3x2

5 +p4_x dx:

Karena KPK dari2, 3, dan4adalah12, maka dibuat substitusix=u12, dx= 12u11du, dan Z p x+p3x2 5 +p4_x dx = Z p_u12₊q3 (u12₎2 5 +p4u12 12u 11_du_{= 12} Z u6+u8 5 +u3 u 11_du = 12 Z u17+u19 5 +u3 du:

Penyelesaian untuk integrasi fungsi rasional di ruas kanan ditinggalkan sebagai latihan.

Jika integran hanya memuat bentuk

s

ax+b

px+q; dengan a; p6= 0;

maka dibuat substitusi u =

r

ax+b

px+q. Hubungan antara du dan dx dicari seperti

berikut: u2 = ax+b px+q =) u 2₍_px₊_q_{) =}_ax₊_b ₌ ) x pu2 a =b qu2 =₎ x= b qu 2 pu2 _a =) dx= 2qu pu2 a b qu2 2pu (pu2 _a₎2 du:

(43)

Z r_x_{+ 1}

x+ 2 dx: Jika dibuat substitusi

u = r x+ 1 x+ 2; dan dx = 4u u 2 ₁ ₁ ₂_u2 ₂_u (u2 ₁₎2 du= 2u (u2 ₁₎2 du, maka diperoleh Z r_x_{+ 1} x+ 2 dx= Z u 2u (u2 ₁₎2 du= 2 Z _u2 (u2 ₁₎2 du:

Penyelesaian untuk integrasi fungsi rasional di ruas kanan ditinggalkan sebagai latihan.

S

OAL-SOAL UNTUK

S

UBBAB

1.8

Hitung setiap integral berikut ini menggunakan substitusi yang diberikan. (1) Z 4x32 1 +x13 dx; x=u6 (2) Z 1 1 +x13 dx; x=u3 (3) Z ₁ p 1 +e2x dx; u 2 _{= 1 +}_e2x ₍₄₎ Z ₁ xpx3 ₈ dx; u 2 ₌_x3 ₈

Hitung setiap integral berikut ini menggunakan suatu substitusi yang sesuai. (5) Z x p x+ 2 dx (6) Z x2 p x+ 4 dx (7) Z 1 4 +px dx (8) Z _x 1 +px dx (9) Z p_x 1 +p3_x dx (10) Z _x2 3 8 +x12 dx (11) Z ₁ x23 + 1 dx (12) Z ₁ 1 +px dx (13) Z _x 1 +x23 dx (14) Z _{1 +}p x 2 +px dx (15) Z ₁ p x 1 +x32 dx (16) Z _{1 +}p x 1 x32 dx (17) Z r 3x 2 4x+ 3 dx (18) Z r 1 +1 x dx (19) Z r 1 1 x dx (20) Z ₁ x r lnx ln (x) 1 dx

(44)

1.9 Substitusi

tan

1₂

x

Jika integran memuat suatu pernyataan berbentuk (a+bsin (x)) atau (a+bcos (x)), maka substitusi berikut bisa membantu dalam penghitungan integral. Substitusi akan mentransformasikan integran ke bentuk rasional.

BENTUK (a+bsin (x)) atau (a+bcos (x)). Diandaikan bahwa u = tan 1₂x , maka dipunyai sin (x) = 2u 1 +u2; cos (x) = 1 u2 1 +u2; dan dx= 2 1 +u2 du: Lebih lanjut, (1) Z ₁ a+bsin (x) dx= Z 2 1+u2 a+b₁₊2_u2 du= Z ₂ a(1 +u2_{) + 2}_bu du (2) Z ₁ a+bcos (x) dx= Z 2 1+u2 a+b1₁₊u_u22 du= Z ₂ a(1 +u2_{) +}_b₍₁ _u2₎ du

Z ₁

1 + sin (x) + cos (x) dx:

Jika dibuat substitusiu= tan 1₂x , dx= 2

1 +u2 du, maka Z 1 1 + sin (x) + cos (x) dx = Z 1 1 + 2u 1 +u2 + 1 u2 1 +u2 2 1 +u2 du = Z ₂ 1 +u2_{+ 2}_u_{+ 1} _u2 du = Z ₂ 2 + 2u du= Z ₁ 1 +u du = ln_j1 +u_j+k = ln 1 + tan 1 2x +k:

SOAL-SOAL UNTUK

SUBBAB

1.9

(1) Z ₁ 2 + sin (x) dx (2) Z ₁ 2 sin (x) dx (3) Z ₁ 4 + cos (x) dx (4) Z ₁ sin (x) + cos (x) dx (5) Z ₁ sin (x) cos (x) dx (6) Z ₁ 2 sin (x) + 3 cos (x) dx

(45)

(7) Z ₁ 3 + cos (x) dx (8) Z ₁ 3 cos (x) dx (9) Z _{sin (}_x₎ sin (x) + cos (x) dx (10) Z _{cos (}_x₎ sin (x) cos (x) dx (11) Z _{1 + sin (}_x₎ 1 sin (x) dx (12) Z ₁ _{cos (}_x₎ 1 + cos (x) dx (13) Z 2 + cos (x) 2 cos (x) dx (14) Z 2 cos (x) 2 + cos (x) dx (15) Z ₂ _{sin (}_x₎ 3 + cos (x) dx

(46)

Integral Tentu

2.1 Integral Riemann

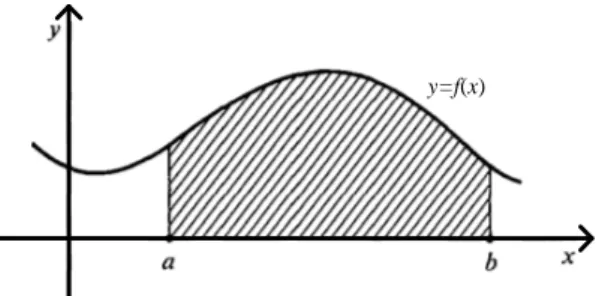
Di sini kita mencoba untuk mencari luas bidang datar dari daerah di bawah kurva

y=f(x)dariasampaib, dimanaf adalah suatu fungsi kontinu, seperti dalam Gambar 2.1.

y=f(x)

Gambar 2.1: Daerah di bawah suatu kurva.

Untuk menaksir luas bidang datar, kita mulai dengan membagi interval [a; b] menjadi

ninterval bagian:

[x0; x1];[x1; x2];[x2; x3]; :::;[xn 1; xn] yang mempunyai lebar sama x= b a

n (sehingga xi =a+i x). Titik-titik x0,x1,

...,xn dinamakan titik-titik diskrit.

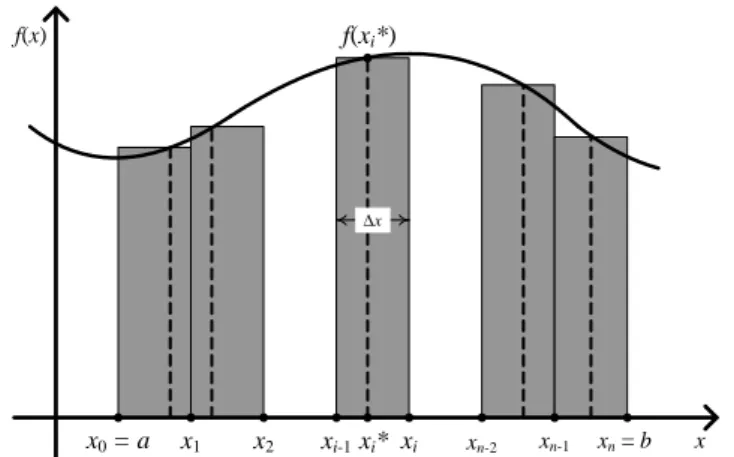
Pada setiap interval bagian [xi 1; xi], kita membentuk persegi panjang dengan tinggi

f(x_i), dimanax_i ₂[xi 1; xi], lihat Gambar 2.2. Persegi panjang ke-iakan mempunyai luas

f(x_i) x:

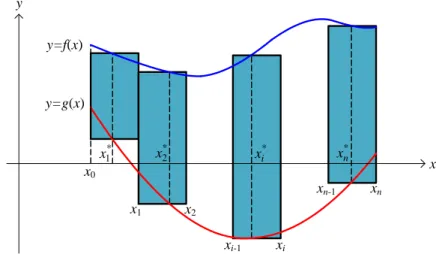
Dari Gambar 2.2, kita bisa melihat bahwa jumlah dari luas semua persegi panjang ham-pir mendekati luas daerah di bawah kurva. Jumlahan ini dinamakan suatu Jumlahan Riemann dan sama dengan

n

X

i=1

f(x_i) x=f(x₁) x+f(x₂) x+ +f(x_n) x:

(47)

x0= a x1 x2 xi-1xi* xi f(xi*) f(x) x xn=b xn-1 xn-2 x ∆

Gambar 2.2: Persegi-persegi panjang di bawah suatu kurva.

Kita bisa memperkenalkan luas eksak dari bidang datar di bawah gra…kf(x) dengan limit: A= lim n!1 n X i=1 f(x_i) x:

Ketika f adalah kontinu, nilai limit tidak tergantung dari titik-titik sampel x_i yang digunakan.

Limit tersebut dinyatakan oleh

Z b a

f(x) dx, dan dinamakan integral tentu (de…nite integral) untukf dari asampai b:

Z b a f(x) dx= lim n!1 n X i=1 f(x_i) x:

Berikut ini diberikan suatu contoh bagaimana bagaimana menghitung integral tentu secara langsung dari de…nisi.

Contoh 2.1 Dicari nilai dari integral tentu

Z 1 0

x2dx:

Kita membagi interval[0;1]menjadinsubinterval dengan lebar sama, sehingga x= 1

n

dan xi =

i

n. Berikutnya kita harus memilih suatu titik xi dalam setiap subinterval

[xi 1; xi]. Di sini kita akan menggunakan titik ujung kanan dari setiap subinterval,

x_i = i

n, lihat Gambar 2.3(a). Aturan ini dinamakan Aturan Sisi Kanan. Karena itu

jumlahan Riemann yang berasosiasi dengan partisi tersebut adalah

R= n X i=1 i n 2 1 n = 1 n3 n X i=1 i2 = 1 n3 2n3+ 3n2+n 6 = 2n3+ 3n2+n 6n3 :

(48)

Jadi, _Z 1 0 x2dx= lim n!1 2n3+ 3n2+n 6n3 = 1 3:

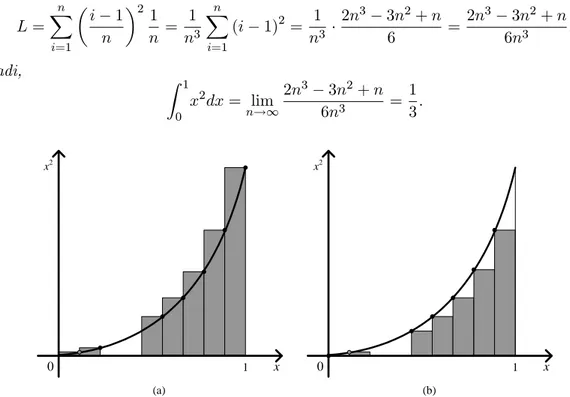
Untuk memeriksa bahwa hasil tidak tergantung pada titik-titik sampel yang digunakan, diulangi penghitungan menggunakan titik ujung kiri dari setiap subinterval, lihat Gam-bar 2.3(b). Aturan ini dinamakan Aturan Sisi Kiri. Hasilnya adalah

L= n X i=1 i 1 n 2 1 n = 1 n3 n X i=1 (i 1)2= 1 n3 2n3 3n2+n 6 = 2n3 3n2+n 6n3 : Jadi, Z 1 0 x2dx= lim n!1 2n3 3n2+n 6n3 = 1 3: 0 x2 x 1 0 x2 x 1 (a) (b)

Gambar 2.3: Jumlahan Riemann: (a) Aturan Sisi Kanan; (b) Aturan Sisi Kiri.

SOAL-SOAL UNTUK

SUBBAB

2.1

Dalam Soal 1 24, hitung jumlahan Riemann menggunakan Aturan Sisi Kanan. Di-gunakan notasi

b

X

a

untuka dan b menyatakan bahwa subinterval pertama dimulai di

adan subinterval akhir berakhir dib. (1) 1 X 0 (3x+ 1) x; x= 1₃ (2) 1 X 0 (3x+ 1) x; x= 2₅ (3) 1 X 1 (3x+ 1) x; x= 1₄ (4) 1 X 0 2x2 x; x= 1₄ (5) 1 X 1 2x2 x; x= 1₄ (6) 5 X 0 (2x 1) x; x= 1 (7) 5 X 0 (2x 1) x; x= 2 (8) 1 X 1 x2 1 x; x= 1₂ (9) 2 X 0 x2 1 x; x= 1₂ (10) 1 X 1 x2 1 x; x= ₁₀3