TESIS
Diajukan untuk memenuhi sebagian syarat memperoleh gelar Magister Pendidikan Program Studi Pendidikan Matematika
oleh Puji Yulianti NIM 1308104
PROGRAM STUDI PENDIDIKAN MATEMATIKA SEKOLAH PASCASARJANA
UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG
2015
IMPLEMENTASI PENDEKATAN METAKOGNITIF DAN PROBLEM POSING DALAM PENCAPAIAN KEMAMPUAN PEMECAHAN MASALAH
DAN SELF-EFFICACY MATEMATIS SISWA
Oleh Puji Yulianti
S.Pd. Universitas Prof. DR. Hamka (Uhamka), 2000
Sebuah Tesis yang diajukan untuk memenuhi salah satu syarat memperoleh gelar Magister Pendidikan (M.Pd.) pada Program Studi Matematika
© Puji Yulianti 2015 Universitas Pendidikan Indonesia
Agustus 2015
Hak Cipta dilindungi undang-undang.
Tesis ini tidak boleh diperbanyak seluruhnya atau sebagian, dengan dicetak ulang, difotokopi, atau cara lainnya tanpa ijin dari penulis. DALAM PENCAPAIAN KEMAMPUAN PEMECAHAN MASALAH
DAN SELF-EFFICACY MATEMATIS SISWA
LEMBAR PENGESAHAN
PUJI YULIANTI
Disetujui dan disahkan oleh pembimbing Pembimbing
Prof. Dr. Wahyudin, M.Pd. NIP. 195108081974121001
Mengetahui
Ketua Program Studi Pendidikan Matematika
DR. Sufyani Prabawanto, M.Ed NIP.196008301986031003
IMPLEMENTASI PENDEKATAN METAKOGNITIF DAN PROBLEM POSING DALAM PENCAPAIAN KEMAMPUAN PEMECAHAN MASALAH
DAN SELF-EFFICACY MATEMATIS SISWA
ABSTRAK
Puji Yulianti (2015): Implementasi Pendekatan Metakognitif dan Problem Posing Dalam Pencapaian Kemampuan Pemecahan Masalah dan Self- Efficacy Matematis Siswa (Studi Eksperimen terhadap Salah Satu SMP Swasta di Jakarta)
Penelitian ini bertujuan untuk menelaah perbedaan capaian Kemampuan Pemecahan Masalah Matematis (KPMM) dan Self-Efficacy Matematis (SEM) antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing. Penelitian ini merupakan penelitian kuasi eksperimen dengan desain penelitian perbandingan kelompok statik. Subjek penelitian adalah siswa kelas VIII salah satu SMP swasta di Jakarta terdiri dari dua kelas yakni 33 siswa diberi pendekatan pembelajaran metakognitif dan 36 siswa diberi pendekatan pembelajaran problem posing. Hasil analisis data diketahui bahwa: (1) ada perbedaan capaian KPMM yang signifikan antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing; (2) berdasarkan KAM: tidak ada perbedaan capaian KPMM yang signifikan antara kelompok siswa kategori tinggi yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing, namun untuk kelompok siswa kategori sedang dan rendah masing-masing disimpulkan ada perbedaan capaian KPMM yang signifikan antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing; (3) ada perbedaan capaian KPMM yang signifikan siswa yang memperoleh pendekatan pembelajaran metakognitif berdasarkan KAM; (4) ada perbedaan capaian KPMM yang signifikan siswa yang memperoleh pendekatan pembelajaran problem posing berdasarkan KAM; (5) tidak ada pengaruh interaksi yang signifikan antara faktor pendekatan pembelajaran dan KAM dalam capaian KPMM siswa; (6) ada perbedaan capaian SEM yang signifikan antara siswa yang memperoleh pendekatan pembelajaran metakognitif dan problem posing; (7) berdasarkan KAM: kelompok siswa kategori tinggi dan rendah masing-masing disimpulkan tidak ada perbedaan capaian SEM yang signifikan antara kelompok siswa yang memperoleh pendekatan pembelajaran metakognitif dan problem posing, namun ada perbedaan capaian SEM yang signifikan antara kelompok siswa kategori sedang yang memperoleh pendekatan pembelajaran metakognitif dan problem posing.
ABSTRACT
Puji Yulianti (2015): Implementation of Metacognitive and Problem Posing Approach In Achievement Problem Solving Ability and Mathematical Self-Efficacy (Experimental Study on One Private School in Jakarta)
This study aimed to analyze the differences in achievement mathematical problem solving ability and self-efficacy between students in acquiring mathematical learning by metacognitive and problem posing approach. This study is a quasi-experimental by using statics comparison group design. Subjects in this study were students of class VIII in one private junior high school in Jakarta. Research samples were taken in two classes consists of 33 students who were given a metacognitive approach and 36 students were given a problem posing approach learning. Results analysis of the data showed that: (1) there is a significant difference achievement of mathematical problem solving ability between the students who obtain a learning metacognitive and problem posing approach; (2) Based on Early Mathematical Ability: there is no significant difference in achievement of mathematical problem solving ability on group of students who obtain a learning by metacognitive and problem posing approach but there are significant differences in achievement of mathematical problem solving ability for groups of students with medium and low categories; (3) There is a significance of achievements of mathematical problem solving ability for the group of students categories of high, medium, and low on learning by metacognitive approach (4) there is a significant difference of achievements of mathematical problem solving ability on student group categories of high, medium, and low on learning by problem posing approach; (5) there is no influences interaction together a significant between learning approaches factor and early mathematical ability in mathematical problem solving ability ’s student achievement; (6) there is a significant differences mathematical self-efficacy between students who received learning by metacognitive and problem posing approach; (7) Based on early mathematical ability: there was no significant difference on matehmatical self-efficacy between groups of high categories of students who obtain a metacognitive and problem posing approach; the same with groups of low catagories of students. But there is a significant differences for groups of medium students who obtain a metacognitive and problem posing approach.
Keywords: metacognitive approach, problem posing approach, mathematical problem
solving ability, and mathematical self-efficacy
DAFTAR ISI
LEMBAR PENGESAHAN
PERNYATAAN ... i
UCAPAN TERIMA KASIH ... ii
PERSEMBAHAN ... iv
KATA PENGANTAR ... v
ABSTRAK ... vi
DAFTAR ISI ... viii
DAFTAR GAMBAR ... xi
DAFTAR TABEL ... xi
DAFTAR LAMPIRAN ... xiii
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah ... 1
1.2 Rumusan Masalah ... 9
1.3 Tujuan Penelitian ... 10
1.4 Manfaat Penelitian ... 11
1.5 Definisi Operasional ... 12
BAB II KAJIAN PUSTAKA 2.1 Pemecahan Masalah ... 14
2.1.1 Pemecahan Masalah sebagai Proses Kognitif ... 14
2.1.2 Kemampuan Pemecahan Masalah Matematis ... 15
2.2 Self-Efficacy 2.2.1 Pengertian Self-Efficacy ... 23
2.2.2 Self-Efficacy Matematis dan Skala Perngukurannya ... 27
2.3 Teori Belajar Pendukung ... 30
2.4 Pendekatan Metakognitif ... 32
2.4.1 Pengertian Metakognisi ... 32
2.4.2 Pembelajaran Matematika dengan Pendekatan Metakognitif 35
2.5 Pendekatan Problem Posing ... 40
2.7 Kerangka Berpikir ... 45
2.8 Hipotesis Penelitian ... 48
BAB III METODE PENELITIAN 3.1 Desain Penelitian ... 49
3.2 Populasi dan Sampel Penelitian ... 51
3.3 Instrumen Penelitian... 51
3.3.1 Instrumen Tes Kemampuan Awal Matematis (KAM) ... 51
3.3.2 Instrumen Tes Kemampuan Pemecahan Masalah Matematis (KPMM) ... 51
3.3.3 Instrumen Angket Skala Self-Efficacy Matematis (SEM) ... 58
3.3.4 Instrumen Perangkat Pembelajaran ... 59
3.4 Prosedur Penelitian ... 61
3.5 Teknik Analisis Data ... 62
BAB IV HASIL PENELITIAN DAN PEMBAHASAN 4.1 Analisis Data Hasil Penelitian ... 70
4.1.1 Analisis Data Hasil Tes KAM Siswa... 70
4.1.2 Analisis Data Hasil Tes KPMM Siswa Berdasarkan Pendekatan Pembelajaran ... 72
4.1.3 Analisis Data Hasil Tes KPMM Siswa Berdasarkan Kategori KAM ... 74
4.1.4 Analisis Data Hasil Tes KPMM Siswa Berdasarkan Kategori KAM setiap Pendekatan Pembelajaran ... 76
4.1.5 Interaksi antara Pendekatan Pembelajaran dan KAM dalam Capaian KPMM ... 79
4.1.6 Analisis Angket Skala Self-Efficacy Matematis Siswa ... 80
4.2 Pembahasan Hasil Penelitian ... 86
4.2.1 Capaian Kemampuan Pemecahan Masalah Matematis Siswa berdasarkan Pendekatan Pembelajaran ... 87
4.2.3 Capaian Self-Efficacy Matematis Siswa ... 93
4.2.4 Hasil Observasi Guru oleh Observer ... 95
4.3 Keterbatasan Penelitian ... 96
BAB V SIMPULAN, IMPLIKASI, DAN REKOMENDASI 5.1 Simpulan ... 98
5.2 Implikasi ... 100
5.3 Rekomendasi ... 102
DAFTAR PUSTAKA ... 101
DAFTAR GAMBAR
Gambar 2.1 Jalinan kinerja Human Learning, Gagne (1983) ... 15
DAFTAR TABEL Tabel 2.1 Aspek Pemecahan Masalah, Indikator, dan Kompetensi Pencapaiannya ... 21
Tabel 2.2 Penskoran pada proses pemecahan masalah ... 22
Tabel 2.3 Indonesian Adaptation of General Self-efficacy Scale ... 28
Tabel 2.4 Karakteristik tinggi rendahnya Self-Efficacy ... 28
Tabel 2.5 Aspek penilaian self-efficacy dan indikator pencapaian ... 29
Tabel 2.6 Hubungan fase pemecahan masalah dan fungsi metakognitif 37 Tabel 2.7 Kartu pemantauan metakognitif bentuk RC ... 38
Tabel 2.8 Komponen metakognitif, tipe, dan terminologi ... 39
Tabel 3.1 Keterkaitan antara kemampuan/skala yang diukur berdasarkan pendekatan pembelajaran dan kategori KAM ... 50
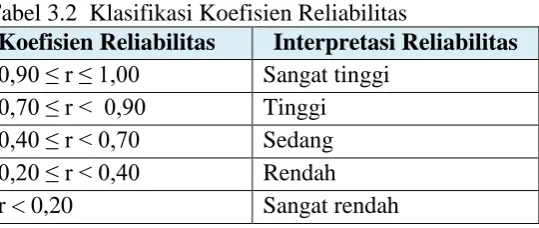
Tabel 3.2 Klasifikasi koefisien reliabilitas ... 54
Tabel 3.3 Koefisien r hasil uji coba tes KAM dan tes KPMM ... 54
Tabel 3.4 Klasifikasi koefisien validitas ... 54
Tabel 3.5 Validitas butir soal hasil uji coba tes KAM ... 55
Tabel 3.6 Validitas butir soal hasil uji coba tes KPMM ... 56
Tabel 3.7 Indeks kesukaran sebuah tes ... 56
Tabel 3.8 Indeks daya pembeda sebuah tes ... 57
Tabel 3.9 Indeks kesukaran dan daya pembeda hasil ujicoba tes KAM 57 Tabel 3.10 Indeks kesukaran dan daya pembeda hasil ujicoba tes KPMM 58 Tabel 3.11 Hipotesis penelitian dan jenis uji statistik yang digunakan .... 62
Tabel 4.1 Data hasil tes KAM pada dua kelompok eksperimen... 70
Tabel 4.4 Pengelompokkan siswa berdasarkan data hasil tes KAM... 72
Tabel 4.5 Data hasil tes KPMM pada dua kelompok eksperimen ... 72
Tabel 4.6 Data hasil uji asumsi tes KPMM siswa ... 73
Tabel 4.7 Data hasil uji beda rata-rata tes KPMM siswa ... 73
Tabel 4.8 Data hasil tes KPMM siswa berdasarkan pendekatan pembelajaran dan faktor KAM ... 74
Tabel 4.9 Data hasil uji asumsi tes KPMM berdasarkan pendekata5 dan faktor KAM ... 74
Tabel 4.10 Data hasil uji beda rata-rata tes KPMM berdasarkan pendekatan pembelajaran dan faktor KAM ... 75
Tabel 4.11 Data hasil uji asumsi tes KPMM siswa berdasarkan KAM pada setiap pendekatan pembelajaran ... 76
Tabel 4.12 Data hasil uji anava satu jalur KPMM kelompok siswa kategori KAM dengan pendekatan pembelajaran metakognitif ... 77
Tabel 4.13 Multiple comparisons hasil uji Scheffe (Pendekatan Metakognitif) ... 77
Tabel 4.14 Data hasil uji anava satu jalur KPMM kelompok siswa kategori KAM dengan pendekatan pembelajaran problem posing... 78
Tabel 4.15 Multiple Comparisons hasil uji Scheffe (Pendekatan Problem Posing)... 78
Tabel 4.16 Data hasil uji asumsi dan tes KPMM berdasarkan pendekatan pembelajaran dan faktor KAM ... 78
Tabel 4.17 Data hasil uji anava dua jalur tes KPMM berdasarkan pendekatan pembelajaran dan faktor KAM... 80
Tabel 4.18 Data skor angket skala self-efficacy matematis (SEM) siswa 81 Tabel 4.19 Data skor angket skala self efficacy matematis (SEM) siswa berdasarkan KAM ... 84
Tabel 4.20 Data hasil uji asumsi angket skala SEM berdasarkan pendekatan pembelajaran ... 82
Tabel 4.22 Data hasil uji asumsi angket skala SEM berdasarkan KAM 83
Tabel 4.23 Data hasil uji t angket skala SEM kelompok siswa
kategori sedang dan rendah ... 83
Tabel 4.24 Data hasil uji Mann Whitney angket skala SEM kelompok siswa kategori tinggi ... 84
Tabel 4.25 Rangkuman hasil pengujian hipotesis KPMM dan KAM 85 Tabel 4.26 Persentase hasil angket skala self-efficacy matematis siswa 94 TABEL LAMPIRAN LAMPIRAN A Lampiran A.1 Peta konsep garis singgung lingkaran ... 111
Lampiran A.2 RPP dan LKS pendekatan metakognitif ... 112
Lampiran A.3 RPP dan LKS pendekatan problem posing ... 146
Lampiran A.4 Format lembar observasi aktivitas siswa ... 179
Lampiran A.5 Format lembar observasi aktivitas guru ... 183
LAMPIRAN B Lampiran B.1 Kisi-kisi tes kemampuan awal matematis siswa ... 187
Lampiran B.2 Soal tes kemampuan awal matematis siswa ... 193
Lampiran B.3 Analisis data hasil ujicoba tes KAM siswa ... 197
Lampiran B.4 Rekap hasil ujicoba tes KAM siswa ... 207
Lampiran B.5 Data hasil tes KAM siswa (pembelajaran dengan pendekatan metakognitif) ... 208
Lampiran B.6 Data hasil tes KAM siswa (Pembelajaran dengan pendekatan problem posing) ... 209
Lampiran C.2 Soal tes kemampuan pemecahan masalah matematis siswa 217 Lampiran C.3 Rubrik penilaian tes kemampuan awal matematis siswa 218 Lampiran C.4 Analisis data hasil ujicoba tes kemampuan pemecahan masalah matematis siswa ... 221 Lampiran C.5 Data hasil tes kemampuan pemecahan masalah matematis siswa (pembelajaran dengan pendekatan metakognitif) ... 226 Lampiran C.6 Data hasil tes kemampuan pemecahan masalah matematis siswa (pembelajaran dengan pendekatan problem posing) ... 228 Lampiran C.7 Analisis uji statistik data hasil tes KPMM ... 230 Lampiran C.8 Analisis uji statistik data hasil tes KPM kelompok siswa
kategori tinggi ... 234 Lampiran C.9 Analisis uji statistik data hasil tes KPMM kelompok siswa Kategori sedang ... 238 Lampiran C.10 Analisis uji statistjuyd hasil tes KPMM
kelompok siswa kategori rendah ...’ 242 Lampiran C.11 Analisis uji anava satu jalur tes KPMM siswa
(pembelajaran dengan pendekatan metakognitif) ... 246 Lampiran C.12 Analisis uji asumsi dan uji anava satu jalur tes KPMM siswa (pembelajaran dengan pendekatan problem posing) ... 250 Lampiran C.13 Analisis uji anava dua jalur data hasil tes KPMM... 253 LAMPIRAN D
(Pembelajaran dengan pendekatan problem posing) ... 278
Lampiran D.8 Analisis uji statistik data hasil angket skala SEM siswa berdasarkan pendekatan pembelajaran ... 286
Lampiran D.9 Analisis uji statistik data hasil angket skala SEM siswa berdasarkan KAM... 289
Lampiran D.10 Persentase capaian self- efficacy matematis siswa ... 296
LAMPIRAN E Lampiran E.1 Jadwal penelitian ... 297
Lampiran E.2 Dokumentasi penelitian (kegiatan siswa) ... 298
Lampiran E.3 Rekaman jawaban tes KPMM siswa ... 310
Lampiran E.4 Rekaman catatan perencanaan belajar siswa ... 318
Lampiran E.5 Lembar observasi aktivitas siswa (pembelajaran dengan pendekatan metakognitif) ... 321
Lampiran E.6 Lembar observasi aktivitas siswa (pembelajaran dengan pendekatan problem posing) ... 327
Lampiran E.7 Rekap hasil observasi aktivitas guru ... 333
BAB I
PENDAHULUAN
1.1 Latar Belakang Masalah
Matematika sebagai ilmu yang universal mempunyai peranan penting dalam kehidupan dan perkembangan ilmu pengetahuan di berbagai disiplin ilmu. Setiap disiplin ilmu memerlukan keterampilan matematika yang sesuai sebagai upaya memecahkan masalah yang dihadapi dalam kehidupan sehari-hari dan ketercapaian kecakapan hidup. Menilik betapa pentingnya matematika dalam kehidupan, maka dipandang perlu mengajarkan matematika kepada siswa sejak dini melalui proses pendidikan.
Sebagaimana tercantum dalam Permendikbud No. 58 Tahun 2014, proses pendidikan dikatakan sebagai proses perubahan kognitif, afektif, dan psikomotorik kearah kedewasaan sesuai dengan kebenaran logika. Proses perubahan ketiga aspek itu tercermin dalam proses pembelajaran matematika. Proses pembelajaran matematika memberikan kesempatan kepada siswa untuk mengembangkan potensi dirinya dan meningkatkan kemampuan mengkonstruksi pengetahuan. Schoenfeld (2013) menyatakan bahwa proses pembelajaran matematika di tingkat kelas menfokuskan pada empat standar kemampuan, yakni pemecahan masalah, penalaran, komunikasi dan koneksi.
2
Pemecahan masalah sebagai proses aktivitas mental yang paling tinggi dalam pembelajaran matematika dapat membantu siswa belajar konsep dan keterampilan intelektual. Siswa harus didorong untuk terlibat dalam pemecahan masalah matematis agar mereka terbantu memahami lebih lanjut arti dari pengetahuan yang diperoleh sehingga dapat memfasilitasi transfer pengetahuan dalam skenario kehidupan nyata.. Hal ini sejalan dengan pendapat Schoenfeld (2013) yang menyatakan bahwa tujuan utama siswa belajar pemecahan masalah adalah agar siswa belajar matematika karena matematika bukan hanya belajar fakta dan prosedur tetapi juga belajar bagaimana siswa dapat mengajukan dan menyelesaikan masalah.
Terkait mengenai pemecahan masalah sebagai proses aktivitas mental dalam pembelajaran matematika, kemampuan pemecahan masalah matematis menjadi salah satu fokus yang diajarkan di sekolah. Omrod (2009a) menyatakan bahwa siswa mengerjakan pemecahan masalah jika guru telah melakukan apa yang seharusnya dikerjakan. Siswa memandang pemecahan masalah matematis sebagai usaha yang cepat dan tidak memerlukan pemikiran. Hal ini sejalan dengan fenomena yang terjadi pada siswa di tingkat Sekolah Menengah Pertama (SMP).
Ajang kompetisi matematika merupakan wadah pengembangan potensi bagi siswa yang memiliki kemampuan berpikir tingkat tinggi. Hal ini dikarenakan soal-soal pada ajang kompetisi tersebut merupakan jenis soal pemecahan masalah. Dari tujuh SMP Negeri dan 21 SMP swasta di kecamatan Cilandak Jakarta Selatan, hanya sedikit SMP negeri dan swasta yang mewakili wilayah sampai ke babak final. Berdasarkan data dari MGMP provinsi DKI Jakarta, diketahui sejak tahun 2010 tidak lebih dari dua SMP baik negeri maupun swasta yang mewakili wilayah kecamatan Cilandak sampai ke babak final.
Berikut contoh soal kompetisi matematika Provinsi DKI Jakarta babak penyisihan yang merupakan kategori soal pemecahan masalah.
Soal 1.
Diketahui xy= 42, yz = 63, dan xz = 54. Nilai x2 + y2+ z2 adalah ....
Soal 2.
Gambar disamping adalah tiga buah kaleng cat yang dililit oleh
sebuah plester. Jika panjang diameter masing-masing kaleng cat
14 cm, maka panjang plester minimal yang diperlukan untuk
dililitkan pada ketiga kaleng cat itu adalah ....
Kedua soal diatas merupakan soal tidak rutin terkait materi kelas VII dan VIII. Soal pertama adalah soal kelas VII materi bilangan bulat. Soal kedua adalah soal kelas VIII materi garis singgung lingkaran. Soal pertama dapat diselesaikan dengan terlebih dahulu mencari Faktor Persekutuan Terbesar (FPB) dan soal kedua adalah soal sabuk lilitan yang dapat diselesaikan dengan terlebih dahulu
merepresentasikan masalah kedalam gambar berikut. Kemudian siswa dapat menyelesaikan masalah dengan cara:
3(2r) + 3(120o x keliling lingkaran) = 6r + keliling lingkaran 360o
Bukti empiris tersebut diperkuat dengan beberapa hasil penelitian yang menunjukkan persoalan pemecahan masalah. Persoalan pemecahan masalah matematis sudah sejak lama menjadi perhatian khusus untuk diteliti. Gagne (1983) menyatakan bahwa makalah dari National Council of Teachers of Mathematics (NCTM) yang dibacanya mengenai pemecahan masalah ternyata
sudah terlebih dahulu dijabarkan dalam penelitiannya.
2r 2r
120º 120º
4
Lester sudah 20 tahun lalu melakukan penelitian tentang pemecahan masalah. Hingga saat ini, konsentrasi Lester tetap konsisten pada penelitian tentang pemecahan masalah. Lester (2013) menyatakan bahwa pemecahan masalah memerlukan kedekatan pengetahuan pedagogis dan keahlian guru dalam pengambil keputusan untuk mengembangkan kemampuan pemecahan masalah siswa. Selain itu, kemampuan pemecahan masalah merupakan salah satu tolok ukur pencapaian kompetensi dalam kajian Trends in International Mathematics and Science Study (TIMSS) dan Program for International Student Assessment
(PISA). Hal ini diidentifikasi dari soal-soal TIMSS dan PISA yang merupakan jenis soal pemecahan masalah.
Menurut Garofalo & Lester (1985) dan Silver (dalam Kuzle, 2013), rendahnya kinerja pemecahan masalah siswa bukan karena ketidakcukupan konten pengetahuan matematika dan fakta, tetapi lebih dikaitkan dengan ketidakmampuan siswa untuk menganalisis masalah, memahami, menilai kecukupan informasi yang diberikan, mengatur pengetahuan dan fakta-fakta yang mereka miliki dengan tujuan menyusun rencana, mengevaluasi kelayakan pelaksanaan rencana yang disusun sebelumnya, dan mengevaluasi kewajaran hasilnya. Newell, Shaw, & Simon (1958) memprediksi kinerja pemecah masalah dalam menangani tugas-tugas tertentu melibatkan penggunaan berulang informasi yang tersedia untuk memulai eksplorasi, pada gilirannya mengungkapkan informasi lebih lanjut sampai ditemukan cara penyelesaian akhir.
Self-efficacy sebagai mediasi pemecahan masalah matematis (Pajares &
Miller, 1994) memiliki peran sentral dalam kontribusi pembelajaran yang memotivasi seseorang untuk belajar (Bandura, 1994). Schunk (1987) dan Bandura (1994) menyatakan bahwa siswa cenderung akan termotivasi untuk mencoba melakukan tugas sendiri jika mereka mengamati keberhasilan orang lain terhadap tugas tersebut. Sebaliknya, siswa yang mengamati orang lain gagal dapat menyebabkan mereka tidak memiliki kompetensi untuk berhasil.
Self-efficacy dan sistem kepercayaan siswa pada daya dan kegunaan
matematika dapat dipengaruhi oleh keberagaman latar belakang pengetahuan mereka (Omrod, 2009a), gender, dan pengalaman sebelumnya pada mekanisme umum (Pajares & Miller, 1994). Selanjutnya, Omrod (2009a) menyatakan bahwa keberagaman semacam itu secara alamiah akan mempengaruhi kemampuan mereka dalam menyelesaikan tugas-tugas yang melibatkan pemikiran tingkat tinggi. Pajares (dalam Ramdass & Zimmerman, 2008) menyatakan bahwa ketika penilaian self-efficacy dibuat khusus untuk sebuah tugas, maka mereka dapat memprediksi kinerja yang lebih baik dari tindakan konsep diri.
Bandura (1994) menyatakan bahwa perasaan self-efficacy yang kuat akan membuat semakin tinggi tujuan dan komitmen. Siswa yang memiliki rasa keberhasilan tinggi akan memvisualisasikan skenario sukses yang memberikan panduan positif dan mendukung kinerja. Sedangkan siswa yang meragukan keberhasilan akan menvisualisasikan skenario kegagalan dan memikirkan banyak hal yang salah. Hal ini diperkuat oleh bukti empiris hasil kajian PISA tahun 2012 yang memberikan informasi bahwa self-efficacy matematis memiliki hubungan kuat dengan kinerja.
6
Kuzle (2013) menjelaskan bahwa proses metakognitif diperlukan dalam proses pemecahan masalah dan perubahan perilaku afektif seperti ketekunan, kegigihan, keyakinan, dan frustrasi. Perilaku afektif akan berubah selama proses pemecahan masalah, dan berhubungan dengan keberhasilan siswa ketika memecahkan masalah. Dalam situasi transisi, tindakan metakognitif paling sering ditangani pada saat tahap pemecahan masalah sebagai hasil dari umpan balik.
Mokos & Kafoussi (2013) memberikan kontribusi hasil studinya bahwa setiap jenis masalah akan memunculkan strategi metakognitif secara spontan yang ditandai dengan pengakuan siswa terhadap jenis masalah matematika. Hal ini dapat membantu guru untuk menekankan sejumlah aspek strategi metakognitif siswa, dan merancang rencana intervensi dalam rangka meningkatkan fungsi kontrol metakognitif utamanya dalam masalah yang kompleks. Mevarech & Arami (dalam Mokos & Kaffoussi, 2013) menyatakan bahwa melalui bimbingan metakognitif dalam kelompok kecil, siswa dapat memperoleh kinerja pemecahan masalah yang baik dan menciptakan masalah lingkungan sosial yang interaktif.
Dalam pemantauan metakognitif, Zimmerman & Schunk (dalam Ramdass & Zimmerman, 2008) menyatakan bahwa perencanaan strategis dan keyakinan self-efficacy merupakan prekursor pemikiran untuk belajar atau kinerja. Tahap
kinerja melibatkan proses, seperti penerapan strategi pembelajaran dan pemantauan metakognitif. Lester (2013) berpandangan bahwa kegiatan matematika memberikan peran menonjol dalam aktivitas metakognitif baik oleh individu maupun kelompok. Kegiatan rutin dan terus menerus adalah fitur kunci keberhasilan pada tugas-tugas matematika yang kompleks.
Pendekatan berikutnya yang dianggap dapat meningkatkan kemampuan pemecahan masalah adalah pendekatan problem posing. Pendekatan problem posing menekankan hubungan antara ide-ide matematika dan aktivitas
pembelajaran matematika. Aktivitas pembelajaran matematika dengan pendekatan problem posing dapat merangsang berpikir tingkat tinggi dan berpikir divergen
(Ghasempour, Bakar, & Jahanshahloo, 2013), sehingga membantu siswa dalam menguasai kemampuan pemecahan masalah (Silver, 1994).
Pendekatan problem posing dapat membantu siswa dalam berkreasi tentang suatu ide baru dari materi yang sedang dipelajari. Siswa harus diberi kesempatan untuk mengajukan pertanyaan atau membuat soal. Siswa dituntut memahami soal itu dengan baik sebagai tahap awal dalam pemecahan masalah. Keterkaitan ini diperkuat dengan hasil penelitian Abu-Elwan (1999) yang menunjukkan bahwa efektivitas strategi pengajuan atau pembuatan soal (problem posing) dapat meningkatkan kemampuan pemecahan masalah. Lebih lanjut
Abu-Elwan menyatakan bahwa siswa yang memiliki kemampuan rendah dapat mengembangkan kemampuan pemecahan masalah melalui bekerja secara kooperatif.
Brown & Walter (2005) menyatakan bahwa fokus pada problem posing dapat memberikan kesempatan siswa untuk memperoleh kualitas pengembangan kemampuan dalam menerima dan mengubah masalah. Secara alami, ketika siswa memulai memecahkan masalah dengan pertanyaan (posing) yang sederhana, kemudian pertanyaan itu dikembangkan lebih spesifik,”apa yang terjadi jika tidak?”, bagaimana jika seharusnya?” dapat diprediksi siswa akan memiliki kebiasaan menciptaan masalah baru atau memodifikasi masalah.
Selain dapat membantu dalam menguasai kemampuan pemecahan masalah, pendekatan problem posing juga berpengaruh terhadap perasaan self-efficacy matematis (Akay & Boz, 2010). Silver (1994) menyatakan bahwa
8
Berdasarkan uraian tentang pendekatan metakognitif dan pendekatan problem posing, kedua pendekatan ini dipandang sebagai pendekatan yang
diperkirakan dapat digunakan dalam capaian kemampuan pemecahan masalah matematis dan memiliki hubungan dengan perasaan self-efficacy. Untuk menciptakan kebermaknaan dalam proses pembelajaran dengan penerapan pendekatan pembelajaran tersebut maka faktor kemampuan awal matematis siswa perlu menjadi bahan pertimbangan. Menurut Suryadi (2005) kemampuan matematika siap pakai yang dimiliki siswa menjadi salah satu faktor yang harus menjadi perhatian guru agar tercipta proses pembelajaran matematika yang memberikan hasil optimal.
Kemampuan Awal Matematis (KAM) merupakan kemampuan yang dapat menjadi dasar untuk menerima pengetahuan baru. Dalam teori belajar bermakna, Ausubel & Fitzgerald (1961) menyatakan bahwa belajar bermakna timbul jika siswa dapat mencoba menghubungkan pengetahuan baru dengan pengetahuan sebelumnya yang dimiliki. Prajitno & Mulyatini (dalam Murni, 2013) menyatakan bahwa kemampuan siswa untuk mempelajari ide-ide baru bergantung pada pengetahuan awal mereka dan struktur kognitif yang sudah ada. Struktur kognitif tersebut berfungsi untuk mengaitkan antara konsep dan prosedur.
Omrod (2009a) menyatakan bahwa matematika bersifat hirarkis, yakni konsep dan prosedur yang kompleks merupakan pengembangan dari konsep yang lebih sederhana dan prosedur yang lebih mendasar. Konsep sederhana dan prosedur yang lebih mendasar didapat dari pengetahuan awal yang dimiliki siswa. Semakin sering siswa memanggil informasi dari pengetahuan awal semakin mudah mereka memanggil informasi baru yang diperlukan (Schunk, 1987) sehingga hubungan ini dapat meningkatkan prestasi matematika siswa secara dramatis (Trianto, 2011).
pembelajaran yang digunakan dengan kemampuan awal matematis yang siswa miliki. Dengan demikian, studi ini berfokus pada penerapan pendekatan pembelajaran yang diperkirakan dapat memberikan capaian kemampuan pemecahan masalah dan self-efficacy matemaits siswa lebih optimal. Oleh karena studi ini dilaksanakan di Sekolah Menengah Pertama (SMP) maka judul penelitiannya adalah “Implementasi Pendekatan Metakognitif dan Problem Posing dalam Pencapaian Kemampuan Pemecahan Masalah dan Self-Efficacy
Matematis Siswa (Studi Eksperimen terhadap Salah Satu SMP Swasta di Jakarta)”
1.2 Rumusan masalah
Berdasarkan latar belakang masalah di atas, masalah dalam penelitian ini dirumuskan sebagai berikut.
1. Apakah terdapat perbedaan capaian kemampuan pemecahan masalah matematis antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing?
2. Berdasarkan KAM:
a. Apakah terdapat perbedaan capaian kemampuan pemecahan masalah matematis kelompok siswa yang memiliki KAM tinggi antara yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing?
b. Apakah terdapat perbedaan capaian kemampuan pemecahan masalah matematis kelompok siswa yang memiliki KAM sedang antara yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing?
10
3. Apakah terdapat perbedaan capaian kemampuan pemecahan masalah matematis antara siswa yang memiliki KAM tinggi, sedang, dan rendah yang memperoleh pembelajaran dengan pendekatan metakognitif?
4. Apakah terdapat perbedaan capaian kemampuan pemecahan masalah matematis antara siswa yang memiliki KAM tinggi, sedang, dan rendah yang memperoleh pembelajaran dengan pendekatan problem posing?
5. Apakah terdapat pengaruh interaksi antara faktor pendekatan pembelajaran (metakognitif dan problem posing) dan KAM terhadap capaian kemampuan pemecahan masalah matematis siswa?
6. Apakah terdapat perbedaan capaian self-efficacy matematis antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing?
7. Apakah terdapat perbedaan capaian self-efficacy matematis antara siswa yang memiliki KAM tinggi, sedang, dan rendah yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing?
1.3 Tujuan Penelitian
Berdasarkan rumusan masalah di atas, tujuan penelitian ini adalah untuk menelaah pencapaian siswa terkait kemampuan pemecahan masalah dan self-efficacy matematis akibat diterapkan pendekatan metakognitif dan problem
posing. Adapun tujuan penelitian secara rinci diuraikan sebagai berikut:
1. Menelaah perbedaan capaian kemampuan pemecahan masalah matematis antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing. a. Menelaah perbedaan capaian kemampuan pemecahan masalah matematis
kelompok siswa yang memiliki KAM tinggi antara yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing. b. Menelaah perbedaan capaian kemampuan pemecahan masalah matematis
c. Menelaah perbedaan capaian kemampuan pemecahan masalah matematis kelompok siswa yang memiliki KAM rendah antara yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing. 3. Menelaah perbedaan capaian kemampuan pemecahan masalah matematis
antara siswa yang memiliki KAM tinggi, sedang, dan rendah yang memperoleh pembelajaran dengan pendekatan metakognitif.
4. Menelaah perbedaan capaian kemampuan pemecahan masalah matematis antara siswa yang memiliki KAM tinggi, sedang, dan rendah yang memperoleh pembelajaran dengan pendekatan problem posing.
5. Menelaah pengaruh interaksi antara faktor pendekatan pembelajaran (metakognitif dan problem posing) dan KAM terhadap capaian kemampuan pemecahan masalah matematis siswa?
6. Menelaah perbedaan capaian self-efficacy matematis antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing.
7. Menelaah perbedaan capaian self-efficacy matematis siswa yang memiliki KAM tinggi, sedang, dan rendah antara yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing.
1.4 Manfaat Penelitian
Penelitian ini dapat memberikan kontribusi dalam pencapaian kualitas pembelajaran matematika secara umum dan khusus. Adapun manfaat penelitian ini sebagai berikut:
1. Segi teori
12
2. Segi praktik
Hasil penelitian ini dapat memberikan gambaran alternatif sudut pandang bagi guru dalam mengembangkan pembelajaran dan penentuan penilaian yang tepat. Hasil penelitian ini dapat pula menjadi alternatif bagi guru dalam menvariasikan atau mengkombinasikan pendekatan pembelajaran yang digunakan dalam proses pembelajaran matematika.
3. Segi isu atau aksi sosial
Bahan acuan, pertimbangan, dan pengembangan penelitian sejenis bagi para peneliti lainnya.
1.5 Definisi Operasional
Untuk menghindari perbedaan penafsiran, maka perlu diberikan batasan istilah atau definisi operasional sebagai berikut:
1. Kemampuan pemecahan masalah matematis
Kemampuan pemecahan masalah matematis yang di maksud dalam penelitian ini adalah kemampuan yang diperoleh dari proses kegiatan siswa (perseorangan atau kelompok) yang menggabungkan aspek konsep dan aturan yang diperoleh dari pengetahuan sebelumnya (pemahaman masalah), keterampilan memecahkan masalah dengan strategi yang tepat, dan kemampuan dalam melakukan refleksi.
2. Self-efficacy matematis
Self-efficacy matematis yang dimaksud dalam penelitian ini adalah keyakinan
dalam belajar matematika khususnya penilaian kemampuan siswa untuk memecahkan masalah matematika tertentu, dan melakukan tugas-tugas yang berhubungan dengan matematika. Proses pengembangan self-efficacy matematis dilakukan pada kegiatan awal, inti, dan diakhir pembelajaran yang meliputi:
a. penguasaan pengalaman;
b. pengalaman mengamati kesuksesan dan kegagalan orang lain; c. persuasi sosial;
3. Pendekatan metakognitif
Pendekatan metakognitif yang dimaksud dalam penelitian ini adalah pendekatan yang menanamkan kesadaran bagaimana siswa dituntut cerdas dalam memanfaatkan kecerdasannya dalam merancang, memonitor, serta mengontrol apa yang dilakukannya. Pendekatan metakognitif yang dimaksud bertujuan untuk menentukan penyelesaian dari suatu permasalahan, memfokuskan pertanyaan kepada pemahaman masalah, pengembangan hubungan antara pengetahuan yang lalu dan sekarang, penggunaan strategi penyelesaian permasalahan yang tepat, merefleksikan proses dan solusi, serta membantu siswa untuk mengembangkan konsep dirinya. Prinsip yang akan diterapkan kepada siswa dalam penelitian ini mengadaptasi dari Lester (2013) yakni prinsip keterlibatan berkepanjangan (siswa terlibat dalam tugas yang teratur selama jangka waktu lama), prinsip berbagai tugas (kesempatan siswa menyelesaikan tugas pemecahan masalah dari berbagai jenis masalah), prinsip interaksi kelompok (siswa terlibat kerja pada kelompok kecil).
4. Pendekatan problem posing
Pendekatan Problem Posing yang dimaksud dalam penelitian ini adalah pendekatan pembelajaran yang melatih siswa untuk merumuskan atau mengajukan masalah dari situasi yang tersedia kemudian melakukan penyelesaian terhadap pertanyaan atau masalah yang diajukan tersebut.
5. Kelompok Kemampuan Awal Matematis (KAM)
49
BAB III
METODE PENELITIAN
3.1 Desain Penelitian
Dalam penelitian ini, diperlukan upaya untuk mengungkapkan cara pencapaian kemampuan pemecahan masalah dan self-efficacy matematis siswa. Pada implementasinya, pemanipulasian dilakukan karena adanya keterbatasan dalam hal faktor-faktor yang kemungkinan dapat mengintervensi situasi pembelajaran. Penelitian ini melibatkan dua kelas sampel yang telah ada sebelumnya dengan penempatan subjek tidak secara acak. Subjek yang tidak dikelompokkan secara acak bertujuan agar penelitian ini tidak mengganggu jadwal pelajaran dan efektivitas pembelajaran yang sedang berjalan. Dengan demikian, studi penelitian ini merupakan kuasi eksperimen.
Adapun desain yang digunakan adalah desain perbandingan kelompok statis. Desain penelitian yang dimaksud disajikan sebagai berikut.
X1 O
X2 O (Ruseffendi, 2010)
Desain ini melibatkan dua kelompok yang diberikan perlakuan pembelajaran dengan pendekatan pembelajaran berbeda. Kelompok pertama (X1) diberi perlakuan pembelajaran dengan pendekatan metakognitif, dan kelompok kedua (X2) diberi perlakuan pembelajaran dengan pendekatan problem posing. Selanjutnya di akhir pembelajaran, kedua kelompok diberi postes (O) berupa tes kemampuan pemecahan masalah matematis dan angket skala self-efficacy matematis.
Selain melibatkan pendekatan pembelajaran, desain penelitian ini juga melibatkan faktor Kemampuan Awal Matematis (KAM). KAM dibagi ke dalam kelompok kategori tinggi (atas), sedang (tengah), dan rendah (bawah). Materi yang digunakan untuk mengukur KAM memuat standar kompetensi tentang bilangan, aljabar, dan geometri.
Dampak yang diteliti dan muncul pada subjek penelitian berupa capaian kemampuan pemecahan masalah dan self-sefficacy matematis siswa. Dampak tersebut merupakan akibat dari perlakuan pembelajaran yang ditetapkan yakni pembelajaran dengan pendekatan metakognitif dan problem posing serta faktor KAM. Berikut desain yang dapat direpresentasikan terkait hubungan antara kemampuan pemecahan masalah matematis atau skala self-efficacy yang diukur berdasarkan pendekatan pembelajaran dan kategori KAM.
Tabel 3.1 Keterkaitan antara Kemampuan/Skala yang Diukur Berdasarkan Pendekatan Pembelajaran dan Kategori KAM
Keterangan
PmM(T,S,R): Kemampuan pemecahan masalah matematis kelompok siswa kategori tinggi, sedang, rendah yang diberikan pendekatan metakognitif
PmP(T,S,R): Kemampuan pemecahan masalah matematis kelompok siswa kategori tinggi, sedang, rendah yang diberikan pendekatan problem posing.
SeM(T,S,R): Self-Efficacy matematis kelompok siswa kategori tinggi, sedang, rendah yang diberikan pendekatan metakognitif
SeP(T,S,R): Self-Efficacy matematis kelompok siswa kategori tinggi, sedang, rendah yang diberikan pendekatan problem posing.
KAM
51
3.2 Populasi dan Sampel Penelitian
Populasi penelitian ini adalah seluruh siswa kelas VIII SMP PGRI 12 Cilandak, Jakarta Selatan sebanyak 264 orang. Pertimbangan mengambil SMP swasta agar penelitian lebih representatif dalam melihat kemampuan pemecahan masalah dan self-efficacy matematis siswa. Sampel penelitian adalah siswa kelas VIII-3 sebanyak 33 orang dan VIII-4 sebanyak 36 orang. Peneliti mengambil subjek sampel kelas VIII dengan pertimbangan:
1. Pemilihan tingkat kelas disesuaikan dengan kebutuhan penelitian yakni kematangan berpikir. Siswa kelas VIII dan IX SMP dianggap telah cukup siap dalam menerima dan melakukan tugas berpikir. Namun, kelas IX tidak memungkinkan untuk dijadikan subjek penelitian karena sedang menfokuskan untuk menghadapi ujian akhir.
2. Berdasarkan psikologi perkembangan kognitif, siswa kelas VIII merupakan individu-individu yang sedang mengalami masa transisi. Akibat dari masa ini tidak sedikit dari siswa kelas VIII mengalami kemunduran dalam hal belajar. Pembentukan motivasi dan self-efficacy dipandang perlu diberikan di kelas ini. Oleh karena itu, peneliti merasa tepat menjadikan siswa kelas VIII sebagai sampel yang mewakili penelitian.
3.3 Instrumen Penelitian
Instrumen yang dikembangkan pada penelitian ini terdiri dari instrumen pengumpul data dan perangkat pembelajaran. Instrumen pengumpul data terdiri dari tes Kemampuan Awal Matematis (KAM), tes Kemampuan Pemecahan Masalah Matematis (KPMM), dan angket skala Self-Efficacy Matematis (SEM). Perangkat pembelajaran terdiri dari Rencana Pelaksanaan Pembelajaran (RPP), Lembar Kerja Siswa (LKS), dan lembar observasi aktivitas siswa dan guru.
3.3.1 Instrumen Tes Kemampuan Awal Matematis (KAM)
Instrumen tes KAM berupa soal pilihan ganda berjumlah 25 butir dengan empat pilihan jawaban. Indikator dan soal instrumen tes KAM diadopsi dari beberapa sumber bank soal yakni soal Uji Coba Ujian Nasional (UCUN), soal Ulangan Kenaikan Kelas (UKK), soal Ulangan Akhir Semester (UAS), soal Tes Uji Kompetensi Peserta Didik (TUKPD), bank soal persiapan Ujian Nasional (UN), dan soal UN tahun 2012 (ada pada lampiran B.1 dan B.2 hal. 187 s.d. 193).
Pembuatan instrumen tes KAM diawali dengan penyusunan kisi-kisi. Pembuatan instrumen tes ini terlebih dahulu melalui proses diskusi dengan rekan sejawat yang berlatar belakang pendidikan matematika. Setelah itu, instrumen tersebut mendapat timbangan dari ahli (dosen pembimbing). Timbangan berupa kesesuaian antara indikator dan butir soal.
Sebelum digunakan, tes KAM diujicobakan terlebih dahulu kepada siswa kelas IX di salah satu SMP swasta di wilayah Cilandak, yakni SMP Bakti Idhata Jakarta. Tujuan ujicoba tes adalah untuk memastikan instrumen tersebut laik digunakan dalam penelitian ini. Kelaikan instrumen tes berdasarkan hasil reliabilitas, validitas. Selain itu, dilihat pula tingkat kesukaran dan daya pembedanya.
Selanjutnya setelah instrumen tes KAM dianggap laik, maka instrumen ini digunakan terhadap subjek penelitian sebelum diberikan perlakuan pembelajaran dengan pendekatan metakognitif dan problem posing. Hasil tes KAM digunakan untuk mengelompokkan siswa. Pengelompokkan dilakukan berdasarkan proporsi area dibawah kurva normal. Daerah yang digunakan berkisar antara z = -1 dan z = +1 yang berada pada persentase kurang lebih dari daerah satu simpangan baku yakni 68%. Adapun rumus yang ekuivalen untuk melakukan transisi dari skor z kedalam skor mentah adalah = ̅ ± �� dengan ̅ = rerata dan �� = simpangan baku (Wahyudin, 2012). Dalam hal pengelompokkan siswa berdasarkan KAM, maka merupakan skor hasil tes KAM dengan kriteria dibawah ini. Hasil pengelompokkan ada pada lampiran B.8 halaman 213.
≥ ̅ + �� (kelompok siswa kategori atas/tinggi)
̅ − �� < < ̅ + �� (kelompok siswa kategori tengah/sedang)
53
3.3.2 Instrumen Tes Kemampuan Pemecahan Masalah Matematis (KPMM)
Tes kemampuan pemecahan masalah digunakan untuk melihat capaian belajar siswa setelah mendapatkan perlakuan pembelajaran dengan menggunakan pendekatan metakognitif dan problem posing. Instrumen tes pemecahan masalah matematis berbentuk uraian yang terdiri dari lima butir soal. Selengkapnya ada pada lampiran C.1 dan C.2 hal. 215 s.d. 217
Pembuatan instrumen tes pemecahan masalah matematis terdiri dari penyusunan kisi-kisi, penyusunan soal, dan rubrik penilaian. Pembuatan instrumen tes ini terlebih dahulu melalui proses diskusi dengan rekan sejawat yang berlatar belakang pendidikan matematika. Setelah itu, instrumen tersebut mendapat timbangan dari ahli (dosen pembimbing). Timbangan terhadap kedua instrumen tes berupa timbangan kesesuaian antara indikator dan butir soal, serta keterbacaan soal baik berupa kalimat, gambar, dan ukuran-ukuran yang disajikan.
Sama halnya dengan tes KAM, tes pemecahan masalah diujicobakan kepada siswa kelas IX di SMP Bakti Idhata Jakarta. Tujuan ujicoba tes adalah untuk memastikan instrumen laik digunakan untuk penelitian ini. Kelaikan instrumen tes berdasarkan hasil reliabilitas, validitas, dilihat pula tingkat kesukaran dan daya pembedanya.
Dalam penelitian ini, uji yang di maksud menggunakan sofware anates versi 4.1.0 dan 4.0.7. Anates versi 4.1.0 digunakan untuk soal pilihan ganda, sedang anates versi 4.0.7 digunakan untuk soal uraian. Namun secara klasik, perhitungan tersebut dapat dilakukan dengan menggunakan rumus-rumus statistik yang terdapat dalam buku-buku statistik. Adapun rumus-rumus yang digunakan pada uji reliabilitas, validitas, tingkat kesukaran, dan daya pembeda disajikan berikut.
1. Reliabilitas tes
Tabel 3.2 Klasifikasi Koefisien Reliabilitas anates selengkapnya ada pada lampiran B.3 dan C.4 hal. 197 dan 222.
Tabel 3.3 Koefisien r Hasil Uji Coba Tes Kam dan Tes KPMM Instrumen Uji Coba Koefisien r Interpretasi
Tes KAM 0,87 Tinggi
Tes KPMM 0,73 Tinggi
2. Validitas tes
Validitas empirik digunakan untuk menentukan tinggi rendahnya koefisien validitas alat evaluasi. Sebuah tes jika dikatakan reliabel belum tentu valid, akan tetapi jika instrumen tes valid maka instrumen tes itu reliabel (Ruseffendi, 2010).
Berdasarkan hasil koefisien reliabilitas, instrumen tes KAM dan tes KPMM memiliki reliabel yang tinggi. Selanjutnya akan dianalisis validitas instrumen tes tersebut. Interpretasi validitas disajikan pada tabel 3.4.
Tabel 3.4 Klasifikasi Koefisien Validitas
Koefisien Validitas Interpretasi Validitas
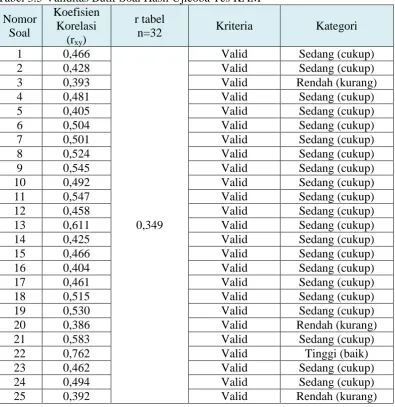
Hasil perhitungan uji coba tes KAM dengan anates diketahui nilai r hitung untuk 25 butir soal seperti disajikan pada tabel 3.5 sedangkan nilai r tabel untuk n= 32, df (n-2) dan α= 0,05 adalah 0,349. Soal dikatakan valid jika r hitung > r tabel. Hasil perhitungan validitas tes KAM disajikan pada lampiran B.3 hal. 197.
55
Adapun ringkasan hasil perhitungan koefisien korelasi rxy tiap butir soal sebagai berikut.
Tabel 3.5 Validitas Butir Soal Hasil Ujicoba Tes KAM Nomor
Tabel 3.6 Validitas Butir Soal Hasil Uji Coba Tes KPMM
Derajat kesukaran suatu butir soal dinyatakan dengan indeks kesukaran (Difficulty Index). Tingkat kesukaran suatu soal menunjukkan apakah soal
tergolong soal yang sukar, sedang, atau mudah. Rusenffedi (2010) menyatakan bahwa soal yang paling baik adalah soal yang mempunyai tingkat kesukaran sedang. Interpretasi tingkat kesukaran disajikan dalam tabel 3.7.
Tabel 3.7 Indeks Kesukaran Sebuah Tes
(Suherman, 2003)
Interpretasi indeks kesukaran memiliki kekuatan soal yang berbeda-beda. Kekuatan itu untuk membedakan siswa yang pandai (siswa kelompok unggul) dan siswa yang kurang pandai (siswa kelompok bawah) Untuk melihat kemampuan soal dalam membedakan hal tersebut digunakan daya pembeda.
4. Daya Pembeda
Pembeda item dapat diketahui dengan melihat besar kecilnya angka indeks diskriminasi item. Berikut ini disajikan rumus indeks daya pembeda untuk instrumen tes KAM berbentuk pilihan ganda. Interpretasi daya pembeda dapat dilihat pada tabel 3.8.
Indeks Kesukaran Interpretasi Indeks Kesukaran
�� = 1,00 Terlalu mudah 0,70 < �� < 1,00 Mudah
0,30 < ��≤ 0,70 Sedang 0,00 < ��≤ 0,30 Sukar
57
Tabel 3.8 Indeks Daya Pembeda Sebuah Tes
(Suherman, 2003)
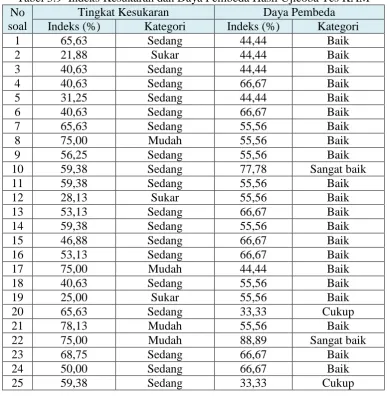
Hasil perhitungan tes KAM dan tes KPMM dengan anates selengkapnya disajikan dalam lampiran B.3 dan lampiran C.4 hal. 197 dan 222. Ringkasan hasil perhitungan disajikan sebagai berikut.
Tabel 3.9 Indeks Kesukaran dan Daya Pembeda Hasil Ujicoba Tes KAM No
Indeks Daya Pembeda Interpretasi Daya Pembeda 0,70 < DP ≤ 1,00 Sangat Baik
0,40 < DP ≤ 0,70 Baik 0,20 < DP ≤ 0,40 Cukup 0,00 < DP ≤ 0,20 Jelek
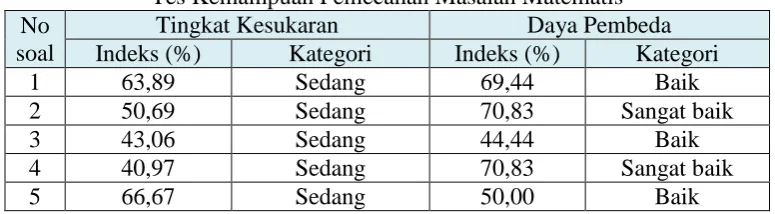
Tabel 3.10 Indeks Kesukaran dan Daya Pembeda Hasil Ujicoba
Berdasarkan hasil perhitungan reliabilitas, validitas, tingkat kesukaran dan daya pembeda maka dapat diputuskan instrumen tes KAM dan tes pemecahan masalah matematis memenuhi kelaikan untuk digunakan pada penelitian ini.
3.3.3 Instrumen Angket Skala Self-Efficacy Matematis (SEM)
Angket Skala Self-efficacy matematis digunakan untuk mengungkapkan gairah atau tingkat kepercayaan siswa terhadap tugas matematika khususnya yang berkaitan dengan pemecahan masalah. Sandaran dalam membuat angket skala self-efficacy matematis adalah teori dan pendapat ahli yang mengkhususkan pada
Mathematics Self-Efficacy Scale (MSES).
Pembuatan instrumen angket diawali dengan penyusunan kisi-kisi angket skala SEM (ada pada lampiran D.1 hal. 256). Pembuatan instrumen angket ini terlebih dahulu melalui proses diskusi dengan rekan sejawat yang berlatar belakang pendidikan konseling. Setelah itu, instrumen tersebut mendapat timbangan dari ahli (dosen pembimbing). Timbangan terhadap angket skala SEM berupa timbangan kesesuaian antara indikator dan pernyataan.
Angket skala SEM pada penelitian ini berdasarkan empat sumber self-efficacy yakni pengalaman kinerja, pengalaman orang lain, dukungan sosial, dan
indeks fisiologis. Indikator penilaian self-efficacy matematis yang tinggi berdasarkan karakteristik rasa berprestasi, kemauan dalam mengambil resiko, akurat evaluasi diri, dan rasa percaya diri (Frank, 2011)
59
Setuju (STS). Skala tidak menggunakan pilihan netral bertujuan untuk menghindari keraguan siswa dalam menentukan pilihan yang diajukan. Selengkapnya angket skala SEM ada pada lampiran D.2 hal. 257.
Penskoran ditentukan secara empirik berdasarkan distribusi jawaban responden yang direkam pada saat uji coba instrumen angket skala SEM. Data hasil skor ditansformasi menggunakan program tambahan (add-in) pada excel yakni stat.97.xla yang berisi Methode of Successive Interval (MSI).
Dari hasil analisis uji reliabilitas dan validitas dengan sofware IBM SPSS Statistics 22 diketahui r tabel untuk n = 32 dan taraf siginifikasi 5% adalah 0,349.
Secara ringkas koefisien reliabilitas dan validitas lebih dari 0,349. Maka dapat disimpulkan bahwa 35 butir pernyataan angket skala SEM dapat digunakan untuk penelitian. Data hasil uji coba untuk instrumen angket skala SEM selengkapnya ada pada lampiran D.4 dan D.5 hal. 265 s.d. 269.
3.3.4 Instrumen Perangkat Pembelajaran
Perangkat pembelajaran digunakan untuk mendukung proses penelitian ini. Perangkat pembelajaran terdiri dari Rencana Pelaksanaan Pembelajaran (RPP), Lembar Kerja Siswa (LKS), lembar observasi aktivitas siswa dan guru. Perangkat pembelajaran dibuat melalui proses timbangan dari dosen pembimbing. Pembimbing melihat kesesuaian antara tujuan pembelajaran dan kegiatan pembelajaran yang menggunakan pendekatan metakognitif maupun problem posing. Kemudian revisi instrumen dilakukan setelah timbangan ini.
Perangkat pembelajaran RPP dikembangkan berdasarkan materi pada silabus matematika kelas VIII semester II yakni materi garis singgung lingkaran. Perangkat dibuat untuk lima kali tatap muka terkait pembelajaran dengan menggunakan pendekatan metakognitif dan lima kali tatap muka untuk pembelajaran dengan pendekatan problem posing. RPP selengkapnya ada pada lampiran A.2 dan A3 hal. 112 s.d. 146.
pada tatap muka saat itu. LKS dibuat dan disesuaikan dengan pendekatan pembelajaran yang digunakan. Bentuk LKS selengkapnya dapat dilihat pada lampiran A.2 dan A.3 hal. 112 s.d. 146.
Perangkat pembelajaran lembar observasi adalah suatu proses pengamatan dan pencatatan secara sistematis, logis, objektif, dan rasional mengenai berbagai fenomena, baik dalam situasi yang sebenarnya maupun dalam situasi buatan untuk mencapai tujuan tertentu. Lembar observasi digunakan untuk memperoleh gambaran tentang suasana pembelajaran terkait dengan aktivitas dan interaksi antara siswa dengan siswa, atau siswa dengan guru. Format lembar observasi ada pada lampiran A.4 dan A.5 hal. 179 s.d. 186.
Proses pembelajaran siswa diamati dan dicatat setiap pertemuan. Lembar observasi aktivitas siswa menggunakan penskoran angka 0 dan 1 dengan interpretasi 1 jika jawaban ya dan 0 jika jawaban tidak. Sedangkan lembar observasi guru menggunakan rubrik penskoran angka antara 1 sampai dengan 4. Adapun ketentuan menggunakan angka 1 sampai dengan 4 mengacu pada Pedoman Penilaian Pencapaian Kompetensi Peserta Didik Sekolah Menengah Pertama yang diterbitkan oleh Kemdikbud tahun 2014. Adapun untuk menghitung hasil observasi aktivitas siswa dan guru pada proses pembelajaran dengan pendekatan metakognitif dan problem posing digunakan rumus:
� = �� × (Wahyudin, 2012)
Keterangan:
� = persentase tiap kategori
= frekuensi atau banyaknya kasus dalam setiap kategori
� = banyaknya kasus dalam kategori
Selanjutnya untuk mengetahui efektivitas pendekatan pembelajaran tersebut diberikan kriteria yang menggunakan nilai skala 1 sampai dengan 4 sebagai berikut:
3,33 < skor ≤ 4,00 : Sangat Baik
2,33 < skor ≤ 3,3 : Baik
1,33 < skor ≤ 2,33 : Cukup
61
3.4 Prosedur Penelitian
Tahapan yang digunakan dalam penelitian adalah sebagai berikut. 1. Tahap Persiapan Penelitian
Kegiatan yang dilakukan pada tahap ini adalah:
a. Mengidentifikasi permasalahan dan melakukan kajian pustaka terhadap variabel kemampuan pemecahan masalah matematis, self- efficacy matematis, pendekatan metakognitif, dan pendekatan problem posing. b. Menyusun proposal, seminar proposal dan perbaikan proposal.
c. Menyusun instrumen tes, membuat rencana pembelajaran, merancang bahan ajar di bawah bimbingan dosen pembimbing.
d. Mengurus perijinan untuk melaksanakan penelitian di sekolah yang bersangkutan.
e. Melakukan uji coba instrumen tes, dilanjutkan dengan menganalisis hasil uji coba (uji reliabilitas, validitas, tingkat kesukaran, dan daya pembeda). f. Memilih sampel kelas untuk diberikan perlakukan.
g. Menyusun perangkat pembelajaran. 2. Tahap Pelaksanaan
Tahap pelaksanaan adalah tahap pembelajaran matematika yang menggunakan pendekatan metakognitif dan pendekatan problem posing. Tahap pelaksanaan sebagai berikut:
a. Melakukan observasi kelas yang akan menjadi kelas penelitian.
b. Menemui guru mata pelajaran yang kelasnya dipinjam untuk penelitian. Kemudian menjelaskan skenario pelaksanaan pembelajaran sesuai pendekatan yang akan diteliti dan menyerahkan lembar observasi guru. c. Memberikan tes KAM pada kedua kelas untuk mengetahui kemampuan
awal matematis siswa.
d. Melaksanakan pembelajaran dengan pendekatan metakognitif dan pendekatan problem posing pada kelas yang berbeda.
e. Memberikan postes pada kedua kelas.
3. Tahap Pengumpulan Data
Data yang dikumpulkan kemudian dianalisis. Data hasil tes KAM dan data hasil postes tentang pemecahan masalah dianalisis secara statistik. Data angket skala self-efficacy matematis ditransformasi menggunakan Method of Successive Interval (MSI) kemudian dianalisis. Sedangkan data kualitatif
yang berasal dari hasil observasi dianalisis secara deskriptif. 4. Tahap Analisis Data
Pengolahan data kuantitatif yang berasal dari tes KAM dan tes pemecahan masalah matematis siswa dilakukan dengan menggunakan bantuan software anates versi 4.1.0, anates versi 4.0.7, microsoft excel 2010, dan IBM SPSS Statistics 22.
3.5 Teknik Analisis Data
Data tes KPMM digunakan untuk melihat perbedaan capaian KPMM siswa. Begitu pula dengan data angket skala SEM digunakan untuk melihat perbedaan SEM siswa. Setelah data diperoleh kemudian data dianalisis.
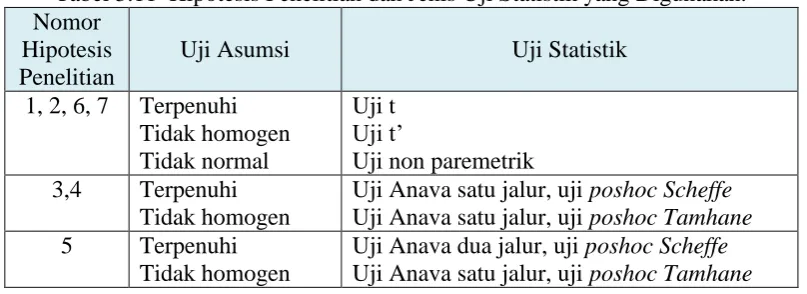
Analisis data difokuskan untuk menguji hipotesis-hipotesis yang diajukan. Terdapat tujuh hipotesis penelitian yang harus di uji secara statistik. Uji statistik yang digunakan meliputi uji t, uji Anava satu jalur dan uji Anava dua jalur. Sebelum dilakukan perhitungan uji tersebut, terlebih dahulu dilakukan uji asumsi yakni uji persyaratan yang terdiri dari ujia normalitas dan uji homigenitas. Berikut disajikan tabel keterkaitan antara hipotesis penelitian yang diajukan dan jenis uji statistik yang akan digunakan.
Tabel 3.11 Hipotesis Penelitian dan Jenis Uji Statistik yang Digunakan. Nomor
Uji Anava satu jalur, uji poshoc Scheffe Uji Anava satu jalur, uji poshoc Tamhane 5 Terpenuhi
Tidak homogen
63
1. Uji Asumsi
a. Normalitas
1) Hipotesis penelitian untuk sampel data KPMM kelompok metakognitif
H0: Data KPMM siswa yang memperoleh pendekatan pembelajaran metakognitif berdistribusi normal
H1: Data KPMM siswa yang memperoleh pendekatan pembelajaran metakognitif berdistribusi tidak normal
Hipotesis penelitian untuk sampel data KPMM kelompok problem posing
H0: Data KPMM siswa yang memperoleh pendekatan pembelajaran problem posing berdistribusi normal
H1: Data KPMM siswa yang memperoleh pendekatan pembelajaran problem posing berdistribusi tidak normal
Hipotesis penelitian untuk sampel data SEM kelompok metakognitif
H0: Data SEM siswa yang memperoleh pendekatan pembelajaran metakognitif berdistribusi normal
H1: Data SEM siswa yang memperoleh pendekatan pembelajaran metakognitif berdistribusi tidak normal
Hipotesis penelitian untuk sampel data SEM kelompok problem posing
H0: Data SEM siswa yang memperoleh pendekatan pembelajaran problem posing berdistribusi normal
H1: Data SEM siswa yang memperoleh pendekatan pembelajaran problem posing berdistribusi tidak normal
2) Taraf signifikansi dan uji yang dipakai.
Uji dilakukan pada taraf konfidensi 95% atau signifikansi α = 0,05. Uji normalitas menggunakan uji Kolmogrov-Smirnov Adapun perhitungannya menggunakan bantuan sofware IBM SPSS Statistics 22.
3) Kriteria Pengujian (Acuan pengambil keputusan):
4) Kesimpulan
Keputusan menerima atau menolak H0 dilakukan berdasarkan nilai probabilitas atau signifikansi (sig.) yang terdapat pada hasil perhitungan dari SPSS 22 dan dikonfirmasi dengan acuan pengambil keputusan.
b. Uji Homogenitas
Uji homogenitas dilakukan untuk melihat apakah dua buah distribusi atau lebih pada kedua kelompok memiliki variansi yang sama atau tidak. Uji homogenitas menggunakan uji varians dua buah peubah bebas karena sampel yang diteliti merupakan sampel saling bebas. Berikut langkah-langkah uji homogenitas.
1) Hipotesis
Hipotesis penelitian untuk data KPMM
H0: Data KPMM antara kelompok siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing memiliki varians yang homogen
H1: Data KPMM antara kelompok siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing memiliki varians yang tidak homogen
Hipotesis penelitian untuk data SEM
H0: Data SEM antara kelompok siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing memiliki varians yang homogen
H1: Data SEM antara kelompok siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan problem posing memiliki varians yang tidak homogen
Hipotesis statistik
65
Keterangan
: Varians kelompok siswa dengan pendekatan pembelajaran metakognitif
: Varians kelompok siswa dengan pendekatan pembelajaran problem posing.
2) Taraf signifikansi dan uji yang dipakai.
Uji dilakukan pada taraf konfidensi 95% atau taraf signifikansi α = 0,05. Dalam sofware IBM SPSS Statistics 22, uji homogenitas dapat diketahui dari hasil F pada Lavene statistics.
3) Kriteria Pengujian (Acuan pengambil keputusan):
Jika nilai Sig. (p-value) < α (α = 0,05), maka H0 ditolak. Jika nilai Sig. (p-value) ≥ α (α = 0,05), maka H0 diterima. 4) Kesimpulan
Keputusan menerima atau menolak H0 dilakukan berdasarkan nilai probabilitas (p value) atau signifikansi (sig.) yang terdapat pada hasil perhitungan di SPSS dan acuan pengambil keputusan.
2. Uji Statistik
Untuk memperoleh kedalaman analisis dilakukan analisis statistik sesuai dengan hipotesis penelitian. Pengujian ini bertujuan untuk melakukan sebuah generalisasi. Untuk menguji hipotesis penelitian yang telah ditetapkan pada bab II maka digunakan uji t (parametrik), uji Mann Whitney (non parametrik), uji Anava satu jalur, dan uji Anava dua jalur.
Uji t yang digunakan adalah uji t dua sampel independen. Uji t digunakan untuk mengetahui perbedaan dua rata-rata. Seperti yang telah jelaskan sebelumnya, jika data berdistribusi tidak normal maka kelanjutan uji statistiknya menggunakan uji non parametrik. Uji non parametrik yang digunakan dalam penelitian ini adalah uji Mann Whitney.
pendekatan problem posing. Uji Anava dua jalur digunakan untuk mengetahui atau mengidentifikasi kemungkinan adanya pengaruh dua faktor (pendekatan pembelajaran dan KAM) yang mungkin menyebabkan perbedaan dalam kemampuan pemecahan masalah matematis siswa. Pada uji Anava, jika uji asumsi terpenuhi dan H0 dinyatakan ditolak maka dilanjutkan dengan uji poshoc Scheffe. Namun apabila uji asumsi menyatakan varians tidak homogen maka uji lanjutan digunakan uji poshoc Tamhane.
a. Uji t atau Uji Mann Whitney
1) Hipotesis
Hipotesis penelitian untuk capaian kemampuan pemecahan masalah
matematis siswa berdasarkan pendekatan pembelajaran yang digunakan
H0: tidak ada perbedaan capaian kemampuan pemecahan masalah matematis yang signifikan antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing.
H1: ada perbedaan capaian kemampuan pemecahan masalah matematis yang signifikan antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing.
Hipotesis penelitian untuk capaian kemampuan pemecahan masalah
matematis siswa berdasarkan kategori KAM (tinggi/sedang/ rendah)
H0: tidak ada perbedaan capaian kemampuan pemecahan masalah matematis yang signifikan antara kelompok siswa kategori (tinggi/sedang/rendah) yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing. H1: ada perbedaan capaian kemampuan pemecahan masalah matematis yang
67
Hipotesis penelitian untuk capaian self-efficacy matematis siswa
berdasarkan pendekatan pembelajaran yang digunakan
H0: tidak ada perbedaan capaian self-efficacy matematis yang signifikan antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing.
H1: ada perbedaan capaian self-efficacy matematis yang signifikan antara siswa yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing. Hipotesis penelitian untuk capaian self-efficacy matematis siswa
berdasarkan kategori KAM (tinggi/sedang/rendah)
H0: tidak ada perbedaan capaian self-efficacy matematis yang signifikan antara kelompok siswa kategori (tinggi/sedang/rendah) yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing.
H1: ada perbedaan capaian self-efficacy matematis yang signifikan antara kelompok siswa kategori (tinggi/sedang/rendah) yang memperoleh pembelajaran dengan pendekatan metakognitif dan yang memperoleh pembelajaran dengan pendekatan problem posing.
Hipotesis Statistik
H : � = �
H : � ≠ �
2) Taraf Signifikansi
Taraf signifikansi yang digunakan adalah 5% atau α = 0,05 3) Kriteria Pengujian (acuan pengambil keputusan)
Daerah penerimaan H0 untuk uji dua arah adalah –t tabel < t hitung < t tabel Namun karena menggunakan perhitungan SPSS 22 maka acuan pengambil keputusan adalah nilai probabilitas atau nilai signifikansi dari output. Jika nilai Sig. (2-tailed) < α (α = 0,05), maka H0 ditolak.
4) Kesimpulan
Keputusan menerima atau menolak H0 diketahui dari nilai sig. pada hitungan SPSS. Selanjutnya dikonfirmasi dengan acuan pengambil keputusan sehingga keputusan terima atau tolak H0 dapat diketahui. Berdasarkan hasil konfirmasi perhitungan dengan SPSS 22 dan kriteria pengujian maka dapat dibuat sebuah kesimpulan terdapat perbedaan atau tidak terdapat perbedaan yang signifikan.
b. Uji Anava Satu Jalur
1) Hipotesis
Hipotesis penelitian pada uji Anava satu jalur merupakan hipotesis penelitian terhadap kemampuan pemecahan masalah matematis siswa berdasarkan kategori KAM pada setiap pembelajaran.
Hipotesis penelitian KPMM berdasarkan kategori KAM pada
pendekatan pembelajaran metakognitif.
H0: tidak ada perbedaan capaian kemampuan pemecahan masalah matematis yang signifikan antara kelompok siswa kategori tinggi, sedang, dan rendah yang memperoleh pembelajaran pendekatan metakognitif.
H1: ada paling sedikit satu yang berbeda capaian kemampuan pemecahan masalah matematis secara signifikan antara kelompok siswa kategori tinggi, sedang, dan rendah yang memperoleh pembelajaran pendekatan metakognitif.
Hipotesis penelitian KPMM berdasarkan kategori KAM pada
pendekatan pembelajaran problem posing.
H0: tidak ada perbedaan capaian kemampuan pemecahan masalah matematis yang signifikan antara kelompok siswa kategori tinggi, sedang, dan rendah yang memperoleh pembelajaran pendekatan problem posing. H1: ada paling sedikit satu yang berbeda capaian kemampuan pemecahan