ANALISIS METODE NEAREST NEIGHBOUR DAN METODE CLARKE AND WRIGHT SAVINGS UNTUK PENYELESAIAN CAPACITATED VEHICLE ROUTING PROBLEM WITH TIME WINDOWS

(1)

ANALISIS METODE NEAREST NEIGHBOUR DAN METODE CLARKE AND WRIGHT SAVINGS UNTUK PENYELESAIAN

CAPACITATED VEHICLE ROUTING PROBLEM WITH TIME WINDOWS

SKRIPSI

EVA CRISDAYANTI SIAHAAN 160803087

PROGRAM STUDI S1 MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2021

(2)

CAPACITATED VEHICLE ROUTING PROBLEM WITH TIME WINDOWS

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

EVA CRISDAYANTI SIAHAAN 160803087

PROGRAM STUDI S1 MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2021

(3)

PERNYATAAN ORISINALITAS

ANALISIS METODE NEAREST NEIGHBOUR DAN METODE CLARKE AND WRIGHT SAVINGS UNTUK PENYELESAIAN

CAPACITATED VEHICLE ROUTING PROBLEM WITH TIME WINDOWS

SKRIPSI

Saya menyatakan bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, 13 Oktober 2021

Eva Crisdayanti S 160803087

(4)

(5)

ii

ANALISIS METODE NEAREST NEIGHBOUR DAN METODE CLARKE AND WRIGHT SAVINGS UNTUK PENYELESAIAN

CAPACITATED VEHICLE ROUTING PROBLEM WITH TIME WINDOWS

ABSTRAK

Capacitated Vehicle Routing Problem with time windows sebagai bentuk pengembangan dari Capacitated Vehicle Routing Problem dan Vehicle Routing Problem with time windows membutuhkan metode penyelesaian yang efektif.

Capacitated Vehicle Routing Problem with time windows akan diselesaikan dengan beberapa metode yaitu metode nearest neighbour dan metode Clarke and Wright Saving. Kedua metode ini memiliki tujuan yaitu untuk mencari solusi yang optimal. Dalam hal ini, dilakukan analisis pada tiap-tiap metode dan membandingkan metode mana yang paling efektif dalam menyelesaikan masalah Capacitated Vehicle Routing Problem with time windows. Tujuan dari penelitian ini adalah mengkaji setiap metode untuk memperlihatkan karakteristik, kelebihan dan kekurangan yang dimiliki setiap metode. Hasil penelitian menunjukkan bahwa jika dilihat dari alur kerja pada tiap metode dan banyak iterasi, metode nearest neighbour merupakan metode yang paling sederhana tetapi belum memberikan hasil yang optimal sedangkan metode Clarke and Wright Saving merupakan metode yang paling optimal pada contoh kasus dan waktu perhitungannya lebih lama.

Kata Kunci : Capacitated Vehicle Routing Problem with time windows (CVRPTW), Clarke And Wright Saving, Graf, Nearest Neighbour, Rute

(6)

iii

ANALYSIS OF THE NEAREST NEIGHBOUR METHOD AND THE CLARKE AND WRIGHT SAVINGS METHOD FOR

SOLVING CAPACITATEDVEHICLE ROUTING PROBLEM WITH TIME WINDOWS

ABSTRACT

The Capacitated Vehicle Routing Problem with time windows as a form of development of the Capacitated Vehicle Routing Problem and the Vehicle Routing Problem with time windows requires an effective solution method. The Capacitated Vehicle Routing Problem with time windows will be solved by several methods, namely the nearest neighbor method and the Clarke and Wright Saving method. Both of these methods have the goal of finding the optimal solution. In this case, an analysis is carried out on each method and compares which method is the most effective in solving the Capacitated Vehicle Routing Problem with time windows. The purpose of this study is to examine each method to show the characteristics, advantages and disadvantages of each method. The results show that when viewed from the workflow of each method and many iterations, the nearest neighbor method is the simplest method but does not provide optimal results, while the Clarke and Wright Saving method is the most optimal method in case examples and the calculation time is longer.

Keywords : Capacitated Vehicle Routing Problem with time windows (CVRPTW), Clarke And Wright Saving, Graph, Nearest Neighbour, Route

(7)

iv

PENGHARGAAN

Puji syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa, karena berkat rahmat dan karunia-Nya penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Analisis Metode Nearest Neighbour Dan Metode Clarke And Wright Savings Untuk Penyelesaian Capacitated Vehicle Routing Problem with Time Windows. Tujuan penulisan skripsi ini adalah sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.

Dalam penyusunan skripsi ini, tidak sedikit hambatan yang penulis hadapi.

Namun penulis menyadari bahwa kelancaran dalam penyusunan skripsi ini tidak lain berkat bantuan, arahan, dan dorongan dari berbagai pihak. Oleh karena itu pada kesempatan ini, penulis ingin mengucapkan terima kasih kepada:

1. Bapak Dr. Sawaluddin, M.IT selaku Dosen Pembimbing yang telah memberikan bimbingan, arahan, dan saran kepada penulis dalam pengerjaan skripsi ini.

2. Bapak Parapat Gultom, MSIE, Ph.D dan Bapak Dr. Syahriol Sitorus, M.IT selaku Dosen Pembanding yang telah memberikan arahan, kritik, dan saran yang membangun kepada penulis dalam pengerjaan skripsi ini.

3. Bapak Prof. Dr. Saib Suwilo, M.Sc selaku penasihat akademik yang telah memberikan bimbingan dan arahan kepada penulis selama penulis belajar di FMIPA USU

4. Ibu Dr. Mardiningsih, M.Si sebagai Ketua Departemen Matematika FMIPA USU

5. Seluruh dosen dan pegawai Departemen Matematika FMIPA USU.

6. Bapak Dr. Kerista Sebayang, MS selaku Dekan FMIPA USU beserta jajarannya.

7. Bapak Dr. Muryanto Amin, S.Sos, M.Kom selaku Rektor Universitas Sumatera Utara beserta jajarannya.

(8)

v

8. Ayahanda Andar Herlan Siahaan dan Ibunda Tutur Rismawati Sirait serta Adinda Silvia Srirezeki Siahaan, Khans Chong Agung Siahaan, dan Sandi Tio Luhur yang telah memberikan dukungan, semangat, motivasi, dan doa kepada penulis dalam pengerjaan skripsi ini.

9. Teman-teman penulis yaitu Astri, Ayu, Esra, Dayan, Dean, Jessica, Ruth, Maya dan Matematika 2016 yang selalu mendukung dan selalu memotivasi penulis disetiap suka dan duka dalam pengerjaan skripsi ini.

Penulis menyadari bahwa skripsi ini masih jauh dari kata sempurna, baik pada teknis penulisan maupun materi, mengingat akan kemampuan yang penulis miliki.

Untuk itu kritik dan saran yang membangun dari semua pihak sangat penulis harapkan demi penyempurnaan pembuatan skripsi ini. Akhir kata penulis berharap semoga skripsi ini dapat bermanfaat dan menjadi sumbangan pemikiran bagi pihak yang membutuhkan, khususnya bagi penulis sehingga tujuan yang diharapkan dapat tercapai, Amin.

Medan, 13 Oktober 2021

Eva Crisdayanti S 160803087

(9)

vi

DAFTAR ISI

PENGESAHAN SKRIPSI i

ABSTRAK ii

ABSTRACT iii

PENGHARGAAN iv

DAFTAR ISI vi

DAFTAR TABEL viii

DAFTAR GAMBAR x

DAFTAR LAMPIRAN xi

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Rumusan Masalah 2

1.3 Batasan Masalah 3

1.4 Tujuan Penelitian 3

1.5 Manfaat Penelitian 4

BAB 2 TINJAUAN PUSTAKA 5

2.1 Graf 5

2.1.1 Defenisi Graf 5

2.1.2 Jenis-jenis Graf 5

2.1.3 Keterhubungan 7

2.2 Travelling Salesman Problem (TSP) 7

2.3 Vehicle Routing Problem 9

2.3.1 Pengertian Vehicle Routing Problem 9 2.3.2 Klasifikasi Jenis-jenis Vehicle Routing Problem 10 2.4 Capacitated Vehicle Routing Problem with Time Windows 11 2.4.1 Pengertian Capacitated Vehicle Routing Problem with Time

Windows 11

2.4.2 Formulasi bentuk umum CVRPTW 11

(10)

vii

2.4.3 Metode Penyelesaian Capacitated Vehicle Routing Problem

with Time Windows 13

BAB 3 METODE PENELITIAN 14

3.1 Jenis Penelitian 14

3.2 Sumber dan Jenis Data 14

3.2.1 Sumber Data 14

3.2.2 Jenis Data 14

3.3 Rancangan Penelitian 15

3.4 Metodologi Penelitian 16

BAB 4 HASIL DAN PEMBAHASAN 17

4.1 Penyelesaian Masalah Capacitated Vehicle Routing Problem with

Time Windows (CVRPTW) 17

4.1.1 Kasus 1 17

4.1.2 Penentuan Solusi Optimal 20

4.1.2.1 Metode Nearest Neighbour 20

4.1.2.2 Metode Clarke and wright Saving 26

4.2 Kasus 2 35

4.2.1 Penentuan Solusi Optimal 40

4.3 Perbandingan Metode Nearest Neighbour dan Metode Clarke and

Wright Saving terhadap dua Contoh Kasus 42

BAB 5 KESIMPULAN DAN SARAN 44

5.1 Kesimpulan 44

5.2 Saran 44

DAFTAR PUSTAKA 44

LAMPIRAN 46

(11)

viii

DAFTAR

TABEL

Nomor

Tabel Judul Halaman

4.1 Matriks Jarak dari Gudang ke setiap Agen 17 4.2 Data Permintaan, Time Windows, dan

Waktu Pelayanan 18

4.3 Waktu Tempuh Kendaraan 18

4.4 Perolehan Rute Kendaraan 25

4.5 Bentuk Umum Matriks Jarak 26

4.6 Bentuk Umum Saving Matrix 26

4.7 Nilai Saving Matrix 28

4.8 Metode Clarke And Wright Saving Iterasi 1 28 4.9 Metode Clarke And Wright Saving Iterasi 2 29 4.10 Metode Clarke And Wright Saving Iterasi 3 29 4.11 Metode Clarke And Wright Saving Iterasi 4 30 4.12 Metode Clarke And Wright Saving Iterasi 5 30 4.13 Metode Clarke And Wright Saving Iterasi 6 31 4.14 Metode Clarke And Wright Saving Iterasi 7 31

4.15 Waktu Distribusi 32

4.16 Perolehan Rute Kendaraan 32

4.17 Perbandingan Dua Metode untuk

Menentukan Solusi Optimal 33

4.18 Time Windows Konsumen 33

4.19 Data Permintaan, Time Windows, dan

Waktu Pelayanan 34

4.20 Jarak Tempuh Kendaraan 35

4.21 Waktu Tempuh Kendaraan 36

4.22 Perolehan Rute Kendaraan Nearest 38

(12)

ix

Neighbour

4.23 Perolehan Rute Kendaraan Clarke And

Wraight Saving 38

4.24

Perbandingan Hasil Metode Nearest Neighbour dan Metode Clarke and Wright Saving terhadap Contoh Kasus

40

(13)

x

DAFTAR

GAMBAR

Nomor

Gambar Judul Halaman

2.1 Graf Sederhana 6

2.2 Graf Berarah 6

2.3 Graf Berbobot 6

2.4 Graf G 7

2.5

Ilustrasi Pola Rute Masalah Travelling Salesmen Problem dan Vehicle Routing Problem

9

(14)

xi

DAFTAR

LAMPIRAN

Nomor

Lampiran Judul Halaman

1 Tabel Iterasi 46

(15)

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Vehicle Routing Problem merupakan suatu permasalahan yang bertujuan untuk mendesain rute-rute yang mungkin dari suatu depot ke sekumpulan titik (node) yang tersebar dengan meminimumkan total jarak tempuh kendaraan. VRP merupakan perkembangan atau perluasan dari Travelling Salesman Problem (TSP). Terdapat perbedaan antara VRP dan TSP, VRP menggunakan banyak kendaraan untuk menyelesaikan permasalahan rute perjalanan sedangkan TSP menggunakan seorang salesman untuk melakukan perjalanan menuju kota dalam menyelesaikan permasalahan perjalanan. Permasalahan m-TSP sering disebut sebagai Vehicle Routing Problem (VRP). Tujuan dari VRP adalah mengantarkan barang ke konsumen dengan rute yang optimum dan meminimalisasi jumlah kendaraan yang digunakan untuk keluar masuk depot.

Jenis permasalahan VRP berdasarkan kendalanya antara lain Capacitated Vehicle Routing Problem (CVRP) dengan kendala setiap kendaraan mempunyai kapasitas yang terbatas dalam mengantarkan barang ke suatu tempat, Vehicle Routing Problem with Time Windows (VRPTW) dengan kendala setiap konsumen yang dilayani oleh kendaraan memiliki batas waktu menerima pelayanan, Multiple Depot Vehicle Routing Problem (MDVRP) dengan kendala distributor memiliki banyak depot untuk menyuplai pelanggan, Vehicle Routing Problem with Pick-up and Delivering (VRPPD) dengan kendala pelanggan mungkin mengembalikan barang pada depot asal.

Capacitated Vehicle Routing Problem with Time Windows (CVRPTW) adalah gabungan dari permasalahan capacitated vehicle routing problem (CVRP) dengan vehicle routing problem with time windows (VRPTW). Tujuan dari CVRPTW adalah membentuk rute optimal untuk memenuhi permintaan pelanggan dengan kendala kapasitas dan waktu pelayanan agar diperoleh waktu dan jarak yang minimum.

Wahyu R et al. (2018) menyatakan dalam jurnalnya bahwa penggunaan metode Clarke And Wright Savings dalam pemecahan persoalan rute distribusi

(16)

mampu memberikan hasil optimal berupa diperolehnya jarak terpendek yang akan menjadi rute pendistribusian baru dan dapat meminimasi waktu pendistribusian produk kepada pelanggan, yang dapat mengakibatkan pemborosan dari segi waktu, jarak, dan biaya pendistribusian.

Cahyaningsih (2015) meneliti tentang penyelesaian capacitated vehicle routing problem (CVRP) Menggunakan algoritma sweep untuk optimasi rute distribusi surat kabar kedaulatan rakyat membuktikan bahwa algoritma nearest neighbour dapat menghasilkan rute yang lebih efektif daripada rute sebelumnya.

Tujuan dilakukannya pengoptimalan rute distribusi adalah mengetahui rute optimal untuk kendaraan yang dimiliki oleh perusahaan, sehingga jarak tempuh dan waktu selama pendistribusian diperoleh lebih optimal dan semua konsumen dilayani dengan memperhatikan interval waktu setiap konsumen. Dalam melakukan pengoptimalan rute distribusi, terdapat banyak metode yang bisa digunakan, yaitu metode nearest neighbour dan metode clarke and wright savings. Metode clarke and wright savings dipilih karena dipublikasikan sebagai suatu algoritma yang digunakan sebagai solusi untuk permasalahan rute kendaraan dimana sekumpulan rute pada setiap langkah ditukar untuk mendapatkan sekumpulan rute yang lebih baik, metode nearest neighbour dipilih karena pemecahan masalah pemilihan rutenya dengan cara mencari jarak terpendek untuk menempuh lokasi pengiriman. Oleh karena itu, penulis memberi judul penelitian ini yaitu Analisis Metode Nearest Neighbour dan Metode Clarke And Wright Savings untuk Penyelesaian Capacitated Vehicle Routing Problem.

1.2 Rumusan Masalah

Sesuai dengan uraian pada latar belakang penelitian ini, maka yang menjadi pokok permasalahan pada penelitian ini adalah:

1. Membentuk model capacitated vehicle routing problem with time windows.

2. Mengkaji dan menyelesaikan bentuk capacitated vehicle routing problem with time windows menggunakan metode nearest neighbour dan metode clarke and wright savings.

(17)

3

3. Menguji keoptimalan setiap metode dengan mengaplikasikan pada contoh kasus dan melihat apakah solusi yang diperoleh sudah merupakan solusi yang optimal atau tidak.

1.3 Batasan Masalah

Agar penelitian yang dilakukan dapat menghasilkan penelitian yang fokus dan akurat, maka diberikan batasan masalah dalam penelitian iniyaitu:

1. Mengoptimalkan rute yang dimaksud dalam penelitian ini adalah dengan menyelesaikan bentuk capacitated vehicle routing problem with time windows menggunakan metode nearest neighbour dan metode clarke and wright savings.

2. Contoh kasus dan data yang digunakan yaitu studi kasus dan data sekunder yang diperoleh dari buku dan jurnal.

1.4 Tujuan Penelitian

Tujuan yang ingin dicapai pada penelitian ini adalah:

1. Mengetahui pembentukan model capacitated vehicle routing problem with time windows.

2. Menyelesaikan capacitated vehicle routing problem with time windows dan membandingkan metode yang digunakan yaitu nearest neighbour dan clarke and wright savings.

3. Melakukan analisis karakteristik dari kedua metode yaitu metode nearest neighbour dan metode clarke and wright savings, dengan melihat kelebihan dan kelemahan setiap metode sehingga suatu metode dapat disimpulkan sebagai metode optimal.

(18)

1.5 Manfaat Penelitian

Manfaat dari penelitian ini adalah:

1. Sebagai bahan referensi dalam menambah wawasan dan memperkaya literatur dalam bidang operasi riset yang berhubungan dengan penerapan metode nearest neighbour dan metode clarke and wright savings.

2. Memberikan informasi dan menambah pengetahuan pembaca dalam memahami konsep atau teori-teori mengenai metode nearest neighbour dan metode clarke and wright savings dalam penyelesaian permasalahan capacitated vehicle routing problem with time windows.

3. Menyusun laporan penelitian dalam bentuk skripsi.

(19)

BAB 2

TINJAUAN PUSTAKA

2.1 Graf

2.1.1 Defenisi Graf

Graf pertama kali dikenal pada saat seorang matematikawan Swiss, bernama Leonhard Euler tahun 1736, berhasil mengungkap misteri teka-teki jembatan Koningsberg mengalir sebuah sungai bernama sungai Pregel yang membelah kota.

Bagian aliran sungai tersebut ada yang mengapit suatu pulau dan kemudian aliran sungai bercabang menjadi 2 bagian. Dengan demikian aliran sungai Pregel membelah kota Koningsberg dan memisahkan daratannya menjadi 4 bagian (misal daratan A, B, C dan D). Untuk menghubungkan keempat daratan tersebut dibuat 7 jembatan. Euler menyederhanakan permasalahan tersebut dengan mempresentasikan setiap daratan yang dipisahkan oleh sungai Pregel sebagai titik dan jembatan sebagai sisi.

Graf adalah suatu diagram yang memuat informasi tertentu dan dilambangkan dengan suatu keterhubungan antar titik. Graf digunakan untuk menggambarkan berbagai objek-objek diskrit dan hubungan antarobjek tersebut.

Secara matematis, Graf G didefinisikan sebagai pasangan himpunan , ditulis dengan notasi , yang dalam hal ini adalah himpunan tidak kosong dari simpul-simpul (vertices atau node) dan adalah himpunan sisi (edges atau arcs) yang menghubungkan sepasang simpul.

2.1.2 Jenis-jenis Graf

Munir (2007) mengatakan bahwa sesuai dengan kekhasan strukturnya, graf dapat diklasifikasikan dalam beberapa jenis yaitu graf sederhana, berarah, berbobot, dan sebagainya.

1. Graf sederhana (simple graph)

Graf sederhana adalah graf yang tidak memiliki rusuk ganda dan gelang. Rusuk ganda adalah dua rusuk yang menghubungkan dua simpul yang sama, sedangkan

(20)

gelang adalah suatu simpul yang menghubungkan suatu simpul dengan simpul itu sendiri (loop).

Contoh graf sederhana dapat dilihat pada gambar .

Gambar 2.1. Graf Sederhana 2. Graf berarah (directed graph)

Graf berarah adalah graf yang setiap rusuknya memiliki orientasi arah. Arah rusuk yang menghubungkan dua buah simpul dilambangkan dengan anak panah.

Contoh graf berarah dapat dilihat pada gambar .

Gambar 2.2. Graf berarah 3. Graf berbobot (Weightedgraph)

Graf berbobot adalah graf yang setiap sisinya diberi sebuah harga (bobot). Bobot pada tiap sisi dapat berbeda-beda bergantung pada masalah yang dimodelkan dengan graf. Bobot pada graf berbobot dapat menyatakan jarak antara dua buah pelanggan, biaya perjalanan, waktu tempuh, dan lain-lain.

Contoh graf berbobot dapat dilihat pada gambar .

Gambar 2.3. Graf berbobot

(21)

7

2.1.3 Keterhubungan

Gambar 2.4. Graf G 1. Perjalanan (Walks)

Perjalanan dalam sebuah graf adalah barisan terhingga dengan bentuk { } dimana rusuk menghubungkan titik dengan titik .

Contoh suatu perjalanan pada Graf adalah , , , , , , , , , , . 2. Lintasan (Trails)

Lintasan adalah perjalanan dengan semua rusuk dalam barisan berbeda.

Contoh suatu lintasan pada graf adalah . 3. Jalur (Path)

Jalur adalah perjalanan dengan semua titik dalam barisan berbeda.

Contoh suatu jalur pada graf adalah . 4. Sirkuit (Circuit)

Sirkuit adalah lintasan yang berawal dan berakhir pada titik yang sama.

Contoh suatu sirkuit pada graf adalah .

2.2 Travelling Salesman Problem (TSP)

Travelling Salesman Problem (TSP) dikemukakan pada abad ke-18 oleh seorang ahli matematika dari Irlandia yaitu William Rowam Hamilton dan ahli matematika dari Britania yaitu Thomas Penyngton Kirkman. TSP adalah masalah optimasi dalam mencari rute untuk salesman yang dimulai dari lokasi awal, mengunjungi serangkaian kota kemudian kembali ke lokasi semula sedemikian sehingga jarak total yang ditempuh adalah jarak minimal dan setiap kota dikunjungi tepat satu kali (Gutin dan Punnen, 2007). TSP merupakan bagian dari permasalahan transportasi yang banyak kita jumpai di kehidupan sehari-hari.

Beberapa contoh aplikasi Travelling Salesman Problem ini adalah sebagai berikut:

(22)

1. Sebuah pabrik yang menghasilkan barang atau komoditi tertentu melalui satu salesman pada lokasi yang berbeda, akan mendistribusikan barang ke berbagai tempat yang memerlukan dengan jumlah kebutuhan yang sudah tertentu.

2. Sebuah mobil pos ditugaskan mengambil surat dari kotak pos yang tersebar pada buah lokasi di berbagai sudut kota. Graf dengan simpul dapat digunakan untuk menyajikan persoalan. Satu simpul menyatakan kantor pos tempat mobil pos mulai berangkat.

3. Penggunaan lengan robot untuk mengencangkan mur pada beberapa buah peralatan mesin dalam sebuah jalur perakitan. Lengan robot mulai berada dari posisi awalnya, lalu berturut-turut pindah ke mur-mur berikutnya dan kembali lagi ke posisi awalnya. Siklus yang dibentuk merupakan perjalanan mengunjungi simpul-simpul sebuah graf.

Menurut Gutin dan Punnen (2007) secara matematis, permasalahan TSP dapat diformulasikan sebagai:

Fungsi tujuan

∑ ∑

(2.1) Dengan kendala

∑

(2.2)

∑

(2.3)

(2.4)

Dimana merepresentasikan jarak perjalanan dari simpul ke simpul . Sedangkan

merepresentasikan ada tidaknya jalur dari simpul ke simpul . Sesuai dengan kendala, bernilai 0 jika tidak ada jalur yang menghubungkan simpul ke dan

bernilai 1 jika ada jalur yang menghubungkan dari simpul ke simpul . Setiap node dilalui tepat satu kali, tetapi solusi dapat lebih dari satu sub siklus (terjadi subtour). Subtour adalah perjalanan yang tidak mengunjungi semua node.

Secara garis besar, TSP tergolong menjadi tiga masalah, yaitu simetris travelling salesman problem (sTSP), asymmetric travelling salesman problem

(23)

9

(aTSP), dan multi travelling salesman problem (mTSP), yaitu jenis TSP yang menambahkan kendala jumlah salesman, sehingga terdapat sejumlah m salesman untuk mengunjungi seluruh tujuan.

2.3 Vehicle Routing Problem

2.3.1 Pengertian Vehicle Routing Problem

Vehicle Routing Problem (VRP) pertama kali dipelajari oleh Dantzig dan Ramser tahun 1959 dalam bentuk rute dan penjadwalan truk yang paling dikenal dengan The Truck Dispatching Problem yang merupakan perutean optimal armada truk pengangkut bensin antara terminal massal dan sejumlah besar stasiun layanan yang dipasok oleh terminal. VRP merupakan perluasan dari Traveling Salesman Problem (TSP) sehingga sering disebut sebagai -TSP. TSP mempertimbangkan satu kendaraan yang mengunjungi banyak pelanggan sebelum kembali ke depot, sementara total waktu perjalanan atau jarak kendaraan diminimalkan. Selanjutnya, ketika menyangkut batasan kapasitas kendaraan menjadi VRP.

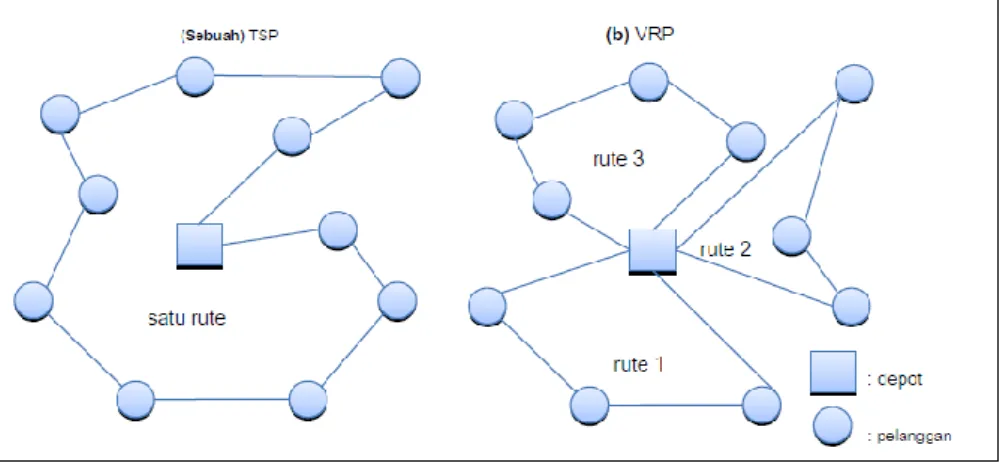
Perbedaan antara VRP dan TSP adalah bahwa VRP dapat menghasilkan banyak rute untuk melewati semua node pelanggan di bawah batasan kapasitas kendaraan. Perbedaan antara TSP dan VRP diilustrasikan pada Gambar 2.5, di mana TSP adalah masalah kombinasi layanan node rute tunggal tanpa batasan kapasitas kendaraan dan VRP adalah masalah kombinasi layanan node multi rute dengan batasan kapasitas kendaraan.VRP menjadi TSP pada saat hanya terdapat satu alat angkut yang kapasitasnya tak hingga (Rupiah et al., 2017).

Gambar 2.5 Ilustrasi Pola Rute Masalah Travelling Salesman Problem (TSP) dan Vehicle Routing Problem (VRP)

(24)

Tujuan umum VRP menurut Toth dan Vigo (2002) adalah:

1. Meminimalkan jarak dan biaya tetap yang berhubungan dengan penggunaan kendaraan.

2. Meminimalkan banyaknya kendaraan yang dibutuhkan untuk melayani permintaan seluruh konsumen.

3. Menyeimbangkan rute-rute dalam hal waktu perjalanan dan muatan kendaraan.

4. Meminimalkan pinalti sebagai akibat dari pelayanan yang kurang memuaskan terhadap konsumen, seperti keterlambatan pengiriman dan lain sebagainya.

2.3.2 Klasifikasi Jenis-jenis Vehicle Routing Problem

Banyak faktor yang muncul pada penggunaan VRP dalam dunia nyata. Faktor-faktor tersebut berpengaruh pada munculnya variasi dari VRP.

1. Capacitated Vehicle Routing Problem (CVRP)

Setiap kendaraan mempunyai kapasitas yang terbatas dalam mengantarkan barang ke suatu tempat.

2. Vehicle Routing Problem with Time Windows (VRPTW)

Setiap konsumen yang dilayani oleh kendaraan memiliki batas waktu menerima pelayanan.

3. Capacitated Vehicle Routing Problem with Time Windows (CVRPTW)

Mempunyai kendala kapasitas kendaraan yang homogen dan waktu pelayanan.

4. Multiple Depot Vehicle Routing Problem (MDVRP)

Distributor memiliki banyak depot untuk menyuplai pelanggan.

5. Vehicle Routing Problem with Pick-up and Delivering (VRPPD) Pelanggan mungkin mengembalikan barang pada depot asal.

6. Split Delivery Vehicle Routing Problem (SDVRP) Pelanggan dilayani dengan kendaraan berbeda.

7. Stochastic Vehicle Routing Problem (SVRP)

Munculnya ‘random values’ seperti jumlah pelanggan, jumlah permintaan, waktu pelayanan atau waktu perjalanan.

8. Periodic Vehicle Routing Problem

Pengantaran hanya dilakukan dihari-hari tertentu.

(25)

11

2.4 Capacitated Vehicle Routing Problem with Time Windows

2.4.1 Pengertian Capacitated Vehicle Routing Problem with Time Windows

Capacitated Vehicle Routing Problem with Time Windows (CVRPTW) adalah gabungan dari permasalahan capacitated vehicle routing problem (CVRP) dengan vehicle routing problem with time windows (VRPTW). Tujuan dari CVRPTW adalah membentuk rute optimal untuk memenuhi permintaan pelanggan dengan kendala kapasitas dan waktu pelayanan agar diperoleh waktu dan jarak yang minimum.

Kendala pertama pada CVRPTW adalah kendala kapasitas. Kendala kapasitas yang dimaksud adalah bahwa setiap kendaraan memiliki kapasitas tertentu dan jika kapasitas kendaraan sudah penuh, maka kendaraan tersebut tidak dapat melayani konsumen selanjutnya. Kendala berikutnya adalah kendala time windows pada masing-masing konsumen dan time windows pada depot. Time windows pada masing-masing konsumen [ ] adalah interval waktu yang ditentukan oleh masing-masing konsumen bagi setiap kendaraan untuk dapat melakukan pelayanan pada konsumen tersebut. Kendaraan dapat memulai pelayanan di antara waktu awal konsumen dan waktu akhir konsumen . Namun kendaraan juga harus menunggu sampai waktu awal konsumen dapat dilayani, apabila kendaraan tersebut datang sebelum waktu awal konsumen, sedangkan time windows pada depot [ ] didefinisikan sebagai interval waktu yang menunjukkan waktu awal keberangkatan kendaraan dari depot dan waktu kembalinya kendaraan ke depot, itu artinya kendaraan tidak boleh meninggalkan depot sebelum waktu awal depot dan harus kembali ke depot sebelum waktu akhir depot .

2.4.2 Formulasi bentuk umum CVRPTW

Hassani et al. (2008) bentuk umum dari CVRPTW adalah:

Fungsi tujuan:

Min ∑∑( ∑ ) (2.5) Kendala

1. Setiap konsumen hanya dikunjungi tepat satu kali oleh kendaraan yang sama

∑ ∑ ∑

(2.6)

(26)

2. Total jumlah permintaan konsumen dalam satu rute tidak melebihi kapasitas kendaraan yang melayani rute.

Misalkan terdapat rute dari i ke j dengan kendaraan k, maka

(2.7)

(2.8)

3. Jika ada perjalanan dari konsumen ke ke konsumen ke , maka waktu memulai pelayanan di konsumen ke lebih dari atau sama dengan waktu kendaraan ke untuk memulai pelayanan di konsumen ke ditambah waktu pelayanan konsumen ke dan ditambah waktu tempuh perjalanan dari konsumen ke ke konsumen ke .

(2.9) 4. Waktu kendaraan untuk memulai pelayanan di pelanggan ke harus berada pada

selang waktu [ ].

(2.10)

5. Setiap rute perjalanan pasti diawali oleh depot

∑ ∑

(2.11)

6. Setiap rute perjalanan pasti diakhiri oleh depot

∑ ∑

(2.12)

7. Kekontinuan rute, artinya kendaraan yang mengunjungi setiap konsumen, setelah selesai melayani akan meninggalkan konsumen tersebut

∑

(2.13) 8. Variabel keputusan merupakan integer biner

{ } (2.14)

(27)

13

2.4.3 Metode Penyelesaian Capacitated Vehicle Routing Problem with Time Windows

1. Metode Nearest Neighbour

Metode nearest neighbour merupakan metode yang digunakan untuk memecahkan masalah pemilihan rute dengan cara mencari jarak terpendek untuk menempuh lokasi pengiriman. Prinsip dasar dari metode ini adalah membentuk rute dengan memilih konsumen yang terdekat dari lokasi awal.

2. Metode Clarke and Wright Saving

Algoritma Clarke and Wright Savings adalah algoritma yang digunakan untuk menentukan rute distribusi produk ke daerah tujuan dengan cara menentukan rute distribusi yang harus dilalui dan jumlah kendaran berdasarkan kapasitas dari kendaraan tersebut agar diperoleh rute terpendek dan biaya transportasi yang minimal. Algoritma Clarke and Wright Savings melakukan perhitungan penghematan yang diukur dari seberapa banyak dapat dilakukan pengurangan jarak tempuh dan waktu yang digunakan dengan menghubungkan titik–titik yang ada dan menjadikannya sebuah rute berdasarkan nilai saving yang terbesar yaitu jarak tempuh antara titik sumber dan titik tujuan.

(28)

BAB 3

METODOLOGI PENELITIAN

3.1 Jenis Penelitian

Penelitian ini merupakan penelitian aplikatif, yaitu jenis penelitian yang hasilnya dapat secara langsung diterapkan untuk memecahkan permasalahan yang dihadapi.

Penelitian ini menggunakan pendekatan studi literatur dan deskriptif.

Pada studi literatur dilakukan dengan cara mengumpulkan bahan-bahan pustaka yang dibutuhkan oleh peneliti sebagai acuan dalam menyelesaikan penelitian. Sedangkan pendekatan deskriptif kuantitatif yaitu dengan menganalisis data dan menyusun data yang sudah ada sesuai dengan kebutuhan peneliti. Pada penelitian ini, teori yang diuji adalah teori capacitated vehicle routing problem with time windows yang diterapkan pada hasil optimum suatu rute pendistribusian.

3.2 Sumber dan Jenis Data 3.2.1 Sumber Data

Pada penelitian ini data yang digunakan adalah data sekunder. Data sekunder adalah data yang diperoleh dari buku-buku, hasil penelitian, jurnal-jurnal ataupun sarana- sarana lainnya yang biasa diambil dari instansi terkait. Peneliti memperoleh data dari penelitian terdahulu oleh Yan Anisa Dewi (2017), yaitu data rute pendistribusian raskin. Data yang dipakai adalah data jumlah permintaan, jarak antara depot ke setiap pelanggan, jumlah kendaraan yang tersedia, kapasitas setiap kendaraan, waktu pendistribusian yaitu jam buka dan tutup tempat tujuan dan waktu pelayanan. Data tersebut digunakan karena menggunakan Metode Genetika untuk menentukan rute optimum pendistribusian barang.

3.2.2 Jenis Data

Jenis data yang digunakan dalam penelitian ini adalah data kuantitatif yaitu data yang diperoleh dari pabrik dalam bentuk angka-angka seperti jarak antara gudang dan

(29)

15

pelanggan, jumlah permintaan, kapasitas kendaraan, dan biaya transportasi selama perjalanan.

3.3 Rancangan Penelitian

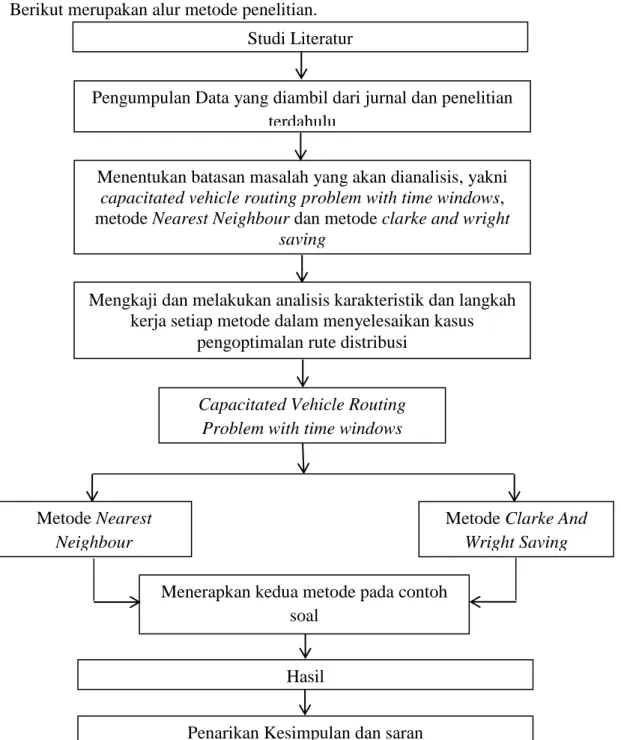
Berikut merupakan alur metode penelitian.

Gambar 3.1 Diagram Rancangan Penelitian Studi Literatur

Menentukan batasan masalah yang akan dianalisis, yakni capacitated vehicle routing problem with time windows, metode Nearest Neighbour dan metode clarke and wright

saving

Penarikan Kesimpulan dan saran

Pengumpulan Data yang diambil dari jurnal dan penelitian terdahulu

Mengkaji dan melakukan analisis karakteristik dan langkah kerja setiap metode dalam menyelesaikan kasus

pengoptimalan rute distribusi

Capacitated Vehicle Routing Problem with time windows

Hasil

Metode Clarke And Wright Saving Metode Nearest

Neighbour

Menerapkan kedua metode pada contoh soal

(30)

3.4 Metodologi Penelitian

Langkah yang dilakukan dengan data yang telah dikumpulkan adalah sebagai berikut:

1. Mengumpulkan sumber informasi

Mengumpulkan dan mempelajari berbagai sumber informasi, berupa buku-buku ataupun jurnal-jurnal yang berhubungan dengan capacitated vehicle routing problem with time windows, metode Nearest Neighbour dan metode clarke and wright savings.

2. Menjelaskan setiap metode optimisasi capacitated vehicle routing problem with time windows, khususnya metode Nearest Neighbour dan metode clarke and wright savings.

3. Melakukan analisis setiap metode dan penggunaan masing-masing metode.

4. Menerapkan dalam penyelesaian contoh kasus dengan metode yang sudah dianalisis.

5. Membuat kesimpulan dan saran.

(31)

BAB 4

HASIL DAN PEMBAHASAN

4.1 Penyelesaian Masalah Capacitated Vehicle Routing Problem with Time Windows (CVRPTW)

4.1.1

Kasus 1

Kasus berikut diperoleh dari penelitian Saraswati R et al. (2017). Pendistribusian koran X diketahui untuk proses distribusi hariannya menggunakan dua buah armada yang memiliki kapasitas masing-masing 3000 eksemplar. Armada ini digunakan sebagai sarana transportasi mendistribusikan koran ke 9 agen yang dimiliki. Kebutuhan untuk masing-masing agen ditunjukkan pada Tabel 4.1

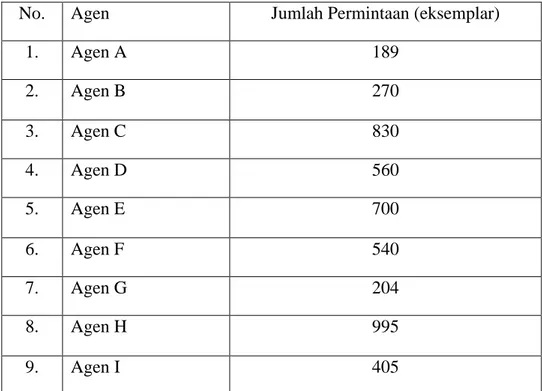
Tabel 4.1 Permintaan setiap agen

No. Agen Jumlah Permintaan (eksemplar)

1. Agen A 189

2. Agen B 270

3. Agen C 830

4. Agen D 560

5. Agen E 700

6. Agen F 540

7. Agen G 204

8. Agen H 995

9. Agen I 405

(32)

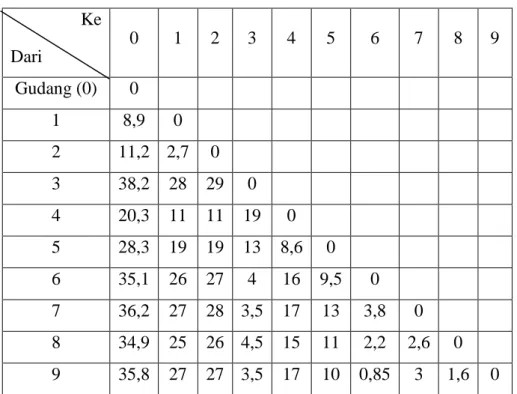
Tabel 4.2 Matriks jarak dari gudang ke setiap agen dan antaragen Ke

0 1 2 3 4 5 6 7 8 9

Dari

Gudang (0) 0

1 8,9 0

2 11,2 2,7 0 3 38,2 28 29 0 4 20,3 11 11 19 0 5 28,3 19 19 13 8,6 0 6 35,1 26 27 4 16 9,5 0 7 36,2 27 28 3,5 17 13 3,8 0 8 34,9 25 26 4,5 15 11 2,2 2,6 0 9 35,8 27 27 3,5 17 10 0,85 3 1,6 0

Tabel 4.3 Data Permintaan, Time Windows, dan Waktu Pelayanan No Agen Jumlah Permintaan

Time Windows

1 Gudang 0 0 315 15

2 Agen 1 189 0 240 4

3 Agen 2 270 0 300 6

4 Agen 3 830 45 240 17

5 Agen 4 560 0 300 13

6 Agen 5 700 0 300 14

7 Agen 6 540 0 270 11

8 Agen 7 204 60 240 5

9 Agen 8 995 45 270 20

10 Agen 9 405 30 240 9

keterangan:

= batas awal time windows pada = batas akhir time windows pada = waktu pelayanan pada

(33)

19

Tabel 4.4 Waktu Tempuh Kendaraan

Gudang 1 2 3 4 5 6 7 8 9

Gudang 0

1 13,35 0

2 16,8 4,05 0

3 57,3 42 43,5 0

4 30,45 16,5 16,5 28,5 0

5 42,45 28,5 28,5 19,5 12,9 0

6 52,65 39 40,5 6 24 14,25 0

7 54,3 40,5 42 5,25 25,5 19,5 5,7 0 8 52,35 37,5 39 6,75 22,5 16,5 3,3 3,9 0 9 53,7 40,5 40,5 5,25 25,5 15 1,275 4,5 2,4 0 Tim operasional perusahaan tersebut ingin memiliki rute tetap yang terbaik agar total jarak dan total waktu distribusi minimum dengan batasan kapasitas kendaraan yang dimemiliki. Dengan demikian tujuan yang ingin dicapai dari kasus ini adalah:

Fungsi tujuan:

Min ∑∑( ∑ ) Kendala

1. Setiap konsumen hanya dikunjungi tepat satu kali oleh kendaraan yang sama

∑ ∑ ∑

2. Total jumlah permintaan konsumen dalam satu rute tidak melebihi kapasitas kendaraan yang melayani rute.

{ } { }

3. Jika ada perjalanan dari konsumen ke ke konsumen ke , maka waktu memulai pelayanan di konsumen ke lebih dari atau sama dengan waktu kendaraan ke untuk memulai pelayanan di konsumen ke ditambah waktu pelayanan konsumen ke dan ditambah waktu tempuh perjalanan dari konsumen ke ke konsumen ke .

(34)

Misalkan terdapat rute dari ke dengan kendaraan k, maka

{ } { }

4. Waktu kendaraan untuk memulai pelayanan di pelanggan ke harus berada pada selang waktu [ ].

{ } { } 5. Setiap rute perjalanan pasti diawali oleh depot

∑ ∑

{ } { } 6. Setiap rute perjalanan pasti diakhiri oleh depot

∑ ∑

{ } { }

7. Kekontinuan rute, artinya kendaraan yang mengunjungi setiap konsumen, setelah selesai melayani akan meninggalkan konsumen tersebut

∑

{ } { } 8. Variabel keputusan merupakan integer biner

{ } { } { } Penyelesaian:

Untuk menyelesaikan permasalahan capacitated vehicle routing problem with time windows diatas, maka dapat dilakukan langkah-langkah sebagai berikut:

4.1.2 Penentuan Solusi Optimal

Ada tiga metode yang digunakan untuk menentukan solusi optimal yaitu:

a. Metode Nearest Neighbour b. Metode Clarke and wright Saving

4.1.2.1 Metode Nearest Neighbour

Metode nearest neigbor adalah metode yang sederhana, dimana setiap iterasinya dilakukan pencarian pelanggan terdekat dengan pelanggan yang terakhir untuk ditambahkan pada akhir rute tersebut. Berikut merupakan algoritma penyelesaian metode nearest neighbour:

(35)

21

Langkah 1 : Cari konsumen ke-j yang memiliki waktu tempuh terpendek dari titik awal i.

Langkah 2 : Hitung total waktu tempuh kendaraan (Wt = t + waktu pelayanan i + Wtij,t). Untuk maka . Jika maka lanjut ke Langkah 3. Jika , maka lanjut ke Langkah 5.

Langkah 3 : Hitung permintaan kendaraan (demand = demand + qi). Jika demand ≤ Q, maka lanjut ke Langkah 4. Jika demand > Q, maka lanjut ke Langkah 5.

Langkah 4 : Set konsumen ke-j sebagai titik awal, kemudian ulangi ke Langkah 2.

Langkah 5 : Batalkan pemilihan konsumen, kemudian pilih konsumen yang belum dilayani dan yang terdekat dengan titik awal berdasarkan keterurutan dan kembali ke Langkah 2. Jika semua konsumen tidak ada yang layak, lanjutkan ke Langkah 6.

Langkah 6 : Kembali ke depot dan lanjut ke Langkah 8.

Langkah 7 : Jika pada saat kembali ke depot , maka batalkan konsumen terakhir dan kembali ke depot.

Untuk melihat bagaimana proses pada metode nearest neighbour menemukan solusi optimal, maka dilakukan contoh permasalahan capacitated vehicle routing problem with time windows pada subbab 4.1.1.

Pembentukan rute pertama

Langkah 1 : Perjalanan berawal dari gudang menuju agen yang akan dilayani berdasarkan matriks waktu tempuh terkecil dari depot, yaitu agen 1 dengan waktu tempuh 13,35 14 menit.

Langkah 2 : Waktu tempuh dari gudang ke agen 1 ( ) adalah 14 menit , maka agen mulai dilayani pada pukul 03.14 dengan lama pelayanan ( ) 4 menit

Langkah 3 : Total demand 189 eksemplar < kapasitas kendaraan.

Jadi, rute sementara yang terbentuk adalah 0 – 1 dengan waktu tempuh total = + s1 = 14 + 4 = 18 menit, total demand =

(36)

189 eksemplar, dan kendaraan selesai melayani agen 1 pada pukul 03.18.

Langkah 4 : Agen yang terakhir dikunjungi adalah agen 1, maka agen yang akan dikunjungi selanjutnya adalah agen yang memiliki waktu tempuh terkecil dari agen 1, yaitu agen 2 dengan waktu tempuh 4,05 5 menit.

Kembali ke langkah 2

Langkah 2 : Waktu tempuh dari agen 1 ke agen 2 ( ) adalah 5 menit, maka total waktu tempuh sementara adalah 23 menit , agen mulai dilayani pada pukul 03.23 dengan lama pelayanan ( ) 6 menit

Langkah 3 : Total demand 189 + 270 = 459 eksemplar < kapasitas kendaraan.

Jadi, rute sementara yang terbentuk adalah 0 – 1 – 2 dengan waktu tempuh total = menit, total demand = 459 eksemplar, dan kendaraan selesai melayani agen 2 pada pukul 03.29.

Langkah 4 : Agen yang terakhir dikunjungi adalah agen 2, maka agen yang akan dikunjungi selanjutnya adalah agen yang memiliki waktu tempuh terkecil dari agen 2, yaitu agen 4 dengan waktu tempuh 16,5 17 menit.

Langkah 2 : Total waktu tempuh sementara adalah 46 menit , agen mulai dilayani pada pukul 03.46 dengan lama pelayanan ( ) 13 menit

Langkah 3 : Total demand 189 + 270 + 560 = 1019 eksemplar < kapasitas kendaraan.

Jadi, rute sementara yang terbentuk adalah 0 – 1 – 2 – 4 dengan waktu tempuh total menit, total demand = 1019 eksemplar, dan kendaraan selesai melayani agen 4 pada pukul 03.59.

(37)

23

Langkah 4 : Agen yang terakhir dikunjungi adalah agen 4, maka agen yang akan dikunjungi selanjutnya adalah agen 5 dengan waktu tempuh 12,9 13 menit

Langkah 3 : Total demand 189 + 270 + 560 + 700 = 1719 eksemplar <

kapasitas kendaraan.

Jadi, rute sementara yang terbentuk adalah 0 – 1 – 2 – 4 – 5 dengan waktu tempuh total menit, total demand = 1719 eksemplar, dan kendaraan selesai melayani agen 5 pada pukul 04.26.

Langkah 3 : Total demand 189 + 270 + 560 + 700 + 540 = 2259 eksemplar <

kapasitas kendaraan.

Jadi, rute sementara yang terbentuk adalah 0 – 1 – 2 – 4 – 5 – 6 dengan waktu tempuh total = menit, total demand = 2259 eksemplar, dan kendaraan selesai melayani agen 6 pada pukul 04.52.

(38)

Langkah 3 : Total demand 189 + 270 + 560 + 700 + 540 + 405 = 2664 eksemplar < kapasitas kendaraan.

Jadi, rute sementara yang terbentuk adalah 0 – 1 – 2 – 4 – 5 – 6 – 9 dengan waktu tempuh total menit, total demand = 2664 eksemplar, dan kendaraan selesai melayani agen 9 pada pukul 05.03.

Lanjut ke langkah 6

Langkah 6 : Menutup rute dengan menambahkan gudang pada akhir perjalanan

Rute 1 : Gudang – agen 1 – agen 2 – agen 4 – agen 5 – agen 6 – agen 9 – Gudang

Langkah 1 : Perjalanan berawal dari gudang menuju agen yang akan dilayani berdasarkan matriks waktu tempuh terkecil dari depot, yaitu agen 8 dengan waktu tempuh 52,35 53 menit.

Langkah 2 : Waktu tempuh dari depot ke agen 8 ( ) adalah 53 menit , maka agen mulai dilayani pada pukul 03.53 dengan lama pelayanan ( ) 20 menit

Langkah 3 : Total demand 995 eksemplar < kapasitas kendaraan.

Jadi, rute sementara yang terbentuk adalah 0 – 8 dengan waktu tempuh total = menit, total demand = 995 eksemplar, dan kendaraan selesai melayani agen 8 pada pukul 04.13.

(39)

25

Langkah 3 : Total demand 995 + 204 = 1199 eksemplar < kapasitas

kendaraan. Jadi, rute sementara yang terbentuk adalah 0 – 8 – 7 dengan waktu tempuh total menit, total demand = 1199 eksemplar, dan kendaraan selesai melayani agen 7 pada pukul 04.22.

Langkah 3 : Total demand 995 + 204 + 830 = 2029 eksemplar < kapasitas kendaraan.

Jadi, rute sementara yang terbentuk adalah 0 – 8 – 7 – 3 dengan waktu tempuh total menit, total demand = 2029 eksemplar, dan kendaraan selesai melayani agen 3 pada pukul 04.45.

Lanjut ke langkah 6

Langkah 6 : Menutup rute dengan menambahkan gudang pada akhir perjalanan

Rute 2: Gudang – agen 8 – agen 7 – agen 3 – gudang

Solusi akhir dari penyelesaian menggunakan metode nearest neighbour untuk permasalahan contoh soal capacitated vehicle routing problem with time windows pada subbab 4.1.1, diperoleh:

(40)

Tabel 4.5 Perolehan Rute Kendaraan

Rute Urutan Pengiriman

Total Kapasitas (eksemplar)

Total Jarak (km)

Lama Pendistrib

usian (menit) 1 Gudang – agen 1 – agen 2 – agen 4 – agen 5

– agen 6 – agen 9 – gudang 2664 77,35 177

2 Gudang – agen 8 – agen 7 – agen 3 –

gudang 2029 79,2 163

Total 156,55 340

4.1.2.2 Metode Clarke and wright Saving

Metode ini merupakan salah satu pendekatan heuristik yang digunakan sebagai solusi untuk permasalahan rute kendaraan dimana sekumpulan rute pada setiap langkah ditukar untuk mendapatkan sekumpulan rute yang lebih baik. Metode ini didasari pada suatu konsep yang disebut savings.

Berikut merupakan algoritma penyelesaian metode Clarke and wright Saving:

Langkah 1 : Buat matriks jarak dari gudang ke agen dan antar agen.

Tabel 4.6 Bentuk Umum Matriks Jarak

... ... ...

0

... 0

0

... 0

0

... 0

0

keterangan:

= depot = node ke = node ke

= jarak dari depot ke node

= jarak dari node i ke node

(41)

Langkah 2 : Hitung nilai penghematan ( ) menggunakan persamaan

pada setiap agen untuk mengetahui nilai penghematan.

Langkah 3 : Membuat matriks penghematan

Tabel 4.7 Bentuk Umum Saving Matriks

... ... ...

0

... 0

0

... 0

0

... 0

0

keterangan:

= Nilai penghematan jarak dari node ke node

Langkah 4 : Menentukan agen yang ditugaskan pada rute dengan cara memilih kombinasi agen dengan nilai saving terbesar.

Langkah 5 : Hitung banyaknya jumlah permintaan dari agen yang telah terpilih.

Langkah 6 : Cek kembali jika Jumlah permintaan ≤ kapasitas kendaran dan total waktu pelayanan ≤ waktu kendaraan, kembali ke langkah 4, jika tidak lanjut ke langkah 7

Langkah 7 : Membuat rute baru, kembali ke langkah 4

Untuk melihat bagaimana proses pada metode Clarke and wright Saving menemukan solusi optimal, maka dilakukan contoh permasalahan Capacitated Vehicle Routing Problem with time windows sebelumnnya.

Langkah 1 : Membuat matriks jarak dari gudang ke agen dan antaragen.

Dapat dilihat pada Tabel 4.1 .

(42)

Langkah 2 : Menghitung nilai saving menggunakan persamaan

Untuk perhitungan nilai saving agen 1 dan agen 2 dengan persamaan diatas diperoleh

Sehingga diperoleh nilai saving untuk semua agen.

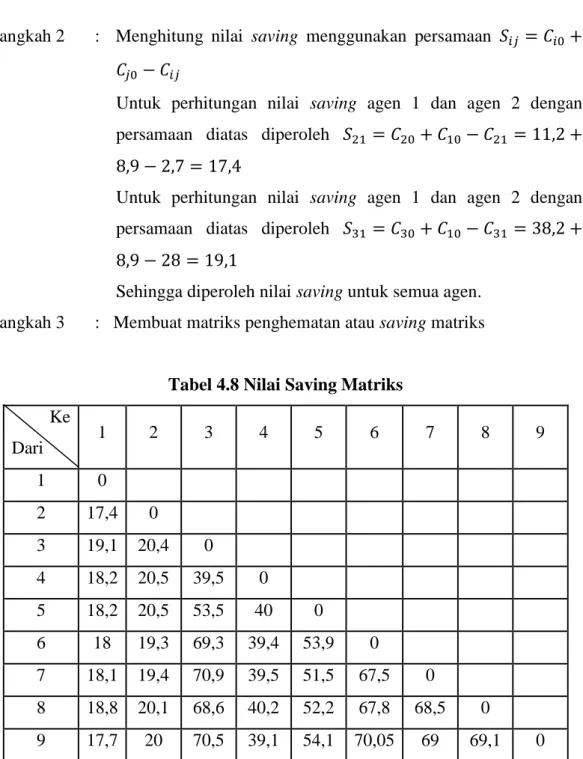
Langkah 3 : Membuat matriks penghematan atau saving matriks

Tabel 4.8 Nilai Saving Matriks

Ke 1 2 3 4 5 6 7 8 9

Dari

1 0

2 17,4 0

3 19,1 20,4 0

4 18,2 20,5 39,5 0

5 18,2 20,5 53,5 40 0

6 18 19,3 69,3 39,4 53,9 0

7 18,1 19,4 70,9 39,5 51,5 67,5 0

8 18,8 20,1 68,6 40,2 52,2 67,8 68,5 0

9 17,7 20 70,5 39,1 54,1 70,05 69 69,1 0

Langkah 4 : Menentukan agen yang ditugaskan pada rute dengan cara memilih kombinasi agen dengan nilai saving terbesar.

(43)

29

Tabel 4.9 Metode Clarke And Wright Saving Iterasi 1 Ke

1 2 3 4 5 6 7 8 9

Dari

1 0

2 17,4 0

3 19,1 20,4 0

4 18,2 20,5 39,5 0

5 18,2 20,5 53,5 40 0

6 18 19,3 69,3 39,4 53,9 0

7 18,1 19,4 70,9 39,5 51,5 67,5 0

8 18,8 20,1 68,6 40,2 52,2 67,8 68,5 0

9 17,7 20 70,5 39,1 54,1 70,05 69 69,1 0 Memilih nilai penghematan terbesar dalam matriks penghematan, yaitu yang letaknya berada di baris 7 dan kolom 3. Agen 7 dan agen 3 gabung menjadi satu rute dalam rute kendaraan 1, sehingga permintaannya dan masih belum melebihi kapasitas kendaraan yaitu 3000 eksemplar.

Langkah 5 :

Tabel 4.10 Metode Clarke And Wright Saving Iterasi 2

Ke 1 2 3 4 5 6 7 8 9

Dari

1 0

2 17,4 0

3 19,1 20,4 0

4 18,2 20,5 39,5 0

5 18,2 20,5 53,5 40 0

6 18 19,3 69,3 39,4 53,9 0

7 18,1 19,4 70,9 39,5 51,5 67,5 0

8 18,8 20,1 68,6 40,2 52,2 67,8 68,5 0

9 17,7 20 70,5 39,1 54,1 70,05 69 69,1 0

(44)

Memilih nilai penghematan terbesar selanjutnya dalam matriks penghematan, yaitu yang letaknya berada di baris 9 dan kolom 6. Agen 9 dan agen 6 gabung menjadi satu rute dalam rute kendaraan 1, sehingga permintaannya dan masih belum melebihi kapasitas kendaraan yaitu 3000 eksemplar.

Langkah 6 :

Ke 1 2 3 4 5 6 7 8 9

Dari

1 0

2 17,4 0

3 19,1 20,4 0

4 18,2 20,5 39,5 0

5 18,2 20,5 53,5 40 0

6 18 19,3 69,3 39,4 53,9 0

7 18,1 19,4 70,9 39,5 51,5 67,5 0

8 18,8 20,1 68,6 40,2 52,2 67,8 68,5 0

9 17,7 20 70,5 39,1 54,1 70,05 69 69,1 0 Memilih nilai penghematan terbesar selanjutnya dalam matriks penghematan, yaitu yang letaknya berada di baris 8 dan kolom 7. Karena agen 7 sudah masuk ke dalam rute, maka langkah selanjutnya adalah menambahkan agen 8 ke dalam rute kendaraan 1, sehingga permintaannya dan belum melebihi kapasitas kendaraan.

(45)

31

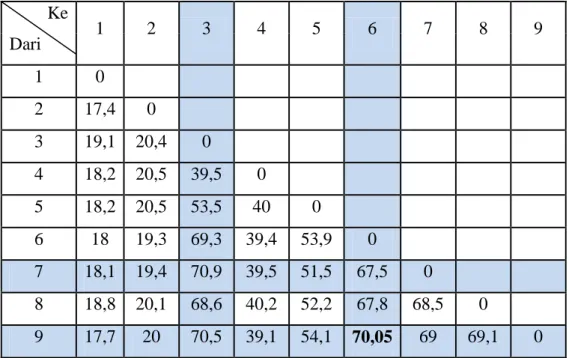
Langkah 7 :

1 2 3 4 5 6 7 8 9

Dari

1 0

2 17,4 0

3 19,1 20,4 0

4 18,2 20,5 39,5 0

5 18,2 20,5 53,5 40 0

6 18 19,3 69,3 39,4 53,9 0

7 18,1 19,4 70,9 39,5 51,5 67,5 0

8 18,8 20,1 68,6 40,2 52,2 67,8 68,5 0

9 17,7 20 70,5 39,1 54,1 70,05 69 69,1 0 Memilih nilai penghematan terbesar selanjutnya dalam matriks penghematan, yaitu yang letaknya berada di baris 6 dan kolom 5. Agen 6 sudah masuk ke dalam rute kendaraan 1 tetapi jika agen 5 digabung ke dalam rute kendaraan 1, maka akan melebihi kapasitas kendaraan, maka agen 5 dibuat dalam rute baru, dengan permintaannya .

Langkah 8 :

1 2 3 4 5 6 7 8 9

Dari

1 0

2 17,4 0

3 19,1 20,4 0

4 18,2 20,5 39,5 0

5 18,2 20,5 53,5 40 0

6 18 19,3 69,3 39,4 53,9 0

7 18,1 19,4 70,9 39,5 51,5 67,5 0

8 18,8 20,1 68,6 40,2 52,2 67,8 68,5 0

9 17,7 20 70,5 39,1 54,1 70,05 69 69,1 0

(46)

Memilih nilai penghematan terbesar selanjutnya dalam matriks penghematan, yaitu yang letaknya berada di baris 5 dan kolom 4. Karena agen 5 sudah masuk ke dalam rute kendaraan 1, maka langkah selanjutnya adalah memasukkan agen 4 dalam rute kendaraan 2, dengan permintaannya dan belum melebihi kapasitas kendaraan.

Langkah 9 :

Ke 1 2 3 4 5 6 7 8 9

Dari

1 0

2 17,4 0

3 19,1 20,4 0

4 18,2 20,5 39,5 0

5 18,2 20,5 53,5 40 0

6 18 19,3 69,3 39,4 53,9 0

7 18,1 19,4 70,9 39,5 51,5 67,5 0

8 18,8 20,1 68,6 40,2 52,2 67,8 68,5 0

9 17,7 20 70,5 39,1 54,1 70,05 69 69,1 0 Memilih nilai penghematan terbesar selanjutnya dalam matriks penghematan, yaitu 2 yang letaknya berada di baris 4 dan kolom 2. Karena agen 4 sudah masuk ke dalam rute kendaraan 1, maka langkah selanjutnya adalah memasukkan agen 2 menjadi satu rute dalam rute kendaraan 2, dengan permintaannya dan belum melebihi kapasitas kendaraan yaitu 3000.

(47)

33

Langkah 10 :

1 2 3 4 5 6 7 8 9

Dari

1 0

2 17,4 0

3 19,1 20,4 0

4 18,2 20,5 39,5 0

5 18,2 20,5 53,5 40 0

6 18 19,3 69,3 39,4 53,9 0

7 18,1 19,4 70,9 39,5 51,5 67,5 0

8 18,8 20,1 68,6 40,2 52,2 67,8 68,5 0

9 17,7 20 70,5 39,1 54,1 70,05 69 69,1 0 Memilih nilai penghematan terbesar selanjutnya dalam matriks penghematan, yaitu yang letaknya berada di baris 3 dan kolom 1. Karena agen 3 sudah masuk ke dalam rute kendaraan 1, maka agen 1 dimasukkan ke dalam rute kendaraan 2, dengan permintaannya . Setelah semua agen masuk ke dalam rute pendistribusian, maka hitung waktu selama pendistribusian barang dengan rumus sebagai berikut:

Sehingga diperoleh

Tabel 4.16 Waktu Distribusi

Lokasi 1 Lokasi 2 Pukul Lama Pendistribusian (menit)

0 7 03:55-04:00

188

7 3 04:06-04:23

3 9 04:29-04:38

9 6 04:40-04:51

6 8 04:55-05:15

8 0 06:08

0 5 03:43-03:57

129

5 4 04:10-04:23

4 2 04:40-04:46

2 1 04:51-04:55

1 0 05:09

Total 317

(48)

Tabel 4.17 Perolehan Rute Kendaraan No

Rute Urutan Pengiriman

Total Kapasitas (eksemplar)

Total Jarak

(km) 1 Gudang – agen 7 – agen 3 – agen 9 – agen 6 – agen

8 – gudang 2974 81,15

2 Gudang – agen 5 – agen 4 – agen 2 – agen 1 –

gudang 1719 59,5

Total 140,65

Dari jawaban kedua metode diatas dapat dilihat pada Tabel 4.18 berikut:

Tabel 4.18 Perbandingan Terhadap Parameter

Parameter Metode Nearest Neighbour Metode Clarke and Wright Savings

Jumlah Rute 2 2

Total Jarak

minimum (km) 156,55 140,65

Waktu

Pendistribusian (menit)

340 317

Persentasi Rata-rata Efisiensi Kapasitas (%)

61% 78%

Dari kedua metode yang telah diuraikan maka akan diperlihatkan perbandingan tiap-tiap metode yaitu metode nearest neighbour dan metode clarke and wright saving dalam menentukan solusi optimal.

Tabel 4.19 Analisa Terhadap 2 Metode Untuk Menentukan Solusi Optimal No. Metode Nearest Neighbour Metode Clarke And Wright

Saving 1. Pada metode ini penyelesaian

permasalahan dilakukan dengan menambahkan pelanggan terdekat

Pada metode ini penyelesaian permasalahan dilakukan dengan membuat tabel iterasi

2. Tidak perlu mencari nilai saving Untuk mencari solusi optimal dilakukan dengan mencari nilai saving

3. Pada metode ini waktu Pada metode ini memerlukan

(49)

35

penyelesaiannya lebih singkat karena pada prosesnya tidak memerlukan iterasi

waktu yang lebih lama dibandingkan metode nearest neighbour karena pada prosesnya harus menghitung nilai penghematan dan mengurutkannya

Pada contoh soal yang penulis berikan pada uraian sebelumnya, solusi yang diperoleh dari metode nearest neighbour yaitu total jarak tempuh 156,55 km, lama pendistribusian 340 menit dan dengan metode clarke and wright saving yaitu total jarak tempuh 140,65 km, lama pendistribusian 317 menit. Kedua metode menghasilkan solusi yang berbeda, meskipun pengerjaan metode nearest neighbour cukup mudah dengan menambahkan agen selanjutnya berdasarkan waktu tempuh paling minimum dari agen sebelumnya belum dapat memberikan hasil optimum untuk digunakan perusahaan. Sedangkan metode clarke and wright saving dapat menghasilkan jarak dan waktu yang minimum.

4.2 Kasus 2

Kasus ini dikutip dari penelitian Yan Anisa Dewi (2017) tentang Implementasi Algoritma Genetika Dengan Variasi Seleksi Dalam Penyelesaian Capacitated Vehicle Routing Problem With Time Windows (CVRPTW) Untuk Optimasi Rute Pendistribusian Raskin.

Proses pendistribusian raskin saat ini tidak terdapat ketentuan baku mengenai titik distribusi mana yang harus didatangi diawal, tetapi proses pendistribusian biasanya dilakukan dengan menyelesaikan beberapa kelurahan terlebih dahulu yang terdapat pada kecamatan yang sama. Untuk menganalisis permasalahan pengoptimalan rute distribusi, diperlukan data sebagai berikut:

Tabel 4.20 Time Windows Kelurahan

No. Kelurahan Time Windows

1. Bener 08.00 – 12.00

2. Kricak 08.00 – 12.00

3. Karangwaru 08.00 – 12.00

4. Tegalrejo 08.00 – 12.00

(50)

5. Bumijo 08.00 – 12.00

6. Gowongan 08.00 – 12.00

7. Cokrodiningratan 08.00 – 12.00

8. Demangan 08.00 – 13.00

9. Terban 08.00 – 12.00

10. Kotabaru 08.00 – 12.00

11. Baciro 08.00 – 12.00

12. Klitren 09.00 – 13.30

13. Suryamatjan 10.00 – 12.30

14. Tegalpanggung 08.00 – 12.00

15. Bausasran 08.00 – 12.00

Tabel 4.21 Data Jumlah Permintaan, Time Windows, dan Waktu Pelayanan

No Kelurahan

Jumlah Permintaan

(kg)

Time Windows

(menit)

1 Gudang 0 0 360 120

2 Bener 3.990 0 240 51,15

3 Kricak 11.250 0 240 144,23

4 Karangwaru 5.655 0 240 72,5

5 Tegalrejo 5.460 0 240 70

6 Bumijo 7.215 0 240 92,5

7 Gowongan 5.325 0 240 68,27

8 Cokrodiningratan 3.330 0 240 42,69

9 Demangan 2.340 0 300 30

10 Terban 1.965 0 240 25,19

11 Kotabaru 660 0 240 8,46

12 Baciro 5.505 0 240 70,58

13 Klitren 3.630 60 270 46,54

14 Suryamatjan 3.045 120 150 39,04

15 Tegalpanggung 8.145 0 240 104,42

(51)

37

16 Bausasran 3.345 0 240 42,88

(52)

Tabel 4.22 Jarak Tempuh Kendaraan (km)

Ke 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Dari

0 0

1 14,1 0

2 13,7 2,6 0

3 13,5 3,3 1,1 0

4 14,3 2,1 2,8 3,3 0

5 13,2 2,2 1,8 2,2 1,2 0

6 12,8 3,1 2,2 1,9 3,2 1 0

7 12,3 2,6 1,6 1,2 2,8 1,8 1 0

8 9,9 5,9 4,9 4,7 4,9 4 4,1 4,3 0

9 11,5 3,5 2,9 2,9 3,7 2,7 2,1 2,4 2,3 0

10 11,7 3,8 3,3 3,1 3,6 2,6 2,7 2,7 2,5 1,1 0 11 11,2 5,6 4,8 4,6 4,6 3,7 3,8 4,2 1,4 2,6 1,6 0 12 10 6,3 4,6 4,2 5,4 4,4 4,5 3,7 0,85 3,2 2,2 1,9 0 13 13 4,2 3,4 3,2 2,9 2 2,5 2,8 3,8 2,4 2,1 2,5 3,4 0 14 12,2 4,6 3,8 3,6 3,3 2,4 2,1 3,2 3 1,6 1,3 2,3 2,6 0,75 0 15 12,5 5,1 4,6 4,5 4,2 3,2 3,3 4 2,5 2,6 1,6 1,2 2,6 1,3 1,2 0