LANDASAN TEORI
2.1 Teori graf 2.1.1 Defenisi graf
Graf G adalah pasangan { , } dengan adalah himpunan terhingga
yang tidak kosong dari objek-objek yang disebut titik (vertex) dan adalah
himpunan pasangan tidak berurutan dari titik-titik berbeda di yang disebut sisi (edge). Misalkan graf G yang memuat himpunan titik dan himpunan sisi
seperti berikut ini. = { , , , , }
= { , , , , , , , , , , , , , } Graf G tersebut dapat dilihat pada Gambar 2.1 (Munir 2009).
a b
G:
b d e Gambar 2.1 Graf G
2.1.2 Graf Terhubung (Connected Graph)
Graf G dikatakan terhubung jika untuk setiap pasangan verteks dalam G terdapat
Gambar 2.2 Graf Terhubung
2.1.3 Graf Berbobot (Weighted Graph)
Graf berbobot adalah graf yang setiap nilainya diberi sebuah nilai atau bobot.
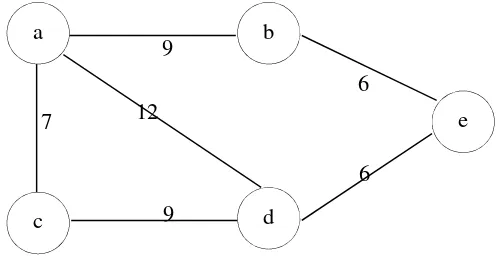
Bobot pada setiap sisi graf dapat berbeda-beda bergantung pada masalah yang dimodelkan. Dalam tugas akhir ini, bobot pada setiap graf menyatakan jumlah permintaan pelanggan. Contoh graf berbobot dapat dilihat pada Gambar 2.3.
Gambar 2.3 Graf Berbobot
2.1.4 Graf Berarah (Directed Graph)
Graf berarah adalah graf yang setiap edge nya memiliki orientasi arah atau panah.
Pada graf berarah , ≠ , . Contoh graf berarah dapat dilihat pada
Gambar 2.4.
6 9
12
6 7
9 a
b
c
d
a
c d
b
Gambar 2.4 Graf Berarah
2.1.5 Graf Tidak Berarah (Undirected Graph)
Graf tidak bearah adalah graf yang edge nya tidak mempunyai orientasi arah atau panah. Pada graf ini, urutan pasangan verteks yang dihubungkan oleh edge tidak
diperhatikan. Jadi , = , . Contoh graf tak berarah dapat dilihat pada
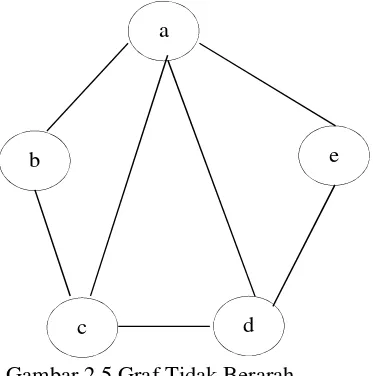
Gambar 2.5.
Gambar 2.5 Graf Tidak Berarah
2.2 Vehicle Routing Problem (VRP)
VRP diperkenalkan pertama kali oleh Dantziq dan Ramser pada tahun 1959 dan semenjak itu dipelajari secara luas. VRP didefnisikan sebagai sebuah pencarian
a
c d
b
e
b
a
c
e
atau penggunaan yang efisien untuk sejumlah kendaraan (vehicle) dimana
kendaraan tersebut harus mengunjungi sejumlah tempat untuk mengantar dan/atau menjemput orang/barang. Istilah pelanggan digunakan untuk menunjukkan tempat pemberhentian. Dan seorang pelanggan hanya boleh dilayani oleh sebuah kendaraan (vehicle) saja. Hal ini dilakukan untuk meminimalkan biaya yang diperlukan dengan mempertimbangkan kapasitas sebuah kendaraan dalam satu
kali pengantaran.
Bentuk dasar VRP berkaitan dengan masalah penentuan suatu himpunan kendaraan (vehicle) yang melayani satu himpunan konsumen yang diasosiasikan dengan vertex dan demand (permintaan) yang diketahui dan rute yang menghubungkan depot dengan satu konsumen dengan konsumen yang lain. VRP sering disebut sebagai Multi Traveling Salesman Problem (MTSP) di mana VRP
merupakan masalah kombinatorial dari dua masalah, yaitu Traveling Salesman Problem (TSP) dan Bin Packing Problem (BPP) (Toth dan Vigo 2002).
BPP dan TSP dikategorikan sebagai permasalahan NP-hard problem, sehingga VRP juga dapat dikategorikan sebagai NP-hard problem, dalam
optimasi kombinatorial yang mungkin belum ditemukan metode eksak untuk mencari nilai optimalnya. Untuk memecahkan VRP berskala kecil dengan beberapa pelanggan dan semua kendaraannya mempunyai kapasitas yang sama, algoritma branch and bound terbukti sebagai metode terbaik dalam mencari solusi optimal. Dan untuk memecahkan VRP berskala besar dapat diselesaikan secara heuristik. Heuristik adalah algoritma berbasis kira-kira, yang berusaha mencari
solusi optimal secepat mungkin. Metaheuristik adalah aturan-aturan penyelesaian secara umum yang memperluas ruang solusi untuk mengidentifikasi solusi yang
baik dan sering menyimpan beberapa susunan rute standar serta perbaikan
heuristik.
Tujuan yang ingin dicapai dalam VRP, antara lain:
1. Meminimalkan biaya perjalanan secara keseluruhan yang dipengaruhi oleh keseluruhan jarak yang ditempuh dan jumlah kendaraan yang digunakan. 2. Meminimalkan jumlah kendaraan yang digunakan untuk melayani semua
3. Menyeimbangkan rute.
4. Meminimalkan keluhan pelanggan.
Secara matematis VRP dapat dinyatakan sebagai suatu graf = ,
dengan = {0,1, … , } menyatakan himpunan vertex yang menunjukkan lokasi konsumen dan = { , ! | , ! , ≠ !} yaitu himpunan sisi berarah yang menyatakan jalan penghubung antar lokasi konsumen. Vertex 0 menunjukkan depot, yaitu tempat menyimpan kendaraan yang digunakan untuk distribusi dan
+ ,%9 = + ,9 ; ∀5 = 1,2, … , 6 ∀: = 1,2, … ,
Fungsi objektif dari VRP (2.1) adalah meminumkan total biaya perjalanan,
dengan &% adalah biaya perjalanan dari konsumen i menuju konsumen j. Variabel
keputusan ,% bernilai 1 jika rute dari konsumen i menuju konsumen j dilayani
oleh kendaraan k dan bernilai nol jika selainnya. Pada kendala (2.2) dan (2.3) dipastikan tepat satu kendaraan yang datang dan pergi dari konsumen i, sedangkan kendala (2.4) dan (2.5) memastikan bahwa tepat satu kendaraan yang pergi dan tiba di depot untuk satu rute. Kendala (2.6) memastikan kekontinuan rute dari
setiap kendaraan yang beroperasi. Kendala (2.7) memastikan total permintaan ($%) pada satu rute tidak melebihi kapasitas kendaraan & yang beroperasi pada rute
tersebut (Kritikos & Ioannou 2004).
Menurut Agus Purnomo (2010), variasi dari VRP antara lain: 1. Capasitated VRP (CVRP)
Faktor: Setiap kendaraan punya kapasitas yang terbatas 2. VRP with Time Windows (VRPTW)
Faktor: Setiap pelanggan harus disuplai dalam jangka waktu tertentu 3. Multiple Depot VRP (MDVRP)
Faktor: Distributor memiliki banyak depot untuk menyuplai pelanggan 4. VRP With Pick-up and Delievering (VRPPD)
Faktor: Pelanggan mungkin mengembalikan barang pada depot asal. 5. Split Delievery VRP (SDVRP)
Faktor: Munculnya random values (seperti jumlsh pelanggan, jumlah permintaan, waktu pelayanan atau waktu perjalanan.
7. Periodic VRP
Faktor: Pengantaran hanya dilakukan di hari tertentu.
2.2 Capasitated Vehicle Routing Problem (CVRP)
CVRP adalah sebuah VRP di mana diberikan sejumlah kendaraan dengan kapasitas tersendiri yang harus melayani sejumlah permintaan pelanggan yang telah diketahui untuk satu komoditas dari sebuah depot dengan biaya transit
minimum. Oleh karena itu, CVRP sama seperti VRP dengan faktor tambahan yaitu tiap kendaraan punya kapasitas tersendiri untuk satu komoditas. CVRP dapat dijabarkan sebagai berikut:
1. Tujuan: Meminimalisasi jumlah kendaraan dan total waktu perjalanan, dan total permintaan barang untuk tiap rute tidak boleh melebihi kapasitas
kendaraan yang melewati rute tersebut.
2. Kelayakan: Solusi dikatakan ‘layak’ jika jumlah total barang yang diatur untuk tiap rute tidak melebihi kapasitas kendaraan yang melewati rute tersebut.
3. Perhitungan: Misalkan K melambangkan kapasitas sebuah kendaraan. Secara matematis, solusi untuk CVRP sama dengan VRP, tapi dengan batasan
tambahan total permintaan pelanggan pada rute @% tidak boleh melebihi
kapasitas kendaraan atau ∑ $C%. % ≤ B, di mana @% merupakan rut ke-i.
Tonci Caric and Hrvoje Gold, (2008) mendefinisikan CVRP sebagai suatu graf berarah = , dengan = {#D, # , # , … , #/, #/E } adalah himpunan
sebesar $%. Himpunan B = {5 , 5 , … , 5/} merupakan himpunan kendaraan dengan kapasitas yang terbatas yaitu Q, sehingga panjang setiap rute dibatasi oleh
kapasitas kendaraan. Setiap node #%, # memiliki jarak tempuh &% yaitu jarak
dari node ke node !. Jarak perjalanan ini diasumsikan simetrik yaitu &% = &%
dan&%% = 0. Permasalahan dari CVRP adalah menentukan himpunan dari K rute kendaraan yang memenuhi kondisi berikut:
1. Setiap rute berawal dan berakhir di depot
2. Setiap konsumen harus dilayani tepat satu kali oleh satu kendaraan
3. Total permintaan konsumen dari setiap rute tidak melebihi kapasitas
kendaraan
4. Total jarak dari semua rute diminimumkan.
2.3 Algoritma Clarke and Wright’s Savings
Clarke dan Wright (1964) menemukan sebuah metode sederhana untuk mengoptimalkan rute pengiriman, di mana terdapat banyak kendaraan pengangkut dengan berbagai kapasitas yang berasal dari satu pusat yang akan mengirimkan barang-barang ke banyak tempat. Rute terpendek antara dua titik diberikan pada sistem. Tujuan yang ingin dicapai adalah bagaimana mengalokasikan kendaraan
pengangkut, sehingga semua barang dapat terkirim dengan biaya pengirirman serta operasional minimal. Algoritma ini didasari pada suatu konsep savings. Algoritma ini adalah sebuah algoritma heuristik, di mana terjadi perubahan prosedur dalam setiap langkah sehingga menghasilkan yang lebih baik.
Formulasi dari algoritma Clarke and Wrigh’s Savings yaitu sejumlah kendaraan dengan kapasitas dan jumlah permintaan untuk didistribusikan ke beberapa titik berawal dari depot, dengan jarak antar node &% , di antara beberapa
Algoritma Clarke and Wright’s Savings melakukan perhitungan penghematan yang diukur dari seberapa banyak dapat dilakukan pengurangan jarak tempuh dan waktu yang digunakan dengan mengaitkan node-node yang ada dan menjadikannya sebuah rute berdasarkan nilai penghematan yang terbesar yaitu jarak tempuh antara node awal dan node tujuan. Untuk proses perhitungannya, metode ini tidak hanya menggunakan jarak sebagai parameter,
tetapi juga waktu untuk memperoleh nilai penghematan yang terbesar kemudian disusun menjadi sebuah rute yang terbaik. Langkah-langkah pada metode ini adalah sebagai berikut (Clarke and Wright, 1964):
1. Menentukan jumlah kapasitas maksimum kendaraan yang tersedia dan alokasi kendaraan yang digunakan untuk pengiriman barang ke pelanggan, mengasumsikan bahwa setiap node permintaan pada rute awal suatu
kendaraan secara terpisah. Di mana setiap node membentuk rute tersendiri yang dilayani oleh kendaraan yang berbeda. Seperti pada Gambar 2.6 yaitu rute 0-i-0 dilayani oleh satu kendaraan, dan rute 0-j-0 dilayani oleh kendaraan lain yang berbeda, dalam hal ini 0 untuk depot, i dan j untuk node yang lain.
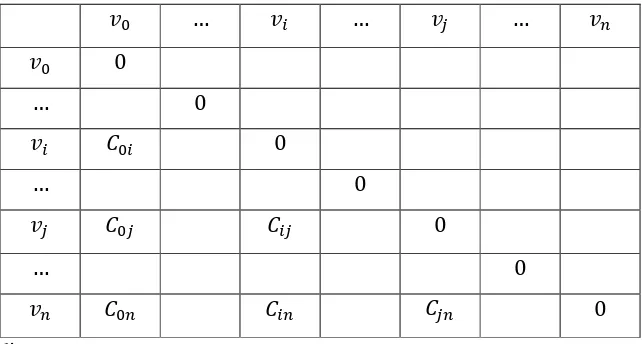
2. Membuat matriks jarak yaitu matriks jarak antara depot dengan node dan antar node. Matriks jarak ini termasuk matriks simetrik karena pengukuran jari dari node A ke node B sama dengan jarak dari node B ke node A. Bentuk umum matriks jarak ini dapat dilihat pada Tabel 2.1.
Tabel 2.1 Bentuk Umum Matriks Jarak
#D … #% … # … #/
#D 0
… 0
#% &D% 0
… 0
# &D &% 0
… 0
#/ &D/ &%/ &/ 0
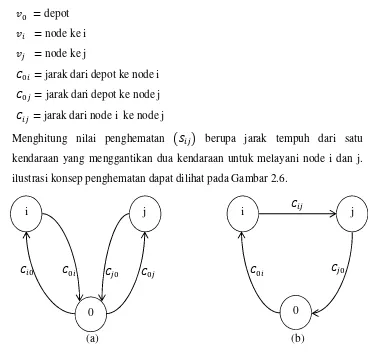
#D = depot ilustrasi konsep penghematan dapat dilihat pada Gambar 2.6.
(a) (b)
Gambar 2.6 Ilustrasi Konsep Penghematan
Nilai penghematan adalah jarak yang dapat dihemat jika rute 0-i-0 digabungkan dengan rute 0-j-0 menjadi rute tunggal 0-i-j-0 yang dilayani oleh
satu kendaraan seperti yang ditunjukkan pada Gambar 2.6 (b). Berdasarkan Ekuivalen dengan rute kendaraan IM pada Gambar 2.6 (b)
IM= &D%+ &% + &D 2.10 Dengan menggabungkan kedua rute diperoleh nilai penghematan:
&D%+ &%D+ &D + &D= &D%+ &% + &D = H% &D%+ &%D+ &D + &D− &D% − &% − &D = H%
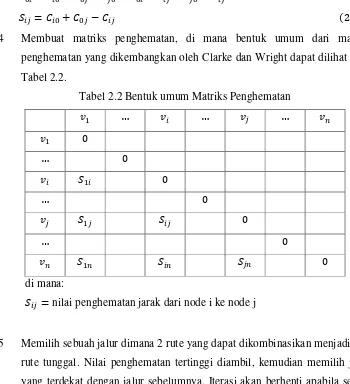
H% = &%D+ &D − &% 2.11 4 Membuat matriks penghematan, di mana bentuk umum dari matriks
penghematan yang dikembangkan oleh Clarke dan Wright dapat dilihat pada Tabel 2.2.
Tabel 2.2 Bentuk umum Matriks Penghematan
# … #% … # … #/
# 0
… 0
#% H % 0
… 0
# H H% 0
… 0
#/ H / H%/ H/ 0
di mana:
H% = nilai penghematan jarak dari node i ke node j
5 Memilih sebuah jalur dimana 2 rute yang dapat dikombinasikan menjadi satu rute tunggal. Nilai penghematan tertinggi diambil, kemudian memilih jarak yang terdekat dengan jalur sebelumnya. Iterasi akan berhenti apabila semua
entri dalam baris dan kolom sudah terpilih.
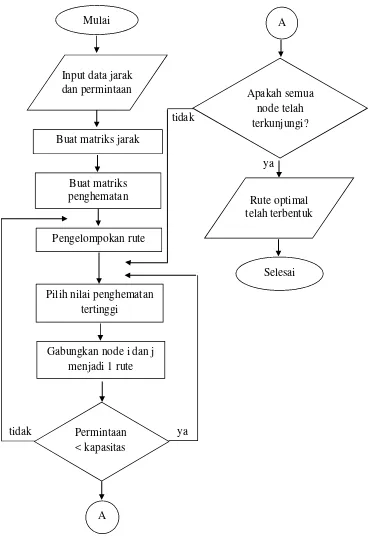
Gambar 2.7 Flowchart Pengerjaan Algoritma Clarke and Wright’s Savings ya
tidak
tidak ya
Mulai
Input data jarak dan permintaan
Buat matriks jarak
Buat matriks penghematan
Pilih nilai penghematan tertinggi
Permintaan < kapasitas Gabungkan node i dan j
menjadi 1 rute
Apakah semua node telah terkunjungi?
A
A
Selesai Rute optimal telah terbentuk