KAJIAN TEORITIS TRANSFORMASI METRIK SCHWARZSCHILD DALAM SISTEM DUA KOORDINAT
SKRIPSI
SABAM PARSIHOLAN SIMBOLON 090801004
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2013
KAJIAN TEORITIS TRANSFORMASI METRIK SCHWARZSCHILD DALAM SISTEM DUA KOORDINAT
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
SABAM PARSIHOLAN SIMBOLON 090801004
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2013
PERNYATAAN
KAJIAN TEORITIS TRANSFORMASI METRIK SCHWARZSCHILD DALAM SISTEM DUA KOORDINAT
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, 25 Juni 2013
SABAM PARSIHOLAN SIMBOLON 090801004
PENGHARGAAN
Terpuji dan termulialah Yesus Kristus yang sampai saat ini, Dia masih tetap memberikan yang terbaik dalam kehidupan saya,terutama dalam penulisan skiripsi ini. Saya sangat menyadari dan percaya tanpa campur tanganNYA perjalanan perkuliahan saya dan penulisan skiripsi ini tidak akan pernah selesai. Semua hanya karena ANUGRAH semata, sesungguhnya saya tidak pernah sanggup dan tidak pernah layak. Saya hanya sedang belajar dan punya kerinduan untuk berjuang hidup benar. Sering saya gagal dan banyak mengalami kejatuhan, Namun saya belajar untuk tetap setia dalam menjalaninya dengan ikhlas hati dan penuh senyuman dalam menghadapinya serta berpengharapan pada-NYA selalu. Saya menyadari bahwa tidak akan pernah ada keberhasilan tanpa adanya dukungan, oleh karena itu dalam kesempatan ini, penulis ingin mengucapkan terima kasih yang sebesar-besarnya kepada mereka yang telah mendukung saya bahkan sampai pada penyelesaian skiripsi ini.
1. Kepada Bapak Drs. Tenang Ginting, M.S dan Bapak Tua Raja Simbolon, S.Si, M.Si selaku pembimbing saya dalam menyelesaikan skiripsi ini yang selalu terbuka dalam memberikan bimbingan maupun motivasi dalam penulisan skripsi ini dan kepada Bapak/Ibu penguji Bapak Drs. Kurnia Sembiring, M.S, Bapak Drs.
Syahrul Humaidi, M.Sc, dan Ibu Dr. Susilawati, S.Si, M.Si
2. Kepada Bapak ibu dosen Departemen FISIKA USU, mulai dari Bapak Dr.Marhaposan Situmorang sebagai ketua departemen FISIKA USU dan kepada Bapak Drs. Syahrul Humaidi, M.Sc selaku sekretaris jurusan beserta staff pegawai di kantor Departemen FISIKA USU yang senantiasa membantu penulis dalam melengkapi administrasi.
3. Kepada orang tua Bapak J. Simbolon (Alm) dan Ibu yang tetap berjuang mendukung dan memotivasi saya selalu dalam kehidupan saya P. br. Siringo-ringo yang saya sayangi dan yang saya cintai, yang selalu memberikan kasih sayang kepada penulis yang tak ternilai dan juga nasehat-nasehatnya yang telah membangun kepribadian saya.
4. Kepada kakak saya R. br Simbolon, L. br Simbolon dan lae L. Hutabalian dan R .P. Sibarani serta bere saya Grace Sibarani, Intan Hutabalian, Gesika Yolanda Sibarani dan Welfrido Hutabalian saya mengucapkan banyak terima kasih untuk setiap dukungan doa dan motivasinya.
5. Kepada Tulang P. Siringo-ringo, M. Siringo-ringo dan Nantulang T. br Simbolon, P. br Sinaga dan Op.Parpunguan Sinaga, Op.Restu br. Simbolon, Bapak Tua Ranto Simbolon, Bapak Tua Basa Ria Simbolon (ALM), Inanguda Binton br.
Sinaga (Alm), B’Hotmian Simbolon, B’Ranto Simbolon, B’Binton Simbolon, saya banyak mengucapkan terima kasih untuk setiap motivasi dan dukungan doanya.
6. Kepada Bapak Dr. Mester Sitepu, M.Sc selaku dosen wali penulis, terima kasih untuk arahan dan bimbinganya.
7. Kepada kelompok kecil saya ‘HARVEST”, ada B’Donal Siregar, S.T dan Riris Hasibuan, terimakasih untuk setiap dukungan doa, kebersamaanya dan bimbingan Rohaninya yang telah saya dapat.
8. Kepada sahabat-sahabat saya di FISIKA stambuk Breaving : Kalam, Sony, Poltak, Enra, Nurjanah, Sukira, Tanu, Helen, Jeni, Suhartina, Rieni, Esra, Agusningsih,Fitri, Agus, Monora, Septiana, Andiko, Istas, Zai, Eldo, Ferdi, Timbul, Josua, Andrian, Arpila, Herdiana, Natanael, Emi, Silvi, Ade, Valentina, Wenni, Stevani, Resdina, saya banyak mengucapkan terimakasih atas kebersamaanya dan setiap motivasinya. Dan kepada seluruh kawan-kawan yang ada di FISIKA USU.
9. Dan kepada teman-teman sepelayanan yang saya cintai di Koordinasi KMKS periode XXIII dan XXIV : Irza, Santy, Budi, Dosma, Inel, Polmer, Selfi, Reynal, Rouli, Plani, Berto, Agustina, Maria, Rianto, Eko, Ruth, Marta, Hanna, Edi, Riris, Myke, Grace, Randy, Linggom, Lenggem, Everson, Franky, Vera, Ervina, Frans, Dinadio, Asni, Simson dan Riswanta terima kasih atas dukungan doa, motivasi dan kebersamaanya yang tak terlupakan.
10. Keluarga besar laboratorium Fisika Inti USU, terima kasih untuk kesempatan mengembangkan diri sebagai seorang asisten dan menimba Ilmu Fisika secara
praktek kepada Ibu Dra. Sudiati, M.Si. Dan kepada teman-teman asisten (K’Fitri, B’Iwan, Fitri, Nurjanah, Arpila, Silvi, Andrian).
11. Kepada B’Hendri Diapari Siregar S.Si dan K’Meli, S.Si, B’Indra Tarigan dan Lae Jeri Harianja, S.T atas dukungan dan motivasinya.
12. Kepada Angkasa Pura II yang memberikan bantuan/beasiswa kepada penulis saya banyak mengucapkan terima kasih.
13. Dan kepada mereka yang tidak saya sebutkan namanya yang telah mendukung penulis , saya ucapkan terima kasih.
Penulis menyadari dalam penulisan skiripsi ini masih jauh dari kesempurnaan, oleh karena itu kritik dan saran yang sifatnya membangun sangat diharapkan untuk penyempurnaan karya-karya penulis selanjutnya.
Akhir kata semoga skripsi ini dapat bermanfaat terutama bagi penulis dan pembaca, terutama juga kepada mereka yang ingin melanjutkan penelitian ini.
Terima kasih….. Syalom Tuhan Yesus memberkati……..
Medan, 25 Juni 2013
Penulis
KAJIAN TEORITIS TRANSFORMASI METRIK SCHWARZSCHILD DALAM SISTEM DUA KOORDINAT
ABSTRAK
Telah dilakukan kajian teoritis mengenai transformasi metrik Schwarzschild dalam sistem dua koordinat, pengkajian transformasi metrik Schwarzschild dalam sistem dua koordinat ini, yaitu koordinat kartesian dan ruang- waktu dipercepat seragam dalam ruang waktu datar serta efek lokal suatu medan gravitasi pada ruang lengkung. Medan gravitasi pada ruang lengkung ini dipilih medan Schwarzschild yang biasanya dinyatakan dalam ruang spatial bola. Melalui transformasi tersebut, metriknya mengandung dua suku : (1) suku yang berhubungan dengan elemen garis dalam kerangka dipercepat seragam, dan (2) suku yang berhubungan dengan kelengkungan serta berkaitan dengan penyimpangan geodesik yang merupakan efek dari kelengkungan ruang waktu. Sehingga dari hasil yang diperoleh memperlihatkan adanya kesamaan antara massa gravitasi dan massa inersial yang kaitannya dengan Teori Relativitas Umum dapat menjelaskan efek lokal dalam suatu medan gravitasi.
Kata kunci : transformasi, koordinat, metrik Schwarzschild
THEORETICAL STUDY OF THE TRANSFORMATION OF THE SCHWARZSCHILD METRIC IN THE SYSTEM OF TWO
COORDINATES
ABSTRACT
Teoritical studies have been made regarding the transformation of the Schwarzschild metric in two coordinates, the Schwarzschild metric transformation study in two coordinates: coordinates Cartesian and accelerated time-space uniform in no time flat spaces as well as local effects of a gravitational field in curved space. Gravitational field in curved space is chosen the Schwarzschild field is usually expressed in spatial space balls. Through these transformations, their metrics contain two people: (1) the rates associated with elements within the framework of the accelerated line uniform, and (2) the tribe associated with the curvature and geodesic deviation with regard to the effect of the curvature of space time. So that the results obtained from the existence of similarities between inertial mass and gravitational mass are relation with the theory of general relativity can explain local effect in the gravitational field .
Key words: Transformation, coordinates, Schwarzschild’s metric
DAFTAR ISI
Halaman
Persetujuan i
Pernyataan ii
Penghargaan iii
Abstrak vi
Abstract vii
Daftar Isi viii
Daftar Simbol x
Daftar Istilah xi
Bab 1 Pendahuluan
1.1 Latar Belakang 1
1.2 Rumusan Masalah 2
1.3 Batasan Masalah 2
1.4 Tujuan Penelitian 2
1.5 Manfaat Penelitian 3
1.6 Metode Penulisan 3
1.7 Sistematika Penulisan 4
Bab 2 Tinjauan Pustaka
2.1 Teori Gravitasi Newton 5
2.1.1 Hukum Gravitasi Universal Newton 6
2.1.2 Potensial Gravitasi 7
2.2 Prinsip Relativitas 8
2.2.1 Hukum Newton dan Kerangka Inersial 9
2.2.2 Relativitas Newton 10
2.3 Teori Relativitas Umum Einstein 12
2.3.1 Analisis Tensor 13
2.3.1.1 Transformasi koordinat 16
2.3.2 Koordinat Kurvalinier 19
2.3.2.1 Koordinat Kuvalinier Ortogonal 19 2.3.2.2 Vektor Satuan dalam sistem koordinat Kurvalinier 19 2.3.2.3 Koordinat Kurvalinier Umum 20
2.3.3 Prinsip Ekuivalensi 22
2.3.4 Prinsip Kovariansi umum 23
2.3.5 Kelengkungan Ruang Waktu 23
2.4 Asas Kesetaraan 25
2.4.1 Asas Kesetaraan dan Geodesik Ruang Waktu Lengkung 26
2.4.2 Metrik Schwarzschild 27
2.4.2.1 Teori Relativitas Umum dalam Metrik Schwarzschild 29 2.4.2.2 Medan Gravitasi dalam Ruang Waktu Schwarzschild Like 30 Bab 3 Metodologi penelitian
3.1 Diagram Alir Penelitian 32
Bab 4 Hasil dan Pembahasan
4.1 Konsekuensi Prinsip Kesetaraan 33
4.2 Transformasi Metrik Schwarzschild 35
4.3 Kerangka Dipercepat Seragam 38
Bab 5 Kesimpulan dan Saran
4.1 Kesimpulan 43
4.2 Saran 44
DAFTAR PUSTAKA 45
LAMPIRAN A : Beberapa Besaran Fisika dan Alfabet Yunani 47 LAMPIRAN B : Komponen-Komponen Koneksi Affine dan Tensor Ricci
Dalam Metrik Simetri Bola Statik 48
LAMPIRAN C : Hubungan simbol Chritoffel dengan tensor metrik 52 LAMPIRAN D : Jumlah kuadrat persamaan (4.11) 54
DAFTAR SIMBOL
Simbol-simbol yang digunakan dalam skripsi ini dan fungsinya:
𝐹 = Gaya
𝐺 = Konstanta gravitasi (6,67 × 10−11𝑁𝑚2/𝑘𝑔2) 𝑟 = Jarak radial
𝑚 = Massa objek
𝑀 = Massa bintang (matahari) 𝜌 = Rapat massa
𝑉 = Energi potensial gravitasi
= Nabla
𝜙 = Potensial gravitasi 𝑅 = Jari-jari matahari
𝑥𝜇 = Koordinat (𝑥0, 𝑥1, 𝑥2, 𝑥3 = 𝑐𝑡, 𝑥1, 𝑥2, 𝑥3) 𝑚𝐼 = Massa inersial
𝑚𝐺 = Massa gravitasi 𝑐 = Kecepatan cahaya u = Kecepatan partikel g = Percepatan gravitasi a = Percepatan objek K = Tetapan Integrasi
h =konstanta momentum sudut 𝑔𝜇𝜈 = Tensor metric
𝜕 = Differensial parsial
𝛿𝜈𝜇 = Delta kronecker [+1(𝜇 = 𝜈), 0(𝜇 ≠ 𝜈)]
𝑑𝜏 = Waktu pribadi 𝑅𝜇𝜈 = Tensor Ricci
𝑔𝑟𝑟 = 𝑔𝜙𝜙 = 𝑔𝑡𝑡 = 𝑔𝜃𝜃= Komponen tensor metric
DAFTAR ISTILAH
Istilah-istilah yang digunakan dalam penulisan skripsi ini adalah:
Kovariansi = Memiliki bentuk yang sama dalam setiap kerangka acuan Ekuivalensi = Kesetaraan
Invariant = Besaran yang tidak berubah walaupun mengalami transformasi
Homogen = Memiliki besar yang sama (seragam)
Geodesik = Lintasan teerpendek partikel dalam ruang-waktu lengkung Kerangka inersial = Kerangka yang diam atau bergerak dengan kecepatan tetap Ruang Euklidean = Ruang datar atau ruang dengan koordinat kartesius
Ruang Non-Euklidean= Ruang lengkung
Isotropik = Keseragaman dalam semua orientasi
BAB I
PENDAHULUAN
Salah satu fondasi teori relativitas umum adalah prinsip kesetaraan (principle of equivalence). Ohanian (1977) menyatakan bahwa ada dua jenis prinsip kesetaraan. Jenis pertama adalah prinsip kesetaraan lemah (weak principle of equivalence) yang menyatakan bahwa dalam suatu medan gravitasi, seluruh partikel uji dengan kecepatan awal yang sama akan jatuh dengan percepatan yang sama. Jenis yang kedua adalah prinsip kesetaraan kuat (strong principle of equivalence) yang berbunyi, dalam seluruh laboratorium yang jatuh bebas serta tak berotasi, hasil- hasil dari sembarang percobaan lokal adalah sama, tidak tergantung dari medan gravitasi yang berada di sekitar laboratorium tersebut.
1.1 Latar Belakang Masalah
Teori Relativitas Umum (TRU) Einstein adalaah teori yang menyatakan bahwa gravitasi bukan seperti halnya gaya lain, namun gravitasi merupakan efek dari kelengkungan ruang-waktu karena adanya penyebaran massa dan energi didalam ruang waktu tersebut.
Teori Relativitas Umum (TRU) ini dibangun oleh dua asas, yaitu yang pertama : Asas kesetaraan (Principle of equivalence) dan yang kedua adalah kovariansi umum (General Covarince).
Asas kesetaraan berbunyi, “Tidak ada percobaan yang dapat dilakukan dalam daerah kecil (Lokal) yang dapat membedakan medan gravitasi dengan sistem dipercepat yang setara”. Salah satu impliksai asas kesetaraan adalah kesamaan massa gravitasi dan massa inersia. Sifat ini memungkinkan untuk menghilangkan efek gravitasi yang muncul dengan menggunakan kerangka acuan yang sesuai. Hal ini merupakan konsekuensi dari medan gravitasi yaitu semua benda yang berada di dalamnya akan merasakan percepatan yang sama serta tidak bergantung pada ukuran maupun massanya.
1.2 Rumusan Masalah
Adapun rumusan masalah dalam penulisan skripsi ini adalah bagaimana hubungan antara kerangka dipercepat seragam dalam ruang waktu datar serta efek lokal suatu medan gravitasi dengan menggunakan transformasi metrik Schwarzschild.
1.3 Batasan Masalah
a. Penjelasan Teori Relativitas Umum (TRU) tentang transformasi metrik Schwarzschild dalam dua koordinat.
b. Prinsip kesetaraan konsekuensi pada kesamaan antara Massa Gravitasi (MG) dan Massa Inersial (MI).
c. Hubungan antara kerangka dipercepat seragam dalam ruang waktu datar serta efek lokal suatu medan gravitasi pada ruang lengkung.
1.4 Tujuan penelitian
1. Untuk mengkaji prinsip Teori Relativitas Umum yang diterapkan di dalam transformasi metrik Schwarzschild ke dalam sistem dua koordinat.
2. Untuk mengkaji prinsip kesetaraan pada kesamaan antara Massa Gravitasi dan Massa Inersial.
3. Untuk mengkaji hubungan antara kerangka dipercepat seragam dalam ruang waktu datar serta efek lokal suatu Medan gravitasi pada ruang lengkung.
1.5 Manfaat penelitian
1. Sebagai sumber pustaka mengenai transfomasi metrik Schwarzschild
2. Sebagai penambahan wawasan bagi penulis maupun pembaca mengenai transfomasi metrik Schwarzschild.
3. Sebagai sumber informasi mengenai prinsip kesetaraan yang membawa konsekuensi pada kesamaan antara massa gravitasi dan massa inersial.
1.6 Metode penulisan
Metode kajian pustaka dipilih dalam penelitian ini dengan menggunakan beberapa literatur dari berbagai sumber pustaka terkait. Kegiatan studi penelitian ini diuraikan secara lebih rinci dibawah ini.
1. Studi Literatur
Merupakan tahap pengumpulan literatur mengenai : Teori Relativitas Umum, Kelengkungan Ruang waktu, Analisis Tensor, Massa Gravitasi Einstein, dan Schwarzschild.
2. Pengkajian Literatur
Merupakan tahap penyelesaian dengan permasalahan yang akan dibahas dalam penelitian sehingga didapat informasi yang diinginkan.
3. Pengolahan Informasi
Merupakan tahap untuk menganalisa informasi sehingga didapat informasi yang dapat digunakan untuk menyelesaikan permasalahan dalam penelitian.
4. Merangkum Kesimpulan
Merupakan jawaban dari setiap permasalahan yang akhirnya suatu fakta ilmiah mengenai fenomena yang ditinjau.
5. Penulisan Laporan
Merupakan tahap penulisan laporan penelitian yang telah dilakukan dalam bentuk skripsi.
1.7 Sistematika Penulisan
Sistematika penulisan masing-masing bab adalah sebagai berikut : BAB I Pedahuluan
Bab ini merupakan Latar Belakang, Rumusan Masalah, Batasan Masalah, Tujuan Penelitian, Manfaat Penelitian, Metode Penulisan, dan Sistematika Penulisan dari Tugas Akhir ini.
BAB II Tinjauan Pustaka
Bab ini berisi teori yang mendasari penelitian ini.
BAB III Metodologi Penelitian
Bab ini membahas tentang metode yang digunakan dan diagram alir dari penelitian.
BAB IV Hasil dan Pembahasan
Bab ini mencakup hasil penelitian berupa penejelasan transformasi metrik Schwarzschild dalam sistem dua koordinat.
BAB V Kesimpulan dan Saran
Bab ini berisi kesimpulan yang diperoleh dari bab sebelumnya yaitu hasil dan pembahasan terkait dari tujuan penelitian. Dan juga saran yang diberikan untuk kajian lebih lanjut dari skripsi ini.
BAB II
TINJAUAN PUSTAKA
2.1 Teori Gravitasi Newton
Beberapa teori dapat membandingkan ketelitian ramalannya dengan teori gravitasi universal Newton. Ramalan mekanika benda angkasa untuk posisi planet sesuai dengan pengamatan. Penemuan Neptunus dan Ceres adalah diantara kesuksesan spektakuler yang memberikan dukungan untuk ketelitian teori ini. Tetapi teori Newton tidak sempurna : ramalan gerak untuk planet dalam (inner) menyimpang sedikit dari nilai yang di amati.
Dalam kasus merkurius kelebihan presesi perihelion sebanyak 43 detik-sudut per abad.
Penyimpangan kecil ini diamati melalui perhitungan oleh Le Verrier pada 1845 dan diperhitungkan kembali oleh Newcomb pada 1882. Penjelasan dari presesi adalah salah satu kesuksesan awal dari teori gravitasi relativistik Einstein. (Hans C. Ohanian, 1976)
Walaupun teori Newton tidak sempurna, teori ini adalah suatu pendekatan yang luar biasa dalam limit kasus gerak pada kecepatan rendah dan dalam suatu medan gravitasi lemah. Setiap teori relativistik gravitasi harus sesuai dengan teori Newton dalam limit kasus ini. Oleh karena itu, akan dimulai dengan suatu penjelasan singkat beberapa aspek dari teori Newton yang telah beliau kemukakan dalam tulisanya seperti hukum gravitasi Newton yang diaplikasikan untuk memprediksi dan menghitung secara teliti gerak planet, bulan, satelit dan objek lain di alam semesta ini.
2.1.1 Hukum Gravitasi Universal Newton
Hukum gravitasi Newton bersama dengan hukum gerak Newton telah diaplikasikan untuk memprediksi dan menghitung secara teliti gerak planet, bulan, satelit, dan objek lain di alam semesta. Berdasarkan Newton, hukum yang menentukan interaksi gravitasi adalah
”Gaya tarik gravitasi antara setiap dua benda di alam semesta secara langsung sebanding pada perkalian massanya dan berbanding terbalik terhadap kuadrat jarak antara kedua benda ”. Jika salah satu massa berada pada titik asal dan yang lain berada pada suatu jarak radial r , maka persamaan gaya mengambil bentuk matematika :
𝐅 = −𝐺𝑚𝑚′
𝑟2 𝐫̂ (2.1)
dengan G = 6,67 x 10-11 N m2/Kg2 , 𝐫̂ adalah vektor satuan. Gaya gravitasional termasuk gaya sentral yaitu gaya yang bergantung pada jarak radial dan beraksi sepanjang arah radial. (Atam P. Arya, 1990)
Berdasarkan hukum Newton, gravitasi adalah aksi pada suatu jarak: massa pada suatu titik beraksi secara langsung dan seketika pada massa lain, bahkan walaupun massa tersebut tidak bersentuhan dengannya. Newton mempunyai rasa khawatir yang serius tentang tarik-menarik khayal yang demikian dari massa yang jauh dan menyarankan bahwa interaksi akan disampaikan oleh material medium. Pandangan modernnya adalah bahwa gravitasi beraksi secara lokal melalui medan: suatu massa pada suatu titik menghasilkan suatu medan, dan medan ini beraksi pada massa apapun yang berhubungan dengannya. Medan gravitasi mungkin dipandang sebagai material medium yang dicari Newton; medan adalah material karena memiliki suatu rapat energi. Gambaran interaksi dengan memakai medan lokal mempunyai keuntungan lanjutan yang membimbing pada teori relativistik yang mana efek gravitasional merambat pada kecepatan berhingga.
Dalam sistem tata surya, teori Newton adalah suatu penaksiran yang luar biasa.
Persamaan gaya (2.1) dapat diturunkan dari suatu energi potensial
𝑉(𝑟) = −𝐺𝑚𝑚′
𝑟 (2.2)
Pada umumnya, dapat dikatakan bahwa efek relativistik akan menjadi kecil, jika energi potensial jauh lebih kecil dari energi massa diam dan kecepatannya jauh lebih kecil daripada kecepatan cahaya. Untuk suatu massa m yang bergerak dengan kecepatan v sekitar suatu pusat massa 𝑚′ kita dapat menggambarkan kondisi ini sebagai
|𝑉| ≪ 𝑚𝑐2 dan 𝑣 ≪ 𝑐
Dimana 𝑐 adalah kecepatan cahaya. Perhatikan bahwa pembentuk kondisi adalah ekuivalen pada 𝑟 ≫ 𝐺𝑚′/𝑐2. Oleh karena itu, penyimpangan dari teori Newton diharapkan menjadi sangat kecil jika jarak dari pusat massa cukup besar dan kecepatannya cukup rendah. Untuk matahari, dengan suatu massa 𝑚′ = 𝑀⊙ ≅ 2 × 1033 𝑔 , dengan 𝐺𝑚′/𝑐2 ≅ 2 𝐾𝑚 dan kondisi 𝑟 ≫ 2 𝑘𝑚 adalah dengan jelas sangat memuaskan, bahkan untuk komet dengan suatu perihelion yang begitu dekat terhadap permukaan matahari. (Hans C. Ohanian, 1976)
2.1.2 Potensial Gravitasi
Medan gravitasi yang kita pandang sebagai pembawa interaksi didefenisikan sebagai gaya persatuan massa,
𝐠(𝐫) = 1
𝑚 𝐅(𝐫) (2.3)
Potensial gravitasi yang bersesuaian didefenisikan sebagai 𝛷(𝐫) ≡ 1
𝑚 𝑉(𝐫) = − ∑ 𝐺𝑚𝑖
|𝐫 − 𝐫𝑖|
𝑖
(2.4)
Defenisi ini membuat potensial negatif, seperti yang diperkirakan untuk suatu gaya tarik.
Potensial gravitasi kadang-kadang didefenisikan dengan tanda yang berlawanan dari
persamaan (2.4), tetapi lebih baik untuk dipilih tanda ini dengan menganalogikannya terhadap elektrostatik. Untuk distribusi massa kontinu seperti persamaan dibawah ini :
𝛷(𝐫) = − ∫𝐺 𝜌(𝐫′)
|𝐫 − 𝐫′|𝑑3𝑟′ (2.5)
Dengan 𝜌(𝐫′) adalah rapat massa. Persamaan (2.5) menyatakan bahwa Φ mematuhi persamaan poisson
∇2𝛷(𝐫) = +4 𝜋 𝐺𝜌(𝐫) (2.6)
2.2 Prinsip Relativitas
Pada intinya, teori relativitas Einstein (baik teori relativitas khusus maupun teori relativitas umum) adalah teori fisika modern dari ruang dan waktu, yang telah mengganti konsep ruang dan waktu absolut Newton dengan ruang-waktu.
Semula dalam fisika, relativitas berarti penghapusan ruang absolut, suatu penyelidikan yang telah dikenal sebagaimana yang diinginkan sejak Newton. Dan ini tentu saja apa yang disempurnakan dua teori Einstein : relativitas khusus, teori ruang waktu datar, menghapuskan ruang mutlak dalam peranan Maxwellian sebagai ‘eter’ yang membawa medan elektromagnetik, dan khususnya gelombang cahaya, sedangkan relativitas umum, teori ruang-waktu lengkung, menghapuskan ruang waktu mutlak juga dalam peranan Newtonian-nya mengenai standar ada dimana-mana dan tidak dapat dipengaruhi dari gerak seragam atau diam. Anehnya, dan tidak secara terencana tetapi agak sebagai satu hasil sampingan yang tidak dapat dihindarkan, teori Einstein juga menghapuskan konsep waktu mutlak Newton.
Defenisi yang lebih modern dan positif dari relativitas telah disusun dari teori relativitas yang sebenarnya. Berdasarkan pandangan ini, relativitas dari setiap teori fisika menggambarkan dirinya sendiri dalam grup transformasi yang menentukan hukum teori invariant dan oleh karena itu menggambarkan kesimetrian, sebagai contoh ruang dan
waktu dari teori ini. Maka seperti yang akan dilihat, mekanika Newton memiliki relativitas yang disebut grup Galilean, relativitas khusus memiliki relativitas dari grup Poincaré (atau grup Lorentz), relativitas umum memiliki relativitas grup lengkap transformasi ruang-waktu. Dan berbagai ilmu kosmologi memiliki relativitas simetri yang bermacam-macam dengan skala besar alam semesta yang dipercaya. Bahkan suatu teori yang hanya berlaku pada ruang Euclidean mutlak, memberikan bahwa secara fisik homogen dan isotropik, akan memiliki relativitas, yang dinamakan grup rotasi dan translasi. (Wolfgang Rindler, 2006)
2.2.1 Hukum Newton Dan Kerangka Inersial
Ketika menggambarkan fenomena fisika di bumi, biasanya digunakan sistem koordinat dengan titik asal pada pusat bumi. Tetapi, sistem koordinat ini tidak ideal untuk menggambarkan gerak planet disekitar matahari. Sistem koordinat dengan titik asal pada pusat matahari lebih natural. Karena matahari bergerak sekitar pusat galaksi, tidak ada yang spesial tentang sistem koordinat dengan titik asal pada pusat matahari.
Kerangka acuan fundamental Newton disebut ‘ruang mutlak’. Sifat geometri dari ruang ini diberikan oleh geometri Euclidean biasa. Ruang ini dapat didekati oleh sistem koordinat kartesian. Kerangka acuan non-rotasi yang diam, atau yang bergerak secara seragam dalam ruang mutlak disebut kerangka acuan Galilean. Dengan memilih titik asal dan orientasi, sistem telah ditetapkan. Newton juga mengenalkan waktu universal yang berdetik pada laju yang sama pada semua posisi dalam ruang. (Grøn Ø., Hervik S., 2007)
Relatif terhadap kerangka acuan Galillean, semua mekanika berkelakuan berdasarkan tiga hukum Newton:
(i) Partikel bebas bergerak dengan vektor kecepatan konstan.
𝐮 = 𝑑𝐫
𝑑𝑡 = 𝑘𝑜𝑛𝑠𝑡𝑎𝑛
dengan r adalah vektor posisi.
(ii) Vektor gaya pada suatu partikel sama dengan hasil kali massanya dengan vektor percepatan : F = m.a
(iii) Gaya dari aksi dan reaksi adalah sama dan berlawanan; sebagai contoh, jika partikel A memberikan gaya F pada partikel B, maka B memberikan suatu gaya –F pada A.
Hukum fisika biasanya dinyatakan relatif terhadap kerangka acuan, yang mengijinkan kuantitas fisika seperti kecepatan, medan listrik dan lain-lain, untuk didefinisikan. Diantara kerangka yang lebih disukai adalah kerangka tegar yang inersial.
Selanjutnya hukum Newton diaplikasikan didalamnya.
Hukum pertama Newton menyajikan untuk memilih kerangka inersial di antara kerangka tegar : kerangka tegar disebut kerangka inersial jika partikel bebas bergerak tanpa percepatan relatif terhadapnya. Dan selama kehadirannya, hukum Newton digunakan secara sama dalam semua kerangka inersial. Bagaimanapun, Newton mempostulatkan keberadaan dari ruang mutlak dimana dia berpikir pusat massa dari sistem tata surya adalah dalam keaadaan diam dan baginya, ini adalah daerah utama untuk mekanikanya. Bahwa hukum-hukum yang secara sama sah dalam semua kerangka acuan lain yang bergerak secara seragam terhadap ruang mutlak (kerangka inersial) adalah teorema yang menarik baginya. (Wolfgang Rindler, 2006)
2.2.2 Relativitas Newton
Dengan mengingat bahwa suatu kerangka inersial adalah suatu kerangka tegar yang mana hukum pertama Newton berlaku. Anggap kerangka S pada Gambar 2.1 adalah inersial.
Karena, menurut transformasi Galileo kecepatan tetap dalam S bertransformasi ke
kecepatan konstan dalam 𝐒′, dapat dilihat bahwa semua partikel bebas dalam S bergerak secara seragam dalam 𝐒′, yang oleh karena itu juga inersial. Dengan kata lain, hanya kerangka yang bergerak secara seragam relatif ke S yang dapat menjadi inersial. Untuk titik tetap dalam setiap kerangka inersial adalah partikel bebas potensial, sehingga semuanya harus bergerak secara seragam relatif terhadap S.
S v
(x,y,z,t) (x’,y’,z’,t’)
Y’
X’
y x vt x’
x
z Z’ S’
O O’
Gambar 2.1 Kerangka S′ Bergerak dengan Kecepatan Konstan Terhadap Kerangka S. (Ronald Gautreau, 2002)
Dalam transformasi koordinat Galilean, hubungan antara pengukuran (𝑥, 𝑦, 𝑧, 𝑡) milik O dengan pengukuran (𝑥′, 𝑦′, 𝑧′, 𝑡′) milik O’ untuk sebuah kejadian tertentu dipeoleh dengan mengkaji gambar (2.1) diatas adalah :
𝑥′= 𝑥 − 𝑣𝑡 ; 𝑦 = 𝑦′ ; 𝑧′= 𝑧 𝑑𝑎𝑛 𝑡 = 𝑡′ (2.7)
Sekarang, dari invariansi percepatan dapat dilihat bahwa semua yang dibutuhkan agar tiga hukum Newton invarian diantara kerangka inersial adalah (i) suatu aksioma bahwa massa m adalah invarian, dan (ii) aksioma bahwa setiap gaya adalah invarian.
Kedua asumsi ini tentu saja bagian dari teori Newton. Menghasilkan sifat dari mekanika Newton bahwa hal ini berlaku sama pada semua kerangka inersial yang disebut relativitas Newtonian (atau Galilean). (Wolfgang Rindler, 2006)
Dalam mekanika Newton, dianggap bahwa massa inersial dari benda tidak bergantung pada kecepatan benda. Maka massa benda di S sama seperti di 𝐒′. Sehingga gaya 𝐅′, diukur dalam 𝐒′ adalah
𝐅′= 𝑚𝑑𝐮′
𝑑𝑡′ = 𝑚𝑑𝐮
𝑑𝑡 = 𝐅 (2.8)
Oleh karena itu, gaya di 𝐒′ sama seperti di S. Hasil ini mungkin digambarkan dengan mengatakan bahwa hukum kedua Newton invarian dibawah transformasi Galliean; yaitu ditulis dalam cara yang sama dalam setiap kerangka acuan Galilean (inersial). Dengan kata lain, prinsip relatvitas Newtonin (Galilean) menyatakan bahwa ‘setiap sistem mekanika akan berkelakuan dalam cara yang sama dalam semua kerangka Galilean (inersial)’. (Grøn Ø., Hervik S., 2007)
2.3 Teori Relativitas Umum Einstein
Untuk setiap sistem fisis, setiap hukum yang menghubungkan besaran fisis tidak akan bergantung kepada sistem pemilihan sistem koordinat. Hal ini berarti, persamaan gerak sistem akan memiliki bentuk yang tetap (tidak berubah) di dalam semua sistem koordinat. Persamaan yang tidak berubah bentuknya terhadap transformasi koordinat dikatakan memiliki sifat kovarian terhadap transformasi tersebut. Sifat inilah yang menyebabkan tensor banyak digunakan untuk menelaah suatu sistem fisis.
Tensor adalah besaran yang merupakan perluasan dari vektor, seperti halnya vektor merupakan perluasan dari besaran skalar. Tensor memiliki komponen-komponen seperti halnya vektor. Besaran vektor sangat penting dalam fisika karena ia menyatakan objek dengan kaedah-kaedah yang tetap sama meskipun kerangka acuan yang dipilih berubah-ubah. Perubahan kerangka acuan memang menyebabkan nilai komponen tensor berubah pula, namun kaedah-kaedah yang berlaku bagi komponen tensor tetap tidak berubah.
Teori relativitas umum adalah salah satu teori fisika modern yang cukup besar peranannya dalam menerangkan struktur ruang waktu dan jagad raya. Teori ini adalah teori yang indah memiliki daya pikat ramalan terhadap gejala alam yang cukup menarik, namun memiliki persyaratan matematika berupa analisis tensor. Karena itu akan disajikan analisis tensor sebagai jembatan untuk memahami teori relativitas umum.
2.3.1 Analisis Tensor
Tensor adalah besaran yang merupakan perluasan besaran vektor seperti halnya vektor adalah perluasan besaran skalar. Yang terakhir disebut ini adalah besaran yang hanya ditentukan oleh angkanya saja, seperti harga barang, ukuran panjang, suhu dan lain-lain.
Sedangkan vektor adalah besaran yang selain ditentukan oleh besar (angkanya) dan juga oleh arahnya. Misalnya kecepatan, kekuatan tarik, gaya, dan lain-lain. Sebagai contoh bila kita mengatakan tiupan angin yang berkecepatan sepuluh kilometer per jam, maka kita harus menyebut pula angin itu bertiup dari mana kemana, misalnya dari arah barat ke timur. Jadi faktor arah juga harus disertakan untuk melengkapi pernyataan kecepatan.
Begitu juga dengan gaya, kita harus menyebut pula kemana arah dorongannya.
Sedangkan tensor lebih luas dari vektor, yaitu besaran yang selain ditentukan oleh besar (angkanya) dan arahnya juga ditentukan oleh sejumlah faktor lain.
Semua sifat-sifat vektor yang telah dikenal akan dimiliki juga oleh tensor dan penggunaan tensor juga didalam fisika, umumnya akan membuat hukum-hukum fisis yang mempunyai bentuk yang lebih umum dan sederhana. Besaran tensor sangat penting dalam geometri karena mereka menyatakan objek geometri yang sebagaimana diketahui pada hakikatnya tetap sama walaupun sistem koordinat yang kita pilih untuk menyatakan objek geometri tersebut dalam ungkapan analisis atau koordinat. (Hans. J. Wospakrik, 1972). Untuk setiap sistem fisis, setiap hukum yang menghubungkan besaran fisis tidak akan bergantung kepada pemilihan sistem koordinat. Hal ini berarti, persamaan gerak sistem (baik zarah maupun medan) akan memiliki bentuk yang tetap (tidak berubah)
didalam semua sistem koordinat. Persamaan yang tidak berubah bentuknya terhadap transformasi koordinat dikatakan memiliki sifat kovarian terhadap transformasi tersebut.
Sifat inilah yang menyebabkan tensor banyak digunakan untuk menelah sistem fisis.
Didalam analisis tensor ada tiga indeks yang digunakan, yang jika semua indeks berada diatas disebut dengan tensor kontravarian, sebaliknya jika semua indeks berada dibawah disebut dengan tensor kovarian dan apabila indeks berada diatas dan dibawah disebut dengan tensor campuran. Jumlah indeks menyatakan rank dari tensor.
Teori Relativitas Umum (TRU) merupakan teori fisika modern yang cukup besar peranannya dalam menerangkan struktur ruang waktu dan jagad raya. Teori ini merupakan salah satu teori yang indah, memiliki daya pikat ramalan terhadap gejala alam yang cukup menarik, namun memiliki persyaratan matematik berupa analisis tensor, karena itulah sangat dibutuhkan analisis tensor sebagai jembatan untuk memahami teori relativitas umum. Namun demikian, tensor juga dapat dibedakan berdasarkan hukum transformasi yang dimilikinya yaitu :
1. Vektor Kontravarian
Fungsi 𝐵𝑝 dalam sistem koordinat (𝑦1, 𝑦2, … , 𝑦𝑛) disebut vektor kontravarian jika pada suatu transformasi koordinat 𝑈𝑛 → 𝑈𝑛, sehingga fungsi 𝐵𝑝 akan ditransformasikan menjadi
𝐵𝑝→ 𝐵̅𝑝 = ∑𝜕𝑦̅𝑝
𝜕𝑦𝑞𝐴𝑞 , 𝑝 = 1, 2, … , 𝑛
𝑛
𝑞=1
dimana 𝐵̅𝑝 merupakan fungsi dalam sistem koordinat (𝑦1, 𝑦̅2, … , 𝑦̅𝑛).
𝐵̅𝑝 =𝜕𝑦̅𝑝
𝜕𝑦𝑞𝐵𝑞 (2.9)
disebut komponen vektor kontravarian atau tensor kontravarian rank satu.
2. Vektor Kovarian
Fungsi 𝐵𝑝 dalam sistem koordinat (𝑦1, 𝑦2, … , 𝑦𝑛) disebut vektor kovarian jika pada suatu transformasi koordinat 𝑈𝑛 → 𝑈𝑛, sehingga fungsi 𝐵𝑝 akan ditransformasikan menjadi
𝐵𝑝 → 𝐵̅𝑝 = ∑𝜕𝑦𝑞
𝜕𝑦̅𝑝𝐵𝑞 , 𝑝 = 1, 2, … , 𝑛
𝑛
𝑞=1
dimana 𝐵̅𝑝 merupakan fungsi dalam sistem koordinat (𝑦̅1, 𝑦̅2, … , 𝑦̅𝑛).
𝐵̅𝑝 =𝜕𝑦𝑞
𝜕𝑦̅𝑝𝐵𝑞 (2.10)
disebut komponen vektor kovarian atau tensor kovarian rank satu atau order satu.
3. Invarian
Suatu fungsi 𝐵 = 𝐵 (𝑦1, 𝑦2, … , 𝑦𝑛) disebut invarian jika pada suatu transformasi koordinat 𝑈𝑛 → 𝑈𝑛, sehingga fungsi 𝐵 akan ditransformasikan menjadi
𝐵 (𝑦𝑛) → 𝐵̅ (𝑦̅𝑛) = 𝐵 (𝑦𝑛) (2.11)
4. Tensor Campuran
Dalam konsep tensor, suatu tensor campuran adalah tensor yang bukan jenis kovarian kuat maupun kontravarian kuat. Fungsi 𝐵𝑞𝑝 dalam sistem koordinat (𝑦1, 𝑦2, … , 𝑦𝑛) disebut tensor campuran yang memiliki komponen kontravarian rank satu dan komponen kovarian rank satu. Jika pada suatu transformasi koordinat 𝑈𝑛 → 𝑈𝑛, maka fungsi 𝐵𝑞𝑝 ditransformasikan menjadi
𝐵𝑞𝑝 → 𝐵̅𝑞𝑝 = ∑ ∑𝜕𝑦̅𝑝
𝜕𝑦𝑟
𝜕𝑦𝑠
𝜕𝑦̅𝑞
𝑛
𝑟=1 𝑛
𝑠=1
𝐵𝑠𝑟, 𝑝, 𝑞 = 1, 2, … , 𝑛
dimana 𝐵̅𝑞𝑝 merupakan fungsi dalam sistem koordinat (𝑦̅1, 𝑦̅2, … , 𝑦̅𝑛). Diperoleh 𝐵̅𝑞𝑝 = 𝜕𝑦̅𝑝
𝜕𝑦𝑟
𝜕𝑦𝑠
𝜕𝑦̅𝑞 𝐵𝑠𝑟 (2.12)
yang menyatakan komponen tensor campuran.
Dengan menggunakan defenisi dari tensor campuran di atas akan ditunjukkan bahwa 𝛿𝑝𝑝 juga merupakan suatu tensor campuran. Sekarang perhatikan persamaan transformasi berikut
𝛿̅𝑞𝑝 = 𝜕𝑦̅𝑝
𝜕𝑦𝑟
𝜕𝑦𝑠
𝜕𝑦̅𝑞 𝛿𝑠𝑟 𝛿̅𝑞𝑝= 𝜕𝑦̅𝑝
𝜕𝑦𝑟
𝜕𝑦𝑟
𝜕𝑦̅𝑞
𝛿̅𝑞𝑝 = 𝛿𝑞𝑝 (2.13)
dimana 𝛿𝑞𝑝= {0, 𝑝≠𝑞1, 𝑝=𝑞 dan 𝛿̅𝑞𝑝 = {1, 𝑝 = 𝑞0, 𝑝 ≠ 𝑞. Jadi diketahui bahwa 𝛿𝑞𝑝 merupakan tensor campuran dengan kontravarian dan kovarian masing-masing ber-rank satu atau biasa dinamakan dengan delta kronecker.
2.3.1.1 Transformasi Koordinat
Misalkan koordinat-koordinat tegak lurus (x, y, z) dari sebarang titik dinyatakan sebagai fungsi-fungsi sehingga
𝑥 = 𝑥(𝑢1, 𝑢2, 𝑢3), 𝑦 = 𝑦(𝑢1, 𝑢2, 𝑢3), 𝑧 = 𝑧(𝑢1, 𝑢2, 𝑢3) (2.14)
Andaikan bahwa bentuk di atas dapat dipecahkan untuk 𝑢1, 𝑢2, 𝑢3 dalam 𝑥, 𝑦, 𝑧, yakni 𝑢1 = 𝑢1(𝑥, 𝑦, 𝑧), 𝑢2 = 𝑢2(𝑥, 𝑦, 𝑧), 𝑢3 = 𝑢3(𝑥, 𝑦, 𝑧) (2.15)
Fungsi-fungsi dalam persamaan (2.14) dan (2.15) dianggap tunggal dan memiliki turunan-turunan yang kontinu sehingga kaitan (𝑥, 𝑦, 𝑧) dengan (𝑢1, 𝑢2, 𝑢3) adalah tunggal.
Misalkan diketahui sebuah titik P dengan koordinat-koordinat tegak lurus (𝑥, 𝑦, 𝑧) maka dari persamaan (2.14) dapat diasosiasikan suatu himpunan koordinat-koordinat (𝑢1, 𝑢2, 𝑢3) yang tunggal yang disebut koordinat-koordinat kurvilinier dari P. Himpunan persamaan (2.14) dan (2.15) mendefenisikan suatu transformasi koordinat.
y
x z
Gambar 2.2 Kurva-kurva dan garis koordinat. (J. D. Anand, 2003)
Selanjutnya, akan didefenisikan transformasi koordinat menyangkut sistem koordinat lain dengan dimensi yang lebih tinggi. Untuk itu perlu diketahui terlebih dahulu mengetahui ruang dengan sebarang dimensi dan membahas sifat-sifat transformasi daripada ruang tersebut.
Sebuah ruang berdimensi n, dimana n adalah sembarang bilangan bulat positif, adalah merupakan himpunan daripada susunan yang teratur,
𝑥 = (𝑥1, 𝑥2, … , 𝑥𝑛) (2.16)
kurva 𝑢1
P
kurva 𝑢2 kurva 𝑢3
𝑢3= 𝑐3 𝑢1= 𝑐1
𝑢2= 𝑐2
dan yang memenuhi sifat-sifat daripada sebuah ruang vektor. Komponen sebuah vektor dalam ruang berdimensi n tersebut akan dinyatakan dengan indeks tertentu. Suatu kurva di dalam sebuah ruang berdimensi n adalah himpunan dari titik-titik x yang memenuhi n buah persamaan, yaitu 𝑥𝛼= 𝑥𝛼(𝑡), dimana t adalah parameter dan 𝛼 = 1, 2, … , 𝑛. Jika 𝑅𝑛 dianggap sebagai subruang dari 𝑅𝑁 (n < N) maka 𝑅𝑛 ditunjukkan oleh
𝑥𝛼= 𝑥𝛼(𝑡1, 𝑡2,… , 𝑡𝑛) dengan 𝑡𝑖, 𝑖 = 1, 2, … , 𝑛 menyatakan n buah parameter dan 𝛼 = 1, 2, … , 𝑛.
Kemudian diberikan sistem koordinat mencakup ruang tersebut, yaitu 𝑥1, 𝑥2, 𝑥3, 𝑥4 yang membentuk sistem koordinat di 𝑅𝑛. Setiap 𝑥̅ = (𝑥1, 𝑥2, … , 𝑥𝑛) menyatakan titik pada ruang 𝑅𝑛. Misalkan ada transformasi dari suatu sistem koordinat ke sistem yang lain maka bentuk perubahan koordinatnya dinyatakan sebagai berikut:
𝑥1′ = 𝑥1′(𝑥1, 𝑥2, 𝑥3, 𝑥4) 𝑥2′ = 𝑥2′(𝑥1, 𝑥2, 𝑥3, 𝑥4) . . . . . . . . .
𝑥𝑛′ = 𝑥𝑛′(𝑥1, 𝑥2, … , 𝑥𝑁)
Dengan demikian, diferensial untuk 𝑑𝑥1, 𝑑𝑥2, 𝑑𝑥3, 𝑑𝑥4 dapat ditulis sebagai berikut:
𝑑𝑥1′ =𝜕𝑥1′
𝜕𝑥1𝑑𝑥1+𝜕𝑥1′
𝜕𝑥2𝑑𝑥2 +𝜕𝑥1′
𝜕𝑥3𝑑𝑥3+𝜕𝑥1′
𝜕𝑥4𝑑𝑥4 𝑑𝑥2′ =𝜕𝑥2′
𝜕𝑥1𝑑𝑥1 +𝜕𝑥2′
𝜕𝑥2𝑑𝑥2+𝜕𝑥2′
𝜕𝑥3𝑑𝑥3+𝜕𝑥2′
𝜕𝑥4𝑑𝑥4 . . . . . . . . . 𝑑𝑥𝑛′ =𝜕𝑥𝑛′
𝜕𝑥1𝑑𝑥1+𝜕𝑥𝑛′
𝜕𝑥2𝑑𝑥2+ … +𝜕𝑥𝑛′
𝜕𝑥𝑁𝑑𝑥𝑁 Atau dapat juga disederhanakan menjadi
𝑑𝑥𝑛′ = ∑𝜕𝑥𝜇′
𝜕𝑥𝛼𝑑𝑥𝛼
𝑁
𝛼=1
(2.17) dengan 𝜇 = 1,2,3,4, … , 𝑛
2.3.2 Koordinat Kurvalinier
2.3.2.1 Koordinat Kurvalinier Ortogonal
Jika diperhatikan pada Gambar 2.2 permukaan-permukaan 𝑢1 = 𝑐1, 𝑢2 = 𝑐2, 𝑢3 = 𝑐3 dimana 𝑐1, 𝑐2, 𝑐3 adalah konstanta, disebut permukaan-permukaan koordinat, dan setiap pasangan permukaan-permukaan ini berpotongan melalui kurva-kurva yang disebut kurva-kurva dan garis-garis koordinat (Gambar 2.2). Bila permukaan-permukaan koordinat ini berpotongan tegak lurus, maka sistem koordinatnya disebut ortogonal.
Kurva-kurva koordinat 𝑢1, 𝑢2 𝑑𝑎𝑛 𝑢3 dari sistem kurvalinear ini analog dengan sumbu- sumbu koordinat (𝑥, 𝑦, 𝑧) dalam sistem koordinat tegak lurus.
2.3.1.2 Vektor Satuan dalam Sistem Koordinat Kurvalinier
Misalkan 𝑟 = 𝑥̂𝑖 + 𝑦̂𝑗 + 𝑧̂𝑘 adalah vektor kedudukan dari sebuah titik P. maka persamaan (2.14) dapat ditulis sebagai 𝑟 = 𝑟(𝑢1, 𝑢2, 𝑢3). Sebuah vektor singgung pada kurva 𝑢1 di P (dengan 𝑢2 dan 𝑢3 adalah konstanta) adalah
𝜕𝑟
𝜕𝑢1, 𝜕𝑟
𝜕𝑢2, 𝜕𝑟
𝜕𝑢3 (2.18)
masing-masing adalah vektor singgung terhadap kurva dengan koordinat: 𝑢1, 𝑢2, 𝑢3. Maka vektor-vektor satuan dalam masing-masing arah koordinat kurvalinier ini adalah:
ê1 =
𝜕𝑟
𝜕𝑢1
| 𝜕𝑟
𝜕𝑢1|
= 1 ℎ1
𝜕𝑟
𝜕𝑢1 , ê2 =
𝜕𝑟
𝜕𝑢2
| 𝜕𝑟
𝜕𝑢2|
= 1 ℎ2
𝜕𝑟
𝜕𝑢2, ê3 =
𝜕𝑟
𝜕𝑢3
| 𝜕𝑟
𝜕𝑢3|
= 1 ℎ3
𝜕𝑟
𝜕𝑢3 (2.19)
dengan
ℎ1 = | 𝜕𝑟
𝜕𝑢1|, ℎ2 = | 𝜕𝑟
𝜕𝑢2| , ℎ3 = | 𝜕𝑟
𝜕𝑢3|
adalah panjang vektor-vektor singgung yang bersangkutan atau disebut juga sebagai faktor skala.
Uraian di atas memberikan bentuk pernyataan untuk sistem koordinat ortogonal yang ditinjau dengan berlaku syarat:
ê1. ê2 = ê2. ê3 = ê3. ê1 = 0 (2.20)
yang ketiga vektor satuan ê1, ê2, ê3 ini membentuk himpunan vektor satuan koordinat kurvalinier (Gambar 2.3). Dalam hal seperti ini penggunaan sistem koordinat kurvalinier yang sesuai seperti koordinat bola ternyata mengalihkan persoalan menjadi sederhana untuk ditangani.
2.3.2.3 Koordinat Kurvalinier Umum
z
y
x u1
u2 er
eφ
eθ θ
φ r
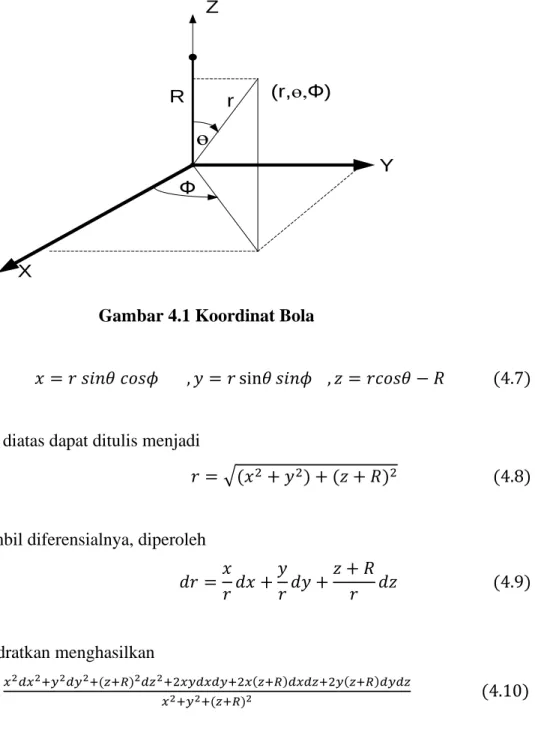
P(r,ө,Ф)
Gambar 2.3 Sistem koordinat kurvalinier bola. (Melly Frizha, 2012)