Skripsi. Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Fisika. Oleh: Margareta Inke Mayasari NIM :

PERHITUNGAN BATAS TERENDAH NILAI PERBANDINGAN ANTARA SUHU DEBYE DAN SUHU KRISTAL SECARA NUMERIK UNTUK MENENTUKAN PENGARUH SUHU TERHADAP PANAS JENIS KRISTAL

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Fisika

Oleh:

Margareta Inke Mayasari NIM : 023214002

PROGRAM STUDI FISIKA JURUSAN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SANATA DHARMA

YOGYAKARTA 2007

MOTTO DAN PERSEMBAHAN

" Dan apa saja yang kamu minta dalam doa dengan penuh

kepercayaan, kamu akan menerimanya " ( Matius 21:22)

PERSEMBAHAN :

"Skripsi ini aku persembahkan untuk Ayah dan Ibuku

serta kakakku mas Robert yang selalu memberikan

dukungan, semangat, doa, dan kasih sayang sepanjang

hidupku"

PERHITUNGAN BATAS TERENDAH NILAI PERBANDINGAN ANTARA SUHU DEBYE DAN SUHU KRISTAL SECARA NUMERIK UNTUK MENENTUKAN PENGARUH SUHU TERHADAP PANAS JENIS KRISTAL

ABSTRAK

Telah dilakukan perhitungan secara numerik terhadap batas terendah nilai perbandingan antara suhu Debye dan suhu kristal yang digunakan dalam perhitungan panas jenis Debye satu dimensi, dua dimensi dan tiga dimensi dengan menggunakan paket program Mathematica 5.0. Hasil perhitungan secara numerik menunjukkan bahwa untuk D _k

x T <

θ

nilai integral I bergantung pada suhu T , sedangkan untuk

k D

x

T ≥

θ

nilai integral I konstan. Nilai untuk satu dimensi adalah , untuk dua dimensi , dan untuk tiga dimensi adalah .

k x xk≥19 22 ≥ k x xk≥25

CALCULATION OF THE RATIO VALUE LOWER LIMIT BETWEEN DEBYE AND CRYSTAL TEMPERATURES NUMERICALLY FOR DETERMINING THE TEMPERATURE EFFECT ON THE CRYSTAL

SPECIFIC HEAT ABSTRACT

The calculations of the ratio value lower limit between Debye temperature and crystal temperature which is used on the calculation of the Debye heat specific for one, two, and three dimension(s) have been performed numerically by using

Mathematica 5.0 package program. The numerical results show that the values of the

integral I for k D

x T <

θ

are depend on the temperature (T), meanwhile for k D

x

T ≥

θ

the values of the I are constants. The values of the are , , and

corresponding to one, two, and three dimension (s) respectively. k

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Yesus Kristus atas segala kasih dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini dengan baik. Skripsi ini berjudul : ”PERHITUNGAN BATAS TERENDAH NILAI PERBANDINGAN ANTARA SUHU DEBYE DAN SUHU KRISTAL SECARA NUMERIK UNTUK MENENTUKAN PENGARUH SUHU TERHADAP PANAS JENIS KRISTAL”, yang diajukan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Fisika Universitas Sanata Dharma Yogyakarta.

Penulis mengucapkan terima kasih kepada semua pihak yang telah membantu penulis baik berupa waktu, tenaga, bimbingan, dorongan, dan sumbang saran yang penulis butuhkan dalam penyelesaian skripsi ini. Pada kesempatan ini penulis ingin mengucapkan terima kasih kepada:

1. Bapak Drs. Drs. Vet. Asan Damanik, M.Si. selaku dosen pembimbing yang telah banyak meluangkan waktu untuk membimbing, mendampingi, memberikan dorongan dan semangat dalam pengerjaan tugas akhir ini.

2. Ayah dan Ibuku tercinta yang tanpa henti memberikan dukungan, dorongan, doa, dan kasihnya sehingga penulis dapat menyelesaikan skripsi ini.

3. Kakakku tercinta mas Robert yang selalu memberikan semangat dan doanya pada waktu penulis mengerjakan skripsi ini.

4. Erig yang selama ini selalu menemaniku, memberikan dorongan, semangat dan doanya pada waktu pengerjaan tugas akhir ini.

5. Adik sepupuku Wahyu dan Angga yang senantiasa memberikan dukungannya.

6. Mbak Asti dan mas Anto yang selama ini telah memberikan dukungannya.

7. Temen-teman kosku terutama Chika, Jule dan Anis yang selalu memberikan semangat dan menjadi sahabat yang baik bagiku serta menemaniku mengerjakan skripsi.

8. Temen-teman fisika yang selama bertahun-tahun selalu berjuang bersamaku.

9. Dr. Edi Santosa, M.S. selaku dosen pendamping akademik yang sudah banyak memberikan pendampingan selama menjadi mahasiswa.

10. Seluruh Staff Pengajar Jurusan Fisika yang telah memberikan pengajaran dan pendampingan.

11. Semua pihak yang tidak dapat disebutkan satu demi satu. Terimakasih atas segala bantuannya.

Penulis menyadari bahwa dalam penulisan ini masih banyak kekurangan, oleh karena itu penulis sangat mengharapkan saran dan kritik yang sangat membangun dari berbagai pihak.

Akhirnya penulis berharap semoga skripsi ini dapat bermanfaat bagi dunia pendidikan dan khususnya pembaca.

Yogyakarta, Juni 2007

DAFTAR ISI

HALAMAN JUDUL………... HALAMAN PERSETUJUAN PEMBIMBING………... HALAMAN PENGESAHAN .……….. HALAMAN MOTO PERSEMBAHAN …………...………. ABSTRAK ………. ABSTRACT ……….. KATA PENGANTAR ………... PERNYATAAN KEASLIAN KARYA………. DAFTAR ISI ………. DAFTAR GAMBAR ……… BAB I. PENDAHULUAN………. 1.1. Latar Belakang ………. 1.2. Perumusan Masalah ………. 1.3. Batasan Masalah ……….. 1.4. Tujuan dan Manfaat Penelitian ……… 1.4.1. Tujuan Penelitian ………... 1.4.2. Manfaat Penelitian ………. 1.5. Sistematika Penulisan ………... BAB II. DASAR TEORI ………...

i ii iii iv v vi vii x xi xiv 1 1 4 5 5 5 6 6 7

2.1. Panas Jenis Zat Padat ……… 2.2. Panas Jenis Menurut Teori Klasik ……… 2.3. Panas Jenis Menurut Teori Einstein ………. 2.4. Panas Jenis Menurut Teori Debye………. 2.4.1. Panas Jenis Zat Padat Dalam Satu Dimensi ………... 2.4.2. Panas Jenis Zat Padat Dalam Dua Dimensi ... 2.4.3. Panas Jenis Zat Padat Dalam Tiga Dimensi ….…………. 2.5. Integrasi Numerik Dengan Menggunakan Mathemetica 5.0…….

BAB III. METODOLOGI PENELITIAN ………. 3.1. Jenis Penelitian ………. 3.2. Sarana Penelitian ……….. 3.3. Langkah-Langkah Penelitian ……… BAB IV. HASIL DAN PEMBAHASAN ………. 4.1. Hasil Integrasi Numerik ……… 4.1.1. Panas Jenis Zat Padat Satu dimensi ………... 4.1.2. Panas Jenis Zat Padat Dua Dimensi ... 4.1.3. Panas Jenis Zat Padat Tiga Dimensi ……….. 4.2. Pembahasan ……….. BAB V. PENUTUP ………... 5.1. Kesimpulan ………... 5.2. Saran ………. 7 9 13 16 17 18 20 23 24 24 24 24 26 26 26 27 28 29 33 33 34

DAFTAR PUSTAKA ……… LAMPIRAN A

LAMPIRAN B LAMPIRAN C

DAFTAR GAMBAR Gambar 1.1 Gambar 1.2 Gambar 4.1 Gambar 4.2 Gambar 4.3 Gambar 4.4

Panas jenis Cu pada volume tetap sebagai fungsi T

Panas Jenis Cu pada volume tetap dengan K

E=240

θ

Grafik I sebagai fungsi x untuk kristal satu dimensi Grafik I sebagai fungsi x untuk kristal dua dimensi Grafik I sebagai fungsi x untuk kristal tiga dimensi Gabungan grafik satu dimensi, dua dimensi dan tiga dimensi 1 3 27 28 29 32

BAB I

PENDAHULUAN

1.1. Latar Belakang

Dalam fisika diketahui ada tiga model atau teori mengenai panas jenis suatu zat padat, yaitu teori Klasik, teori Einstein dan teori Debye. Menurut teori Klasik nilai panas jenis suatu zat padat pada volume tetap

( )

c tidak bergantung _v

pada suhu

(

. Dengan kata lain, panas jenis suatu zat pada volume tetap menurut teori Klasik adalah

)

T

R

c_v=3 (1.1) dengan R tetapan gas umum ( R=8.31×103J / kmol K = 1.99 kcal / kmol K).

Berdasarkan hasil eksperimen, nilai panas jenis suatu zat pada volume tetap bergantung pada suhu atau secara matematis dapat dituliskan

( )

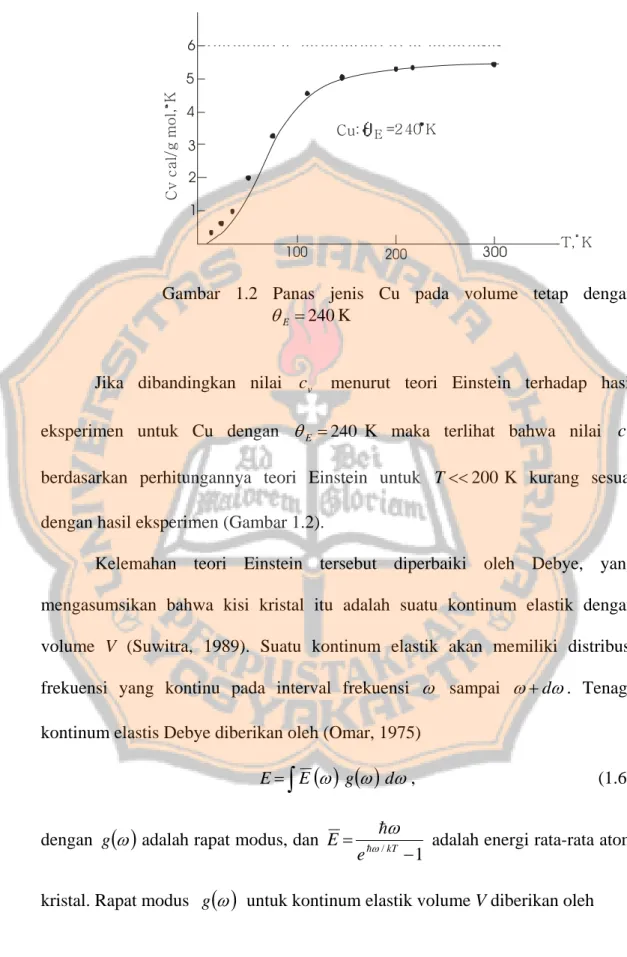
T c

c_v≡ _v . (1.2) Sebagai contoh, panas jenis Cu berdasarkan hasil eksperimen (Omar, 1975) diperlihatkan pada Gambar 1.1

6 5 4 2 1 100 300 3 200 Cu: _E=2 40 K C v c a l/ g m o l, K T, K

Dari gambar 1.1 terlihat bahwa nilai pada suhu tinggi mendekati (sesuai dengan teori Klasik), tetapi pada suhu rendah nilai sangat bergantung pada v c 3R v c T .

Untuk mengatasi kelemahan teori Klasik tersebut, Einstein merumuskan teori panas jenis pada volume tetap dengan menganggap (mengandaikan) bahwa zat padat tersusun dari atom-atom yang bergetar secara bebas (independen) disekitar titik kesetimbangannya satu dengan yang lainnya. Dengan asumsi tersebut, Einstein memperoleh energi rata-rata sebesar (Omar, 1975) :

∑

∑

∞ = − ∞ = − = 0 / 0 / n kT E n kT E n n n e e E E (1.3) dengan E_n n ⎟_hω_E ⎠ ⎞ ⎜ ⎝ ⎛ + = 2 1

(_{h tetapan Planck tereduksi,}

π

2

h

=

h dan ω frekuensi _E

getar), sehingga (Sears dan Salinger, 1975)

(

_/

)

2 / 2 1 3 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ∂ ∂ = T T E v E E e e T R T E c θ θ θ . (1.4)

Pada suhu tinggi nilai menurut teori Einstein mendekati nilai (sesuai teori Klasik) dan pada suhu rendah (Omar, 1975)

v c 3R T E v E e T R c / 2 3 θ ⎟ −θ ⎠ ⎞ ⎜ ⎝ ⎛ = (1.5)

6 5 4 2 1 100 300 3 200 Cu: E=2 40 K C v c a l/ g m o l, K T, K

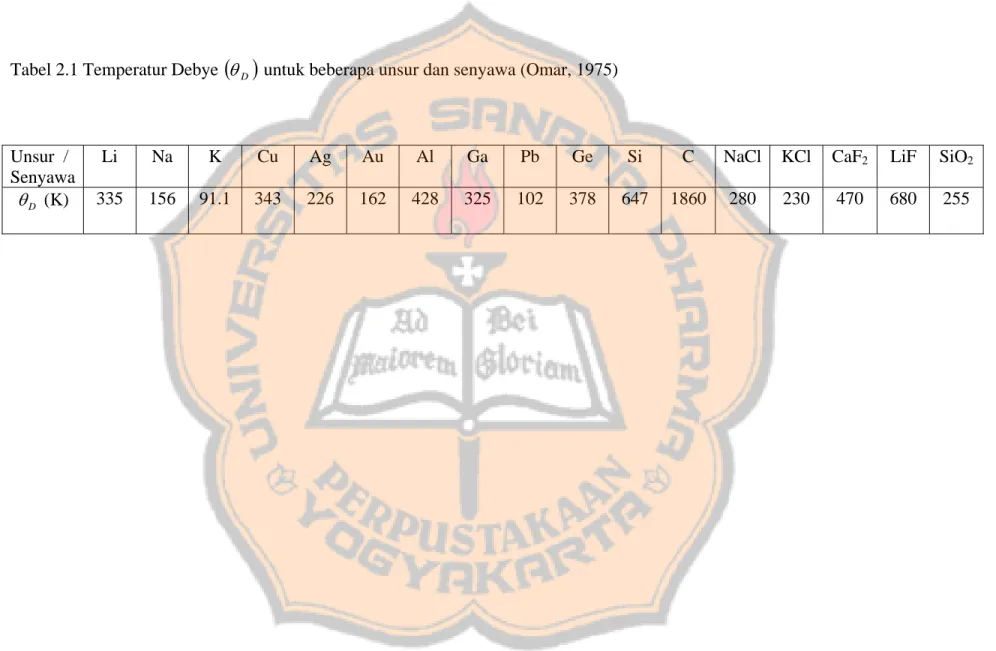
Gambar 1.2 Panas jenis Cu pada volume tetap dengan

240 =

E

θ K

Jika dibandingkan nilai menurut teori Einstein terhadap hasil eksperimen untuk Cu dengan

v

c

240 =

E

θ K maka terlihat bahwa nilai berdasarkan perhitungannya teori Einstein untuk

v

c

200 <<

T K kurang sesuai dengan hasil eksperimen (Gambar 1.2).

Kelemahan teori Einstein tersebut diperbaiki oleh Debye, yang mengasumsikan bahwa kisi kristal itu adalah suatu kontinum elastik dengan volume V (Suwitra, 1989). Suatu kontinum elastik akan memiliki distribusi frekuensi yang kontinu pada interval frekuensi ω sampai ω+dω. Tenaga kontinum elastis Debye diberikan oleh (Omar, 1975)

( ) ( )

ω g ω dω E

E=

∫

, (1.6) dengan g

( )

ω adalah rapat modus, dan

1 / − = kT e E _ω ω h

h _{adalah energi rata-rata atom}

( )

3_{2 3}2 2 v_s L g ω π ω = (1.7)

dengan L panjang rusuk volume V, ω frekuensi kontinum elastik, dan kecepatan gelombang. Sehingga persamaan (1.6) dapat dituliskan menjadi

s v

∫

₋ = D d e v V E _kT s ω ω ω ω π ₀ / 3 3 2 1 2 3 h h _{. (1.8)} Jika didefenisikan kT x=hω , kT xD D ω h = , dan kθ_D =_hω_D atau h D D kθ ω = (θ _D adalah suhu Debye), maka panas jenis pada volume tetap diberikan oleh

T E c_v ∂ ∂ =

(

)

dx e e x T R D x x x x D

∫

= − ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 0 2 4 3 1 9 θ . (1.9) 1.2. Perumusan Masalah

Dari persamaan (1.9) terlihat bahwa nilai integral

(

)

∫

= − = D x x x x dx e e x I 0 2 4 1 (1.10)

untuk suhu rendah

(

T<<θ_D

)

adalah

15 4π4

(suatu konstanta). Secara umum hasil

integral persamaan (1.10) masih merupakan fungsi θ dan T atau _D

(

T

)

I

I≡ θD, . (1.11) Yang menjadi permasalahan adalah berapa batas terendah nilai

T D θ

agar hasil

1.3. Batasan Masalah

Masalah yang diteliti dalam penelitian ini dibatasi pada masalah

1. Penentuan batas terendah nilai T

D θ

agar hasil integral persamaan (1.9)

untuk suhu rendah terpenuhi.

2. Implikasi batas terendah nilai T

D θ

terhadap panas jenis Debye pada

panjang tetap, luas tetap dan volume tetap.

1.4. Tujuan dan Manfaat Penelitian 1.4.1. Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk:

1. Menentukan batas terendah nilai T

D θ

agar hasil integral pada

persamaan (1.10) untuk suhu rendah terpenuhi.

2. Mengetahui implikasi batas terendah nilai T

D θ

terhadap panas jenis

suatu zat pada panjang tetap, luas tetap dan volume tetap

( )

c_v .

1.4.2. Manfaat Penelitian

Penelitian ini bermanfaat untuk pengembangan ilmu pengetahuan khususnya pengetahuan terhadap panas jenis pada panjang tetap, luas tetap dan volume tetap dan kaitannya dengan suhu Debye θ dan ._D T

1.5. Sistematika Penulisan

Sistematika penulisan penelitian ini adalah sebagai berikut: BAB I. PENDAHULUAN

Pada Bab I dijelaskan mengenai latar belakang masalah, rumusan masalah, batasan masalah, tujuan dan manfaat penelitian, dan sistematika penulisan. BAB II. DASAR TEORI

Dalam Bab II dijabarkan teori panas jenis zat padat menurut teori Klasik, Einstein, dan Debye.

BAB III. METODOLOGI PENELITIAN

Pada Bab III akan dijelaskan tentang jenis penelitian, sarana penelitian dan langkah-langkah penelitian.

BAB IV. HASIL DAN PEMBAHASAN

Pada Bab IV akan ditampilkan hasil penelitian secara numerik serta pembahasannya

BAB V. KESIMPULAN DAN SARAN

BAB II

DASAR TEORI

2.1. Panas Jenis Zat Padat

Zat padat terbentuk dari atom-atom (berupa ion atau atom netral) atau molekul yang sangat tersusun dengan posisi sangat berdekatan. Energi zat padat dapat dikelompokkan menjadi dua kelompok, yaitu energi termal dan energi lain. Energi lain dapat berasal dari energi kinetik, energi potensial listrik, energi potensial magnetik energi rotasi, energi potensial gravitasi, dll. Perubahan energi termal tiap satu satuan perubahan suhu disebut kapasitas panas C (Suwitra, 1989)

T E C ∂ ∂ = . (2.1) Selain konsep kapasitas panas, dikenal juga konsep panas jenis yang didefenisikan sebagai jumlah kalor atau energi yang diperlukan oleh satu mol zat untuk menaikkan suhunya sebesar 1K. Secara matematis, panas jenis dituliskan sebagai T E m c ∂ ∂ = 1 (2.2)

dengan c panas jenis ( satuan J / kmol atau kcal / kmol K) dan m adalah besarnya massa satu mol zat. Jika suatu sistem bekerja pada volume tetap, maka panas jenis itu disebut panas jenis pada volume tetap (c_v), secara matematis dituliskan

v v T E m c ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = 1 (2.3)

Menurut hukum I termodinamika, jika sejumlah kalor dQ diberikan kepada suatu sistem, maka kalor/energi tersebut dapat digunakan oleh sistem

untuk mengubah energi dalamnya

( )

dU dan untuk melakukan sejumlah kerja . Hukum termodinamika tersebut dapat dituliskan sebagai (Nainggolan, 1978)

(

dW

)

dW dU

dQ= + (2.4) Energi dalam sistem ditentukan oleh volume

( )

V dan suhu sistem sehingga (Sears dan Salinger, 1975)

( )

T dV V U dT T U dU T v ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = (2.5) Jika persamaan (2.5) disubstitusikan ke persamaan (2.4) maka diperoleh

dW dV V U dT T U dQ T v + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = (2.6) Mengingat , persamaan (2.6) dapat dituliskan kembali dalam bentuk dV p dW = . dV p V U dT T U dQ T v ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = (2.7)

Maka kapasitas panas

(

C

)

pada volume tetap

(

dV=0

)

diberikan oleh . v v v T U T Q C ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = (2.8) Selain konsep kapasitas panas, dikenal juga konsep panas jenis

(

yang didefenisikan sebagai jumlah kalor atau energi yang diperlukan oleh satu mol zat untuk menaikkan suhunya sebesar 1K. Secara matematis panas jenis

(

pada volume tetap dituliskan

)

v c

)

v c

v v T U m T Q m c ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = ∂ ∂ = 1 1 (2.9)

Selanjutnya panas jenis zat padat ditinjau menurut tiga teori, yaitu teori Klasik, teori Einstein, dan teori Debye.

2.2. Panas Jenis Menurut Teori Klasik

Menurut teori klasik dengan menggunakan teori kinetik gas, jika suatu kotak yang mempunyai volume V diisi N molekul gas dengan masing-masing molekul memiliki massa m dan bergerak dengan kecepatan (searah sumbu x), maka akan terjadi tumbukan antara molekul dengan luasan (A) dinding kotak sehingga perubahan momentum sebelum dan sesudah terjadinya tumbukan adalah

. x v x v m 2

Besarnya perubahan momentum dalam interval sampai diberikan oleh (Bradbury, 1984)

x

v v_x+dv_x

Δp_x=2mAxdn(v_x)v_x (2.10) dengan x adalah panjang lintasan, dan adalah jumlah molekul tiap satu satuan volume sebagai fungsi . Perubahan momentum tersebut terjadi dalam interval waktu ) (v_x dn x v x v x t= Δ . (2.11) Perubahan gaya yang dihasilkan dalam luasan A akibat terjadinya tumbukan adalah

(

x x x x mAv dn v t p dF =2 2 Δ

)

Δ = . (2.12) sehingga

(

∫

∞ = 0 2 2 x x x Am v dn v F

)

. (2.13) Nilai v2_x diberikan oleh (Bradbury, 1984)

( )

( )

( )

V N v dn v v dn v dn v v x x x x x x / 2 0 2 2 2

∫

∫

∫

∞ ∞ + ∞ − +∞ ∞ − ₌ = . (2.14)

Jika persamaan (2.13) dan (2.14) digabungkan, maka akan diperoleh

V v N m A F P x x 2 = = (2.15) dengan P adalah tekanan. Persamaan (2.15) dapat dituliskan dalam bentuk

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 2 2 1 3 2 v m N PV , (2.16) sebab vx2 =v2y =v2z dan 2 2 2 2 z y x v v v

v = + + . Dengan demikian energi kinetik molekul gas dapat dituliskan menjadi

T k v m 2 3 2 1 2 = . (2.17)

Pada persamaan (2.17) digunakan relasi PV=NkT (Martin, 1986)

Selain memiliki energi kinetik, molekul-molekul gas tersebut juga memiliki energi potensial. Dari persamaan (2.11) dan (2.12) diperoleh relasi

x p v dFx x x Δ = atau x x x v p dF x =Δ Δ (2.18)

Besarnya gaya dalam luasan A adalah

( )

x _t x dn x A m dF t _x= _Δ Δ 2 ( ) (2.19)

Persamaan (2.19) dapat dituliskan menjadi

( )

x dn t x A m dF t _{x 2} 2 ) ( 2 Δ = Δ . (2.20)

Meningat nilai x adalah 2

∫

∫

∞ ∞ − ∞ ∞ − = ) ( ) ( 2 2 x dn x dn x x (2.21)

sehingga dari persamaan (2.20) diperoleh

V N t dF t A m V N x dn x x x⎟⎟Δ ⎠ ⎞ ⎜⎜ ⎝ ⎛ Δ = =

∫

∫

∞ ∞ 0 0 2 2 1 ) ( 2 . (2.22)

Dari persamaan (2.15) diperoleh

A dF

dP= x . (2.23)

Jika ruas kiri dan kanan persamaan (2.23) dikalikan xΔ , maka diperoleh

x dF dP x AΔ = _x Δ x x tv dF dP x AΔ = Δ

atau x x tdF v dP V =

∫

Δ (2.24)

Jika persamaan (2.24) diintegralkan, maka dihasilkan

∫

∞ Δ = 0 x x tdF v V P

Jika dimasukkan ke dalam persamaan (2.22)

V N t dF t A m x x⎟⎟Δ ⎠ ⎞ ⎜⎜ ⎝ ⎛ Δ =

∫

∞ 0 2 1 t V N v PV mA x Δ = / / 1 2 x V t v N A m PV x Δ = 2 x V t v N A m kT N x A = _Δ 2 x V N t v N A m kT A x Δ = atau 2 2 1 2 1 x t N V v N A m T k A x Δ = (2.25) Jika c t N V v N A m A x =

2 2 1 2 1 x c T k = (2.26)

sehingga besarnya energi potensial adalah adalah kT

2 1

.

Dengan demikian besarnya panas jenis (satu dimensi) menurut teori klasik ditinjau dari teori kinetik gas adalah sebesar (Omar, 1975)

v c k N c_v = _A R c_v = . (2.27)

Untuk panas jenis (c_v) tiga dimensi c_v =3R

Berdasarkan hasil eksperimen (Gambar 1.1) panas jenis zat padat bergantung pada suhu T khususnya pada suhu rendah. Pada suhu tinggi

mendekati 3R. Oleh sebab itu teori panas jenis klasik masih memiliki kelemahan

karena tidak dapat menjelaskan kebergantungan terhadap T.

v

c

v

c

2.3. Panas Jenis Menurut Teori Einstein

Menurut teori panas jenis Einstein osilasi zat padat mengikuti statistik Bose-Einstein (Suwitra, 1989). Einstein juga mengajukan asumsi bahwa semua fonon (osilator) memiliki frekuensi yang sama. Tiap atom berprilaku sebagai tiga osilator harmonis yang independen. Menurut mekanika kuantum, tenaga osilator harmonik diberikan oleh (Alonso dan Finn, 1968)

ω 2 1 ⎟_h ⎠ ⎞ ⎜ ⎝ ⎛ + = n E_n , n=0,1,2,3,... (2.28)

dengan ω frekuensi osilator harmonik,

π

2

h

=

h . Tenaga rata-rata osilator harmonik diberikan oleh (Omar, 1975)

∑

∑

∞ = − ∞ = − = 0 / 0 / n kT E n kT E n n n e e E E (2.29) Jika dituliskan kT 1 =

β , maka persamaan (2.29) dapat dituliskan

∑

∑

∞ = − ∞ = − = 0 0 n E n E n n n e e E E β β (2.30)

Untuk memudahkan perhitungan persamaan (2.30) digunakan substitusi

∑

∞ = − = 0 n E_n e Z β (2.31)

yang dikenal sebagai fungsi partisi (Mandl, 1988). Dengan demikian, maka tenaga rata-rata pada persamaan (2.30) menjadi

(

Z Z Z E 1 ln β β ∂

)

∂ − = ∂ ∂ − = (2.32)

Jika persamaan (2.28) disubstitusikan ke dalam persamaan (2.30) maka diperoleh

∑

∞ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = 0 2 1 n n e Z ωβ h

∑

∞ = − − = 0 2 / n n e e hωβ hωβ =e−hωβ/2

(

1+e−hωβ +e−2hωβ +e−3hωβ +...

)

(2.33)

Jika _hωβ>0, maka , sehingga bentuk deret pada persamaan (2.32) dapat dituliskan menjadi

1 << −hωβ e ωβ ωβ ωβ ωβ h h h h − − − − − = + + + + e e e e 1 1 ... 1 2 3

Dengan demikian fungsi partisi dapat dituliskan menjadi

ωβ ωβ h h − − − = e e Z 1 2 / (2.34)

Dengan substitusi persamaan (2.34) ke dalam persamaan (2.32) diperoleh tenaga rata-rata osilator harmonik satu dimensi sebesar

(

Z

)

E ln β ∂ ∂ − =

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{− − −} ∂ ∂ − = _ωβ ωβ β 2h ln 1 eh 1 _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − + = 1 1 2 1 ωβ ω h h e (2.35)

Jika ditinjau osilator tiga dimensi dan ada sejumlah N osilator, maka tenaga total

osilator harmonik sebesar

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + = = 1 1 2 1 3 3 _kT/ e N E N E _hω _hω (2.36)

Kalau ada satu mol zat (kristal), maka N=NA (bilangan Avogadro). Dengan demikian panas jenis c_v diberikan oleh

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = T E c_v

(

_/

)

2 / 2 1 3 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = kT kT A e e kT k N ω ω ω h h h

(

_/

)

2 / 2 1 3 − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = kT kT E E E e e T R θ θ θ (2.37) dengan R=NA k dan ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = k E ω

θ h yang dikenal sebagai suhu Einstein.

Untuk mengetahui daya prediksi panas jenis Einstein tersebut, ditinjau dua keadaan ekstrim yaitu pada suhu rendah dan suhu tinggi. Pada suhu tinggi

E T>>θ atau <<1 T E θ sehingga T

eθE/T ≈1+θE _{. Jadi panas jenis Einstain pada}

suhu tinggi dapat dituliskan

2 3 2 3 2 2 ... ... 1 3 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = T T T T T T T R c E E E E E E E v θ θ θ θ θ θ θ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ≈ T R ₁ θE 3 (2.38)

Pada suhu rendah

R c_v ≈3 E T<<θ atau >>1 T E θ , sehingga . Jika ,

maka faktor . Jadi panas jenis Einstein pada suhu rendah dapat dituliskan 1 /T _>> E eθ _eθE/T >>1 T T E E _e eθ / −1≈ θ / T E v E e T R c / 2 3 θ ⎟ −θ ⎠ ⎞ ⎜ ⎝ ⎛ = (2.39)

Model panas jenis Einstein hanya cocok untuk suhu tinggi, sedangkan pada suhu rendah kurang sesuai.

2.4. Panas Jenis Menurut Teori Debye

Debye mengembangkan suatu model dengan mengasumsikan bahwa kisi kristal itu adalah suatu kontinum elastik dengan volume V (Suwitra, 1989). Pada

model Debye, suatu kontinum elastik akan memiliki distribusi frekuensi yang kontinu pada interval frekuensi ω sampai ω+dω, dan tenaga total diberikan oleh

( ) ( )

ω ω ω ω d E g E D

∫

= 0 (2.40)

dengan g(ω) adalah rapat modus dan ω adalah frekuensi Debye. Rapat modus _D didefenisikan

( )

ω ω d dN g = (2.41)

dengan N adalah jumlah modus.

2.4.1. Panas jenis zat padat dalam satu dimensi

Jumlah modus fonon untuk satu dimensi adalah

λ

L

N= (2.42)

dengan λ adalah panjang gelombang. Mengingat

λ π λ k 2 = , persamaan (2.42) dapat dituliskan menjadi

λ π k L N ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = 2 . (2.43)

Sebab k dapat juga dituliskan sebagai

s v k_λ =ω , maka s v L N ω π 2 = . (2.44)

Jadi rapat modus untuk satu dimensi adalah

( )

s v L g π ω 2 = (2.45)

Dengan menggunakan persamaan (2.44), frekuensi ω untuk gelombang satu dimensi diberikan oleh

L N v_s π

ω=2 (2.46)

Dengan demikian tenaga kontinum elastis satu dimensi diberikan oleh

( )

ω _ω ω ω ω d e g E D _kT 1 / 0 − =

_∫

h h ω ω π ω ω d e v L E D kT s

∫

− = 0 / 1 2 h h _(2.47) Jika didefenisikan kT x=hω , kT x D D ω h = , dan kθ_D =hω_D atau h D D kθ

ω = (θ adalah suhu Debye), maka panas jenis zat padat satu dimensi D diberikan oleh L c T E c_L ∂ ∂ =

∫

− = D x x x s dx e e x T k v L 0 2 2 2 ) 1 ( h π (2.48) atau T c_L ≈ (2.49)

2.4.2. Panas jenis zat padat dalam dua dimensi Jumlah modus fonon dua dimensi

2 2 2π kλ L N ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ₂ 2 2 2 v_s L ω π = (2.50)

Sehingga rapat modus diberikan oleh

( )

2_{2 2} 2 vs L g ω π ω = , (2.51)

dan frekuensi ω untuk gelombang dua dimensi diberikan oleh

2 1 2 2 2 2 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = L N v_s π ω (2.52)

Jadi tenaga kontinum elastis dua dimensi diberikan oleh

( )

ω _ω ω ω ω d e g E D _kT 1 2 _/ 0 − =

_∫

h h ω ω π ω ω d e v L E D kT s

∫

− = 0 / 2 2 2 2 1 2 2 h h _(2.53)

Mengingat kT x=hω, kT xD D ω h = , dan kθ_D =_hω_D atau h D D kθ ω = (θ adalah suhu _D Debye), maka panas jenis zat padat untuk dua dimensi diberikan oleh

T E c_A ∂ ∂ = dx e e x T k v L xD x x s

∫

− = 0 2 3 2 2 3 2 2 2 ) 1 ( h π (2.54) atau 2 T c_A≈ (2.55)

2.4.3. Panas jenis zat padat dalam tiga dimensi Jumlah modus fonon tiga dimensi

3 3 3 4 2 λ π π k L N ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = ₃ 3 2 3 6 v_s L ω π = (2.56)

sehingga rapat modus diberikan oleh

( )

3_{2 3}2 2 v_s L g ω π ω = , (2.57)

dan frekuensi ω untuk gelombang tiga dimensi diberikan oleh

3 1 3 3 2 6 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = L N vs π ω (2.58)

Jadi tenaga kontinum elastis tiga dimensi dapat dituliskan sebagai atau Mengingat

( )

ω _ω ω ω ω d e g E D _kT 1 3 _/ 0 − =

∫

h h ω ω π ω ω d e v L E D kT s

∫

− = 0 / 3 3 2 3 1 2 3 h h (2.59) kT x=hω, kT x D D ω h = , dan kθD =hωD atau h D D kθ ω = (θ adalah suhu D Debye), maka panas jenis untuk zat padat tiga dimensi adalah

Bentuk integrasi numerik yang terdapat dalam panas jenis Debye satu dimensi (persamaan (2.48)), dua dimensi (persamaan (2.54)), dan tiga dimensi (persamaan (2.60)) akan diselesaikan dengan menggunakan paket program

Mathematica 5.0 3 T c_v ≈ v c T E cv = ∂ ∂ dx e e x T k v L xD x x s

∫

− = 0 2 4 3 3 4 3 2 3 ) 1 ( 2 3 h π (2.61) (2.60)

Unsur / Senyawa

Li Na K Cu Ag Au Al Ga Pb Ge Si C NaCl KCl CaF2 LiF SiO2

D

θ (K) 335 156 91.1 343 226 162 428 325 102 378 647 1860 280 230 470 680 255 Tabel 2.1 Temperatur Debye

( )

θ untuk beberapa unsur dan senyawa (Omar, 1975) _D

2.5. Integrasi Numerik Menggunakan Mathematica 5.0

Bentuk- bentuk integrasi numerik yang ada di dalam persamaan (2.48), (2.54) dan (2.60) akan diselesaikan secara numerik dengan menggunakan paket program Mathematica 5.0. Secara umum penyelesaian integrasi numerik untuk

dengan menggunakan paket program Mathematica 5.0 adalah

( )

∫

= max min x x dx x f I

NIntegrate[f, {x, xmin, xmax}], dengan f adalah fungsi yang akan diintegralkan , xmin adalah batas bawah, xmaks adalah batas atas, dan NIntegrate adalah perintah

yang digunakan untuk mengevaluasi integrasi numeriknya.

Selain itu ada juga penyelesaian integrasi numerik dengan

Table[NIntegrate[f, {x, xmin, y}],{y,ymin,ymaks}], dimana {y,ymin,ymaks}

dihitung dahulu nilai integralnya kemudian hasilnya akan digunakan sebagai batas dalam {x, xmin, y}.

Contoh 1: In[1]:= NIntegrate[Exp[-x^3], {x, 0, Infinity}] Out[1]= 0.89298

Hasil penyelesaian contoh diatas tersebut hanya untuk satu nilai dalam suatu daerah integral.

Contoh 2 : In[2]:= Table[NIntegrate[(x^3)/(Exp[x]-1),{x,0,y}],{y,0,8}] Out[2]=

{0.,0.224805,1.17634,2.55222,3.87705,4.89989,5.58586,6.00317,6.23962}

Hasil penyelesaian contoh 2 tidak seperti hasil penyelesaian contoh 1. Hasil penyelesaian contoh 2 berupa nilai-nilai hasil integrasi numerik sekaligus dalam interval tertentu untuk nilai x tertentu.

BAB III

METODOLOGI PENELITIAN

3.1. Jenis Penelitian

Jenis penelitian yang dilakukan dalam penulisan skripsi ini adalah penelitian studi pustaka dan paket program Mathematica 5.0.

3.2. Sarana Penelitian

Sarana yang dibutuhkan dalam peyelesaian skripsi ini adalah buku-buku yang berhubungan dengan panas jenis zat padat yang terdapat di UPT Perpustakaan Sanata Dharma Yogyakarta.

3.3. Langkah – langkah penelitian

Langkah – langkah yang dilakukan dalam penelitian ini adalah sebagai berikut:

1. Menelusuri bahan – bahan mengenai teori panas jenis Klasik, Einstein dan Debye serta integrasi numerik dengan menggunakan paket program Mathematica 5.0.

2. Mengelaborasi teori-teori panas jenis Klasik, Einstein dan Debye secara analitik.

3. Menyelesaikan teori panas jenis Debye secara numerik dengan menggunakan paket program Mathematica 5.0.

4. Batasan angka desimal numerik yang akan diambil untuk panas jenis satu dimensi dan dua dimensi adalah lima digit sedangkan

untuk panas jenis tiga dimensi adalah empat digit. Batasan angka desimal numerik yang akan diambil mengikuti paket program

Mathematica 5.0.

5. Menentukan batas terendah nilai T

D θ

agar hasil integral pada

persamaan (1.10) untuk suhu rendah terpenuhi.

6. Menarik kesimpulan dan saran dari penelitian yang telah dilakukan.

BAB IV

HASIL DAN PEMBAHASAN

4.1. Hasil Integrasi Numerik

Sebagaimana diketahui dari persamaan (2.48), (2.54) dan (2.60) bahwa panas jenis kristal pada panjang tetap

( )

cL , luas tetap

( )

cA dan volume tetap tergantung pada nilai integrasi

( )

cv

( )

∫

= D x dx x f I 0

Dengan adalah fungsi yang bentuknya bersesuaian dengan dimensi kristal. Dari berbagai studi literatur (Omar, 1975 ; Sears, 1975 ; Mandl, 1988) nilai integral I konstan.

( )

x f

4.1.1. Panas Jenis Zat Padat Satu Dimensi

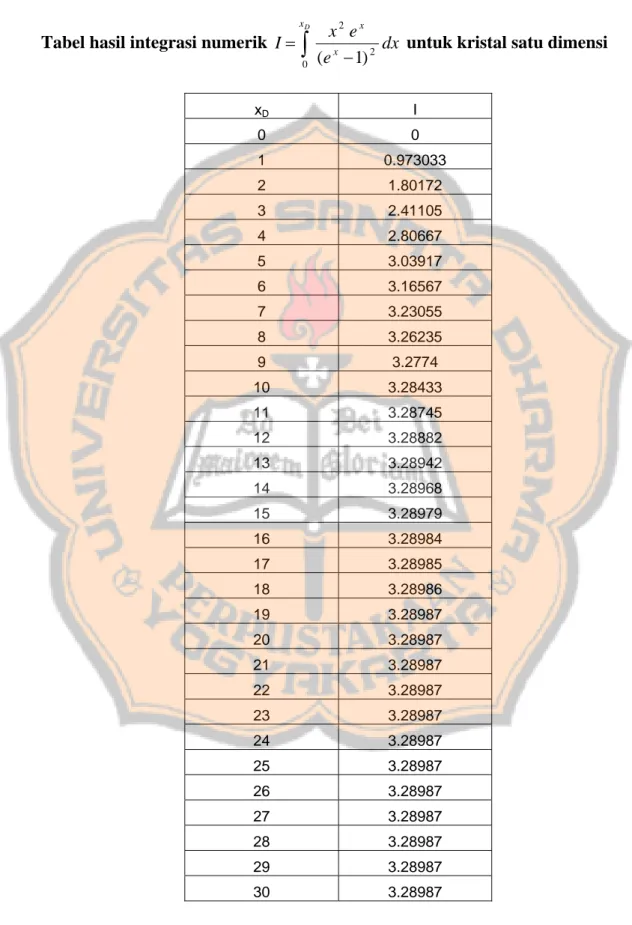
Untuk panas jenis satu dimensi hasil integrasi numerik dari

dx e e x D x x x

∫

₋ 0 2 2 ) 1

( dapat dilihat pada Lampiran A dan jika hasil integrasi numerik

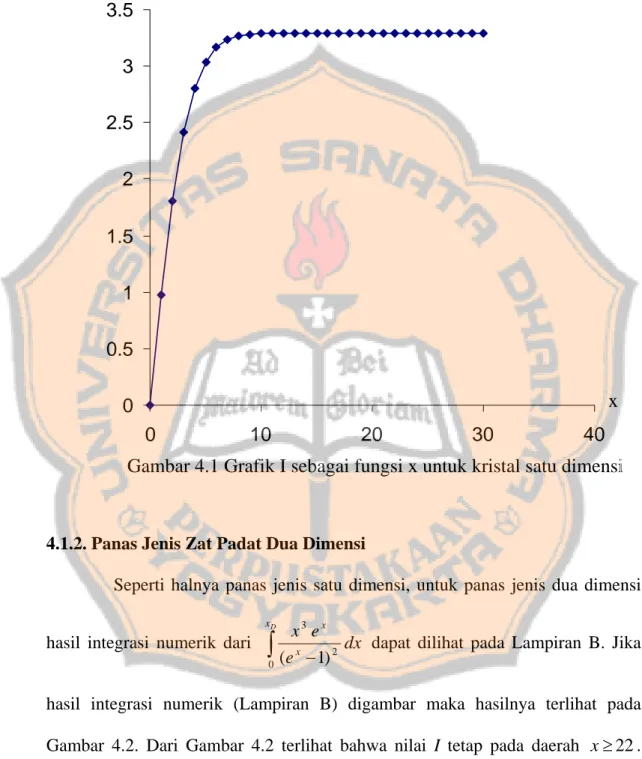
(Lampiran A) digambar maka hasilnya terlihat pada Gambar 4.1. Dari gambar 4.1 terlihat bahwa nilai I tetap pada daerah . Sedangkan untuk daerah

nilai I bergantung pada x.

19 ≥

Gambar 4.1 Grafik I sebagai fungsi x untuk kristal satu dimensi 0 0.5 1 1.5 2 2.5 3 3.5 0 10 20 30 40 x I

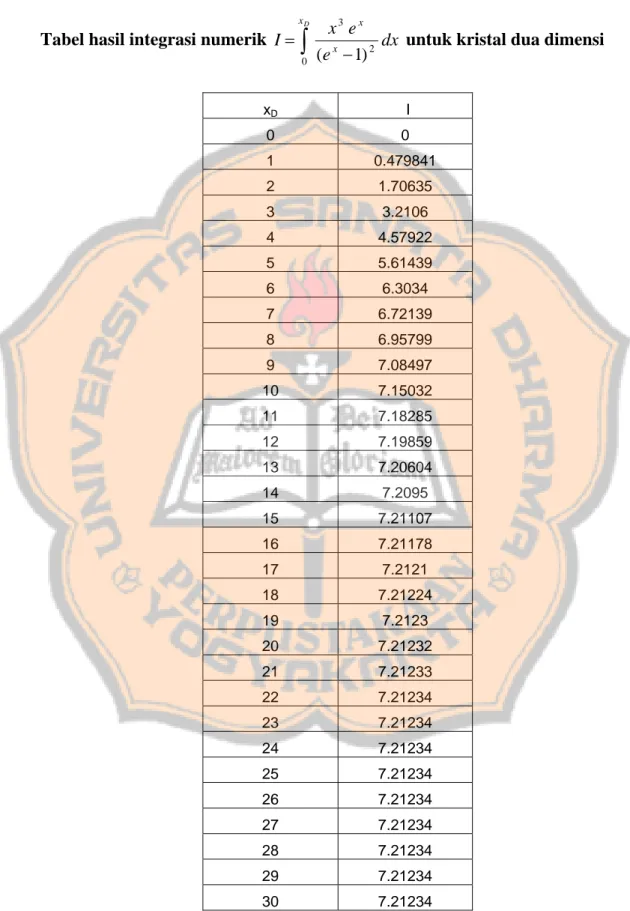
4.1.2. Panas Jenis Zat Padat Dua Dimensi

Seperti halnya panas jenis satu dimensi, untuk panas jenis dua dimensi

hasil integrasi numerik dari dx e e x D x x x

∫

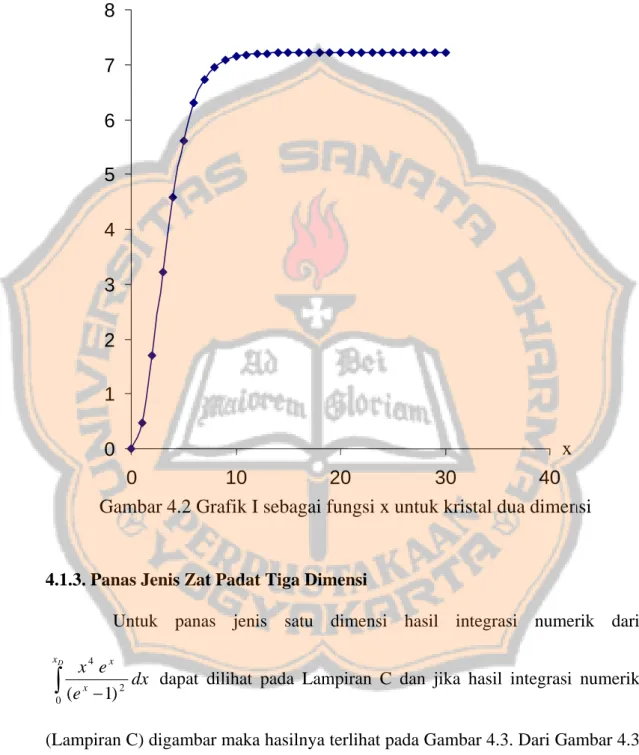
₋ 0 2 3 ) 1

( dapat dilihat pada Lampiran B. Jika

hasil integrasi numerik (Lampiran B) digambar maka hasilnya terlihat pada Gambar 4.2. Dari Gambar 4.2 terlihat bahwa nilai I tetap pada daerah . Sedangkan untuk daerah nilai I bergantung pada x.

22 ≥ x 22 < x

Gambar 4.2 Grafik I sebagai fungsi x untuk kristal dua dimensi 0 1 2 3 4 5 6 7 8 0 10 20 30 40 x I

4.1.3. Panas Jenis Zat Padat Tiga Dimensi

Untuk panas jenis satu dimensi hasil integrasi numerik dari

dx e e x D x x x

∫

₋ 0 2 4 ) 1

( dapat dilihat pada Lampiran C dan jika hasil integrasi numerik

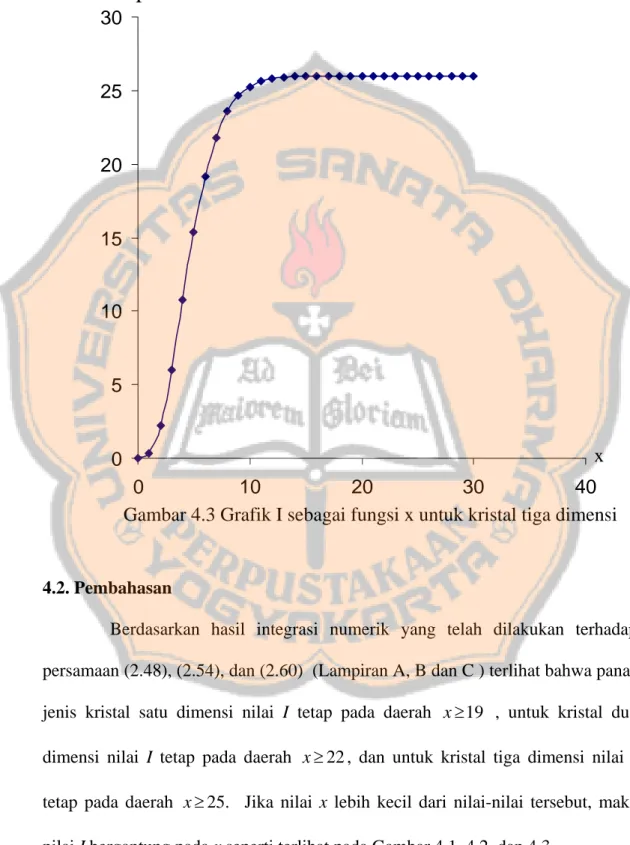
(Lampiran C) digambar maka hasilnya terlihat pada Gambar 4.3. Dari Gambar 4.3 terlihat bahwa nilai I tetap pada daerah . Sedangkan untuk daerah

nilai I bergantung pada x.

25 ≥

4.2. Pembahasan

Gambar 4.3 Grafik I sebagai fungsi x untuk kristal tiga dimensi 0 5 10 15 20 25 30 0 10 20 30 40 x I

Berdasarkan hasil integrasi numerik yang telah dilakukan terhadap persamaa

nilai I bergantung pada x seperti terlihat pada Gambar 4.1, 4.2, dan 4.3.

n (2.48), (2.54), dan (2.60) (Lampiran A, B dan C ) terlihat bahwa panas jenis kristal satu dimensi nilai I tetap pada daerah x≥19 , untuk kristal dua dimensi nilai I tetap pada daerah x≥22, dan untuk kristal tiga dimensi nilai I tetap pada daerah x≥25. Jika nilai x lebih kecil dari nilai-nilai tersebut, maka

Berdasark ai-nilai x yang telah diperoleh, dapat dihitung suhu k kristal (satu, dua, dan tiga dimensi) dengan menggunakan relasi berikut:

an nil kT xD D ω h = h D D kθ ω = T x D D θ =

Jika nilai xD dan θD diketahui, maka nilai T dapat diperoleh. Contohnya unsur Li (pada Tabel 2.1) untuk tiga dimensi, θ_D =335, x_D =25, nilai T dapat dihitung

ng an

dengan me gunak persamaan diatas, yaitu

T x D D θ = T 335 25= K T=13.4

Nilai T yang telah dihitung untuk beberapa unsur dan senyawa berdasarkan relasi

T

x D

D

θ

= dan data Tabel 2.1 disajikan pada Tabel 3.1. Unsur / senyawa θ_D T (K)

Na 156 6.24

Cu 343 13.72

Ag 226 9.04

D D x T<θ

Berdasarkan perhitungan yang telah dilakukan, jika nilai maka

nilai panas jenis bergantung pada suhu. Tetapi jika nilai D x

T≥θD mak i panas

Sears, 1975 ; Mandl, 19

a nila

jenis mendekati klasik.

Sebagaimana yang telah diketahui dari buku-buku teks (Omar, 1975 ; 88) yang memuat panas jenis Debye bahwa nilai integrasi

pada persamaan (1.9) adalah sebesar 15 4π4

untuk kristal tiga dimensi (suatu

pada persamaan (1.9) untuk daerah x≥2 alah sama dengan yang ada di buku-konstanta). Dengan menggunakan paket program Mathematica 5.0 nilai integrasi

ad

buku teks yaitu

5

15 4π4

. Tetapi untuk x<25 nilai integral persamaan (1.9)

bergantung pada nilai x.

I ters

jenisnya adalah sebesar (untuk kristal tiga dimensi), sedangka

Nilai-nilai ebut akan mempengaruhi panas jenis Debye, dimana jika pada daerah x≥25 panas 3R

n jika pada daerah x<25 nilainya tertentu atau dengan kata lain panas jenisnya buka . Demikian juga dengan panas nis kristal satu dimensi, dua dimensi dan tiga dimensi, yang masing-masing memiliki batas daerah dimana nilai integrasinya ulai konstan.

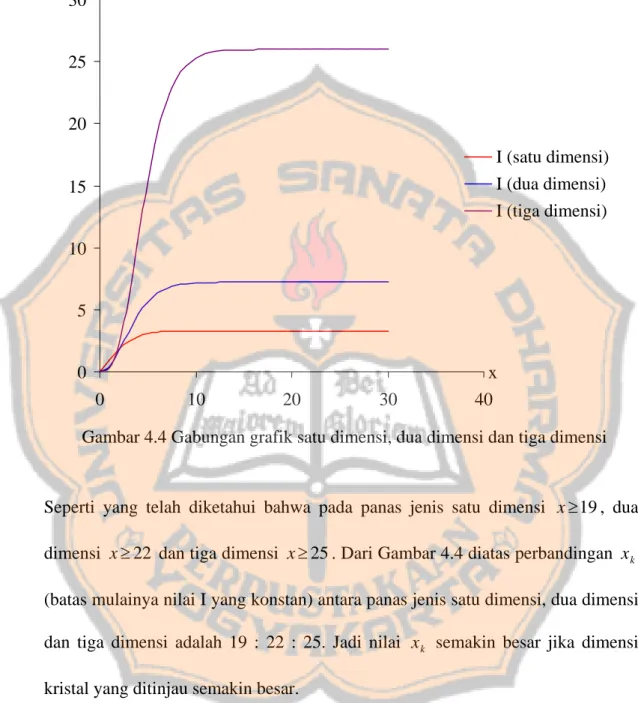
Jika ketiga grafik pada Gambar 4.1, 4.2, dan 4.3 digabungkan, maka diperoleh gambar grafik seperti te

n 3R je

m

Gambar 4.4 Gabungan grafik satu dimensi, dua dimensi dan tiga dimensi 0 5 10 15 20 25 30 0 10 20 30 40 x I I (satu dimensi) I (dua dimensi) I (tiga dimensi)

Seperti yang telah diketahui bahwa pada panas jenis satu dimensi , dua dimensi dan tiga dimensi . Dari Gambar 4.4 diatas perbandingan (batas mulainya nilai I yang konstan) antara panas jenis satu dimensi, dua dimensi dan tiga dimensi adalah 19 : 22 : 25. Jadi nilai semakin besar jika dimensi kristal yang ditinjau semakin besar.

19 ≥ x 22 ≥ x x≥25 x_k k x

BAB V

PENUTUP

5.1. Kesimpulan

Berdasarkan keseluruhan proses yang telah dilakukan dalam penelitian ini dapat diperoleh kesimpulan sebagai berikut

1. Pada panas jenis zat padat satu dimensi nilai I tetap ( konstan ) pada daerah , dua dimensi pada daerah dan tiga dimensi pada daerah .

19 ≥ x x≥22 25 ≥ x

2. Nilai I tetap ( konstan ) jika k D

x T ≥ θ

( adalah batas mulainya

nilai I yang konstan ). Sedangkan untuk k x k D x T < θ nilai I bergantung pada x.

3. Untuk suhu yang sangat rendah khususnya pada daerah , , dan 19 < x 22 <

x x<25 nilai I sangat bergantung suhu (T), pengaruh suhu terhadap panas jenis zat padat satu dimensi , dua dimensi , dan tiga dimensi menyebabkan besarnya panas jenis satu dimensi , dua dimensi

, dan tiga dimensi

T c_L ~ 2 ~ T cA 3 ~ T c_v

( )

T I T cL ~

( )

T I T c_A~ 2 c_v ~T3 I

( )

T .

5.2. Saran

Saran yang dapat diberikan untuk penyempurnaan dan pengembangan tulisan ini adalah

1. Perlu dilakukan penelitian lanjutan tentang perbandingan hasil integrasi numerik menggunakan paket program Mathematica 5.0 dengan paket program lainnya.

2. Untuk suhu yang sangat rendah khususnya pada daerah , , dan 19 < x x<22 25 <

x nilai I sangat bergantung suhu (T), oleh karena itu nilai I haruslah diperhitungkan karena akan mempengaruhi besarnya panas jenis zat padat satu dimensi, dua dimensi, dan tiga dimensi.

DAFTAR PUSTAKA

Alonso, M., dan Finn, E.J., 1986, Quantum and Statistical Physics, United States of America: Addison-Wesley Publishing Company.

Bradbury, T. C., 1984, Mathematical Methods with Applications to Problem in

the Physical Sciences, Canada: Addison–Wesley Publishing

Company.

Mandl, F., 1988, Statistical Physics, Manchester : John Wiley & Sons.

Martin, M. C., 1986, Elements of Thermodynamics, New Jersey : Prentice – Hall. Nainggolan, W.S., 1978, Thermodinamika, Bandung: Penerbit Armico.

Omar, M. A., 1975, Elementary Solid State Physics, Massachussets : Addison– Wesley Publishing Company.

Sears, F. W., dan Salinger, G. L., 1975, Thermodynamics, Kinetic Theory, and

Statistical Thermodynamics, Massachusetts : Addison-Wesley

Publishing Company.

Suwitra, N., 1989, Pengantar Fisika Zat Padat, Jakarta : Depertemen Pendidikan dan Kebudayaan.

Zeemansky, M. W., dan Dittman, R. H., 1981, Heat and Thermodynamics, New York : McGraw-Hill Book Company.

Wolfram, S., 2007, Mathematica6.0, http://reference.wolfram.com/mathematica/ tutorial/NumericalIntegration.html.

LAMPIRAN A

Tabel hasil integrasi numerik dx e e x I D x x x

∫

₋ = 0 2 2 ) 1

( untuk kristal satu dimensi

xD I 0 0 1 0.973033 2 1.80172 3 2.41105 4 2.80667 5 3.03917 6 3.16567 7 3.23055 8 3.26235 9 3.2774 10 3.28433 11 3.28745 12 3.28882 13 3.28942 14 3.28968 15 3.28979 16 3.28984 17 3.28985 18 3.28986 19 3.28987 20 3.28987 21 3.28987 22 3.28987 23 3.28987 24 3.28987 25 3.28987 26 3.28987 27 3.28987 28 3.28987 29 3.28987 30 3.28987

LAMPIRAN B

Tabel hasil integrasi numerik dx e e x I D x x x

∫

₋ = 0 2 3 ) 1

( untuk kristal dua dimensi

xD I 0 0 1 0.479841 2 1.70635 3 3.2106 4 4.57922 5 5.61439 6 6.3034 7 6.72139 8 6.95799 9 7.08497 10 7.15032 11 7.18285 12 7.19859 13 7.20604 14 7.2095 15 7.21107 16 7.21178 17 7.2121 18 7.21224 19 7.2123 20 7.21232 21 7.21233 22 7.21234 23 7.21234 24 7.21234 25 7.21234 26 7.21234 27 7.21234 28 7.21234 29 7.21234 30 7.21234

LAMPIRAN C

Tabel hasil integrasi numerik dx e e x I D x x x

∫

₋ = 0 2 4 ) 1

( untuk kristal tiga dimensi

xD I 0 0 1 0.317244 2 2.20109 3 5.96482 4 10.7319 5 15.3598 6 19.123 7 21.8212 8 23.584 9 24.6565 10 25.2737 11 25.6132 12 25.7933 13 25.886 14 25.9324 15 25.9552 16 25.9661 17 25.9713 18 25.9737 19 25.9748 20 25.9754 21 25.9756 22 25.9757 23 25.9757 24 25.9757 25 25.9858 26 25.9858 27 25.9858 28 25.9858 29 25.9858 30 25.9858

BIOGRAFI

Nama lengkap penulis Margareta Inke Mayasari, lahir di Margodadi, 9 mei 1985, merupakan anak kedua dari pasangan Bapak Hadi Suprapto dan Ibu Maria Sumiyati. Pada waktu SD (tahun 1990) bersekolah di SDN I Margodadi, SMP (1996) bersekolah di SMP Xaverius Pringsewu, SMU (tahun 1999) bersekolah di SMU Xaverius Pringsewu, kemudian pada tahun 2002 melanjutkan jenjang pendidikannya di Universitas Sanata Dharma Yogyakarta, Fakultas Matematika dan Ilmu Pengetahuan Alam, Jurusan Fisika.